
A New Approach to GraphMaps, a System Browsing
Large Graphs as Interactive Maps
Debajyoti Mondal
1
and Lev Nachmanson
2
1
Department of Computer Science, University of Saskatchewan, Saskatoon, SK, Canada
2
Microsoft Research, Redmond, WA, U.S.A.
Keywords:
Network Visualization, Layered Drawing, Geometric Spanners, Competition Mesh, Network Flow.
Abstract:
A GraphMaps is a system that visualizes a graph using zoom levels, which is similar to a geographic map
visualization. GraphMaps reveals the structural properties of the graph and enables users to explore the graph
in a natural way by using the standard zoom and pan operations. The available implementation of GraphMaps
faces many challenges such as the number of zoom levels may be large, nodes may be unevenly distributed
to different levels, shared edges may create ambiguity due to the selection of multiple nodes. In this paper,
we develop an algorithmic framework to construct GraphMaps from any given mesh (generated from a 2D
point set), and for any given number of zoom levels. We demonstrate our approach introducing competition
mesh, which is simple to construct, has a low dilation and high angular resolution. We present an algorithm
for assigning nodes to zoom levels that minimizes the change in the number of nodes on visible on the screen
while the user zooms in and out between the levels. We think that keeping this change small facilitates smooth
browsing of the graph. We also propose new node selection techniques to cope with some of the challenges of
the GraphMaps approach.
1 INTRODUCTION
Traditional data visualization systems render all the
vertices and edges of the graph on a single screen. For
large graphs, this approach requires rendering many
objects on the screen, which overwhelms the user. A
GraphMaps system confronts the challenge of visu-
alizing large graphs by enabling the users to browse
the graphs as interactive maps. Like Google or Bing
Maps, a GraphMaps system visualizes the high pri-
ority features on the top level, and as we zoom in,
the low priority entities start to appear in the subse-
quent levels. To achieve this effect, for a given graph
G and a positive integer k > 0, GraphMaps creates
the graphs G
1
,G
2
,...,G
k
, where G
i
, 1 ≤ i < k, is an
induced subgraph of G
i+1
, and G
k
= G.
The graph G
i
, where 1 ≤ i ≤ k, corresponds to
the ith zoom level. Assume that the nodes of G
are ranked by their importance. The discussion on
what a node importance is and how the ranking is ob-
tained, is out of the scope of the paper, but by default
GraphMaps uses Pagerank (Brin and Page, 2012) to
obtain such a ranking. Let V (G
i
) be the nodes of
G
i
. We build graphs G
i
in such a way that the nodes
of G
i
are equally or more important than the nodes
of V (G
i+1
) \V (G
i
). At the top view, we render the
graph G
1
. As we zoom in and the zoom reaches 2
i−1
,
the rendering switches from G
i−1
to G
i
, exposing less
important nodes and their incident edges. To create
spatial stability GraphMaps keeps the node positions
fixed, and the rendering of edges changes incremen-
tally between G
i
and G
i+1
as described in Section 3.
By browsing a graph with GraphMaps, the user
obtains a quick overview of the important elements.
Navigation through different zoom levels reveals the
structure of the graph. In addition, users can interact
with the system. For example, when the user clicks
on a node u, the visualization highlights and renders
all neighbors of u (even those that do not belong to the
current G
i
) and the edges that connect u to its neigh-
bors. By using this interaction the user can explore a
path by selecting a set of successive nodes on the path,
and can answer adjacency questions by selecting the
corresponding pair of nodes.
We draw the nodes as points, and edges as polyg-
onal chains. Each maximal straight line segment in
the drawing is called a rail. The edges may share
rails. Every point where a pair of rails meet is ei-
ther a node or a point which we call a junction. Fig-
ure 1(a) depicts a traditional node-link diagram of a
108
Mondal, D. and Nachmanson, L.
A New Approach to GraphMaps, a System Browsing Large Graphs as Interactive Maps.
DOI: 10.5220/0006618101080119
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages
108-119
ISBN: 978-989-758-289-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(a) (b) (d)
a
a
b
c
d
e
f
g
h
i
(c)
a
(e)
Figure 1: (a) A node-link diagram of a graph G. (b–d) A GraphMaps visualization of G. (e) An example of edge bundling.
graph G. Figures 1(b–c) illustrate a GraphMaps visu-
alization of G on three zoom levels. The gray region
at each level corresponds to a viewport in that level.
The higher ranked nodes of G have the darker color.
The tiny gray dots represent the locations of the nodes
that are not visible in the current layer. Figures 2 illus-
trate the node selection technique and the zoom fea-
ture. The rails rendered by thick lines correspond to
the shortest paths from the selected nodes a and h to
their neighbors.
a
h
a
Figure 2: Node selections and zoom in.
In our scheme, where we change the rendering de-
pending on the zoom level, the quality of the visu-
alization depends both on the quality of the drawing
on each level, and the differences between the draw-
ings of successive zoom levels. We think that a good
drawing of a graph on a single zoom level satisfies the
following properties:
- The angular resolution is large
- The degree at a node or at a junction is small.
- The amount of ink, that is the sum of the lengths
of all distinct rails used in the drawing, is small.
- The edge stretch factor or dilation, that is the ratio
of the length of an edge route to the Euclidean
distance between its end nodes, is small.
These properties help to follow the edge routes, re-
duce the visual load, and thus improve the readability
of a drawing. Since some of the principles contradict
each other, optimizing all of them simultaneously is a
difficult task.
Our algorithm, in addition to creating a good
drawing of each G
i
, attempts to construct these draw-
ings in a way that a switch from G
i
to G
i+1
does not
cause a large change on the screen. We try to keep the
amount of new appearing details relatively small and
also try to keep the edge geometry stable.
1.1 Related Work
A large number of graph visualization tools, e.g.,
Centrifuge, Cytoscape, Gephi, Graphviz, Biolay-
out3d, have been developed over the past few decades
due to a growing interest in exploring network data.
A good visualization requires the careful placement
of nodes, e.g., sometimes nodes with similar proper-
ties are placed close to each other, whereas the nodes
that are dissimilar are placed far away. Force directed
approaches, multi-dimensional scaling and stochastic
neighbor embedding are some common techniques to
generate the node positions (Hu, 2005; Klimenta and
Brandes, 2012; van der Maaten and Hinton, 2008).
Techniques that try to make the visualization readable
by drawing the edges carefully consider various types
of edge bundling (Ersoy et al., 2011; Gansner et al.,
2011; Lambert et al., 2010; Pupyrev et al., 2011) and
edge routing techniques (Dobkin et al., 1997; Holten
and van Wijk, 2009; Dwyer and Nachmanson, 2009).
Informally, the edge bundling technique groups the
edges that are travelling towards a common direc-
tion, and routes these edges through some narrow
tunnel. Figure 1(e) illustrates an example of edge
bundling. Other forms of clutter reduction approaches
include node aggregation (Wattenberg, 2006; Dunne
and Shneiderman, 2013; Zinsmaier et al., 2012),
topology compression (Shi et al., 2013; Brunel et al.,
2014), and sampling algorithms (Gao et al., 2014).
This paper focuses on GraphMaps, proposed by
Nachmanson et al. (Nachmanson et al., 2015), that
reduces clutter by distributing nodes to different
zoom levels and routing edges on shared rails. Like
the clutter reduction approaches, a primary goal of
GraphMaps is to make the visualization more read-
able and interactive in the higher levels of abstrac-
tion. Nachmanson et al. (Nachmanson et al., 2015)
use multidimensional scaling to create the node posi-
tions. To distribute the nodes into zoom levels, they
consider at each level i, an uniform 2
i
×2
i
grid, where
each grid cell is called a tile. The tiles are filled with
nodes, the most important nodes first. While filling
the levels with nodes, they maintain a node and a rail
quota that bound the number of nodes and rails inter-
secting a tile. Whenever an insertion of a new node
creates a tile intersecting more than one fourth of the
A New Approach to GraphMaps, a System Browsing Large Graphs as Interactive Maps
109

Figure 3: A partial display of a flight network with approximately 3K nodes and 19K edges. (left) Traditional node-link
diagram over the airports of North America. (middle) The top-level of a GraphMaps visualization based on our approach,
where the airports TUS and YWG are selected. (right) A view after zoom in.
node quota nodes or more than one quarter of rail
quota rails, a new zoom level is created to insert the
rest of the entities. The visualization of GraphMaps
works in such a way that each viewport is covered
by four tiles of the current level. This ensures that
not more than the node quota nodes and the rail quota
rails are rendered per viewport.
GraphMaps visualization also relates to the hier-
archical visualization of clustered networks (Schaffer
et al., 1996; Balzer and Deussen, 2007). We refer the
reader to the survey (Vehlow et al., 2015) for more
details on visualizing graphs based on graph parti-
tioning. There exist some systems that render large
graphs on multiple layers by using the notion of tem-
poral graphs, e.g., evolving software systems (Coll-
berg et al., 2003; Lambert et al., 2010). A generaliza-
tion of stochastic neighbor embedding renders nodes
on multiple maps (van der Maaten and Hinton, 2012).
Gansner et al. (Gansner et al., 2010) proposed a visu-
alization that emphasizes node clusters as geographic
regions.
1.2 Contribution
The existing implementation of GraphMaps (Nach-
manson et al., 2015) focuses mainly on the quality of
the layout at individual zoom level. The construction
follows a top-down approach, where the successive
levels were obtained by inserting nodes incrementally
in a greedy manner.
We propose an algorithm to construct a
GraphMaps visualization starting from a com-
plete drawing of the graph G(= G
k
) at the bottom
level. Specifically, given an arbitrary mesh and the
edge routes of G
k
on this mesh, our method builds
the edge routes for G
k−1
,...,G
2
,G
1
, in this order.
We introduce a particular type of mesh, called com-
petition mesh, which is of independent interest due to
its low edge stretch factor (2 +
√
2), and high angular
resolution 45
◦
. We then construct GraphMaps visual-
izations by applying our algorithm to this mesh. We
develop a node assignment algorithm that minimizes
the change in the drawing when switching from G
i
to
G
i+1
during zoom in, where 1 ≤i < k. Moreover, we
propose new node selection techniques to cope with
some of the challenges of the GraphMaps approach.
We also carried out experiments on some real-life
datasets (see Figure 3 and Section 5). Our experi-
ments reveal the usefulness of GraphMaps, even in its
basic implementations, for understanding the network
information through interactive exploration.
2 TECHNICAL BACKGROUND
We now introduce the mesh that we use for edge rout-
ing and analyze its properties. Let P be a set of n dis-
tinct points that correspond to the node positions, and
let R(P) be the smallest axis aligned rectangle that
encloses all the points of P. A competition mesh of
P is a geometric graph constructed by shooting from
each point, four axis-aligned rays at the same con-
stant speed (towards the top, bottom, left and right),
where each ray stops as soon as it hits any other ray
or R(P). We break the ties arbitrarily, i.e., if two non-
parallel rays hit each other simultaneously, then arbi-
trarily one of these rays stops and the other ray contin-
ues. If two rays are collinear and hit each other from
the opposite sides, then both rays stop. We denote
this graph by M(P), e.g., see Figure 4. The vertices
of M(P) are the points of P (nodes), and the points
where a pair of the rays meet (junctions). Two ver-
tices in M(P) are adjacent if and only if the straight
line segment connecting them belongs to M(P). A
competition mesh can also be viewed as a variation of
a motorcycle graph (Eppstein et al., 2008), or a ge-
ometric spanner with Steiner points (Bose and Smid,
2013). In the rest of the paper the term ‘vertices’ de-
notes all the nodes and junctions of M(P).
For any point u, let u
x
and u
y
be the x and y-
coordinates of u, respectively, and let l
v
(u) and l
h
(u)
be the vertical and horizontal straight lines through
u, respectively. For any two points p,q in R
2
, let
dist
E
(p,q) be the Euclidean distance between p and
q. For each point u of the plane we define four quad-
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
110

t
s
s
t
v
1
v
2
v
3
w
1
w
2
w
3
v
1
v
2
v
3
w
1
w
2
(a) (b) (c) (d)
P
right
P
right
P
bottom
P
top
P
l
h
(t)
l
v
(t)
t
Figure 4: (a) A point set and its corresponding competition mesh. (b–c) Bounding the bottom-left quadrant of t. (d) A
monotone path inside the bottom-left quadrant of t.
rants formed by the horizontal and vertical lines pass-
ing through u. A path v
1
,...,v
k
is monotone in direc-
tion of vector a if for each 1 ≤ i < k the dot product
a·(v
i+1
−v
i
) is not negative. Lemmas 1–2 prove some
properties of M(P).
Lemma 1. Let u be a node in M(P). Then in each
quadrant of u there is a path in M(P) that starts at u,
ends at some point on R(P), and is monotone in both
horizontal and vertical directions.
Proof. Without loss of generality it suffices to prove
the lemma for the first quadrant of u, which consists of
the set of points v such that v
x
≥ u
x
and v
y
≥ u
y
. Sup-
pose for a contradiction that there is no such path in
this quadrant. Consider a maximal xy-monotone path
Π that starts at u and ends at some node or junction w
of M(P). If w is a node, then we extend Π using the
right or top ray of w, which is a contradiction. There-
fore, w must be a junction in M(P). Without loss of
generality assume that the straight line segment ` in-
cident to w is horizontal. Since Π is a maximal xy-
monotone path, the ray r
`
corresponding to ` must be
stopped by some vertical ray r
0
generated by some
vertex w
0
. Observe that w
y
> w
0
y
, otherwise we can
extend Π towards w
0
. Since r
`
is stopped, the ray r
0
must continue unless there are some other downward
ray r
00
that hits r
0
at w. In both cases we can extend
Π, either by following r
0
(if it continues), or follow-
ing the source of r
00
(if r
0
is stopped by r
00
), which
contradicts to the assumption that Π is maximal.
Lemma 2. For any set P with n points M(P) has O(n)
vertices and edges. The graph distance between any
two nodes of M(P) is at most (2 +
√
2) times the Eu-
clidean distance.
Proof. By construction of M(P), whenever a junction
is created, one ray stops. Since |P| = n there are at
most 4n rails, and therefore we cannot have more than
4n junctions, that proves that the number of vertices in
M(P) is O(n). Since M is a planar graph, the number
of edges is also O(n).
We now show that the ratio of the graph distance
and the Euclidean distance between any two nodes of
M(P) is at most (2 +
√
2). Let C
le f t
,C
right
,C
top
, and
C
bottom
be the four cones with the apex at (0,0) deter-
mined by the lines y = ±x. Let s and t be two nodes
in M(P). Without loss of generality assume that s lo-
cated at (0,0) and t lies on C
right
. Consider now an x-
monotone orthogonal path P
right
= (v
0
,v
1
,v
2
,...,v
q
)
in the mesh such that v
0
coincides with s, for each
0 < i ≤ q, v
i
is a node in M(P) that stops the right-
ward ray of v
i−1
, and v
q
lies on or to the right of l
v
(t),
e.g., see Figure 4(b). Suppose that t is either above
or below P
right
. If t is above P
right
, then consider a y-
monotone path P
top
= (w
0
, w
1
,w
2
,...,w
r
) such that
w
0
coincides with s, for each 0 < i ≤ r, w
i
is a node in
M(P) that stops the upward ray of v
i−1
, and v
r
lies on
or above l
h
(t). If t is below P
right
, then define a path
P
bottom
symmetrically, e.g., see Figure 4(c).
Without loss of generality assume that t is above
P
right
. Observe that the paths P
top
and P
right
remain
inside the cones C
top
and C
right
, respectively, and
bound the bottom-left quadrant of t, as shown in the
shaded region in Figure 4(b). By Lemma 1, t has a
(−x)(−y)-monotone path P that starts at t and reaches
the boundary of R(P), e.g., see Figure 4(d). This
path P must intersect either P
top
or P
right
. Hence
we can find a path P
0
from s to t, where P
0
starts
at s, travels along either P
top
or P
right
depending on
which one P intersects, and then follows P from the
intersection point. We now show that length of P
0
is
at most (2 +
√
2) ·dist
E
(s,t). Since any ray is not
shorter than a ray it stops, the sum of the lengths
of the vertical segments of P
right
is at most the sum
of the lengths of the horizontal segments. Therefore,
the part of P
right
inside the bottom-left quadrant of t
is at most 2t
x
. Similarly, the part of P
top
inside the
bottom-left quadrant of t is at most 2t
y
. Path P is
not longer than t
x
+ t
y
(see Figure 4(d)) . Therefore,
the length of P
0
is at most t
x
+ t
y
+ 2 ·max{t
x
,t
y
)} ≤
√
2·dist
E
(s,t)+2·max{t
x
,t
y
}≤(2+
√
2)·dist
E
(s,t).
In the case when t belongs to P
right
, the length of
path P is zero and the proof easily follows.
The following lemma states that a competition
mesh can be constructed in O(nlogn) time.
Lemma 3. For any set P with n points, the competi-
tion mesh M(P) can be constructed in O(nlogn) time.
A New Approach to GraphMaps, a System Browsing Large Graphs as Interactive Maps
111

Proof. Define for each point w ∈P, a set of eight non-
overlapping cones as follows: The central angle of
each cone is 45
◦
and the cones are ordered counter
clockwise around w. The first cone lies in the first
quadrant of w between the lines y = x +w
x
and y = 0,
as shown in Figure 5(a). Guibas and Stolfi (Guibas
and Stolfi, 1983) showed that in O(n log n) time, one
can find for every point w ∈ P the nearest neigh-
bor of w (according to the Manhattan Metric) in
each of the eight cones of w. Assume that δ
y
=
{min
{a,b}∈P, where a
y
6=b
y
|a
y
−b
y
|}, which can be com-
puted in O(n log n) time by sorting the points accord-
ing to y-coordinates.
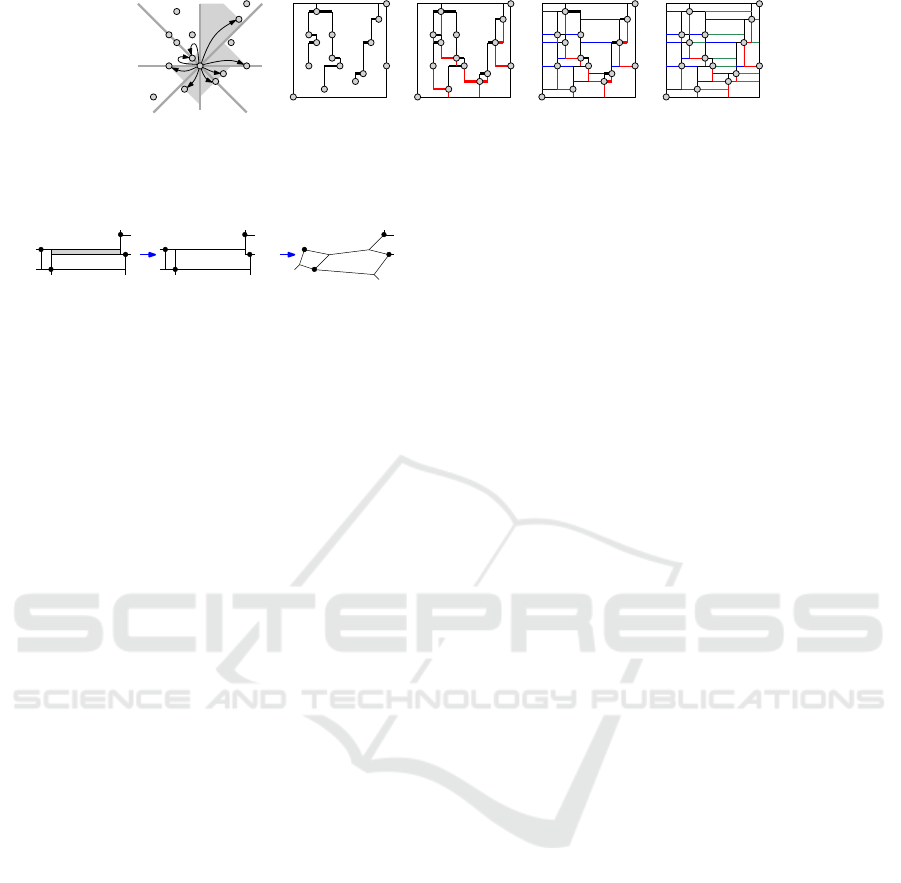
We construct M in four phases. The first phase
iterates through the top rays of the each point w and
finds the point w
0
closest to l(h)
w
(in Manhattan met-
ric) such that |w
0
x
−w
x
| ≤ |w
0
y
−w
y
|. Note that if such
a w
0
exists, then one of the horizontal rays r
0
of w
0
would reach the point (w
x
,w
0
y
) before the top ray r of
w (while all rays are grown in an uniform speed). Ac-
cording to the definition of the competition mesh, we
can continue the ray r
0
and stop growing the ray r. If
no such w
0
exists, then r must hit R(P).
To find the point w
0
, it suffices to compare the
Manhattan distances of the nearest neighbors in the
second and third cones of w (breaking ties arbitrar-
ily). Since the nearest neighbors at each cone can
be accessed in O(1) time, we can process all the top
rays in linear time. Figure 5(b) shows the junctions
and nodes created after the first phase, where all the
rays that stopped growing are shown in thin lines.
The nearest neighbors in the second and third cones
of w are a and b, respectively. Since a is closer to
l
h
(w) than b, the top ray of w does not grow beyond
(w
x
,a
x
). The second phase processes the bottom rays
in a similar fashion, e.g., see Figure 5(c). Both the
first and second phase use a ray shooting data struc-
ture to check whether the current ray already hits an
existing ray. We describe this data structure in the
next paragraph while discussing phase three. Let the
planar subdivision at the end of phase two be S.
In the third phase, we grow each left ray until it
hits any other vertical segment in S, as follows: For
each vertical edge ab in S, construct a segment a
0
b
0
by
shrinking ab by δ
y
/3 from both ends. For each node
and junction w, construct a segment w
1
w
2
such that
w
1
= (w
x
,w
y
−δ
y
/4) and w
2
= (w
x
,w
y
+δ
y
/4). Let S
v
be the constructed segments. Note that the segments
in S
v
are non-intersecting. Giyora and Kaplan (Giy-
ora and Kaplan, 2009) gave a ray shooting data struc-
ture D that can process O(n) non-intersecting verti-
cal rays in O(n log n) time, and given a query point
q, D can find in O(log n) time the segment (if any) in
S
v
immediately to the left of q. Furthermore, D sup-
ports insertion and deletion in O(log n) time. For each
point q ∈ P in the increasing order of x-coordinates,
we shoot a leftward ray r from q, and find the first
segment ab hit by the ray. Assume that a
y
< b
y
and r
hits ab at point x. We update the subdivision S accord-
ingly, then delete segment ab from D, and insert seg-
ment xb in D. Note that these updates keep all the seg-
ments in D non-intersecting. Since there are O(n) left
rays, processing all these rays takes O(n log n) time.
Figure 5(d) illustrates the third phase.
The fourth phase processes the right rays in a
similar fashion, e.g., see Figure 5(e). Since the
preprocessing time of the data structures we use is
O(nlogn), and since each phase runs in O(nlogn)
time, the construction of the computation mesh takes
O(nlogn) time in total.
3 GRAPHMAPS SYSTEM
Our technique for calculating the graphs G
1
,...,G
k
(equivalently, node level assignment) is described in
Section 4. For now, let us assume that the sequence
of graphs is ready. We now show how to route edges
on graphs G
i
.
The computation of edges starts from the bottom.
Namely we build a competition mesh M for graph
G(= G
k
). We route each edge (u, v) ∈ G as a short-
est path P
uv
in M. Let us denote by M
0
the mesh we
obtain after applying these modifications to M. Next
we modify M
0
to make the routes more visually ap-
pealing. We perform local modifications and try to
minimize the total ink of the routes, which is the sum
of lengths of edges of M
0
used in the routes (Gansner
and Koren, 2006), and remove thin faces. During the
modifications we keep the angular resolution greater
or equal than some α > 0, and the minimum distance
between non-incident vertices and edges of M
0
greater
or equal than some β > 0. The local modifications are
described below.
Face refinement: For each face f of M
0
that does
not contain a node of G in its boundary, we compute
the width of f , which is the smallest Euclidean dis-
tance between any two non-adjacent rails of f . If
the width of f is smaller than some given threshold,
then remove the longest edge of f from M
0
(breaking
ties arbitrarily). Figures 6(a–b) depict such a removal,
where the thin face is shown in gray. The edge routes
using the removed edge are rerouted through the re-
maining boundary of f
0
.
Median: Move each junction κ of M
0
toward the
geometric median of its neighbors, i.e., the point that
minimizes the sum of distance to the neighbors, as
long as the restriction mentioned above holds. Iterate
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
112
(a) (b) (c) (d) (e)
C
5
C
6
C
8
C
4
C
7
C
3
C
1
w
C
2
w
a
b
Figure 5: (a) A point set P and the nearest neighbor of w in each of the eight cones around w. (b–e) Construction of the mesh
of P, while processing (b) top rays, (c) bottom rays, (d) left rays and (e) right rays.
(a)
(b)
(c)
Figure 6: (a–b) Removal of thin faces. (b–c) Moving junc-
tions towards median.
the move for a certain number of times, or until the
change becomes smaller than some given threshold.
Figures 6(c–d) illustrate the outcome of this step.
Shortcut: Remove every degree two junction and
replace the two edges adjacent to it by the edge short-
cutting the removed junction, as long as the restriction
mentioned above holds.
In all the above modifications, the routes are
updated accordingly. Modifications “Median” and
“Shortcut” diminish the ink. The final M
0
gives the
geometry of the bottom-level drawing of G in our ver-
sion of GraphMaps.
Given a mesh M
i
representing the geometry for
the drawing of G
i
, where 1 < i ≤ k, we construct
M
i−1
from M
i
by removing from the latter the nodes
V (G
i
) \V (G
i−1
), and by removing the edges that are
not used by any route P
u,v
, where (u,v) is an edge
of G
i−1
. Some routes P
u,v
can be straightened in
M
i−1
. We use the simplification algorithm (Douglas
and Peucker, 1973) to morph the paths of M
i
to paths
of M
i−1
. Figures 7(a–b) illustrate the simplification.
This change in the edge routes geometry dimin-
ishes the consistency between the drawings of succes-
sive levels. To smoothen the differences while transit-
ing from zoom level i to i + 1 we linearly interpolate
between the paths of M
i
and M
i+1
, as demonstrated in
Figures 7(b–d).
The idea of path simplification and transition
via linear interpolation enables us to construct
GraphMaps in a bottom-up approach. In fact, the
above strategy can be applied to transform any mesh
generated from a set of 2D points to a GraphMaps vi-
sualization.
4 COMPUTING NODE LEVELS
Let us consider in more details how the view changes
when we zoom by examining Figures 8(a)–(d). On
the top-left tile of Figure 8(a), the user’s viewport cov-
ers the whole graph, so G
1
is exposed. In Figure 8(d),
the user’s viewport contains only the top-left tile of
Figure 8(a), and the visualization switches to graph
G
2
. Seven new nodes, which were not fully visible
in zoom level 1, become fully visible for the current
viewport, as represented in light gray. If all of a sud-
den, a large number of new nodes become fully visi-
ble, then it may disrupt user’s mental map. Here we
propose an algorithm to keep this change small.
We build the tiles as in (Nachmanson et al., 2015).
In the first level we have only one tile coinciding
with the graph bounding box. On the ith level, where
i > 1, the tiles are obtained by splitting each tile in the
(i −1)th level into a uniform 2 ×2 grid cell. This ar-
rangement of tiles can be considered as a rooted tree
T , where the tiles correspond to the nodes of the tree.
Specifically, the topmost tile is the root of T , and a
node u is a child of another node v if the correspond-
ing tiles t
u
and t
v
lie in two different but adjacent lev-
els, and t
u
⊂t
v
. We refer to T as a tile tree.
For every node v in T , denote by S(v) the num-
ber of fully visible nodes in the tile t
v
. For an edge
e = (v, w) in T , where v is a parent of w, we denote by
δ
e
the number of new nodes that become visible while
navigating from t
v
to t
w
, i.e., δ
e
= |S(w) \S(v)|. We
can control the rate the nodes appear and disappear
from the viewport by minimizing
∑
e∈E(T )
δ
2
e
, where
E(T ) is the set of edges in T . For simplicity we show
how to solve the problem in one dimension, where all
the points are lying on a horizontal line. It is straight-
forward to extend the technique in R
2
.
Problem. BALANCED VISUALIZATION
Input. A set P of n points on a horizontal line,
where every point q ∈ P is assigned a rank r(q).
A tile tree T of height ρ; and a node quota Q, i.e.,
the number of points allowed to appear in each
tile.
Output. Compute a mapping g : P → {1,2,...ρ}
A New Approach to GraphMaps, a System Browsing Large Graphs as Interactive Maps
113
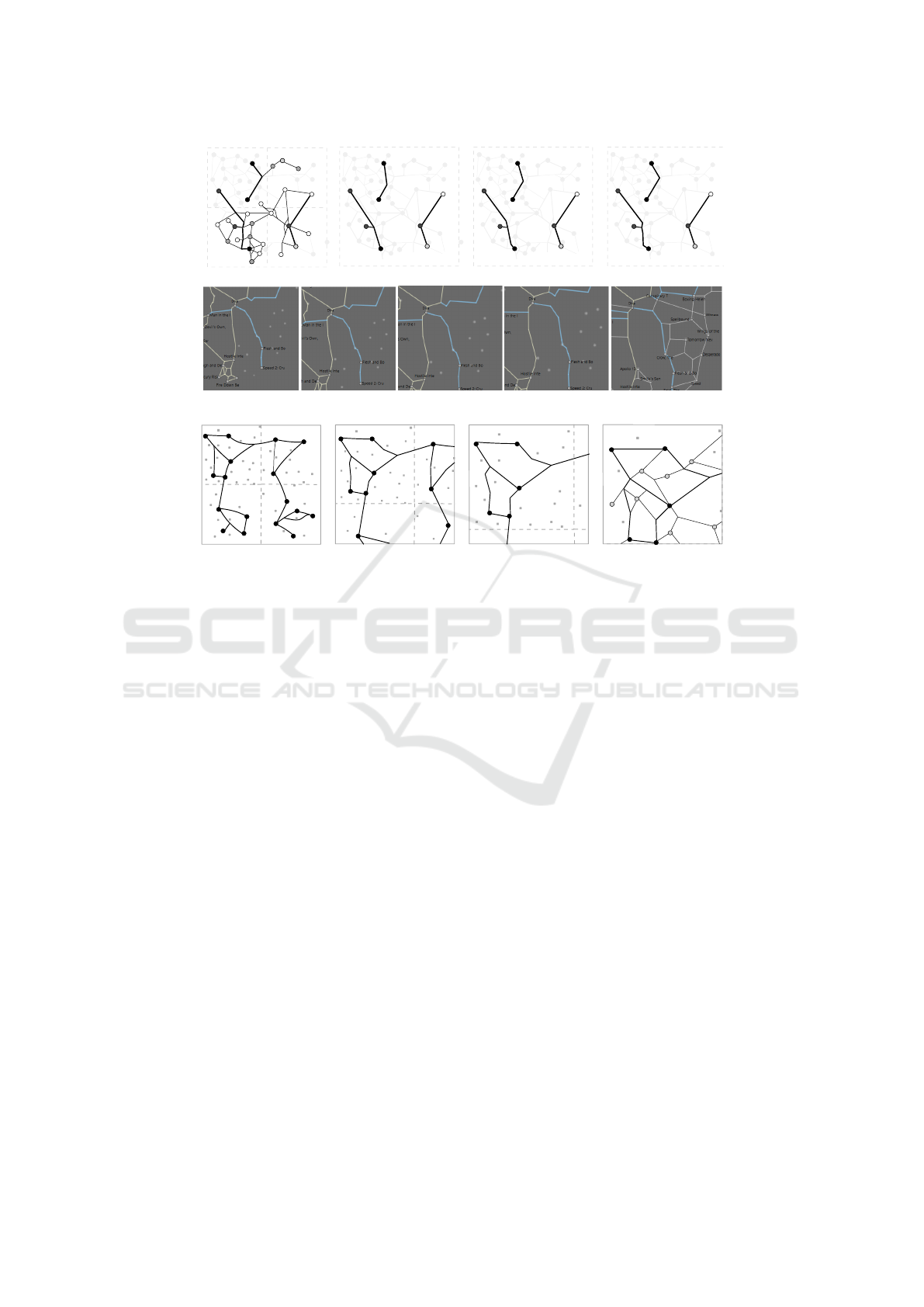
(a) (b) (c) (d)
Figure 7: (a) Zoom level 2. (b–d) Transition from level 1 to 2. (bottom) Transition in our GraphMaps system.
(a)
(b)
(c)
(d)
Figure 8: (a) Zoom level 1. (b–c) Transition from level 1 to 2. (d) Zoom level 2.
(if exists) that
- satisfies the node quota,
- minimizes the objective F =
∑
e∈E(T )
δ
2
e
, and
- for every pair of points q,q
0
∈ P with r(q) ≥
r(q
0
), satisfies the inequality g(q) ≤ g(q
0
),
which we refer to as the rank condition.
If the rank of all the points are distinct, then the
solution to BALANCED VISUALIZATION is unique,
and can be computed in a greedy approach. But the
problem becomes non-trivial when many points may
have the same rank. In this scenario, we prove that the
BALANCED VISUALIZATION problem can be solved
in O(τ
2
log
2
τ) + O(nlogn) time, where τ is the num-
ber of nodes in T . This is quite fast since the maxi-
mum zoom level is a small number, i.e., at most 10,
in practice. We reduce the problem to the problem of
computing a minimum cost maximum flow problem,
where the edge costs can be convex (Orlin, 1993; Or-
lin and Vaidyanathan, 2013), e.g., quadratic function
of the flow passing through the edge. Figure 9(a) de-
picts a set of points on a line, where the associated
tiles are shown using rectangular regions. The num-
bers in each rectangle is the number of points in the
corresponding tile. Figure 9(b) shows a correspond-
ing network G, where the source is denoted by s, and
the sinks are denoted by T
1
,T
2
,...,T
8
. The excess at
the source and the deficit at the sinks are written in
their associated squares. We allow each internal node
w (unfilled square) of the tile tree to pass at most Q
units of flow through it. This can be modeled by re-
placing w by an edge (u,v) of capacity Q, where all
the edges incoming to w are incident to u and the out-
going edges are incident to v. This transformation is
not shown in the figure. Set the capacity of all other
edges to ∞.
The production of the source is n units, and the
units of flow that each sink can consume is equal to
the number of points lying in the corresponding tile.
The cost of sending flows along the tree edges (solid
black) is zero. The cost of sending flows along the
dotted edge connecting the source and the tree root is
also zero. The cost of sending x units of flow along
the dashed edges is x
2
; sending x units of flow through
a dashed edge corresponds to x new nodes that are be-
coming visible when we zoom in at the tile of the edge
target. Figure 9(c) illustrates a solution to the mini-
mum cost maximum flow problem, where the flows
are interpreted as follows:
(A) The number in a square denotes the number of
points that would be visible in the associated tile.
(B) The edges (s,w), where w is not the root, are la-
beled by numbers. Each such number corresponds
to the new nodes that will appear while zooming
in from the tile associated to parent(w) to the tile
associated to w. Thus the cost of this network flow
is the sum of the squares of these numbers, i.e., 35.
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
114
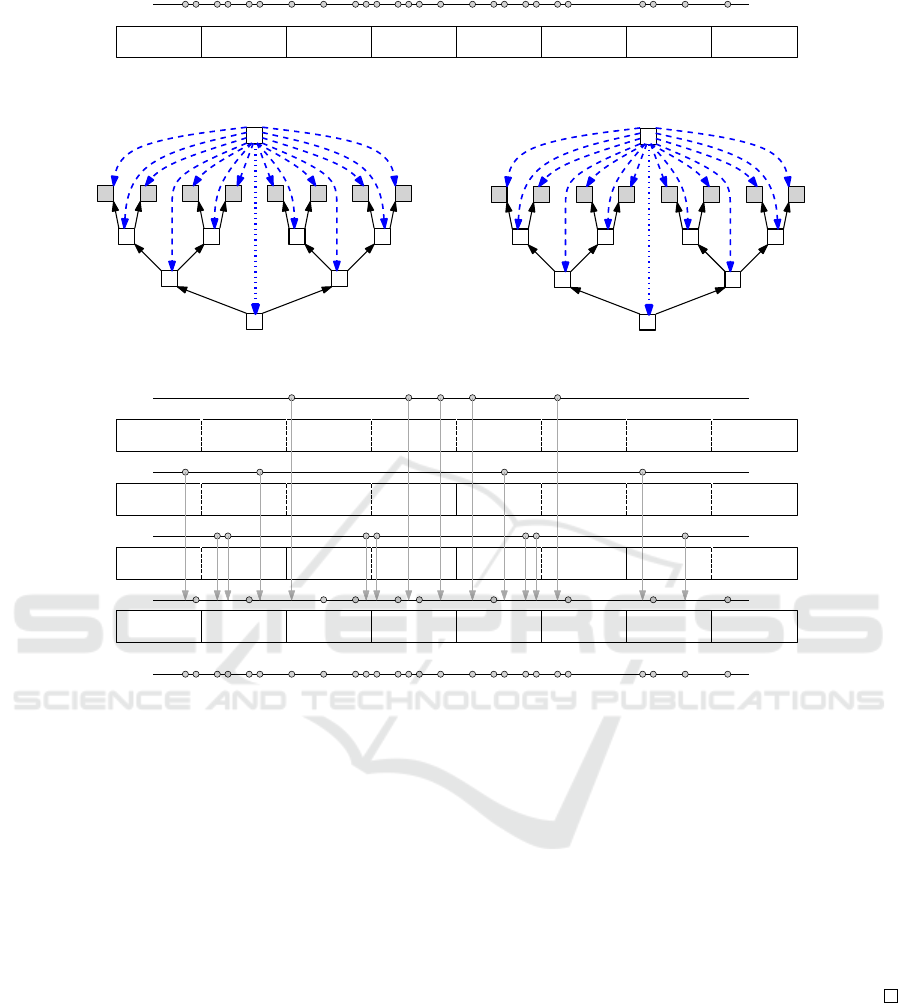
2 4 4 5 5 2 3 1
2
4
4
5
2
5
3
1
26
2 4
4
5 2
5
3 1
26
5
2
2
2
1
1
2
2
2
1
2
1
1
1
1
3
1
3
2
4
1
2
2
3
3
1
3
2
5
5
4
5
5
4
2
2 4 4 5 5 2 3 1
2 4 4 5 5 2 3 1
2 4 4 5 5 2 3 1
2 4 4 5 5 2 3 1
(a)
(b) (c)
(d)
T
1
T
8
s
s
T
8
T
1
root
root
Figure 9: (a) A set of points on a line and the associated tiles are shown using rectangular regions. (b) A corresponding
network G. (c) A solution to the minimum cost maximum flow problem. (d) A solution to the BALANCED VISUALIZATION
problem that corresponds to the network flow.
(C) Each edge of (u,v) of T is labeled by the number
of nodes that are fully visible both u and in v.
(D) Any one unit source-to-sink flow corresponds
to a point of P, where the flow path source,
u
1
,u
2
,...,u
k
(= sink) denotes that the point ap-
peared in all the tiles associated to u
1
,...,u
k
.
Lemma 4. A minimum cost maximum flow in G mini-
mizes the objective function F of the BALANCED VI-
SUALIZATION problem.
Proof. If the amount of flow consumed at sink is
smaller than n, then we can find a cut in G with to-
tal capacity less than n. Thus even if we saturate the
corresponding tiles with points from P, we will not be
able to visualize all the points without violating the
node quota. Therefore, we can visualize all the points
if and only if the flow is maximum and the total con-
sumption is n. Therefore, the only concern is whether
the solution with cost λ obtained from flow-network
model minimizes the sum of the squared node differ-
ences between every parent and child tiles. Suppose
for a contradiction that there exists another solution
of BALANCED VISUALIZATION with cost λ
0
< λ. In
this scenario we can label the edges of the network
according to the interpretation used in (A)–(D) to ob-
tain a maximum flow in G with cost λ
0
. Therefore, the
minimum cost computed via the flow-network model
cannot be λ, a contradiction.
Given a solution to the network flow, we can con-
struct a corresponding solution to the BALANCED VI-
SUALIZATION problem as described below.
- For each point w, set g(w) = ∞.
- For each zoom level z from ρ to 1, process the tiles
of zoom level z as follows. Let W be a tile in zoom
level z. Find the amount of flow x incoming to W
from s in G. Note that this amount x corresponds
to the difference in the number of points between
A New Approach to GraphMaps, a System Browsing Large Graphs as Interactive Maps
115

W and parent(W ). Therefore, we find a set L of x
lowest priority points in W with zoom level equal
to ∞, then for each w ∈ L, we set g(w) = z. Fig-
ure 9(d) illustrates a solution to the BALANCED
VISUALIZATION problem that corresponds to the
network flow of Figure 9(c).
If the resulting mapping does not satisfy the rank con-
dition, then the instance of BALANCED VISUALIZA-
TION does not have any affirmative solution. The
best known running time for solving a convex cost
network flow problem on a network of size O(τ) is
O(τ
2
log
2
τ) (Orlin, 1993; Orlin and Vaidyanathan,
2013). Besides, it is straightforward to compute the
corresponding node assignments in O(nlogn) time
augmenting the merge sort technique with basic data
structures. Hence we obtain the following theorem.
Theorem 1. Given a set of n points in R, a tile tree of
τ nodes, and a quota Q, one can find a balanced visu-
alization (if exists) in O(τ
2
log
2
τ)+O(nlogn) time.
While implementing GraphMaps, we need to
choose a node quota Q depending on the given total
number of zoom levels ρ. Using a binary search on
the number of nodes, in O(logn) iterations, one can
find a minimal node quota that allow visualizing all
the points of P satisfying the rank condition.
5 EXPERIMENTS
The GraphMaps system proposed previously (Nach-
manson et al., 2015) uses
1
to obtain the graph for
routing edges on a level. Our approach does not de-
pend on Triangle, but uses Competition Mesh. This
has several advantages. For example, Competition
Mesh usually produces less edges than Triangle. As
a result the edge routing runs much faster. With the
same initial layout for the nodes, the GraphMaps sys-
tem based on our approach sped up the initial pro-
cessing significantly, up to 8 times on some graphs.
The graph with 38395 nodes and 85763 edges was
processed in the new system within 1 hour and 45
minutes, where the previous GraphMaps system took
6 hours (Nachmanson et al., 2015). Besides, Com-
petition Mesh is more robust than Triangle. We did
not experience failures, which were reported on Tri-
angle (Nachmanson et al., 2015).
The previous GraphMaps (Nachmanson et al.,
2015) supports node selection, which is initiated by
the user clicks. Selection of a node highlights the
paths to its neighbors in red. This may create am-
biguity. For example, Figure 10(top-left) shows a
1
https://www.cs.cmu.edu/
∼
quake/triangle.html
Figure 10: Node selection in previous GraphMaps (Nach-
manson et al., 2015).
Figure 11: Selection of multiple nodes: (a) previous
GraphMaps (Nachmanson et al., 2015), and (b) our ap-
proach.
graph of Burglary events (April 2015) in Manchester,
UK, where two events are adjacent if they are lo-
cated within 1km of each other. Selection of the node
‘Burnaby Street’ highlights a rail very close to the
node ‘Shopping area’, which gives a false impres-
sion that these nodes are adjacent. After zooming
in one can see that there is a detour that carries the
highlighted path away from ‘Shopping area’, e.g., see
Figure 10(top-right). This also give a wrong impres-
sion of the node degree. Besides, since the edges may
share rails, selection of multiple nodes may obscure
the adjacency relationship, e.g., see Figure 11(left).
We introduce new visualizations that allow the
user to better understand the node neighborhood.
Clicking on a node toggles its status from selected to
not selected. When a node is selected, its neighbors
are highlighted in yellow color, and the edges con-
necting the clicked node with the neighbors are high-
lighted with some unique color. If the mouse pointer
hovers over a node highlighted by yellow color, then
a tooltip appears with the list of the node neighbors,
e.g., see Figure 11(right). When a selected node is
unselected, then every edge adjacent to it is rendered
in the default color, and the highlighting is removed
from each neighbor, unless it is a neighbor of another
selected node. These visualization measures help to
resolve some ambiguities caused by edge bundling.
Note that our approach does not create any detour,
and thus avoids the circular artifacts (rails) around the
nodes. Exploring the node adjacencies and degree be-
comes comparatively easy, and less number of rails
aids faster level transition.
Like the previous GraphMaps, our approach can
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
116

Figure 12: A visualization of gemstone trade-relation among countries (≈7K edges) in 2015 (https://resourcetrade.earth).
Selected nodes: (left) Iraq, Sudan, Cuba, and (right) China.
also revel the structural properties of the graph. Fig-
ure 12 depicts a gemstone trade graph, where the
countries with most trade relation, e.g., China, are
in the central position and the countries with small
number of trade relations fall into the periphery. Fig-
ure 13 visualizes a drugs-crime event in Manchester,
UK, where the events are connected if they are lo-
cated within a distance of (left) 1Km and (right) 5Km
of each other. The high risk events form clusters in
the top-level visualizations.
Figure 14 shows an experiment with the graph of
include dependencies of the C++ sources of
2
. The de-
veloper was interested in how his files are used by the
rest of the system. He clicked node ‘lar solver.h’ rep-
resenting an important header file of his files and cre-
ated the neighborhood in red color (the upper draw-
ing). Then he noticed that file ‘theory lra.cpp’ in-
cludes ‘lar solver.h’ and clicked the former, creating
the blue neighborhood (in the lower drawing). Then
he noticed two files, marked by the black oval, that
were included into ‘theory lra.cpp’ by mistake.
In another experiment, a user was analyzing col-
laboration between Chinese and Russian composers
in 20-th and 21-st centuries. By highlighting the
neighborhoods of Chinese composers of 20-th cen-
tury, the user saw that there were no connections be-
tween the composers of these two countries in this
period. In 21-st century the only relation of such
kind that he found was between Tan Dun and Sofia
Gubaidulina. More details can be seen in a video
3
.
2
https://github.com/Z3Prover/z3
3
https://www.youtube.com/watch?v=qCUP20dQqBo&
feature=youtu.be
6 LIMITATIONS
Adjacency relations and node degrees are readily
visible in small size traditional node-link diagrams,
GraphMaps can process large networks, but it looses
those two aspects at an expense of avoiding clutter.
The users need to select nodes to explore the adjacen-
cies and node degrees. Currently, we use colors to
disambiguate node selections, which limits us to the
selection of a small number of nodes avoiding ambi-
guity. GraphMaps is sensitive to node quota or the
maximum number of nodes per tile. Selecting a large
node quota may increase the interaction latency dur-
ing level transitions. On the other hand, selecting a
small node quota may select few nodes on the top-
level, which may fail to give an overview of the graph
structure. An appropriate choice of the node quota
based on the graph size and node layout is yet to dis-
cover. For simplicity, we used polygonal chains to
represent the edges, different colors for multiple node
selections, and color transparency to avoid ambiguity.
It would be interesting to find ways of improving the
visual appeal of a GraphMaps visualization, e.g., us-
ing splines for edges, enabling tooltip texts for show-
ing quick information and so on.
7 CONCLUSION
We described our algorithm to construct GraphMaps
Visualizations using competition mesh. Recall that
the edge stretch factor of the competition mesh we
created is at most (2 +
√
2). A natural open question
is to establish tight bound on the edge stretch factor of
the competition mesh. It would also be interesting to
A New Approach to GraphMaps, a System Browsing Large Graphs as Interactive Maps
117
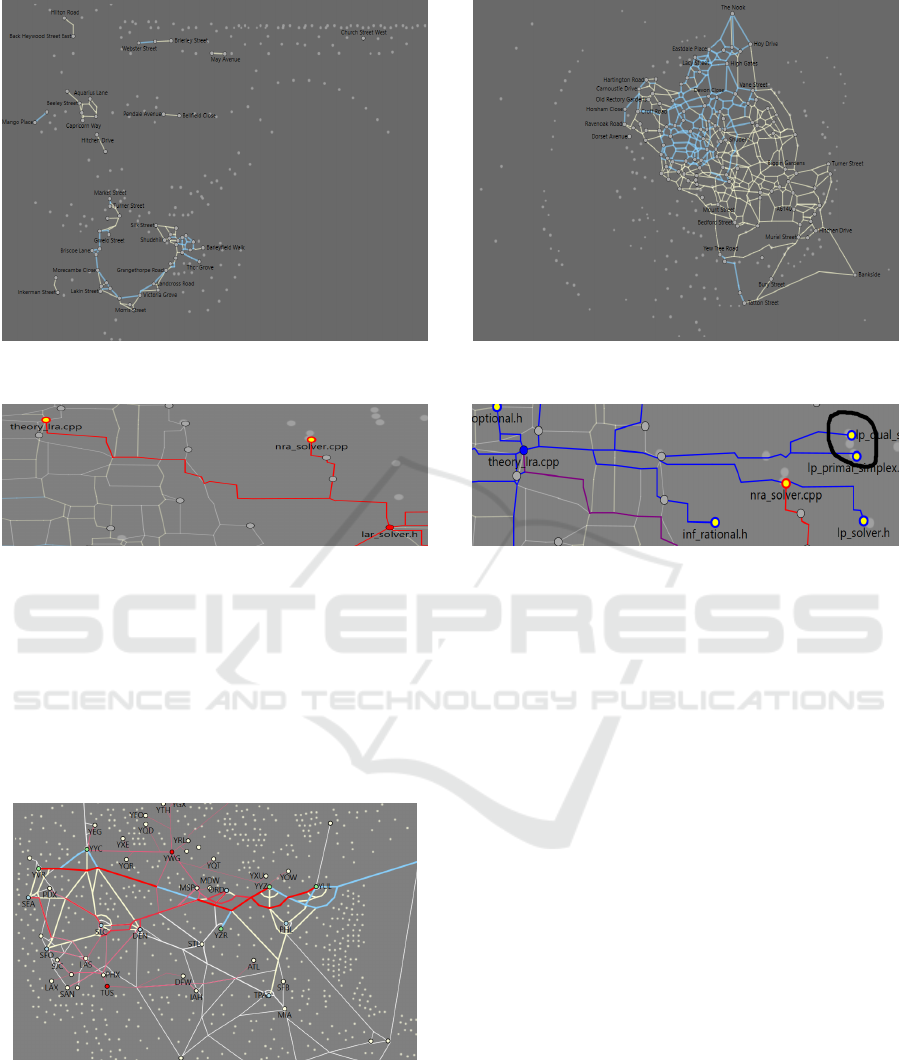
Figure 13: A visualization of drugs-crime event in Manchester, UK, with approximately (left) 0.5K edges, and (right) 8K
edges. The rails in light blue and white illustrate the first and second zoom levels, respectively.
Figure 14: Highlighting the neighborhood in a unique color helps to understand relations.
find bounded degree spanners (possibly with Steiner
points) that are monotone and have low stretch fac-
tor. We refer the reader to (Bose and Smid, 2013;
Dehkordi et al., 2015; Felsner et al., 2016) for more
details on such geometric mesh and spanners. We
leave it as a future work to examine how the quality
of a GraphMaps system may vary depending on the
choice of geometric mesh.
Figure 15: A visualization of the flight network
dataset (https://openflights.org/data.html) using previous
GraphMaps (Nachmanson et al., 2015).
The previous GraphMaps (Nachmanson et al.,
2015) uses an incremental mesh generation, which
does not require path simplification. Since the con-
struction of the upper levels does not take the lower
level nodes into account, the top-level view is usually
sparse, e.g., see Figure 15. Our approach is powerful
in the sense that any mesh can be transformed into a
GraphMaps visualization. But the upper levels are the
simplification of the bottom level mesh, and thus the
quality of the top-level depends on both the bottom
level mesh and the simplification process. It will be
interesting to further explore the pros and cons of both
approaches. We believe that our results will inspire
further research to enhance the appeal and usability
of GraphMaps visualizations.
ACKNOWLEDGEMENTS
This work was initiated when the first author was
a summer intern at Microsoft Research, Redmond,
USA. His subsequent work was partially supported
by NSERC.
REFERENCES
Balzer, M. and Deussen, O. (2007). Level-of-detail vi-
sualization of clustered graph layouts. In Asia-
Pacific Symp. on Visualization (APVIS), pages 133–
140. IEEE Computer Society.
Bose, P. and Smid, M. H. M. (2013). On plane geometric
spanners: A survey and open problems. Computa-
tional Geometry, 46(7):818–830.
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
118

Brin, S. and Page, L. (2012). Reprint of: The anatomy of a
large-scale hypertextual web search engine. Computer
Networks, 56(18):3825–3833.
Brunel, E., Gemsa, A., Krug, M., Rutter, I., and Wagner,
D. (2014). Generalizing geometric graphs. J. Graph
Algorithms Appl., 18(1):35–76.
Collberg, C. S., Kobourov, S. G., Nagra, J., Pitts, J., and
Wampler, K. (2003). A system for graph-based visu-
alization of the evolution of software. In ACM Symp.
on Software Visualization (SOFTVIS), pages 77–86.
ACM.
Dehkordi, H. R., Frati, F., and Gudmundsson, J. (2015).
Increasing-chord graphs on point sets. J. Graph Al-
gorithms Appl., 19(2):761–778.
Dobkin, D. P., Gansner, E. R., Koutsofios, E., and North,
S. C. (1997). Implementing a general-purpose edge
router. In Graph Drawing (GD), volume 1353 of
LNCS, pages 262–271. Springer.
Douglas, D. and Peucker, T. (1973). Algorithms for the re-
duction of the number of points required to represent
a digitized line or its caricature. The Canadian Car-
tographer, 10(2):112–122.
Dunne, C. and Shneiderman, B. (2013). Motif simplifica-
tion: improving network visualization readability with
fan, connector, and clique glyphs. In ACM SIGCHI
Conference on Human Factors in Computing Systems
(CHI), pages 3247–3256. ACM.
Dwyer, T. and Nachmanson, L. (2009). Fast edge-routing
for large graphs. In Graph Drawing (GD), volume
5849 of LNCS, pages 147–158. Springer.
Eppstein, D., Goodrich, M. T., Kim, E., and Tamstorf, R.
(2008). Motorcycle graphs: Canonical quad mesh par-
titioning. Comput. Graph. Forum, 27(5):1477–1486.
Ersoy, O., Hurter, C., Paulovich, F. V., Cantareiro, G., and
Telea, A. (2011). Skeleton-based edge bundling for
graph visualization. IEEE Trans. Vis. Comput. Graph.,
17(12):2364–2373.
Felsner, S., Igamberdiev, A., Kindermann, P., Klemz, B.,
Mchedlidze, T., and Scheucher, M. (2016). Strongly
monotone drawings of planar graphs. In Symposium
on Computational Geometry, volume 51 of LIPIcs,
pages 37:1–37:15.
Gansner, E. R., Hu, Y., and Kobourov, S. G. (2010). Gmap:
Visualizing graphs and clusters as maps. In IEEE Pa-
cific Visualization Symp. (PacificVis), pages 201–208.
Gansner, E. R., Hu, Y., North, S. C., and Scheidegger, C. E.
(2011). Multilevel agglomerative edge bundling for
visualizing large graphs. In IEEE Pacific Visualization
Symp. (PacificVis), pages 187–194.
Gansner, E. R. and Koren, Y. (2006). Improved circular
layouts. In Graph Drawing, LNCS, pages 386–398.
Springer.
Gao, R., Hu, P., and Lau, W. C. (2014). Graph property
preservation under community-based sampling. In
IEEE Global Communications Conference (GLOBE-
COM), pages 1–7.
Giyora, Y. and Kaplan, H. (2009). Optimal dynamic vertical
ray shooting in rectilinear planar subdivisions. ACM
Transactions on Algorithms, 5(3).
Guibas, L. J. and Stolfi, J. (1983). On computing all north-
east nearest neighbors in the l
1
metric. Information
Processing Letters, 17(4):219–223.
Holten, D. and van Wijk, J. J. (2009). Force-directed edge
bundling for graph visualization. Comput. Graph. Fo-
rum, 28(3):983–990.
Hu, Y. (2005). Efficient and high quality force-directed
graph drawing. The Mathematica Journal, 10:37–71.
Klimenta, M. and Brandes, U. (2012). Graph drawing
by classical multidimensional scaling: New perspec-
tives. In Graph Drawing (GD), volume 7704 of LNCS,
pages 55–66. Springer.
Lambert, A., Bourqui, R., and Auber, D. (2010). Winding
roads: Routing edges into bundles. Comput. Graph.
Forum, 29(3):853–862.
Nachmanson, L., Prutkin, R., Lee, B., Riche, N. H., Hol-
royd, A. E., and Chen, X. (2015). Graphmaps: Brows-
ing large graphs as interactive maps. In Graph Draw-
ing & Network Visualization (GD), volume 9411 of
LNCS, pages 3–15. Springer.
Orlin, J. B. (1993). A faster strongly polynomial minimum
cost flow algorithm. Operations Research, 41:377–
387.
Orlin, J. B. and Vaidyanathan, B. (2013). Fast algorithms
for convex cost flow problems on circles, lines, and
trees. Networks, 62(4):288–296.
Pupyrev, S., Nachmanson, L., Bereg, S., and Holroyd, A. E.
(2011). Edge routing with ordered bundles. In Graph
Drawing (GD), volume 7034 of LNCS, pages 136–
147. Springer.
Schaffer, D., Zuo, Z., Greenberg, S., Bartram, L., Dill, J.,
Dubs, S., and Roseman, M. (1996). Navigating hier-
archically clustered networks through fisheye and full-
zoom methods. ACM Trans. Comput.-Hum. Interact.,
3(2):162–188.
Shi, L., Liao, Q., Sun, X., Chen, Y., and Lin, C. (2013).
Scalable network traffic visualization using com-
pressed graphs. In IEEE Int. Conference on Big Data,
pages 606–612.
van der Maaten, L. and Hinton, G. E. (2008). Visualizing
data using t-SNE. Journal of Machine Learning Re-
search, 9:1–48.
van der Maaten, L. and Hinton, G. E. (2012). Visualiz-
ing non-metric similarities in multiple maps. Machine
Learning, 87(1):33–55.
Vehlow, C., Beck, F., and Weiskopf, D. (2015). The State of
the Art in Visualizing Group Structures in Graphs. In
Borgo, R., Ganovelli, F., and Viola, I., editors, Eu-
rographics Conference on Visualization (EuroVis) -
STARs. The Eurographics Association.
Wattenberg, M. (2006). Visual exploration of multivariate
graphs. In Proc. of the Conference on Human Factors
in Computing Systems (CHI), pages 811–819. ACM.
Zinsmaier, M., Brandes, U., Deussen, O., and Strobelt,
H. (2012). Interactive level-of-detail rendering of
large graphs. IEEE Trans. Vis. Comput. Graph.,
18(12):2486–2495.
A New Approach to GraphMaps, a System Browsing Large Graphs as Interactive Maps
119
