
Anomaly Detection in Crowded Scenes Using Log-Euclidean Covariance
Matrix
Efsun Sefa Sezer and Ahmet Burak Can
Department of Computer Engineering, Hacettepe University, Beytepe, Ankara, Turkey
Keywords:
Anomaly Detection, Video Surveillance, Log-Euclidean Covariance Matrices, One-class SVM.
Abstract:
In this paper, we propose an approach for anomaly detection in crowded scenes. For this purpose, two impor-
tant types of features that encode motion and appearance cues are combined with the help of covariance matrix.
Covariance matrices are symmetric positive definite (SPD) matrices which lie in the Riemannian manifold and
are not suitable for Euclidean operations. To make covariance matrices suitable for use in the Euclidean space,
they are converted to log-Euclidean covariance matrices (LECM) by using log-Euclidean framework. Then
LECM features created in two different ways are used with one-class SVM to detect abnormal events. Exper-
iments carried out on an anomaly detection benchmark dataset and comparison made with previous studies
show that successful results are obtained.
1 INTRODUCTION
In recent years, abnormal crowd behavior analysis
has become a popular topic of research in computer
vision. Due to increasing security concerns, secu-
rity cameras are used in many areas such as airports,
metro stations, shopping malls and hospitals. This
has led to the amount of video data being acquired.
Processing these data manually is very hard and time
consuming. The visual attention module of the human
brain (Wang et al., 2017) is limited and thus, human
attention shows a great decline after a certain period
of time. This is a serious problem in manual anal-
ysis of large amounts of data. Therefore, intelligent
surveillance systems have a vital role to play. These
systems reduce the need for human power and enable
to obtain meaningful information from large amount
of video data. The main purposes of intelligent video
surveillance systems are to analyze videos effectively,
distinguish between normal and abnormal conditions
and alert security personnel about abnormal events.
Although various methods are used to design intelli-
gent surveillance systems, general approach is mod-
eling normal events and identifying abnormal events
that do not fit into the model. The reasons for re-
searcher to prefer mentioned approach are that the
anomaly definition varies according to the content,
namely, situations considered abnormal for a particu-
lar scene may be considered normal in another scene
and the difficulties in finding the abnormal training
samples.
In this work, we propose an efficient approach to
detect anomalies in videos. For that, log-Euclidean
covariance matrices are used with one-class SVM
classification method. Covariance matrices are cre-
ated with appearance and motion cues. For appear-
ance cues, gradient-based features are chosen. For
motion cues, optical flow-based features are used.
Unlike traditional methods, which utilize gradient-
based or optical flow-based features for motion rep-
resentation, two important types of features that en-
code motion and appearance cues are combined with
the help of covariance matrix. Covariance matri-
ces are symmetric positive definite (SPD) matrices
which lie in the Riemannian manifold and are not
suitable for traditional Euclidean operations. Most of
the computer vision algorithms are developed for data
points located in Euclidean space. For this reason,
covariance matrices are mapped to Euclidean space
by utilizing log-Euclidean framework (Arsigny et al.,
2007). The model building process, which is the first
step in the detection of abnormal situations, is per-
formed by using features obtained from normal events
and one-class SVM (OCSVM). In the detection pro-
cess, dissimilar events meaning that do not fit the
model are marked as abnormal. Figure 1 shows the
overview of our approach. We evaluate our approach
on UMN (umn, 2006) anomaly detection benchmark
dataset. Experiments reveal that successful results are
obtained and the proposed method detects abnormal
events as soon as they occur. We organize the rest of
Sezer, E. and Can, A.
Anomaly Detection in Crowded Scenes Using Log-Euclidean Covariance Matrix.
DOI: 10.5220/0006618402790286
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages
279-286
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
279

Figure 1: Overview of the proposed approach. First, motion and appearance features are extracted. Then they are combined
with the help of covariance matrix. Log-Euclidean framework is employed to use the covariance matrices in the Euclidean
space. Anomaly detection is performed using log-Euclidean covariance features with OCSVM.
this paper as follows: Previous works are expressed in
Section 2. LECM features and log-euclidean frame-
work are described in Section 3. Anomaly detection
with OCSVM is explained in Section 4. Experimen-
tal results, comparison with previous approaches are
given in Section 5. Finally, we conclude this paper in
Section 6.
2 RELATED WORKS
Anomaly detection is the problem of finding situa-
tions that do not conform to the expected behavior
and it is an important topic that has been explored in
different application areas. Various approaches have
been proposed for anomaly detection. They can be
divided into two main categories: trajectory analysis
and motion analysis.
In trajectory-based approaches (Piciarelli et al.,
2008; Marsden et al., 2016; Fu et al., 2005), model-
ing crowd behaviors requires the separation and track-
ing of each objects in the scene. Object detection
and tracking cannot be done sufficiently in crowded
scenes due to the variable structure of crowded envi-
ronments. This makes the applicability of trajectory-
based approaches to crowded scenes considerably dif-
ficult.
In motion-based approach, as opposed to
trajectory-based approaches, behavioral analysis is
carried out without object tracking. Thus, they per-
form well in crowded scenes with difficult problems
such as closure and noise. For example, (Mehran
et al., 2009) use social force model to identify and
localize abnormal behaviors in crowded scenes. So-
cial force model is a method of mathematical crowd
behavior modeling based on Newton principles. (Lee
et al., 2013) propose motion influence matrix for
anomaly detection. In this study, anomaly detection
is performed according to the value of the motion
influence matrix which is high for abnormal events
and low for normal events. (Shi et al., 2010) calculate
the motion vectors between two consecutive frames
using phase correlation. Then normal events are mod-
eled using STCOG (spatial-temporal co-occurrence
Gaussian Mixture Models) and events that do not
fit into the model are marked as abnormal. (Wang
and Snoussi, 2015) extract the histogram of the
optical flow orientation (HOFO) features for motion
representation. Using the HOFO features with
kernel principal component analysis and one-class
SVM, they obtain favorable results. (Colque et al.,
2017) use spatio-temporal feature descriptor called
HOFM (Histograms of Optical Flow Orientation and
Magnitude) to determine the anomalies. HOFM is
generated by the direction and magnitude information
of the optical flow. Since the process of obtaining
magnitude and direction information does not require
complex operations, this work is suitable for use
in real-time systems. When anomaly detection
is conducted using only motion information, it is
difficult to identify the anomalies originating from
the size and appearance of the object. Considering
this situation, (Reddy et al., 2011) use appearance
information in addition to motion information. They
model features separately for efficient computation.
Classification is done using up to two classifiers. In
the first stage, velocity information is checked. If the
anomaly is not detected, it is passed to the second step
where anomaly detection is performed using size and
texture information. (Mahadevan et al., 2010) model
crowd behavior using Mixture of Dynamic Texture
(MDT). MDT represents motion and appearance
cues together. However, it has high computational
complexity. (Ryan et al., 2011) use textures of optical
flow with Gaussian Mixture Model (GMM). (Zhang
et al., 2016) deal with abnormal event detection in
two parts, appearance and motion. For abnormal
situations caused by appearance such as unusual
objects, unexpected appearance, strange positions,
unidentified objects, they use spatio-temporal gradi-
ent features with Support Vector Data Description
(SVDD). For motion anomaly, statistical histogram
is used. In the final part, the results obtained from the
motion and appearance detection are combined.
The process of identifying unusual events in com-
plex scenes requires use of high dimensional features
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
280

(Sabokrou et al., 2015). Training with these fea-
tures is very difficult and leads to problems such as
a decrease in the prediction power of the model. To
overcome these limitations, sparse methods have been
proposed. For instance, (Cong et al., 2011) propose
Multi-scale Histogram of Optical Flow (MHOF) to
detect abnormal events. MHOF is formed by combin-
ing two optical flow histograms according to a certain
threshold value and it represents motion in more de-
tail than the standard optical flow histogram. They in-
troduce the sparse reconstruction cost (SRC) over the
normal dictionary to distinguish anomalies from nor-
mal ones. (Huo et al., 2012) use MHOF features with
the multi-instance learning method. Unlike (Cong
et al., 2011), MHOF features are extracted from only
moving pixels. Different from previous studies, (Pen-
nisi et al., 2016) propose a real-time method based
on segmentation and without the need for a training
phase. They use entropy and TOV (Temporal Occu-
pancy Variation) to identify abnormal events.
3 LOG-EUCLIDEAN
COVARIANCE MATRIX (LECM)
When previous studies are examined, it is seen that
the optical flow feature which represents motion
of the crowd is frequently used in determining the
anomalies (Colque et al., 2017; Cong et al., 2011;
Wang and Snoussi, 2015). In this way, it is possible
to detect irregularities in the direction of movement
and speed. As is known, in application such as object
recognition, object tracking, action recognition, ab-
normal event detection successful result are obtained
by combining motion and appearance cues (Shotton
et al., 2006; Sanin et al., 2013; Zhang et al., 2016) . In
this study, both approaches are followed by creating
two different forms of covariance matrix. In the first
form of the covariance matrix, optical flow-based and
gradient-based features are used together. In the sec-
ond form, only optical flow-based features are used.
For optical flow estimation, Horn-Schunk (Horn and
Schunck, 1981) method is used.
Covariance matrix is introduced by (Tuzel et al.,
2006) to computer vision community for pedestrian
detection, object recognition. Later, they have been
successfully applied many areas such as object track-
ing, face recognition, action recognition (Sanin et al.,
2013; Guo et al., 2013). Let I(x,y,t) denote a video
sequence and F = { f
k
} be the feature vectors. Then
the covariance matrix is defined as:
C
t
=
1
N − 1
N
∑
k=1
( f
k
− µ)( f
k
− µ)
T
(1)
where N is the size of the feature set and µ is the mean
of the feature vectors. The use of covariance matrix
has many advantages:
• It is a simple and effective way of integrating var-
ious features.
• It is a low dimensional descriptor. Dimension of
covariance feature is independent of the size of the
region where it is computed.
While the advantages listed above make the covari-
ance matrix based approaches attractive, it is an im-
portant problem that the covariance matrices are de-
fined in the Riemannian manifold and not suitable for
the Euclidean operations. In order to make the co-
variance matrices suitable for Euclidean operations,
the log-Euclidean metric (Arsigny et al., 2007) is pro-
posed.
3.1 Log-Euclidean Framework on
Symmetric Positive Definite
Matrices
Covariance matrix is a symmetric positive definite
(SPD) matrix and SPD matrices do not lie in a vector
space. In order to make covariance matrices suitable
for use in the Euclidean space, log-Euclidean frame-
work is employed. According to this framework, co-
variance matrices are mapped to the Euclidean space
by using the matrix logarithm operation. The log-
covariance matrix estimation is performed as follows.
Let SPD(n) and S(n) denote the space of n × n real
SPD matrices and n × n real symmetric matrices, re-
spectively. The eigen-decomposition of a covariance
matrix S ∈ S(n) is S = UΛU
T
, where U is an or-
thonormal matrix and Λ = Diag(λ
1
,...,λ
n
) is a diago-
nal matrix that contains the eigenvalues λ
i
of S. If S is
positive definite matrix, S ∈ SPD(n), then λ
i
> 0 for
i = 1,...,n. Using eigen-decomposition, the exponen-
tial of a S ∈ S(n) can be calculated as follows:
exp(S) = U.Diag(exp(λ
1
),...,exp(λ
n
)).U
T
(2)
Logarithm of S ∈ SPD(n) is the following form:
log(S) = U.Diag(log(λ
1
),...,log(λ
n
)).U
T
(3)
Because the covariance matrix is a symmetric matrix,
half-vectorization is performed and final representa-
tion contains
n(n+1)
2
values.
3.2 LECM-1 Feature
In this section, we explain the first form of the pro-
posed covariance descriptor. When the previous stud-
ies are reviewed, it is commonly seen that gradi-
ent and optical flow-based features are used together
Anomaly Detection in Crowded Scenes Using Log-Euclidean Covariance Matrix
281

(Zhang et al., 2016; Zhu et al., 2016). These two fea-
tures are complementary to each other and give in-
formation about appearance and motion, respectively.
When they are used together, they produce good re-
sults. The feature vector f
1
(x,y,t) which is extracted
from (x,y,t) pixel position is the following form:
f
1
(x,y,t) = [x,y,t,g,o]
T
(4)
where
g =
h
|I
x
|,|I
y
|,|I
xx
|,|I
yy
|,
q
I
2
x
+ I
2
y
i
(5)
o =
u,v,
∂u
∂t
,
∂v
∂t
,
∂u
∂x
+
∂v
∂y
,
∂v
∂x
−
∂u
∂y
(6)
g and o represent appearance and motion cues. The
first four gradient-based features in (5) denote the first
and second order intensity gradients at pixel location
(x,y,t) and the last term is the gradient magnitude.
The optical flow-based features in (6) denote the hor-
izontal and vertical components of the flow vector
(u,v), the first order derivatives of the horizontal and
vertical components of the optical flow with respect to
time (∂u/∂t, ∂v/∂t). The last two optical flow based
features are the spatial divergence and vorticity of the
flow field (Ali and Shah, 2010).
3.3 LECM-2 Feature
The second form of covariance matrix is created by
using only optical flow-based features. The feature
vector f
2
(x,y,t) which is extracted from (x,y,t) pixel
position is the following form:
f
2
(x,y,t) = [x,y,t,o]
T
(7)
where o =
u,v,
∂u
∂t
,
∂v
∂t
,
∂u
∂x
+
∂v
∂y
,
∂v
∂x
−
∂u
∂y
,Gten,Sten
(8)
The optical flow-based features in (8) denote the hor-
izontal and vertical components of the flow vector
(u,v), the first order derivatives of the horizontal and
vertical components of the optical flow with respect
to time (∂u/∂t, ∂v/∂t) and the spatial divergence and
vorticity of the flow field. Gten, Sten are tensor invari-
ants which remain unchanged no matter which coor-
dinate system they are referenced in (Ali and Shah,
2010). Gten,Sten are derived from gradient tensor of
optical flow and the rate of strain tensor. The gradient
tensor of optical flow ∇u(x,y,t) is a 2×2 dimensional
matrix and defined as:
∇u(x,y,t) =
∂u
∂x
∂u
∂y
∂v
∂x
∂v
∂y
(9)
The rate of strain tensor S(x, y,t) is defined as follows:
S(x,y,t) =
1
2
(∇u(x,y,t) + ∇
T
u(x,y,t)) (10)
Gten and Sten are defined using ∇u(x,y,t) and
S(x,y,t) as follows:
Gten(x, y,t) =
1
2
(tr
2
(∇u(x,y,t) − tr(∇
2
u(x,y,t)))
(11)
Sten(x,y,t) =
1
2
(tr
2
(S(x,y,t)− tr(S
2
(x,y,t))) (12)
where tr(.) represents the trace operation.
4 DETECTION OF ANOMALOUS
EVENTS
Abnormal event detection is a daunting task due to its
context-dependent nature. This means that, an event
considered abnormal in one scenario may be consid-
ered normal in another scenario. In automatic surveil-
lance systems, abnormal event detection is performed
by modeling expected patterns in a given dataset and
finding patterns that do not conform to expected be-
havior. The expected behaviors are modeled using
normal samples.
In this work, we use one-class SVM for building
normal models. The main reasons for preferring one-
class classification methods in the detection of abnor-
mal events are that there are a wide range of abnormal
events and difficulties in collecting samples of these
cases. For that purpose, (Sch
¨
olkopf et al., 2001) pro-
pose a method that adapts the classical SVM method-
ology to the one class classification problem. In one-
class SVM, firstly the distribution of normal data is
determined. Classification is done according to the
presence or absence of the test data in this distribu-
tion. Let x
1
,x
2
,...,x
l
be training examples belonging
to one class X and Φ : X → H. H is a feature space
and Φ is a kernel map that transforms training sam-
ples to another space. The process of separating the
normal samples from the others using the kernel is
achieved by solving the following quadratic program-
ming problem :
min
1
2
||w||
2
+
1
vl
l
∑
i=1
ξ
i
− ρ (13)
subject to
(w.Φ(x
i
)) ≥ ρ − ξ
i
i = 1, 2, ...,l ξ
i
≥ 0 (14)
where w is a vector defining the hyper-plane,, v is reg-
ularization parameter, l is the number of training sam-
ples, ξ
i
is the slack variable and ρ the distance to the
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
282

Figure 2: Example frames from the UMN dataset. Top line: normal events. Bottom line: abnormal events.
origin in feature space.
The decision function is defines as:
f (x) = sign((w.Φ(x)) − ρ) (15)
The function in (15) will produce a positive value for
the samples in the training set.
5 EXPERIMENTAL RESULTS
In this section, firstly, we provide information about
the abnormal crowd behavior dataset UMN and eval-
uation metrics. Then qualitative and quantitative re-
sults are given.
5.1 Dataset
The UMN dataset (umn, 2006) is used to measure the
performance of the proposed method. It contains 11
video and 7739 frames with a 320 × 240 resolution.
Videos are captured in 1 indoor and 2 outdoor scenes.
Each video starts with normal behavior and ends with
an abnormal behavior of escape. Example scenes are
shown in Figure 2.
5.2 Evaluation Metric
In order to conduct a quantitative analysis on the pro-
posed method, ROC (Receiver Operating Character-
istics) curve and Area Under Curvature (AUC) are
used. For the ROC curve and the area under the curve
(AUC), the true positive rate (TPR) and the false pos-
itive rate (FPR) should be determined. TPR and FPR
values are calculated using the false positive (FP), true
positive (TP), false negatives (FN) and true negatives
(TN).
T PR =
T P
T P + FN
(16)
FPR =
FP
FP + T N
(17)
where TP denotes the correctly detected abnor-
mal events, FN denotes incorrectly detected nor-
mal events, FP denotes incorrectly detected abnormal
events, TN denotes correctly detected normal events.
5.3 Results
This section contains the results of the proposed
methods and comparison with previous studies. ROC
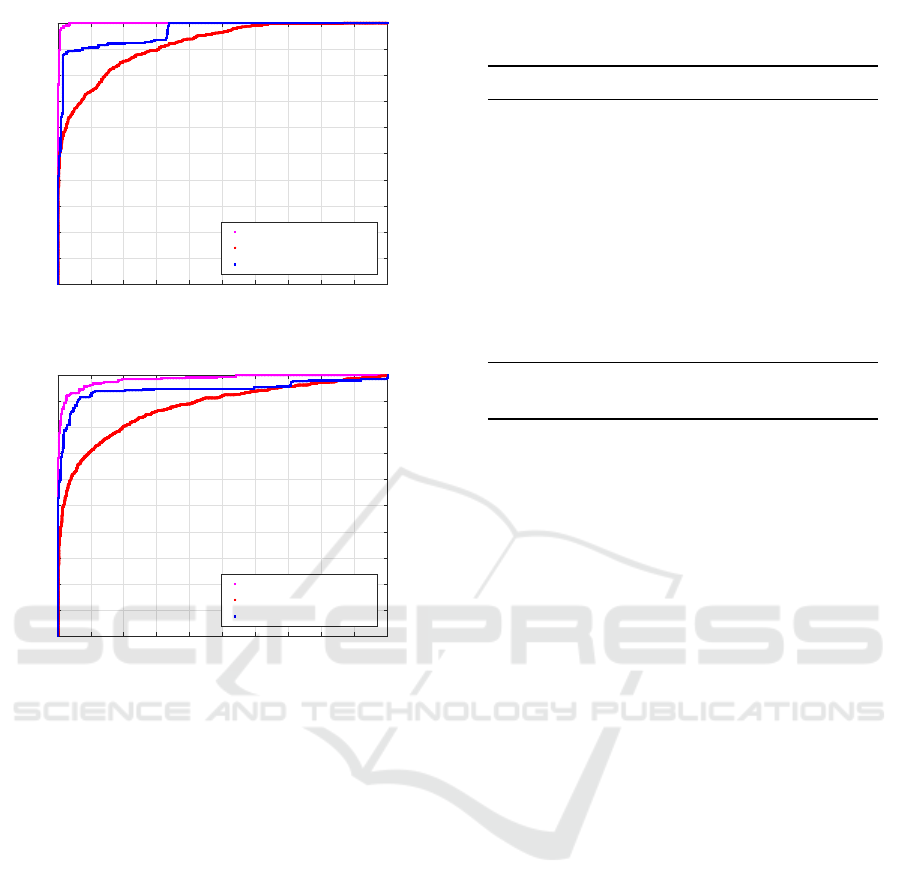
curves for LECM-1 and LECM-2 features are pre-
sented in Figure 5 and Figure 6, respectively. Re-
sults show that LECM-1 feature produces better re-
sults than LECM-2. Both approaches produce a lower
AUC value in the second scene than the other scenes.
This is due to the fact that the Scene-2 is dim light
indoor scene and there are changes in lighting con-
ditions. These problems adversely affect feature ex-
traction stage, and thus the system performance is
reduced. Figure 3 and Figure 4 show the qualita-
tive results for LECM-1 and LECM-2. It is observed
that LECM-1 makes the transition between abnormal
and normal events better than LECM-2. Especially
in the second scene, LECM-2 features cannot cor-
rectly detect the end of abnormal events. The rea-
son is that LECM-1 is constructed by using features
that are complementary to each other. The results also
Anomaly Detection in Crowded Scenes Using Log-Euclidean Covariance Matrix
283

Figure 3: The qualitative results of the abnormal behavior
detection using LECM-1. Each row shows detected ab-
normal events in three different videos. The ground truth
bar and the proposed approach bar show the labels of each
frame for that video. In that bars, green color indicates nor-
mal events and red color indicates abnormal events.
show that combining motion and appearance cues im-
proves detection accuracy and can also reduce false
alarms. In systems designed to detect anomalies, it
is important to define the moments of transition from
normal events to abnormal events correctly. In this
sense, LECM-1 features give alarms with a high de-
gree of accuracy from the moment when abnormal
conditions have begun to be seen.
We compare our approach with other methods
in Table 1. These methods are : SR (Cong et al.,
2011), MI (Lee et al., 2013), HF (Marsden et al.,
2016), MIDL (Huo et al., 2012), CMA (Zhang et al.,
2016), STCOG (Shi et al., 2010), FSCB (Pennisi
et al., 2016), HOFO SVM and HOFO PCA (Wang
and Snoussi, 2015), SF and OF (Mehran et al., 2009).
Figure 4: The qualitative results of the abnormal behavior
detection using LECM-2. Each row shows detected ab-
normal events in three different videos. The ground truth
bar and the proposed approach bar show the labels of each
frame for that video. In that bars, green color indicates nor-
mal events and red color indicates abnormal events.
LECM-1 outperforms SF, OF, STCOG, MIDL, HF
and is comparable to SR, MI, CMA, HOFO SVM
and HOFO PCA. It is important to note that we ob-
tained comparable or better results in comparison to
other methods using a very simple classification tech-
nique. The computational cost of our work is lower
than SR and MIDL which are complex dictionary
learning-based approaches. Furthermore, unlike the
FSCB method, segmentation is not used in the pro-
posed approach. In crowded scenes, it is very dif-
ficult to perform segmentation because there are too
many components to be analyzed and they have clo-
sure problems. When Table 1 is examined, it is seen
that the highest performance is achieved by HOFO
PCA. HOFO feature contains only motion informa-
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
284
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
FPR
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
TPR
Scene-1 AUC = 0.9986
Scene-2 AUC = 0.9181
Scene-3 AUC = 0.9667
Figure 5: The ROCs for LECM-1.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
FPR
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
TPR
Scene-1 AUC = 0.9857
Scene-2 AUC = 0.8790
Scene-3 AUC = 0.9468
Figure 6: The ROCs for LECM-2.
tion and are not discriminative enough for detecting
anomalies arising form object shapes and appearance.
In contrast to HOFO, LECM-1 feature contains both
appearance and motion cues and can provide success-
ful results when used with more advanced classifica-
tion methods.
6 CONCLUSIONS
In this study, log-Euclidean covariance matrix is
formed in two different ways and used with OCSVM
effectively to detect abnormal events. As mentioned
before, it is difficult to collect anomalous event in-
stances in the detection of abnormal events. For this
reason, OCSVM, which has been popular in recent
years, is preferred. In this respect, the method has
a simple and effective structure which is different
from the complicated works in the literature. Also,
our method is suitable for use in crowded scenes be-
cause object tracking, detection are not performed
and there is no need to set any threshold value dur-
ing anomaly detection. Experiments carried out on
Table 1: Performance comparison according to ROC curves
on the UMN dataset.
Approach Scene-1 Scene-2 Scene-3
SR 0.995 0.975 0.964
MI 0.995 0.853 0.98
HF 0.953 0.913 0.964
MIDL 0.8927 0.7541 0.9482
CMA 0.993 0.969 0.988
STCOG 0.9362 0.7759 0.9661
FSCB 09641 0.8764 0.9750
HOFO SVM 0.9845 0.9037 0.9815
HOFO PCA 0.9992 0.9880 0.9989
SF 0.96
OF 0.84
LECM-1 0.9986 0.9181 0.9667
LECM-2 0.9857 0.8790 0.9468
the UMN dataset indicate that the proposed method
provides satisfying results. The best results are ob-
tained by combining appearance and motion informa-
tion with the help of the covariance matrix. For future
work, we aim to make the proposed approach suitable
for use in scenes where local abnormal events are ob-
served.
REFERENCES
(2006). University of Minnesota, Unusual crowd
activity data set. http://(http://mha.cs.
umn.edu/Movies/Crowd-Activity-All.avi).
Ali, S. and Shah, M. (2010). Human action recognition in
videos using kinematic features and multiple instance
learning. IEEE transactions on pattern analysis and
machine intelligence, 32(2):288–303.
Arsigny, V., Fillard, P., Pennec, X., and Ayache, N. (2007).
Geometric means in a novel vector space structure on
symmetric positive-definite matrices. SIAM journal
on matrix analysis and applications, 29(1):328–347.
Colque, R. V. H. M., Caetano, C., de Andrade, M. T. L.,
and Schwartz, W. R. (2017). Histograms of opti-
cal flow orientation and magnitude and entropy to
detect anomalous events in videos. IEEE Transac-
tions on Circuits and Systems for Video Technology,
27(3):673–682.
Cong, Y., Yuan, J., and Liu, J. (2011). Sparse reconstruc-
tion cost for abnormal event detection. In Computer
Vision and Pattern Recognition (CVPR), 2011 IEEE
Conference on, pages 3449–3456. IEEE.
Fu, Z., Hu, W., and Tan, T. (2005). Similarity based vehicle
trajectory clustering and anomaly detection. In Im-
age Processing, 2005. ICIP 2005. IEEE International
Conference on, volume 2, pages II–602. IEEE.
Guo, K., Ishwar, P., and Konrad, J. (2013). Action recog-
nition from video using feature covariance matrices.
Anomaly Detection in Crowded Scenes Using Log-Euclidean Covariance Matrix
285

IEEE Transactions on Image Processing, 22(6):2479–
2494.
Horn, B. K. and Schunck, B. G. (1981). Determining optical
flow. Artificial intelligence, 17(1-3):185–203.
Huo, J., Gao, Y., Yang, W., and Yin, H. (2012). Ab-
normal event detection via multi-instance dictionary
learning. Intelligent Data Engineering and Automated
Learning-IDEAL 2012, pages 76–83.
Lee, D.-G., Suk, H.-I., and Lee, S.-W. (2013). Crowd
behavior representation using motion influence ma-
trix for anomaly detection. In Pattern Recognition
(ACPR), 2013 2nd IAPR Asian Conference on, pages
110–114. IEEE.
Mahadevan, V., Li, W., Bhalodia, V., and Vasconcelos, N.
(2010). Anomaly detection in crowded scenes. In
Computer Vision and Pattern Recognition (CVPR),
2010 IEEE Conference on, pages 1975–1981. IEEE.
Marsden, M., McGuinness, K., Little, S., and O’Connor,
N. E. (2016). Holistic features for real-time crowd
behaviour anomaly detection. In Image Process-
ing (ICIP), 2016 IEEE International Conference on,
pages 918–922. IEEE.
Mehran, R., Oyama, A., and Shah, M. (2009). Abnormal
crowd behavior detection using social force model.
In Computer Vision and Pattern Recognition, 2009.
CVPR 2009. IEEE Conference on, pages 935–942.
IEEE.
Pennisi, A., Bloisi, D. D., and Iocchi, L. (2016). On-
line real-time crowd behavior detection in video se-
quences. Computer Vision and Image Understanding,
144:166–176.
Piciarelli, C., Micheloni, C., and Foresti, G. L. (2008).
Trajectory-based anomalous event detection. IEEE
Transactions on Circuits and Systems for video Tech-
nology, 18(11):1544–1554.
Reddy, V., Sanderson, C., and Lovell, B. C. (2011). Im-
proved anomaly detection in crowded scenes via cell-
based analysis of foreground speed, size and texture.
In Computer Vision and Pattern Recognition Work-
shops (CVPRW), 2011 IEEE Computer Society Con-
ference on, pages 55–61. IEEE.
Ryan, D., Denman, S., Fookes, C., and Sridharan, S. (2011).
Textures of optical flow for real-time anomaly de-
tection in crowds. In Advanced Video and Signal-
Based Surveillance (AVSS), 2011 8th IEEE Interna-
tional Conference on, pages 230–235. IEEE.
Sabokrou, M., Fathy, M., Hoseini, M., and Klette, R.
(2015). Real-time anomaly detection and localization
in crowded scenes. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition
Workshops, pages 56–62.
Sanin, A., Sanderson, C., Harandi, M. T., and Lovell, B. C.
(2013). Spatio-temporal covariance descriptors for ac-
tion and gesture recognition. In Applications of Com-
puter Vision (WACV), 2013 IEEE Workshop on, pages
103–110. IEEE.
Sch
¨
olkopf, B., Platt, J. C., Shawe-Taylor, J., Smola, A. J.,
and Williamson, R. C. (2001). Estimating the support
of a high-dimensional distribution. Neural computa-
tion, 13(7):1443–1471.
Shi, Y., Gao, Y., and Wang, R. (2010). Real-time abnor-
mal event detection in complicated scenes. In Pattern
Recognition (ICPR), 2010 20th International Confer-
ence on, pages 3653–3656. IEEE.
Shotton, J., Winn, J., Rother, C., and Criminisi, A. (2006).
Textonboost: Joint appearance, shape and context
modeling for multi-class object recognition and seg-
mentation. In European conference on computer vi-
sion, pages 1–15. Springer.
Tuzel, O., Porikli, F., and Meer, P. (2006). Region covari-
ance: A fast descriptor for detection and classification.
Computer Vision–ECCV 2006, pages 589–600.
Wang, C., Yao, H., and Sun, X. (2017). Anomaly detection
based on spatio-temporal sparse representation and vi-
sual attention analysis. Multimedia Tools and Appli-
cations, 76(5):6263–6279.
Wang, T. and Snoussi, H. (2015). Detection of abnor-
mal events via optical flow feature analysis. Sensors,
15(4):7156–7171.
Zhang, Y., Lu, H., Zhang, L., and Ruan, X. (2016). Com-
bining motion and appearance cues for anomaly de-
tection. Pattern Recognition, 51:443–452.
Zhu, Z., Wang, J., and Yu, N. (2016). Anomaly detec-
tion via 3d-hof and fast double sparse representation.
In Image Processing (ICIP), 2016 IEEE International
Conference on, pages 286–290. IEEE.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
286
