
Infrared Image Enhancement in Maritime Environment with
Convolutional Neural Networks
Purbaditya Bhattacharya
1
, J
¨
org Riechen
2
and Udo Z
¨
olzer
1
1
Department of Signal Processing and Communications, Helmut Schmidt University, Hamburg, Germany
2
WTD 71 Military Service Center for Ships, Naval Weapons, Maritime Technology and Research, Eckernf
¨
orde, Germany
Keywords:
Image Processing, Convolutional Neural Network, Denoising, Super-resolution.
Abstract:
Image enhancement approach with Convolutional Neural Network (CNN) for infrared (IR) images from mar-
itime environment, is proposed in this paper. The approach includes different CNNs to improve the resolution
and to reduce noise artefacts in maritime IR images. The denoising CNN employs a residual architecture
which is trained to reduce graininess and fixed pattern noise. The super-resolution CNN employs a similar ar-
chitecture to learn the mapping from a low-resolution to multi-scale high-resolution images. The performance
of the CNNs is evaluated on the IR test dataset with standard evaluation methods and the evaluation results
show an overall improvement in the quality of the IR images.
1 INTRODUCTION
Optical cameras contain sensors that are able to de-
tect light of wavelength in the range of 450 - 750 nm
and hence limited by the availability of light. Infrared
(IR) cameras and thermographic cameras in particular
have sensors that detect thermal radiation and are in-
dependent from the amount of ambient visible light.
The thermal radiation of the object determines how
salient or detailed it will be in an infrared image and
can provide useful information, otherwise not avail-
able in a normal image. IR imagery has become con-
siderably popular over the last years because of its us-
age in multiple fields of application including medical
imaging, material testing, military surveillance. Due
to its effectiveness, IR imaging is used extensively
in maritime environment for maritime safety and se-
curity application, activity detection, object tracking,
and environment monitoring.
IR images suffer from low signal-to-noise ratio
(SNR) because of the non-uniformity of the detec-
tor array responses and their underlying processing
circuits. The ambient temperature plays a very im-
portant role since the IR camera has to be calibrated
accordingly (Zhang et al., 2010). In this context,
outdoor maritime environment poses a bigger chal-
lenge compared to an indoor environment due to the
temperature fluctuations, atmospheric loss, wind, and
rain. In spite of regular camera calibrations and er-
ror correcting techniques (Zhang et al., 2010), the
(a) Original (b) Enhanced
Figure 1: An example of enhancement in IR images.
image suffers from spot noise, fixed pattern noise,
graininess, blur and other artefacts. Traditional digital
image processing techniques of image enhancement
have been extensively used over the years. The classi-
cal approaches include the usage of adaptive median
filters, gradient based approach like the total varia-
tion denoising (Micchelli et al., 2011), (Goldstein and
Osher, 2009), wavelet based approach (Zhou et al.,
2009), non-local self similarity (NSS) based methods
(Dabov et al., 2007), (J.Xu et al., 2015), and meth-
ods on sparse representation based dictionary learning
Bhattacharya, P., Riechen, J. and Zölzer, U.
Infrared Image Enhancement in Maritime Environment with Convolutional Neural Networks.
DOI: 10.5220/0006618700370046
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages
37-46
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
37

(Elad and Aharon, 2006). In recent years deep learn-
ing has become a very popular topic due to its success
in solving many computer vision problems. Convolu-
tional neural network (CNN) is the most popular deep
learning tool and has been employed already in many
image enhancement problems e.g., denoising, super-
resolution, and compression artefact removal. This
paper applies a deep learning approach with CNNs to
solve the enhancement problem in maritime IR im-
ages. An example is shown in Figure 1.
2 RELATED WORK
The present work is influenced by the recent suc-
cess of CNNs in image super-resolution and denois-
ing problems. An artificial neural network is used
for image denoising in (Jain and Seung, 2009). It is
shown in (Burger et al., 2012) that multi layer per-
ceptrons (MLP) can outperform state-of-the-art stan-
dard denoising techniques. In the area of resolution
improvement, the ”Super-Resolution Convolutional
Neural Network” (SRCNN) (Dong et al., 2015) has
trained a CNN architecture to learn the mapping be-
tween a low and high resolution image. The end to
end learning has yielded very good results but the cor-
responding training convergence is slow. In (He et al.,
2016) it is already established that residual connec-
tions or skip connections in a network increase the
learning speed and improve the overall performance.
Residual networks are particularly useful if the train-
ing data and the ground truth data have high corre-
lation. In this context, CNNs with residual learn-
ing has yielded better results from the perspective of
speed and accuracy. In (Kim et al., 2016) it is estab-
lished that the super-resolution with a deep residual
architecture subsequently improved the performance.
Recently residual learning for image denoising with
CNNs have been used successfully in (Pan et al.,
2016) and (Zhang et al., 2017). Due to the improved
performance of residual networks the present work
has employed residual architectures for the enhance-
ment application.
3 PROPOSED APPROACH
A CNN is a layered architecture primarily compris-
ing of linear multi dimensional convolution kernels
and non-linear activation functions usually appear-
ing alternately in a basic architecture. Apart from
the two layers mentioned, other important layers in-
clude pooling, batch normalization, and fully con-
nected layers and the usage of these layers depends
L
Label
Output
Update
+
Input
Blur
Noise Patch
CNN
Loss
Figure 2: An overview of the denoising method.
on the computer vision application. The layers are ar-
ranged in different combinations to create flexible net-
work architectures that are trained iteratively with an
objective function to solve different computer vision
problems. In order to perform a supervised training of
a CNN, it is necessary to create a dataset of image and
ground truth pairs. The purpose of the training is to
learn and generalize the relationship between the im-
ages and the corresponding ground truth images in the
dataset. The dataset is usually divided into training,
validation and test data. The final goal of a trained
CNN is to perform the desired action on an unseen
test data. The following sections provide the details
of the denoising and super-resolution CNNs.
3.1 Denoising Method
The denoising method overview is shown in Figure 2.
In the first step the dataset is prepared for the denois-
ing task. The primary goal of this work is to suc-
cessfully denoise the IR images from the WTD 71
dataset. For training the CNN the RGB-NIR scene
database (Brown and S
¨
usstrunk, 2011) from the EPFL
Lausanne is used. The database contains a collection
of near infrared (NIR) and color images of indoor and
outdoor scenes from which the NIR images are used
for training. In the second step the CNN is described,
setup and trained.
3.1.1 Data Preparation
Figure 3: Sample clean images from the RGB-NIR training
dataset.
From the RGB-NIR database 400 images and 60 im-
ages are selected for training and validation respec-
tively. To create the training and validation dataset
the clean NIR images are initially resampled and de-
graded with noise to create the input dataset for the
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
38

Loss
*
ReLU
Conv
Input
Output
Label
L
+
*
Conv
49
21
21
21
49
3
3
1
64
64
21
2121
7
7
1
49
21
21
21
21
21
21
64
21
21
Figure 4: The architecture of denoising CNN.
CNN, and the clean NIR images are used as the
ground truth or reference dataset. Figure 3 shows
some example images from the database. A majority
of the test IR images from WTD 71 have noisy arte-
facts of varying intensities and properties. A consid-
erable number of noise patches are extracted from the
IR images from areas of uniform background intensi-
ties. Additionally, noisy frames from videos with uni-
form background, containing 35 mm film grain, are
extracted and added to the collection of noise patches.
During the creation of the CNN dataset, the noise
patches are randomly augmented and are added to the
clean images after mean subtraction and resizing to
produce the noisy images. The image and ground
truth image pairs of both training and validation data
are divided into patches of 21×21 pixels to create the
final dataset. During the training process the image
patches are randomly flipped.
3.1.2 Network Architecture
The example architecture for denoising is shown in
Figure 4. As illustrated in the figure, the network
is composed of alternate convolutional (Conv) layers
and rectified linear units (ReLU), with the exception
of the first two layers which are convolutional. The
network is only composed of Conv layers and ReLU
layers. There are 7 Conv layers and 5 ReLU layers
in the network and 13 layers altogether including the
Loss layer. The Conv layer performs linear convolu-
tion on each incoming feature map tensor or a tensor
of input image patch with the defined kernels to pro-
duce the output feature maps. As shown in Figure 4
the depth of the convolution kernel should match the
depth of the input feature map and the depth of the
output feature map tensor is equal to the number of
kernels in the Conv layer. Hence the number of ker-
nels used in the final Conv layer should be 1 in or-
der to obtain a target output image with a depth or
channel of 1. The convolution operation in each Conv
layer also retains the height and the width of the in-
put feature map to that layer by correct padding. The
depth of the convolution kernel is equal to the depth of
the input feature map tensor. Thus a convolution of a
21×21×1 image patch with 49 kernels of size 7×7×1
produces a feature map tensor of size 21×21×49 in
the first layer. The first two Conv layers use 7×7×1
and 3×3×49 kernels respectively and the last Conv
layer uses 3×3×64 kernel. The kernels in the first
Conv layer are initialized with sparse matrices where
most of the elements are zero valued and the remain-
ing elements have a value of 1. The remaining Conv
layers use 5×5×64 kernels with ReLU layers in be-
tween. The ReLU layer truncates the negative values
in a feature map as given by,
y = max(0, x), (1)
where x denotes the input to the ReLU function, y
denotes the output of the ReLU function, and max
denotes the maximum operator. Before the Loss
layer the input is added to the output so that the net-
work learns to estimate the noise residue. Table 1
shows the information about the network architec-
ture, where Id. denotes the layer index, and w and
b denote weight and bias respectively. The table
also provides the size of each kernel in the form of
height×width×depth×number of kernels. The leak-
age factor (Lk) of the ReLU layer weights the neg-
ative values from the input feature maps instead of
truncating them.
3.1.3 Objective
The objective of the training process is to minimize
a combination of losses defined by the correspond-
ing loss functions. The CNN is trained iteratively to
minimize a weighted combination of loss functions in
order to find an optimal solution of the free or train-
able parameters. The combination consists of the L
1
and L
2
regression loss functions which operate pixel
wise. The individual loss functions are given in the
below equations,
L
1
(y, ˆy) =
1
V
||y − ˆy||
1
, (2)
Infrared Image Enhancement in Maritime Environment with Convolutional Neural Networks
39

Table 1: The denoising CNN architecture.
Id. Name Kernel Size Lk lr (w, b)
1 Conv 7×7×1×49 - 1e-4, 1e-4
2 Conv 3×3×49×64 - 1e-2, 1e-4
3 ReLU - 0.2 -
4 Conv 5×5×64×64 - 1e-2, 1e-4
5 ReLU - 0.2 -
6 Conv 5×5×64×64 - 1e-2, 1e-4
7 ReLU - 0.2 -
8 Conv 5×5×64×64 - 1e-2, 1e-4
9 ReLU - 0.2 -
10 Conv 5×5×64×64 - 1e-2, 1e-4
11 ReLU - 0.2 -
12 Conv 3×3×64×1 - 1e-2, 1e-4
13 Loss - - -
and
L
2
(y, ˆy) =
1
V
||y − ˆy||
2
2
, (3)
where ˆy denotes the estimated CNN output, y denotes
the ground truth data, and V denotes the volume of
the CNN output or the ground truth data tensor. The
advantage of the L
1
loss is that it has edge preserving
qualities since the L
1
norm solves for the median. The
optimization problem is given by,
ˆy = f
θ
(x), (4)
θ
∗
= arg min E
y, ˆy
[
K
∑
i=1
α
i
L
i
(y, ˆy))], (5)
where, θ
∗
denotes the optimal solution of the free
or trainable parameters denoted by θ, f
θ
denotes the
CNN model, x denotes the input image, L
i
(·) denotes
a loss function, α
i
is the weighting factor for com-
bining the K loss functions, and E
y, ˆy
[·] denotes the
expected value of the combination of loss functions.
From the loss layer the gradients starts backpropa-
gating through each layer following the chain rule of
derivatives. The kernel weights are then updated with
the calculated gradients for the corresponding layers
and the amount of update is controlled by a user spec-
ified learning rate parameter. In order to update the
weights, the adaptive momentum (Adam) optimiza-
tion (Kingma and Ba, 2014) is used, due to its fast
convergence. The weights of the Conv layers are ini-
tialized with Xavier initialization (Glorot and Bengio,
2010) and the weight decay regularization parameter
of 0.001 is used to counter overfitting problems. It is
noteworthy that a CNN is usually not trained with one
image per iteration but with a batch of images as de-
termined by a user specified batch size. Images inside
a batch are randomly selected from the entire dataset
which leads to the stochastic nature of the training
process. In this case a batch size of 64 is used during
the training. During the training process, the learn-
ing rates as shown in Table 1 are adapted by reducing
them by a factor of 2 at every 10th epoch. The net-
work is trained for 90 epochs.
3.2 Super-resolution Method
L
Label
Output
Update
Bicubic
CNN
Loss
Input
Figure 5: An overview of the super-resolution method.
In this section the CNN model for super-resolution is
described. For super-resolution the RGB-NIR dataset
is used as well. The method overview is shown in
Figure 5. The model for the super-resolution CNN has
differences from the denoising CNN in terms of the
network architecture and data preparation.
3.2.1 Data Preparation
The dataset is prepared with 360 training images and
60 validation images. The training is performed with
both the NIR images as well as with the Y channel of
the color images converted to YCbCr, with the results
from the latter being discussed in this work because
of more stable performance. To create the training
and validation dataset the clean images are initially
resampled with bicubic interpolation to create the in-
put dataset for the CNN and the clean images are used
as the ground truth data. The CNN is trained with re-
sampling factors of 2, 3, and 4 separately. The image
and ground truth pairs of both training and validation
data are divided into patches of 224×224 pixels to
create the final dataset. During the training process
the image patches are randomly flipped as a form of
batch augmentation.
3.2.2 Network Architecture
The CNN architecture example for super-resolution
is shown in Figure 6. The network is primarily com-
posed of alternate Conv and ReLU layers and a con-
catenation (Concat) layer. The network has 13 Conv
layers, 12 ReLU layers, 1 Concat layer, and has 27
layers in total including the Loss layer. Each Conv
layer uses 3×3×64 kernel except the first layer which
uses a 5×5×1 kernel and the layer after the Concat
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
40

Loss
*
ReLUReLU
Conv
Concat
Conv
*
Input
Output
Label
L
+
5
5
1
64
64
3
3
64
224
224
224
224
224
224
64
224
224
64
224
224
64 64 64 64 64
224
224
224
224
224
224
64
224
224
224
224
64
Figure 6: The architecture of super-resolution CNN.
layer which uses 5×5×320 kernel. All the layers em-
ploy 64 The learning rate (lr) of the Conv layers is the
same. Before the last 2 Conv layers there is a Con-
cat layer that collects feature maps from selected lay-
ers along the 3rd dimension of the feature tensor, as
shown in Figure 6. In this particular case the feature
maps from layers 6, 10, 14, 18, and 22, of a depth
of 64 each, are concatenated along the 3rd dimen-
sion of the feature tensor resulting in a feature tensor
with a depth of 320. The Concat layer ensures that
the inference be made from feature maps from layers
of multiple depths and hence multiple resolution with
respect to the information content. The original im-
age is added to the output by a skip connection and
the network learns to estimate the residual high fre-
quency details of the image. Table 2 shows the infor-
mation about the network architecture. As mentioned
previously the depth of the kernel in each Conv layer
equals the depth of the corresponding input feature
map. Hence, the kernel depth in the Conv layer fol-
lowing the Concat layer is 320 as given in Table 2.
For super-resolution factors of 3 and 4, the same net-
work architecture with different kernel depths (32), is
used.
3.2.3 Objective
The super-resolution CNN is trained with a similar
combination of loss functions as in the case of de-
noising. The goal of the training is to minimize the
expected combined loss as given in Equation (5). The
weights of the Conv layers are initialized with the im-
proved Xavier initialization. The weight decay regu-
larization parameter of 0.0005 is used and a batch size
of 8 is used during training. The Adam optimizer is
used to update the weights and biases in the Conv lay-
ers. During the training, the learning rate is adapted
by reducing it by a factor of 2 after every 20th epoch.
Training of the network with different resampling fac-
tors are performed separately for 230 epochs.
Table 2: The super-resolution CNN architecture.
Id. Name Kernel Size Lk lr (w, b)
1 Conv 5×5×1×64 - 1e-2, 1e-5
2 ReLU - 0 -
3 Conv 3×3×64×64 - 1e-2, 1e-5
4 ReLU - 0 -
5 Conv 3×3×64×64 - 1e-2, 1e-5
6 ReLU - 0 -
7 Conv 3×3×64×64 - 1e-2, 1e-5
8 ReLU - 0 -
9 Conv 3×3×64×64 - 1e-2, 1e-5
10 ReLU - 0 -
11 Conv 3×3×64×64 - 1e-2, 1e-5
12 ReLU - 0 -
13 Conv 3×3×64×64 - 1e-2, 1e-5
14 ReLU - 0 -
15 Conv 3×3×64×64 - 1e-2, 1e-5
16 ReLU - 0 -
17 Conv 3×3×64×64 - 1e-2, 1e-5
18 ReLU - 0 -
19 Conv 3×3×64×64 - 1e-2, 1e-5
20 ReLU - 0 -
21 Conv 3×3×64×64 - 1e-2, 1e-5
22 ReLU - 0 -
23 Concat - - -
24 Conv 3×3×320×64 - 1e-2, 1e-5
25 ReLU - 0 -
26 Conv 3×3×64×1 - 1e-2, 1e-5
27 Loss - - -
4 EVALUATION
The training of the CNNs are performed in MATLAB
with the MatConvNet toolbox (Vedaldi and Lenc,
2015) on one Nvidia GTX 980Ti GPU. Training the
individual networks took only a few hours. The per-
formance of the networks are evaluated with the IR
images from WTD 71. For evaluation of the qual-
ity of denoising and super-resolution, relatively clean
images are selected from the database and are cor-
Infrared Image Enhancement in Maritime Environment with Convolutional Neural Networks
41

rupted with film grain of 35 mm and fixed pattern
noise. Some of the images from the dataset are shown
in Figure 7. The results are also compared with estab-
lished denoising methods BM3D (Dabov et al., 2007)
and PGPD (J.Xu et al., 2015) and the DnCNN (Zhang
et al., 2017).
Figure 7: Sample clean images from WTD 71 test dataset.
4.1 Standard Evaluation
The results of the CNNs are evaluated with the stan-
dard peak signal-to-noise ratio (PSNR) and struc-
tural similarity (SSIM) metric and are compared with
the results from a selected number of denoising and
super-resolution methods publicly available for test-
ing. Figure 8 shows the improvement of average
PSNR by our denoising CNN on a batch of the val-
idation data over each training epoch. Denoising is
performed on 44 test images. Figure 9 and Figure 10
show a few denoising examples of granular noise with
BM3D, PGPD, our CNN and DnCNN. The denoising
CNN is not trained to denoise Gaussian noise but is
tested with Gaussian noise of standard deviation (σ)
of 25, to test its robustness. Figure 11 shows an ex-
ample denoising result for Gaussian noise. Each of
the denoising examples show selected areas inside the
original image, while the PSNR values represent the
entire original image. The average performance of
the CNN for both granular noise and Gaussian noise
is shown in Table 3. The results show that the denois-
ing CNN is capable of performing well even without
being explicitly trained for a particular kind of noise
profile. The results also show that the CNN can per-
form well on different noise profiles without explicit
manual parameter setup usually required by standard
Gaussian denoisers. In other words, irrespective of
the noise content in terms of the type of noise or the
noise power, the CNN generalizes the denoising prob-
lem well, while other methods need prior information
about the noise for good performance. Another ad-
vantage of the denoising CNN is that it does not de-
grade a clean image or an image with negligible noise
content, when operated on, proving its robustness as
well.
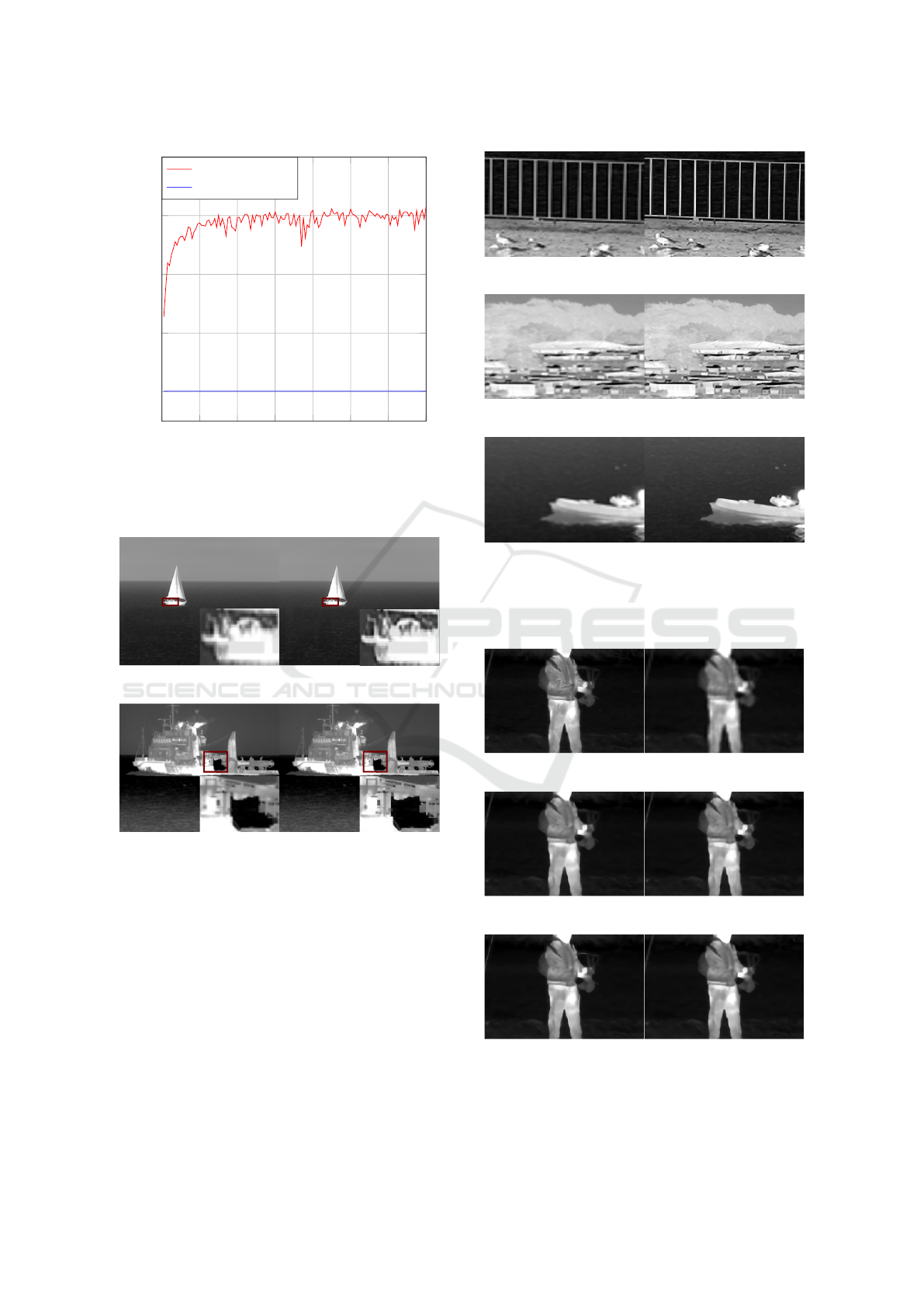
Similar to the denoising CNN, an improvement of
the average PSNR by the super-resolution CNN on a
0 20 40
60
80
26
28
30
32
34
36
Epoch
PSNR in dB
denoised
noisy
Figure 8: Comparison of average PSNR of a set of noisy
and denoised validation images at every training epoch.
(a) Original (b) Noisy (33.68 dB)
(c) CNN (Ours) (40.82 dB) (d) BM3D (40.58 dB)
(e) PGPD (37.95 dB) (f) DnCNN (39.40 dB)
Figure 9: Denoising of granular noise in selected section in
an IR image by different methods.
batch of the validation data over each training epoch,
can be seen in Figure 12. For testing, super-resolution
is performed on the aforementioned test images for
three upsampling ratios. Figure 13 shows two exam-
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
42

(a) Original (b) Noisy (33.19 dB)
(c) CNN (Ours) (42.33 dB) (d) BM3D (41.52 dB)
(e) PGPD (38.10 dB) (f) DnCNN (41.65 dB)
Figure 10: Denoising of granular noise in selected section
in an IR image by different methods.
Table 3: Evaluation of average denoising performance
(SSIM, PSNR in dB).
Method
Image Grain Gaussian (σ = 25)
PSNR SSIM PSNR SSIM
None 33.3 0.763 20.58 0.190
CNN 39.47 0.947 33.69 0.841
BM3D 39.42 0.942 33.83 0.848
PGPD 37.47 0.901 32.94 0.802
DnCNN 38.00 0.904 33.99 0.850
ple super-resolution results and Figure 14 shows ex-
ample results for multiple super-resolution factors.
The performance of our super-resolution CNN is also
compared with SRCNN (Dong et al., 2015), DnCNN
(Zhang et al., 2017), and VDSR (Kim et al., 2016),
which are some of the standard state-of-the-art super-
resolution methods. The methods are applied on the
WTD71 dataset and the corresponding results are tab-
ulated in Table 4 and Table 5. Figure 15 shows an ex-
ample from the application of each of these methods
for a super-resolution factor of 4. The results indi-
cate that our CNN is very competitive with respect to
VDSR and DnCNN. Our super-resolution CNN also
has lesser number of training parameters compared to
the other deep networks.
(a) Original (b) Noisy (20.93 dB)
(c) CNN (Ours) (33.29 dB) (d) BM3D (32.07 dB)
(e) PGPD (31.95 dB) (f) DnCNN (32.05 dB)
Figure 11: Denoising of Gaussian noise (σ=25) in selected
section in an IR image by different methods.
Table 4: Comparison of super-resolution performance
(PSNR).
Method
PSNR (dB)
×2 ×3 ×4
Bicubic 37.25 34.75 33.29
CNN (ours) 39.21 36.15 34.45
SRCNN 38.76 35.91 34.17
VDSR 39.22 36.20 34.54
DnCNN 38.79 36.02 34.45
Table 5: Comparison of super-resolution performance
(SSIM).
Method
SSIM
×2 ×3 ×4
Bicubic 0.92 0.87 0.84
CNN (ours) 0.94 0.90 0.87
SRCNN 0.94 0.89 0.86
VDSR 0.94 0.90 0.88
DnCNN 0.93 0.88 0.85
4.2 Blind Denoising
In real world images, prior knowledge of the degra-
dation is unknown. In this context the test IR images
can only be subjectively evaluated and the improve-
Infrared Image Enhancement in Maritime Environment with Convolutional Neural Networks
43
0 20 40
60
80 100 120 140
38
40
42
44
46
Epoch
PSNR in dB
super-resolution
bicubic
Figure 12: Comparison of average PSNR of a set of bicubic
and super-resolved (×2) validation images at every training
epoch.
(a) Bicubic (36.06 dB) (b) CNN (Ours) (38.64 dB)
(c) Bicubic (35.07 dB) (d) CNN (Ours) (37.68 dB)
Figure 13: Comparison between bicubic interpolation and
super-resolution (×2) of selected IR images.
ment can be compared through observation. The test
images comprise of 20 IR images corrupted by natu-
ral artefacts. A selection of the original and denoised
image sections are shown in Figure 16. From the ex-
ample images it can be observed that the images con-
tain noise artefacts and the intensity of noise is not
very high. The images are a collection of frames from
specific videos and have the appearance of graininess
and repetitive patterns. Areas from the original im-
ages and the processed versions of the images in Fig-
ure 16 show the denoising performance of the CNN.
From the images it can be observed that the graininess
(a) Bicubic (23.78 dB) (b) CNN (Ours) (26.73 dB)
(c) Bicubic (24.60 dB) (d) CNN (Ours) (25.78 dB)
(e) Bicubic (29.97 dB) (f) CNN (Ours) (31.28 dB)
Figure 14: Comparison between (a) bicubic and (b) super-
resolution (×2) (c) bicubic and (d) super-resolution (×3)
and (e) bicubic and (f) super-resolution (×4) of selected sec-
tions of IR images.
(a) Original (b) Bicubic (35.07 dB)
(c) CNN (Ours) (38.27 dB) (d) SRCNN (37.75 dB)
(e) VDSR (38.11 dB) (f) DnCNN (38.06 dB)
Figure 15: Super-resolution (×4) of a selected section in an
IR image by different super-resolution methods.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
44

Figure 16: Example of denoising of natural images with original image areas shown in the left column and the corresponding
denoised areas shown in the right column (best observed on a monitor).
of the images is reduced while preserving the edges
considerably well. The differences are best observed
on a monitor.
5 CONCLUSION
In this paper we have proposed image enhancement
approaches for maritime IR images. We use two
CNNs with residual architectures based on regression
losses to denoise and super-resolve IR images. The
training images are created by adding noise content in
clean images. From the objective and subjective eval-
uation based on example images it can be concluded
that the denoising and super-resolution performs well
with our networks. The results show that the CNNs
are able to improve the quality of IR images. The
results also encourage further investigation of simple
CNN structures and improving their robustness to dif-
ferent types of noise, different intensities of noise and
different grain sizes since the present network is lim-
ited to the data it is trained with. Further investigation
can be made on the training data requirement, e.g.,
training with thermal images only, for better domain
specific learning. It is also noteworthy that other vi-
sion tasks like segmentation, detection, and stabiliza-
tion also benefit from the enhancement of images and
the influence can be investigated in the future.
REFERENCES
Brown, M. and S
¨
usstrunk, S. (2011). Multispec-
tral SIFT for scene category recognition. In
Computer Vision and Pattern Recognition
(CVPR11), 177-184, Colorado Springs. IEEE.
Infrared Image Enhancement in Maritime Environment with Convolutional Neural Networks
45

doi:10.1109/CVPR.2011.5995637. Retrieved from
http://ivrl.epfl.ch/supplementary material/cvpr11/.
Burger, H. C., Schuler, C. J., and Harmeling, S. (2012).
Image denoising: Can plain neural networks compete
with BM3D? In IEEE Conference on Computer Vi-
sion and Pattern Recognition, 2392-2399. IEEE. doi:
10.1109/CVPR.2012.6247952.
Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.
(2007). Image denoising by sparse 3-d transform-
domain collaborative filtering. In IEEE Transac-
tions on Image Processing, 16(8), 2080-2095. IEEE.
doi:10.1109/TIP.2007.901238.
Dong, C., Loy, C. C., He, K., and Tang, X. (2015). Im-
age super-resolution using deep convolutional net-
works. In IEEE Transactions on Pattern Analy-
sis and Machine Intelligence, 38(2), 295-307. IEEE.
doi:10.1109/TPAMI.2015.2439281.
Elad, M. and Aharon, M. (2006). Image denoising via
learned dictionaries and sparse representation. In
IEEE Computer Society Conference on Computer Vi-
sion and Pattern Recognition (CVPR), 1, 895-900.
IEEE. doi:10.1109/CVPR.2006.142.
Glorot, X. and Bengio, Y. (2010). Understanding the
difficulty of training deep feedforward neural net-
works. In Proceedings of the Thirteenth Inter-
national Conference on Artificial Intelligence and
Statistics, 9, 249-256. JMLR. Retrieved from
http://proceedings.mlr.press/v9/glorot10a.html.
Goldstein, T. and Osher, S. (2009). The split breg-
man method for L1 regularized problems. In SIAM
Journal on Imaging Sciences, 2(2), 323-343. Society
for Industrial and Applied Mathematics Philadelphia.
doi:10.1137/080725891.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep
residual learning for image recognition. In IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), 770-778. IEEE. doi:10.1109/CVPR.2016.90.
Jain, V. and Seung, S. (2009). Natural image de-
noising with convolutional networks. In Ad-
vances in Neural Information Processing Systems
21, 769-776. Curran Associates, Inc. Retrieved
from http://papers.nips.cc/paper/3506-natural-image-
denoising-with-convolutional-networks.pdf.
J.Xu, L.Zhang, Zuo, W., Zhang, D., and Feng, X. (2015).
Patch group based nonlocal self-similarity prior learn-
ing for image denoising. In IEEE International Con-
ference on Computer Vision (ICCV), 244-252. IEEE.
doi:10.1109/ICCV.2015.36.
Kim, J., Lee, J. K., and Lee, K. M. (2016). Accurate
image super-resolution using very deep convolutional
networks. In IEEE Computer Society Conference on
Computer Vision and Pattern Recognition (CVPR),
1646-1654. IEEE. doi:10.1109/CVPR.2016.182.
Kingma, D. P. and Ba, J. (2014). Adam: A method for
stochastic optimization. In 3rd International Confer-
ence for Learning Representations. CoRR. Retrieved
from http://arxiv.org/abs/1412.6980.
Micchelli, C. A., Shen, L., and Y.Xu (2011). Prox-
imity algorithms for image models: denoising.
In Inverse Problems, 27(4). Retrieved from
http://stacks.iop.org/0266-5611/27/i=4/a=045009.
Pan, T., Zhongliang, F., Lili, W., and Kai, Z. (2016).
Perceptual loss with fully convolutional for image
residual denoising. In T. Tan et al. (eds.) Chinese
Conference on Pattern Recognition (CCPR), 122-132.
Springer. Retrieved from https://doi.org/10.1007/978-
981-10-3005-5 11.
Vedaldi, A. and Lenc, K. (2015). Matconvnet: Con-
volutional neural networks for matlab. In Pro-
ceedings of the 23rd ACM international confer-
ence on Multimedia. CoRR. Retrieved from
http://arxiv.org/abs/1412.4564.
Zhang, K., Zuo, W., Chen, Y., Meng, D., and Zhang, L.
(2017). Beyond a gaussian denoiser: Residual learn-
ing of deep cnn for image denoising. In IEEE Transac-
tions on Image Processing, 26(7), 3142-3155. IEEE.
doi:10.1109/TIP.2017.2662206.
Zhang, Z. M., Tsai, B. K., and G.Machin (2010). Radiomet-
ric Temperature Measurements. Elsevier, 1st edition.
Zhou, Z., Cao, J., and Liu, W. (2009). Contourlet-
based image denoising algorithm using adaptive win-
dows. In 4th IEEE Conference on Industrial Elec-
tronics and Applications (ICIEA), 3654-3657. IEEE.
doi:10.1109/ICIEA.2009.5138888.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
46
