
360 Panorama Super-resolution using Deep Convolutional Networks
Vida Fakour-Sevom
1,2
, Esin Guldogan
1
and Joni-Kristian K
¨
am
¨
ar
¨
ainen
2
1
Nokia Technologies, Finland
2
Laboratory of Signal Processing, Tampere University of Technology, Finland
Keywords:
Super-resolution, Virtual Reality, Equirectangular Panorama, Deep Convolutional Neural Network.
Abstract:
We propose deep convolutional neural network (CNN) based super-resolution for 360 (equirectangular)
panorama images used by virtual reality (VR) display devices (e.g. VR glasses). Proposed super-resolution
adopts the recent CNN architecture proposed in (Dong et al., 2016) and adapts it for equirectangular panorama
images which have specific characteristics as compared to standard cameras (e.g. projection distortions). We
demonstrate how adaptation can be performed by optimizing the trained network input size and fine-tuning
the network parameters. In our experiments with 360 panorama images of rich natural content CNN based
super-resolution achieves average PSNR improvement of 1.36 dB over the baseline (bicubic interpolation) and
1.56 dB by our equirectangular specific adaptation.
1 INTRODUCTION
Super-resolution (SR) is one of the actively investi-
gated problems of image processing where the main
objective is to recover the original high resolution
(HR) image from a low resolution (LR) one(s) (Yang
et al., 2014). Due to the limitation in the avail-
able information, loss of details, super-resolution is
generally an ill-posed problem. Super-resolution al-
gorithms are divided into two main groups: Multi-
frame SR (Hung and Siu, 2009; Btz et al., 2016)
(traditional method) which exploit information avail-
able in multiple frames and Single Image Super-
resolution (SISR) (Tang and Chen, 2013; Tsurusaki
et al., 2016; Cheng et al., 2017) which tries to recover
original information from a single image. The SISR
methods are further divided into Learning-based and
Interpolation-based methods. In this paper, we focus
on the learning-based single image super-resolution.
Freeman (Freeman et al., 2002) introduced the
concept of learning-based super-resolution for the
first time and proposed an example-based method.
In (Yang et al., 2008) the authors presented sparse
coding based SR using sample images for training an
over-complete dictionary. Recently, deep learning has
set the state-of-the-arts in many computer vision tasks
including super-resolution (Ji et al., 2016; Dong et al.,
2016), denoising and removing artifacts (Quijas and
Fuentes, 2014; Ji et al., 2016).
360 panorama images and videos have recently
gained momentum due to availability of consumer
level display devices such as Samsung Gear VR and
HTC Vive VR. The users are used to experience high
quality and high resolution images and videos due to
availability of professional level sensors such as high-
end Nokia OZO capturing device which uses 8 wide
angle lenses and provides 4K image per eye. The cap-
tured videos/images are stitched together to make a
single content which might suffer from stitching arti-
facts. Moreover, an equirectangular panorama image
is generated very differently than traditional images.
Equirectangular panorama mapping takes spherical
input and maps the latitude and longitude coordi-
nates onto a single rectangular plane. This may cause
strong distortions on the produced image (equirect-
angular panorama projection). Therefore, it is inter-
esting to study whether the previous SR methods still
work or do they need special adaptation.
In this work we adopt the deep convolutional neu-
ral network super-resolution approach by Dong et
al. (Dong et al., 2016) (SRCNN) to recover high-
resolution 360 (equirectangular) panorama images
from their low resolution versions. We adapt the ex-
isting methodology by studying the effects of input
sub-image size to the network and fine-tuning with
the different number of iterations on 360 panorama
dataset. In our experiments the SRCNN provides
clear improvement as compared to the baseline (bicu-
bic interpolation) and our adaptation techniques fur-
ther improve the results.
Fakour-Sevom, V., Guldogan, E. and Kämäräinen, J-K.
360 Panorama Super-resolution using Deep Convolutional Networks.
DOI: 10.5220/0006618901590165
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages
159-165
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
159

Contributions – The novel contributions of our
work are:
• We demonstrate effective learning-based super-
resolution for 360 (equirectangular) panorama im-
ages by adopting the recent SRCNN method for
standard images.
• We adapt the methodology to the characteristics
of high-resolution 360 panorama images by opti-
mizing the network input size and fine-tuning with
360 panorama training set.
• We create a dataset to benchmark 360 degree
panorama image super-resolution methods.
2 RELATED WORK
Image Super-resolution (SR) – Addressing the
problem of recovering a HR image from a given LR
image is known as single image super-resolution. In
many works, SISR is divided into Learning-based and
Interpolation-based methods (Zhou et al., 2012). In
early interpolation-based methods, it is assumed that
a LR input image is the downsized version of a HR
image. Hence, the HR image, considering aliasing, is
recovered from upscaling the LR input image (Siu and
Hung, 2012). Currently, learning-based approaches
are widely used in order to make a mapping func-
tion between LR images and their corresponding HR
ones. Freeman in (Freeman et al., 2002) for the first
time introduced the concept of learning-based super-
resolution and proposed an example-based method.
The main idea behind the learning-based approach is
using the spatial similarities between Low-Resolution
and High-Resolution images and making a mapping
function in order to predict the HR image for a given
LR input image. Methods in (Yang et al., 2008; Tim-
ofte et al., 2013) use a learned over-complete dictio-
nary based on sparse signal representation. The main
idea is based on the assumption of existing the same
sparse coefficient in LR and their corresponding HR
patches.
Deep CNN SR – Lately, Convolutional Neural Net-
work (CNN) approaches have been popular in many
vision applications including super-resolution (Cui
et al., 2014; Shi et al., 2016; Kim et al., 2016; Schulter
et al., 2015) where they had noticeable performance
improvements over the previous state-of-the-arts.
SRCNN (Dong et al., 2016), known as a represen-
tative state-of-the-art method for deep learning, ap-
plies a single image super-resolution where the net-
work end-to-end learns a mapping between LR and
HR images. Moreover, it is shown that existing sparse
coding methods might be considered as a deep learn-
ing. In (Ji et al., 2016), a HR image is created over
iterative refinement and back projection methods. An
extension of SRCNN method is seen in (Youm et al.,
2016) where a single system’s input is replaced by a
multi-channel one. In this method the input contains
original LR image, corresponding edge-enhanced and
interpolated ones. Single image super-resolution us-
ing deep learning and gradient transformation is an-
other recent approach proposed in (Chen et al., 2016).
In their extension, closest gradient to the one in the
original image is estimated by transforming observed
gradient in the upscaled images using a gradient trans-
formation network.
3 DEEP MULTI-RESOLUTION
In our work we utilized the deep super-resolution
convolutional neural network architecture by (Dong
et al., 2016) since it recently demonstrated state-of-
the-art accuracy for various datasets and over many
competitive non-CNN based competitors. The main
idea of SRCNN is to learn a mapping from low res-
olution images to high resolution images by devising
a suitable network structure and error function, and
then train the network with a large dataset.
In our case, the main target is to input a low-
resolution equirectangular panorama image to the
SR model and reconstruct its corresponding high-
resolution version. In the training phase, we in-
put multi-resolution input sub-images (the network
training input is not the whole image but randomly
cropped regions called as sub-images) to the network
in order to study the effect of multi-resolution sub-
images on the super-resolution results. It is likely
that equirectangular panorama exhibits different char-
acteristics to standard images and therefore requires
adaptation.
The first step in SRCNN is to perform a standard
bicubic interpolation for the input image of any size
(denoted as X) to the desired output size of the HR
image: f : X → Y . The aim of the next CNN forward
pass step is to recover the high resolution details for
Y to make an image (denoted as F(Y)) that is sim-
ilar to the original high quality image. The desired
above-mentioned mapping function (denoted as F) is
composed of the three convolution layers: patch ex-
traction, non-linear mapping and reconstruction.
In the first layer the patches are extracted by con-
volving the image with a set of filters. Afterwards,
the patches are represented using a set of pre-trained
bases. The first layer is shown as an operation F
1
:
F
1
(Y ) = max(0, W
1
∗Y + B
1
) (1)
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
160

where ∗ denotes convolution, moreover, W
1
and B
1
show the filters and biases, respectively. Assuming
c as a number of channels of an image and f
1
as
a filter size, n
1
convolutions with the kernel size of
c × f
1
× f
1
are applied on the image. Each element of
the n
1
-dimensional B
1
vector is corresponding to a fil-
ter individually. Hence, extracting an n
1
-dimensional
feature for each patch is the final output of this step.
In the second layer, other n
2
-dimensional vectors
are created from the mapped n
1
-dimensional vectors
(previous step). The corresponding operation is:
F
2
(Y ) = max(0, W
2
∗ F
1
(Y ) + B
2
) (2)
where W
2
and B
2
correspond to the first layer equa-
tion filters and biases, respectively. However this
time there are n
2
filters of size n
1
× f
2
× f
2
and n
2
-
dimensional B
2
vector. Eventually, the output of this
layer is a high-resolution patch which will be used for
the next layer i.e. reconstruction.
In the last layer, a convolutional layer is defined
where the final high-resolution image is produced:
F(Y ) = W
3
∗ F
2
(Y ) + B
3
(3)
where W
3
is c filters of size n
2
× f
3
× f
3
and B
3
is a c-dimensional vector. Minimizing the loss be-
tween reconstructed images and ground truth image
makes estimating the above-mentioned parameters,
i.e. W
1
, W
2
, W
3
, B
1
, B
2
, B
3
possible. These parameters
are needed for learning the mapping function. Mean
Square Error is used as the network loss function:
L(θ) =
1
n
n
∑
i=1
kF(Y
i
;θ) − X
i
k
2
, (4)
where θ = {W
1
, W
2
, W
3
, B
1
, B
2
, B
3
}, n is the num-
ber of training images.
3.1 Training
The three mentioned steps together result the SR-
CNN convolutional neural network. Training is per-
formed by cropping training images (X
i
) to random
f
sub
× f
sub
-pixel sub-images (in experimental part we
use various sizes). Low-resolution samples are cre-
ated by downscaling and upscaling the sub-images af-
ter making them blurred using Gaussian kernel. The
downscaling and upscaling are completed via Bicubic
interpolation where the same scaling factor (in our ex-
periments is 3) is used. In order to avoid the border
effect, padding is not used in the network. Hence, the
output size of a sub-image based on the network filter
sizes (( f
sub
− f
1
− f
2
− f
3
+ 3)
2
× c) is smaller than
the input size. Training model is implemented using
Caffe package which is also used in our implementa-
tion. Once training is done and network parameters
are created, the SRCNN trained model is applied to
test images of any size.
4 EXPERIMENTS
We first experimented our equirectangular panorama
images with the existing training model (using orig-
inal training and test images). Next, we examined
the training phase with our own images and studied
the effect of using equirectangular images instead of
the traditional ones on the results. Subsequently, the
training parameters, number of iterations and network
input sub-image size, are adaptively changed based on
our images.
4.1 Data
Figure 1: Video frames of the size 3840 × 1081 captured
using a Nokia OZO high-end VR camera.
The dataset which we use consists of 34 high qual-
ity equirectangular panorama images which are single
frames of various 360-video scenes captured using a
Nokia OZO VR camera
1
(Figure 1). For comparison,
the small training set, used in the original paper, with
91 images is used. The sub-images size is set to a
fixed size i.e. f
sub
= 33 in SRCNN, but in our exper-
iments two f
sub
= 65 and f
sub
= 129 are also studied.
The sub-images are extracted from the ground truth
images with a stride of 14 (same as default setting in
the original paper for f
sub
= 33) and then we increase
it to 30 and 62, for f
sub
= 65 and f
sub
= 129, respec-
tively.
4.2 Settings
The baseline model in our experiments is the origi-
nal network proposed in (Dong et al., 2016) which
uses 33 × 33 sub-image input and their own dataset
1
https://ozo.nokia.com/vr/
360 Panorama Super-resolution using Deep Convolutional Networks
161
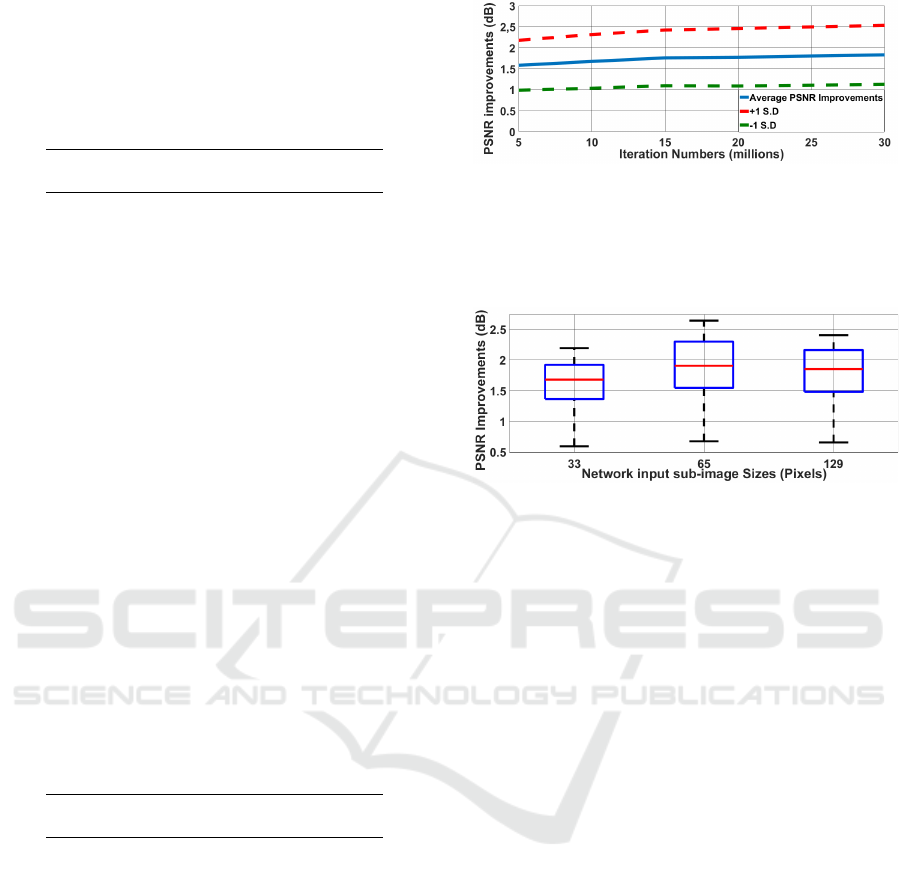
Table 1: Super-resolution results for all 34 frames from 5-
fold cross-validation where 6-7 images selected for the test
set. Bicubic results correspond to bicubic interpolation, SR-
CNN is (Dong et al., 2016) and SRCNN-ft is fine-tuned
with our equirectangular panorama data using the original
settings (33× 33 patch size) and after 15 million fine tuning
iterations.
PSNR (dB)
Frame# Bicubic SRCNN SRCNN-ft
F01 34.38 35.26 35.43
F02 30.13 31.24 31.46
F03 23.13 23.56 23.66
F04 30.44 32.36 32.51
F05 35.79 36.50 36.54
F06 32.24 33.35 33.48
F07 38.97 40.12 40.28
F08 28.02 28.98 29.19
F09 34.70 35.59 35.69
F10 28.14 29.12 29.32
F11 27.18 28.14 28.29
F12 30.54 32.50 32.70
F13 34.74 37.12 37.18
F14 32.20 33.29 33.40
F15 38.94 40.48 41.17
F16 37.49 39.15 39.60
F17 40.09 41.04 42.02
F18 23.16 23.68 23.83
F19 33.78 34.78 34.91
F20 28.54 29.68 29.79
F21 27.52 28.22 28.28
F22 41.39 42.82 42.98
F23 32.32 33.46 33.65
F24 38.67 40.23 40.52
F25 36.31 38.62 38.67
F26 35.56 37.89 38.08
F27 35.69 37.57 37.63
F28 40.95 42.54 42.69
F29 36.01 38.02 38.28
F30 37.55 38.91 39.47
F31 33.59 34.72 34.91
F32 32.53 34.59 34.69
F33 32.98 34.59 34.72
F34 33.03 34.68 34.79
avg. improv. [dB] - 1.36 1.56
avg. improv. [%] - 4.1% 4.7%
for training the model with batch size 128 The net-
work settings are: c = 3, f
1
= 9, f
2
= 1, f
3
= 5,
n
1
= 64 and n
2
= 32. The results have been evaluated
with the scaling factor equal to 3. For our experiment
we downscaled the original images by the factor of 3,
meaning that the input image is subsampled and the
resolution is one third of the initial size in horizontal
and vertical directions, then it is again upsampled by
the factor of 3 to the initial size.
We conducted our experiments using 5-fold cross-
validation and the results for single images have been
selected from the folds where these images were
not used in training. For our experiments we tested
fine-tuning the original network with equirectangular
panorama images for 5, 10, 15, 20 and 30 million it-
erations keeping the original batch size and using var-
ious network input sub-image sizes (33 × 33, 65 × 65
Figure 2: Average and plus/minus one standard deviation
movement of SR improvement (dB) over all equirectangu-
lar panorama images as the function of the number of fine-
tuning iterations. The average training time takes roughly
11 hours for 5M iterations running on NVIDIA GEForce
GTX980 GPU.
Figure 3: Box plots of the average PSNR improvements for
SR with different network input sub-image sizes.
and 129×129). For the largest sub-image size we de-
creased the learning rate from 0.0001 to 0.00001 to
avoid overfitting. As our performance measure we re-
port the peak signal-to-noise ration (PSNR) defined in
decibels (dB). Moreover, we report also bicubic inter-
polation as the baseline method to epmhasize overall
superiority of deep learning based super-resolution.
4.3 Results
Using the standard SRCNN for our equirectangu-
lar dataset improved the results quite significantly
(+1.36dB/+4.1%) as compared to the baseline (see
Table 1) and in the remaining experiments we inves-
tigated the different adaptation strategies.
Fine-tuning – In the first experiment we fine-
tuned the SRCNN network with our equirectangular
panorama images. Note that the images are from dif-
ferent video clips and therefore there is no imme-
diate correlation between the contents. Fine tuning
was performed 15 million iterations with the original
learning rate 0.0001 and using the original sub-image
input size and batch size The results are reported for
5-fold cross-validation where image specific numbers
are taken as averages from folds where that image
was only in the test set. The results for the fine-
tuned network (SRCNN-FT) are shown in Table 1.
For all images the SR results improved and demon-
strated the average improvement 1.36dB → 1.56dB
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
162

(a) A high density equirectangular panorama image captured using a Nokia OZO VR camera.
(b) Original (c) Bicubic / 31.15 dB (d) SRCNN / 31.74 dB (e) SRCNN FT / 32.95 dB
(f) Original (g) Bicubic / 30.67 dB (h) SRCNN / 33.49 dB (i) SRCNN FT / 34.53 dB
Figure 4: Equirectangular panorama super-resolution examples.
over all contents. Clearly the fine-tuning is beneficial
for the process as the network learns equirectangu-
lar specific characteristics such as the lens distortion
which is very strong vertically.
Number of Iterations – In this experiment we kept
the network structure fixed to the same as the previous
one, but experimented the limits of fine-tuning by in-
creasing the number of iterations. In Figure 2 the av-
erage and standard deviation of SR improvement are
shown in dB over all images. It is noteworthy that the
improvement continues beyond 15 million iterations
and reaches improvement 1.56dB which is signifi-
cantly better than with the original SRCNN (1.34dB).
Network Input Sub-image Size – In this experi-
ment we fixed the network structure and parameters
and kept the number of iterations 15M and then ap-
plied the multi-resolution sub-image experiment. The
sub-image sizes are changed from 33 × 33 to 65 × 65
and 129 × 129. The PSNR box plots for the average
improvements as compared to the bicubic baseline are
shown in Figure 3. It is noteworthy that there is clear
improvement from the sub-image size from 33 × 33
to 65 × 65, but the results got worse with the larger
sub-image size of 129 × 129. In general, the results
should improve for large sub-image sizes, but then
the network becomes more sensitive to overfitting and
therefore results got worse.
360 Panorama Super-resolution using Deep Convolutional Networks
163

(a) A high density equirectangular panorama image captured using a Nokia OZO VR camera.
(b) Original (c) Bicubic / 30.53 dB (d) SRCNN / 32.68 dB (e) SRCNN FT / 35.52 dB
(f) Original (g) Bicubic / 36.22 dB (h) SRCNN / 38.6535 dB (i) SRCNN FT / 42.28 dB
Figure 5: Equirectangular panorama super-resolution examples.
4.4 Examples
Visual comparison of the applied Bicubic interpola-
tion and super-resolution images using SRCNN and
SRCNN FT are given in Figure 4-5. Two random
regions, with the size of 150 × 150, are extracted
from our three input equirectangular images. Apply-
ing Bicubic, SRCNN and SRCNN
FT showed that
the SRCNN method has a high accuracy in terms
of sharpness and removing artifacts to the baseline
(bicubic interpolation). Our multi-resolution fine-
tuned SRCNN makes notable improvements over SR-
CNN by equirectangular specific adaptation.
5 CONCLUSIONS
We proposed a learning-based super-resolution
method for equirectangular panorama images by
adopting the recently introduced deep convolutional
neural network based super-resolution architecture
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
164

SRCNN. We investigated the different parameters of
the architecture for equirectangular panorama images
and showed how special adaptation by larger network
input layer sub-images and dedicated fine-tuning im-
prove the results as compared to the baseline (bicubic
interpolation) and also to the original SRCNN. In our
future work we will develop novel VR applications of
image super-resolution.
REFERENCES
Btz, M., Koloda, J., Eichenseer, A., and Kaup, A. (2016).
Multi-image super-resolution using a locally adaptive
denoising-based refinement. In 2016 IEEE 18th Inter-
national Workshop on Multimedia Signal Processing
(MMSP), pages 1–6.
Chen, J., He, X., Chen, H., Teng, Q., and Qing, L. (2016).
Single image super-resolution based on deep learning
and gradient transformation. In 2016 IEEE 13th In-
ternational Conference on Signal Processing (ICSP),
pages 663–667.
Cheng, P., Qiu, Y., Wang, X., and Zhao, K. (2017). A new
single image super-resolution method based on the in-
finite mixture model. IEEE Access, 5:2228–2240.
Cui, Z., Chang, H., Shan, S., Zhong, B., and Chen, X.
(2014). Image super-resolution as sparse representa-
tion of raw image patches. In 2014 Computer Vision-
ECCV, pages 49–64.
Dong, C., Loy, C., He, K., and Tang, X. (2016). Image
super-resolution using deep convolutional networks.
IEEE Trans. on PAMI, 38(2).
Freeman, W. T., Jones, T. R., and Pasztor, E. C. (2002).
Example-based super-resolution. IEEE Computer
Graphics and Applications, 22(2):56–65.
Hung, K.-W. and Siu, W. C. (2009). New motion com-
pensation model via frequency classification for fast
video super-resolution. In 2009 16th IEEE Interna-
tional Conference on Image Processing (ICIP), pages
1193–1196.
Ji, X., Lu, Y., and Guo, L. (2016). Image super-resolution
with deep convolutional neural network. In 2016
IEEE First International Conference on Data Science
in Cyberspace (DSC), pages 626–630.
Kim, J., Lee, J. K., and Lee, K. M. (2016). Accurate image
super-resolution using very deep convolutional net-
works. In 2016 IEEE Conference on Computer Vision
and Pattern Recognition (CVPR), pages 1646–1654.
Quijas, J. and Fuentes, O. (2014). Removing jpeg block-
ing artifacts using machine learning. In 2014 South-
west Symposium on Image Analysis and Interpreta-
tion, pages 77–80.
Schulter, S., Leistner, C., and Bischof, H. (2015). Fast
and accurate image upscaling with super-resolution
forests. In 2015 IEEE Conference on Computer Vision
and Pattern Recognition (CVPR), pages 3791–3799.
Shi, W., Caballero, J., Huszr, F., Totz, J., Aitken, A. P.,
Bishop, R., Rueckert, D., and Wang, Z. (2016). Real-
time single image and video super-resolution using an
efficient sub-pixel convolutional neural network. In
2016 IEEE Conference on Computer Vision and Pat-
tern Recognition (CVPR), pages 1874–1883.
Siu, W. C. and Hung, K. W. (2012). Review of image inter-
polation and super-resolution. In Proceedings of The
2012 Asia Pacific Signal and Information Processing
Association Annual Summit and Conference, pages 1–
10.
Tang, Y. and Chen, H. (2013). Matrix-value regression for
single-image super-resolution. In 2013 International
Conference on Wavelet Analysis and Pattern Recogni-
tion, pages 215–220.
Timofte, R., De, V., and Gool, L. V. (2013). An-
chored neighborhood regression for fast example-
based super-resolution. In 2013 IEEE International
Conference on Computer Vision, pages 1920–1927.
Tsurusaki, H., Kameda, M., and Ardiansyah, P. O. D.
(2016). Single image super-resolution based on total
variation regularization with gaussian noise. In 2016
Picture Coding Symposium (PCS), pages 1–5.
Yang, C.-Y., Ma, C., and Yang, M.-H. (2014). Single-
Image Super-Resolution: A Benchmark, pages 372–
386. Springer International Publishing, Cham.
Yang, J., Wright, J., Huang, T., and Ma, Y. (2008). Image
super-resolution as sparse representation of raw im-
age patches. In 2008 IEEE Conference on Computer
Vision and Pattern Recognition, pages 1–8.
Youm, G. Y., Bae, S. H., and Kim, M. (2016). Image super-
resolution based on convolution neural networks us-
ing multi-channel input. In 2016 IEEE 12th Image,
Video, and Multidimensional Signal Processing Work-
shop (IVMSP), pages 1–5.
Zhou, F., Yang, W., and Liao, Q. (2012). Interpolation-
based image super-resolution using multisurface fit-
ting. IEEE Transactions on Image Processing,
21(7):3312–3318.
360 Panorama Super-resolution using Deep Convolutional Networks
165
