
Slice-based Visualization of Brain Fiber Bundles
A LIC-based Approach
Stefan Philips
1
, Mario Hlawitschka
2
and Gerik Scheuermann
1
1
Leipzig University, Image and Signal Processing Group, Leipzig, Germany
2
Leipzig University of Applied Sciences, Faculty of Computer Science, Mathematics and Natural Sciences, Leipzig,
Germany
Keywords:
Fiber Bundles Visualization, Slice, MRI, dw-MRI, Tractography, Visualization, 2D.
Abstract:
The reconstruction of brain fibers from diffusion MRI data is a widely studied field. There is a great variety
of algorithms to generate fiber tracts. Despite the many possibilities to create fiber tractograms, it is not
very common within the medical community to make use of them. We think there are two reasons why the
acceptance of this technique is so low. The first reason is that most time the degree of detail provided by
singular fibers is neither justified nor needed. Second, within the medical domain tractography visualization
is still uncommon. To solve the first problem it is common to apply clustering algorithms which aggregate the
single fibers to fiber bundles. In this paper, we display the fiber bundles within slices. The presentation within
slices is common within the medical community and very intuitive to examine. Furthermore, our visualization
allows the spatial assignment of fiber bundles to the brain structure provided as T1 images. Among many
neuroscientists and physicians, T1 images are the main source for spatial orientation within the brain.
1 INTRODUCTION
Diffusion-weighted magnetic resonance imaging
(dw-MRI) is the only data source to reconstruct the
neuronal connections of a living brain. A dw-MR
image stores for each voxel the hydrogen diffusion
profile. Brain fibers/axons are ensheathed by myelin,
which is about 40 % water. Therefore the orientations
of the axons influence the hydrogen diffusion profiles.
Hence, it is possible to reconstruct nerve fibers from
dw-MR images with tractography algorithms.
The dw-MR images are differentiated by their an-
gular resolution. The most commonly used diffusion
tensor images (DTI) with at least six measurements in
different directions allows it to derive one main diffu-
sion direction. The use of high angular resolution data
imaging (HARDI) with more measurements in, e.g.
60, different directions makes it possible to compute
a more realistic and detailed model of the diffusion
profile per voxel. With the help of HARDI it is pos-
sible to extract several prominent diffusion directions
per voxel.
The diffusion characteristic can be described by
the diffusion orientation distribution function (ODF).
The diffusion ODF is the marginal probability of dif-
fusion in a given direction, which is computed for
each voxel. Tuch 2004 introduced the diffusion ODF
for dw-MRI. For our method, we use the improved
variant of Aganj et al. 2010.
For a better comprehension of the remaining text
we define the terms brain fiber, fiber and fiber bundle:
Brain Fiber: the actual biological
Fiber: a trajectory reconstructed from the dw-MR
data using a tractography algorithm
Fiber Bundle: a set of anatomically similar fibers
Especially the differentiation between a brain
fiber and a fiber, which is reconstructed, is impor-
tant. One has to be aware that a 7 T Scanner has a
maximal voxel resolution of 1 mm edge length and
a typical axon has a diameter of 1 µm. Consider-
ing this, ten thousands of axons can run through one
voxel. With this in mind, one has to think of a recon-
structed fiber as a representative for many real brain
fibers. Since a reconstructed fiber is already a sim-
plification, it makes sense for many use cases sense
to reduce the data even more. This leads to the next
logical step: the clustering of the reconstructed fibers
by similarity. This clustering is done by fiber bun-
dle algorithms, which typically use geometric shape
and position of the fibers to measure similarity. The
similarity, in turn, is used to group the fibers. These
groups are the fiber bundles.
Philips, S., Hlawitschka, M. and Scheuermann, G.
Slice-based Visualization of Brain Fiber Bundles - A LIC-based Approach.
DOI: 10.5220/0006619402810288
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages
281-288
ISBN: 978-989-758-289-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
281

The awareness of the structural brain connectivity
should be very helpful for clinical and scientific ap-
pliances as well. But despite the fiber tractography
algorithms are well explored, the acceptance within
the medical community, especially in the clinical en-
vironment, is low.
(Hlawitschka et al., 2013) mentions the feedback
from neuroscience experts for slice-based methods is
very positive. The preference for slice-based visual-
izations among these experts has the following rea-
sons:
• A simple but undeniable fact is the familiarity
of neuroscientists and physicians with the slice-
based data presentation. Slices allow them to ex-
plore and focus the data in a familiar way.
• Especially during the exploration of brain related
data, the anatomical context is a very important
asset. This can be achieved by combining a sparse
slice visualization with anatomical image slices,
e.g. T1 images.
• Slice-based techniques avoid occlusions.
• Medical documentation is often done in 2D.
Further Munzner 2014 gives a comprehensive
overview of possible disadvantages resulting from 3D
visualizations.
In this work, we introduce a visualization tech-
nique that has all the aforementioned advantages.
Furthermore, our visualization works for difficult
fiber configurations, like kissing or crossing fibers,
and it can be used in combination with 3D fiber vi-
sualizations.
2 RELATED WORK
Our visualization approach relies on two kinds of pre-
processing algorithms. It needs a fiber tracking and a
fiber clustering algorithm.
There are a multitude of different fiber tracking
algorithms. Behrens et al. 2014 give an overview of
all three types of tractography algorithms. (Fillard
et al., 2011) benchmarks different approaches. Prob-
abilistic tractography algorithms are a special type of
fiber tracking algorithm, which do not generate 3D
trajectories as fibers. Briefly explained: Probabilistic
tractography algorithms compute for each voxel of a
dataset the connection likeliness to a seed voxels.
The trajectories of the aforementioned tractogra-
phy algorithms can be clustered by a fiber clustering
algorithm. Also for this task exists several algorithms.
The visualization of tractograms as 3D polylines
is a competing and complementing approach to our
technique as well. Therefore subsection 2.1 refers to
work that displays fibers as 3D polylines.
In the last subsection, we present alternative slice-
based dMRI-related visualization techniques. This
overview of alternative techniques allows us to com-
pare our method to them.
2.1 Visualization of 3D Trajectories as
Polylines
The visualization of 3D trajectories has many appli-
cations and is therefore thematized by several pub-
lications which are not specifically related to recon-
structed brain fibers, e.g. Zöckler et al. 1996 or Mallo
et al. 2005.
Eichelbaum et al. 2013 addressed the problem
of the spatial and the structural perception of recon-
structed brain fibers to each other. With their LineAO
approach, they contributed an algorithm to display
fibers with better spatial and structural perception.
2.2 Slice-based Visualization
Approaches
There already exist different approaches to visualize
reconstructed brain fiber data in a slice based manner.
Goldau et al. 2011 introduced a technique to vi-
sualize probabilistic tractograms slice-wise. This ap-
proach was improved regarding the perception of
tract probability by Hlawitschka et al. 2013. Lately
Reichenbach et al. 2015b adapted the approach to
HARDI data, that means they were able to illus-
trate possible kissing or crossing tracts of probabilis-
tic tractograms.
Höller et al. 2012 proposed a slice-based tech-
nique which is based on a three-dimensional LIC. The
necessary directions for the LIC is gained by extract-
ing up to two maxima from the diffusion ODFs. The
directions of the corresponding first maxima are used
to apply a color coding to the LIC results. Höller et
al. 2014 modify their slice visualization approach by
replacing the input noise for the LIC algorithm with
an image of diffusion glyphs.
Calamante et al. 2011 introduced track-density
imaging (TDI). This technique counts the fibers cross-
ing each voxel of a high resolution grid, allowing
more insight into the white matter structure. Color
coding can visualize the diffusion direction.
3 METHOD
In this section we introduce our slice-wise visualiza-
tion of fiber bundles. In combination with a T1 image
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
282
as an anatomical context, this allows a clear assign-
ment of fiber bundles to the brain anatomy. These
fiber bundles shall be distinguishable and traceable
within the slice. We start by explaining the necessary
preprocessing steps – fiber tracking and fiber cluster-
ing. After that, we provide the detailed steps of our
approach to achieve the aforementioned visualization.
This includes:
• the creation of direction images for each bundle
• the creation of a noise texture, that allows the
blending of the fiber bundle LIC-images
• the blending of the LIC-images
3.1 Preprocessing
The basic data input for our visualization method is a
diffusion MRI dataset. Based on this data, our visu-
alization method needs two preprocessing algorithms,
the fiber tractography algorithm, and an algorithm to
cluster the created fibers by similarity. The depen-
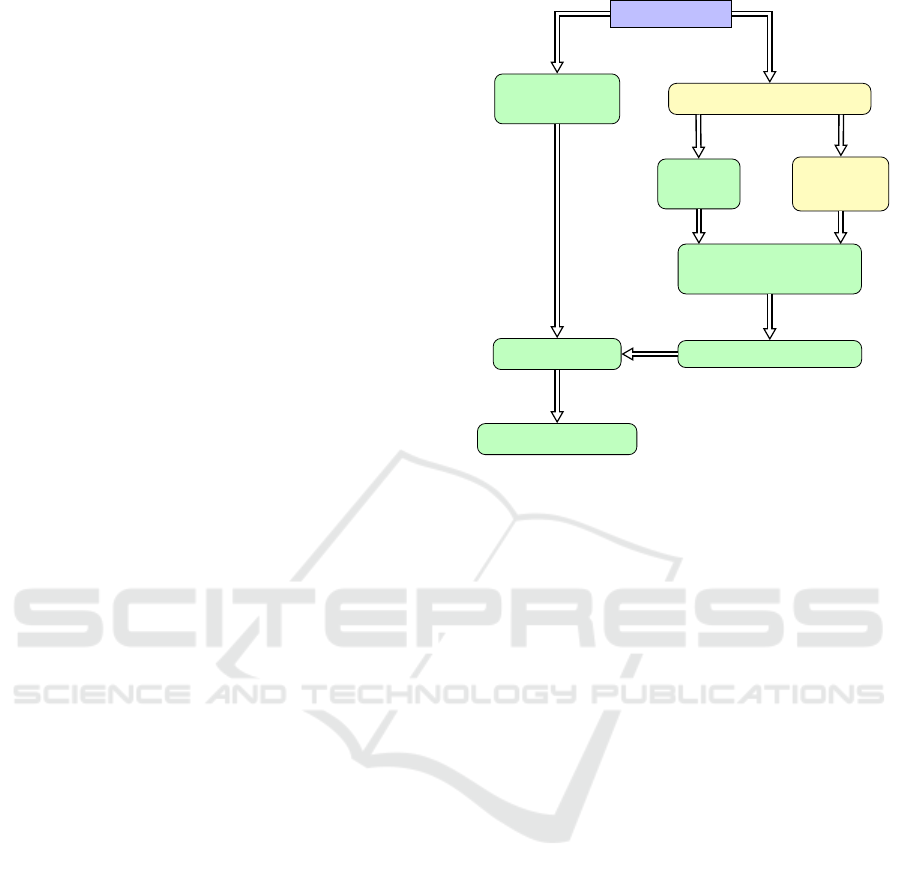
dence of our processes is shown in Figure 1, where
the preprocessing algorithms are marked yellow.
For both steps, tracking and clustering exist a
bunch of algorithms. Behrens et al. 2014 give an
overview of tractography algorithms and the work by
Fillard et al. 2011 compares several fiber tracking al-
gorithms. (Reichenbach et al., 2015a) compare their
fiber clustering approach to four other techniques.
The preprocessing for our visualization starts with
a given diffusion MRI dataset. This is used to cre-
ate a fiber tractogram with a tracking algorithm. This
tractogram is then clustered by a fiber clustering ap-
proach. The preprocessing data-flow is illustrated in
Figure 1.
3.2 Processing
Once the preprocessing is done, three types of data
are available for our visualization method. These are
the dMRI dataset, the tractography and the clustering
of the fibers. The process flow can be seen in Fig-
ure 1, where the actual visualization processes of our
method are marked green.
The overall bundle-slice creation process of the
bundle slices can be outlined the following four steps:
1. Create 2D direction images
(a) Voxelize Fibers:
calculate for each fiber which voxels it crosses
(b) Median bundle direction for each voxel:
calculate for each voxel the median direction
from all fiber of a bundle
(c) Extract 2D-Directions:
create for each bundle per voxel the direction
dMRI dataset
Tractography algorithm
Voxelize
Fibers
Fiber
Clustering
Median bundle direc-
tion for each voxel
Extract 2D directions
Create Glyph
Noise Texture
LIC algorithm
Blend LIC images
Figure 1: Data-flow during the processing. The colors pur-
ple, yellow or green mark if the boxes represent data, pre-
processing or processing steps, respectively.
2. Create Glyph Noise Texture:
create a noise texture for the LIC algorithm using
HARDI glyphs
3. LIC algorithm:
compute a LIC image for each fiber bundle of the
slice by using the 2D directions images from step
1 and the noise image from step 2
4. Blend LIC images:
combine the different LIC images into one image
3.2.1 Create 2D Directions Image
Voxelize Fibers
input: fiber tractography, fiber clustering
output: voxels with directions with annotated fiber
cluster number
We calculate for each fiber which voxel it passes and
store in each crossed voxel the local fiber direction.
Currently, the resolution of the voxelized fibers is de-
termined by the input dMRI dataset.
In detail the voxelization algorithm works as fol-
low: The algorithm walks along the fiber points and
processes two consecutive points after another. To
determine which voxels are crossed by a fiber seg-
ment between two consecutive points p
i
and p
j
, we
use the rasterization algorithm Glassner (1990) which
is based on the Bresenham algorithm 1965. The seg-
ment direction, annotated with the fiber cluster num-
ber of the currently processed fiber, is stored in every
Slice-based Visualization of Brain Fiber Bundles - A LIC-based Approach
283

voxel that is determined by the aforementioned raster-
ization algorithm.
The result of this process are sets of directions
B
1
, B
2
, B
3
, . . . in each voxel. These sets group the di-
rections, which are derived from the fibers, to the dif-
ferent fiber bundles.
Bundle Median Direction for Each Voxel
input: voxels with directions with annotated fiber
cluster number
output: representative 3D direction for each fiber
bundle for each crossed voxel
Now that we have the sets of directions B
1
, B
2
, B
3
, . . .
in each voxel with B
i
= {d
i1
, d
i2
, d
i3
, . . .}, we need to
derive one representative direction for each set. Let
B
i
be one of these sets. We find the spatial median di-
rection d
i,med
∈ B
i
according to the following formula
d
i,med
= argmin
d∈B
i
n
∑
j=1
^(d
i j
, d), (1)
where ^(a, b) is the angle between the directions a
and b.
Extract 2D Directions
input: representative 3D direction for each fiber bun-
dle for each crossed voxel
output: 2D vector images for each visualized bundle
For each fiber bundle, that crosses the current slice, a
2D vector image needs to be created. We obtain the
2D direction d
2D
of the fiber bundle i by mapping the
3D direction d
3D
∈ B
i
to the slice plane. Given that our
slices are aligned to the XY-, XZ- or YZ-plane, this
can be done by taking the respective values of the 3D
vector. For example the 3D direction d
3D
= (x, y, z)
T
mapped to the XY-plane leads to d
2D
= (x, y)
T
.
3.2.2 Noise Image
The original LIC algorithm was proposed by Cabral
and Leedom 1993 and uses two images as input: a
2D vector image and a noise image. The creation of
the 2D vector image is described in the previous para-
graph. Usually an image with white noise is as an
input for the LIC-algorithm.
Glyph-based Noise Image
input: dMRI dataset
output: 2D gray scale image with glyphs
Höller et al. 2014 use samples of fiber-orientation-
density (FOD) glyphs to generate a noise image for
the LIC. The fiber orientations for the FOD glyphs are
computed by using spherical deconvolution (Tournier
et al., 2004) on the HARDI input. Then the glyph
samples are placed along a path which results from a
deterministic tracking within the slice.
For our visualization we use like Höller et al. 2014
a from glyphs generated noise image. For our goal to
display clustered fibers within slices, we cannot use
this a deterministic tracking algorithm. The determin-
istic tracking would most likely differ from the fibers
to display and would be computational expensive.
Therefore we had to find a good placement
scheme for the glyphs within the noise image. At a
first glance the well-known glyph packing strategy by
Kindlmann and Westin 2006 seems a suitable choice
for the glyph placement problem, but it is designed
for DTI Glyphs and would have to be extended for
HARDI glyphs. Even if an extended variant would
be available, it would be unnecessary complex for the
actual task. In our case, the potential overlapping of
some glyphs within the noise image is not problem-
atic at all.
We tested three glyph placement strategies. The
first one is a simple two-dimensional regular place-
ment. The second variant distributes the glyphs uni-
form randomly within the slice. And the third variant
uses Poisson-disk distribution to distribute the glyphs
within the slice.
Points of a Poisson-disk distribution are ran-
domly distributed and must be no closer than a spec-
ified value. To create this distribution we used
the sampling algorithm proposed by Dunbar and
Humphreys 2006. Our concrete implementation com-
putes points within the 2D-range of [0..1] × [0..1].
These coordinates are scaled to the full image size.
Figure 2 shows examples for the different glyph
distributions. In Figure 2a one can see that the regu-
lar distribution pattern causes a regular pattern in the
result image. The uniform random distribution causes
a wild pattern in the resulting image, Figure 2b. The
Poisson-disk distribution results in straight lines, Fig-
ure 2c.
The actual glyphs are created as follows: A icosa-
hedron is tessellated with triangles to a certain degree.
Then the normalized triangle vertex coordinates are
used as input for the spherical harmonic function of
the ODF. The resulting values describe the surface of
the spherical function. This results in spherical har-
monics glyphs like shown in Figure 3. The tessel-
lation degree for these example glyphs is 2, which
means each consists of 162 vertices. The coloring is
done by using the absolute values of the normalized
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
284

(a) Regular glyph distribution
Left: Noise image with regularly placed glyphs.
Right: The resulting visualization for regulary placed glyphs.
(b) Uniform random glyph distribution
Left: Noise image with uniform randomly placed glyphs.
Right: The resulting visualization for uniform randomly
placed glyphs.
(c) Poisson-disk glyph distribution
Left: Noise image with Poisson-disk distributed glyphs.
Right: The resulting visualization for Poisson-disk dis-
tributed glyphs.
Figure 2: Different glyph distributions and the correspond-
ing result of the algorithm.
Euclidean direction as RGB color.
3.2.3 Special Case: Orthogonal Bundles
Fiber bundles which run orthogonal or almost orthog-
onal to the displayed slice would not be visualized in a
reasonable way by the LIC-method. This results from
the fact that there is not enough directional informa-
tion for this bundles within the slice.
Therefore we determine the orthogonal bundles
and display them by coloring their slice area with their
Figure 3: Spherical harmonics glyphs composited from 162
vertices. The absolute values of the Euclidean direction vec-
tors are used as RGB color vector (RGB coloring).
transparent cluster color (alpha value 0.5). Which
fiber bundles are considered to be orthogonal bundles
is determined by the percentage of the average bundle
direction-vector-component that is orthogonal to the
current slice.
3.2.4 LIC Process and Coloring
input: direction image for each bundle that crosses
the current slice and the glyph noise image
output: a LIC image for each bundle that crosses that
crosses the current slice
The LIC implementation is the original algorithm like
it was proposed by Cabral and Leedom 1993, but of
course it uses the adapted noise image. The coloring
is done bundle-wise, apart from that the actual color
of each fiber bundle can be arbitrary selected. For ex-
ample one can use RGB direction coloring, selection
coloring or any other bundle-wise coloring.
3.2.5 Blending the Bundle Layers
input: a LIC image for each bundle that crosses the
current slice
output: final slice
After the LIC algorithm is done for every bundle. It
is necessary to merge the output of all LIC processes
into one image. This is done by drawing one LIC im-
age after another into the space left by the previous
LIC images. A pixel with RGB color c is considered
free if kck
max
< 0.2 is true. The blending order is de-
termined by the size of the bundles within the slice.
The blending process starts with the LIC image of
the smallest bundle. This should ensure the maximum
visibility of the fiber bundles in the slice.
4 RESULTS
We tested our visualization with two datasets. The
first one is the synthetic Fiber Cup phantom dataset
(Fillard et al., 2011). The Fiber Cup dataset is a
dw-MRI scan of a hardware phantom. It was orig-
inally created to test tractography algorithms. We
Slice-based Visualization of Brain Fiber Bundles - A LIC-based Approach
285

Table 1: Properties of the datasets to test the visualization.
Dataset Fiber Cup Human brain
voxel size (mm
3
) 3 × 3 × 3 1.7 × 1.7 × 1.7
dimensions 64 × 64 × 3 128 × 128 × 72
diffusion directions 128 60
choose this one because of its clear structure and the
known ground truth. It has typical difficult fiber bun-
dle configurations like kissing, crossing and spread-
ing fiber bundles. The second one is a dw-MR im-
age of a healthy human brain. It was acquired with
a 3 T Siemens Trio MRI scanner using single echo
spin echo Echo-Planar Imaging (EPI) sequence with
GRAPPA on a 32 channel coil. Table 1 shows the
image properties of both datasets.
4.1 Fiber Cup Dataset
Figure 4a shows the whole dataset using our visual-
ization. The planar shape and the different fiber bun-
dle configurations make the Fiber Cup dataset ideal
to demonstrate slice based visualization approaches.
Since we know the ground truth of the Fiber Cup
dataset we reduced it by removing identified out-
liers to 250 fibers. The fibers were generated with
the streamline tractography algorithm by Lazar et
al. 2003 using the implementation from tensor toolkit
1.4
1
. Except for FA
1
= 0.2 and FA
2
= 0.3 we used
the default parameter. We used the QuickBundles
(Garyfallidis et al., 2012) algorithm to cluster the trac-
tograms. Heuristically we determined the parameter
θ = 225 to get a clustering close to the known ground
truth of 7 fiber bundles.
For the visualization example in Figure 4a we
used a Poisson-disk radius of 0.0045, a glyph size
of 0.4 and 30 LIC steps at maximum. The separate
fiber bundles are clearly identifiable and the course at
crossings is also traceable. The close-ups of cross-
ings in Figure 4b and 4c show that the bundles are
clearly differentiable The image shows also a disad-
vantage of the current implementation: Due to the low
resolution of the voxelized fibers, the displayed fiber
bundles overlap the white matter. The low resolution
is also the reason for the raw block shape of the dis-
played fibers.
4.2 Human Brain Dataset
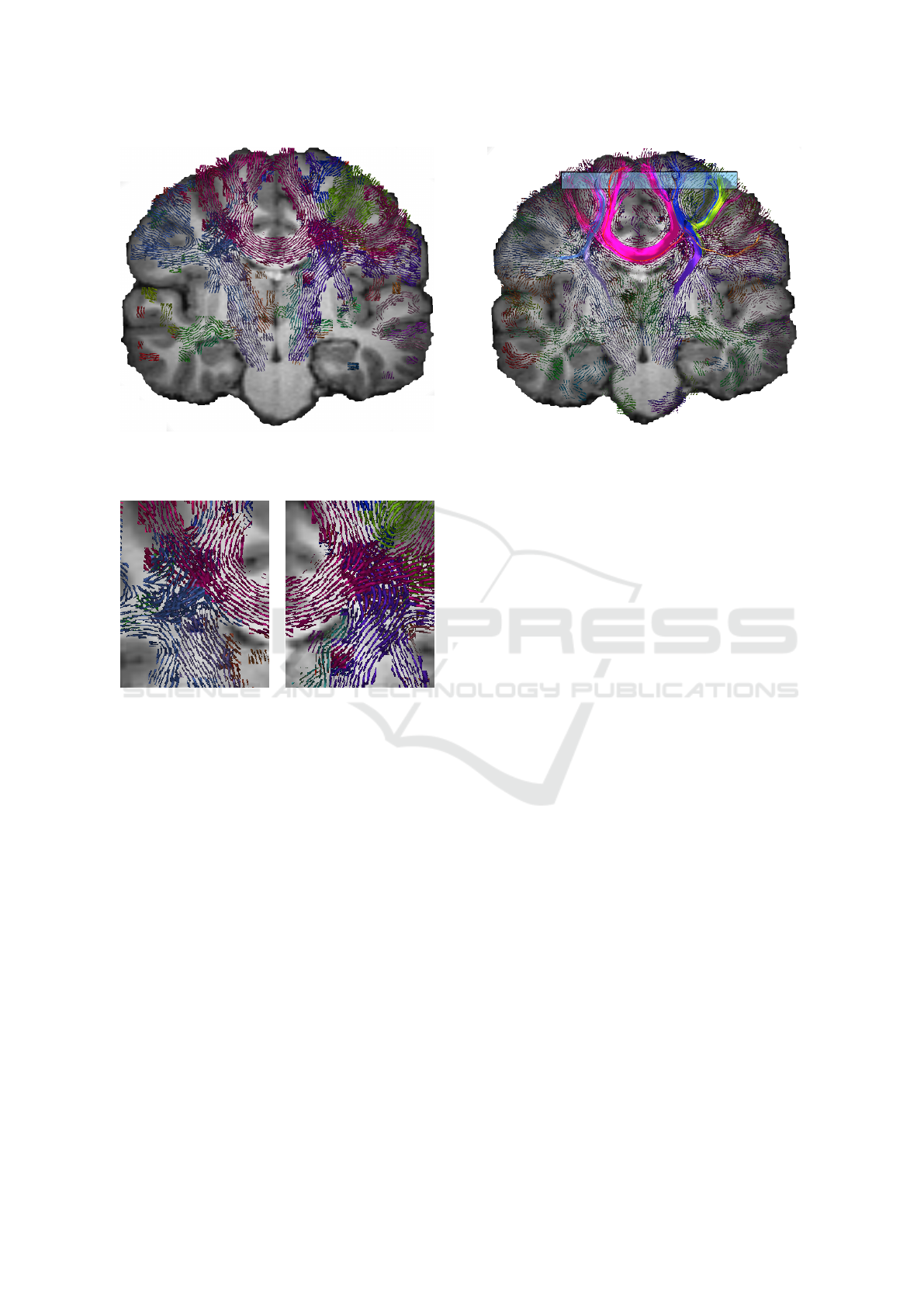
The dataset of a healthy human brain allows us to
show a real world example. Figure 5a visualizes a
frontal view of a coronal slice. We used the determin-
istic spherical-deconvolution (SD) (Tournier et al.,
1
https://gforge.inria.fr/projects/ttk
(a) Visualization for the fibercup dataset bundles.
(b) Detail of the crossing
in the upper-right area.
(c) Detail of the crossing in
the bottom-middle area.
Figure 4: The presented algorithm applied to the Fiber Cup
dataset, including three detail views.
2004) based fiber tracking algorithm from MRtrix
2
with its default parameters. The clustering was done
with the approach by Reichenbach et al. 2015a. For
the visualization, we used the same parameter as be-
fore, a Poisson-disk radius of 0.0045, a glyph size of
0.4 and 30 LIC steps at maximum. We selected a slice
where the corticospinal tracts (CST, blue) and the cor-
pus callosum (CC, red) cross. The detail views of the
crossings in the left and right hemisphere are shown
in Figure 5c and 5b, respectively. The corticospinal
tract is traceable crossing the corpus callosum.
Figure 6 shows the LineAO approach by Eichel-
baum et al. 2013 and our slice-based visualization
combined. To select the displayed 3D trajectories,
we used a Region-of-Interest (ROI) box. By using
this combination, the user can benefit from the advan-
tages of 2D and 3D visualization. Whereas the 3D
trajectories provide a good overview, the strength of
2
http://jdtournier.github.io/mrtrix-
0.2/tractography/tracking.html
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
286
(a) Visualization for a coronal slice. Showing among
other fiber bundles the corpus callossum (CC, red) and
the cortico spinal tract (CST, blue.)
(b) Crossing of CC (red)
and CST (blue) in the right
hemisphere.
(c) Crossing of CC (red)
and CST (blue) in the left
hemisphere.
Figure 5: Visualization of Coronal slice and two detail
views. Orthogonal fiber bundles are suppressed.
our approach is the fast view into spatial details, with-
out using a ROI box and the clear perception of the
anatomical context, represented as T1 image.
4.3 Comparison to Existing
Visualizations
Depending on the application the presented method
has advantages over the previously mentioned visual-
ization approaches.
In contrast to 3D polylines, a slice based fiber
bundle visualization allows the easy assignment to an
anatomical context by using T1 images. Besides the
slice-wise view to medical data is well-established.
Given that slice-based methods are two-dimensional,
they are suitable for clinical documentation purposes.
The advantage of the presented method over the
Figure 6: The combination of 3D streamline and slice-based
visualization.
approach by Höller et al. 2014 is the use of recon-
structed tractograms. Höller et al. 2014 perform an
own tracking for their visualization. This tracking is
reduced to the currently displayed slice. Because of
this locality, it does not cover the complex task of fiber
reconstruction from diffusion MRI data. The com-
parison of fiber tractography algorithms by Fillard et
al. 2011 suggests that especially the use of global in-
formation is advisable. The presented method can use
many available fiber tractography algorithms. The in-
formation complexity of the reconstructed fiber con-
figurations is further decreased by the use of a fiber
bundle algorithm.
The method by Reichenbach et al. 2015b is spe-
cialized for probabilistic tractograms. The adaptation
to general fiber tractograms would be possible, but the
visualization of deterministic fiber tractograms in a
glyph-based manner is counter-intuitive and increases
unnecessarily the visual complexity.
The aforementioned TDI approach (Calamante
et al., 2011) generates a super-resolution T1-like im-
age from a tractogram. TDI does not aim to visualize
concrete fibers or fiber bundles.
5 SUMMARY
We presented a new visualization approach that al-
lows a slice-wise examination of fiber bundles. This
slice-wise inspection has several useful properties and
is intended as a supplement to conventional 3D trajec-
tory visualization of fiber bundles. The combination
of this visualization techniques is shown in Figure 6.
Further, the slice-wise presentation allows a clear
assignment of the fiber bundles to the structural infor-
Slice-based Visualization of Brain Fiber Bundles - A LIC-based Approach
287

mation provided by a T1 image. Many neuroscien-
tists use the structural information provided by a T1
image as spatial orientation. The familiarity of medi-
cal staff with slice-based data can also be considered
as an advantage of the method. Furthermore, a 2D vi-
sualization is well suited for medical documentation.
Another inherent advantage of a 2D approach is the
avoidance of occlusion.
We have shown that the visualization works also
for difficult fiber bundle configurations like crossings,
see the Figures 5b, 5c, 4b, and 4c. The visibility of
the relation between the fiber bundles and anatomy
is a strength of the visualization method, too. The
Figures 4a and 5a allow it to relate the fiber bundle to
structural information given by T1 image.
REFERENCES
Aganj, I., Lenglet, C., Sapiro, G., Yacoub, E., Ugurbil, K.
and Harel, N. (2010). Reconstruction of the orientation
distribution function in single-and multiple-shell q-ball
imaging within constant solid angle. Magnetic Reso-
nance in Medicine 64, 554–566.
Behrens, T. E., Sotiropoulos, S. N. and Jbabdi, S. (2014).
MR Diffusion Tractography. In Diffusion MRI - Sec-
ond Edition, (Johansen-Berg, H. and Behrens, T. E., eds),
chapter 19, pp. 429–451. Elsevier Inc. London.
Bresenham, J. E. (1965). Algorithm for computer control
of a digital plotter. IBM Systems journal 4, 25–30.
Cabral, B. and Leedom, L. C. (1993). Imaging Vector
Fields Using Line Integral Convolution. In Proceed-
ings of the 20th Annual Conference on Computer Graph-
ics and Interactive Techniques SIGGRAPH ’93 pp. 263–
270, ACM, New York, NY, USA.
Calamante, F., Tournier, J.-D., Heidemann, R. M., Anwan-
der, A., Jackson, G. D. and Connelly, A. (2011). Track
density imaging (TDI): validation of super resolution
property. Neuroimage 56, 1259–1266.
Dunbar, D. and Humphreys, G. (2006). A Spatial Data
Structure for Fast Poisson-disk Sample Generation. In
ACM SIGGRAPH 2006 Papers SIGGRAPH ’06 pp.
503–508, ACM, New York, NY, USA.
Eichelbaum, S., Hlawitschka, M. and Scheuermann, G.
(2013). LineAO — Improved Three-Dimensional Line
Rendering. IEEE TVCG 19, 433–445.
Fillard, P., Descoteaux, M., Goh, A., Gouttard, S., Jeuris-
sen, B., Malcolm, J., Ramirez-Manzanares, A., Reisert,
M., Sakaie, K., Tensaouti, F., Yo, T., Mangin, J.-F. and
Poupon, C. (2011). Quantitative evaluation of 10 tractog-
raphy algorithms on a realistic diffusion MR phantom.
NeuroImage 56, 220 – 234.
Garyfallidis, E., Brett, M., Correia, M. M., Williams, G. B.
and Nimmo-Smith, I. (2012). Quickbundles, a method
for tractography simplification. Frontiers in neuroscience
6, 175.
Glassner, A. (1990). Graphics Gems I.
Goldau, M., Wiebel, A., Gorbach, N. S., Melzer, C.,
Hlawitschka, M., Scheuermann, G. and Tittgemeyer, M.
(2011). Fiber Stippling: An Illustrative Rendering for
Probabilistic Diffusion Tractography. In IEEE BioVis
Proceedings pp. 23–30, IEEE.
Hlawitschka, M., Goldau, M., Wiebel, A., Heine, C. and
Scheuermann, G. (2013). Hierarchical Poisson-Disk
Sampling for Fiber Stipples. In 3rd Intl. Workshop on
VMLS pp. 19–23, Eurographics, Leipzig.
Höller, M., Otto, K. M., Klose, U., Groeschel, S. and
Ehricke, H. H. (2014). Fiber Visualization with LIC
Maps Using Multidirectional Anisotropic Glyph Sam-
ples. Journal of Biomedical Imaging 2014, 9:9–9:9.
Höller, M., Thiel, F., Otto, K.-M., Klose, U., Ehricke,
H.-H. and Schwedenschnaze, Z. (2012). Visualization
of High Angular Resolution Diffusion MRI Data with
Color-Coded LIC-Maps. In GI-Jahrestagung pp. 1112–
1124, GI.
Kindlmann, G. and Westin, C.-F. (2006). Diffusion tensor
visualization with glyph packing. IEEE Transactions on
Visualization and Computer Graphics 12.
Lazar, M., Weinstein, D. M., Tsuruda, J. S., Hasan, K. M.,
Arfanakis, K., Meyerand, M. E., Badie, B., Rowley,
H. A., Haughton, V., Field, A. et al. (2003). White matter
tractography using diffusion tensor deflection. Human
brain mapping 18, 306–321.
Mallo, O., Peikert, R., Sigg, C. and Sadlo, F. (2005). Illu-
minated lines revisited. In VIS 05. IEEE Visualization,
2005. pp. 19–26, IEEE.
Munzner, T. (2014). Visualization analysis and design.
CRC press.
Reichenbach, A., Goldau, M., Heine, C. and Hlawitschka,
M. (2015a). V-Bundles: Clustering Fiber Trajectories
from Diffusion MRI in Linear Time. In MICCAI (1),
(Navab, N., Hornegger, J., III, W. M. W. and Frangi,
A. F., eds), vol. 9349, of LNCS pp. 191–198, Springer.
Reichenbach, A., Goldau, M. and Hlawitschka, M. (2015b).
Fiber Stipples for Crossing Tracts in Probabilistic Trac-
tography. In Proc. of VCMB ’15 pp. 113–122, EG.
Tournier, J.-D., Calamante, F., Gadian, D. G. and Connelly,
A. (2004). Direct estimation of the fiber orientation den-
sity function from diffusion-weighted MRI data using
spherical deconvolution. NeuroImage 23, 1176–1185.
Tuch, D. S. (2004). Q-ball imaging. Magnetic resonance in
medicine 52, 1358–1372.
Zockler, M., Stalling, D. and Hege, H.-C. (1996). Interac-
tive visualization of 3D-vector fields using illuminated
stream lines. In Visualization’96. Proc. pp. 107–113,
IEEE.
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
288
