Subtle Motion Analysis and Spotting using the Riesz Pyramid

Carlos Andres Arango, Olivier Alata, R

emi Emonet, Anne-Claire Legrand and Hubert Konik

Univ. Lyon, UJM-Saint-Etienne, CNRS, Institut d Optique Graduate School, Laboratoire Hubert Curien UMR 5516,

F-42023, Saint-Etienne, France

Keywords:

Subtle Motion, Temporal Spotting, Riesz Pyramid, Quaternion Representation.

Abstract:

Analyzing and temporally spotting motions which are almost invisible to the human eye might reveal interest-

ing information about the world. However, detecting these events is difﬁcult due to their short duration and

low intensities. Taking inspiration from video magniﬁcation techniques, we design a workﬂow for analyzing

and temporally spotting subtle motions based on the Riesz pyramid. In addition, we propose a ﬁltering and

masking scheme that segments motions of interest without producing undesired artifacts or delays. In order to

be able to evaluate the spotting accuracy of our method, we introduce our own database containing videos of

subtle motions. Experiments are carried out under different types and levels of noise. Finally, we show that

our method is able to outperform other state of the art methods in this challenging task.

1 INTRODUCTION

Although the human visual system is capable of de-

tecting a plethora of objects and phenomena that

surround us it has limited spatio-temporal sensitiv-

ity. There are some movements of low-spatial am-

plitude that are difﬁcult to detect by the human eye

which might conceal interesting information about

the world (Liu et al., 2005). For instance it has been

reported that the cyclical movement of blood in the

human body causes the head to move in a subtle peri-

odic motion which has been used to calculate the heart

rate in a non invasive manner (Balakrishnan et al.,

2013)(Irani et al., 2014). For this reason motion mag-

niﬁcation techniques have been developed in order to

reveal almost invisible signals in videos. These tech-

niques have been used for modal analysis (the study

of the dynamic properties of structures under vibra-

tional excitation) (Chen et al., 2015), for enhancing

the motion of the blood ﬂow in the ﬁnger veins for

liveness detection (Raghavendra et al., 2015), to en-

hance the movement of facial expressions for anti-

spooﬁng in a face biometric system (Bharadwaj et al.,

2013), for amplifying the motion of pulsating arteries

during an endoscopic surgery (McLeod et al., 2014)

and for micro-expression recognition (Park and Kim,

2009).

The main problem with motion magniﬁcation

methods is that they exaggerate the motion on a video

rather than explicitly estimating it. However, our

careful examination showed that intermediate repre-

sentations produced by these methods can be used as

proxies for motion. Furthermore, considering that a

lot of real-life applications require to detect when an

event takes place, these representations could poten-

tially be used to temporally spot subtle events (ﬁnd-

ing the temporal locations of subtle movements from

a video sequence). Thus, we propose a method to an-

alyze and spot subtle motions in a video by analyz-

ing the phase variations between frames based on the

Riesz Pyramid. This paper is organized as follows.

Section 2 serves as an introduction to the theoreti-

cal material to understand the Riesz Pyramid outputs,

its quaternionic representation and ﬁltering. Section

3 describes our proposed methodology and contribu-

tions. Section 4 describes some potential applica-

tions, our experiments, results and discussion. Fi-

nally, section 5 presents our conclusions.

2 BACKGROUND

Eulerian motion magniﬁcation is a family of tech-

niques that ampliﬁes subtle motion in videos. They

are inspired by the Eulerian perspective, in reference

to ﬂuid dynamics where the properties of a voxel of

ﬂuid, such as pressure and velocity, evolve over time.

The ﬁrst of these techniques (Wu et al., 2012) exag-

gerates motion by amplifying temporal color changes

at ﬁxed positions. However, this method can signif-

446

Arango, C., Alata, O., Emonet, R., Legrand, A-C. and Konik, H.

Subtle Motion Analysis and Spotting using the Riesz Pyramid.

DOI: 10.5220/0006620004460454

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

446-454

ISBN: 978-989-758-290-5

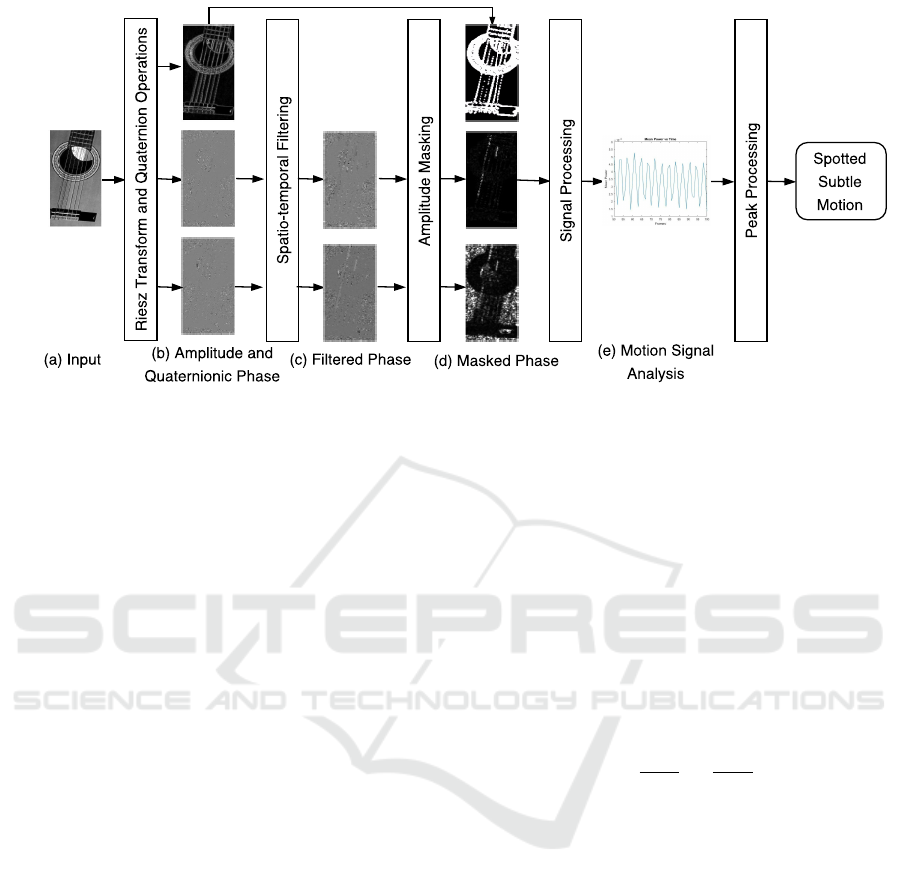
Figure 1: Subtle motion analysis framework. Each frame from an input video (a) is processed with the Riesz Pyramid to

obtain the local amplitude and the quaternionic phase (b). We apply an improved spatio-temporal ﬁlter to the quaternionic

phase (c). Then we use local amplitude to mask relevant areas in the quaternionic phase (d). The phase is processed into a

1-D signal (e) and we detect and classify the resulting peaks to spot the subtle motions.

icantly amplify noise when the magniﬁcation factor

is increased. Another method proposed by (Wadhwa

et al., 2013), ampliﬁes the phase variation over time

within each image subband using the steerable pyra-

mid (an over-complete transform that decomposes

an image according to spatial scale, orientation, and

position). However, the main disadvantage of this

method comes from the complex steerable pyramids

which are very overcomplete and costly to construct.

Later on, (Wadhwa et al., 2014a) propose a new

method based on the Riesz pyramid which produced

motion-magniﬁed videos of comparable quality to the

previous one, but the videos can be processed in one

quarter of the time, making it more suitable for real-

time or online processing applications.

Although, video magniﬁcation is a powerful tool

for magnify subtle motions in videos, it doesn’t in-

dicate the moment when these motions take place.

However, the ﬁltered quaternionic phase differ-

ence obtained during the Riesz magniﬁcation ap-

proach (Wadhwa et al., 2014b) seems to be a good

proxy of motion, thus it could potentially be used for

analyzing and temporally segmenting subtle motions.

In this section, we do an introduction to the Riesz

pyramid, its quaternionic representation and quater-

nionic ﬁltering.

2.1 Riesz Monogenic Signal

The Riesz pyramid is constructed by ﬁrst breaking the

input image into non-oriented subbands using an ef-

ﬁcient, invertible replacement for the Laplacian pyra-

mid, and then taking an approximate Riesz transform

of each band. The key insight into why this repre-

sentation can be used for motion analysis is that the

Riesz transform is a steerable Hilbert transformer and

allows us to compute a quadrature pair that is 90 de-

grees out of phase with respect to the dominant ori-

entation at every pixel. This allows us to phase-shift

and translate image features only in the direction of

the dominant orientation at every pixel.

Following (Unser et al., 2009), in two dimensions,

the Riesz transform is a pair of ﬁlters with transfer

functions

−i

−→

ω k

,−i

−→

ω k

(1)

with

−→

ω = [ω

,ω

] being the signal dimensions in the

frequency domain. If we ﬁlter a given image subband

I using Eq. 1, the result is the pair of ﬁlter responses,

). The input I and Riesz transform (R

) to-

gether form a triple (the monogenic signal) that can

be converted to spherical coordinates to yield the lo-

cal amplitude A, local orientation θ and local phase φ

using the equations

I = A cos(φ)

= A sin (φ)cos(θ)

= A sin (φ) sin(θ)

(2)

2.2 Quaternion Representation of Riesz

Pyramid

The Riesz pyramid coefﬁcient triplet (I; R

) can

be represented as a quaternion r with the original sub-

band I being the real part and the two Riesz transform

Subtle Motion Analysis and Spotting using the Riesz Pyramid

447

components (R

) being the imaginary i and j com-

ponents of the quaternion.

r = I + iR

+ jR

(3)

The previous equation can be rewritten using (4) as:

r = A cos(φ) + iAsin (φ)cos (θ) + jA sin(φ)sin (θ)

(4)

However, the decomposition proposed by (4) is not

unique. That means that both (A,φ,θ) and (A,−φ,θ +

π) are possible solutions. This can be solved if we

consider

φcos (θ),φ sin(θ) (5)

which are invariant to this sign ambiguity. If the Riesz

pyramid coefﬁcients are viewed as a quaternion, then

Eq. 5 is the quaternion logarithm of the normalized

coefﬁcient

. Thus, the local amplitude A and quater-

nionic phase deﬁned in Eq. 5 are computed:

A = krk (6)

iφcos (θ) + jφ sin (θ) = log (r/krk) (7)

2.3 Filtering of Quaternionic Phase

In previous Eulerian motion ampliﬁcation papers,

motions of interest were isolated and denoised with

temporal ﬁlters. However, the quaternionic phase

cannot be naively ﬁltered since it is a wrapped quan-

tity (Wadhwa et al., 2014b). Therefore a technique

developed in (Lee and Shin, 2002) is used to ﬁlter a

sequence of unit quaternions (by ﬁrst unwrapping the

quaternionic phases in time and then using a linear

time invariant (LTI) ﬁlter). This technique is used to

ﬁlter the Riesz pyramid coefﬁcients at each pixel in

each scale in time. It is also assumed that the local

orientation is roughly constant in time and space.

Suppose at a single frame n, a single pixel (x,y) in

a single scale ω

the normalized Riesz pyramid coef-

ﬁcients are:

= cos (φ

) + i sin(φ

)cos (θ

)

+ j sin (φ

)sin (θ

)

(8)

In the case of ordinary complex phase unwrap-

ping, we would take the principal value of the differ-

ence between successive terms and then do a cumula-

tive sum to give an unwrapped sequence in which the

difference between two successive terms is always in

the interval (−π,π]. We compute the principal value

of the difference between two successive coefﬁcients

by dividing them and then taking the logarithm:

log(r

),log (r

−1

),. .. ,log (r

−1

n−1

) (9)

An extended review of the quaternionic representa-

tion icluding complex exponentiation and logarithms can be

found in (Wadhwa et al., 2014b).

If we assume that θ

= θ + ε, that is that the lo-

cal orientation is roughly constant over time at every

pixel, the k term will be close to zero. More speciﬁ-

cally,

−1

n−1

= cos (φ

−φ

n−1

)

+isin (φ

−φ

n−1

)cos (θ)

+ j sin (φ

−φ

n−1

)sin (θ) + O(ε)

(10)

by ignoring the O(ε) term, the logarithm is

i([φ

−φ

n−1

])cos (θ) + j([φ

−φ

n−1

])sin (θ) (11)

The second step is to perform a cumulative sum of (9)

u,(φ

+ [φ

−φ

])u,. ..,

∑

l=2

[φ

−φ

n−1

]

(12)

where u = i cos θ + j sin θ. If we let

= φ

∑

l=2

[φ

−φ

n−1

] the series can be written

as:

iφ

cos(θ) + jφ

sin(θ) (13)

Afterwards we can isolate motions of interest in the

quaternionic phase signal using an LTI ﬁlter. Further-

more, the signal-to-noise ratio (SNR) of the phase sig-

nal can be increased by spatially denoising each frame

with an amplitude-weighted spatial blur with Gaus-

sian Kernel K

with standard deviation ρ on the i and

j components of the temporally ﬁltered signal.

Aφ

cos(θ) ∗K

A ∗K

+ j

Aφ

sin(θ) ∗K

A ∗K

(14)

Assuming that the orientation does not change sub-

stantially in the support of K

, then cos(θ) and sin(θ)

can be moved outside of the convolution in Eq. 14 to

get:

icos (θ)φ

+ j sin(θ)φ

(15)

where

Aφ

∗K

A ∗K

(16)

where (15) is the ﬁltered quaternionic phase obtained

for each pixel of each subband in each frame. This

signal is then multiplied by a magniﬁcation factor and

the pyramid is reconstructed to obtain the magniﬁed

video (Wadhwa et al., 2014a). In the following sec-

tion, we show how this signal can be used to analyze

subtle motions.

3 SUBTLE MOTION ANALYSIS

Our proposed algorithm goes as follows: ﬁrst we

use the Riesz Pyramid to calculate the amplitude

and quaternionic phase of the images. Secondly, we

implement a proper spatio-temporal ﬁltering scheme

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

448

which can enhance motions of interest without pro-

ducing delays or undesired artifacts. Thirdly, we iso-

late areas of potential subtle motion based on the com-

puted amplitude. Finally, we measure the dissimilar-

ities of quaternionic phases over time and transform

them into a 1-D signal, which is used to estimate the

moment when the subtle moment is taking place. A

graphic representation of our framework can be seen

in Figure 1.

3.1 Temporal Filtering Considerations

For an image sequence of N frames we perform the

process described in Sec.2.1 and Sec.2.2 for each

frame n ∈ N. However, not all levels of the pyramid

are able to provide useful information about the subtle

motion. Thus, after processing our video using differ-

ent pyramid levels, we select the one that shows more

subtle changes. We then obtain both local amplitude

and quaternionic phase (φ

cos(θ), φ

sin(θ)). We

apply the process described in Sec. 2.3 to obtain φ

(Eq. 16). However, since we are aiming to detect any

signiﬁcant quaternionic phase shifts between frames

and to compensate for the cumulative sum made in

(12), we calculate the difference of two consecutive

ﬁltered quaternionic phases:

∆φ

u = φ

u −φ

n−1

u (17)

where u = i cosθ + j sinθ. The previous work in eule-

rian motion magniﬁcation have given their users free-

dom to choose any temporal ﬁltering method avail-

able. However, since we require to pinpoint the ex-

act moment when subtle motion is detected we can-

not use traditional causal ﬁlters which may delay the

signal response (Figure 2c). Therefore we propose to

use a digital non-causal zero-phase ﬁnite impulse re-

sponse (FIR) ﬁlter.

u = b

∆φ

u +

∑

k=1

(∆φ

n+k

u + ∆φ

n−k

u) (18)

where p is an even number and b

is a coefﬁcient

of a FIR ﬁlter of length 2p + 1. One limitation of

this method is that non-causal ﬁlters requires to use

the previous and following p frames from the current

frame (therefore for online applications there must be

a delay of at least p frames). Another element to

consider is that Eulerian ampliﬁcation methods are

tailored for a particular task. These methods aim to

amplify subtle periodical movements (such as human

breathing, the vibration of an engine, the oscillations

of a guitar string, etc) by temporally band-passing

some potential movements and amplify them. How-

ever, these methods do not consider subtle non peri-

odical movements (such as blinking or facial MEs).

(a) (b)

Figure 2: A comparison of different ﬁlter responses for sub-

tle motion detection. (a) is an slice in time of an input im-

age sequence with subtle non periodical motion (The purple

dashed lines indicate when the subtle movement starts and

ends). (b) is the calculated quaternionic phase shift ∆φ

(a). We reduce the noise in (b) using three different ﬁltering

schemes: (c) an IIR Butterworth causal ﬁlter which delays

the signal; (d) a FIR non-causal band-pass ﬁlter which does

not delay the signal but it creates some artifacts before and

after the motion has taken place (Gibbs phenomenon); (e) a

FIR non-causal low-pass ﬁlter (our proposal).

The latter type of motion, when band-passed, creates

some large oscillations near the beginning and the end

of the subtle motion (Figure 2d) as stated by Gibbs

phenomenon. Therefore we decided to use low-pass

ﬁltering for this type of signals (Figure 2e).

3.2 Amplitude Masking

The ﬁrst step is to simplify the quaternionic phase by

discarding the orientation and calculate the euclidean

norm of the phase thus:

|Φ

| =

(Φ

sinθ)

+ (Φ

cosθ)

(19)

One thing to consider before trying to detect sub-

tle motion is the problem of image noise. Assuming

the general case of two static images corrupted with

some level of additive Gaussian noise, their quater-

nionic phase difference would be non-zero (|Φ

|> 0)

even after the phase SNR is improved by ways of

spatial and temporal ﬁltering (Sec. 2.3). We have

observed that the Φ

values could have a high vari-

ance in areas where local amplitude A has a rela-

tive low value regardless of the presence of motion.

Considering that the motion phase-signal in regions

of low amplitude is not meaningful (Wadhwa et al.,

2013) we decide to isolate these areas using a thresh-

old of validation computed from the local amplitude.

However, since the scale of local amplitude might

vary from subject to subject (Some videos might have

objects with stronger edges compared to others) we

need to normalize the local amplitude before we can

Subtle Motion Analysis and Spotting using the Riesz Pyramid

449

(a) (b)

Figure 3: Quaternionic phase masked. (a) is an input video

in which the ﬁrst string of the guitar is subtly oscillating.

(b) is the calculated quaternionic phase shift ∆φ and (c) is

its local amplitude. (d) is the result of masking (b) with (c).

threshold it.

M =

(

1 if β ≤

0 if β >

(20)

where A

is the calculated local amplitude of the im-

age at frame n, A

is the 95-percentile of the empirical

distribution of the amplitudes along the video and β is

a threshold selected by the user (See Section 4.2.3).

The mask can be further reﬁned using morphological

opening. Finally, we mask the phase norm (Φ

) with

M (as seen in Figure 3d). By masking the areas of low

amplitude we have effectively selected the regions in

which subtle motion can be detected.

3.3 Motion Spotting

Although the amplitude masking step aims to discard

any area that could contribute with noisy data, some

spurious pixels might get through this step. Thus, for

each masked frame ∆φ, we select the values smaller

than the 90-percentile. This is done to avoid outliers

caused by noisy pixels which do not represent the sub-

tle motion. From the selected pixels we calculate the

average power:

L−1

∑

l=0

|∆φ

n,l

(21)

where l is the index of the selected pixels and L is

the total number of selected pixels. P

is a one-

dimensional signal which peaks or local maxima rep-

resents changes in the image sequence.

In order to distinguish relevant peaks (subtle mo-

tions) from local magnitude variations and back-

ground noise, we use a method to contrast the differ-

ences of P

proposed by (Li et al., 2017). This method

compares the differences of P

within a speciﬁed in-

terval. Since subtle motions might take more than 2

consecutive frames, we analyze micro-intervals of K

frames (an odd number bigger than 2). Then, for each

current frame value, we subtract the average of the

k-th frame value before the current frame and the k-th

frame value after the current frame, where

k =

(K −1) (22)

Thus, for the n-th value in the contrasted difference

vector C(φ) is calculated by:

= P

−

n−k

+ P

n+k

) (23)

Finally, we select from C

the peaks or local maxima

that go over a threshold T and that are separated for

at least K frames. The threshold is calculated as:

T = C

median

+ p ×(C

max

−C

median

) (24)

where C

median

and C

max

are the median and maximum

value of C

for the whole video and p is a percentage

parameter in the range [0,1].

4 RESULTS

Our proposed method allows an user to analyze sub-

tle motions in videos. Although, the eulerian am-

pliﬁcation methods are able to reveal imperceptible

phenomena not previously visualized on video, our

method goes further and is able to quantify this mo-

tion. Thus, in the following section, we decide to

show some potential applications using the videos

provided in the supplemental material of (Wadhwa

et al., 2013; Wadhwa et al., 2014a).

4.1 Preliminary Evaluation

We select a video of a baby sleeping under a blanket in

a cradle that, when it’s magniﬁed, ampliﬁes the sub-

tle movements of the baby breathing (See Figure 4a).

We decided to test our method using the same ﬁltering

parameters suggested by the supplemental material of

(Wadhwa et al., 2013; Wadhwa et al., 2014a). For

the Riesz transform step we select the second level of

the pyramid. We design a non-causal FIR bandpass

FIR temporal ﬁlter of order 10 with passband between

0.04 and 0.4 Hz. We use a Gaussian Kernel K

with

standard deviation ρ = 2 for spatial ﬁltering. For the

amplitude masking step we select a threshold β = 0.3

(See Figure 4b). The segmented areas are transformed

into a 1-D signal using mean power. As we can see

in Figure 4c, the local maxima in the signal corre-

spond to the moment when the breathing motion is at

its peak, thus we can estimate the breathing patter of

the baby.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

450

(a)

(b)

50 60 70 80 90 100 110 120 130 140 150

Frames

2.2

2.4

2.6

2.8

3.2

3.4

3.6

3.8

Mean Power

-4

Mean Power vs Time

(c)

Figure 4: Subtle motion detection for breathing measure-

ment. (a) is the a frame of a video of a baby sleeping, (b) is

the masked phase norm and (c) is the obtained signal.

We also select a video of a drum, for which the

motion ampliﬁcation method, magniﬁes its vibrations

(See Figure 5a). For this example we decided to de-

sign a ﬁltering using a passband between 60 and 90

Hz instead of the narrow passband between 74 and 78

suggested by (Wadhwa et al., 2013). This video was

recorded using a high speed camera at 1900 fps. For

the Riesz transform step we select the third level of

the pyramid. The following parameters are the ones

suggested in the supplemental material of (Wadhwa

et al., 2013; Wadhwa et al., 2014a). We design a

non-causal FIR bandpass FIR temporal ﬁlter of order

44. with passband between 60 and 90 Hz. We use a

Gaussian Kernel K

with standard deviation ρ = 2 for

spatial ﬁltering. For the amplitude masking step we

select a threshold β = 0.15 (See Figure 5b). The seg-

mented areas are transformed into a 1-D signal using

mean power. As we can see in Figure 5c, the detected

vibration behaves like a combination of sinusoidal

waves (which is expected since the drum is emitting

acoustic waves). We can further analyze the signal

spectrum using the fast Fourier transform. As we can

see from Figure 5d, there are some frequency peaks

outside the narrow spectrum considered by (Wadhwa

et al., 2013) which could better characterize the fre-

quency of the drum vibration.

4.2 Experiments

Although, the examples presented in the previous sec-

tion show the potential of our method for subtle mo-

tion analysis, we would also like to measure its spot-

ting accuracy and robustness. Thus, we have designed

an experiment to compare the performance of our

method compared with methods in the state of the art

under different levels of noise.

4.2.1 Database

To the extent of our knowledge, there is not a public

labeled subtle motion database available. Thus we de-

cide to create our own database consisting of image

sequences with subtle motions. We create 18 image

sequences using real and artiﬁcially generated images

which elements are for the most part static with the

exception of one or two instances of subtle motion.

We simulate the subtle motion by translating either an

object in the image or the whole image by one pixel

per frame during two or three frames. We also la-

bel the time when the subtle motion starts (onset) and

ends (offset).

4.2.2 Method Comparison

We decide to compare our proposed method against

other classical approaches for motion detection. First,

the image is divided into a grid of equal-sized blocks.

Then, we extract information from each block using

three different feature descriptors: local binary pat-

tern (LBP) (Ojala et al., 2002), histogram of oriented

gradients (HOG) (Dalal and Triggs, 2005) and optical

ﬂow (OF) using the Lucas-Kanade method (Barron

et al., 1994). Then we use the feature difference anal-

ysis method proposed by (Li et al., 2017) to compare

the differences of the appearance-based features for

each block within a speciﬁed interval. The difference

between HOG and LBP histograms is calculated us-

ing the Chi-Squared (χ

) distance. Then we sort the

feature difference values from the blocks and calcu-

late the mean of the greatest values that surpass the

80−percentile. Finally, we use the method to con-

trast the differences and the peak detection discussed

in section 3.3 (Eq. 23 and 24 respectively).

4.2.3 Parameter Selection

We select the parameters for the spotting methods

which will work in all videos without added noise.

For our spotting method we select the second level

of the Riesz pyramid. We design a FIR non-causal

low-pass temporal ﬁlter with cutoff frequency of 30

Hz, corresponding to a ﬁlter of order 10. We use a

Gaussian Kernel K

with standard deviation ρ = 2 for

spatial ﬁltering. For the amplitude masking step we

select a threshold β = 0.25.

For the LBP method we divide the image into

a grid of 6 × 6 equal-sized blocks. The LBP de-

scriptor has a radius of 3 pixels with 16 neigh-

bors. For the HOG method we use the function

extractHOGFeatures from Matlab. For each block

produced by the function there are 2 ×2 cells of [8,8]

pixels. For the OF method, we divide the image into

a grid of 6 ×6 and compute the ﬂow’s amplitude

We don’t extract the orientation since it doesn’t provide

Subtle Motion Analysis and Spotting using the Riesz Pyramid

451

(a)

(b)

0 50 100 150 200 250 300 350 400 450

Frames

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

Mean Power

-3

Mean Power vs Time

(c)

0 50 100 150

f (Hz)

0.5

1.5

2.5

3.5

4.5

-4

Power Spectral Density

(d)

Figure 5: Subtle motion analysis for spectral analysis. (a) is the a frame of a video of a vibrating drum, (b) is the masked

phase norm,(c) is the obtained sinusoidal signal and (d) is its magnitude spectrum.

4.2.4 Image Noise Measurement

Considering that subtle motions have low amplitude

and, in some cases, they could be mistaken for noise,

we decide to test the robustness of the motion de-

tection methods in the presence of different levels of

noise. We choose to test the videos under Gaussian

additive noise and Salt and Pepper noise. In order

to do a standard measurement of the noise among

the different videos, we measure it using the peak

signal-to-noise ratio (PSNR). PSNR is deﬁned by the

mean square error (MSE). Given a noise-free u ×v

monochrome image I and the image with added noise

K, MSE is deﬁned as:

MSE =

u−1

∑

i=0

v−1

∑

j=0

[I(i, j) −K(i, j)]

(25)

The PSNR (in dB) is deﬁned as:

PSNR = 10 ·log



MAX

√

MSE



(26)

where MAX

is the maximum possible pixel value of

the image.

4.2.5 Evaluation Methodology

The ﬁrst step is, for each video, to add a speciﬁc

level of noise. Then we evaluate the methods accu-

racy by comparing all the detected peak frames in

each method with the ground truth labels from each

video in order to tell whether they are true or false

positive subtle motions. Within a certain threshold

level (p = 0.75 see Eq. 24), if one spotted peak is lo-

cated within the frame range of [ONSET, OFFSET] of

a labeled subtle motion video, the detected sequence

is be considered as one true positive subtle motion.

any important information about the instant when a subtle

motion takes place.

Otherwise a penalization of a possible detected subtle

motion (ψ frames) is counted as false positive. Since

the noise is added randomly we repeat the test and

measure the methods’ accuracy 20 times.

We deﬁne the true positive rate (TPR) as the per-

centage of frames of correctly detected subtle motion

divided by the total number of ground truth subtle mo-

tion frames in the database. The false positive rate

(FPR) is calculated as the percentage of incorrectly

spotted frames divided by the total number of non-

subtle motion frames from all the image sequences.

We evaluate the performance of the subtle motion de-

tection methods by tracing curves with TPR and FPR

as the y axis and PSNR as the x axis.

4.2.6 Experimental Results

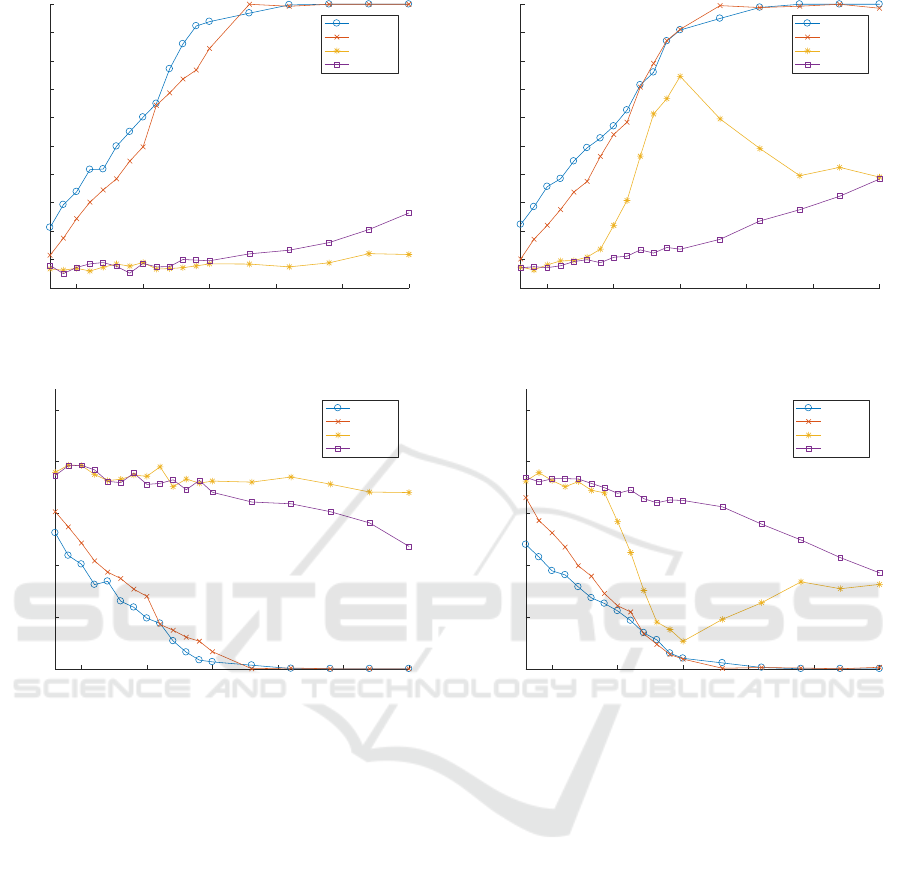
The spotting results under different levels of Gaus-

sian noise are presented in Figure 6. Our method has

shown to have an equal or higher TPR in the pres-

ence of most levels of Gaussian noise compared to the

other methods except when the PSNR is between 20

and 23 dB in which the OF method has a higher TPR.

Similarly, the FPR of our method is equal or lower in

most levels of Gaussian Noise except when the PSNR

is between 20 and 23 dB. The LBP and HOG method

had a lower TPR and a higher FPR compared to our

method and the OF method.

The spotting results under different levels of den-

sity of Salt and Pepper noise are presented in Figure 7.

Our method has shown to have an equal or higher

TPR in the presence of most levels of Salt and Pep-

per noise compared to the other methods except when

the PSNR is between 19 and 26 dB in which the OF

method has a higher TPR. Similarly, the FPR of our

method is equal or lower in most levels of Salt and

Pepper Noise except when the PSNR is between 19

and 26 dB. The LBP and HOG method had a lower

TPR and a higher FPR compared to our method and

the OF method. However, the LBP method seems to

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

452

10 15 20 25 30 35

PSNRdB

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

TPR

TPR vs PSNRdB

Riesz Pyr

LBP

HOG

(a)

10 15 20 25 30 35

PSNRdB

0.05

0.1

0.15

0.2

0.25

FPR

FPR vs PSNRdB

Riesz Pyr

LBP

HOG

(b)

Figure 6: Performance curves of different subtle motion

spotting techniques in presence of different levels of Gaus-

sian noise.

have a better performance between 18 and 23 dB than

HOG.

4.2.7 Discussion

The results in the previous section show that our

method has, in general, a better spotting accuracy

compared to the other methods tested. However, a

closer examination of our database has shown that our

method performs better in images with overall strong

edges and its performance decreased in images with

blurry edges. A possible explanation for this behav-

ior is that our amplitude masking method (see sec-

tion 3.2) aims to bypass areas of higher amplitude

in which the phase noise is lower and discard areas

of low amplitude in which the phase noise is higher.

However, in images with blurry edges, the computed

amplitude will be low all over the image and our sys-

10 15 20 25 30 35

PSNRdB

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

TPR

TPR vs PSNRdB

Riesz Pyr

LBP

HOG

(a)

10 15 20 25 30 35

PSNRdB

0.05

0.1

0.15

0.2

0.25

FPR

FPR vs PSNRdB

Riesz Pyr

LBP

HOG

(b)

Figure 7: Performance curves of different subtle motion

spotting techniques in presence of different levels of Salt

and Pepper noise.

tem will end up bypassing areas of higher noise, thus,

compromising our method’s accuracy.

The performance of the OF method is comparable

to our method. Since the Lucas-Kanade optical ﬂow

method was formulated under the temporal persis-

tence assumption (motion remains small from frame

to frame), it seems like an appropriate method for de-

scribing subtle motion (Kamate and Yilmazer, 2015).

However, in videos with color gradients and certain

levels of noise, the optical ﬂow accuracy is decreased.

The accuracy of the HOG method was low be-

cause image gradients are sensible to noise. The

accuracy of the LBP method was also low because

LBP is sensitive to noise and sometimes may clas-

sify two or more different patterns falsely to the same

class (Rassem and Khoo, 2014). However, the overall

results suggest that our method better describes subtle

motion than LBP and HOG descriptors.

Subtle Motion Analysis and Spotting using the Riesz Pyramid

453

5 CONCLUSIONS

We presented a subtle motion analysis and spot-

ting method based on the Riesz pyramid. Our

method adapted the quaternionic representation of the

Riesz monogenic signal by proposing a new ﬁltering

scheme. We were also able to mask regions of inter-

est where subtle motion might take place in order to

reduce the effect of noise using the image amplitude.

Furthermore, we illustrated the power of our subtle

motion analysis method by brieﬂy presenting a couple

of potential real-life applications. After testing our

method using our own database under different levels

of Gaussian additive noise and salt and peper noise,

we can conclude that our method surpasses other state

of the art methods.

Due to the unavailability of a public labeled subtle

motion database we had to test our experiments in a

rather limited dataset. Further tests will require us to

create or ﬁnd a more complete database in order to

obtain more statistically signiﬁcant results.

The quaternionic representation of phase and ori-

entation from the Riesz monogenic signal is a power-

ful tool that could potentially be exploited in the fu-

ture for more focused applications like modal analy-

sis, biomedical signals processing, and facial micro-

expression spotting and recognition.

REFERENCES

Balakrishnan, G., Durand, F., and Guttag, J. (2013). Detect-

ing Pulse from Head Motions in Video. In 2013 IEEE

Conference on Computer Vision and Pattern Recogni-

tion, pages 3430–3437.

Barron, J. L., Fleet, D. J., and Beauchemin, S. S. (1994).

Performance of optical ﬂow techniques. International

Journal of Computer Vision, 12(1):43–77.

Bharadwaj, S., Dhamecha, T. I., Vatsa, M., and Singh, R.

(2013). Computationally Efﬁcient Face Spooﬁng De-

tection with Motion Magniﬁcation. In 2013 IEEE

Conference on Computer Vision and Pattern Recog-

nition Workshops, pages 105–110.

Chen, J. G., Wadhwa, N., Cha, Y.-J., Durand, F., Freeman,

W. T., and Buyukozturk, O. (2015). Modal identiﬁca-

tion of simple structures with high-speed video using

motion magniﬁcation. Journal of Sound and Vibra-

tion, 345:58–71.

Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-

dients for human detection. In 2005 IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition (CVPR’05), volume 1, pages 886–893

vol. 1.

Irani, R., Nasrollahi, K., and Moeslund, T. B. (2014). Im-

proved Pulse Detection from Head Motions Using

DCT. Institute for Systems and Technologies of In-

formation, Control and Communication.

Kamate, S. and Yilmazer, N. (2015). Application of Object

Detection and Tracking Techniques for Unmanned

Aerial Vehicles. Procedia Computer Science, 61:436–

441.

Lee, J. and Shin, S. Y. (2002). General construction of time-

domain ﬁlters for orientation data. IEEE Transactions

on Visualization and Computer Graphics, 8(2):119–

128.

Li, X., Hong, X., Moilanen, A., Huang, X., Pﬁster, T.,

Zhao, G., and Pietikainen, M. (2017). Towards Read-

ing Hidden Emotions: A Comparative Study of Spon-

taneous Micro-expression Spotting and Recognition

Methods. IEEE Transactions on Affective Computing,

PP(99):1–1.

Liu, C., Torralba, A., Freeman, W. T., Durand, F., and Adel-

son, E. H. (2005). Motion Magniﬁcation. In ACM

SIGGRAPH 2005 Papers, SIGGRAPH ’05, pages

519–526, New York, NY, USA. ACM.

McLeod, A. J., Baxter, J. S. H., de Ribaupierre, S., and

Peters, T. M. (2014). Motion magniﬁcation for en-

doscopic surgery. volume 9036, pages 90360C–

90360C–8.

Ojala, T., Pietikainen, M., and Maenpaa, T. (2002). Mul-

tiresolution gray-scale and rotation invariant texture

classiﬁcation with local binary patterns. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

24(7):971–987.

Park, S. and Kim, D. (2009). Subtle facial expression recog-

nition using motion magniﬁcation. Pattern Recogni-

tion Letters, 30(7):708–716.

Raghavendra, R., Avinash, M., Marcel, S., and Busch, C.

(2015). Finger vein liveness detection using motion

magniﬁcation. In 2015 IEEE 7th International Con-

ference on Biometrics Theory, Applications and Sys-

tems (BTAS), pages 1–7.

Rassem, T. H. and Khoo, B. E. (2014). Completed local

ternary pattern for rotation invariant texture classiﬁca-

tion. The Scientiﬁc World Journal, 2014.

Unser, M., Sage, D., and Ville, D. V. D. (2009). Multires-

olution Monogenic Signal Analysis Using the Riesz-

Laplace Wavelet Transform. IEEE Transactions on

Image Processing, 18(11):2402–2418.

Wadhwa, N., Rubinstein, M., Durand, F., and Freeman, W.

(2014a). Riesz pyramids for fast phase-based video

magniﬁcation. In 2014 IEEE International Confer-

ence on Computational Photography (ICCP), pages

1–10.

Wadhwa, N., Rubinstein, M., Durand, F., and Freeman,

W. T. (2013). Phase-based Video Motion Processing.

ACM Trans. Graph., 32(4):80:1–80:10.

Wadhwa, N., Rubinstein, M., Durand, F., and Freeman,

W. T. (2014b). Quaternionic representation of the

riesz pyramid for video magniﬁcation. Technical re-

port.

Wu, H.-Y., Rubinstein, M., Shih, E., Guttag, J., Durand, F.,

and Freeman, W. (2012). Eulerian Video Magniﬁca-

tion for Revealing Subtle Changes in the World. ACM

Trans. Graph., 31(4):65:1–65:8.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

454