TabularVis – A Circos-inspired Interactive Web Client based Tool for

Improving the Clarity of Tabular Data Visualization

orgy Papp and Roland Kunkli

Department of Computer Graphics and Image Processing, Faculty of Informatics, University of Debrecen, Debrecen,

Hungary

Keywords:

Data Visualization, Circular Layout, Sorting, Table, Diagram, Search Algorithm.

Abstract:

Table visualization is one of the earliest problems in the ﬁeld of data visualization, and there are many appli-

cations which provide different solutions to this task. One of the most popular ones is Circos, a well-known

genome visualization software package based on the so-called circular layout technique. In this work, we

present an interactive web-based visualization tool inspired by Circos’ table viewer web application, in which

we provide new extensions and techniques beyond its existing main ideas, for improving the clarity of the

generated visualization. One of them is making the links easier to follow by giving an automatic solution to

reduce the number of intersections between the links. We also present different tools which could be particu-

larly useful in such situations, in which the table’s data induce extreme scatter, i.e., the difference between the

data is signiﬁcantly large or small. Our proposed visualization accepts tables with non-negative numbers, and

the amount of efﬁciently displayable data depends on the number of zeros in the table. In the paper, besides

describing our contributions in detail, we also compare the outputs of our method and Circos table viewer to

conﬁrm the legitimacy of our application and the implemented techniques it contains.

1 INTRODUCTION

Nowadays, it is difﬁcult to ﬁnd a scientiﬁc or indus-

trial ﬁeld, in which the relationships between data do

not play an important role. Almost everything affects

something else, and it is crucial to notice these de-

pendencies and understand the relationships that they

describe. The connections are often represented by

values, and each one can indicate the related connec-

tion’s type or property.

Tables have a long history in database manage-

ment and computer science, and they suit well to store

information about relationships. In this paper, we deal

with connections which are represented by numbers.

However, organizing these connections into a table

does not make them easily readable or understandable

by itself, because when a table is formed by many

rows and columns, it becomes harder to work with

it. There are a lot of various reasons and purposes

why the users want to visualize tables, and what they

want to see in the resulting image. By using tabu-

lar visualization, our goal is to display relationship

information. There are a lot of different techniques

to achieve this goal, but the circular layout is one of

the most prominent ones. It is used in the ﬁeld of

graph drawing and many visualization applications,

including the highly cited and popular Circos soft-

ware package (Krzywinski et al., 2009). In this paper,

we present an improved approach of how Circos vi-

sualizes connections based on tables, by giving new

tools for displaying the value, the direction, and the

pattern of the connections. Sometimes it is confus-

ing to follow the links in a diagram, so we introduce

a sorting method as well, to make the diagrams more

transparent by reducing the number of intersections

between the connections. Multiple search and opti-

mization algorithms were implemented for this task,

and we compare them with each other to ﬁnd the one

with the best performance.

In this work, ﬁrst, we discuss the related works,

then in Section 3.2, we introduce our visualization

method in detail. Also, we brieﬂy present Circos to

make the comparison of the two visualization solu-

tions easier. After this, we propose our solution for

reducing the intersections of the connections. At the

end of the paper, we introduce the features and the

performance of our self-developed application, which

was implemented to present our results.

120

Papp, G. and Kunkli, R.

TabularVis – A Circos-inspired Interactive Web Client based Tool for Improving the Clarity of Tabular Data Visualization.

DOI: 10.5220/0006620701200131

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages

120-131

ISBN: 978-989-758-289-9

2 RELATED WORK

Circular layout is often used to visualize connections,

especially for genomic data or graphs. However, its

advantages, which come from its simplicity and sym-

metry, make it perfect to visualize other general data

as well. The rotation invariant property, the ability to

reduce the number of eye movements, and weakening

the reading order implications are just three of these

advantages, which are discussed in the work of Chuah

and Eick (Chuah and Eick, 1998).

In these referenced works we can see examples of

genome (Katapadi et al., 2012; Burkart-Waco et al.,

2012; Schmutz et al., 2014; Tine et al., 2014), net-

work (Lin et al., 2014; Dang et al., 2015; Irimia and

Horn, 2013; Irimia and Van Horn, 2014), and general

(Blasco-Sopl

on et al., 2015; Pan et al., 2013; Fuji-

wara, 2015; Nicholas et al., 2014) data visualization

by researchers from different disciplines. There are a

lot of studies which show good use cases for how the

circular layout can easily visualize the connections;

here we would like to mention some of them. Circos

is an open-source and free application licensed under

GPL. Also, it is widely used in the ﬁeld of genome

research, because of its success in displaying varia-

tion in genome structure and positional relationship

between genomic intervals. Besides, it can show dif-

ferent plot types inside the tracks of the diagram, to

provide more information about genomes. However,

despite the fact that Circos is a powerful visualiza-

tion tool, unfortunately, it is not user-friendly at all. It

is a command line application written in Perl, and it

uses conﬁguration ﬁles to create the diagrams. More-

over, learning how to use the software can be hard and

time consuming for researchers with basic IT skills.

There are numerous applications, for example, ggbio

(Yin et al., 2012), Rcircos (Zhang et al., 2013), or

OmicCircos (Hu et al., 2014), which aim to provide

a more user-friendly and improved circular genome

visualization. These mentioned applications are pack-

ages which have been developed for the R statistical

software environment. By using them, it is ensured

that the users can take the advantages of R while they

are creating visualizations. However, only static im-

ages can be generated with all the applications that

we mentioned so far, and this makes it signiﬁcantly

harder to customize the diagrams after they were cre-

ated. The possibly used third party software or any

framework assumes the knowledge of them, and they

can make the installation of the application more com-

plex and time-consuming. The circular layout com-

bined with interactive data visualization techniques

(e.g. in Mizbee (Meyer et al., 2009) or J-Circos (An

et al., 2015)) can help the users to understand their

data better and faster. Unfortunately, the possibility

of customizing the diagram in the way of removing

or changing its elements is missing in these two men-

tioned applications. In turn, this functionality could

help to make the diagram more personalized. Addi-

tionally, these software still operate with one or more

conﬁguration ﬁles, which is still not the most user-

friendly solution. However, both applications have

inspired us to extend the possibilities of visualizing

the connections’ values in a diagram.

Beside genomic data, there is a demand for soft-

ware solutions and tools for visualizing relationships

and connections based on more general data. The

R package called circlize (Gu et al., 2014) can cre-

ate diagrams based on non-genomic data. The main

purpose of circlize is still the genomic analysis, but

thanks to its low-level graphic functions, the user can

use it for displaying other kinds of data. Circos can

visualize general data as well, but they have to be

given in one of the required formats. The InfoVis li-

brary (Li, 2012) has a visualization tool called Smith-

Graph which uses bars on the circle’s circumference.

A similar visualization method is Jen Lowe’s solution

(Bayer, 2011), with which she has won the WikiViz

2011 challenge.

There is a trend to bring the visualization right

into the browser and make it as interactive as much

as possible. Probably the most used tools for this

kind of purpose are the D3.js (Bostock et al., 2011)

and the WebGL libraries. There are many examples

in the Chrome Experiments website (creative coding

community, 2009), and WebGL also has been used in

different scientiﬁc visualization projects (Mwalongo

et al., 2015; Andrews and Wright, 2014; Bornel

et al., 2014; Cui et al., 2016). Circos also has an on-

line application for tabular data visualization, but it

has less much less functionality than the desktop ver-

sion of the software.

As we have pointed out above, the circular layout

has proven its ability to visualize both genomic and

general data. Also, few examples have been shown

how the lack of interactive functionality can nega-

tively affect the usability of an application. Besides,

we have seen that there is a need for an easily acces-

sible and user-friendly web-based application.

It is easy to imagine that a diagram can quickly

become crowded if there are too many connections

in it, and this may prevent the user from understand-

ing the data. Decreasing the number of intersections

between graph edges during a circular graph drawing

is a well-known problem in the ﬁeld of graph theory.

In the work of Baur et al. (Baur and Brandes, 2005)

we can see an example to construct a graph using a

two-phase heuristic algorithm. The ﬁrst phase mini-

TabularVis – A Circos-inspired Interactive Web Client based Tool for Improving the Clarity of Tabular Data Visualization

121

mizes the total length of the edges of the graph, and

the second one uses the shifting heuristic to optimize

the result of the previous step locally. Another exam-

ple is the work of Gansner et al. (Gansner and Koren,

2007), which tries to ﬁnd the best node placement by

minimizing the length of the edges separately using a

heuristic algorithm as well. Edge bundling (Lhuillier

et al., 2017) is an efﬁcient alternative to reduce the

number of intersections in a diagram. Another way

of avoiding crowded diagrams is the exterior routing

and in the work of Gansner et al. (Gansner and Ko-

ren, 2007) we can see an example for that. However,

we do not use the edge bundling because we want to

keep the connections thickness in the diagram. We

also want to make the diagram more transparent by

performing a sort on any predeﬁned order and pre-

serving the relative position of selected elements.

3 TABLE VISUALIZATION

In this section, we introduce how Circos creates dia-

grams based on tabular data, and we compare it with

our proposed technique because our improvements

were inspired by Circos. We also point out a few

shortcomings of its visualization method (which uses

circular layout and B

ezier curves), and we suggest so-

lutions to them.

3.1 Circos’ Visualization

Circos can visualize connections between the

columns and the rows of a given table. A connec-

tion is represented by a cell and its value. Therefore,

the cell’s position determines which row and column

are affected, and the value describes the relationship

between them. The software visualizes these connec-

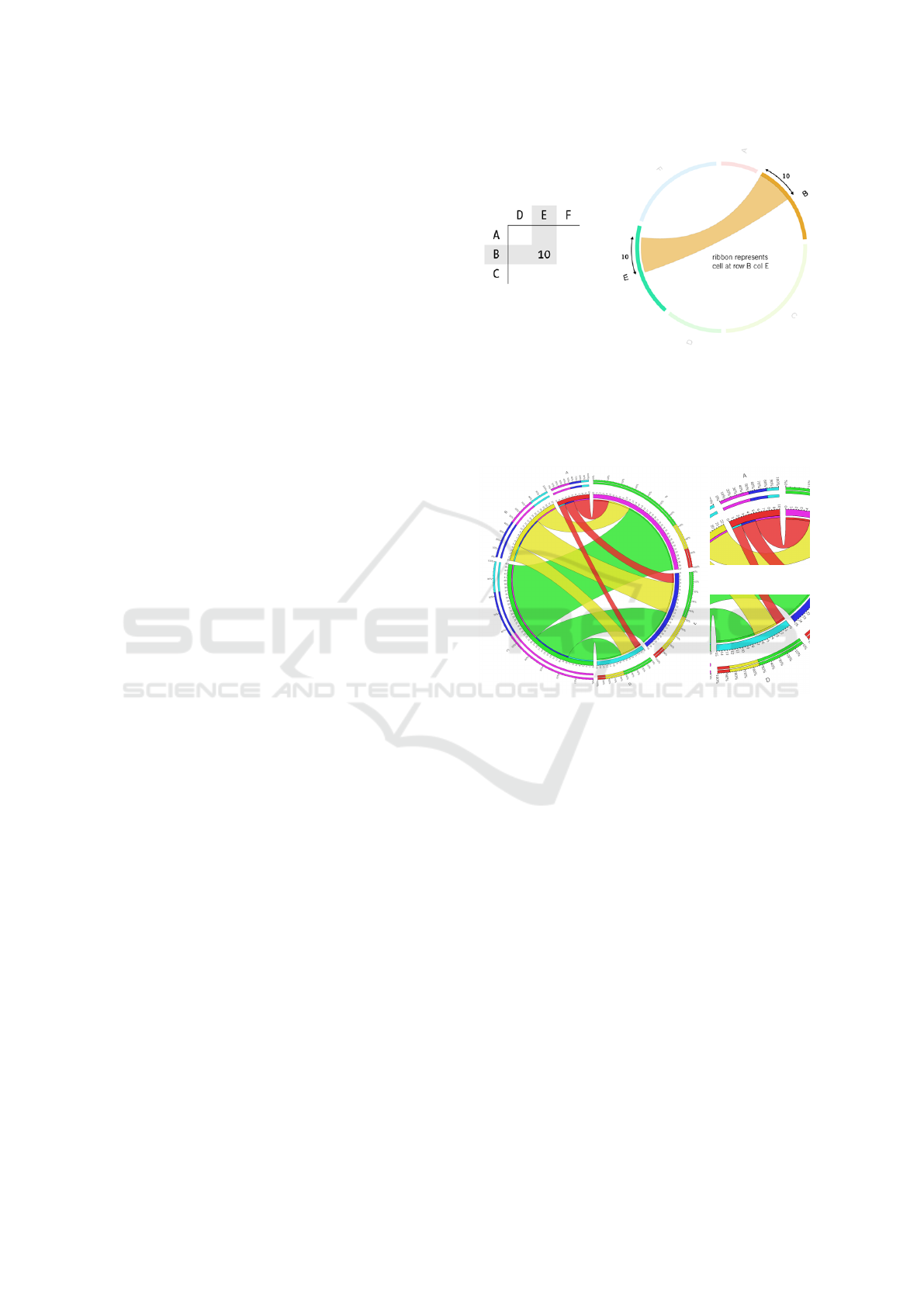
tions as we can see in Figure 1. The main concept in

Circos is that a cell can only contain a non-negative

value, and zero means no connection.

There are smaller angular segments (so-called ribbon

caps) located at the end of the connections (see Fig-

ure 2). These indicate which segment is the other par-

ticipant in the relationship, using the color of the con-

nected segment. We can see in Figure 1 that the rib-

bon caps do not always appear in the diagram. The

contribution tracks can be placed above each segment

to show the relative values of its contained row and

column and the sum of them.

3.2 Our Visualization Method

In this paper, our goal is to improve the previously in-

troduced visualization in Subsection 3.1, by increas-

Figure 1: Circos’ way to visualize connections (Krzywin-

ski, 2008). The ribbon represents the value 10 of the cell at

row B and column E. Rows and columns are represented by

circular arranged segments, and their angular size is based

on the summarized values of the corresponding one. The

thickness of the ribbon is deﬁned by the cell’s value.

(a)

(b)

(c)

Figure 2: Circos’ visualization in detail: (a) shows the con-

tribution tracks outside the circle, the so-called tick marks

and tick labels on the segments, and the track. While (b)

shows that the links start from a row segment, (c) displays

that they end at the column segments. (b) and (c) also pro-

vide a closer look at the ribbon caps.

ing its clarity in common situations, depending on

the intentions of the user. Therefore, we speciﬁed

the following criteria to create our visualization tech-

nique based on them. The ﬁrst one was to construct

a connection between two objects that helps the user

to track and identify the visualized relationship. The

second was about to give the ability to determine

and compare the value of the connections easily and

quickly. Lastly to provide more space for the labels

and to give the possibility of grouping the table’s rows

and columns. We use circular layout in our solution as

well, because of the advantages that it provides; and

similarly to Circos we also use B

ezier curves for con-

structing the connections. Circos can effectively dis-

play the relationships in many cases. However, there

are many situations where its visualization makes im-

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

122

portant details harder to perceive. Also, it works well

when the differences between the matrix’s values are

signiﬁcant because in this case the relationships rep-

resented by thick ribbons are easily and quickly no-

ticeable. However, it is harder to decide which re-

lationships have larger values in the case of minor

differences. Furthermore, the comparison of the val-

ues is not an easy task, especially if the segments are

placed far from each other. The so-called tick marks

and tick labels help this comparison by showing the

row or column values at the top of the segments (see

Figure 2).

Figure 3: The extensions of the connections and the bars

together form a block, and they can be arranged into groups

like block C and block D. The height and the angular length

of a bar have the same meaning, and they are both used

for representing the value of a link. There are concentric

circles behind the bars to make their values easier to read

and compare, even if they are far from each other.

One of our main ideas is to remove Circos’ segments

– which represent the rows and the columns – and

replace them with angular segments. These are cre-

ated as an extension of the connections in both di-

rections, and we call them bars in the rest of the pa-

per. We use them to make the values easy to read and

compare, and this is one of our mentioned criteria in

Section 3.2. The newly deﬁned bars have the same

thickness as the links themselves, but they have differ-

ent height based on the connections’ value. They are

positioned a little bit farther from connections’ ends.

Figure 3 shows that the bars are used together with

the concentric circles to make the values easier to read

and compare (see Figure 4). The blocks represent the

row and the column from the table. It is created by

placing the bars belong to the same row or column

next to each other and marking them with the same

color. Additionally, these blocks can be arranged into

groups to represent rows and columns close to each

other (see Figure 3).

(a) (b)

Figure 4: The left image (a) shows how the bars can easily

indicate the values with concentric circles, while in Circos

(b) it is harder to read and compare the values of the con-

nections.

In Circos, wider ribbons represent larger values in the

table, and they can grab our attention immediately,

which is very useful in some cases. But if the scat-

ter in the table’s values is signiﬁcant, then thick con-

nections may cover other ones and make them hardly

visible. This situation is perfect for ﬁnding out which

row and column have the largest or smallest value, but

it makes the patterns – formed by the connections or

the direction of the ribbons – hard to recognize.

(a) (b)

Figure 5: The left image (a) shows our visualization with

uniﬁed connection sizes, while in (b) we can see the result

using Circos. We can recognize that the pattern of the con-

nections is much more visible in the case of (a) than (b).

As a solution to this problem, we decided to make

it possible to create all relationships equally visible

by unifying the thickness of the links and the bars in

the diagram. This way the links represent only the

existence of a relationship between two bars (see Fig-

ure 5(a)), and as a result, thinner connections become

more visible in the diagram, than before. Further-

more, the links with uniﬁed length make the pattern

formed by the connections easier to perceive, instead

of drawing our attention to a particular part of the di-

agram, while the bars’ height still represents the rela-

TabularVis – A Circos-inspired Interactive Web Client based Tool for Improving the Clarity of Tabular Data Visualization

123

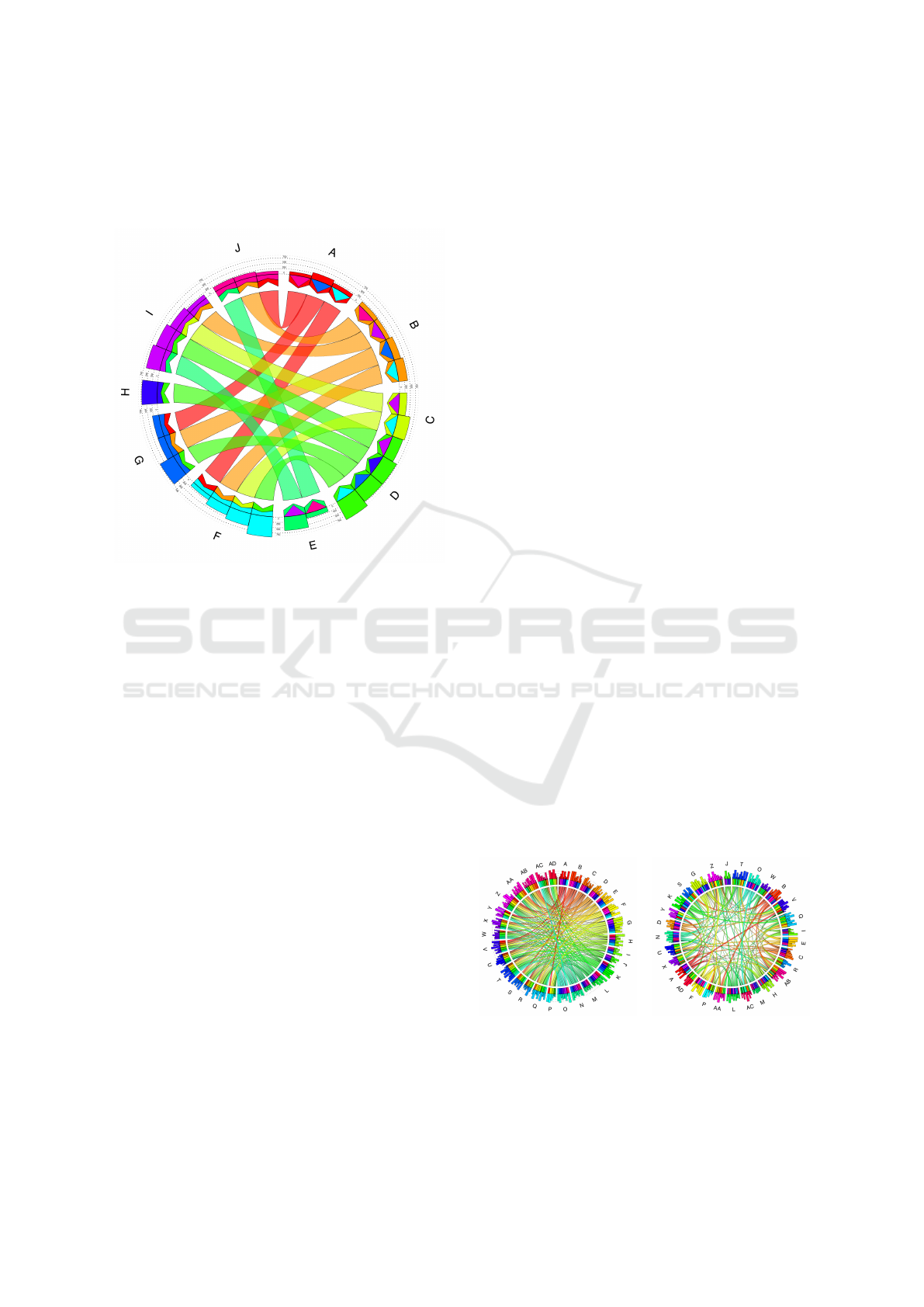
tionships’ values (see Figure 5). Moreover, the equal

thickness of the bars increases the visibility and the

comparability of them. With this feature, the redun-

dancy mentioned at Figure 3 can be eliminated.

Figure 6: Shows the connections with uniﬁed length and our

arrow-style shapes to indicate the directions. The shapes

below block e indicate the connections’ source, and the ones

below block h show its target.

In some situations, it could come in handy to be able

to determine the connections’ direction and to decide

which row or column is the start or the end of a rela-

tionship. Circos indicates the direction of a relation-

ship by distinguishing a ribbon’s starting and ending

position. However, this way of representing the direc-

tions may not clear enough for somebody who does

not have any preconception about the visualization

method to ﬁnd out the direction. We intended to offer

a different and more informative way to display the

connections’ direction. Therefore we added a shape

between the block and the link in a way that Figure 6

shows us to indicate the link’s direction and the other

block of the link. This solution works best when the

connections have equal width since in this case the

mentioned new shape does not deform and keeps the

original arrow-style form without losing its meaning.

This shape is always attached to the bar, and it has

three different forms. Two of them are shown in Fig-

ure 6, and the third one, which is used for represent-

ing an undirected relationship, has a similar shape like

Circos’ ribbon cap with a different height. Our previ-

ously mentioned improvements are suffered from the

problem of barely perceptible bars when the value of

the represented relationship is too small. Because in

this case, the height of the bar could be so small that

it appears only as a circular arc. The proposed arrow-

like shapes can increase the visibility of the bars in

this case as well.

Our application provides these modiﬁcations as

optional features since they are suitable for different

situation, so the users can decide which one is the

most appropriate for their purpose.

4 SORTING THE CONNECTIONS

One of the most important aspects of a visualization

is that it should be easily understood. In our case, the

position of the blocks and groups controls where the

connections are placed, so any change in their order

affects on the number of the intersections in the di-

agram. Because the intersections of the connections

make the diagram less transparent and make the links

harder to follow, the blocks’ and groups’ order has a

huge inﬂuence on the clarity of the diagram. There-

fore, it may be important to ﬁnd an easy and fast way

for modifying their order. In the rest of the paper,

we reference the process of changing the blocks’ and

groups’ order as sorting the connections. Figure 7

shows an example where sorting can help to avoid the

clutter in the diagram. However, Circos do not pro-

vide an automatic solution to perform a sorting of the

connections, which means that the user has to do it

manually. This sorting problem is known as the cir-

cular crossing minimization problem in the ﬁeld of

graph drawing. it is an NP-hard problem, and re-

searchers often use heuristic ways to deal with it (e.g.

(Baur and Brandes, 2005; Gansner and Koren, 2007)).

Because of the problem’s complexity, our goal is to

automatically ﬁnd one of the sequences of the blocks

and the groups, which can remove a large number of

intersections from the diagram by using a heuristic

approach as well.

(a) (b)

Figure 7: Example of how the sorting of the connections

makes the diagram more transparent. The left image (a)

shows the diagram without sorting, and the right image (b)

shows the result that we get after applying it.

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

124

4.1 Used Algorithms

To get the desired order of the blocks and the groups,

we tried and used two local search algorithms (hill

climbing and max-conﬂicts) and three optimization

methods (cross-entropy, simulated annealing, and

bees algorithm), which are all discussed in more detail

in (Brownlee, 2011) and (Russell and Norvig, 2010).

These algorithms try to search the best possible po-

sition of the groups and the blocks to minimize the

number of the intersections in the diagram. However,

as we mentioned earlier, this is an NP-hard problem,

and these methods only can give an approximation

of the best “theoretical” solution. But in most cases,

their results are good enough to remarkably increase

the clarity of the visualization (see Figure 7).

However, not all parts of the diagram are con-

trolled by the search, because the position of the

bars is determined by the order of the blocks and

the groups. This is done by creating a temporary list

from the result of the search, starting with the block

which contains the bar we want to set, then adding the

blocks followed by it from the result. By reversing

this newly created order, we can set the bars’ position

in the block.

The used algorithms produce a result within sec-

onds or in the case of tables (20 × 20) approximately

in ≈ 17 seconds. More detailed information about the

run time of the algorithms can be found in Table 1. In

the next subsections, we brieﬂy introduce the methods

and their time complexity.

Table 1: The running times in seconds for all algorithms

and table sizes.

5 × 5 10 × 0 15 ×15 20 ×20

Hill climbing 0 s 6 s 106 s 724 s

Min-conﬂicts 0 s 1 s 5 s 19 s

Cross-entropy 0 s 1 s 5 s 18 s

Cross-entropy

and

Min-conﬂicts

0 s 11 s 111 s 475 s

Simulated

annealing

0 s 1 s 4 s 14 s

Bees algorithm 0 s 4 s 37 s 154 s

4.2 Search Space

Before we could start to discuss the used algorithms,

we have to deﬁne a search space for the methods. It

consists of states that store all possible combinations

of the positions of the groups and the blocks. More-

over, it contains the actions of how the search meth-

ods can modify the states. The sorting methods are

operating in this search space to ﬁnd better order for

the groups and blocks. This is a simple deﬁnition of

the problem, and it contains only the necessary infor-

mation for the search, the position of the blocks and

the groups and the relationships between the blocks.

This information is enough for us to ﬁnd a better or-

der, which generates fewer intersections than the ini-

tial state. In the diagram, the position of the groups

and the blocks determines the location of the connec-

tions, but during the sorting, instead of using the exact

location of them, we just deal with their order. After

the search, we can easily get back their position from

this. Also, to be able to get information about the con-

nected blocks, we store the position of a connection’s

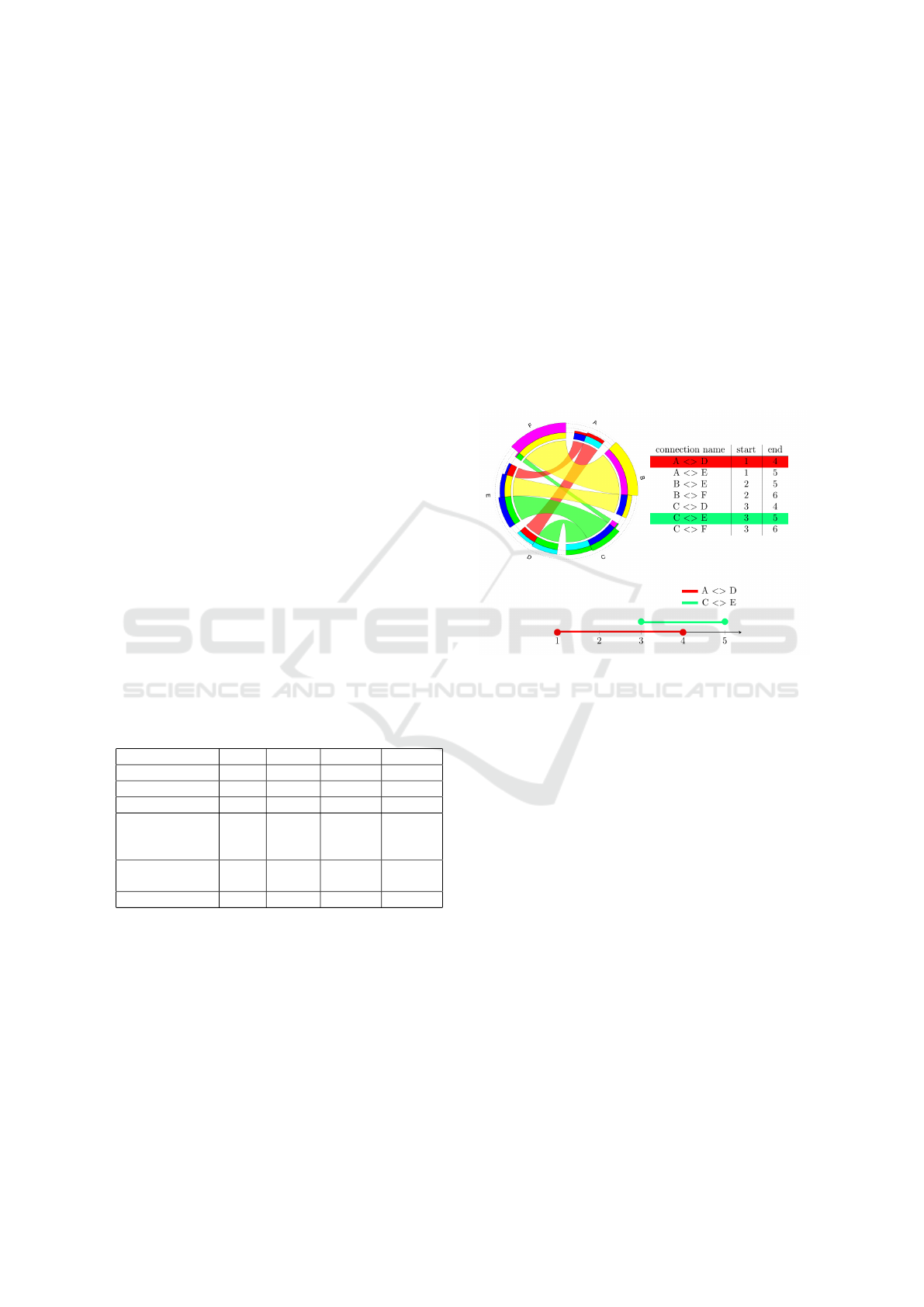
start and end segments. Figure 8 shows information

about the groups and blocks, which is stored in a state.

Figure 8: In the picture, we can see the information, which

is stored in a state. At the bottom, it also displays that by

testing the overlap of the ranges – created from the connec-

tions – we can determine whether they are intersecting or

not.

The state has to know whether the given action can

apply to it or not and if yes, the result also has to be

known. We deﬁned our actions to move the groups

and the blocks to a new position in the order, and

since we do not want to prioritize any of the actions,

we have the same cost for all of them. Beside this, it

is important to make a difference between two states,

so they store the number of intersections to describe

the goodness of their status and give the basis for

the comparison of them. This number can be calcu-

lated by using the analogy of testing for overlapping

ranges, which were created from the stored positions

of the connection as Figure 8 shows. If two ranges

overlap, then the two connections intersect each other.

Otherwise, there is no intersection between them. To

decide whether two ranges overlap each other or not,

we have to deﬁne their midpoint. We have to use a

distance function as well, and we used the following:

f (a, b) =



2π −

a − b

> π

a − b

π, otherwise

TabularVis – A Circos-inspired Interactive Web Client based Tool for Improving the Clarity of Tabular Data Visualization

125

Also, we have to deﬁne a function, which normalize

the given value to the range [0, 2π]

l(a) = a −

j

2π

· 2π



The function g(a,b), that ﬁnds the midpoint of two

given points, is given in the following form:

g(a, b) =





a+b

+ π



a − b

> π



a+b



, otherwise

It is also important to know when a point is inside in

the given range and we can ﬁnd out this by using the

h(a, b, c) function.

h(a, b, c) = f (g(a, b), c) −

f (a, b)

The overlap of two ranges is tested by using the

sgn(h(a, b, c)) function for both ranges and all of their

points.

k(a, b, c, d) = sgn (h(a, b, c) · h (a, b, d)) +

sgn(h (c, d, a) · h (c, d,b))

We denote the connections as c

, . . . , c

where n is the

number of the links in the diagram. Our connections

are deﬁned with their start and end positions, which

are denoted with two functions, s(c

) and e(c

) respec-

tively i ∈ [1, n]. The existence of an intersection is cal-

culated from the overlap function (k(a, b, c, d)) in the

following way:

q(i, j) = 1+sgn



−1 −

k(s(c

), e(c

), s(c

), e(c

)))



With testing all connections with each other we can

calculate the number of the intersections in the dia-

gram in the following way:

∑

i=1

∑

j=1

j6=i

q(i, j).

The result of the sum is 1 if there is an intersection

between the two given edges (e

, e

) and 0 otherwise.

Therefore this function was used as an optimization

criterion to minimize the intersections in the diagram.

4.3 Hill Climbing

Our ﬁrst choice was the well-known hill climbing

method because it visits all the neighbors of a state

during the search, and thus it is more likely to get bet-

ter results. Sometimes the search could trap in a lo-

cal minimum, so to avoid this, we modiﬁed it to ran-

domly choose another state if there is no better one

around it. The algorithm has two parameters. The

ﬁrst one controls how many times it can jump to a

random state (the value used by us 10), and the sec-

ond one speciﬁes how many iterations it can do (we

used 100). This search algorithm does not use any

knowledge or heuristic about the problem, it is just a

brute force method to ﬁnd a better state and therefore

its running time is long.

4.4 Min-conﬂicts

This method is based on the idea, that the number of

intersections can be signiﬁcantly reduced by replac-

ing the block, that causes the most intersections in

the diagram. The algorithm searches for this block

in every iteration, and then it tries to ﬁnd a better po-

sition for the block. This method has only one pa-

rameter, which speciﬁes the number of the iteration

that it can do before it has to stop (we used 10). The

min-conﬂicts algorithm is faster than the hill climbing

because it visits less state during the search.

4.5 Cross-entropy

This algorithm uses the statistics of the blocks’ po-

sition, which is updated from a speciﬁed number of

generated states in every iteration. This statistical data

is stored in a matrix, which contains the percentage of

the blocks’ occurrences for every position. The ma-

trix’s values will converge to the best position of the

blocks which means that eventually, we will ﬁnd a

good solution. This algorithm has multiple parame-

ters in order to ﬁll and maintain the matrix, but the

two most important are the number of the states gen-

erated by the algorithm in every iteration (which was

10 in our implementation) and the number of the used

ones as elite states (the value used by us 2) to update

the matrix.

4.6 Cross-entropy and Min-conﬂicts

We merged the cross-entropy and min-conﬂicts

method to get better result. We implemented the min-

conﬂicts methods’ idea in the cross-entropy to in-

crease the “goodness” of the elites. This means that in

every iteration a min-conﬂicts search is performed on

each newly generated state to get a state with fewer

intersections.

4.7 Simulated Annealing

This global optimization algorithm is based on a prob-

abilistic technique. It mimics the physical process of

heating a material ﬁrst and then slowly cooling it to

improve its conditions. In our case, this means, that

the method can accept worse orders of blocks and

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

126

groups at the beginning, but as the temperature drops

with each iteration, it accepts only the better orders

with fewer intersections. The algorithm has three pa-

rameters, the acceptance ratio (we used 0.8), that we

want to reach during the preheat process, the number

of iterations per temperature (which was 10 in our ap-

plication), and a maximum iteration number (we used

100 in our implementation).

4.8 Bees Algorithm

The last algorithm is also a global optimization

method, and it tries to ﬁnd the best state by simulat-

ing the movements of the bees searching for pollen.

This means that in every iteration the method gener-

ates a speciﬁed number of random state, then it se-

lects the best of them to perform further search on

each of them. In our case, this means that we run the

min-conﬂicts method on all of the best states. The al-

gorithm’s three important parameters are the number

of the generated states, the number of the best states,

and the number of min-conﬂicts runs per best state

(we used the following values respectively: 20,2,10).

4.9 Algorithms Time Complexity

To present the time complexity of the proposed algo-

rithms, we introduce the following notations.

• b : the number of the blocks in the diagram

• o : the number of the groups in the diagram

• m : the maximum number of iterations of the al-

gorithm

• n : the number of the newly generated states

• w : the time complexity of quicksort

• u : the time complexity of updating all elements

of a matrix with the size of (b + o) × (b + o)

• p : the maximum number of iterations to ﬁnd the

best starting temperature for simulated annealing

• t : the number of iterations on each temperature

• r : the maximum number of iterations to ﬁnd the

best reheat temperature for simulated annealing

• z : the number of random searches per iteration to

ﬁnd new states in the bees algorithm

• j : the number of the best states through the whole

• v : the number of min-conﬂicts runs per best state

in the bees algorithm

The time complexity of the used algorithms can be

seen in Table 2 to make the comparison between them

easier.

Table 2: The time complexity of the used algorithms.

Algorithms Time complexity

Hill climbing O



m ·



− b





− o



Min-conﬂicts O



m · (b − 1) ·



− o



Cross-entropy O



m · (n + w + u)



Cross-entropy

and

Min-conﬂicts



m · ((n · (b − 1)) + u)



Simulated

annealing



p + (m ·t) + r



Bees algorithm O



m · (z + ( j · v))



4.10 The Result of the Algorithms

These methods were tested on randomly ﬁlled tables

with four different sizes (5 × 5, 10 × 10, 15 × 15, and

20 × 20), and 100 tables were generated for each size

to run the sorting on them. The overall result of the

tests are shown in Figure 9, and it shows us that the

algorithms effectively reduce the number of intersec-

tions in the diagram, and the average reduction of in-

tersections was ≈ 55%.

120

300

500

700

100

Hill climbing

Min-conﬂicts

Cross entropy

Cross entropy and min-conﬂicts

Simulated annealing

Bees algorithm

The number

of rows and

columns

Time(s) Reduced

intersections(%)

Figure 9: Parallel coordinates visualization of the algo-

rithms’ performance tested on different table sizes.

However, the comparison of the sorting algo-

rithms’ running time shows large differences when

the number of the rows and columns increases in the

table. The fastest ones (min-conﬂict, cross-entropy,

and simulated annealing) need around 17 seconds in

average to give results, while the rest of them require

minutes to do the same for a table with the size of

20 × 20.

TabularVis – A Circos-inspired Interactive Web Client based Tool for Improving the Clarity of Tabular Data Visualization

127

45 50 55 60

100

150

Reduced intersections(%)

Time(s)

Hill climbing

Min-conﬂicts

Cross-entropy

Cross-Entropy and min-conﬂicts

Simulated annealing

Bees algorithm

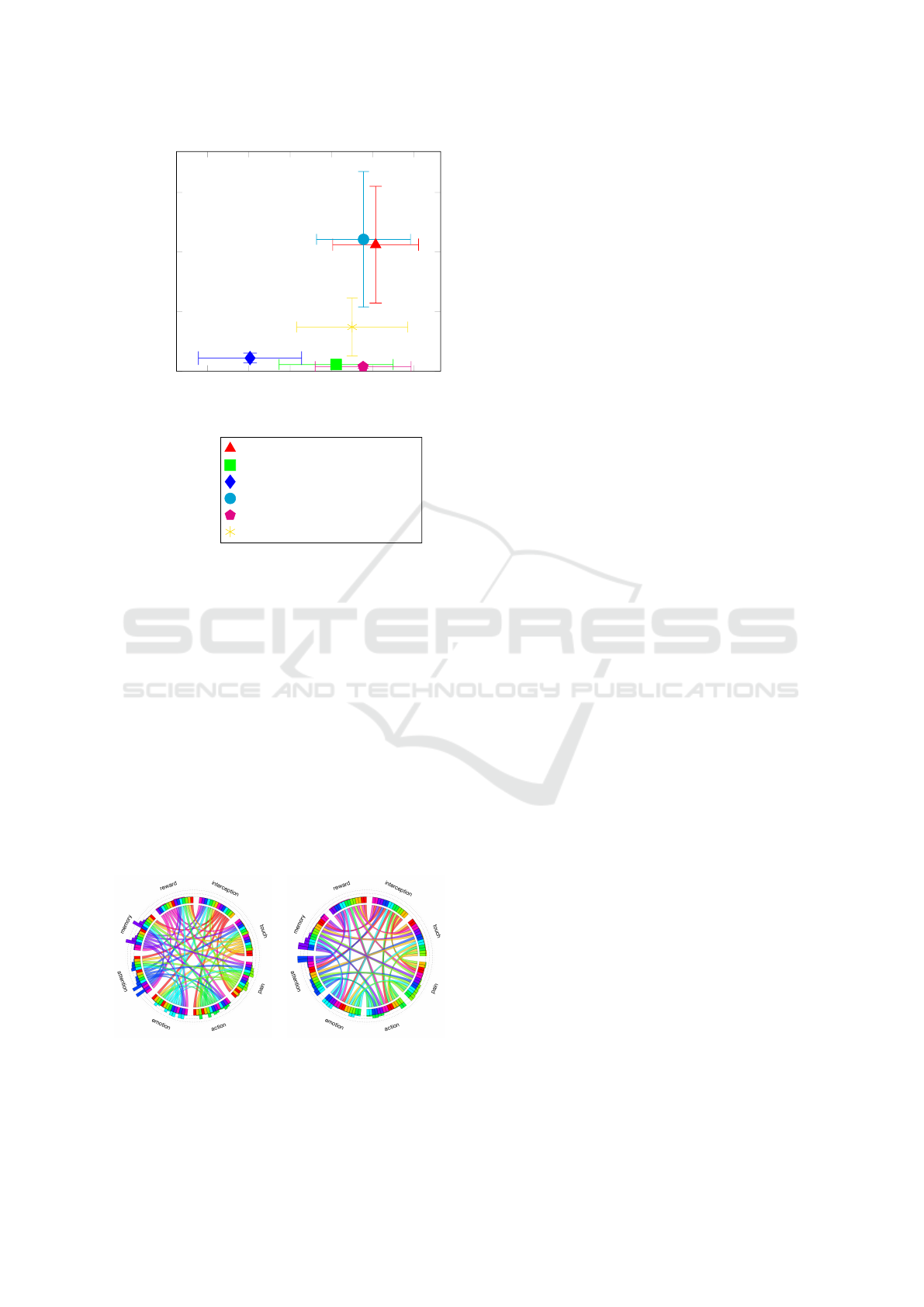
Figure 10: Comparison of the search algorithms’ execution

time and the resulting reduced intersections on 100 tables

with 15 rows and columns.

When the results of the tests are grouped by sizes,

the differences between the tested methods become

clearer and more noticeable (see Figure 10). The

cross-entropy method’s performance is really poor

compared to the others, and its running time is also

not the best. However, its modiﬁed version has a bet-

ter performance, but it requires way too much time to

give a result. The hill climbing has the best perfor-

mance, but the user has to wait too long for the algo-

rithm to ﬁnish the sorting. The min-conﬂicts and the

bees algorithms have a good performance, but there

is a faster method with better performance, and this is

the simulated annealing.

(a) (b)

Figure 11: These diagrams are created based on the heat

maps from the work of Cauda et al. (Cauda et al., 2012).

The left one shows the diagram (a) without sorting, and the

right one (b) is created by applying the sorting feature.

Based on these results, it seems that the best pos-

sible choices for sorting are the hill climbing, the

simulated annealing, the min-conﬂicts, and the bees

algorithm. There are not big differences between

the selected methods’ performance (≈ 5%), so when

we choose an algorithm for our sorting process, we

need to consider two important things, which are

the following. How fast is the selected method and

how much of the differences between the algorithms

are visible in the current diagram. In the case of

small table sizes, for example, tables with 5 rows and

columns, the differences between the algorithms’ re-

sults can be easily noticeable as Figure 12 shows us.

But on the other hand, this small difference is almost

negligible when the table’s size is 20 × 20. Beside

this, in Figure 12 we can also see in both cases, that

even a bit worse result is way better than the original

diagram without applying any sorting on it.

The selected algorithms have multiple parameters,

and we focused on keeping the balance between the

performance and the running time while we searched

the best settings for them. All of the images in this pa-

per are generated by using the previously mentioned

parameters in the description of each method. Fur-

thermore, we also used them in our application as de-

fault parameter values for the sorting algorithms.

5 APPLICATION

We have implemented a web application to present

the proposed visualization method and the sorting of

the connections. The software was written in the

Dart programming language, and it uses WebGL for

displaying the diagrams. These choices gave us the

opportunity to make a fully interactive application,

which lets the user modify (the data and the posi-

tion of the segments and connections) and customize

(change the visual appearance, like the color or the

shape of the segments and the connections) the di-

agram. However, the sorting feature is not interac-

tive, because the search methods need time to reduce

the number of intersections. The position of the seg-

ments can be changed in real time, and the customiza-

tion of its appearance is also possible. Our software

supports to change the connections’ shape by modi-

fying the parameters of the B

ezier curves. It offers

different predeﬁned coloring scheme for the blocks

and the connections. The application can work with

Circos’ data ﬁles and Excel spreadsheets as well, in

which the values are not limited to integers. Fur-

thermore, our software has its own editor, with which

the user can enter numbers in the table. These men-

tioned features allow easy data entry. The result of

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

128

(a) (b) (c)

(d) (e) (f)

Figure 12: Comparison of search algorithms based on two different table sizes. A 5 × 5 table was used for the upper set of

images ((a), (b), (c)) and one with 20 rows and columns was used for creating the lower diagrams ((d), (e), (f)). From the

images above, (a) and (d) (sorted with simulated annealing) have the least number of intersections, (b) and (e) (sorted with

bees algorithm) contain ≈ 5% more intersections, and the last two, (c) and (f) have not been sorted.

the sorting can be downloaded as a PNG ﬁle, and

it is also possible to download the input data in the

format, which is used by Circos. The application

is available at https://arato.inf.unideb.hu/

kunkli.roland/tabularvis/index.html (at the

current state of the development, our application

works properly only with the latest stable ver-

sion of Google’s Chrome browser), and the source

code is shared on GitHub (https://github.com/

pappgyorgy/TabularVis).

6 CONCLUSION

We introduced some improvements to an existing tab-

ular visualization technique, with which we can in-

crease the clarity of the visualization in various cases.

Replacing the segments with bars makes the values

easy to read and compare, if the scatter in the values of

the table is insigniﬁcant. The conception of concen-

tric circles also serves this purpose. We used uniﬁed

thickness for the connections to provide the ability to

see the pattern more clearly, which are formed by the

connections. This feature can provide more space for

labeling in cases, when the differences between the ta-

bles’ values are large. We also introduced a new way

for representing the direction of the links with arrow-

like shapes. Moreover, an efﬁcient solution was pro-

vided to the problem of reducing the number of inter-

sections between the links in the diagram, by modify-

ing the order of the elements around the circle, based

on different local search algorithms and global opti-

mization methods. We also implemented our visual-

ization and sorting method in a client-side web appli-

cation which is available for public usage.

The proposed techniques have some limitations

which give opportunities for further improvement.

First of all, our method can only visualize tables ﬁlled

with non-negative numbers, and it gives the best re-

sult in the case when there are elements, which are

not connected with each other. This means that some

TabularVis – A Circos-inspired Interactive Web Client based Tool for Improving the Clarity of Tabular Data Visualization

129

of the table’s cells contain zeros. Furthermore, dense

tables with a large number of rows and columns can

cause problems for our visualization method. Be-

cause in cases when the size of the tables is larger

than 20×20 and it contains only a few zeros, then the

middle part of the diagram becomes dense, and as a

result, the connections will be hard to follow. Also, in

this case, the sorting method is not effective because

it may require minutes to complete the computations.

Based on these limitations, a possible future im-

provement can be to ensure that the visualization

method works with tables ﬁlled with rational num-

bers. Because changing the position of a B

ezier curve

can cause intersections between the connections also

in the case of when its end positions do not justify

that, a modiﬁcation of the sorting method to detect

this kind of intersections can be a part of future work.

The maximization of the used area inside the circle by

modifying the parameters of the used B

ezier curves

individually is another potential way of improving our

work. Besides these, we are planning to give de-

tailed information about the connections or the seg-

ments (e.g., statistical information) by hovering the

mouse over them. Because of the mentioned reason

at the end of Section 2, we did not use edge bundling

to avoid clutter in the diagram. However, it can be

worth the effort to combine this technique with our

proposed modiﬁcation.

ACKNOWLEDGEMENTS

Supported by the

UNKP–17–4 New National

Excellence Program Of The Ministry Of Human Ca-

pacities.

REFERENCES

An, J., Lai, J., Sajjanhar, A., Batra, J., Wang, C., and Nel-

son, C. C. (2015). J-circos: an interactive circos plot-

ter. Bioinformatics, 31(9):1463–1465.

Andrews, K. and Wright, B. (2014). FluidDiagrams: Web-

Based Information Visualisation using JavaScript and

WebGL. In Elmqvist, N., Hlawitschka, M., and

Kennedy, J., editors, EuroVis - Short Papers. The Eu-

rographics Association.

Baur, M. and Brandes, U. (2005). Crossing Reduction in

Circular Layouts, pages 332–343. Springer Berlin

Heidelberg, Berlin, Heidelberg.

Bayer, T. (2011). A thousand ﬁbers connect us”

– wikiviz 2011 winner visualizes wikipedia’s

global reach. Retrieved May 14, 2017, from

https://blog.wikimedia.org/2011/10/06/a-

thousand-fibers-connect-us-wikiviz-

winner-visualize-wikipedias-global-reach/.

Blasco-Sopl

on, L., Grau-Valldosera, J., and Minguill

on, J.

(2015). Visualization of enrollment data using chord

diagrams. In Proceedings of the 10th International

Conference on Computer Graphics Theory and Ap-

plications, GRAPP 2015, pages 511–516, Portugal.

SCITEPRESS - Science and Technology Publications,

Lda.

Bornel

ov, S., Marillet, S., and Komorowski, J. (2014). Ciru-

vis: a web-based tool for rule networks and interaction

detection using rule-based classiﬁers. BMC Bioinfor-

matics, 15(1):139.

Bostock, M., Ogievetsky, V., and Heer, J. (2011). D3 data-

driven documents. IEEE Transactions on Visualiza-

tion and Computer Graphics, 17(12):2301–2309.

Brownlee, J. (2011). Clever Algorithms: Nature-Inspired

Programming Recipes. Lulu.com, 1st edition.

Burkart-Waco, D., Josefsson, C., Dilkes, B., Kozloff, N.,

Torjek, O., Meyer, R., Altmann, T., and Comai, L.

(2012). Hybrid incompatibility in arabidopsis is de-

termined by a multiple-locus genetic network. Plant

Physiology, 158(2):801–812.

Cauda, F., Torta, D. M.-E., Sacco, K., Geda, E., D’Agata,

F., Costa, T., Duca, S., Geminiani, G., and Amanzio,

M. (2012). Shared “core” areas between the pain and

other task-related networks. PLOS ONE, 7(8):1–10.

Chuah, M. C. and Eick, S. G. (1998). Information rich

glyphs for software management data. IEEE Com-

puter Graphics and Applications, 18(4):24–29.

creative coding community, C. E. (2009). Chrome Ex-

periments - WebGL Experiments. Retrieved June

5, 2017, from https://www.chromeexperiments.

com/webgl.

Cui, Y., Chen, X., Luo, H., Fan, Z., Luo, J., He, S., Yue,

H., Zhang, P., and Chen, R. (2016). Biocircos.js:

an interactive circos javascript library for biological

data visualization on web applications. Bioinformat-

ics, 32(11):1740–1742.

Dang, Q., Lin, X., and Konar, M. (2015). Agricultural vir-

tual water ﬂows within the united states. Water Re-

sources Research, 51(2):973–986.

Fujiwara, Y. (2015). Visualizing open data of input-output

tables in kobe city. In SIGGRAPH Asia 2015 Visu-

alization in High Performance Computing, SA ’15,

pages 18:1–18:1, New York, NY, USA. ACM.

Gansner, E. R. and Koren, Y. (2007). Improved Circular

Layouts, pages 386–398. Springer Berlin Heidelberg,

Berlin, Heidelberg.

Gu, Z., Gu, L., Eils, R., Schlesner, M., and Brors, B. (2014).

circlize implements and enhances circular visualiza-

tion in r. Bioinformatics, 30(19):2811–2812.

Hu, Y., Yan, C., Hsu, C.-H., Chen, Q.-R., Niu, K., Komat-

soulis, G. A., and Meerzaman, D. (2014). Omiccircos:

A simple-to-use r package for the circular visualiza-

tion of multidimensional omics data. Cancer Infor-

matics, 13:13–20.

Irimia, A. and Horn, J. D. V. (2013). The structural, con-

nectomic and network covariance of the human brain.

NeuroImage, 66(Supplement C):489 – 499.

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

130

Irimia, A. and Van Horn, J. (2014). Systematic network

lesioning reveals the core white matter scaffold of the

human brain. Frontiers in Human Neuroscience, 8:51.

Katapadi, V. K., Nambiar, M., and Raghavan, S. C. (2012).

Potential g-quadruplex formation at breakpoint re-

gions of chromosomal translocations in cancer may

explain their fragility. Genomics, 100(2):72 – 80.

Krzywinski, M. (2008). Articles // CIRCOS Circu-

lar Genome Data Visualization. ’Visualizing Ta-

bles’ section, ﬁrst image, Retrieved February 3,

2017, from http://circos.ca/presentations/

articles/vis_tables1/.

Krzywinski, M., Schein, J., Birol,

I., Connors, J., Gas-

coyne, R., Horsman, D., Jones, S. J., and Marra, M. A.

(2009). Circos: An information aesthetic for compar-

ative genomics. Genome Research, 19(9):1639–1645.

Lhuillier, A., Hurter, C., and Telea, A. (2017). State of the

art in edge and trail bundling techniques. Comput.

Graph. Forum, 36(3):619–645.

Li, Z. (2012). Infoviz: information visualization library. Re-

trieved May 13, 2017, from http://infoviz.org/.

Lin, X., Dang, Q., and Konar, M. (2014). A network anal-

ysis of food ﬂows within the united states of america.

Environmental science & technology, 48(10):5439–

5447.

Meyer, M., Munzner, T., and Pﬁster, H. (2009). Mizbee: A

multiscale synteny browser. IEEE Transactions on Vi-

sualization and Computer Graphics, 15(6):897–904.

Mwalongo, F., Krone, M., Becher, M., Reina, G., and Ertl,

T. (2015). Remote visualization of dynamic molecu-

lar data using webgl. In Proceedings of the 20th Inter-

national Conference on 3D Web Technology, Web3D

’15, pages 115–122, New York, NY, USA. ACM.

Nicholas, M., Archambault, D., and Laramee, R. S.

(2014). Interactive Visualisation of Automotive War-

ranty Data Using Novel Extensions of Chord Di-

agrams. In Elmqvist, N., Hlawitschka, M., and

Kennedy, J., editors, EuroVis - Short Papers. The Eu-

rographics Association.

Pan, K.-X., Zhu, H.-X., Chang, Z., Wu, K.-H., Shan, Y.-L.,

and Liu, Z.-X. (2013). Estimation of coal-related co2

emissions: The case of china. Energy & Environment,

24(7-8):1309–1321.

Russell, S. and Norvig, P. (2010). Artiﬁcial Intelligence:

A Modern Approach. Prentice Hall Series in Artiﬁ.

Prentice Hall.

Schmutz, J., McClean, P. E., Mamidi, S., Wu, G. A., Can-

non, S. B., Grimwood, J., Jenkins, J., Shu, S., Song,

Q., Chavarro, C., et al. (2014). A reference genome

for common bean and genome-wide analysis of dual

domestications. Nature genetics, 46(7):707–713.

Tine, M., Kuhl, H., Gagnaire, P.-A., Louro, B., Desmarais,

E., Martins, R. S., Hecht, J., Knaust, F., Belkhir, K.,

Klages, S., et al. (2014). European sea bass genome

and its variation provide insights into adaptation to

euryhalinity and speciation. Nature communications,

5:5770.

Yin, T., Cook, D., and Lawrence, M. (2012). ggbio: an

r package for extending the grammar of graphics for

genomic data. Genome Biology, 13(8):R77.

Zhang, H., Meltzer, P., and Davis, S. (2013). Rcircos: an r

package for circos 2d track plots. BMC Bioinformat-

ics, 14(1):244.

TabularVis – A Circos-inspired Interactive Web Client based Tool for Improving the Clarity of Tabular Data Visualization

131