Unsupervised Learning for Color Constancy

Nikola Bani

c and Sven Lon

cari

Image Processing Group, Department of Electronic Systems and Information Processing,

Faculty of Electrical Engineering and Computing, University of Zagreb, 10000 Zagreb, Croatia

Keywords:

Clustering, Color Constancy, Illumination Estimation, Unsupervised Learning, White Balancing.

Abstract:

Most digital camera pipelines use color constancy methods to reduce the inﬂuence of illumination and camera

sensor on the colors of scene objects. The highest accuracy of color correction is obtained with learning-based

color constancy methods, but they require a signiﬁcant amount of calibrated training images with known

ground-truth illumination. Such calibration is time consuming, preferably done for each sensor individually,

and therefore a major bottleneck in acquiring high color constancy accuracy. Statistics-based methods do

not require calibrated training images, but they are less accurate. In this paper an unsupervised learning-based

method is proposed that learns its parameter values after approximating the unknown ground-truth illumination

of the training images, thus avoiding calibration. In terms of accuracy the proposed method outperforms all

statistics-based and many state-of-the-art learning-based methods. The results are presented and discussed.

1 INTRODUCTION

Beside other abilities the human visual system (HVS)

can recognize colors of scene objects even under var-

ious illumination. This ability is known as color con-

stancy (Ebner, 2007) and most digital cameras have

computational color constancy implemented in their

image processing pipelines (Kim et al., 2012). The

main task of computational color constancy is to per-

form an accurate illumination estimation, which is

then used to chromatically adapt the image in order

to remove the inﬂuence of the illumination on colors.

The most commonly used image f formation model

for this problem with included Lambertian assump-

tion is (Gijsenij et al., 2011)

(x) =

I(λ, x)R(λ, x)ρ

(λ)dλ (1)

where c ∈ {R, G, B} is a color channel, x is a given

image pixel, λ is the wavelength of the light, ω is

the visible spectrum, I(λ, x) is the spectral distribution

of the light source, R(λ, x) is the surface reﬂectance,

and ρ

(λ) is the camera sensitivity of color channel c.

To make the problem simpler, uniform illumination is

usually assumed and by removing x from I(λ, x), the

observed light source color is given as

e =









I(λ)ρ(λ)dλ. (2)

By knowing only the direction of e, an image can

be successfully chromatically adapted (Barnard et al.,

2002). With only image pixel values f given and

both I(λ) and ρ(λ) unknown, calculating e is an ill-

posed problem, which needs additional assumptions

to be solved. Many illumination estimation methods

with different assumptions have been proposed. In

the ﬁrst of two main groups of illumination estima-

tion methods are low-level statistics-based methods

such as White-patch (Land, 1977; Funt and Shi, 2010)

and its improvements (Bani

c and Lon

cari

c, 2013;

Bani

c and Lon

cari

c, 2014a; Bani

c and Lon

cari

2014b), Gray-world (Buchsbaum, 1980), Shades-of-

Gray (Finlayson and Trezzi, 2004), Grey-Edge (1st

and 2nd order) (Van De Weijer et al., 2007a), us-

ing bright and dark colors (Cheng et al., 2014).

The second main group consists of learning-based

methods, all of which are supervised, like gamut

mapping (pixel, edge, and intersection based) (Fin-

layson et al., 2006), using high-level visual infor-

mation (Van De Weijer et al., 2007b), natural im-

age statistics (Gijsenij and Gevers, 2007), Bayesian

learning (Gehler et al., 2008), spatio-spectral learn-

ing (maximum likelihood estimate, and with gen.

prior) (Chakrabarti et al., 2012), simplifying the illu-

mination solution space (Bani

c and Lon

cari

c, 2015a;

Bani

c and Lon

cari

c, 2015b; Bani

c and Lon

cari

2015b), using color/edge moments (Finlayson, 2013),

using regression trees with simple features from color

Bani

c, N. and Lon

cari

c, S.

Unsupervised Learning for Color Constancy.

DOI: 10.5220/0006621801810188

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages

181-188

ISBN: 978-989-758-290-5

181

distribution statistics (Cheng et al., 2015), performing

various kinds of spatial localizations (Barron, 2015;

Barron and Tsai, 2017), using convolutional neural

networks (Bianco et al., 2015; Shi et al., 2016; Hu

et al., 2017). Statistics-based methods are character-

ized by a relatively high speed, simplicity, and usu-

ally lower accuracy, while with the learning-based

methods it is vice versa. However, several recently

proposed learning-based methods are not only highly

accurate, but also as fast as statistics-based meth-

ods (Bani

c and Lon

cari

c, 2015b; Cheng et al., 2015).

Nevertheless, since all well-known learning-based

methods are supervised, a major obstacle for their ap-

plication is that for a given sensor, despite proposed

workarounds (Gao et al., 2016), supervised learning-

based methods have to be trained on calibrated images

taken by preferably the same sensor (Aytekin et al.,

2017). To calibrate the images, a calibration object

has to be placed in the scenes of these images and

later segmented to extract the ground-truth illumina-

tion. The amount of manual work required for such

calibration is the main bottleneck in enabling highly

accurate color constancy for a given sensor.

To try to avoid such calibration, in this paper an

unsupervised learning-based method is proposed that

learns its parameter values from non-calibrated im-

ages with unknown ground-truth illumination. Such

learning is possible by clustering the approximated

ground-truth illuminations of images from the train-

ing set and then extracting useful information. The

method is fast, hardware-friendly, and it outperforms

most state-of-the-art methods in terms of accuracy. To

the best of the authors’ knowledge this is the ﬁrst suc-

cessful unsupervised learning-based color constancy

method evaluated on benchmark datasets and thus

also a contribution to the color constancy philosophy.

The paper is structured as follows: Section 2 lays

out the motivation for the proposed method, Section 3

describes the method, in Section 4 the experimental

results are presented and discussed, and ﬁnally Sec-

tion 5 concludes the paper.

Figure 1: The rb-chromaticities of the ground-truth illumi-

nations and Gray-world illumination estimations for images

of the Samsung benchmark dataset (Cheng et al., 2014).

2 MOTIVATION

Ground-truth illumination of training images for su-

pervised learning-based methods is extracted from

calibration objects placed in the image scenes. As

explained in the introduction, obtaining the ground-

truth illumination is time consuming, but it enables

supervised learning and high illumination estimation

accuracy. To speed things up signiﬁcantly, usage of

calibration objects has to be dropped out. Then in

place of the real ground-truth illumination, some kind

of its approximation has to be used instead, e.g. illu-

mination estimations obtained by means of statistics-

based methods that require no previous learning. But

since they are usually less accurate than learning-

based methods, using their estimations as the ground-

truth illumination may be counterproductive. How-

ever, instead of only image-based illumination esti-

mation, there are other kinds of information that such

methods provide. Namely, even illumination estima-

tions of the simplest statistics-based methods appear

”to correlate roughly with the actual illuminant” (Fin-

layson, 2013) as shown in Fig 1 i.e. they occupy

roughly the same region in the chromaticity plane. To

have a better insight into this phenomenon, some ad-

ditional numerical analysis is required.

Figure 2: Values of SAE averaged over 1000 random sub-

sets of the Sony benchmark dataset (Cheng et al., 2014) for

various subset sizes.

As described in more detail later in Section 4.1,

the error measure for accuracy of illumination esti-

mation is the angular error i.e. the angle between the

vectors of ground-truth illumination and illumination

estimation. One way to see how well a set of illu-

mination estimations numerically resembles the set

of ground-truth illuminations in terms of occupying

the same region in the chromaticity space is to rear-

range the existing illumination estimations between

images in order to minimize the sum of overall an-

gular errors obtained for such rearranged illumination

estimations. More formally this is the same as mak-

ing pairs of illumination points under three following

constraints: ﬁrst, in each pair one point comes from

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

182

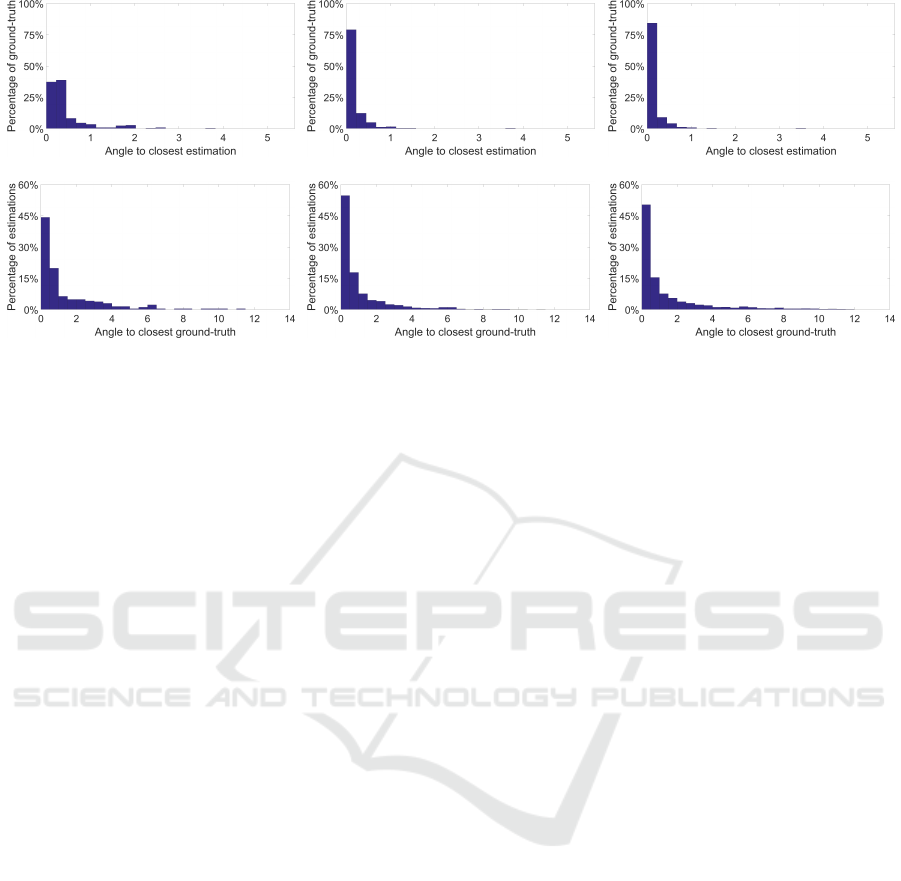
(a) (b) (c)

Figure 3: Percentage of ground-truth with speciﬁed angle to the closest estimation (ﬁrst row) and vice versa (second row)

obtained with Shades-of-Gray on images of the Sony benchmark dataset (Cheng et al., 2014) for (a) n = 1, (b) n = 4, and

the set of ground-truth illuminations and the other

from the set of illumination estimations; second, ev-

ery point from both sets is a member of exactly one

pair; and third, the pairs are formed so that the the sum

of angular errors between all pair points is minimized.

Effectively, this boils down to solving the optimal as-

signment problem (Burkard et al., 2012). In the rest

of the paper the minimal possible mean angular error

between pair points for given sets will be denoted as

Sets’ Angular Error (SAE). It must be clearly stressed

here that a low SAE does not implicate an accurate

method; by deﬁnition an inaccurate method can un-

der certain conditions produce estimations with a low

SAE. As the number of points in the sets grows, SAE

should decrease since every point will have more pair-

ing opportunities. This is shown in Fig. 2 where the

values of SAE averaged over 1000 random subsets of

the Sony benchmark dataset (Cheng et al., 2014) de-

crease as the size of the used subsets increases. Based

on the empirical evidence, including the results shown

in Fig. 2, the impact of the method choice on SAE

seems to be higher then the impact of the set size.

These results show that by applying well chosen

methods to a sufﬁcient number of given images it is

possible to obtain a low SAE, which is a proof of con-

cept that a relatively accurate approximation of the

set of unknown ground-truth illuminations for these

images is feasible. This deﬁnitely motivates to ex-

ploit the demonstrated concept further, but to have

a practical use of it, at least two questions need to

be answered: ﬁrst, what other information useful for

a more accurate illumination estimation can be ex-

tracted from a set of ground-truth illumination ap-

proximations, and second, how to obtain such approx-

imated sets that have a low SAE?

As for the ﬁrst question, the ground-truth illumi-

nations or their approximations for many images can

reveal in which chromaticity space regions are future

illumination estimations of new images most likely

to appear. There are several methods that rely on

such kind of information (Bani

c and Lon

cari

c, 2015a;

Mazin et al., 2015; Cheng et al., 2015; Bani

c and

Lon

cari

c, 2015b) with probably the least demand-

ing one being the Color Dog method (Bani

c and

Lon

cari

c, 2015b). During the training phase it clus-

ters the ground-truth illuminations by using the k-

means clustering (Vassilvitskii, 2007) with angular

instead of Euclidean distance. The cluster centers

obtained in this process become the only illumina-

tion estimations that the method will ever produce

when used later in production. When applied to a

new image, Color Dog ﬁrst runs the parameterless

White-patch and Gray-world methods. The angular

distances between their illumination estimations and

the learned cluster centers are used as weighted votes

to determine which center should represent the illu-

mination on the given image. Well positioned centers

in the chromaticity plane result in relatively small er-

rors (Bani

c and Lon

cari

c, 2015b) and despite its sim-

plicity, Color Dog was reported to be very successful.

The centers and their number are learned by means of

nested cross-validation (Japkowicz and Shah, 2011).

Since accurate ground-truth illuminations are needed

for such learning, using approximations gives poor re-

sults, but the main idea of Color Dog can be the basis

for a method that learns from approximations. Such a

new method is proposed in the following section.

Unsupervised Learning for Color Constancy

183

(a) (b)

Figure 4: The rb-chromaticities of the ground-truth illuminations and SoG illumination estimations for n = 8 on images of

the Samsung benchmark dataset (Cheng et al., 2014) (a) before and (b) after trimming with t = 0.3 (best viewed in color).

3 THE PROPOSED METHOD

Nested cross-validation can be circumvented by sim-

ply ﬁxing the number of centers. Using more cen-

ters increases the upper limit for accuracy because

of the ﬁner chromaticity space splitting, but it also

poses a harder classiﬁcation problem for which the

upper accuracy limit may be rarely reached. Thus

the new method proposed here uses only two cen-

ters and assumes that most images can be classiﬁed

as having either a warmer i.e. reddish or a cooler i.e.

blueish illumination, which is effectively a simpliﬁca-

tion of the Planckian locus (Schanda, 2007) that has

already been used for illumination estimation (Bani

and Lon

cari

c, 2015a; Mazin et al., 2015). A some-

what similar rough division to an indoor and outdoor

type illumination has been successfully used for a

slightly different purpose in (Cheng et al., 2016).

With the answer to the ﬁrst question from the pre-

vious section proposed, it remains to resolve the sec-

ond one i.e. which illumination estimations should

be clustered to get centers that are well positioned

among the ground-truth illumination? A single

statistics-based method with ﬁxed parameter values

may achieve a relatively low SAE, but with unknown

ground-truth illuminations, it cannot be said which

parameter values will result in minimal SAE. To solve

this problem, it can be assumed that for any set of pa-

rameter values for a statistics-based method in most

cases there will be a number of training images for

which the method’s illumination estimations will be

accurate. Other parameter values should again give

accurate estimations for some other images. If this

is repeated for more sets of parameter values, then

the region with the actual ground-truth illumination

should be more densely ﬁlled with illumination esti-

mations than other regions. Such behaviour can also

be observed for the Shades-of-Gray (SoG) (Finlayson

and Trezzi, 2004) method, which uses the Minkowski

norm p for illumination estimation



( f

(x))



= ke

(3)

where k is a constant that assures the unit length of

e. SoG already offers a diversity of illumination esti-

mations by only changing the value of its single pa-

rameter. While other statistics-based methods like

Gray-Edge may be more accurate, this holds only if

their multiple parameters are well chosen. In order

to avoid possible problems related to parameter value

tuning, the proposed method clusters combined SoG

illumination estimations for p ∈ {1, 2, ..., n}. Fig. 3

shows the inﬂuence of n on percentage of ground-

truth with speciﬁed angle to the closest estimation and

vice versa. It can be observed that using combined

SoG estimations for various values of p can indeed

result in a more accurate coverage of the chromatic-

ity plane regions populated with ground-truth illumi-

nations. Theoretically this should also improve the

accuracy of obtained clustering centers.

Figure 5: Percentage of SoG estimations for n = 8 with

speciﬁed angle to the closest ground-truth for the Sony

benchmark dataset (Cheng et al., 2014).

However, beside putting more points around the

actual chromaticity plane region with the ground-

truth, combining estimations for several values of

p also introduces a lot of estimations that are far

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

184

away from all ground-truth illuminations and repre-

sent noise. Under the used assumption such estima-

tions should be scattered and less dense than the es-

timations closer to the ground-truth region and this

could be used to reduce their inﬂuence. A direct so-

lution would be to use clustering techniques that con-

sider outliers and simply ignore them with one ex-

ample being DBSCAN (Ester et al., 1996). How-

ever, since DBSCAN and some other similar meth-

ods determine the number of centers on their own

and additionally the problem here does not involve

some arbitrarily shaped clusters, another solution is

proposed. After the initial clustering with k-means,

for each cluster center 100 · t% of its furthest estima-

tions are removed i.e. trimmed and then clustering is

repeated only on the remaining estimations to obtain

the ﬁnal cluster centers. This trimming procedure is

summarized in Algorithm 1. Fig. 4 shows an exam-

ple of such an outlier removal. The numerical effect

of it can be observed when comparing the lower right

histogram in Fig. 3 and the histogram in Fig. 5, which

shows that after trimming the remaining illuminations

are much closer to the ground-truth. Default parame-

ter values are set to n = 8 and t = 0.3 since they were

empirically found to work well. In the following sec-

tion on experimental results these values have been

used for all benchmark datasets. Tuning them for each

set individually would result in a signiﬁcantly higher

accuracy, but that would defeat the whole purpose of

unsupervised learning since ground-truth illumination

would be needed for such ﬁne tuning of parameters.

For simpler notation in the experimental results

and because the proposed method learns the values

of its parameters from images obtained in the wild

without knowing their ground-truth illumination, it is

named Color Tiger (CT). Now that the whole theo-

retical background with all required assumptions has

been explained, Color Tiger’s training procedure can

be simply described as learning the centers of two

clusters from a speciﬁcally trimmed set of illumina-

tion estimations obtained by applying Shades-of-Gray

to training images for every p ∈ {1, 2, ..., 8}, which is

summarized in Algorithm 2. The illumination estima-

tion for new images resembles the one of Color Dog

and it is given in Algorithm 3.

4 EXPERIMENTAL RESULTS

4.1 Experimental Setup

The following benchmark datasets have been used to

compare the accuracy of the proposed method to the

accuracy of other well-known methods: the GreyBall

Algorithm 1: Trimming.

Input: data D, number of centers k, threshold t

Output: trimmed data T

1: C = kmeans(D, k)  Use angular distance

2: T = {}

3: r = 1 −t

4: for c

∈ C do

5: D

= {d ∈ D | c

= arg min

∈C

∠ (c

, d)}

6: r

= b100 · rc-th percentile of {∠ (c

, d) | d ∈

}

7: D

= {d | ∠ (c

, d) ≤ r

}

8: T.AddAll(D

)

9: end for

Algorithm 2: Color Tiger Training.

Input: images I, SoG upper power n, trimming t

Output: set of two centers C

1: E = {}

2: for I ∈ I do

3: for p ∈ {1, 2, ..., n} do

4: e = ShadesO f Gray(I, p)

5: E.Add(e)

6: end for

7: end for

8: E

= Trimming(E, 2, t)

9: C = kmeans(E

, 2)  Use angular distance

Algorithm 3: Color Tiger Application.

Input: image I, set of two centers C

Output: illumination estimation e

1: e

= GrayWorld(I)

2: e

W P

= W hitePatch(I)

3: e = arg max

∈C



·e

||c

||·||e

·e

W P

||c

||·||e

W P



dataset (Ciurea and Funt, 2003), its approximated

linear version, and eight linear NUS dataset (Cheng

et al., 2014). The ColorChecker dataset (Gehler et al.,

2008; L. Shi, 2015) has not been used to avoid confu-

sion over various results mentioned in numerous pub-

lications during ColorChecker’s history of partially

wrong usage when reporting the results of older meth-

ods despite warnings from leading experts in the area

of color constancy going back as far as 2013 (Lynch

et al., 2013). Since in digital devices illumination es-

timation is mostly performed on linear images (Kim

et al., 2012) similar to the model described by Eq. (1),

linear datasets are preferred over the non-linear ones.

Each dataset has images and their ground-truth il-

luminations obtained by putting a calibration object

Unsupervised Learning for Color Constancy

185

in the image scene, e.g. a color checker or a gray ball

that is masked out during testing to avoid bias.

Various illumination estimation accuracy mea-

sures have been proposed (Gijsenij et al., 2009; Fin-

layson and Zakizadeh, 2014; Bani

c and Lon

cari

2015a). The most commonly used one is the angular

error i.e. the angle between the illumination estima-

tion vector and the ground-truth illumination. All an-

gular errors obtained for a given method on a chosen

dataset are usually summarized by different statistics.

Because of the non-symmetry of the angular error dis-

tribution, the most important of these statistics is the

median angular error (Hordley and Finlayson, 2004).

Cross-validation on all used datasets was per-

formed with the same folds as in other publications.

The source code for recreating the results given

in the following subsection is publicly available at

http://www.fer.unizg.hr/ipg/resources/color constancy/.

Table 1: Combined performance of different color con-

stancy methods on eight NUS dataset (lower median is bet-

ter). The used format is the same as in (Barron and Tsai,

2017).

Algorithm Mean Med. Tri.

Best

25%

Worst

25%

Avg.

White-Patch (Funt and Shi, 2010) 9.91 7.44 8.78 1.44 21.27 7.24

Pixels-based Gamut (Gijsenij et al.,

2010)

5.27 4.26 4.45 1.28 11.16 4.27

Grey-world (Buchsbaum, 1980) 4.59 3.46 3.81 1.16 9.85 3.70

Edge-based Gamut (Gijsenij et al.,

2010)

4.40 3.30 3.45 0.99 9.83 3.45

Shades-of-Gray (Finlayson and Trezzi,

2004)

3.67 2.94 3.03 0.98 7.75 3.01

Natural Image Statistics (Gijsenij and

Gevers, 2011)

3.45 2.88 2.95 0.83 7.18 2.81

Local Surface Reﬂectance

Statistics (Gao et al., 2014)

3.45 2.51 2.70 0.98 7.32 2.79

2nd-order Gray-Edge (Van De Weijer

et al., 2007a)

3.36 2.70 2.80 0.89 7.14 2.76

1st-order Gray-Edge (Van De Weijer

et al., 2007a)

3.35 2.58 2.76 0.79 7.18 2.67

Bayesian (Gehler et al., 2008) 3.50 2.36 2.57 0.78 8.02 2.66

General Gray-World (Barnard et al.,

2002)

3.20 2.56 2.68 0.85 6.68 2.63

Spatio-spectral Statistics (Chakrabarti

et al., 2012)

3.06 2.58 2.74 0.87 6.17 2.59

Bright-and-dark Colors PCA (Cheng

et al., 2014)

2.93 2.33 2.42 0.78 6.13 2.40

Corrected-Moment (Finlayson, 2013) 2.95 2.05 2.16 0.59 6.89 2.21

Color Tiger (proposed) 2.96 1.70 1.97 0.53 7.50 2.09

Color Dog (Bani

c and Lon

cari

2015b)

2.83 1.77 2.03 0.48 7.04 2.03

Shi et al. 2016 (Shi et al., 2016) 2.24 1.46 1.68 0.48 6.08 1.74

CCC (Barron, 2015) 2.38 1.48 1.69 0.45 5.85 1.74

Cheng 2015 (Cheng et al., 2015) 2.18 1.48 1.64 0.46 5.03 1.65

FFCC (Barron and Tsai, 2017) 1.99 1.31 1.43 0.35 4.75 1.44

4.2 Accuracy

Tables 1, 2, and 3 show the comparisons between

the accuracies of the proposed method and other il-

lumination estimation methods on various datasets.

The proposed method outperforms all statistics-based

methods and many learning-based methods. For all

datasets except for the GreyBall dataset its median

Table 2: Performance of different color constancy methods

on the original GreyBall dataset (lower median is better).

Algorithm Mean Median Trimean

do nothing 8.28 6.70 7.25

Low-level statistics-based methods

Gray-world (GW) (Buchsbaum, 1980) 7.87 6.97 7.14

White-Patch (WP) (Funt and Shi, 2010) 6.80 5.30 5.77

Shades-of-Gray (Finlayson and Trezzi, 2004) 6.14 5.33 5.51

General Gray-World (Barnard et al., 2002) 6.14 5.33 5.51

1st-order Gray-Edge (Van De Weijer et al.,

2007a)

5.88 4.65 5.11

2nd-order Gray-Edge (Van De Weijer et al.,

2007a)

6.10 4.85 5.28

Learning-based methods

Pixel-based gamut (Finlayson et al., 2006) 7.07 5.81 6.12

Edge-based gamut (Finlayson et al., 2006) 6.81 5.81 6.03

Intersection-based gamut (Finlayson et al.,

2006)

6.93 5.80 6.05

Natural Image Statistics (Gijsenij and Gevers,

2011)

5.19 3.93 4.31

Exemplar-based learning (Joze and Drew,

2012)

4.38 3.43 3.67

Color Cat (CC) (Bani

c and Lon

cari

c, 2015a) 4.22 3.17 3.46

Smart Color Cat (SCC) (Bani

c and Lon

cari

2015b)

4.62 3.52 3.80

Color Dog

W P,GW

(Bani

c and Lon

cari

c, 2015b)

5.27 3.71 4.16

Color Dog

(Bani

c and Lon

cari

c, 2015b) 4.50 2.86 3.50

Color Dog

SCC

(Bani

c and Lon

cari

c, 2015b) 4.80 3.08 3.71

Color Tiger (proposed) 5.61 3.39 4.31

Table 3: Performance of different color constancy methods

on the linear GreyBall dataset (lower median is better).

Algorithm Mean Median Trimean

do nothing 15.62 14.00 14.56

Low-level statistics-based methods

Gray-world (GW) (Buchsbaum, 1980) 13.01 10.96 11.53

White-Patch (WP) (Funt and Shi, 2010) 12.68 10.50 11.25

Shades-of-Gray (Finlayson and Trezzi, 2004) 11.55 9.70 10.23

General Gray-World (Barnard et al., 2002) 11.55 9.70 10.23

1st-order Gray-Edge (Van De Weijer et al.,

2007a)

10.58 8.84 9.18

2nd-order Gray-Edge (Van De Weijer et al.,

2007a)

10.68 9.02 9.40

Learning-based methods

Pixel-based gamut (Finlayson et al., 2006) 11.79 8.88 9.97

Edge-based gamut (Finlayson et al., 2006) 12.78 10.88 11.38

Intersection-based gamut (Finlayson et al.,

2006)

11.81 8.93 10.00

Natural Image Statistics (Gijsenij and Gevers,

2011)

9.87 7.65 8.29

Exemplar-based learning (Joze and Drew,

2012)

7.97 6.46 6.77

Color Cat (CC) (Bani

c and Lon

cari

c, 2015a) 8.73 7.07 7.43

Smart Color Cat (SCC) (Bani

c and Lon

cari

2015b)

8.18 6.28 6.73

Color Dog

W P,GW

(Bani

c and Lon

cari

c, 2015b)

10.27 7.33 8.20

Color Dog

(Bani

c and Lon

cari

c, 2015b) 8.81 5.98 6.97

Color Dog

SCC

(Bani

c and Lon

cari

c, 2015b) 8.51 5.55 6.56

Color Tiger (proposed) 9.51 7.11 7.66

angular error is below the acceptable 3

◦

(Finlayson

et al., 2005; Fredembach and Finlayson, 2008).

4.3 Discussion

Beyond the fact that the proposed method outper-

formed all statistics-based methods and many state-

of-the-art learning-based methods, a far more im-

portant thing to stress here is that it did so with-

out having any ground-truth illumination data avail-

able. Not only does this show the abundance of in-

formation available in even the simplest natural im-

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

186

age statistics, but it also opens a simple and effec-

tive way of achieving highly accurate illumination es-

timation for a given sensor by only providing train-

ing images without ground-truth illumination data.

Skipping the calibration of training images can save

a signiﬁcant amount of time and in some cases this

can make the proposed method more suitable for

practical applications than other learning-based meth-

ods. Since in production it only executes two of

the fastest statistics-based methods with practically

no memory requirements, namely Gray-world and

White-patch (Cheng et al., 2014), and then performs a

small and constant number of calculations for voting,

the proposed method is hardware-friendly and thus

widely applicable. Unlike Color Dog, the proposed

method is also immune to problems of false ground-

truth data (Zakizadeh et al., 2015). Finally, if the as-

sumptions and steps devised here have led to the de-

scribed results, it is can be assumed that higher accu-

racy could be achieved by using more sophisticated

image statistics, voters, and trimming procedures.

5 CONCLUSIONS AND FUTURE

RESEARCH

A fast and hardware-friendly unsupervised learning-

based method that learns its parameter values from

images with unknown ground-truth illumination has

been proposed. In terms of accuracy the method out-

performs all statistics-based and many state-of-the-art

learning-based methods. This demonstrates how to

achieve highly accurate color constancy for a given

sensor without carrying out the usually time con-

suming calibration of training images. The proposed

method could possibly also be an important step

in color constancy philosophy, especially now when

there are large amounts of uncalibrated images avail-

able on the Internet. Future research will focus on ex-

tracting more useful information from statistics-based

illumination estimations obtained on training images

without ground-truth illumination and on other ways

of outlier removal.

REFERENCES

Aytekin, C¸ ., Nikkanen, J., and Gabbouj, M. (2017). INTEL-

TUT Dataset for Camera Invariant Color Constancy

Research. arXiv preprint arXiv:1703.09778.

Bani

c, N. and Lon

cari

c, S. (2015a). Color Cat: Remember-

ing Colors for Illumination Estimation. Signal Pro-

cessing Letters, IEEE, 22(6):651–655.

Bani

c, N. and Lon

cari

c, S. (2015b). Using the red chro-

maticity for illumination estimation. In Image and

Signal Processing and Analysis (ISPA), 2015 9th In-

ternational Symposium on, pages 131–136. IEEE.

Bani

c, N. and Lon

cari

c, S. (2013). Using the Random

Sprays Retinex Algorithm for Global Illumination Es-

timation. In Proceedings of The Second Croatian

Computer Vision Workshopn (CCVW 2013), pages 3–

7. University of Zagreb Faculty of Electrical Engi-

neering and Computing.

Bani

c, N. and Lon

cari

c, S. (2014a). Color Rabbit: Guid-

ing the Distance of Local Maximums in Illumina-

tion Estimation. In Digital Signal Processing (DSP),

2014 19th International Conference on, pages 345–

350. IEEE.

Bani

c, N. and Lon

cari

c, S. (2014b). Improving the White

patch method by subsampling. In Image Processing

(ICIP), 2014 21st IEEE International Conference on,

pages 605–609. IEEE.

Bani

c, N. and Lon

cari

c, S. (2015a). A Perceptual Measure

of Illumination Estimation Error. In VISAPP, pages

136–143.

Bani

c, N. and Lon

cari

c, S. (2015b). Color Dog: Guiding the

Global Illumination Estimation to Better Accuracy. In

VISAPP, pages 129–135.

Barnard, K., Cardei, V., and Funt, B. (2002). A compar-

ison of computational color constancy algorithms. i:

Methodology and experiments with synthesized data.

Image Processing, IEEE Transactions on, 11(9):972–

984.

Barron, J. T. (2015). Convolutional Color Constancy. In

Proceedings of the IEEE International Conference on

Computer Vision, pages 379–387.

Barron, J. T. and Tsai, Y.-T. (2017). Fast Fourier Color Con-

stancy. In Computer Vision and Pattern Recognition,

2017. CVPR 2017. IEEE Computer Society Confer-

ence on, volume 1. IEEE.

Bianco, S., Cusano, C., and Schettini, R. (2015). Color

Constancy Using CNNs. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion Workshops, pages 81–89.

Buchsbaum, G. (1980). A spatial processor model for object

colour perception. Journal of The Franklin Institute,

310(1):1–26.

Burkard, R., Dell’Amico, M., and Martello, S. (2012). As-

signment problems: revised reprint. SIAM.

Chakrabarti, A., Hirakawa, K., and Zickler, T. (2012). Color

constancy with spatio-spectral statistics. Pattern Anal-

ysis and Machine Intelligence, IEEE Transactions on,

34(8):1509–1519.

Cheng, D., Abdelhamed, A., Price, B., Cohen, S., and

Brown, M. S. (2016). Two Illuminant Estimation

and User Correction Preference. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition, pages 469–477.

Cheng, D., Prasad, D. K., and Brown, M. S. (2014). Illu-

minant estimation for color constancy: why spatial-

domain methods work and the role of the color distri-

bution. JOSA A, 31(5):1049–1058.

Cheng, D., Price, B., Cohen, S., and Brown, M. S. (2015).

Effective learning-based illuminant estimation using

Unsupervised Learning for Color Constancy

187

simple features. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 1000–1008.

Ciurea, F. and Funt, B. (2003). A large image database

for color constancy research. In Color and Imaging

Conference, volume 2003, pages 160–164. Society for

Imaging Science and Technology.

Ebner, M. (2007). Color Constancy. The Wiley-IS&T Se-

ries in Imaging Science and Technology. Wiley.

Ester, M., Kriegel, H.-P., Sander, J., Xu, X., et al. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. In Kdd, volume 96,

pages 226–231.

Finlayson, G. D. (2013). Corrected-moment illuminant es-

timation. In Proceedings of the IEEE International

Conference on Computer Vision, pages 1904–1911.

Finlayson, G. D., Hordley, S. D., and Morovic, P. (2005).

Colour constancy using the chromagenic constraint.

In Computer Vision and Pattern Recognition, 2005.

CVPR 2005. IEEE Computer Society Conference on,

volume 1, pages 1079–1086. IEEE.

Finlayson, G. D., Hordley, S. D., and Tastl, I. (2006). Gamut

constrained illuminant estimation. International Jour-

nal of Computer Vision, 67(1):93–109.

Finlayson, G. D. and Trezzi, E. (2004). Shades of gray and

colour constancy. In Color and Imaging Conference,

volume 2004, pages 37–41. Society for Imaging Sci-

ence and Technology.

Finlayson, G. D. and Zakizadeh, R. (2014). Reproduction

angular error: An improved performance metric for

illuminant estimation. perception, 310(1):1–26.

Fredembach, C. and Finlayson, G. (2008). Bright chroma-

genic algorithm for illuminant estimation. Journal of

Imaging Science and Technology, 52(4):40906–1.

Funt, B. and Shi, L. (2010). The rehabilitation of MaxRGB.

In Color and Imaging Conference, volume 2010,

pages 256–259. Society for Imaging Science and

Technology.

Gao, S., Han, W., Yang, K., Li, C., and Li, Y. (2014). Ef-

ﬁcient color constancy with local surface reﬂectance

statistics. In European Conference on Computer Vi-

sion, pages 158–173. Springer.

Gao, S.-B., Zhang, M., Li, C.-Y., and Li, Y.-J. (2016). Im-

proving Color Constancy by Discounting the Varia-

tion of Camera Spectral Sensitivity. arXiv preprint

arXiv:1609.01670.

Gehler, P. V., Rother, C., Blake, A., Minka, T., and Sharp, T.

(2008). Bayesian color constancy revisited. In Com-

puter Vision and Pattern Recognition, 2008. CVPR

2008. IEEE Conference on, pages 1–8. IEEE.

Gijsenij, A. and Gevers, T. (2007). Color Constancy using

Natural Image Statistics. In CVPR, pages 1–8.

Gijsenij, A. and Gevers, T. (2011). Color constancy using

natural image statistics and scene semantics. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 33(4):687–698.

Gijsenij, A., Gevers, T., and Lucassen, M. P. (2009). Per-

ceptual analysis of distance measures for color con-

stancy algorithms. JOSA A, 26(10):2243–2256.

Gijsenij, A., Gevers, T., and Van De Weijer, J. (2010). Gen-

eralized gamut mapping using image derivative struc-

tures for color constancy. International Journal of

Computer Vision, 86(2):127–139.

Gijsenij, A., Gevers, T., and Van De Weijer, J. (2011).

Computational color constancy: Survey and exper-

iments. Image Processing, IEEE Transactions on,

20(9):2475–2489.

Hordley, S. D. and Finlayson, G. D. (2004). Re-evaluating

colour constancy algorithms. In Pattern Recognition,

2004. ICPR 2004. Proceedings of the 17th Interna-

tional Conference on, volume 1, pages 76–79. IEEE.

Hu, Y., Wang, B., and Lin, S. (2017). Fully Convolutional

Color Constancy with Conﬁdence-weighted Pooling.

In Computer Vision and Pattern Recognition, 2017.

CVPR 2017. IEEE Conference on, pages 4085–4094.

IEEE.

Japkowicz, N. and Shah, M. (2011). Evaluating learning

algorithms: a classiﬁcation perspective. Cambridge

University Press.

Joze, H. R. V. and Drew, M. S. (2012). Exemplar-Based

Colour Constancy. In British Machine Vision Confer-

ence, pages 1–12.

Kim, S. J., Lin, H. T., Lu, Z., S

usstrunk, S., Lin, S., and

Brown, M. S. (2012). A new in-camera imaging

model for color computer vision and its application.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 34(12):2289–2302.

L. Shi, B. F. (2015). Re-processed Version of the Gehler

Color Constancy Dataset of 568 Images.

Land, E. H. (1977). The retinex theory of color vision. Sci-

entiﬁc America.

Lynch, S. E., Drew, M. S., and Finlayson, k. G. D. (2013).

Colour Constancy from Both Sides of the Shadow

Edge. In Color and Photometry in Computer Vision

Workshop at the International Conference on Com-

puter Vision. IEEE.

Mazin, B., Delon, J., and Gousseau, Y. (2015). Estima-

tion of illuminants from projections on the planck-

ian locus. IEEE Transactions on Image Processing,

24(6):1944–1955.

Schanda, J. (2007). Colorimetry: Understanding the CIE

System. John Wiley & Sons.

Shi, W., Loy, C. C., and Tang, X. (2016). Deep Specialized

Network for Illuminant Estimation. In European Con-

ference on Computer Vision, pages 371–387. Springer.

Van De Weijer, J., Gevers, T., and Gijsenij, A. (2007a).

Edge-based color constancy. Image Processing, IEEE

Transactions on, 16(9):2207–2214.

Van De Weijer, J., Schmid, C., and Verbeek, J. (2007b). Us-

ing high-level visual information for color constancy.

In Computer Vision, 2007. ICCV 2007. IEEE 11th In-

ternational Conference on, pages 1–8. IEEE.

Vassilvitskii, S. (2007). K-means: Algorithms, Analyses,

Experiments. Stanford University.

Zakizadeh, R., Brown, M. S., and Finlayson, G. D. (2015).

A Hybrid Strategy For Illuminant Estimation Target-

ing Hard Images. In Proceedings of the IEEE Inter-

national Conference on Computer Vision Workshops,

pages 16–23.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

188