
A Hybrid CPU-GPU Scalable Strategy for Multi-resolution Rendering of
Large Digital Elevation Models with Borders and Holes
Andrey Rodrigues and Waldemar Celes
Tecgraf/PUC-Rio Institute, Computer Science Department,
Pontifical Catholic University of Rio de Janeiro, Rio de Janeiro, Brazil
Keywords:
Digital Elevation Model, Terrain Rendering, Scalable LOD, GPU Tessellation.
Abstract:
Efficient rendering of large digital elevation models remains as a challenge for real-time applications, espe-
cially if those models contain irregular borders and holes. First, direct use of hardware tessellation has limited
scalability; although the graphics hardware is capable of controlling the resolution of patches in a very effi-
cient manner, the whole patch data must be loaded in memory. Second, previous techniques restrict elevation
data resolution and do not handle irregular border or holes. In this paper, we propose an efficient and scalable
hybrid CPU-GPU algorithm for rendering large digital elevation models. Our proposal effectively combines
GPU tessellation with CPU tile management, taking full advantage of GPU processing capabilities while main-
taining graphics-memory use under practical limits. Our proposal also handles models with irregular borders
and holes. Additionally, we present a technique to manage level of detail of aerial imagery mapped on top
of elevation models. Both geometry and texture level of detail management run independently, and tiles are
combined with no need to load extra data.
1 INTRODUCTION
Due to advances in acquisition technologies, large
digital elevation models (DEM), with gigabytes of
data, have been widely available. As a consequence,
an efficient and scalable rendering technique for such
models has been mandatory in different applications.
Without any special treatment, the amount of data eas-
ily exceeds hardware limits in both memory and tri-
angle throughput.
On the other hand, graphics hardware tessellation
has evolved and is currently able to generate complex
geometry on the fly (Schäfer et al., 2014), eliminat-
ing the need to generate the geometry on the CPU,
and thus avoiding transferring a large amount of data
to the graphics pipeline at each frame. In this paper,
we present a hybrid CPU-GPU strategy for handling
large elevation models. Previous works have also
taken advantage of hardware tessellation for DEM
rendering (Yusov and Shevtsov, 2011; Fernandes and
Oliveira, 2012; Kang et al., 2015), trying different
strategies for mapping CPU tiles to GPU patches and
for avoiding cracks along patch interfaces. Our hy-
brid approach makes it possible to control both CPU
and GPU memory and computational loads, by tuning
CPU-tile and GPU-patch sizes, and avoids cracks by
construction.
Furthermore, previous proposals on rendering dig-
ital elevation models restrict tile/patch resolutions,
generally as (2
n
+ 1)× (2
n
+ 1), and do not handle ir-
regular borders and holes. We present a new method
for handling borders and holes in DEMs. We intro-
duce a metric to compute horizontal errors due to bor-
der displacements, as tile/patch resolution is reduced,
and ensure these errors are under control in our level-
of-detail management. Our approach also imposes re-
strictions on tile/patch resolution; however, being able
to deal with holes allows us to easily handle models in
arbitrary resolutions by just filling the “blanks” with
holes. As we shall demonstrate, we are then able to
render very long terrain strips and large seismic sur-
faces with complex holes.
We then extend our proposal to also manage level
of detail of aerial imagery mapped as textures on top
of elevation models. The texture tiles are also stored
in a quadtree structure and the active cut is mandated
by the screen resolution of projected tiles. Both ge-
ometry and texture level-of-detail managements run
independently. As a result, we may end up with a 1-
to-n or n-to-1 mapping between geometry and texture
tiles; both cases are handled smoothly without any ad-
ditional load of data.
The rest of this paper is organized as follows. In
the next section, we discuss related work. Then we
240
Rodrigues, A. and Celes, W.
A Hybrid CPU-GPU Scalable Strategy for Multi-resolution Rendering of Large Digital Elevation Models with Borders and Holes.
DOI: 10.5220/0006621902400247
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 1: GRAPP, pages
240-247
ISBN: 978-989-758-287-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

present our strategy, discuss how we handle irregu-
lar borders and holes, and describe how we combine
aerial level of detail. Next, we present the results of
several computational experiments. Finally, we draw
concluding remarks.
2 RELATED WORK
Several researches have been done to efficiently ren-
der massive terrain data. In (Pajarola and Gobbetti,
2007), the authors presented a comprehensive survey
on multi-resolution approaches for digital terrain ren-
dering, analyzing different choices of data structures
and error metrics. The general idea consists in struc-
turing the data in an hierarchical way to manage adap-
tive level of detail.
Early multi-resolution approaches have opted for
a triangle-based hierarchy. Binary tree hierarchies
were proposed to control triangulation resolution
based on a screen-space error evaluation (Lindstrom
et al., 1996) (Duchaineau et al., 1997) (Lindstrom and
Pascucci, 2001). While simple to implement, these
techniques are limited by CPU-GPU memory transfer
because the geometry has to be loaded to the GPU for
every frame.
In order to overcome this limitation, techniques
such as BDAM (Cignoni et al., 2003a) and P-BDAM
(Cignoni et al., 2003b) opted for a tile-based hier-
archy: each hierarchical node represents a precom-
puted triangle surface tile instead of a single trian-
gle. The elevation data, which is encoded using a
wavelet-based compression technique, can be placed
into the GPU memory for future use. The use of a
tile-based hierarchy is scalable and efficient, at the
cost of decreased adaptivity, processing more trian-
gles than needed. Geometry clipmaps (Losasso and
Hoppe, 2004) use a mipmap pyramid as the terrain
representation and a compression technique to reduce
the storage requirements; however, they simplified the
evaluation of the screen-space error to choose the ap-
propriate level of detail, thus affecting resulting image
quality.
Recent approaches have tried to explore the GPU
tessellation to speedup mesh generation. A crack-free
terrain surface generation with a continuous LOD tri-
angulation algorithm is presented in (Fernandes and
Oliveira, 2012). The method simply estimates the size
of a patch in screen-space and tessellates it accord-
ingly, producing a constant triangle size in pixels. In
(Cervin, 2012), a density map is used, which encodes
the terrain curvature, to choose the appropriate level
of detail in the GPU tessellation stage, creating more
triangles for a high density area (bumpy land) and few
triangles for low density areas (flat land). However,
these techniques do not accurately evaluate geometry
errors in the final triangulation.
The approach proposed in (Yusov and Shevtsov,
2011) is similar to ours. They also subdivide the
model in patches (we call tiles) and then in blocks (we
call patches). However, their approach is not able to
ensure, by construction, crack-free surface along tile
interfaces. To hide gaps along tile interface, they ex-
ploit “vertical skirts” as proposed in (Ulrich, 2000).
Also, no analysis is performed to justify the choice
of tile and patch resolutions. On another hand, Kang
et al. (Kang et al., 2015) have presented an strategy
for avoiding cracks by construction, annotating four
edge LODs for each quadtree node (tile), determined
by using the inner LODs of the current node and its
neighbors. As in their approach each tile is mapped to
a single patch, all tessellation levels are computed in
CPU. We use a similar strategy to avoid crack along
tile interfaces, but our approach maps each CPU tile
to a set of GPU patches, minimizing CPU load. As
a consequence, we also need to avoid cracks along
patch interfaces.
3 GEOMETRY LOD
The proposed algorithm to render multi-resolution el-
evation models is a hybrid CPU-GPU approach. The
CPU is responsible for managing a quadtree of tiles.
Each tile is subdivided into a set of patches that are
sent to the GPU, as illustrated in Figure 1.
3.1 Pre-processing Phase
In a pre-processing phase, the quadtree is built ap-
plying a bottom-up procedure. First, the tile resolu-
tion is chosen, and different choices of resolution af-
fect memory footprint and performance, as we shall
see. The whole elevation data is subdivided into tiles
representing the quadtree leafs. Then, for each four
neighbors, a parent tile is created with half of the chil-
dren’s resolution, filling the quadtree top levels. For
simplicity, we do not apply any filter for reducing tile
resolution; we only eliminate each other line/column
of data, avoiding discontinuities along tile interfaces.
The resolution of each patch, and consequently
the number of patches per tile, also affects perfor-
mance. The maximum resolution is limited by the
graphics hardware. In Section 6, we present the com-
putational test we ran to test different resolutions.
Once tile and patch resolutions are chosen, we are
ready to compute the errors in object space associated
to each tile and each patch.
A Hybrid CPU-GPU Scalable Strategy for Multi-resolution Rendering of Large Digital Elevation Models with Borders and Holes
241

n x n
patches
Figure 1: Geometry tiles are selected to honor a predefined
screen-space error limit; each tile is subdivided into a fixed
number of patches to the GPU.
Tile and patch resolutions must be of dimension
(2
n
+1)× (2
n
+1), because neighbor tiles (or patches)
share the same border pixels. For simplicity, we men-
tion dimension values by power of two (2
n
× 2
n
).
To illustrate the discussion that follows, let us con-
sider that tile’s resolution is 512 × 512 and patch’s is
64× 64. So, each tile is subdivided into 8× 8 patches.
For each tile, we first compute the error in ob-
ject space associated to each patch for different res-
olutions. For the leaf tiles, the error for each patch
at maximum resolution is zero. We denote this by
ε
l
i
64
= 0, where i represents the patch, l the tile
quadtree level, and 64 the patch tessellation level. For
each patch, we then annotate the errors associated to
smaller tessellation levels: ε
l
i
32
, ε
l
i
16
, · · · , ε
l
i
1
.
The error in object space associated to a tile is
given by: E
l
= max
i
ε
l
i
64
, being naturally zero for the
leaf tiles. The errors of patches at upper quadtree lev-
els are inherited from the lower levels with half of the
maximum tessellation:
ε
l−1
i
64
= max
i∈N
ε
l
i
32
(1)
where N represents the set of associated four neigh-
boring patches. This error is then propagated to
smaller tessellation levels and, again, the tile error is
E
l−1
= max
i
ε
l−1
i
64
. For each tile, all patch errors are
annotated and stored in a texture to be accessed in
the GPU-tessellation stage. Figure 2 illustrates this
object-space error computation.
3.2 Rendering Phase
At run time, the error in screen space ρ is computed
in the usual way, either to select tiles on the CPU or
to determine patch tessellation level on the GPU:
ρ = λ
E
d
, with λ =
w
2tan
θ
2
(2)
where E, w, θ and d represent, respectively, the er-
ror in object space, the viewport resolution, the cam-
era field of view and the distance from the camera to
the closest point of the tile’s (or patch’s) 3D bounding
box.
l
i
l
i
l
i
l
i
l
Compute
E
11632
64
,...,
:
,0
,0
111
1
11
11632
3264
64
,...,
:
,max
,max
l
i
l
i
l
i
l
i
Ni
l
i
l
ii
l
Compute
E
l
1l
Figure 2: Computed object-space errors: at leaf tiles, for
each patch at maximum tessellation level, the associated er-
ror is zero; errors are then propagated to other possible tes-
sellation levels. Errors of patches at upper quadtree level
are inherited from the lower levels. The error associated to
each tile is the maximum annotated to patches at maximum
tessellation level.
On the CPU, we use two threads to process the
data. The loading thread is responsible for predicting
camera movement and loading tiles in advance from
disk. The rendering thread is responsible for select-
ing tiles, among the loaded ones, necessary to render
the terrain honoring a prescribed error tolerance for
the current frame. Both threads use the conventional
top-down approach, subdividing the tile if the screen
space error exceed the prescribed tolerance.
Once the frame tiles are selected, the CPU is re-
sponsible for issuing rendering commands for the cor-
responding patches. In the tessellation shader, the
level of detail of each patch is determined. The inner
tessellation level is given by evaluating the screen-
space error of the patch, choosing the lowest pos-
sible resolution. The choice of the outer tessella-
tion level must avoid T-junctions between adjacent
patches. There are two cases, denoted here by the
patch-patch case, for interfaces between two patches
of a same tile, and the tile-tile case, for interfaces be-
tween patches of different tiles.
The patch-patch case is easily handled, because
all the needed data are available within the tile. The
outer tessellation level is given by the maximum sub-
division requested by the interfacing patches, as in
(Yusov and Shevtsov, 2011). So, the coarsest patch
gets refined along the border:
n
outer
= max(n
i
,n
j
) (3)
where n
i
and n
j
represents the computed inner level
of the interfacing patches.
The challenge lies on the tile-tile case; data are not
available within a tile and additional information is
necessary. To overcome this problem, on the CPU, af-
ter performing the LOD algorithm (tile selection), for
each tile, we annotate the difference in level between
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
242
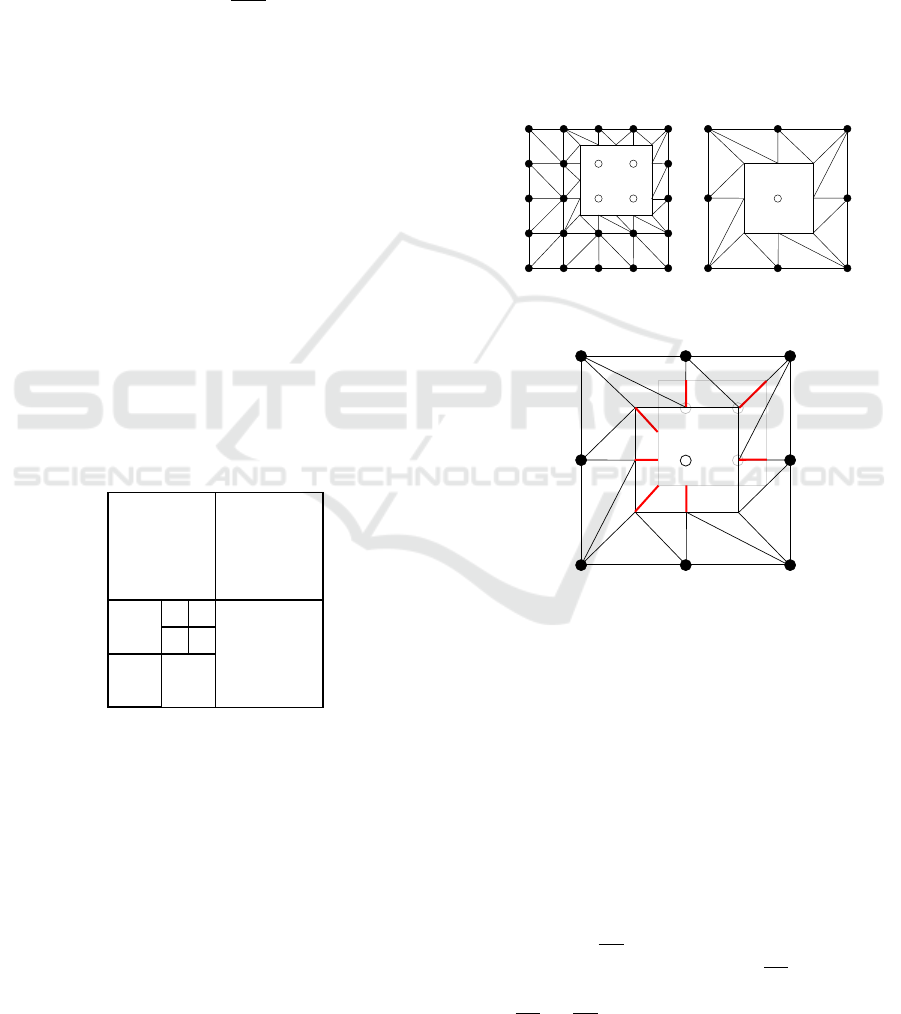
adjacent selected tiles; one value for each tile edge.
If the level of the adjacent tile is equal or higher (the
adjacent is more refined), we annotate the value zero;
if the level of the adjacent tile is lower (it is less re-
fined), we annotate the difference in level: l
tile
− l
ad j
.
Figure 3 illustrates the values annotated for a sample
active quadtree. In the tessellation shader, the outer
tessellation level of a tile-tile interface is given by:
n
outer
=
n
max
2
δ
(4)
where n
max
is the maximum possible subdivision for
the patch and δ is the annotated level difference. This
imposes a limit in the unbalance level of adjacent tiles
equals to log
2
n
max
, which, in practice, tends not to
be a problem. For instance, for a 64 × 64 patch res-
olution, the unbalance between adjacent tiles cannot
exceed a factor of six. If this limit is reached, it is im-
posed a subdivision on the less refined tile. All patch
borders along the tile edge get the same outer tessel-
lation level. Note that this approach makes all inter-
face between tiles refined to the most possible reso-
lution. This induces a small increase in the number
of generated triangles but makes it simple to avoid
T-junctions. As we shall demonstrate, this approach
to ensure crack-free surface does not impact perfor-
mance. Moreover, there is no need to employ ad-
ditional procedures for crack filling, such as to add
flanges, to join tiles with special meshes, or to gener-
ate vertical ribbon meshes(Ulrich, 2000).
0
2
0
2
0
0
0 1
2
1
2
0
0
1
0 1
0
0
0 0
0
0
1 0 0
0
0
1
0
Figure 3: Annotated level differences along tile edges.
For each edge of a selected tile, the neighboring tiles are
checked; if neighbor tile is at same or higher level, zero is
annotated; if neighbor tile is at lower level, level difference
is annotated.
4 BORDERS AND HOLES
We now extend our approach to deal with irregular
borders and holes. In such models, there are regular
vertices (•) and void vertices (◦). We then consider
that there are borders along all the interfaces between
regular and void vertices. Figure 4a (left) illustrates
a 4 × 4 patch with four void vertices and the corre-
sponding defined border. At first, void vertices have
no associated elevation data. In order to render the
border, in a pre-processing phase, we assign, to each
void vertex, an elevation value given by its neighbor-
ing regular vertices.
For computing the error in object space when de-
creasing tile/patch resolution, we need to consider
border displacements, which we identify as horizon-
tal error. Figure 4 shows what happens when decreas-
ing the resolution of the illustrative patch from 4 × 4
to 2 × 2 (Figure 4a). As each other line/column are
eliminated, the border is displaced, and horizontal er-
ror, illustrated in Figure 4b, has to be considered.
(a)
(b)
Figure 4: Horizontal object space errors: (a) illustrative
patch with void vertices and corresponding coarser level;
(b) computed horizontal errors due to border displacement.
Table 1 summarizes all possible cases involving
void vertices when reducing resolution. For each
eliminated vertex in a patch, the error is computed
considering removing the middle vertex of four edges:
horizontal, vertical, forward diagonal, and backward
diagonal. The maximum error is stored per patch con-
sidering all edges of all eliminated vertices. Let as
take as example the second table entry, case A−C − B
as • − • − ◦ (regular, regular, and void vertices), where
vertex C is removed: originally, the border is in the
middle of edge
CB; after removing vertex C, the bor-
der is moved to the middle of edge AB, representing
a displacement equal to ∆/2, where ∆ is the length of
edge AC (or BC).
A Hybrid CPU-GPU Scalable Strategy for Multi-resolution Rendering of Large Digital Elevation Models with Borders and Holes
243
Vertical errors are expressed in the usual way by:
E
v
=
z
A
+ z
B
2
− z
C
(5)
where z
V
represents the elevation value at vertex V .
This is valid for all cases, except for the last table
entry, involving only void vertices; in this case, both
vertical and horizontal errors are zero.
In the pre-processing phase, both maximum errors
are annotated. The combined error, expressed by:
E =
q
E
2
v
+ E
2
h
(6)
is only computed in the rendering phase. The reason
we do that is to allow applying a vertical scale fac-
tor when visualizing the model, which is commonly
employed.
In the rendering phase, the combined error is pro-
jected to compute the error in screen space. Note that
the whole patch is rendered, even triangles with void
vertices. In order to correctly render the border, we
assign an attribute equal to one for regular vertices
and equal to zero for void vertices. This attribute
is interpolated by the rasterizer and, in the fragment
shader, fragments with attribute value less than 0.5
are discarded.
Patches with only void vertices are not rendered,
and tiles with only void vertices are not even rep-
resented in the quadtree. This allows us to pro-
cess rectangular elevation data using regular quadtree
in a effective way. The rectangular data is com-
pleted with void vertices to get the required resolu-
tion (2
n
+ 1 × 2
n
+ 1) but, in the end, we get a non-
complete quadtree, as void tiles are discarded.
5 TEXTURE LOD
On top of the multi-resolution elevation surface, we
map aerial imagery as textures, also managing its
Table 1: Table of corresponding horizontal (E
h
) errors when
eliminating a vertex C in the middle of an edge AB. The
value of ∆ corresponds to the horizontal length of AC or CB.
Note that the edge AB may be horizontal, vertical, forward
diagonal, or backward diagonal, with respect to the patch.
A − C − B E
h
• − • − • 0
• − • − ◦ ∆/2
• − ◦ − • ∆
• − ◦ − ◦ ∆/2
◦ − • − • ∆/2
◦ − • − ◦ ∆
◦ − ◦ − • ∆/2
◦ − ◦ − ◦ 0
level of detail. The challenge here resides on combin-
ing both geometry and texture tiles without loading
additional data. Each LOD manager has to indepen-
dently select the tiles necessary to meet the desired
quality in the final image.
In the preprocessing phase, a conventional
quadtree structure is created to store the texture in dif-
ferent resolutions, using the box filter to reduce reso-
lution of parent tiles. In the rendering phase, again,
a separate thread is used to predict, select, and load
texture tiles necessary for the next frames. The ren-
dering thread selects the tiles needed for each frame,
considering the loaded ones.
The selection of texture tiles also employ the con-
ventional top-down procedure. For each visited tile in
the hierarchy, we compute its longest edge in screen
space, L
pro j
, and compute the magnification rate:
r
mag
=
L
pro j
w
tile
(7)
where w
tile
represents the maximum tile dimension.
In our experiments, we use a limit of value 1.5: if the
magnification rate is less than 1.5, the tile is selected;
otherwise, its four children are processed.
As tile selection runs independently for geom-
etry and texture, we end up having three cases of
geometry-texture tile correspondences: 1-to-1, n-to-
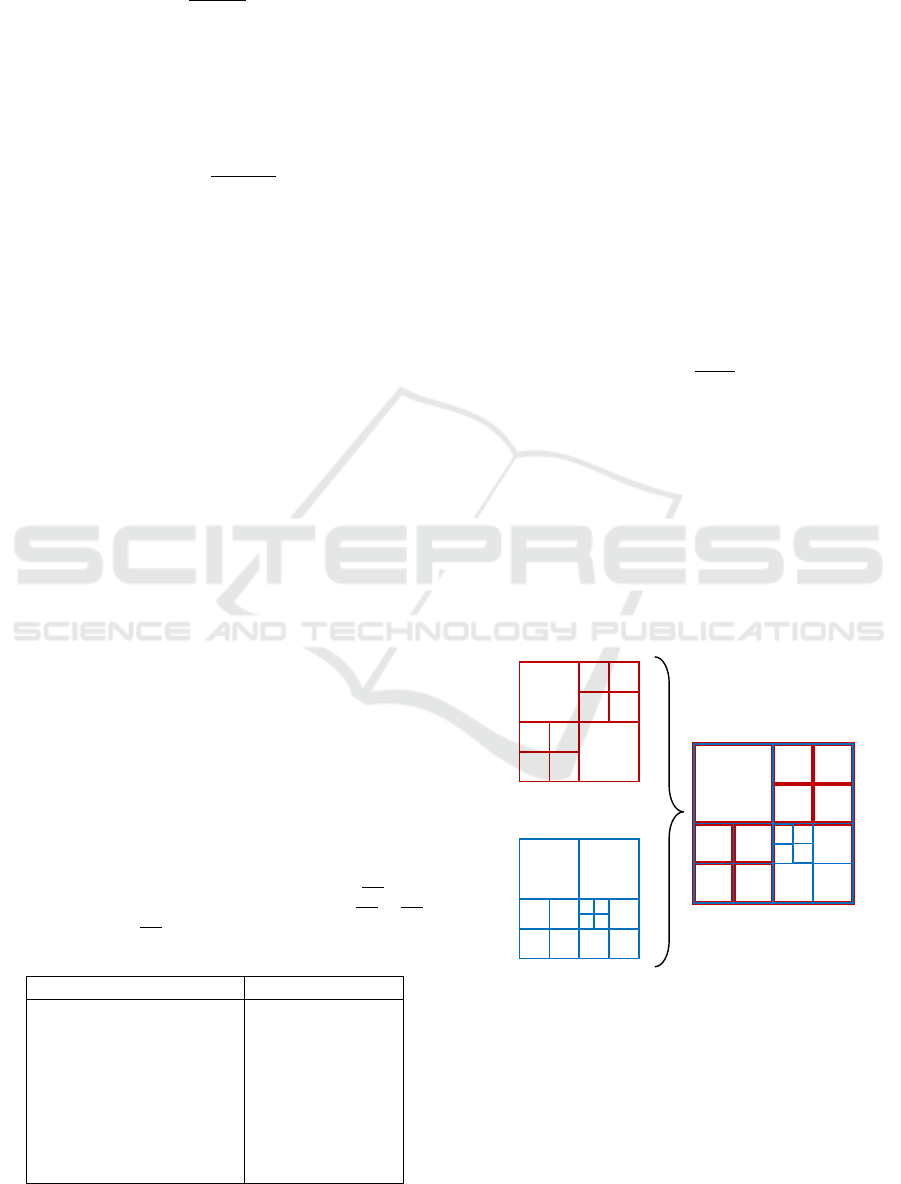
1, 1-to-n. Figure 5 illustrates these different corre-
spondence cases.
Geometry Quadtree
Texture Quadtree
Combined Quadtree
Figure 5: Correspondence among geometry (in red) and
texture (in blue) tiles: at the left quadrants, 1-to-1 corre-
spondence cases are configured; at the upper right quadrant,
there is a n-to-1 case and, at the lower right quadrant, there
is a 1-to-n case, which requires the use of virtual geometry
tiles to be rendered.
The 1-to-1 case is the direct one; we have one ge-
ometry tile for each texture tile: vertices defining the
patches receive texture coordinates from 0.0 to 1.0.
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
244

The n-to-1 case is also simple: there are n geome-
try tiles mapped into one texture tile. Texture coordi-
nates are transformed accordingly, and all geometry
tiles uses the same texture object.
The 1-to-n case is the one that requires a more
elaborated solution: we have one geometry tile that
must be rendered using different texture objects. It
is needed to render the geometry tile multiple times,
one for each texture tile. We see two approaches for
doing this. In the first approach, for each render pass,
we would select the patches covered by each texture
tile. Although this solution seems straightforward, it
presents two important drawbacks: (i) the correspon-
dence factor, n, would be limited by the number of
patches in a geometry tile; (ii) we would need a spe-
cialized algorithm to handle tiles with less patches.
We have opted for a second solution: we generate
a virtual geometry tile for each texture tile. Each vir-
tual tile is subdivided into the same number of patches
as a regular tile, so there is no need to modify the al-
gorithm. What differs is that a virtual tile uses a sub-
set of the elevation data: all virtual tiles are render-
ing using the same elevation data; texture coordinates
to access these data are assigned accordingly. Each
patch of virtual tiles inherits the object-space errors
annotated to the containing real patch.
6 RESULTS AND DISCUSSION
In this section, we describe a set of computational
experiments we used to test and tune the proposed
method. All experiments were run on a i7-3960X pro-
cessor computer with 24GB of RAM, equipped with
a NVIDIA Geforce GTX TITAN graphics card with
6GB of VRAM.
6.1 Tile and Patch Size Analysis
First, we analyze the influence of the geometry tile
size. For this computational experiment, we used a
high-resolution version of the Puget Sound Terrain.
The elevation data has a resolution of 65K × 65K
with 4 meter pixel spacing, using the aerial imagery
mapped as texture with 262K × 262K in size and 1
meter pixel spacing. The dataset was obtained from
(WU, 2017) and (USGS, 2017), totalizing 250GB of
disk space. We set the screen resolution to 1920 ×
1080 and the geometry error tolerance to 1.0 pixel.
To run the experiment, we defined a camera path
over the terrain, crossing flat and bumpy regions along
the way. We run the same experiment with two differ-
ent patch size (32 × 32 and 64 × 64) and tested differ-
ent tile sizes. Figures 6 and 7 show the achieved frame
rate. In this experiment, we got better performance
with 128 × 128 tiles for patches of 32 × 32 and with
256 × 256 tiles for patches of 64 × 64, what suggests
an ideal relation of 4 × 4 patches per tile on this ma-
chine. As we increase tile size, we reduce the height
of the quadtree, thus alleviating CPU workload and
increasing performance. On the other hand, as we in-
crease tile size, we reduce LOD granularity, requir-
ing more GPU memory and processing. Tests with
smaller patches resulted in worse performance.
50
100
150
200
250
Frame Rate
tile 32
tile 64
tile 128
tile 256
tile 512
Figure 6: Achieved frame rate along camera path for patch
size of 32 × 32.
100
150
200
250
Frame Rate
tile 64
tile 128
tile 256
tile 512
Figure 7: Achieved frame rate along camera path for patch
size of 64 × 64.
The following figures show different measure-
ments along the camera path for the 32 × 32 patch;
similar results were achieved for the 64 × 64 patch.
Figure 8 shows the required GPU memory for dif-
ferent tile sizes. The 128 × 128, which delivered
better performance, presents a good compromise be-
tween performance and requested memory resource.
Figure 9 shows the required CPU time to process
the frames along the camera way. As expected,
small tiles increases CPU workload, degrading per-
formance. Figure 10 shows the observed error in
screen space; recall that the used tolerance was set to
1 pixel. Small tiles do not honor the requested image
quality, since the application becomes CPU limited,
not being able to assure the quality in real time.
6.2 Comparison with Other Methods
We compared the rendering performance of our
method with the implementation of the chunked LOD
A Hybrid CPU-GPU Scalable Strategy for Multi-resolution Rendering of Large Digital Elevation Models with Borders and Holes
245

0
200
400
600
·10
6
#Memory
tile 32
tile 64
tile 128
tile 256
tile 512
Figure 8: Required GPU memory (in MB) per frame along
camera path (patch 32 × 32).
0
10
20
CPU Time
tile 32
tile 64
tile 128
tile 256
tile 512
Figure 9: Required CPU processing time (in milliseconds)
per frame along camera path (patch 32 × 32).
approach provided by (Ulrich, 2000). The available
code uses the Puget Sound data with 16k × 16k of
resolution. In the experiment, we set the screen er-
ror tolerance to one pixel and use a similar camera
paths. Figure 11 shows the achieved performance
along the camera path: our approach was in average
6.5x faster than the chunked LOD approach. This rel-
ative gain is higher than the one reported by (Yusov
and Shevtsov, 2011) but our experiment was ran on a
different equipment (they reported their proposal run
3.5x faster than the chunked LOD approach, using
two pixel tolerance on a NVidia GTX480).
6.3 Terrain Strip
In order to demonstrate the ability of our system to
handle terrain with irregular border, we run a sec-
ond experiment using a dataset that represents the el-
evation model of 1,000 kilometers of a terrain strip
that is the site a natural gas/oil pipeline, as shown
in Figure 12. This model is used in an application
to monitor emergency situations along the pipeline.
The raw dataset consists of several partially overlap-
ping terrain patches, one for each kilometer of the
pipe, resulting in 86 GB and 130 GB of elevation
and aerial imagery data, respectively. To pre-process
this dataset, we compose all files into a virtual raster
file, using a common GIS format (Virtual Raster).
The final virtual image resolution was 2
22
x2
22
. How-
ever, since this virtual image contains large amount
of void data, the pre-processing is performed in rea-
1
1.2
1.4
Screen Error(Max)
tile 32
tile 64
tile 128
tile 256
tile 512
Figure 10: Observed maximum screen space error (in pix-
els) per frame along camera path (patch 32 × 32). Recall
we request an error of at most 1 pixel; values above this
number signalize the system is not capable of delivering the
requested quality in real time.
0
500
1,000
1,500
Frame Rate
Our proposal
Ulrich’s approach
Figure 11: Comparison on performance of our approach
and the chunked LOD approach.
sonable time, only persisting tile with valid data. The
proposed system is capable of rendering such model
smoothly, from overview to zoom-in shots.
(a)
Figure 12: A rendered image of an actual terrain strip along
a gas/oil pipeline of 1,000 kilometers.
6.4 Seismic Surface
This last experiment demonstrates our system dealing
with internal holes in the surface. We used a horizon
surface resulted from an actual seismic data process-
ing. This surface is represented by an elevation model
but contains a large amount of void data, and correctly
rendering the holes is crucial for an accurate inter-
pretation of the model. Figure 13 shows a rendered
image. Again, the proposed system was capable of
rendering the model smoothly ensuring image quality
even for the complex structure of such a model.
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
246

Figure 13: A rendered image of an actual horizon surface
from a seismic data.
7 CONCLUSION
We presented a new hybrid CPU-GPU strategy to ren-
der large digital elevation models with aerial imagery
mapped as textures. Level of detail managements,
for geometry (elevation) and texture (aerial imagery),
run independently. On the CPU, a multi-threaded
implementation is responsible for selecting, loading,
and transferring to the GPU active tiles. Geometry
tiles are decomposed into patches, and tessellation
shaders are used to determine tessellation levels for
each patch. The proposed method avoids crack be-
tween patch and tile interfaces by construction. Ge-
ometry and texture tiles are combined with no extra
data load, even in the case where one geometry tile is
covered by a set of different texture tiles.
We also extended the proposal for handling terrain
with irregular borders and surfaces with holes, intro-
ducing the concept of horizontal errors. Dealing with
irregular borders mitigates the constraint of power of
two (plus one for the border) on terrain dimensions;
supporting surfaces with hole has an important ap-
plication on rendering interpreted seismic surfaces of
large datasets.
ACKNOWLEDGEMENTS
We thank CNPq (Brazilian National Council for Sci-
entific and Technological Development) and Petro-
bras (the Brazilian oil company) for the financial sup-
port to conduct this research.
REFERENCES
Cervin, A. (2012). Adaptive Hardware-accelerated Ter-
rain Tessellation. PhD thesis, Linköpings Universitet,
Tekniska Högskolan.
Cignoni, P., Ganovelli, F., Gobbetti, E., Marton, F., Pon-
chio, F., and Scopigno, R. (2003a). BDAM —
Batched Dynamic Adaptive Meshes for High Perfor-
mance Terrain Visualization. Computer Graphics Fo-
rum, 22(3):505–514.
Cignoni, P., Ganovelli, F., Gobbetti, E., Marton, F., Pon-
chio, F., and Scopigno, R. (2003b). Planet-Sized
Batched Dynamic Adaptive Meshes (P-BDAM). In
Proceedings of the 14th IEEE Visualization 2003
(VIS’03), VIS ’03, pages 20–, Washington, DC, USA.
IEEE Computer Society.
Duchaineau, M., Wolinsky, M., Sigeti, D., Miller, M.,
Aldrich, C., and Mineev-Weinstein, M. (1997).
ROAMing terrain: Real-time Optimally Adapting
Meshes. In Visualization ’97., Proceedings, pages 81–
88.
Fernandes, A. and Oliveira, B. (2012). Gpu tessellation:
We still have a lod of terrain to cover. In Cozzi, P. and
Riccio, C., editors, OpenGL Insights, pages 143–160.
CRC Press.
Kang, H., Jang, H., Cho, C.-S., and Han, J. (2015). Multi-
resolution Terrain Rendering with GPU Tessellation.
Vis. Comput., 31(4):455–469.
Lindstrom, P., Koller, D., Ribarsky, W., Hodges, L. F.,
Faust, N., and Turner, G. A. (1996). Real-time, contin-
uous level of detail rendering of height fields. In Pro-
ceedings of the 23rd annual conference on Computer
graphics and interactive techniques, pages 109–118.
ACM.
Lindstrom, P. and Pascucci, V. (2001). Visualization of
large terrains made easy. In Visualization, 2001.
VIS’01. Proceedings, pages 363–574. IEEE.
Losasso, F. and Hoppe, H. (2004). Geometry Clipmaps:
Terrain Rendering Using Nested Regular Grids. In
ACM SIGGRAPH 2004 Papers, SIGGRAPH ’04,
pages 769–776, New York, NY, USA. ACM.
Pajarola, R. and Gobbetti, E. (2007). Survey of semi-regular
multiresolution models for interactive terrain render-
ing. The Visual Computer, 23(8):583–605.
Schäfer, H., sner, M. N., Keinert, B., Stamminger, M., and
Loop, C. (2014). State of the Art Report on Real-time
Rendering with Hardware Tessellation. In Eurograph-
ics, pages 93–117.
Ulrich, T. (2000). Rendering massive terrains using chun-
ked level of detail. ACM SIGGRAPH Course “Super-
size it! Scaling up to Massive Virtual Worlds”.
USGS (2017). US geological survey - USGS.
https://www.usgs.gov/products/maps/gis-data.
WU, G. R. G. (2017). Geomorphological re-
search group - washington university.
http://gis.ess.washington.edu/data/.
Yusov, E. and Shevtsov, M. (2011). High-performance ter-
rain rendering using hardware tessellation. Journal of
WSCG, 19(3):85–92.
A Hybrid CPU-GPU Scalable Strategy for Multi-resolution Rendering of Large Digital Elevation Models with Borders and Holes
247
