Combining 2D to 2D and 3D to 2D Point Correspondences for Stereo

Visual Odometry

Stephan Manthe

, Adrian Carrio

, Frank Neuhaus

, Pascual Campoy

and Dietrich Paulus

Institute for Computational Visualistics, University of Koblenz-Landau, Universit

atsstr. 1, 56070 Koblenz, Germany

Computer Vision & Aerial Robotics Group, Universidad Polit

ecnica de Madrid,

Calle Jos

e Guti

errez de Abascal, 28006 Madrid, Spain

Keywords:

Visual Stereo Odometry, Epipolar Constraint, Bundle Adjustment.

Abstract:

Self-localization and motion estimation are requisite skills for autonomous robots. They enable the robot to

navigate autonomously without relying on external positioning systems. The autonomous navigation can be

achieved by making use of a stereo camera on board the robot. In this work a stereo visual odometry algorithm

is developed which uses FAST features in combination with the Rotated-BRIEF descriptor and an approach for

feature tracking. For motion estimation we utilize 3D to 2D point correspondences as well as 2D to 2D point

correspondences. First we estimate an initial relative pose by decomposing the essential matrix. After that

we reﬁne the initial motion estimate by solving an optimization problem that minimizes the reprojection error

as well as a cost function based on the epipolar constraint. The second cost function enables us to take also

advantage of useful information from 2D to 2D point correspondences. Finally, we evaluate the implemented

algorithm on the well known KITTI and EuRoC datasets.

1 INTRODUCTION

Stereo visual odometry (VO) is a method to compute

the egomotion of a camera system relative to a sta-

tic scene that consists of two cameras. Stereo VO al-

gorithms continuously compute the relative poses be-

tween two consecutive points in time from overlap-

ping images captured by the camera system. By con-

catenating these relative poses they continuously up-

date an absolute pose that describes the camera pose

with relation to an arbitrary initial pose. In order to

estimate the motion over time, VO algorithms track

image parts and make use of structure from motion

techniques to derive the camera system’s motion and

3D structure of the captured scene.

Recently, many applications of VO have been

found in the ﬁeld of robotics, since motion estimation

is essential for many robotic tasks. One reason for

the high interest of VO in robotics are the advantages

of the sensor properties. Due to their wide applica-

tions also in consumer devices: they are cheap, with

a small form factor and lightweight. However, this

comes with the cost of the need to process images,

which is computationally expensive and can be error

prone in scenarios with bad lighting conditions.

Figure 1: Reconstructed trajectory and point cloud. The

trajectory is visualized in red and the point cloud is colored

based on elevation. On the right of the image the current

position of the camera marked by a coordinate system can

be seen.

In this work we adapt the depth enhanced odome-

try approach of Zhang et al. to a pure stereo vision

based approach (Zhang et al., 2014). This enables

us to exploit the previously described advantages of a

pure camera based sensor system. In contrast to their

approach we triangulate features using stereo image

Manthe, S., Carrio, A., Neuhaus, F., Campoy, P. and Paulus, D.

Combining 2D to 2D and 3D to 2D Point Correspondences for Stereo Visual Odometry.

DOI: 10.5220/0006623604550463

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

455-463

ISBN: 978-989-758-290-5

455

pairs instead of associating 2D features with depth

information from a depth map. Following their ap-

proach, we utilize features with and without depth to

maximize information gain. However, we propose for

this a slightly modiﬁed version of their cost function

for features without depth information which returns

a metric error and is essentially based on the epipo-

lar constraint (Hartley and Sturm, 1997). This ena-

bles our algorithm to be extended by tightly coupled

sensor fusion since it allows a normalization of the

error terms. In contrast to the algorithm of Zhang

et al. we do not implement windowed bundle adjus-

tment (BA) and focus on pure frame to frame motion

estimation, which can be considered a pairwise BA

algorithm. This keeps processing times low and ena-

bles us to apply our algorithm on board a robot with

low computational power which is an unmanned ae-

rial vehicle in our case. BA is a further step that im-

proves the results of the very ﬁrst step related to cal-

culating VO from two consecutive stereo image pairs.

This is the reason why we focus our work in this pa-

per on this ﬁrst step, that can of course be improved

by a further BA upon the improvements we present in

this paper. We evaluate the proposed algorithm exten-

sively on two different datasets and present evaluation

results that are similar to that of Zhang et al.

The rest of this paper is structured as follows. In

Section 2 we present the related work. After that, we

revise in Section 3 important basic knowledge before

we give an overview of our algorithm in Section 4. In

Section 5 we introduce our algorithm more in detail

followed by the evaluation of our approach on two

different datasets in Section 6. Finally our work is

summarized in Section 7.

2 RELATED WORK

A lot of work on VO has been done by the Robo-

tics and Perception group at ETH Z

urich, led by Da-

vide Scaramuzza. His two-part tutorial gives an over-

view to common algorithms used in VO (Scaramuzza

and Fraundorfer, 2011; Fraundorfer and Scaramuzza,

2012). In these tutorials also visual-SLAM techni-

ques which are related to VO are explained.

Cvi

c and Petrovi

c recently achieve very accu-

rate results with their method on the KITTI odome-

try benchmark (Cvi

c and Petrovi

c, 2015). They

focus on careful feature selection by making use of

two different keypoint detection algorithms. This al-

lows them to have a high feature acceptance thres-

hold while keeping still enough features for motion

estimation. In contrast to our work the motion esti-

mation of their algorithm is divided into rotation esti-

mation and translation estimation separately. First the

rotation matrix is extracted from an estimated essen-

tial matrix and then the translation vector is estimated

by iteratively minimizing the reprojection error with

a ﬁxed rotation matrix.

Buczko et al. also focused on outlier rejection in

order to achieve high accuracy during motion estima-

tion. The authors presented a new iterative outlier

rejection scheme (Buczko and Willert, 2016b) and

a new ﬂow-decoupled normalized reprojection error

(Buczko and Willert, 2016a). Their method achieves

as well outstanding results in translation and rotation

accuracy on the KITTI odometry benchmark.

The work in this paper is based on the idea of com-

bining information of image features with and wit-

hout known depth information developed by Zhang

et al. They build an odometry system that combines

a monocular camera with a depth sensor. Their al-

gorithm assigns to the tracked features in the camera

images depth information from the depth sensor if this

information is available. During their motion estima-

tion they utilize features with and without depth in

order to achieve a maximum information gain when

recovering the motion. The use of features without

depth enables to compute a relatively accurate pose

even if only a few features with depth information

are available. They evaluated their method with an

Asus Xtion Pro Live RGB-D camera and a sensor sy-

stem consisting of a camera in combination with a

Hokuyo UTM-30LX laser scanner on their own da-

tasets. Additionally they also evaluated on the public

KITTI dataset which provides the depth information

from a Velodyne HDL-64E laser scanner. Our method

differs from theirs as it obtains metric depth informa-

tion from a stereo camera and it does not use BA. As

mentioned before, we also apply a small adaption of

their cost function for 2D to 2D point corresponden-

ces.

Fu et al. compute the depth information of

Zhang’s algorithm by using a stereo camera also (Fu

et al., 2015). However, they do this by using a

block matching algorithm. Furthermore their algo-

rithm uses key frames which can reduce the drift in

situations where the camera is not moving. Also the

rest of their motion estimation is similar to Zhang’s

approach since they apply their motion estimation ap-

proach including BA for their camera system.

3 THEORETICAL BACKGROUND

The VO approach described in this paper solves a BA

problem in order to estimate the most likely motion

given two stereo image pairs from consecutive points

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

456

in time. For this, an optimization problem is setup

that makes use of the epipolar geometry, which des-

cribes the geometrical properties between two came-

ras. Furthermore, the epipolar geometry will also be

used during the feature matching process in our algo-

rithm. In this section, the basics of epipolar geometry

will be described in order to give a better insight into

our algorithm.

The relative pose between two cameras is des-

cribed as a rigid transformation given by a rota-

tion matrix R ∈ IR

3×3

and a translation vector t =

, t

)

∈ IR

. These can be used to transform an

arbitrary 3D point that is deﬁned in the coordinate sy-

stem of a camera c

into the coordinate system of a

second camera c

. With R and t we can also deﬁne

the so called essential matrix

E = R[t]

, (1)

where [t]

is a skew symmetric matrix

[t]





0 −t

−t





. (2)

It maps a homogeneous undistorted point ˜p

in image

coordinates of the ﬁrst camera to a homogeneous

line

l in image coordinates of the second camera

l = E ˜p

. (3)

The projections of any point located on a ray inter-

secting the projection center of the ﬁrst camera and

are projected onto this line. Given the homoge-

neous undistorted point ˜q

in image coordinates of the

second camera, we compute the corresponding homo-

geneous line

˜m = E

˜q

(4)

where ˜m is in image coordinates of the ﬁrst camera.

The constraint that a corresponding point in the se-

cond image of a point from the ﬁrst image has to lie

on an epipolar line is named the epipolar constraint.

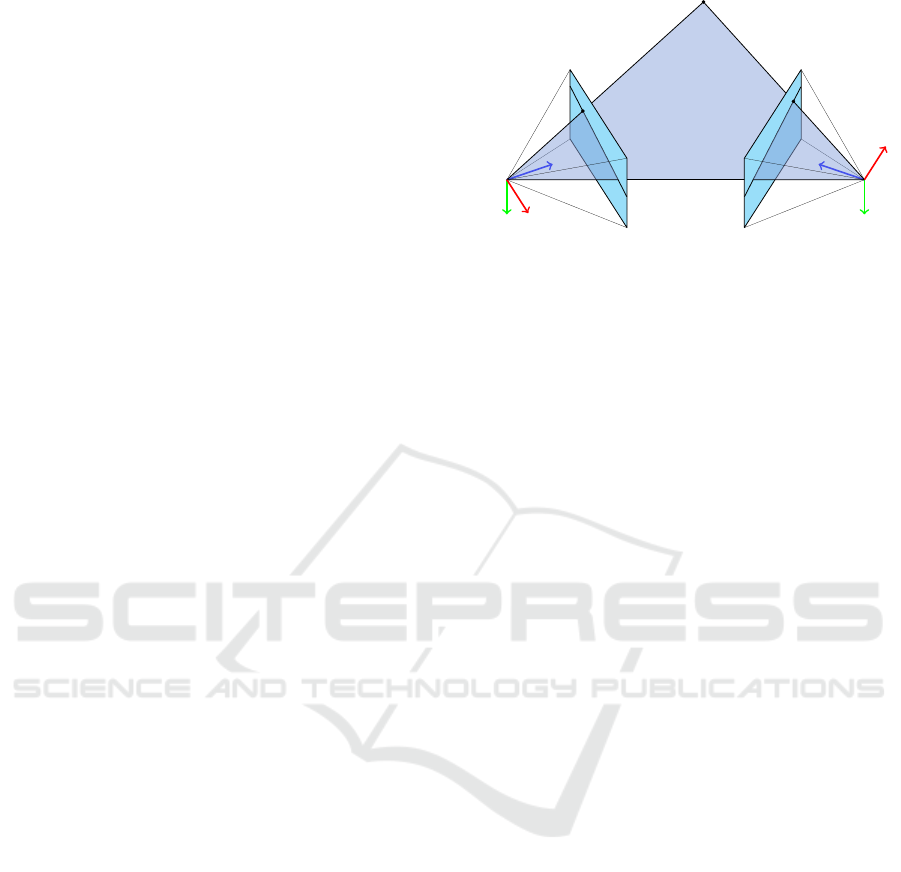
This geometric relation is depicted in Figure 2 and

will be used during motion estimation as well as fea-

ture matching.

Another approach to compute the essential ma-

trix is to use point correspondences from two ima-

ges. This can be done for example by using the 5-

point-algorithm which computes the essential matrix

from 5 point correspondences (Nist

er, 2004). Since

often many more correspondences are available and

not all of them are correct it is often used in combina-

tion with a RANSAC framework. It robustiﬁes the al-

gorithm and classiﬁes the point correspondences into

inliers and outliers. The computed essential matrix

can then be decomposed into a rotation matrix R and

˜m

˜p

˜q

Figure 2: Illustration of the epipolar geometry and the epi-

polar constraint.

a translation vector t. As a result, two possible rota-

tions R and R

as well as two possible translations t

and −t are obtained. Thus the four possible solutions

have to be validated by checking the cheirality con-

straint. It describes that a 3D point lies in front of both

cameras from which it was reconstructed. Therefore,

it is determined with which of the four possible solu-

tions the largest number of 3D points can be correctly

triangulated. Finally the relative pose from which the

most correct triangulated 3D points can be obtained

is chosen (Hartley, 1993). The interested reader may

ﬁnd a more detailed description of how to extract the

correct R and t from an essential matrix in (Hartley

and Zisserman, 2003). However, by making use of 2D

to 2D point correspondences t can only be estimated

up to a scale factor. The scale factor can be recovered

from known 3D to 2D point correspondences as we

show in Section 5.

4 ALGORITHM OVERVIEW

The stereo VO algorithm presented in this work uses

a feature-based approach. It extracts FAST features

(Rosten et al., 2010) from images and guarantees an

equal distribution of them by means of bucketing in

the left and right stereo image (Zhang et al., 1995).

The oriented-BRIEF descriptor is then applied to

the ﬁltered keypoints (Rublee et al., 2011). Even

though FAST is an undirected keypoint extraction

algorithm and oriented-BRIEF cannot make use of

its rotational invariance, we achieved more precise

motion estimation results with it. These probably

come from the machine learning stage of the modi-

ﬁed BRIEF descriptor. At the end of the feature ex-

traction stage we transform all keypoints into undis-

torted image coordinates in order to avoid repeated

distortion and undistortion during the following pro-

cessing.

In order to match keypoints between the left and

the right stereo camera we utilized stereo matching al-

Combining 2D to 2D and 3D to 2D Point Correspondences for Stereo Visual Odometry

457

ong epipolar lines only. This allows to exclude many

wrong matches, which are not possible due to the epi-

polar constraint. We apply the stereo matching twice

from the left to the right image and vice versa. Only

if the matching results in the same correspondence in

both cases, it will be accepted as a correct match.

The search for keypoint correspondences over

time is only done in the left image. For this purpose

we applied the KLT-tracker on the extracted FAST

keypoints (Lucas and Kanade, 1981). During our tests

the tracking of keypoints lead to many more keypoint

correspondences than a keypoint matching approach

and has also been applied in other works (Zhang et al.,

2014; Cvi

c and Petrovi

c, 2015).

For point cloud triangulation between the

keypoints in the left and the right image we used the

optimal triangulation method presented by Hartley

and Sturm (Hartley and Sturm, 1997). By using

these 3D points, the algorithm derives 3D to 2D

point correspondences between time t − 1 and t by

concatenating the results of the previously described

matching and tracking phases. Since our algorithm

is a pure VO algorithm it maintains the keypoint

correspondences only while they are needed for the

following motion estimation. For the purpose of

visualization the algorithm keeps the triangulated 3D

points in memory without any further processing.

In the next phase, the algorithm estimates the re-

lative motion as a rigid transformation between two

successive points in time. This phase is split up into

a motion initialization and a motion reﬁnement step

which are described in more detail in Section 5. Af-

ter the relative pose is computed, it is concatenated

with the initial absolute pose. In the second iteration

and every following iteration the relative pose is con-

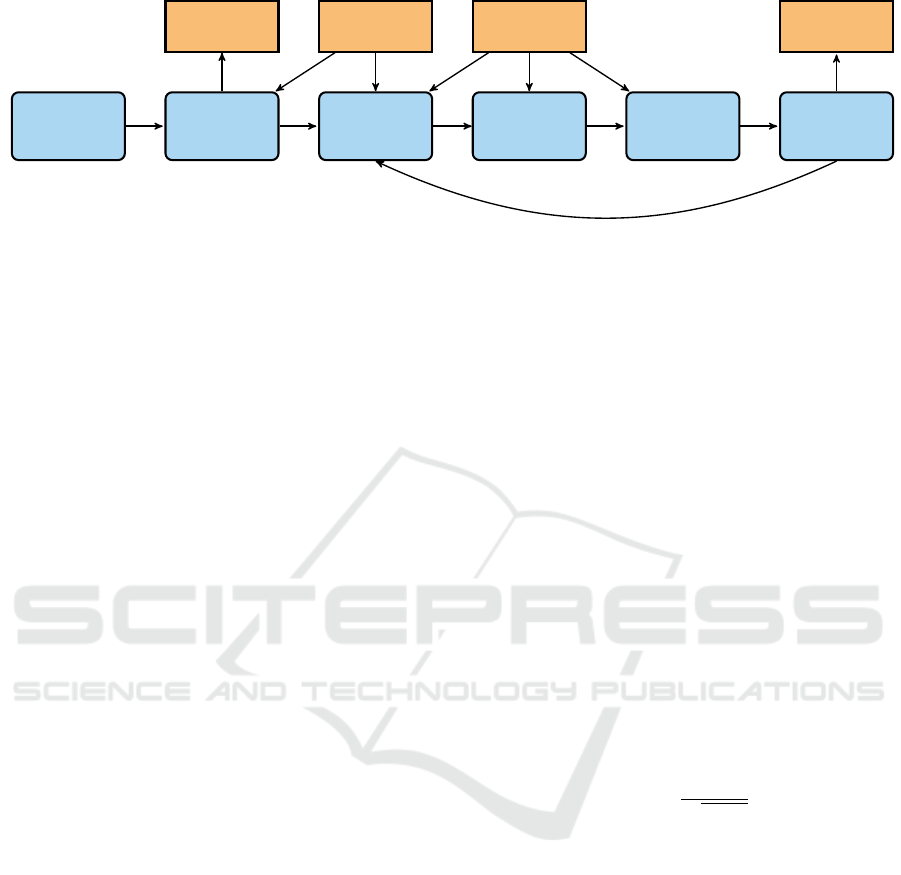
catenated with the previous absolute pose. Figure 3

shows a diagram that visualizes the whole pipeline of

our algorithm.

5 MOTION ESTIMATION

Our motion estimation algorithm estimates for a pe-

riod of time ∆t between two points in time t and t − 1

the motion of the left camera as a rigid transforma-

tion. It is a pure frame to frame motion estimation

and split up into two consecutive steps. The ﬁrst step

is an initial motion estimation that estimates the es-

sential matrix ﬁrst and then extracts the relative pose

from it. With this pose, BA respectively a nonlinear

optimization problem is initialized in a second step. It

minimizes both the reprojection error and an error that

measures how good the current estimated pose fulﬁlls

the epipolar constraint.

5.1 Motion Initialization

Our motion initialization needs 2D to 2D keypoint

correspondences as well as 3D to 2D keypoint cor-

respondences as an input. All 2D to 2D correspon-

dences that are available from the matching will be

used for estimating an essential matrix between two

camera poses of the left camera from different points

in time. After that the scale of the translation is deri-

ved from 3D to 2D point correspondences.

Step 1: Essential Matrix Computation. For mo-

tion initialization, ﬁrst the essential matrix E

∆t

is es-

timated. This is done using a 5-point-algorithm that is

embedded into a RANSAC framework (Nist

er, 2004).

All point correspondences which were classiﬁed as

outliers by the RANSAC algorithm are not used du-

ring the computation of the motion initialization. This

makes the computation robust against wrong keypoint

matches as well as moving keypoints which result

from moving objects.

Step 2: Extraction of the Relative Pose. From E

∆t

the relative pose of the stereo camera between the two

points in time is computed. It is deﬁned by the rota-

tion matrix R

∆t

and the translation vector t

∆t

that is

deﬁned up to a scale factor. Both are computed from

∆t

by the method described in Section 3. For the ini-

tial pose R

∆t

can be used directly but the correct scale

of t

∆t

has to be estimated ﬁrst since it can have large

errors.

Step 3: Scale Computation of the Translation.

The scale of t

∆t

can be computed from a 3D point



, p



, which was triangulated with the

correct scale from the stereo camera and a 3D point



, p



with incorrect scale. The point p

was triangulated from a 2D to 2D point correspon-

dence of the left camera over time. For this R

∆t

and

∆t

with incorrect scale were used. In the next step the

scale factor α of p

is computed as:

α =

. (5)

It can be used to scale t

∆t

to its correct length. Ho-

wever, for being robust against outliers the scale is

computed for all point correspondences. From them

heuristically the 5% of the smallest and 5% of the lar-

gest scale factors are discarded, since they likely con-

tain outliers. With the n remaining scale factors, the

correct scaled translation vector is computed as

∆t

∑

k=0

· t

∆t

(6)

where α

is the k-th scale factor.

The method to derive the initial pose here pre-

sented is inspired by the method described in (Scara-

muzza and Fraundorfer, 2011) to derive a consistent

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

458

Initialization

Store First

Image

Matching

and Tracking

Initial Pose

Stereo

Image Pairs

Point Cloud

Recon-

struction

Motion

Estimation

Replace

Stored Image

Computed

Pose

Sensor Unit

Calibration

Figure 3: Pipeline of the stereo VO algorithm. The ﬁgure depicts the single algorithmic steps and data ﬂows during the

execution of the stereo VO algorithm. Therefore blue boxes with rounded corners indicate algorithmic processes and orange

boxes with sharp corners data. The arrows indicate the data ﬂow.

scaled motion of a monocular camera from 2D to 2D

point correspondences. This method uses also trian-

gulated 3D points but without a metric and another

formula to estimate scale. Also the method for de-

riving the translation vector in (Cvi

c and Petrovi

2015) is similar in the way that it uses reconstructed

3D points triangulated with a metric scale from a pre-

vious stereo image pair. Here during an optimization

procedure the full translation vector whose scale is

derived from the triangulated 3D points is estimated.

However, the method presented here is to the best of

our knowledge not presented in the literature and the-

refore assumed to be new.

5.2 Motion Reﬁnement

The goal of the motion reﬁnement is to reﬁne the co-

arse estimation of R

∆t

and t

∆t

from the motion initia-

lization. We achieve this by setting up a BA problem

that makes use of information from 2D to 2D as well

as 3D to 2D point correspondences. The ﬁrst type of

cost function computes the well known reprojection

error which makes use of 2D to 3D point correspon-

dences. It is important since it is used to derive the

correct scale of the translation vector. In contrast the

second type of cost function uses 2D to 2D point cor-

respondences and quantiﬁes how good two correspon-

ding points satisfy the epipolar constraint. The later

inﬂuences only the rotation matrix and the orientation

of the translation vector.

Reprojection Error. The reprojection error quanti-

ﬁes the distance between a predicted projection of a

3D point and its corresponding observation for a gi-

ven pose of a camera. In order to compute the costs, a

3D point p

t−1

from time t −1 is transformed ﬁrst into

the camera coordinate system of the camera at time t

= R

∆t

· p

t−1

+ t

∆t

. (7)

This one is then projected into image coordinates

= π (p

) (8)

where π is the projection function which computes the

projection of p

as a point p

in image coordinates.

Finally the reprojection error is deﬁned as

r = kq

− p

(9)

where q

is the corresponding point to p

and k · k

the L

-norm.

Epipolar Error. The epipolar error used here quan-

tiﬁes how good the epipolar constraint is satisﬁed for

a given relative pose and two corresponding 2D fea-

tures. This is done by measuring the metric distance

between a point and the epipolar line on which this

point should lie on. First from a homogeneous point

˜p

t−1

in image coordinates the epipolar line

= E

∆t

· ˜p

t−1

(10)

is computed. In a next step the metric distance be-

tween the point ˜q

and





is computed.

Therefore we normalize

(11)

and denote the normalized epipolar line with

. After

that the distance between

and ˜q

is computed as

e =

· ˜q

. (12)

For the second point ˜q

of the point correspondence

the same error measure is computed again but by ma-

king use of E

∆t

These computations are similar to the ones done

by Zhang et al. since it can be shown that the cost

function for 2D to 2D point correspondences he pro-

posed also measures how good the current relative

pose fulﬁlls the epipolar constraint. However, the cost

function he proposed does not work with normalized

lines and points. We decided to compute a metric dis-

tance since it allows us to deﬁne a heuristically es-

timated standard deviation. This is necessary for a

correct weighting between the two different kinds of

Combining 2D to 2D and 3D to 2D Point Correspondences for Stereo Visual Odometry

459

cost functions and it is also a preparation of our algo-

rithm for sensor fusion with inertial information for

example.

Like Zhang et al. we also weight our cost terms

with the Tukey biweight loss function (Huber, 2011).

It assigns a ﬁxed value to costs that are higher than

a certain threshold. Since the result value of this

function does not change as long as the cost term is

higher than this threshold, these functions do not in-

ﬂuence the optimization result. This is similar to an

outlier rejection of wrong keypoint correspondences.

However, since the costs of keypoint corresponden-

ces change during optimization it is possible that a

keypoint that produces costs over that threshold can

have inﬂuence on the optimization result again after

several iterations.

6 EVALUATION

For evaluating our algorithm we used a consumer

Laptop with an Intel



Core

i7-4850HQ 2.30 GHz

CPU and 24 Gb RAM. We implemented the algorithm

in modern C++11 based on the robot operating system

(ROS) which we used for visualization as well as for

evaluation. For nonlinear optimization of the BA we

utilized the Ceres-Solver which ran in parallel with 8

threads (Agarwal et al., 2017). As evaluation datasets

we used the odometry dataset of the KITTI Vision

Benchmark Suite

(Geiger et al., 2012) and the Eu-

ropean Robotics Challenge

(EuRoC) dataset (Burri

et al., 2016).

For evaluation on the KITTI dataset we used the

rotation error e

rot

and translation error e

trans

which

are also used for evaluation by the KITTI odometry

benchmark suite (Geiger et al., 2012). It should give

an idea of about how good our algorithm performs

in comparison to the one by Zhang et al. Additio-

nally, we provide results for the absolute trajectory

error (ATE) (Sturm et al., 2012) which aims to mea-

sure the global consistency of a computed trajectory.

Its computation needs only information about the po-

sition of the camera system and not the orientation.

This is useful since for some EuRoC datasets only po-

sition information is provided.

6.1 Results on the KITTI Dataset

The odometry dataset of the KITTI Vision Bench-

mark Suite were recorded by a moving car. The 22

Web page of the KITTI Vision Benchmark Suite:

http://www.cvlibs.net/datasets/kitti/eval odometry.php

Web page of the EuRoC dataset: http://projects.asl.

ethz.ch/datasets/doku.php?id=kmavvisualinertialdatasets

Table 1: Evaluation results on KITTI dataset.

Dataset ATE [m] e

trans

[%] e

rot

[deg/m]

00 5.20 1.00 0.0032

01 - - -

02 8.57 0.94 0.0031

03 0.70 2.10 0.0034

04 3.11 2.96 0.0032

05 9.12 2.60 0.0054

06 8.12 2.73 0.0072

07 5.14 2.27 0.0104

08 11.29 2.35 0.0043

09 12.18 3.17 0.0046

10 4.99 2.05 0.0047

Average 6.84 2.22 0.0050

datasets are split into eleven training datasets and ele-

ven evaluation datasets. We evaluate our algorithm

only on the eleven training datasets since for the eva-

luation datasets no ground truth is public available.

The ground truth information of the datasets is provi-

ded as a 6D pose and computed from a GPS receiver

with an integrated IMU. The stereo camera system of

the car provides grayscale images at a frame rate of

10 frames per second and a resolution of 1241 × 376

pixels (Geiger et al., 2012).

During our experiments the algorithm matched

approximately 380 keypoints between the left and the

right image and tracked 1290 keypoints between two

consecutive images including outliers. As described

in Section 5.1 and Section 5.2 these outliers were pro-

perly handled by the RANSAC algorithm during mo-

tion initialization and the robust cost functions during

the motion reﬁnement.

Our evaluation results are shown in Table 1. The

algorithm achieves the best results on the datasets 00

and 02 with relation to e

rot

and e

trans

. Except for da-

taset 01 our algorithm is able to compute the whole

trajectory for all datasets. During the processing of

dataset 01 the algorithm is not able to keep track of

the trajectory since the scale computation fails due to

the lack of proper feature correspondences. When the

scale computation fails many feature matches are lo-

cated far away on the horizon where the triangulated

depth information of 3D points can contain large er-

rors.

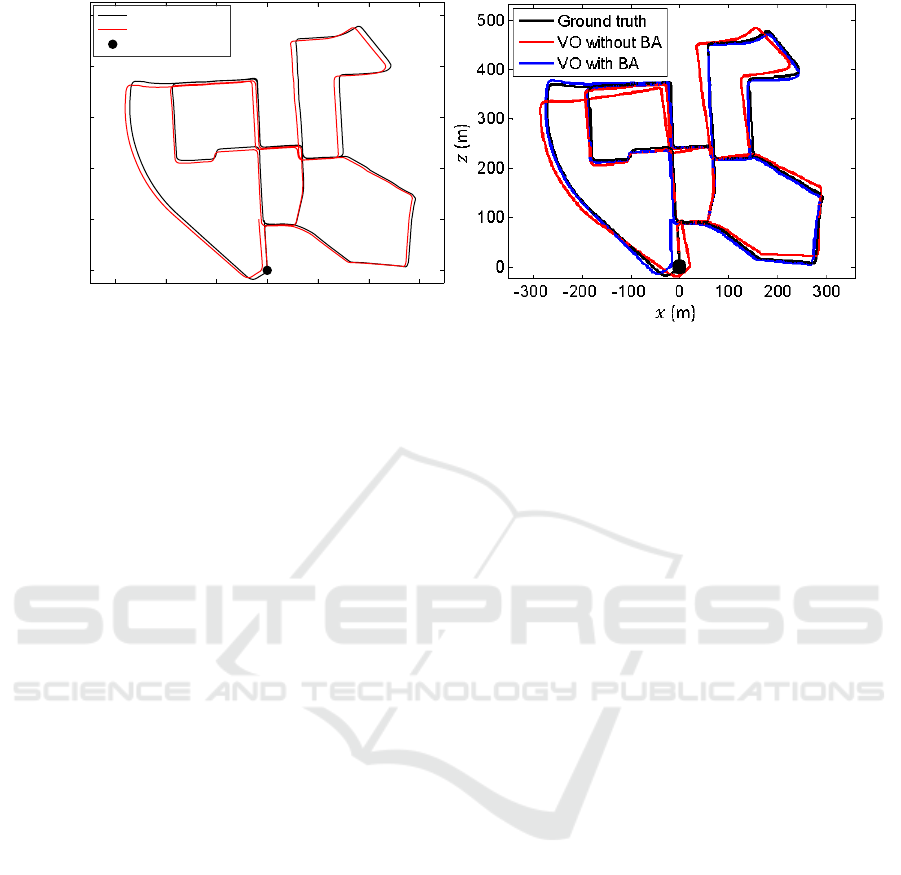
Figure 4(b) shows the trajectory of Zhang’s algo-

rithm in the ground plane with and without windowed

BA for the KITTI dataset 00. By comparing the tra-

jectory without windowed BA to the one with it, it can

be seen how much positive impact it has on the accu-

racy of the trajectories. Due to this fact, the results

of our algorithm cannot be compared with the results

of Zhang et al. since the authors of that work do not

provide evaluation data without windowed BA. Ho-

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

460

−300 −200 −100 0 100 200 300

x (m)

100

200

300

400

500

y (m)

Ground Truth

Our Result

Start point

(a) KITTI 00 in the ground plane. (b) KITTI 00 in the ground plane by Zhang et al. (Zhang

et al., 2014).

Figure 4: Reconstructed trajectories in the ground plane for the dataset KITTI 00.

wever, in comparison to our trajectory visualized in

Figure 4(a) the trajectory of Zhang’s algorithm dif-

fers more from the ground truth trajectory than ours

in the ground plane.

The results of the ATE do not always correlate

with the translational error e

trans

. This apparent lack

of correlation can be attributed to the different charac-

teristics of the error measurements. Especially for tra-

jectories where the vehicle moves only straight ahead

like 03, 04, 07 and 10 this error is very low. In these

cases the computed and the ground truth trajectory

can be aligned very well, which happens during the

computation of the ATE.

The average error values in Table 1 were compu-

ted without considering dataset 01. The processing of

a single stereo image pair of the KITTI dataset took

approximately 180 milliseconds.

6.2 Results on the EuRoC Dataset

The EuRoC dataset contains data records captured

with a hexacopter (Burri et al., 2016). The robot was

equipped with a sensor system that provided synchro-

nized grayscale stereo image pairs which were cap-

tured with a resolution of 768 × 480 pixel at 20 Hz.

The datasets were captured in three different environ-

ments. The “Vicon Room 1” (V1) datasets are captu-

red in a bright room whereas “Vicon Room 2” (V2)

datasets were captured in the same room with less

light and different obstacles. From both environments

respectively datasets with three levels of difﬁculty:

V1-1 and V2-1 easy; V1-2 and V2-2 medium; V1-3

and V2-3 difﬁcult. The different degrees of difﬁculty

result from different motion speeds and lighting con-

ditions. As ground truth a full 6D pose is provided.

The remaining 5 datasets were recorded in a “Ma-

chine Hall” (MH) environment. The degrees of dif-

ﬁculty are here also divided into three levels: MH-1

and MH-2 easy; MH-3 medium; MH-4 and MH-5 dif-

ﬁcult. For these datasets only the ground truth posi-

tion is provided.

Since the resolution of the images from the Eu-

RoC dataset is smaller than for the KITTI dataset less

keypoint matches can be extracted from the images.

These were approximately 380 keypoints between the

left and the right image and 830 for consecutive ima-

ges.

Our evaluation results on the EuRoC dataset are

shown in Table 2. By examining the values of the ATE

it can be noticed that they are smaller than the ones

from the KITTI dataset in general. This comes from

the expansion of the trajectories which is in general

smaller than for the KITTI dataset. By further analy-

sis it can also be noticed that the algorithm seems to

perform better on the Machine Hall datasets. This is

the result of a slower optical ﬂow in the image stream

since almost all objects are further away from the ca-

mera than in the Vicon Room datasets. The keypoint

matching and tracking proﬁts from this. However, at

some parts of the trajectories for MH-4 and MH-5 the

algorithm is almost not able to track the camera sys-

tems egomotion due to bad lighting conditions. These

problems lead to high ATE values.

On the Vicon Room datasets the algorithm works

for the datasets with easy and medium degree of dif-

ﬁculty. For these datasets the algorithm is able to

handle the speed of the optical ﬂow and the resulting

motion blur. Only for the datasets V1-3 and V2-3

our algorithm is not able to track the egomotion of

the camera. In these situations fast changing lighting

conditions which result in almost black images due

to the cameras auto exposure as well as strong mo-

Combining 2D to 2D and 3D to 2D Point Correspondences for Stereo Visual Odometry

461

Table 2: Evaluation results on the EuRoC dataset.

Dataset V1-1 V1-2 V1-3 V2-1 V2-2 V2-3 MH-1 MH-2 MH-3 MH-4 MH-5

ATE [m] 0.60 0.35 - 0.51 0.85 - 0.19 0.21 0.63 1.64 1.52

Figure 5: Visualization of the trajectory of the dataset MH-2

in 3D. The trajectory was aligned by computing an optimal

transformation for the ﬁrst 1100 positions. It can be noticed

that the trajectory starts to drift after a few meters. However,

the trajectory proceeds close to the ground truth even at its

end.

tion blur lead to few and wrong point corresponden-

ces. In consequence the relative pose estimation di-

verges at several points of the trajectory. In order to

overcome the problems resulting from motion blur, a

keypoint tracking method that applies the photometric

error could be utilized.

The processing time for a stereo image pair from

the EuRoC dataset took approximately 140 millise-

conds. This smaller processing time in comparison to

the KITTI dataset comes obviously from the smaller

image size of the dataset and fewer computed featu-

res.

7 CONCLUSION AND FUTURE

WORK

In this work we have presented a pure visual odome-

try approach which adapts the idea of Zhang et al.

(Zhang et al., 2014) to utilize keypoints with and wit-

hout known depth information during motion estima-

tion. In contrast to Zhang et al. we have used a stereo

camera instead of a laser scanner in order to obtain

depth information. Instead our algorithm computes

depth information from keypoint matches which are

obtained by means of keypoint matching and tracking.

These matches are passed to the motion estimation

which is split into a initialization and reﬁnement step.

With our motion initialization we have shown how an

initial estimate for a nonlinear optimization problem

can be derived which is solved during motion reﬁne-

ment. This optimization problem utilizes the infor-

mation from 2D to 2D as well as 3D to 2D keypoint

matches. With this approach we achieved promising

results on the well known EuRoC and KITTI dataset.

However, the algorithm was not able track the trajec-

tory in three cases where many triangulated keypoint

features were far away on the horizon or no keypoints

could be matched due to bad light conditions.

During further developments we would like to ex-

tend our approach with windowed BA which has the

potential to improve the accuracy of the trajectory

a lot. Additionally we also plan to utilize keypoint

correspondences from the right stereo camera in our

motion reﬁnement. This may also make it possible

to avoid the motion initialization step and could also

enable the algorithm to keep track in environments

with bad lighting conditions.

ACKNOWLEDGEMENTS

We thank the German Academic Exchange Service

(DAAD) for partially founding this work.

REFERENCES

Agarwal, S., Mierle, K., and Others (2017). Ceres solver.

http://ceres-solver.org. Version 1.12.

Buczko, M. and Willert, V. (2016a). Flow-decoupled nor-

malized reprojection error for visual odometry. In In-

telligent Transportation Systems (ITSC), 2016 IEEE

19th International Conference on, pages 1161–1167.

IEEE.

Buczko, M. and Willert, V. (2016b). How to distinguish in-

liers from outliers in visual odometry for high-speed

automotive applications. In 2016 IEEE Intelligent

Vehicles Symposium (IV), pages 478–483. IEEE.

Burri, M., Nikolic, J., Gohl, P., Schneider, T., Rehder, J.,

Omari, S., Achtelik, M. W., and Siegwart, R. (2016).

The EuRoC micro aerial vehicle datasets. The Inter-

national Journal of Robotics Research.

Cvi

c, I. and Petrovi

c, I. (2015). Stereo odometry based on

careful feature selection and tracking. In Mobile Ro-

bots (ECMR), 2015 European Conference on, pages

1–6. IEEE.

Fraundorfer, F. and Scaramuzza, D. (2012). Visual odome-

try: Part ii: Matching, robustness, optimization, and

applications. IEEE Robotics & Automation Magazine,

19(2):78–90.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

462

Fu, C., Carrio, A., and Campoy, P. (2015). Efﬁcient visual

odometry and mapping for unmanned aerial vehicle

using arm-based stereo vision pre-processing system.

In Unmanned Aircraft Systems (ICUAS), 2015 Inter-

national Conference on, pages 957–962. IEEE.

Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we ready

for autonomous driving? the KITTI vision benchmark

suite. In Proceedings of the IEEE Computer Society

Conference on Computer Vision and Pattern Recogni-

tion, pages 3354–3361.

Hartley, R. and Zisserman, A. (2003). Multiple view geome-

try in computer vision. Cambridge university press.

Hartley, R. I. (1993). Cheirality invariants. In Proc. DARPA

Image Understanding Workshop, pages 745–753.

Hartley, R. I. and Sturm, P. (1997). Triangulation. Computer

vision and image understanding, 68(2):146–157.

Huber, P. J. (2011). Robust statistics. In International En-

cyclopedia of Statistical Science, pages 1248–1251.

Springer.

Lucas, B. D. and Kanade, T. (1981). An iterative image re-

gistration technique with an application to stereo vi-

sion. In Proceedings of the 7th International Joint

Conference on Artiﬁcial Intelligence, IJCAI ’81, Van-

couver, BC, Canada, August 24-28, 1981, pages 674–

679.

Nist

er, D. (2004). An efﬁcient solution to the ﬁve-point

relative pose problem. IEEE transactions on pattern

analysis and machine intelligence, 26(6):756–770.

Rosten, E., Porter, R., and Drummond, T. (2010). Faster

and better: A machine learning approach to corner

detection. IEEE transactions on pattern analysis and

machine intelligence, 32(1):105–119.

Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.

(2011). Orb: An efﬁcient alternative to sift or surf.

In Computer Vision (ICCV), 2011 IEEE International

Conference on, pages 2564–2571. IEEE.

Scaramuzza, D. and Fraundorfer, F. (2011). Visual odome-

try : Part I: The ﬁrst 30 years and fundamentals. IEEE

Robotics & Automation Magazine, 18(4):80–92.

Sturm, J., Engelhard, N., Endres, F., Burgard, W., and Cre-

mers, D. (2012). A benchmark for the evaluation of

rgb-d slam systems. In 2012 IEEE/RSJ International

Conference on Intelligent Robots and Systems, pages

573–580. IEEE.

Zhang, J., Kaess, M., and Singh, S. (2014). Real-time depth

enhanced monocular odometry. In Intelligent Robots

and Systems (IROS 2014), 2014 IEEE/RSJ Internatio-

nal Conference on, pages 4973–4980. IEEE.

Zhang, Z., Deriche, R., Faugeras, O., and Luong, Q.-T.

(1995). A robust technique for matching two unca-

librated images through the recovery of the unknown

epipolar geometry. Artiﬁcial intelligence, 78(1-2):87–

119.

Combining 2D to 2D and 3D to 2D Point Correspondences for Stereo Visual Odometry

463