Interactive Anisotropic Tearing of Elastic Solids

Omar Hesham, Chris Joslin and Rufino R. Ansara

School of Information Technology, Carleton University, 1125 Colonel By, Ottawa, Canada

Keywords: Anisotropic Tearing, Simulation, Physics.

Abstract: Dynamic models to simulate tearing of soft elastic bodies are an essential element of various medical and

surgical training simulators. These models are also finding increased use in film and gaming applications,

where control of the quality and style of the final output is highly valued. There is a general lack of models

specifically designed to control tearing patterns, and in this paper, we present our work towards a soft-body

tearing method that provides simple parametrizations to control the tear independently from the elastic

properties of the soft body simulation. Our parameters can influence how clean-cut or jagged the tear is, in

addition to allowing anisotropic influence using an embedded fibre model in the elastic body. We also aim

for a real-time implementation suitable for interactive environments. Our meshless solution is discussed in a

context that is aware of the importance of unified physics solvers.

1 INTRODUCTION

Deformable body problems and fracturing

simulations were developed originally to simulate

solutions for the engineering and applied sciences

fields. These methods soon found their way into the

computer graphics field, applying their strengths to

simulate various natural dynamic phenomenon like

cloth, fluids and general soft bodies. Research that is

specific to computer graphics models is geared

towards stability and visual realism, as opposed to

absolute theoretical accuracy. Speed and efficiency

are also valued greatly when comparing methods

against each other. These developments find their

primary application in film, game and medical

simulation. We present a method to simulate fast

tearing in elastic bodies that gives the user control

over the fracture style and direction, while aiming at

a real-time implementation for interactive

environments.

While soft and viscoelastic body simulation can

be done efficiently for highly dynamic real-time

gaming environments, fracturing or tearing those

objects apart remains a challenge at those frame rates.

One efficient approach is pre-fracturing model

geometries and holding the pieces together using

artificial cohesive “glue” values. While this can give

visually appealing results for breakable rigid bodies,

it is very limiting for soft bodies that can tear at

arbitrary locations. This motivated us to formulate a

soft body tearing framework that can run in

interactive environments and allow independent

control over the fracturing style, while interacting

with the physical model used to simulate the body’s

elastic behaviour.

Figure 1: Stylistic control over the tearing process.

Comparing the effects of γ on the tearing pattern, using the

same elastic properties. From left to right: a) Initial state (t

= 0sec); b) = 0:85 (t = 1sec); c) = 0:3 (t = 1sec).

This paper presents our research efforts towards

tearable soft-body simulation with an emphasis on the

following properties: First, a tearing method that

provides stylistic and directional control with simple,

easily implementable parameters that are independent

from, but work together with the underlying material

properties used for the elastic simulation. Second,

have the potential for a real-time implementation

without significantly compromising the accuracy of

the simulation.

Finally, be based on a dynamics framework that

can be embedded or extended into a unified physics

solver (easy transition, extension and coupling with

256

Hesham, O., Joslin, C. and Ansara, R.

Interactive Anisotropic Tearing of Elastic Solids.

DOI: 10.5220/0006623902560263

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 1: GRAPP, pages

256-263

ISBN: 978-989-758-287-5

other physical systems like fluid and cloth dynamics.)

With those goals in mind, we set out to achieve

the following:

Extending Becker et al.’s Smoothed Particle

Hydrodynamics (SPH) elastic simulation framework

(2009) to support topological changes through tearing

(or fracture, terms used interchangeably). Their

meshless framework was chosen for its realistic

simulation of elasticity at real-time rates while also

being extensible to fluid and rigid simulation, as

previously demonstrated by (Solenthaler et al., 2007).

Proposed the concept of a fracture disk that is

inserted at any point of fracture throughout the

simulation domain and, with the aid of an empirically

developed transparency map, affords the end user a

degree of control over the style of the tear (sharp and

clean-cut vs. soft and feathered), decoupled from the

elastic properties of the soft body being torn.

To control the tearing direction, we propose an

anisotropic tearing model that uses a vector field,

called fibres, to influence the orientation of the tear in

an isotropic material. We propose the use of strain-

rate to modulate this influence and to avoid a

completely geometric and artificial tearing pattern.

We also describe a fast and simple method of

maintaining the fibre field definition during the

simulation, while robustly handling situations of

fracture and topological changes in the material.

2 BACKGROUND

Since Terzopoulos et al.’s (1988) seminal work on the

dynamic simulation of deformable bodies and their

fracture, this area of computer graphics research has

seen a rapid increase in development, focusing on

stable, visually realistic and efficient methodologies

for simulating various natural physical phenomenon.

Specific to fracture simulation, earlier methods

heavily featured the Finite Element Method (FEM)

discretization, thanks to its connected mesh definition

and the ease of disconnecting them wherever fracture

events occurred. FEM also provided the desirable

property of convergence (as the resolution of the

mesh increases, the method approaches the true

continuum solution) and facilitated textured surface

embedding by simply treating the boundary faces of

the FEM mesh as the visual surface to render. Early

examples of efficient FEM fracture include O’Brien

et al.’s (1999) and its extension to ductile fracture

(O’Brien et al., 20020) and Irving et al.’s (2004) very

stable formulation for large and even inverted mesh

deformations. FEM found further practical use in

real-time gaming environments (Parker and O’Brien,

2009) and specialized medical and surgical scenarios

(Meier et al., 2005). However, remeshing around

topological changes while avoiding the generation of

irregularly shaped and problematic elements remains

a non-trivial challenge for FEM methods. This is

important in tearing simulation, considering the need

for fracture lines that cut through the mesh at arbitrary

locations.

Recent adaptive remeshing techniques (Hahn and

Wojtan, 2016), have tackled this problem, some even

providing a high level of control of the fracture

dynamics (Pfaff et al., 2014) with convincing visual

realism. Koschier et al., (2017) proposed an approach

based that decouples cut geometry from the

underlying FEM mesh, avoiding the need for

remeshing when tearing complex-shaped objects.

FEM and XFEM methods are still, however, far from

any real-time implementation, making them unviable

for interactive environments.

An approach proposed in Chen et al.’s work

(2014) comes closest to our goals of providing visual

control over the cut features. While fast, it contrasts

to our proposed method in two aspects. First, their

approach is done in a post-process that modifies the

FEM mesh geometrically while ours is done during

runtime. Second, our approach relies on a meshless

physics formulation.

Meshless methods have attracted attention for

their flexibility and resampling freedom. In essence,

the domain is discretized into disconnected particles

(nodes) where the dynamic properties are evaluated,

and each has an influence on the rest of the continuous

body that decreases as we go further away from it.

They do not suffer from the remeshing problems of

FEM methods and have been found particularly

useful for fracture simulation. Müller et al. (2004)

used moving least squares (MLS) to calculate a first-

order-accurate estimation of the deformation gradient

and successfully showcased the versatility of

meshless methods in handling elastic, plastic and

viscoelastic simulation seamlessly in the same

framework and at interactive rates.

Smoothed particle hydrodynamics (SPH) is a

meshless method, originally developed a few decades

ago to model cosmo-galactic events (Gingold and

Monaghan, 1977), that later became very popular in

computer graphics for real-time Lagrangian fluid

simulation due to its ability to handle rapidly

changing neighbourhoods with high temporal

coherency and stability (Müller et al., 2003; Tan and

Yang, 2009). Solenthaler et al., (2007) devised an

SPH framework to model a relatively large variety of

physical phenomenon including rigid, deformable

and fluid objects. However, their elasticity

Interactive Anisotropic Tearing of Elastic Solids

257

formulation suffered from being rotationally variant,

causing incorrect handling of rotating elastic bodies

that relied on an initial reference position. This was

later corrected by Becker et al., (2009) in their

corotated SPH formulation for elastic bodies.

Liu et al., (2011) presented a meshless method to

simulate fracture in brittle solids. They used rigid

dynamics for regular simulation and the Meshless

Local PetricGalerkin (MLPG) method to evaluate

stresses throughout the body during a fracturing

event. User control over the fracture pattern was

allowed through a custom weighted vector field to

guide the clustering part of their algorithm. While this

approach is fast and works well for brittle fracture in

rigid solids, it also forces the creation of a new

partition at every fracturing event, making it

unsuitable for our elastic soft body tearing where

partial cuts are allowed.

One of the few real-time medical simulators that

provides anisotropic tearing is Allard et al.’s cataract

surgery simulator (2009). In their implementation,

they use a 2D FEM model along with a vector field

(they called fibre field) to define the desired direction

of tear propagation. In contrast to the previously

discussed methods, however, their approach is purely

physical, relying on a complete anisotropic elasticity

simulation, which in turn directly results in

anisotropic tearing simulation. While their results are

convincing, their method does not allow for

anisotropic fracture control in isotropic materials.

The proposed method presented in this short paper

is largely based on work first introduced in (Hesham,

2011) which incorporates tearing into Becker’s

(2009) corotated SPH approach, and further

influenced by the concepts in Allard et al.’s (2009)

and Liu et al.’s (2011) research.

3 METHODOLOGY

We start by describing how fracture is visually

encoded using fracture disks and allowed to exist in

semi-arbitrary locations, followed by

parametrizations that allow control over the visual

detail of the fracture pattern without disturbing the

underlying physical mechanics and finally,

incorporating controllable anisotropic influence on

the tearing direction. We apply our tearing

modifications while striving for minimal impact on

the computational cost of the already efficient elastic

simulation.

3.1 Tearing

3.1.1 Fractured Kernel Shape Functions

In FEM or Mass-Spring System (MSS) simulations,

the discretized simulation nodes have well defined

connections that can be removed or split apart to

introduce fracture and topological change into the

model. Meshless methods like SPH, on the other

hand, do not have this kind of explicit connectivity

between its smoothed particles. What we can do,

however, is modify the weighted kernel shape

functions, such that nodes separated due to fracturing

no longer continue to influence the displacement field

gradient calculation, even if those nodes are still

within each other’s neighbourhood radius h.

For this purpose, Baleytschko et al., (2003)

introduced discontinuities in the SPH kernel shape

functions using a visibility criterion. Two nodes

within each other’s neighboorhoods can no longer

interact with each other if the ray passing through

them intersects a crack surface. This prevented the

shape functions from crossing the crack, but

introduced abrupt discontinuities in ▽u on both sides

of the crack, not just across it. This prompted Organ

et al., (1996) to introduce transparency to the

visibility check, providing a smoother outcome for

the modified shape functions and better transitions

near the tip of the crack front. We follow this

approach and develop our own transparency criteria,

motivated by empirical results and the afforded

controllability of the tearing style.

Every particle i stores a visibility value A

 [0, 1]

for every particle j in its neighbourhood, where 0

means the particles can completely see each other and

1 indicates no visibility at all. This is symmetric, so

= A

. The value is used to artificially increase the

distance between 





and 





for the kernel

computation in equation for both particles. So, the

new distance metric used for r becomes:



















  





(1)

A crack surface is defined as a round disk centred at

position c with axis vector a and radius k. Wherever

a fracture event is detected, a new disk is inserted. The

criteria for determining the disk location and

orientation is discussed in sections 3.1.2-3.2.2. Once

inserted, we trigger a visibility check for all nearby

particles: for a given particle i, we trace a ray to each

of its neighbours j and denote the location of

intersection of each ray with the fracture disk as d

The opacity 

at that point on the disk gets added to

the principle opacity A

. The opacity   [0, 1] is

radially defined on the disk as:

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

258







 

  





   





  









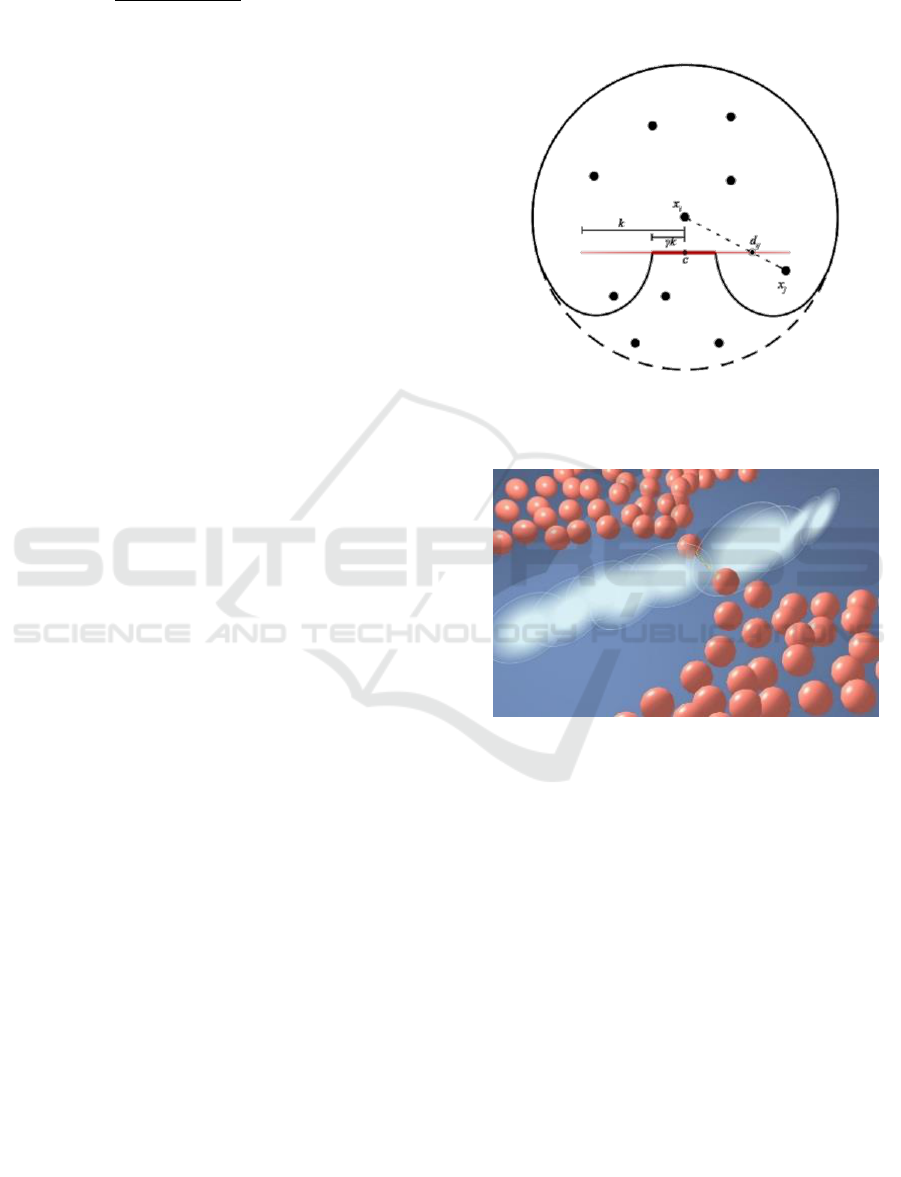
(2)

where γ  [0, 1] defines the rigidity of the fracture

giving the user control over how the fracture

propagates locally. Visually, k can be thought of as

the radius of an inner disk that is completely opaque

(α = 1) and the rest of the disk gets gradually more

trans-parent as we move closer to the outer edge,

radius k, of the disk. Figure 2 shows the gradual effect

of disk transparency on the kernel shape function for

particle i.

The α

value is the same for both particles (α

). If multiple disks are inserted in the same time step

(frame) of animation, the α

obtained from all the disk

visibility checks are treated additively and A

updated before discarding all the disks at the end of

the frame. A

can only increase, as we treat fracture

damage as permanent, and once it reaches 1, the

particles are dropped from each other’s

neighbourhood lists and are never used again in each

other’s ▽u calculation. Also, as a general rule, if the

particles become too distant from each other ||x

- x

> 2.5h, we drop them from their corresponding lists,

regardless of A

. Note that while the visibility check

is done using the current deformed state with

positions x

and x

, the neighbourhood update is done

on the initial state 





and 





as that is where the

elastic structure is originally defined.

High γ values produce very rigid and clean cuts,

whereas lower values produce softness in the fracture

lines and interesting patterns will arise (Figure 3 and

Figure 1). Of course, values can also be defined

globally or specified locally per node. We empirically

found γ =1 to be a suitable default value.

The method presented in this section is a simple user-

friendly way to alter the dynamic style of fracture,

affording flexibility of design and working alongside

(without being restricted by) the physical parameters

used for elasticity simulation.

3.1.2 Fracture Criteria

Fracture or tearing is initiated at any point in the body

where the maximal eigenvalue of the stress tensor

exceeds the material threshold. For an isotropic

material, the crack is propagated orthogonally to the

corresponding eigenvector.

The stress criteria are evaluated at every particle

in the simulation and we can directly begin the crack

at the location of that node. However, arbitrary crack

locations that are not dependent on the particle

distribution are also very easily. Part of what makes

meshless methods attractive for fracture simulation is

their inherent flexibility with resampling, allowing

the freedom to insert particles without worrying about

proper remeshing as with FEM methods.

Figure 2: Effect of a visibility check through a fracture disk

(red) on the kernel shape function (thick line) with

influence radius h (dotted circle).

Figure 3: Effect of transparent fracture disks on the fracture

style. High γ values produce stiff fractures akin to brittle

fracture; while low γ produces “softer” tearing, with

interesting small-scale effects like shown here, where part

of the fractured object still seems to be “hanging by a

thread”, as seen when tearing a fibrous body (e.g. an

orange).

Our goal is still primarily an interactive

application, and although resampling might increase

accuracy, it could result in an unpredictable increase

in the number of simulation nodes and effectively

penalize simulations with a high count of fracturing

events.

Our crack location method begins with a node

whose principal stress (eigenvalue) v

has exceeded

the material fracture threshold. We obtain the

corresponding stress eigenvector 





and the

orthogonal fracture direction z

. A fracture disk is

inserted with c = x

, a = 





and k = h + 2(



 ).

Interactive Anisotropic Tearing of Elastic Solids

259

We then split the neighbourhood of particle i into Left

and Right neighbourhoods by the plane containing z

and whose normal is in 





. The weighted average of

the maximal stresses is calculated for each side

independently as Left and Right:

















 







h



(3)

















 











(4)

The main idea here is to find out which side is more

stressed, and this bias informs us of where the fracture

would have most likely occurred. Finally, we perturb

the crack location from its original position x

along

the stress vector 





by an amount directly

proportional to the difference between Left and Right.

Since meshless methods are inherently denser

than FEM methods, we find this minimal approach

reasonable for finding a physically-motivated

arbitrary crack location without sacrificing

computational efficiency.

3.2 Anisotropic Tearing

In this section we describe the specifics related to

anisotropic control over the tearing direction, using

terminology analogous to fibres found in biological

tissue (Allard et al., 2009).

3.2.1 Fibre Orientation Update

In our physics model, we allow a user-controlled

vector field over the simulation particles to denote the

desired directional influence on the tear propagation.

Each vector is called a fibre, and is conceptualized as

a 1-dimensional thread flowing through the body of

the object. We assume that the fibres fill up the 3D

domain of the simulation. That is, any particle lying

within the continuum of the object has a single fibre

passing through it, indicating the preferred direction

of tearing at that particle. These threads give strength

to the material along their main vector and resist

tearing across it.

The fibrous structure of the object is discretized

into a vector field over our existing set of simulation

particles P. Every particle is initialised with the 3D

vector 



indicating fibre direction through that

particle position. The directions can be defined

globally, generated procedurally (for example

following the curvature of the object), or setup by

hand using 3D brushes or other manual techniques.

Linear, quadratic or quaternion interpolation can be

used to find the intended fibre direction at arbitrary

points throughout the domain.

As the simulation progresses and the object is

deformed by elastic and external forces, we need to

update the direction of the fibre to reflect the true fibre

structure in the deformed state, because elastic forces

do not produce local torque. This was not a problem

in Liu et al.’s (2011) meshless brittle fracture

simulation because they used rigid body dynamics

and could correctly maintain the fibre direction

throughout the simulation. Elastic FEM methods, like

(Allard et al., 2009), can simply embed the fibre

within each triangle (2D) or tetrahedron (3D) and

track the orientation as the simplex deforms.

We initially experimented with an implicit

definition of 



, so for a certain particle i, we chose a

neighbouring particle j such that 





 





as provided

the closest approximation to the user input direction

i. Once initialised, this link between i and j is constant

throughout the simulation. This method was simple to

implement, and gave a very stable non-jittery

definition of 



, but we soon realised its

disadvantages. The first obvious problem was that the

fibre structure became entirely dependent on the

initial distribution of particles, hence we could not

truly define arbitrary fibre directions. Additionally,

having the direction coupled with a single particle j

meant that 



, was no longer aware of deformations

on the opposite side of i and would not update the

fibre at i accordingly. Lastly, further maintenance was

required when a fracturing event separated i from j,

requiring us to find a new suitable neighbour j for i. It

quickly became apparent that this approach was not

robust enough for our tearable simulation.

We opted instead for an explicit definition of 



(Figure 4). Becker et al.’s (2009) corotated SPH

formulation that we already use to evaluate elastic

dynamics, provides a rotation matrix, R

, which

encodes the local rotational variance from the initial

undeformed shape. This gave us a very stable and

efficient way to locally update the current fibre

direction 















(5)

where 



(or 



, we do not differentiate between

them) is now just the initial vector definition of the

fibre, centred at x

and is no longer restricted to the

distribution of the particles, and the current ɸ

is not

affected by fracturing events.

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

260

Figure 4: Fibre orientation maintenance. From left to right:

undeformed particles with initial fibre direction 



;

deformed particles with no update to fibre direction;

deformed particles with explicit fibre update ɸ

= R





3.2.2 Anisotropic Influence of Fibre on the

Tearing Direction

In this section, we describe how fibre orientation is

used to influence the fracture direction z in 3.1.2,

resulting in the desired anisotropic fracture.

Fibres in our simulation are there to resist tearing

across the fibre’s main direction. Given the plane 



whose normal is 



we want to suppress the

component of the fracture vector z

in the direction of

its projection onto 



The new fracture vector is then:











  

















(6)

where 



is a penalty term deciding the magnitude of

the fibre’s influence (0 = completely follow fibre

direction; 1 = no fibre influence at all). What

distinguishes our implementation from previous

penalty-based anisotropy models (Liu et al., 2011) is

that in addition to allowing user-input values for 



we improve the simulation realism by also

considering the physical rate of deformation (strain

rate 



) for varying 



. The faster the rate of

deformation is, the less the fibre can influence the

tear’s

direction. The effect of our approach can be

seen in Figure 5.

4 RESULTS

4.1 Implementation

We implemented our elasticity and tearing models by

extending the open source SPH simulator FLUIDSv.2

(Hoetzlein and Höllerer, 2008), resulting in a system

that can simulate both fluids and tearable elastic

bodies. The code is written in C++ and utilizes

OpenGL for graphical output.

The particles in all of our tests are on average 0.05

units apart with an influence radius h = 0.2. The

number of neighbours a particle can have within its

influence radius is limited to the nearest 20. This

allows us to use an adjacency list to maintain

neighbourhood information quite efficiently. In

addition, we inserted our deforming particles into a

spatial hash as described in Viccione et al. (2008),

which is a standard way to accelerate broad-phase

collision detection and fluid neighbourhoods, but we

also use it to quickly find the grid(s) around an

inserted fracture disk, performing the disk visibility

check on only those particles.

4.2 Performance and Results

We successfully achieve interactive rates in our tests,

with our profiler indicating that our calculations take

an average of 62% of the total processing time per

frame, with the rest for rendering and other processes.

These results, while not distinguished from similar

purely elastic simulation models, show considerable

speed-up when compared to similar fracturing

simulations, in some cases even an order of a

magnitude faster, as shown in Table 1. We do note

that surfacing would incur additional costs, but our

physical fracturing simulation speeds already seem

promising. We compare our method with other

meshless techniques in computer graphics that allow

soft-body tearing. We also include the performance of

Becker et al., (2009), the purely elastic framework

that we extended, to show that our tearing method

does not present a large computational penalty, even

in situations with relatively high particle count. As the

number of fractured partitions increased, our

simulation got faster due to a reduced neighbourhood

list. Figure 5 shows an example of an elastic soft body

hanging from a static support bar (green) and getting

torn by its own weight. Figure 4 shows how we

enhance the realism of anisotropic tearing by

considering the velocity of deformation, strain rate.

As with every physics simulator in computer

graphics, stability is an important factor to consider in

our tests and implementation design. We use the

Verlet variant of the Leapfrog integration (Nealen et

al., 2006), to advance our simulation, which was fast

to solve and provided a high degree of stability.

Complex cases benefited from increasing particle

samples and decreasing the timestep, at an added

computational cost. Generally, SPH fluid pressure

forces were also useful to maintain stability for larger

time steps (Becker et al., 2009; Müller et al., 2004).

We also found it helpful to spread the fracture disk

insertion process over several frames (4 to 10) by

scaling the disk size from 0.25k to k. Aside from being

a reasonable reflection of reality, this had a

favourable impact on our computational and visual

stability.

Interactive Anisotropic Tearing of Elastic Solids

261

Figure 5: An originally rectangular soft body with diagonal

fibres pointing north-east being torn apart by external forces

(green cones). Top: peeling the object slowly allows the

fibre to dictate the tearing direction. Bottom: a faster strain-

rate correctly reduces the anisotropic influence of fibre,

closely resembling tearing in a fibre-free object.

Table 1: Performance results for samples shown in this

report.

Sample

Particles

γ Tear

Rigidity

Δt(ms)

FPS

Figure 3.

700

0.5

Figure 5.

300

0.9

Figure 1b.

24000

0.85

Figure 1c.

24000

0.3

While evaluating our explicit fibre tracking

method (Section 3.2.1), we observed that temporal

coherency of the fibre orientation was not perfect (i.e.

it seemed a bit jittery) for particles near the surface of

newly created fractures. We believe this happens

because the SPH-based rotation estimation R has

lesser accuracy due to a reduced number of

neighbouring particles compared to the neighbours at

the initial reference positions. The effect on the

simulation, however, was negligible and the method

is overall very sufficient for a fairly accurate and

robust maintenance of fibre direction. We also

noticed that it performs quite well with primarily

dilation-based de-formations (stretch and

compression), however it struggles to maintain the

fibre orientation accurately when the object is

subjected to large shear deformations. We attempted,

unsuccessfully, to remedy this by extracting the local

shear information from the Jacobian of the

displacement field to inform the fibre orientation. We

suspect that a mixed explicit-implicit fibre update

method would help greatly in this situation.

5 CONCLUSIONS

This short paper has presented a method for soft-body

tearing that emphasizes controllability, speed and

stability without significantly compromising realism

and accuracy, all of which are desired aspects in

game, film and medical simulation development. We

provided simple parametrizations for two interesting

phenomena in tearing simulation. The first, controls

how clean (brittle-looking) the cuts are; and the

second involved anisotropic control of the tearing

direction for mechanically isotropic materials using

embedded virtual fibres in the de-formable body.

We have shown how to incorporate our approach

into an existing soft-body simulator by extending an

elastic solids SPH framework, chosen due to the

versatility of meshless methods in fracturing

simulations and their suitability for extension into

unified physics solvers that directly interact with

other meshless simulants such as fluids.

While the observed performance of the method in

this poster is encouraging, this work requires further

validation against real-life scenarios, particularly

building a database of parameterization for tearing of

various fibrous objects (e.g. fruits and vegetables) and

organic tissue. It would also benefit from comparative

analysis against the established state-of-the-art in

near real-time soft-body tearing. Blobby-sphere

based surfacing would suffice for rudimentary

examination of the results, but more sophisticated

surfacing methods warrant study.

Medical soft tissue that exhibits highly non-linear

and anisotropic behaviour (Zohdi, 2007) is difficult to

simulate and tear accurately in real-time. This would

involve extending our anisotropic component to

model more sophisticated fibre fields including grids

and 2D strips, in addition to accounting for

anisotropy, not just in tearing, but in the mechanical

behaviour itself where the material stress thresholds

vary across different directions.

ACKNOWLEDGEMENTS

This project was funded by The Interactive and Multi-

Modal Experience Research Syndicate (IMMERSe).

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

262

REFERENCES

Allard, J., Marchal, M. and Cotin, S., 2009. Fiber-based

fracture model for simulating soft tissue tearing. Studies

in health technology and informatics, 142, pp.13-18.

Becker, M., Ihmsen, M. and Teschner, M., 2009, March.

Corotated SPH for Deformable Solids. In NPH (pp. 27-

34).

Belytschko, T., Chen, H., Xu, J. and Zi, G., 2003. Dynamic

crack propagation based on loss of hyperbolicity and a

new discontinuous enrichment. International Journal

for Numerical Methods in Engineering, 58(12),

pp.1873-1905.

Chen, Z., Yao, M., Feng, R. and Wang, H., 2014. Physics-

inspired adaptive fracture refinement. ACM

Transactions on Graphics (TOG), 33(4), p.113.

Gingold, R.A. and Monaghan, J.J., 1977. Smoothed particle

hydrodynamics: theory and application to non-spherical

stars. Monthly notices of the royal astronomical society,

181(3), pp.375-389.

Hahn, D. and Wojtan, C., 2016. Fast approximations for

boundary element based brittle fracture simulation.

ACM Transactions on Graphics (TOG), 35(4), p.104.

Hesham, O., 2011. Fast Meshless Simulation of

Anisotropic Tearing in Elastic Solids (Thesis, Carleton

University Ottawa).

Hoetzlein, R.C. and Höllerer, T., 2008. Analyzing

Performance and Efficiency of Smoothed Particle

Hydrodynamics.

Irving, G., Teran, J. and Fedkiw, R., 2004, August.

Invertible finite elements for robust simulation of large

deformation. In Proceedings of the 2004 ACM

SIGGRAPH/Eurographics symposium on Computer

animation (pp. 131-140).

Koschier, D., Bender, J. and Thuerey, N., 2017. Robust

eXtended finite elements for complex cutting of

deformables. ACM Transactions on Graphics (TOG),

36(4), p.55.

Liu, N., He, X., Li, S. and Wang, G., 2011. Meshless

simulation of brittle fracture. Computer Animation and

Virtual Worlds, 22(2‐3), pp.115-124.

Meier, U., López, O., Monserrat, C., Juan, M.C. and

Alcaniz, M., 2005. Real-time deformable models for

surgery simulation: a survey. Computer methods and

programs in biomedicine, 77(3), pp.183-197.

Müller, M. and Gross, M., 2004, May. Interactive virtual

materials. In Proceedings of Graphics Interface 2004

(pp. 239-246).

Müller, M., Charypar, D. and Gross, M., 2003, July.

Particle-based fluid simulation for interactive

applications. In Proceedings of the 2003 ACM

SIGGRAPH/Eurographics symposium on Computer

animation (pp. 154-159).

Müller, M., Keiser, R., Nealen, A., Pauly, M., Gross, M.

and Alexa, M., 2004, August. Point based animation of

elastic, plastic and melting objects. In Proceedings of

the 2004 ACM SIGGRAPH/Eurographics symposium

on Computer animation (pp. 141-151).

Nealen, A., Müller, M., Keiser, R., Boxerman, E. and

Carlson, M., 2006, December. Physically based

deformable models in computer graphics. In Computer

graphics forum (Vol. 25, No. 4, pp. 809-836).

O'Brien, J.F. and Hodgins, J.K., 1999, July. Graphical

modeling and animation of brittle fracture. In

Proceedings of the 26th annual conference on

Computer graphics and interactive techniques (pp.

137-146).

O'Brien, J.F., Bargteil, A.W. and Hodgins, J.K., 2002.

Graphical modeling and animation of ductile fracture.

ACM transactions on graphics (TOG), 21(3), pp.291-

294.

Organ, D., Fleming, M., Terry, T. and Belytschko, T., 1996.

Continuous meshless approximations for nonconvex

bodies by diffraction and transparency. Computational

mechanics, 18(3), pp.225-235.

Parker, E.G. and O'Brien, J.F., 2009, August. Real-time

deformation and fracture in a game environment. In

Proceedings of the 2009 ACM SIGGRAPH/

Eurographics Symposium on Computer Animation (pp.

165-175).

Pfaff, T., Narain, R., de Joya, J.M. and O'Brien, J.F., 2014.

Adaptive tearing and cracking of thin sheets. ACM

Transactions on Graphics (TOG), 33(4), p.110.

Solenthaler, B., Schläfli, J. and Pajarola, R., 2007. A unified

particle model for fluid–solid interactions. Computer

Animation and Virtual Worlds, 18(1), pp.69-82.

Tan, J. and Yang, X., 2009. Physically-based fluid

animation: A survey. Science in China Series F:

Information Sciences, 52(5), pp.723-740.

Terzopoulos, D. and Fleischer, K., 1988, August. Modeling

inelastic deformation: viscolelasticity, plasticity,

fracture. In ACM Siggraph Computer Graphics (Vol.

22, No. 4, pp. 269-278).

Viccione, G., Bovolin, V. and Carratelli, E.P., 2008.

Defining and optimizing algorithms for neighbouring

particle identification in SPH fluid simulations.

International Journal for Numerical Methods in Fluids,

58(6), pp.625-638.

Zohdi, T.I., 2007. A computational framework for network

modeling of fibrous biological tissue deformation and

rupture. Computer Methods in Applied Mechanics and

Engineering, 196(31), pp.2972-2980.

Interactive Anisotropic Tearing of Elastic Solids

263