A Simple and Exact Algorithm to Solve `

Linear Problems

Application to the Compressive Sensing Method

Igor Ciril

, J

ome Darbon

and Yohann Tendero

DR2I, Institut Polytechnique des Sciences Avanc

ees, 94200, Ivry-sur-Seine, France

Division of Applied Mathematics, Brown University, U.S.A.

LTCI, T

ecom ParisTech, Universit

e Paris-Saclay, 75013, Paris, France

Keywords:

Basis Pursuit, Compressive Sensing, Inverse Scale Space, Sparsity, `

Regularized Linear Problems, Non-

smooth Optimization, Maximal Monotone Operator, Phase Transition.

Abstract:

This paper considers `

-regularized linear inverse problems that frequently arise in applications. One striking

example is the so called compressive sensing method that proposes to reconstruct a high dimensional signal

u P R

from low dimensional measurements R

Q b “ Au, m ! n. The basis pursuit is another example. For

most of these problems the number of unknowns is very large. The recovered signal is obtained as the solution

to an optimization problem and the quality of the recovered signal directly depends on the quality of the

solver. Theoretical works predict a sharp transition phase for the exact recovery of sparse signals. However,

to the best of our knowledge, other state-of-the-art algorithms are not effective enough to accurately observe

this transition phase. This paper proposes a simple algorithm that computes an exact `

minimizer under the

constraints Au “ b. This algorithm can be employed in many problems: as soon as A has full row rank.

In addition, a numerical comparison with standard algorithms available in the literature is exhibited. These

comparisons illustrate that our algorithm compares advantageously: the aforementioned transition phase is

empirically observed with a much better quality.

1 INTRODUCTION

Compressive sensing and sparsity promoting methods

have gained a signiﬁcant interest. These methods are

used for e.g., data analysis, signal and image proces-

sing or inverse problems and amounts to ﬁnd a suita-

ble u which satisﬁes

Au “ b (1)

where b can be seen as some observed data, A P

mˆn

pRq and m ! n. The columns of A can for in-

stance model an acquisition device or may represent

some frame or dictionary designed to adequately en-

code u. The problem (1) is ill-posed. Therefore, some

a priori information is needed. The most standard

assumption is that u is “simple”, i.e., u has minimal

pseudo norm. However, ﬁnding an `

minimizer

of (1) is difﬁcult as the optimization problem is non-

smooth and non-convex. Hence, methods (Foucart,

2013; Jain et al., 2011; Mallat and Zhang, 1993; Pati

et al., 1993; Tropp and Gilbert, 2007; Blumensath

and Davies, 2009; Dai and Milenkovic, 2009; Maleki,

2009) that aim at tackling `

pseudo norm minimiza-

tion usually guarantee only an optimal solution with

high probability and, to the best of our knowledge,

for a speciﬁc class of matrices A. The second class

of methods proposes to use an `

relaxation and the

problem becomes

inf

uPR

}u}

s.t. Au “ b.

)

Problem (P

) is known as the ”basis pursuit pro-

blem”, see, e.g., (Chen et al., 2001). Under vari-

ous assumptions, the minimizers remain the same if

one replaces the `

pseudo-norm by the `

norm (see,

e.g., (Candes and Tao, 2005; Candes and Tao, 2006;

Donoho, 2006; Donoho and Elad, 2003) and the refe-

rences therein). Problem (P

) enjoys strong uniform

guarantees for sparse recovery, see, e.g. (Needell and

Vershynin, 2009). Loosely speaking, one can easily

check if a vector is optimal for (P

) and the theore-

tical works bridge the gap between `

and `

. Yet,

problem (P

) is a convex one but it is a non-smooth

optimization problem in high dimensions (n can be,

e.g., the number of pixels of an image). For these

Ciril, I., Darbon, J. and Tendero, Y.

A Simple and Exact Algorithm to Solve `

Linear Problems - Application to the Compressive Sensing Method.

DOI: 10.5220/0006624600540062

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages

54-62

ISBN: 978-989-758-290-5

reasons developing efﬁcient algorithmic solutions is

still a challenge in many cases. For instance, the stan-

dard CVX solver is not suitable (Grant and Boyd, ,

Sec. 1.3) for very large problems that arise from sig-

nal/image processing applications. Therefore, many

methods have been proposed to solve (P

) for large

signal/images, see, e.g. (Osher et al., 2005; Hale et al.,

2007; Beck and Teboulle, 2009; Yin et al., 2008;

Zhang et al., 2011; Moeller and Zhang, 2016).

This paper proposes a new algorithm that computes an

exact solution to (P

) that can be employed in many

problems. Indeed, we only assume that A is full row

rank. This paper also exhibits a numerical compari-

son with standard algorithms available in the litera-

ture. These comparisons illustrate that our algorithm

compares advantageously: the theoretically predicted

transition phase, see e.g., (Maleki and Donoho, 2010;

Cand

es et al., 2006) is empirically observed with a

much better quality.

Outline of this Paper. The paper is organized as

follows. Section 2 gives a very compact, yet self-

contained, presentation of the formalism that under-

lies the algorithm proposed in this paper. The con-

struction yields to algorithm 1 page 3. Section 3

proposes a numerical evaluation and comparison of

our algorithm with some other state-of-the-art solu-

tion solving (P

). We demonstrate in this section that

our method outperforms other state-of-the-art met-

hods in terms of quality. Discussions and conclusi-

ons are summarized in section 4. The appendix 4 on

page 8 contains a Matlab code of the algorithm propo-

sed in this paper and a glossary containing notations

and deﬁnitions. In the sequel, Latin numerals refer to

the glossary of notations page 9.

2 ALGORITHM

This section presents the algorithm proposed in this

paper and its underlying mathematical formalism.

The method we propose in this paper begins by

computing a solution to the dual problem associated

to (P

) then computes a solution to the primal. The

ﬁrst step involves the exact computation of a ﬁnite se-

quence. The last iterate of this sequence is a solution

to the dual problem. The second step consists in com-

puting a constrained least squares problem. We now

give the formalism that underlies this algorithm then

state the algorithm (see algorithm 1 page 3). Herein-

after, we assume that A P M

mˆn

pRq is full row rank.

Consider the Lagrangian L : R

ˆ R

Ñ R of (P

)

Lpu,λ

λq :“ Jpuq`

xλ

λ,Auy` xλ

λ,´by,

where Jp¨q “ } ¨ }

, and the Lagrangian dual function

g : R

Ñ R Y t`8u deﬁned by

gpλ

λq :“ ´ inf

uPR

Lpu,λ

λq

“ ´ inf

uPR

Jpuq ´

´A

λ,u

´ xλ

λ,´by

“ J

´A

`xλ

λ,by “ χ

´A

` xλ

λ,by.(2)

In 2, J

denotes the Legendre-Fenchel transform (ix)

of the convex function J P Γ

q (see (v) and (vi)

and χ

the convex characteristic function of the

(iii) unit ball B

(vii). (We recall that hereinaf-

ter Latin numerals refer to the glossary of notations

page 9). Consider also the Lagrangian dual problem

inf

λPR

gpλ

λq.

)

(From (Aubin and Cellina, 2012, Prop. 1, p.163 and

Thm. 2, p. 167) problems (P

and (D

) have solu-

tions). We wish to solve (D

). To do so, we consi-

der the evolution equation, explicitly given, for every

t ě 0, by

ptq “ ´Π

p0q

λp0q “ λ

(3)

In (3),

denotes the right-derivative (viii), Bg pλ

λq “

b `

iPS

: η

ě 0, i P S pλ

λq

)

, the matrix

A P

mˆ2n

pRq is deﬁned by the column-wise concatena-

tion

A :“ rA | ´ As and the set S pλ

λq is deﬁned by

Spλ

λq:“

i P t1, ... ,2nu:

λ,

“1

(

, (4)

where e

denotes the i-th canonical vector of R

We further denote by Π

the Euclidean pro-

jection (x) operator on the non-empty closed convex

set Bgpλ

λptqq and λ

P dom Bg (iv) is some initial state.

(We set λ

“ 0 in our experiments).

Using similar arguments to the ones developed

in (Hiriart-Urruty and Lemarechal, 1996a, Chap. 8,

section 3.4), one can easily prove that the trajectory

converges to a solution of (D

) and that it is constant

after some ﬁnite time t

P r0,`8q. It remains to show

how one can compute (3) and then compute a solution

to (P

By the same arguments as the ones developed

in, e.g., (Hiriart-Urruty and Lemarechal, 1996a, Lem.

3.4.5, p. 381) the trajectory (3) is piecewise af-

ﬁne. This means that (3) can be obtained from a

sequence. In other words there exist pd

such

that λ

k`1

“ λ

` pt

k`1

´t

(we set t

“ 0) with

“ ´Π

0q (where Π denotes the projection

operator (x)). It remains to give a formula for the sca-

A Simple and Exact Algorithm to Solve `

Linear Problems - Application to the Compressive Sensing Method

lars pt

k`1

´t

q. The scalars pt

k`1

´t

q are given by

∆t

:“ pt

k`1

´t

q“min

1 ´

,λ

, iPS

,(5)

where S

:“

iPt1, .. ., 2nu:

ą0

(

. (6)

Thus, to compute a solution to (D

) one can simply

compute (3) using (4)-(6). The cornerstone of this

algorithm is the computation of a projection on a con-

vex cone given by the maximal monotone operator Bg.

(One can use for instance a constrained least squares

solver, available in, e.g., Matlab, to compute the so-

lution). The computation of

∆t

is straightforward: it

relies on the evaluation of the signs of inner products.

It remains to compute a solution to (P

) from a solu-

tion

λ of (D

Given a solution of (D

) denoted by

λ, we can

compute a solution

u to (P

) by solving the following

constrained least squares problem

’

min

uPR

}Au ´ b}

s.t. u

ě 0 if x

λ,Ae

y “ ´1,

ď 0 if x

λ,Ae

y “ 1,

“ 0 otherwise,

(7)

where e

denotes the i-th canonical vector of R

. The

construction is now complete. Before we state the al-

gorithm, let us make the following remarks.

Remark 1. The reconstruction formula given by (7)

is different from the reconstruction methods that can

sometimes be found in the literature (see, e.g., (Moel-

ler and Zhang, 2016, algorithm 6, p. 11)). Howe-

ver, for matrices satisfying compressive sensing as-

sumptions (see, e.g., (Candes and Tao, 2006; Donoho,

2006)), the signal can be obtained from an uncon-

strained least-squares solution to Au “ b. Indeed, the

support constraint issued form

λ boils down to sol-

ving, in the least squares sense, Bu “ b, where B

is a sub-matrix formed from A by removing appro-

priate columns. Notice that in this case, there is no

sign constraint on u

contrarily to (7). In addition, in

many cases, the unconstrained least squares solution

can be computed using a Moore-Penrose pseudo in-

verse formula. However, the least squares solution

and (7) will, in general, differ: they have same `

pseudo norms but different `

norms.

Remark 2. To compute d

:“ ´Π

p0q consider

the set G :“

iPSpλ

λq

: η

ě 0, i P S pλ

)

. We

have d

“ ´Π

p´bq ´ b. This vector can be compu-

ted from a constrained least squares problem similar

to (7). For instance, one can use the lsqnonneg Matlab

function. In our implementation, we used (Meyer

Input: Matrix A, b

Output:

u solution to (P

)

Set k “ 0 and λ

“ 0 P R

;

repeat

1. Compute S pλ

q (see (4));

2. Compute d

:“ ´Π

Bgpλ

p0q (see remark (2));

3. Compute S

q then

∆t

(see (6) and (5));

4. Update current point λ

k`1

:“ λ

∆t

;

5. Set k “ k ` 1 and set λ

λ :“

λ}

if }A

λ}

ą 1;

until d

“ 0 (see remark (2));

Compute

u using (7).

Algorithm 1: Algorithm computing

u solution to (P

2013) that is supposedly faster than the Matlab rou-

tine.

The stopping condition, namely d

“ 0, was replaced

by }d

}

∆t

}

ă 10

´10

in all of our ex-

periments. In step (3), to prevent numerical issues, we

test if the computed

∆t

satisﬁes

∆t

ě 0. If

∆t

ă 0

we set

∆t

:“ 0 and which ends the while loop at the

current position.

A Matlab code for algorithm 1 is given in appen-

dix (4). The computations of (2) can be done at re-

latively low precision. Indeed, algorithm 1 converges

for any starting point in Ω :“ tx : A

x P B

u and

step (5) ensures that every iterate belongs to Ω. This

also means that the current error (e.g., due to ﬁnite

quantization of numbers) does not depend on previ-

ous errors: algorithm 1 is error forgetting.

Claim: Algorithm 1 converges after ﬁnitely many

iterations to an `

minimizer under the constraints

Au “ b.

For the sake of completeness we now give some the-

oretical remarks on algorithm 1. The sequence pd

is the steepest Euclidean descent direction for g deﬁ-

ned in (2). The time steps calculated in algorithm 1

step 3 guarantee that g pλ

λpt

k`1

qq ă gpλ

λpt

qq. In other

words, this algorithm can be interpreted as a descent

method on the dual problem (D

). This descent met-

hod is ruled by an evolution equation governed by the

maximal monotone operator (Br

ezis, 1973, Chap. 3)

Bg. It is well known that this evolution converges to a

solution of (D

) (Aubin and Cellina, 2012, Chap. 3).

In addition, since g is polyhedral (Rockafellar, 1997,

Section 19), the evolution equation (3) is piecewise

afﬁne. As we have seen, the trajectory (3) satisﬁes

λptq “ λ

λpt

q for some t

P r0, `8q and any t ě t

Thus, algorithm 1 computes exactly the trajectory (3)

and converges after ﬁnitely many iterations to a so-

lution to (D

). The last step allows us to retrieve a

solution to (P

) using (7).

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

3 NUMERICAL EXPERIMENTS

This section proposes an empirical evaluation of

the following methods to solve (P

): OMP (Pati

et al., 1993), CoSamp (Needell and Tropp, 2009),

AISS (Burger et al., 2013) GISS (Moeller and Zhang,

2016), and algorithm 1. These methods are compa-

red in terms of quality and number of iterations nee-

ded. The ﬁrst paragraph gives the experimental setup

considered. The second paragraph gives the criteria

used for the comparisons in terms of quality. The last

paragraph reports the results in terms of number of

iterations needed.

In these experiments the sensing matrix A always

has 1000 columns. The entries of A are drawn from

i.i.d. realizations of a centered Gaussian distribution.

Without loss of generality we normalize the columns

of A to unit Euclidean norm. The number of rows of

A, i.e., the dimension of the ambient space m, vary

in M :“ t50, .. . ,325u with increments of 25. For

each number of rows, we vary the sparsity level s be-

tween 5% and 40% with increments of 5% and the-

refore consider the discrete set S :“ t0.05,. .. ,0.4u.

The sparsity level is related to the `

norm of u

by “}u}

“ round ps ˆ mq” following (Cand

es et al.,

2006). The positions of the non-zero entries of u are

chosen randomly, with uniform probability. The non-

zero entries of u are drawn from a uniform distribu-

tion on r´1,1s. To do so, for each parameter (i.e.,

sparsity level s, dimension of ambient space m, type

of values for u, i.e., Bernoulli or uniform) we repea-

ted the experiments 1,000 times. The implementation

of CoSamp and OMP we used are due to S. Becker

(code updated on Dec 12th, 2012) and can be found

on Mathworks ﬁle exchange

. The implementation

of AISS and GISS we used are the ones given by the

authors of (Burger et al., 2013; Moeller and Zhang,

2016). The implementation of CoSamp requires an

estimate of the sparsity. In all the experiments we

used an oracle for CoSamp, i.e., provided the exact

sparsity of the source element. We now give the cri-

teria used for the comparisons in terms of quality.

We need to deﬁne the “success” of algorithm 1. In

our opinion, two options can be considered. A natural

choice would be to deﬁne the success as “the output

of algorithm 1 is a solution to (P

)”. However, this

criterion would be veriﬁed for every output. Indeed,

algorithm 1 ends with some

u that numerically veri-

ﬁes an optimality condition to (P

). Thus, this choice

seems uninformative. Another natural choice is to de-

ﬁne the success as “the output of algorithm 1 is equal

to the source element u”. This choice can be justi-

https://fr.mathworks.com/matlabcentral/ﬁleexchange/

32402-cosamp-and-omp-for-sparse-recovery

ﬁed by several theoretical works, see, e.g., (Candes

and Tao, 2005; Candes and Tao, 2006; Donoho, 2006;

Donoho and Elad, 2003). Thus, this second criterion,

namely the output is equal to the source element, is

chosen for the numerical experiments proposed the-

reafter. Note that this criterion seems slightly in favor

of methods speciﬁcally designed for the compressive

sensing method compared to methods that propose to

solve (P

). Here, this means that the comparisons

are slightly biased in favor of (Pati et al., 1993; Nee-

dell and Tropp, 2009). We need to deal with the ﬁ-

nite numerical precision. Thus, we deﬁne that a re-

construction is a success if the relative error satisﬁes

}u´u

est

}

}u}

ă 10

´10

. Hence, for any pm,sq P M ˆS, the

empirical probability of success is given by

pm,sq

:“

# of tests

´u

est

}

ă10

´10

piq, (8)

where u

est

(resp. u

) is the estimated signal (resp.

source signal) and # denotes the cardinality of a set.

Each method is tested on the same data by using the

same random seed. Remark this type of experimen-

tal setup has been used before, for instance in (Jain

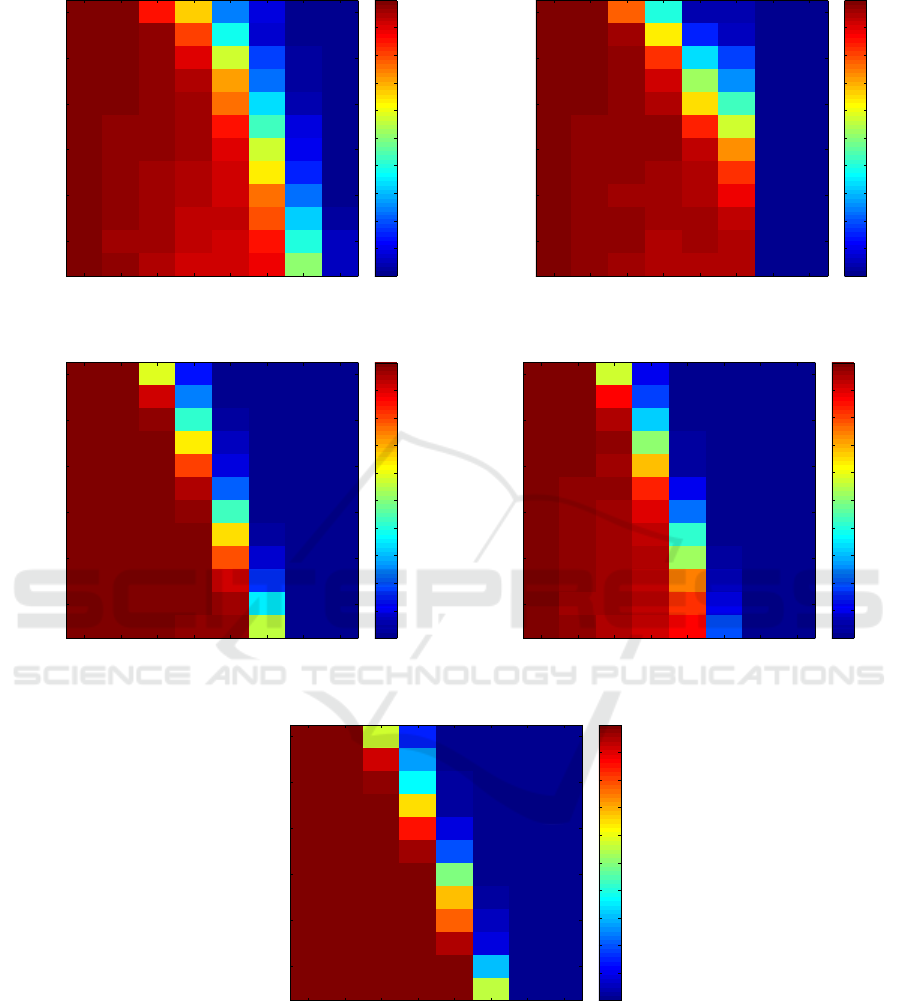
et al., 2011). Figure 2 depicts the empirical probabi-

lity of success 8 for OMP, CoSamp, AISS, GISS and

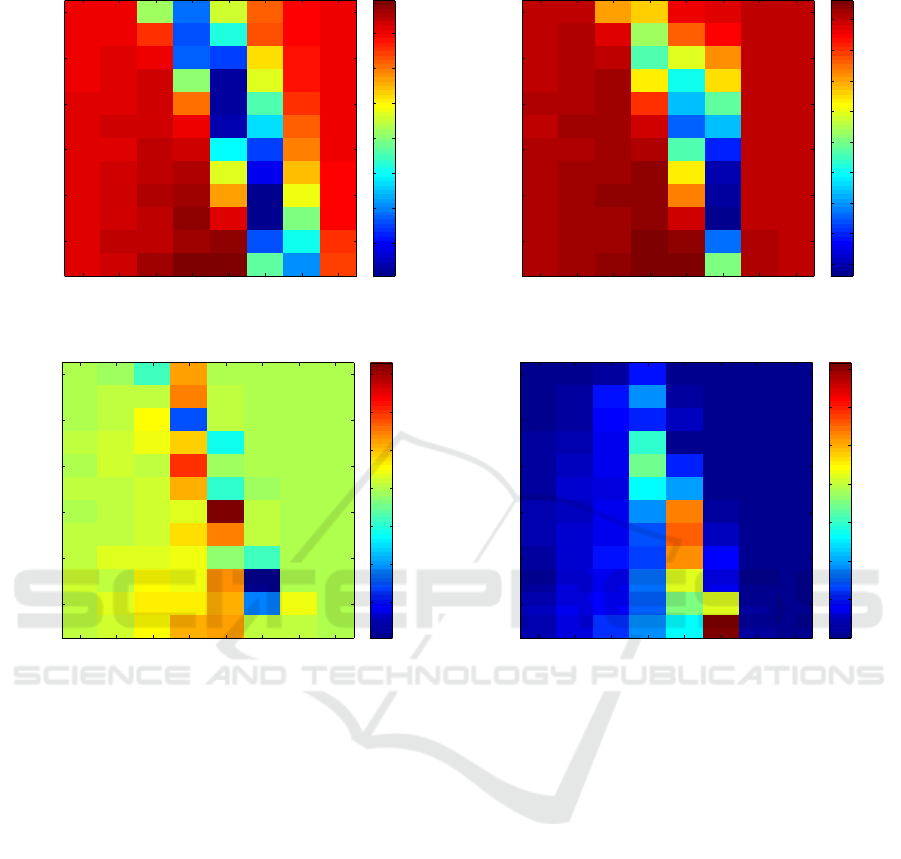
algorithm 1. We also consider the difference of pro-

bability of success between algorithm 1 and the other

methods:

pm,sq

:“ P

algo p1q

pm,sq

´ P

pm,sq

, (9)

where m P M, s P S, P

algo 1

pm,sq

(resp. P

pm,sq

) denotes the

quantity (8) obtained with algorithm 1 (resp. OMP,

CoSamp, AISS or GISS). It is easy to see that if (9)

is positive then algorithm 1 performed better than the

other method in terms of success as deﬁned above.

These differences are depicted in ﬁgure 3. It is ea-

sily seen that OMP and CoSamp succeed at retrieving

the source signal with a probability of approximately

80% for a larger set of parameters than any other met-

hod. However, they produce correct results with a

probability of nearly 100% for a much smaller set of

parameters than AISS, GISS, and algorithm 1. An

overview of the similarities and differences between

OMP (Pati et al., 1993), CoSamp (Needell and Tropp,

2009), AISS (Burger et al., 2013) GISS (Moeller and

Zhang, 2016), and algorithm 1 is given in table 1. In

this table, we recall the assumption(s) on A, the va-

riables to maintain during the iterations, the update

rule and the type of convergence the method enjoys.

In table 1, we also give the empirical probability that

a least x% of signals are successfully reconstructed.

This statistical indicator is deﬁned by

ěx

“

pm,sq P M ˆ S : P

pm,sq

ě x

(

#M ¨ #S

, (10)

A Simple and Exact Algorithm to Solve `

Linear Problems - Application to the Compressive Sensing Method

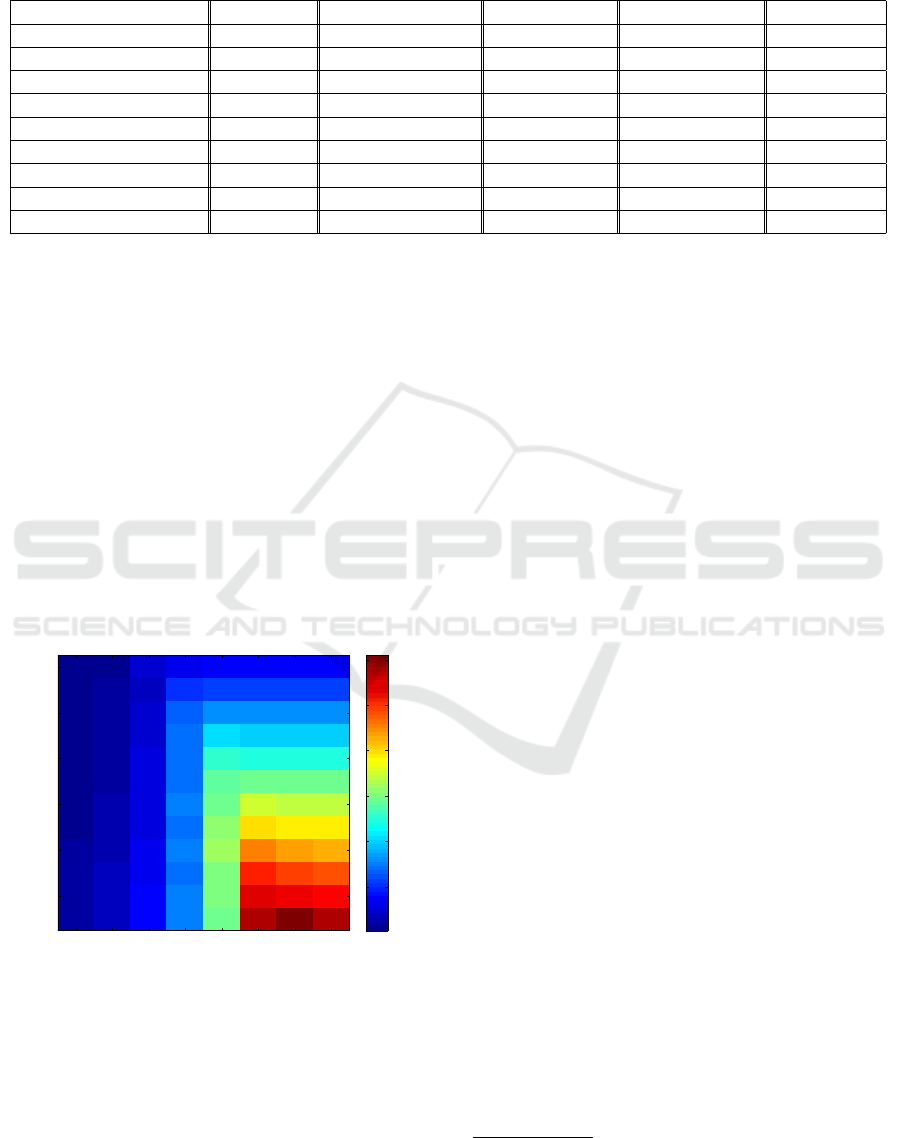
Table 1: Overview of main similarities and differences between OMP, CoSaMP, AISS, GISS and algorithm 1. Below,

ERC stands for exact recovery condition see, e.g., (Pati et al., 1993) and RIC stands for restricted isometry constant see,

e.g., (Needell and Tropp, 2009).

Method OMP (Pati et al., 1993) CoSamp (Needell and Tropp, 2009) AISS (Burger et al., 2013) GISS (Moeller and Zhang, 2016) Algorithm 1

Assumption(s) A satisﬁes ERC A satisﬁes RIC Du P R

: Au “ b A satisﬁes ERC A full row rank

Variable(s) u

P R

and p

P R

and p

P R

Update(s) rule(s) least squares in R

least squares and hard threshold in R

constrained least squares in R

least squares in R

projection onto cone of R

Type of convergence Probabilistic Probabilistic Exact Exact Exact

Probability of at least 90 % of success (10) 0.5104 0.5521 0.4688 0.4063 0.4688

Probability of at least 95 % of success (10) 0.3854 0.4583 0.4375 0.3333 0.4479

Probability of at least 99 % of success (10) 0.1042 0.1250 0.3438 0.1042 0.4271

Probability of at least 99.9 % of success (10) 0 0 0.1250 0 0.3958

Probability of at least 100 % of success (10) 0 0 0.0521 0 0.3958

where P

pm,sq

is deﬁned by (8). We now report results

concerning the number of iterations needed to achieve

convergence.

Figure 1 gives the average number of iterations

needed by algorithm 1. The maximal average number

of iterations is bounded from above by 600. Com-

paring ﬁgures 1 and 2 it can be noticed that when

the algorithm succeeds in recovering the source ele-

ment the average number of iterations remains below

(about) 250. This suggests modifying algorithm 1 to

use an early stopping criterion. The stopping criterion

would be either the optimality condition is reached or

a maximal number of iteration is attained. The com-

putational efﬁciency of the other algorithms conside-

red here can be found in, e.g., (Moeller and Zhang,

2016).

Pseudo l0 norm in percent

Number of observations

Average number of iterations

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

100

200

300

400

500

600

Figure 1: Average number of iteration needed by algo-

rithm 1. This ﬁgure suggest an early stopping criterion. See

text.

4 CONCLUSIONS

In this paper, a new fast algorithm to solve `

regularized linear problems was proposed. The algo-

rithm is exact: it produces an exact `

minimizer un-

der the constraints Au “ b in ﬁnite time. The method

relies on the calculation of a ﬁnite sequence of fea-

sible points of the dual. This sequence converges to

a solution of the dual problem. A solution of the pri-

mal problem is then obtained by a simple least squares

with signs constraints. Numerical comparisons with

existing methods of the literature has been proposed

for the noiseless compressive sensing (also called ba-

sis pursuit) problem. These comparisons allowed us

to illustrate the accuracy of the algorithm developed

in this paper compared to existing methods for the

compressive sensing paradigm. Indeed, the number

of parameters

where the `

reconstruction was nearly

always equal to the `

(sparsest) one is bigger with our

algorithm. The algorithm developed in this paper only

requires that A is full row rank. Hence, it can be used

in many problems. For instance, it can be applied with

matrices that do not comply with RIP-like properties.

The initialization of our algorithm was chosen arbitra-

rily as the null vector. Future work could investigate

the beneﬁts of a smarter initial guess to further speed

up the method. Another ongoing work studies plausi-

ble stopping criteria.

ACKNOWLEDGEMENTS

The authors thanks Said Ladjal and Karim Trabelsi

for their fruitful comments. The authors also thank

the university of Valencia for its hospitality. The Aut-

hors thank M. Mller for providing the implementation

of the GISS algorithm.

pseudo norm, ambient dimension and dimension of

the observed data.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

Pseudo l0 norm in percent

Number of observations

Empirical probability of success: OMP

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(a)

Pseudo l0 norm in percent

Number of observations

Empirical probability of success: CoSamp

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(b)

Pseudo l0 norm in percent

Number of observations

Empirical probability of success: AISS

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(c)

Pseudo l0 norm in percent

Number of observations

Empirical probability of success: GISS

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(d)

Pseudo l0 norm in percent

Number of observations

Empirical probability of success: Algo1

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(e)

Figure 2: Empirical probability of success (8). Panel (a): OMP (Pati et al., 1993), panel (b): CoSamp (Needell and Tropp,

2009), panel (c): AISS (Burger et al., 2013), panel (d) GISS (Moeller and Zhang, 2016) and panel (e) algorithm 1. The

non-zero entries of the source element u are drawn from a uniform distribution on r´1, 1s. The entries in A are drawn from

i.i.d. realization of a Gaussian distribution.

A Simple and Exact Algorithm to Solve `

Linear Problems - Application to the Compressive Sensing Method

Pseudo l0 norm in percent

Number of observations

Difference of empirical probability of success: OMP v.s. Algo1 tresh :1e−10

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

−0.6

−0.5

−0.4

−0.3

−0.2

−0.1

(a)

Pseudo l0 norm in percent

Number of observations

Difference of empirical probability of success: CoSamp v.s. Algo1 tresh :1e−10

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

−0.8

−0.7

−0.6

−0.5

−0.4

−0.3

−0.2

−0.1

(b)

Pseudo l0 norm in percent

Number of observations

Difference of empirical probability of success: AISS v.s. Algo1 tresh :1e−10

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

−0.06

−0.04

−0.02

0.02

0.04

0.06

(c)

Pseudo l0 norm in percent

Number of observations

Difference of empirical probability of success: GISS v.s. Algo1 tresh :1e−10

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

100

150

200

250

300

0.05

0.1

0.15

0.2

0.25

0.3

0.35

(d)

Figure 3: Difference of probability of success (9). Panel (a): Algo 1-OMP (Pati et al., 1993), panel (b): Algo 1-CoSamp (Nee-

dell and Tropp, 2009), panel (c): Algo 1-AISS (Burger et al., 2013) and panel (d) Algo 1-GISS (Moeller and Zhang, 2016).

A positive value indicates that algorithm 1 performs better, a negative value the contrary.

REFERENCES

Aubin, J.-P. and Cellina, A. (2012). Differential Inclusions:

Set-Valued Maps and Viability Theory. Grundlehren

der mathematischen Wissenschaften. Springer Berlin

Heidelberg.

Beck, A. and Teboulle, M. (2009). A fast iterative

shrinkage-thresholding algorithm for linear inverse

problems. SIAM Journal on Imaging Sciences,

2(1):183–202.

Blumensath, T. and Davies, M. E. (2009). Iterative hard

thresholding for compressed sensing. Applied and

Computational Harmonic Analysis, 27(3):265–274.

ezis, H. (1973). Op

erateurs Maximaux Monotones et

Semi-Groupes de Contractions Dans Les Espaces de

Hilbert. North-Holland Publishing Co., American El-

sevier Publishing Co.

Burger, M., M

oller, M., Benning, M., and Osher, S.

(2013). An adaptive inverse scale space method for

compressed sensing. Mathematics of Computation,

82(281):269–299.

Cand

es, E. J., Romberg, J., and Tao, T. (2006). Robust un-

certainty principles: Exact signal reconstruction from

highly incomplete frequency information. IEEE Tran-

sactions on information theory, 52(2):489–509.

Candes, E. J. and Tao, T. (2005). Decoding by linear pro-

gramming. Information Theory, IEEE Transactions

on, 51(12):4203–4215.

Candes, E. J. and Tao, T. (2006). Near-optimal signal re-

covery from random projections: Universal encoding

strategies? Information Theory, IEEE Transactions

on, 52(12):5406–5425.

Chen, S. S., Donoho, D. L., and Saunders, M. A. (2001).

Atomic decomposition by basis pursuit. SIAM review,

43(1):129–159.

Dai, W. and Milenkovic, O. (2009). Subspace pursuit for

compressive sensing signal reconstruction. Informa-

tion Theory, IEEE Transactions on, 55(5):2230–2249.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

Donoho, D. L. (2006). Compressed sensing. Information

Theory, IEEE Transactions on, 52(4):1289–1306.

Donoho, D. L. and Elad, M. (2003). Optimally sparse repre-

sentation in general (nonorthogonal) dictionaries via

`1 minimization. Proceedings of the National Aca-

demy of Sciences, 100(5):2197–2202.

Foucart, S. (2013). Stability and robustness of weak ort-

hogonal matching pursuits. In Recent advances in

harmonic analysis and applications, pages 395–405.

Springer.

Grant, M. C. and Boyd, S. P. The CVX Users Guide, Release

2.1.

Hale, E. T., Yin, W., and Zhang, Y. (2007). A Fixed-

Point Continuation Method for l1-Regularized Mini-

mization with Applications to Compressed Sensing.

CAAM Technical Report TR07-07.

Hiriart-Urruty, J.-B. and Lemarechal, C. (1996a). Convex

Analysis and Minimization Algorithms I: Fundamen-

tals. Grundlehren der mathematischen Wissenschaf-

ten. Springer Berlin Heidelberg.

Hiriart-Urruty, J.-B. and Lemarechal, C. (1996b). Convex

Analysis and Minimization Algorithms II: Advanced

Theory and Bundle Methods. Grundlehren der mat-

hematischen Wissenschaften. Springer Berlin Heidel-

berg.

Jain, P., Tewari, A., and Dhillon, I. S. (2011). Orthogonal

matching pursuit with replacement. In Advances in

Neural Information Processing Systems, pages 1215–

1223.

Maleki, A. (2009). Coherence analysis of iterative thres-

holding algorithms. In Communication, Control, and

Computing, 2009. Allerton 2009. 47th Annual Aller-

ton Conference on, pages 236–243. IEEE.

Maleki, A. and Donoho, D. L. (2010). Optimally tuned ite-

rative reconstruction algorithms for compressed sen-

sing. IEEE Journal of Selected Topics in Signal Pro-

cessing, 4(2):330–341.

Mallat, S. and Zhang, Z. (1993). Matching pursuits with

time-frequency dictionaries. Signal Processing, IEEE

Transactions on, 41(12):3397–3415.

Meyer, M. C. (2013). A simple new algorithm for quadratic

programming with applications in statistics. Commu-

nications in Statistics-Simulation and Computation,

42(5):1126–1139.

Moeller, M. and Zhang, X. (2016). Fast Sparse Recon-

struction: Greedy Inverse Scale Space Flows. Mat-

hematics of Computation, 85(297):179–208.

Needell, D. and Tropp, J. A. (2009). CoSaMP: Iterative

signal recovery from incomplete and inaccurate sam-

ples. Applied and Computational Harmonic Analysis,

26(3):301–321.

Needell, D. and Vershynin, R. (2009). Uniform uncertainty

principle and signal recovery via regularized orthogo-

nal matching pursuit. Foundations of computational

mathematics, 9(3):317–334.

Osher, S., Burger, M., Goldfarb, D., Xu, J., and Yin, W.

(2005). An iterative regularization method for to-

tal variation-based image restoration. Multiscale Mo-

deling & Simulation, 4(2):460–489.

Pati, Y. C., Rezaiifar, R., and Krishnaprasad, P. (1993). Ort-

hogonal matching pursuit: Recursive function approx-

imation with applications to wavelet decomposition.

In Conference Record of The Twenty-Seventh Asilo-

mar Conference on Signals, Systems and Computers,

pages 40–44. IEEE.

Rockafellar, R. T. (1997). Convex Analysis. Princeton Uni-

versity Press, Princeton, NJ.

Tropp, J. A. and Gilbert, A. C. (2007). Signal recovery

from random measurements via orthogonal matching

pursuit. Information Theory, IEEE Transactions on,

53(12):4655–4666.

Yin, W., Osher, S., Goldfarb, D., and Darbon, J. (2008).

Bregman iterative algorithms for zell 1-minimization

with applications to compressed sensing. SIAM Jour-

nal on Imaging Sciences, 1(1):143–168.

Zhang, X., Burger, M., and Osher, S. (2011). A uniﬁed

primal-dual algorithm framework based on bregman

iteration. Journal of Scientiﬁc Computing, 46(1):20–

46.

APPENDIX

Program Code

Matlab code for algorithm 1.

function [solution_primal,solution_dual,nb_iteration]=compute_solution_l1(A,

...,observed_vect, param)

% Step. 0 Initialization

lambda_init=param.initdual;

A=[A -A];

%% Step1. Compute solution dual

[solution_dual,active_set,nb_iteration]=compute_solution_dual(A,

observed_vect,...,lambda_init,param);

%% Step2. Compute solution primal

solution_primal=compute_solution_primal(A,observed_vect,active_set,param);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%NESTED FUNCTIONS: Compute Dual + Primal %%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%% Compute_solution_dual %%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [lambda,active_set,nb_iteration]=compute_solution_dual(A,

observed_vect,...,lambda,param)

%% 0. Initialize DO WHILE loop and pre-compute some stuff

shall_continue=true;

Atransp=A’;

nb_iteration=0;

while shall_continue

% 1. Compute active set

active_set=compute_active_set(A,lambda,param);

% 2. Compute direction

direction=compute_direction(A,observed_vect,active_set,param);

% 3. Compute kick time

timestep=compute_kick_time(A,direction,lambda,param);

% 4. Check termination condition

if (norm(direction*timestep)<param.tolcomputedual...

||norm(direction)<param.tolcomputedual||timestep==realmax)

% 5.1 Stop

shall_continue=false;

else % 5.2 Move current point in dual

A Simple and Exact Algorithm to Solve `

Linear Problems - Application to the Compressive Sensing Method

lambda=update_lambda(Atransp,lambda,direction,timestep,param);

end; % endif

nb_iteration=nb_iteration+1

end; % end whil

end % end compute_solution_dual function

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%% update_lambda %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function lambda=update_lambda(Atransp,lambda,direction,...

timestep,param)

% 0. Safery check : if not valid set t to 0 then quit (termination valid)

if isempty(timestep) timestep=0; end; %end if

% 1. Move in dual feasible set

lambda=lambda+timestep*direction;

% 1.1 : reproject new positon onto feasible set

if (param.leastquarefit_flag)

% compute projection onto dual feasible set

norm_Atransplambda=max(abs(Atransp*lambda))+param.tolcomputedual;

if (norm_Atransplambda>1+param.tolcomputedual)

lambda=(1+param.tolcomputedual)*lambda/norm_Atransplambda;

end;

end; % end if

end % end: update_lambda functon

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%% compute_active_set %%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function active_set=compute_active_set(A,lambda,param)

active_set=(((lambda’)*A)>=1-param.tolcomputedual);

end % end : compute_active_set function

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%% compute_direction %%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function direction=compute_direction(A,observed_vect,active_set,param)

% the next is equal to the proj of 0 onto the set b+ active cols of A

direction=-observed_vect-projection_simplicial_cone(A,-observed_vect,...

active_set,param);

end % end : compute_direction function

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%% compute_kick_time %%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function t=compute_kick_time(A,direction,lambda,param)

% 0. Compute S_Cˆ+(lambda) set

active_set_plus=(((direction’)*A)>param.tolcomputedual);

% 1. Compute kick time

% 1.1: verify possible emptyness

if (˜any(active_set_plus)) % empty active set

t=realmax; %’+infty (from its definition)

else

% 1.2 non empty case

Aactiveplus=A(:,active_set_plus);

t=min((1-((lambda’)*Aactiveplus))./((direction’)*Aactiveplus));

% safety check t must be non negative

if (t<0) t=0; % we set t:=0; then quit (termination condition valid)

end;

end; % end if

end % end: compute_kick_time function

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%% compute_solution_primal %%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function sol_primal=compute_solution_primal(A,observed_vect,...

active_set,param)

[˜,sol_primal]=projection_simplical_cone(A,-observed_vect,...

active_set,param);

sol_primal=-sol_primal(1:end/2)+sol_primal(end/2+1:end);

end % end : compute_solution_primal function

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% END NESTED FUNCTIONS%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

end% end: compute_solution_l1 function

Notations

(i) (Vectors) Vectors of, e.g., R

are denoted in

bold typeface, e.g., x. Other objects like scalars

or functions are denoted in non-bold typeface

(ii) (Inner product) xx, yy “

(iii) (the `

q unit ball) B

“

tu : xu,e

y ď 1, i “ 1, .. ., 2nu where e

de-

notes the canonical vector

(iv) (Effective domain) dom f : The domain of a

convex function f is the (convex, possibly

empty) set dom f “ tx P R

: f pxq P Ru

(v) (Convex function) A function f : R

Ñ R Y

t`8u is said to be convex if @px, yq P R

ˆ R

and @α P p0, 1q f pαx ` p1 ´ αqyq ď α f pxq `

p1 ´ αq f pyq holds true (in R Y t`8u)

(vi) (Set Γ

q) The set of lower semi-continuous,

convex functions with dom f ‰ H is denoted

by Γ

(vii) (Characteristic function of a set) χ

pxq “ 0 if

x P E and χ

pxq “ `8 otherwise

(viii) (Right derivative)

λptq

:“

lim

hÑ0

λpt`hq´λ

λptq

(ix) (Convex conjugate) For any f convex that sa-

tisﬁes dom f ‰ H, the function f

deﬁned by

Q s ÞÑ f

psq :“ sup

xPdom f

txs,xy´ f pxqu.

(See , e.g., (Hiriart-Urruty and Lemarechal,

1996b, Def. 1.1.1, p. 37))

(x) (Euclidean projection) Π

pxq “ arg min

yPC

}y´

for C ‰ H closed and convex

VISAPP 2018 - International Conference on Computer Vision Theory and Applications