A Procedural Model for Snake Skin Texture Generation

Jefferson Magalh

aes Pinheiro

1,2

and Marcelo Walter

Instituto de Inform

atica, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil

Faculdade de Inform

atica, Centro Universit

ario Ritter dos Reis - UniRitter, Porto Alegre, Brazil

Keywords:

Texturing, Procedural Generation, Texture Synthesis, Snakes, Serpents, Mathematical Biology.

Abstract:

There are thousands of snake species in the world, many with intricate and distinct skin patterns. This diversity

becomes a problem for users who need to create snake skin textures to apply on 3D models, as the difﬁculty

for creating such complex patterns is considerable. We present a procedural model capable of synthesizing a

wide range of texture skin patterns from snakes. Our model was derived from a visual assessment of a large

number of snakes, and uses image processing as well as cellular automata to generate textures. Our results

show good visual similarity with real skin found in snakes. The resulting textures can be used not only for

computer graphics texturing, but also in education about snakes and their visual characteristics. We have also

performed a user study to assess the usability of our tool. The score from the System Usability Scale was 85.8,

suggesting a highly effective texturing tool.

1 INTRODUCTION

Snakes (reptiles of the Serpentes suborder) are numer-

ous in species. They are present on every continent,

except Antarctica and some islands (notably Ireland,

Iceland, Greenland, Hawaii and New Zealand) (Bau-

chot, 2006). Some aquatic species live in the Indian

and Paciﬁc oceans as well. Being so widespread, it

is natural that snakes are typically depicted in digi-

tal media – such as computer animations and video

games – where these animals must be digitalized,

which means creating a 3D model and their textures.

When we consider textures, a complicating factor

comes into play: there are over 3600 snake species,

according to The Reptile Database (Uetz et al., 2016),

which means a large variety of colors and patterns.

Creating such textures manually, from scratch, may

prove to be a very time-consuming task. Extract-

ing textures from photos will be difﬁcult because un-

wrapped snake skin textures are not easily found, and

collecting a specimen for photography could also be

a complicating factor. Procedural texture generation

comes as a possible solution to this problem. Another

advantage of procedural generation is that, since the

end result is driven by a mathematical formula, cer-

tain parameters (such as colors and random seed) can

be modiﬁed to generate different patterns, and a col-

lection of visually diverse population. In addition, it

demands no art skills from the user.

This paper introduces a model to procedurally

generate snake skin textures, with the main purpose

of using them in computer graphics applications, such

as animations and games. We also discuss the advan-

tages of this technique over traditional texturing meth-

ods. We have implemented a tool for our model and

we have also assessed the usability of this tool.

2 RELATED WORK

We were unable to ﬁnd any work in the related litera-

ture that focuses on snakes (or any reptilian) skin tex-

ture generation, to apply on a 3D model and use on

a modern renderer. However, this ﬁeld was already

studied in the Mathematical Biology ﬁeld by (Murray

and Myerscough, 1991) and (Cocho et al., 1987a).

These authors discuss how snake skin patterns can

be generated using a mathematical model, which is

precisely the basis for procedural texture generation.

Cocho uses cellular automata, which are further ex-

plained on section 4.1.4, and Murray uses reaction-

diffusion, which is further explained on section 4.1.5.

One drawback of these models for our goals is

that they can generate textures that are visually too

simple to use on many modern applications. For

instance, typically only black-and-white images are

synthesized, and in the case of Cocho’s work, the res-

olution is extremely low (about a dozen pixels wide).

Regardless, these works serve as a good basis for a

Pinheiro, J. and Walter, M.

A Procedural Model for Snake Skin Texture Generation.

DOI: 10.5220/0006626401330144

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 1: GRAPP, pages

133-144

ISBN: 978-989-758-287-5

133

more elaborate (detailed) texture generation method.

Other works focus on snakes in computer graph-

ics, but not speciﬁcally on texture generation. One

of these focuses on snakes (and other materials) iri-

descence (Dhillon et al., 2014). Another two studies,

(Panagiotakis and Tziritas, 2006) and (Miller, 1988),

focus on their movement patterns.

Regarding procedural texturing, there are many

works available in literature. Some works worth men-

tioning include (Turk, 1991) and (Witkin and Kass,

1991), who also used reaction-diffusion. However,

these methods are too generic, and it is unclear how

to apply them to our domain (snakes) such that it cov-

ers all, or most of, snake skin patterns. In addition,

another goal of our procedural model is to be very

fast, allowing for an iterative texture creation process,

and these methods are too computationally intensive.

Other texture synthesis methods such as (Efros

and Leung, 1999) and (Gilet et al., 2014) (the latter

even included a snake as an example) rely on a good

amount and quality of sample input images, therefore,

would be impractical in the case of snakes (due to the

difﬁculty to obtain good photographies for texturing).

(Hendrikx et al., 2013) offers a recent survey on gen-

erating procedural content for games, including tex-

tures.

3 SNAKES BIOLOGY

Snakes are numerous in species and in skin pattern

variation. Some have only a single plain color, while

others have patterns composed of two or more colors.

The pattern can be as simple as stripes or spots, or it

can be so complex that it is even difﬁcult to describe.

The Serpentes suborder is split into 26 fam-

ilies, the most important (numerous) being the

Boidae (Boas), Colubridae (Colubrids), Dipsadi-

dae, Pythonidae (Pythons), Elapidae, and Viperidae

(Vipers and Pit Vipers).

3.1 Skin Pattern

We are mostly interested in the snake’s visual appear-

ance, that is, pattern and colors. When taxonomists

discover a new snake species, they describe, among

other things, their appearance. However, there is not

an international standard for categorization of snake

skin pattern, such as, “if it looks like this then it

should be categorized as Spots; if it looks like that

then it should be categorized as Horizontal Stripes”.

Instead, taxonomists verbally describe the species’

pattern.

The ﬁrst step in our study was therefore to create

a categorization of snakes’ visual pattern, and assign

each snake species to one of these categories. This

will be useful to help determining the pattern synthe-

sis method, and also to determine what pattern types

are mostly present in nature. Since it is very hard to

ﬁnd images of a snake’s ventral side (the underside,

or “belly”), and it is typically not visible, we decided

to consider only the visible dorsal side (“back” and

sides). Also, some species have a signiﬁcantly differ-

ent pigmentation color or pattern on their head or tail

(such as the Apostolepis assimilis, which has no pat-

tern on its body, but its head is black); again, we did

not take this into consideration. Both topics will be

explored in future work.

With the help of a herpetologist, we deﬁned the

following six snake pattern categories. Please note

that when we say “body”, we mean only the dorsal

side of a snake. We show two ﬁgures for each cate-

gory, as examples.

1. No Pattern. The snake shows no pigmentation

pattern, consisting only of a single solid color.

Note that we do not consider head or tail pig-

mentation, thus the Apostolepis assimilis is cat-

egorized as having no pattern.

Figure 1: Left: Philodryas aestiva (source: (Nogueira,

ndb)). Right: Apostolepis assimilis (source: (Nogueira,

nda)).

2. Longitudinal Stripes. The snake shows one or

more stripes aligned along its body, that go from

neck to tail or from head to tail.

Figure 2: Left: Phalotris lemniscatus (source: (Borges-

Martins, 2007b)). Right: Philodryas olfersii (source:

(Sawaya, nd)).

3. Transversal Stripes. The snake shows many

stripes aligned perpendicularly to its body axis,

also known as “rings”. These rings may be in two

alternating colors, or may be in multiple colors.

Typical examples include corals and false corals.

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

134

Figure 3: Left: Micrurus altirostris (coral, source: (Borges-

Martins, 2007a)). Right: Rhinobothryum lentiginosum

(false coral, source: (de Albuquerque, nd)).

4. Spots. The snake shows regular (similar) shapes

on its body, often elliptical.

Figure 4: Left: Liophis miliaris (source: (de Aguiar Pas-

sos, 2013)). Right: Ptychophis ﬂavovirgatus (source: (Di-

Bernardo, nd)).

5. Other Simple Pattern. A few snakes show a

pattern that is easily described and repeats along

its body, but doesn’t fall on any of the categories

above. Examples include the Bothrops alternatus,

which has many C-shaped patterns along its body

(see Figure 5).

Figure 5: Left: Oxyrhopus rhombifer (source: (Timm,

2014)). Right: Bothrops alternatus (source: (Borges-

Martins, 2007c)).

6. Complex. When the pattern is none of the above,

it is categorized as “Complex”. Typically, this in-

cludes intricate (or abstract) camouﬂage patterns,

that would be hard to describe verbally, or with

numerous different elements on its body.

Figure 6: Left: Sibynomorphus turgidus (source: (May,

2010)). Right: Python regius (source: (Campbell, 2005)).

Our goal is to assign each species to one category,

so that we can determine the relative proportions be-

tween different categories. This was done by means

of a visual assessment of each species’ photos.

3.2 Scope Limitation

Naturally, it would be tremendous work to analyze the

skin pattern of all 3600+ snake species. Scope had to

be limited somehow.

For this study, we decided to limit the scope ge-

ographically. In the state of Rio Grande do Sul,

Brazil, there are dozens of snake species, at least 81

of which have been identiﬁed and catalogued in the

book (Abegg and Entiauspe Neto, 2012). In this book,

these 81 species have been described as accurately as

possible, however, in text format (instead of a well-

structured data table).

It is important to note that although we limited the

scope to the snakes in this speciﬁc region, all major

snake families are present in it, with the exception of

Pythonidae. Therefore, we deemed our subset as a

good representation of the whole and use the book as

a guide.

3.3 Skin Pattern Analysis Results

In the studied region the most expressive family is

Dipsadidae, with 59 species (72.8%), followed by

Viperidae (7 species, 8.6%), Colubridae (5 species,

6.1%) and Elapidae (5 species, 6.1%).

After analyzing pictures of these 81 species, we

categorized them as the following pattern types (as

discussed on section 3.1):

Table 1: Pattern types distribution.

Pattern Count % of Total

No Pattern 19 23.46%

Longitudinal Stripes 19 23.46%

Transversal Stripes 7 8.64%

Spots 8 9.88%

Other Simple Pattern 9 11.11%

Complex Pattern 19 23.46%

From this analysis, we have learned that 76.54%

of snake species from the sample region have some

type of skin pattern and would beneﬁt from the cre-

ation of a procedural model.

4 THE PROCEDURAL MODEL

The goal of our procedural model is to generate high

resolution textures (e.g. 1024x1024 to 4096x4096

A Procedural Model for Snake Skin Texture Generation

135

pixels) for use in a modern renderer. As such, it

should generate at least a Color map and a Height

map. We will also generate a Roughness map, which

describes how rough or glossy the surface looks, and

is explained further in Section 4.3. The generated tex-

tures will be applied to a previously-made 3D mesh

and should yield a realistic result. It should also be

very fast, outputting the resulting textures in less than

a second, allowing for an iterative texture creation

process.

In our model, all texture sizes are normalized in

the [0.0;1.0] range, with [0.0;0.0] being the top-left

corner, and [1.0;1.0] the bottom-right corner. The tex-

ture generator can synthesize any texture size, as long

as there is processing power. We now proceed to ex-

plain how the color map is generated, followed by the

height map and roughness map.

4.1 Color Map

The ﬁnal texture’s color map begins with a single

solid color, which forms the “background” of the tex-

ture. This is the snake’s predominant skin color. On

top of this, the speciﬁc pattern type is drawn. We now

proceed to explain how each pattern type is generated,

except “No Pattern”.

4.1.1 Transversal Stripes Pattern

Our model supports up to 4 distinct stripes colors and

sizes. For each color we can deﬁne where it starts and

ends using a two-dimensional vector parameter, with

values ranging from 0.0 to 1.0.

For instance, if the four input colors are red,

green, blue and yellow and the begin/end vectors are

[0.0;0.25], [0.3;0.45], [0.6;0.65] and [0.8;1.0] respec-

tively for each color, the resulting image would be as

seen in Figure 7. Small gray-and-white squares mean

transparency, which will be ﬁlled by the background

color.

Figure 7: Example of generated Transversal Stripes Pattern.

We do not know of any snake species that has

more than 5 colors in its pattern (the background plus

the 4 stripes color), so we did not deem necessary to

allow more colors on the transversal pattern, though

that could be easily implemented. Some of the most

colorful snake are the corals, with 3 colors, typically

red, black and yellow.

4.1.2 Longitudinal Stripes Pattern

The longitudinal pattern implementation can be de-

scribed by the following steps. Figure 8 shows an ex-

ample of each step’s result.

1. A single white stripe is generated with the width

set by the user;

2. The result from step 1 is repeated a number of

times set by the user. If greater than 1, the stripe’s

width will be divided a number of times equal to

the parameter;

3. The result from step 2 is squeezed according to

a parameter set by the user. Texture tiling is dis-

abled at this step;

4. Stripe and background colors are blended with

stripes color (a single color chosen by the user)

and transparency.

Figure 8: Example of generated Longitudinal Stripes Pat-

tern.

4.1.3 Spots Pattern

The spots pattern is generated by the following steps:

1. A single circumference is synthesized. Its inten-

sity is 1.0 at the center and 0.0 at the edges and

decays linearly;

2. Its mid-levels are adjusted so that it turns more

opaque;

3. The spots color (set by the user) is applied to it;

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

136

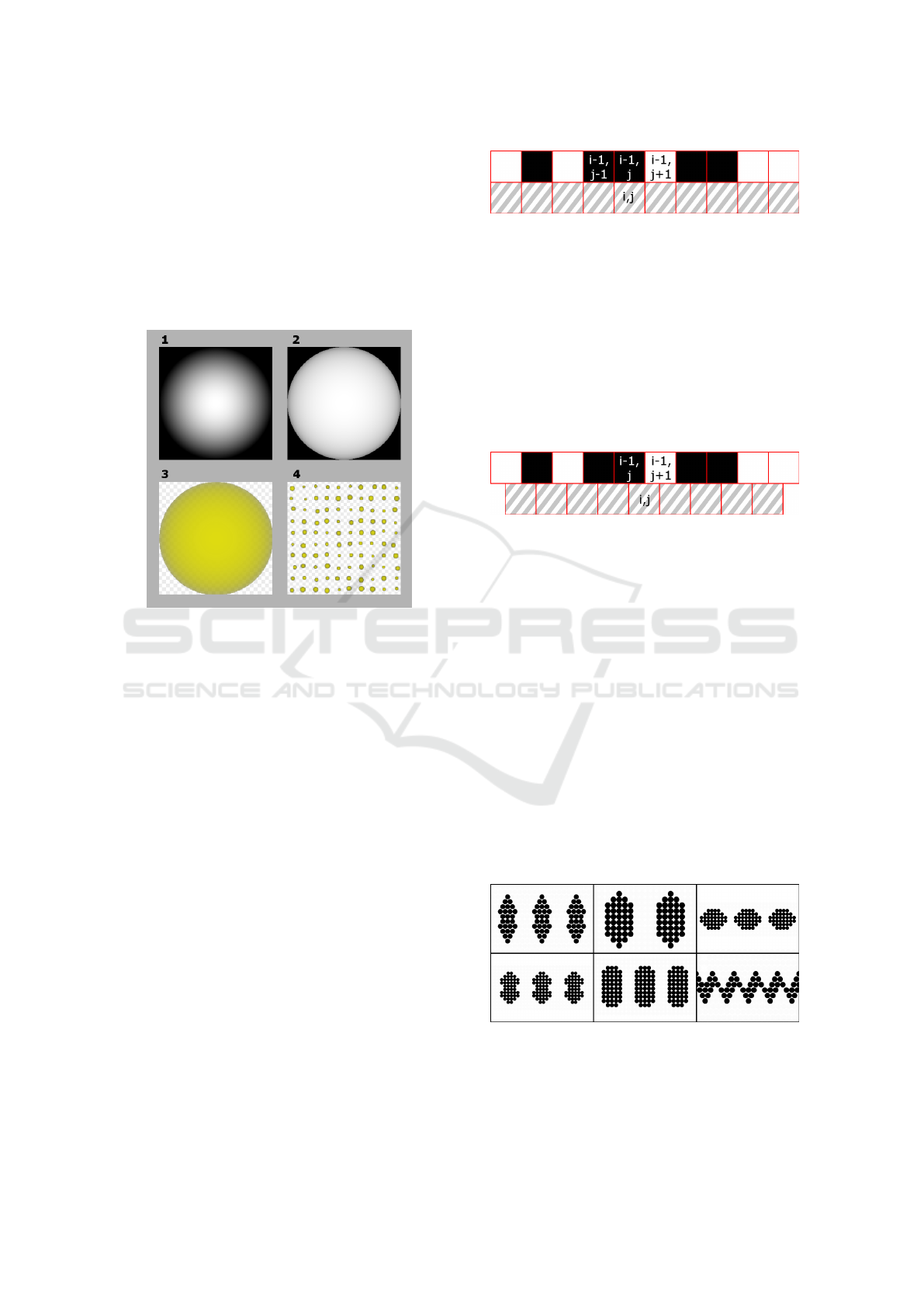
4. It is tiled in a 10x10 grid, and other parameters are

then applied to control the various characteristics

of the pattern, such as tiling, random position vari-

ation, size and random size variation.

Figure 9 shows an example of the generation pro-

cess. The resulting texture has spots that are slightly

different in size and not precisely aligned in the grid

because parameters that control randomness in size

and location have been set.

Figure 9: Example of generated Spots Pattern.

4.1.4 Other Simple Pattern

For the simple pattern group, which includes repeat-

ing geometrical patterns, we took inspiration from the

works of Cocho (Cocho et al., 1987a) (Cocho et al.,

1987b), who used cellular automata to create simple

patterns, including snake skin.

As in (Cocho et al., 1987b), we have two types

of cellular automata: rectangular and triangular, and

both work similarly. The automaton is initialized with

a single row of bits (usually 10 to 25 bits, depending

on the desired pattern size), deﬁned by the user. This

will be the texture’s ﬁrst row: each bit is a pixel, with

zeros being white, and ones being black. Then, for

a predeﬁned number of loops (called “Epochs”), the

next rows are calculated as follows.

For rectangular automata, there is a transition rule

that is deﬁned by four bits. Assume we are calculat-

ing the value for pixel [i,j]. The algorithm takes the

previous row’s pixel value, [i-1,j], and sums it with its

adjacencies, [i-1,j-1] and [i-1,j+1]. See Figure 10.

If the result of this sum is 0, the last (rightmost)

bit of the transition rule is the new pixel value. If the

sum is 1, the 3rd bit is used. If the sum is 2, the 2nd

bit is used, and if the sum is 3, the ﬁrst bit is used.

In case there are no adjacent cells (for calculating the

Figure 10: Values used for calculating position i,j in a rect-

angular automaton.

left-most or right-most cells), the value from the other

end is used (i.e. wrap around).

The triangular automaton works similarly, how-

ever, each odd row is displaced 50% of each element’s

diameter to the right, and only the two cells above

it are used for the sum (see Figure 11). Since the

maximum sum is 2, the transition rule has only 3 bits

(for sums of 0, 1, and 2), following the same logic as

above.

Figure 11: Values used for calculating position i,j in a trian-

gular automaton.

Once all rows have been calculated (given by the

number of epochs), an image is synthesized using the

resulting bit matrix. We paint white circles for zeros

and black circles for ones, and the diameter of these

circles is adjustable (50 pixels by default). While we

could have used the bits as vertices and drawn using

vectors, we deem the circles approach to be simpler

and faster to compute. Afterwards, the resulting im-

age is duplicated above the original and mirrored ver-

tically, to create a symmetrical texture. This mirror

may be displaced horizontally to create interleaving

patterns.

Figure 12 shows some examples of generated im-

ages using this algorithm. All these images represent

a speciﬁc snake species’ pattern. Although simple,

cellular automata can generate many patterns visually

similar to real snakes.

Figure 12: Sample results obtained using cellular automata.

From top-left to bottom-right: Bothrops neuwiedii, Crotalus

viridis, Daboia russelii, Eunectes murinus, Python molurus

and Vipera berus.

After generating the image, additional steps are

A Procedural Model for Snake Skin Texture Generation

137

taken to remove the circles pattern. The image is

blurred and then its contrast is increased. See Figure

13 for an example.

Figure 13: Cellular automaton’s resulting image post pro-

cess. Left: the generated image. Middle: blurred image.

Right: contrast increased.

4.1.5 Complex Pattern

Snakes categorized as having Complex pattern

present spots of different shapes and sizes, often

forming a camouﬂage pattern as seen in many mili-

tary vehicles. This pattern’s form is apparently ran-

dom, being hard to even describe it.

We believe that Murray’s reaction-diffusion sys-

tems would perform well to generate these patterns.

Indeed, complex snake skin patterns have been gen-

erated, as discussed in his paper (Murray and Myer-

scough, 1991). However, the computational cost of

running a reaction-diffusion simulation is high com-

pared to our other methods and therefore Murray’s

method was not implemented and is left as a future

improvement.

4.1.6 Pattern Post-process

One problem up to this point is that the generated pat-

tern is very artiﬁcial. Lines are perfectly straight and

curves are perfectly round. To counter this, we ap-

ply a distortion effect, using two Perlin noises (Per-

lin, 2002) of different granularities: one of low fre-

quency to provide a macro variation, and one of high

frequency to provide a micro variation. The intensity

of these distortions are adjustable. See Figure 14 for

an example.

4.1.7 Pattern Outline

Some snakes, such as the eastern milk snake (Lampro-

peltis triangulum triangulum) and the burmese python

(Python bivittatus) also present a strong color contrast

on the borders of their pattern (see Figure 15). For this

reason, we implemented a pattern outliner.

The outline is created by the following steps:

1. Perform an edge detection on the pattern image;

2. Distort it using the height map from the scales

(scales generation is explained on section 4.2).

Figure 14: Left: input image. Middle: low frequency dis-

tortion applied (above) and the noise used (below). Right:

high frequency distortion applied (above) and the noise used

(below).

Figure 15: Left: Lampropeltis triangulum triangulum

(source: (Rada, 2008)). Right: Python bivittatus (source:

(Andrews II, 2010)).

This is done so that the outline doesn’t matches

perfectly the contour of the pattern, but is ad-

justable;

3. A blur is applied, and contrast is increased. This

is to remove some of the irregularities introduced

in step 2. Both the blur and the contrast intensities

are adjustable.

Figure 16 shows an example of the outline being

created step by step.

Figure 16: Outliner steps. (a) Input image. (b) Edge detec-

tion. (c) Distortion. (d) Blur. (e) Contrast.

4.2 Height Map Generation

Snakes are scaled reptilians; as such, it is important

for our model to reproduce them, and the height map

is used for rendering this. Scales generation begins

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

138

with ﬁrst synthesizing a single scale, which will later

be tiled. We can notice from reference images (see

Figures 1 to 6) that most snake scales are leaf-shaped,

and also that some scales are smooth and others have

a protruding ridge along its longitudinal direction.

Those are called keeled scales, an evolution of smooth

scales seen in some snakes that causes light to dis-

perse through the surface, increasing surface rough-

ness.

Scale generation is performed by the following

steps. See Figure 17 for a visual depiction of each

step’s result.

a A grayscale circumference is generated. Its inten-

sity is 1.0 at the center and linearly decays to 0.0

at the edges;

b Mid-levels are adjusted to make it more solid;

c One copy is created and translated to the left...

d ... to the right...

e ... and blended together by taking the minimal

value between these two. This is to generate the

scale’s leaf shape;

f A blur is applied...

g ... and contrast is increased to make it smoother,

particularly on the top and bottom ends;

h It is multiplied with a linear gradient, ranging

from black to white, to create the scale’s height

map;

i If the scale is keeled, then a thin linear gradient

ranging from black-white-black is blended into

the center of the scale.

Figure 17: Scale generation steps.

Once the single scale is generated, it is dupli-

cated horizontally and vertically a number of times

adjustable by parameters (i.e. the number of scales).

It is also possible to add a random variation to size,

location and rotation for each duplicated scale, so the

result looks more natural. On the left and right ends,

we stretch the texture to create ventral (underside)

scales. See Figure 18.c for an example.

We can also enhance ﬁne details on this texture

by using a high frequency noise. We can notice from

reference images that scales’ surface has some irreg-

ularities, which we model by adding a Fractal Sum

noise texture (Mandelbrot and Pignoni, 1983) to the

height map. The intensity should be very low as its

purpose is only to add micro details.

4.3 Roughness Map

We also synthesize another texture to describe how

glossy or rough the surface looks. This is important

because scales on some snake species have a glossier

appearance than others. The Roughness map is a

grayscale texture where black means the surface is not

rough (i.e., glossy or polished) and white means it is

rough (diffuse). It is used in certain game engines

that use a physically-based renderer, such as Unreal

Engine 4. For more details on physically-based ren-

dering, we recommend (Pharr et al., 2016).

While we could have used a single solid color for

the Roughness map, we chose to use the same frac-

tal sum (Mandelbrot and Pignoni, 1983) noise texture

from the Height map, to add ﬁne details. Output lev-

els are adjustable as a means to adjust the minimal

and maximum surface roughness. Figure 18.d shows

an example of generated Roughness map.

Figure 18 shows all generated textures for the Mi-

crurus altirostris, as an example.

Figure 18: Generated textures for the Micrurus altirostris.

From left to right: color, height and roughness maps.

5 RESULTS

We implemented our model to allow the end-user to

create snake skin textures by changing all available

parameters. It also displays what the generated tex-

tures look like, shows a 3D render of the textures ap-

A Procedural Model for Snake Skin Texture Generation

139

plied on a manually modelled snake mesh, allows to

load and save presets (all parameters values), change

generated textures resolution, and export textures for

use in another software.

To implement the texture generation process,

we used the software Substance Designer version

2017.1.0, by Allegorithmic SAS. It is a node-based

procedural texture generator, which performs many

image processing routines such as blur, levels adjust-

ment (brightness, contrast, minimal output and max-

imal output), 2D transformations and distortion; and

also has several built-in noise generators, such as Per-

lin noise (PERLIN, 1985). We chose this software be-

cause it is easy to use, has most routines we’ll need al-

ready implemented, ready for use, and is well known

and widely used by professional texture artists.

The tool itself was implemented using Unreal En-

gine 4, by Epic Games Inc., which is a real-time game

engine. We chose this game engine because it has in-

tegration with Substance Designer, and also because

it has a user interface designer and a renderer to dis-

play the preview snake mesh. The software’s main

interface can be seen in Figure 19.

Figure 19: The software’s interface.

Our model can generate a multitude of snake skin

textures. Some examples can be seen on Figures 20,

21, 22 and 23. These ﬁgures show snakes with tex-

tures synthesized by our generator in an example en-

vironment, rendered in real-time in Unreal Engine 4.

Background scenario assets (foliage and rocks) were

provided by Epic Games, Inc. To generate these sam-

ples, we looked at reference photos and reproduced

them by manually tweaking parameters, such as pat-

tern type and size, colors, and speciﬁc pattern param-

eters. There are 59 parameters in total.

Figure 24 better shows smooth scales detail, and

Figure 25 shows keeled scales detail.

Figure 26 shows a side-by-side comparison of ref-

erence photos and generated textures. Background on

rendered images was copied from the reference pho-

tos for better comparison.

We can see that our model is capable of generating

Figure 20: Generated Micrurus altirostris textures rendered

on a snake mesh.

Figure 21: Generated Elapomorphus quinquelineatus tex-

tures rendered on a snake mesh.

Figure 22: Generated Philodryas olfersii textures rendered

on a snake mesh.

Figure 23: Generated Crotalus viridis textures rendered on

a snake mesh.

textures that are quite similar to their real-world coun-

terparts, as well as generating ﬁne details, as seen in

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

140

Figure 24: Generated smooth scales.

Figure 25: Generated keeled scales.

Figures 24 and 25.

Although we based our study on real-world

snakes, it is entirely possible to use our model to cre-

ate unrealistic, or fantasy, snake textures. Some ex-

amples can be seen in Figures 27, 28 and 29.

In our test system, equipped with an Intel Core

i5-4670K @ 4.1 GHz, 16GB RAM and NVIDIA

GeForce GTX 1070, it takes an average of 82.73ms

to compute all 4 textures (base color, normal map,

height map and roughness map) at 1024x1024 reso-

lution. Thus the user can change parameters and see

the result in real-time, allowing to work iteratively.

Table 2 shows the average time taken to compute the

4 textures in other resolutions.

Table 2: Average computing times for all 4 textures at dif-

ferent texture resolutions.

Resolution Average time

256x256 51ms

512x512 56.7ms

1024x1024 82.73ms

2048x2048 163.06ms

4096x4096 554.82ms

5.1 User Tests

In order to identify how useful and friendly our tool

is for the average designer, we ran user tests. We se-

lected as subjects students from the 4th semester of

an undergraduate Game Design course at UniRitter,

located in the city of Porto Alegre, Brazil. 13 subjects

participated in the test, most of them between 21 and

26 years old, and most of them males (12 males, 1

female). The test involved 4 tasks:

1. Freely explore the tool;

2. Attempt to reproduce the snake Elapomorphus

quinquelineatus (see Figure 21);

3. Attempt to reproduce any coral snake of their

choice;

4. Attempt to reproduce any snake of their choice.

For each task, users had a maximum working time

of 7 minutes. We chose this time limit because we

take an average time of 3 minutes to create each of

these textures, and added 4 minutes for unexperienced

users.

Users had to look for photos of these snakes on

the internet. The time they had to browse for images

was free (it was not counted in each task’s time limit).

After taking this test, they answered a questionnaire

anonymously.

Among the questions, we asked whether they had

any prior experience in texturing. 30.8% said they had

no prior experience at all, 69.2% said they had some

experience, and no one said they had good experience

or worked with texturing frequently. We also asked if

they were able to reproduce each of the three snakes,

with 3 options: “Yes”, “Yes, partially” and “No”. No

user answered “no” for any snake.

• For the ﬁrst snake (Elapomorphus quinquelinea-

tus), most users managed to reproduce it faithfully

(61.5% “Yes” against 38.5% for “Yes, partially”).

• For the second snake (the coral), again most users

managed to reproduce it faithfully (92.3% “Yes”

against 7.7% for “Yes, partially”).

• For the third snake (user’s choice), most users

only managed to reproduce it partially (30.8%

“Yes” against 69.2% for “Yes, partially”). We

believe this comes from the fact that some users

chose a snake with a complex pattern, which our

method is currently unable to reproduce.

When asked how easy it was to reproduce each

snake, most users reported the Elapomorphus quin-

quelineatus as easy, followed by the coral with mixed

results; and lastly their chosen snake as the most dif-

ﬁcult, likely because some users chose a snake with

a complex pattern, which is not supported by our

model.

Thus, we asked if users realized they couldn’t re-

produce all patterns in the tool (the complex patterns).

30.8% answered “No” (meaning they think all pat-

terns can be reproduced), 38.5% answered “Yes, just

A Procedural Model for Snake Skin Texture Generation

141

Figure 26: Photo reference (left) and textures obtained using our texture synthesizer (right), applied on a 3D mesh. In

reading order: Crotalus Viridis (photo source: (Stuart, 2011)), Liophis miliaris (source: (de Aguiar Passos, 2013)), Elapomor-

phus quinquelineatus (source: (Martins, 2011)), Micrurus altirostris (source: (Borges-Martins, 2007a)), Philodryas olfersii

(source: (Sawaya, nd)) and Mussurana bicolor (source: (Smith, 2015)).

Figure 27: Generated textures for a ﬁctional snake.

Figure 28: Generated textures for a ﬁctional snake.

Figure 29: Generated textures for a ﬁctional snake.

a few”, 30.8% answered “Yes, several”, and 0% an-

swered “Yes, many”.

Lastly, we asked the 10 questions from the Sys-

tem Usability Scale (SUS) by John Brooke (Brooke,

1986). We only adapted the ﬁrst question. The origi-

nal “I think that I would like to use this system fre-

quently” was changed to “I would like to use this

tool in the future to create snake textures”. We also

changed all mentions of “system” to “tool”. The SUS

test result was 85.8 points on average, on a scale that

goes from 0 (bad usability) to 100 (good usability).

This indicates a very good usability, and that users

are likely to use the tool in the future to generate

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

142

snake skin textures. The full test results can be seen

at https://goo.gl/GDEs56.

We’ve also shown our texture generator to a her-

petologist to gather feedback. Although originally in-

tended to use in the game or animation industry, the

herpetologist said the tool is useful to them as well. It

could be used to easily create a visual representation

of a new snake species: according to her, biologists

currently use photos (which aren’t always available

or of good quality) or manually draw using a vec-

tor graphics tool such as CorelDraw. The herpetolo-

gist has also tested our tool, and the System Usability

Scale score was 80.0 (however, keep in mind we had

only one test subject).

6 CONCLUSIONS

From the results we obtained and the positive feed-

back on user tests, we believe our tool proves to be

a quite useful texture synthesizer for snake skin pat-

terns. Even though we based our study only on snakes

found in the Rio Grande do Sul region, we found it

can be used for snakes from other regions as well

without any problem (save the complex patterns we

are unable to reproduce), as well as ﬁctional snakes.

Our tool was made available to download for

free at https://goo.gl/tmGxZB. Within the tool are

the presets (all parameters values) used for all

snakes shown in the results. The Substance De-

signer source ﬁle was also made available for free at

https://share.allegorithmic.com/libraries/3214. Feed-

back from other users is positive (4 reviews, all with

5 stars) and it was downloaded 90 times as of October

31, 2017 (33 days after it was uploaded).

It should also be mentioned that generated tex-

tures can easily be adapted for other scaled reptilians

as well, or indeed, any other animal if the normal map

and height map aren’t used (scales shape go into these

textures only). Some preliminary results can be seen

in Figure 30.

Figure 30: Color textures generated using our method for

different animals. From left to right: Cheetah (Acinonyx

jubatus), cow (Bos taurus) and ﬁve-lined skink (Plestiodon

fasciatus).

Our tool, however, is unable to reproduce textures

of snakes categorized as having the “Complex” pat-

tern type, which was not implemented as discussed

on section 4.1.5, and snakes that combine multiple

pattern types (such as both longitudinal stripes and

spots). We also do not generate head and tail textures

for two reasons. First, these would be dependent on

how the mesh’s UV coordinates were mapped. Sec-

ond, due to the much higher complexity. Scales on the

head often have a speciﬁc amount for each species,

and many different shapes. These improvements are

left for a future work.

Finally, we would like to test our tool with experi-

enced users, that is, professional texture artists.

ACKNOWLEDGEMENTS

We would like to thank Marluci M

uller Rebelato, of

the Biosciences Institute at Universidade Federal do

Rio Grande do Sul, for her advice on snakes biology.

REFERENCES

Abegg, A. D. and Entiauspe Neto, O. M. (2012). Serpentes

do Rio Grande do Sul. Livraria e Editora Werlang

Ltda., Tapera, RS, Brazil.

Andrews II, M. J. (2010). Caramel burmese python.

Bauchot, R. (2006). Snakes: A Natural History. Sterling.

Borges-Martins, M. (2007a). Micrurus altirostris (cope,

1860).

Borges-Martins, M. (2007b). Phalotris lemniscatus trilinea-

tus (boulenger, 1889).

Borges-Martins, M. (2007c). Rhinocerophis alternatus

(dum

eril, bibron and dum

eril, 1854).

Brooke, J. (1986). System usability scale (sus): a quick-

and-dirty method of system evaluation user informa-

tion. Reading, UK: Digital Equipment Co Ltd.

Campbell, C. (2005). Pastel ball python.

Cocho, G., P

erez-Pascual, R., and Rius, J. L. (1987a). Dis-

crete systems, cell-cell interactions and color pattern

of animals. i. conﬂicting dynamics and pattern forma-

tion. Journal of Theoretical Biology, 125:419–435.

Cocho, G., P

erez-Pascual, R., Rius, J. L., and Soto, F.

(1987b). Discrete systems, cell-cell interactions and

color pattern of animals ii. clonal theory and cellular

automata. Journal of Theoretical Biology, 125:437–

447.

de Aguiar Passos, M. (2013). Erythrolamprus miliaris (lin-

naeus, 1758).

de Albuquerque, S. (n.d.). Falsa-coral (rhinobothryum

lentiginosum.

Dhillon, D. S., Teyssier, J., Single, M., Gaponenko, I.,

Milinkovitch, M. C., and Zwicker, M. (2014). Inter-

active diffraction from biological nanostructures. In

Computer Graphics Forum, volume 33, pages 177–

188. Wiley Online Library.

A Procedural Model for Snake Skin Texture Generation

143

Di-Bernardo, M. (n.d.). Ptychophis ﬂavovirgatus gomes,

1915.

Efros, A. A. and Leung, T. K. (1999). Texture synthesis by

non-parametric sampling. In Computer Vision, 1999.

The Proceedings of the Seventh IEEE International

Conference on, volume 2, pages 1033–1038. IEEE.

Gilet, G., Sauvage, B., Vanhoey, K., Dischler, J.-M.,

and Ghazanfarpour, D. (2014). Local random-phase

noise for procedural texturing. ACM Transactions on

Graphics (TOG), 33(6):195.

Hendrikx, M., Meijer, S., Van Der Velden, J., and Iosup, A.

(2013). Procedural content generation for games: A

survey. ACM Transactions on Multimedia Computing,

Communications, and Applications (TOMM), 9(1):1.

Mandelbrot, B. B. and Pignoni, R. (1983). The fractal ge-

ometry of nature, volume 173. WH freeman New

York.

Martins, P. H. (2011). Elapomorphus quinquelineatus. serra

do cip

o, minas gerais, brazil.

May, P. S. (2010). Figure 1 - (fprep393ph) adult, encar-

naci

on, departamento itap

ua (paul smith may 2010).

Miller, G. S. P. (1988). The motion dynamics of snakes and

worms. SIGGRAPH Comput. Graph., 22(4):169–173.

Murray, J. and Myerscough, M. (1991). Pigmentation pat-

tern formation on snakes. Journal of Theoretical Bi-

ology, 149:339–360.

Nogueira, C. (n.d.a). R

epteis squamata do cerrado - apos-

tolepis assimilis.

Nogueira, C. (n.d.b). R

epteis squamata do cerrado -

philodryas aestiva.

Panagiotakis, C. and Tziritas, G. (2006). Snake terrestrial

locomotion synthesis in 3d virtual environments. The

Visual Computer, 22(8):562–576.

Perlin, K. (2002). Improving noise. In Proceedings of the

29th Annual Conference on Computer Graphics and

Interactive Techniques, SIGGRAPH ’02, pages 681–

682, New York, NY, USA. ACM.

Pharr, M., Jakob, W., and Humphreys, G. (2016). Phys-

ically based rendering: From theory to implementa-

tion. Morgan Kaufmann.

Rada, T. (2008). Lampropeltis triangulum triangulum (east-

ern milksnake).

Sawaya, R. (n.d.). Philodryas olfersii (lichtenstein, 1823).

Smith, P. (2015). Bicoloured mussurana mussurana bicolor.

Stuart, J. N. (2011). Prairie rattlesnake (crotalus viridis),

adult.

Timm, C. D. (2014). Falsa-coral (oxyrhopus rhombifer).

Turk, G. (1991). Generating textures on arbitrary surfaces

using reaction-diffusion. In ACM SIGGRAPH Com-

puter Graphics, volume 25, pages 289–298. ACM.

Uetz, P., Freed, P., and (eds.), J. H. (2016). The reptile

database.

Witkin, A. and Kass, M. (1991). Reaction-diffusion tex-

tures. ACM Siggraph Computer Graphics, 25(4):299–

308.

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

144