
Wavelet Correlation of Neural Activity Bursts Generating Spikes
S. V. Bozhokin, I. B. Suslova and D. A. Tarakanov
Peter the Great Saint-Petersburg Polytechnic University, Polytechnicheskaya 29, Saint-Petersburg, Russia
Keywords: Continuous Wavelet Transform, Wavelet Correlation Function, Synchronization of Neurons.
Abstract: We study neural activity synchronization on the basis of instantaneous wavelet correlation function and
simple mathematical model of brain bursts carrying several spikes. The approach allows us to obtain
analytical solution for two neurons generating a given number of spikes and estimate the coupled behavior
of neurons at different time moments. Neural activity is simulated as a superposition of elementary
nonstationary Gaussian signals with some given parameters. Time-frequency properties of neural signals are
studied by continuous wavelet transform with adaptive Morlet mother wavelet function.
1 INTRODUCTION
Synchronization of individual neurons and complex
neuron ensembles plays an important role in the
central nervous system functioning (Hramov et al.,
2015). A neuron as a pacemaker can generate
rhythms of various duration and frequencies, regular
or chaotic. The electric neural activity shows some
bursts consisting of short pulses (spikes) and low-
frequency oscillations associated with slow changes
in the membrane potential. In accordance with the
spike model (Izhikevich, 2006, Kislev, 2016,
Gerstner et al., 2002) the main carriers of
information are the number, duration and the
moments of occurrence of spikes. Synchronization
of neural activity as a way of information transfer
has been considered in numerous experimental and
theoretical works (Izhikevich, 2006, Kislev, 2016,
Gerstner et al, 2002, Xiaojuan et al., 2011).
A large number of mathematical models of
neurons, simulating the dynamics of their electrical
activity, can be divided into several classes. The first
class includes the models based on kinetic equations
simulating the excitation of nerve impulse. Such
models use a detailed description of ion channels
kinetics. The classical Hodgkin-Huxley model and
its various generalizations (Zhou and Kurths, 2003)
belong to this class of models. The requirements for
these models consist in accurate reproduction of the
electrical activity of the mathematical neuron, whose
electrical activity must correspond to a single pulse
or bursts of pulses of the real biological neuron.
The second class of models includes conceptual
models of neurons (Hramov et al., 2015, Izhikevich,
2003). These phenomenological models describe the
effect of ion currents with identical characteristic
scales by using a single variable. In this case, a few
ordinary differential equations are sufficient to
describe the electrical activity of a single neuron.
The third class includes threshold models of neurons
(Nekorkin, 2008, Tuchwell, 1988). In this case, the
system accumulates threshold signals. Their
combined action results in membrane potential
reaching the threshold value. This fixed value is
treated as a spike. Thereafter, the value of the
membrane potential returns to the initial state. The
process of synchronization is described by using
mathematical models of synaptic connections
(Hramov et al., 2015). It should be noted that both
the models of functioning of a neuron ensemble and
synapses connecting the neurons require large
computing powers.
In this paper, we use the simplest model
describing a separate spike in the form of the
Gaussian signal, which has a certain duration. In this
model, we assume that all spikes produced by
neurons have the same shape. The formation of
individual bursts both for a single neuron and for
two coupled neurons is given phenomenologically in
the form of a sequence of individual spikes created
by the neurons. Such a simple model has the
advantage of allowing us to solve analytically the
synchronization problem for two neurons.
It is assumed that the coding of information in
the brain is carried out through spike frequencies for
a single neuron and a group of several neurons
Bozhokin, S., Suslova, I. and Tarakanov, D.
Wavelet Correlation of Neural Activity Bursts Generating Spikes.
DOI: 10.5220/0006635102010207
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 4: BIOSIGNALS, pages 201-207
ISBN: 978-989-758-279-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
201

(Izhikevich and Gally, 2004). A certain stimulus of
electrical activity causes excitation of a specific
group of neurons. In this case, the relative times for
the production of spikes by different neurons in the
group are strictly fixed. The evidence is that
temporal coding serves to represent and process
information in the cerebral cortex (Lowet et al.,
2016). The same set of neurons can encode a large
number of different stimuli. Each stimulus is
characterized by a unique order of spikes emitted by
different neurons. The same is the case with the
spacing between the spikes. The activation of neural
groups, caused by the presence of any stimulus,
assumes the process of creating spikes with strictly
fixed delays between them. This procedure of
creating spikes is observed for all or almost all
participants of the neural groups.
Coherent analysis, instantaneous phase-locking,
entropy transfer, and nonlinear dynamics methods
have been applied to assess the degree of
synchronization of neurons (Lowet et al., 2016,
Mizuno-Matsumoto et al., 2005). Spectral coherence
method based on the Fourier transform (cross-
spectra) and assuming stationarity of signals has
long been considered the main method for
evaluating the interaction of signals related to
rhythmic brain activity. It should be noted that
instantaneous phase synchronization methods are
recognized as more informative.
The study (Quyen et al., 2001) on the
synchronization of neurons at different frequencies
compares the efficiency of Hilbert transform and
wavelet transform. At present, it is possible to
highlight two main directions in the research on the
synchronization of neurons and neural networks: the
construction of more complex and more realistic
models of neurons and their interactions, and the
development of methods that take into account the
nonstationary and nonlinear nature of neural
rhythmic activity.
The purpose of this work is to develop a model
of impulse activity of neurons generating spikes; to
derive analytical wavelet transform that determines
the time-frequency properties of spikes; to calculate
wavelet correlation function analytically for
comprehensive analysis of the synchronization
processes.
2 METHODS
2.1 Mathematical Model of Neural
Rhythmic Activity
In contrast to the complicated models (Hramov et
al., 2015, Izhikevich, 2003, Nekorkin, 2008, Zhou
and Kurths, 2003), which consider in detail the
operation of ion channels, we propose a simple
mathematical model of the coupling activity of two
neurons
and
, and formulate the criteria for
their synchronization. Let the signal
Zt
of
electrical activity of the first
- neuron, be a
superposition of
N
elementary Gaussian signals
L
N
L
L
ttztZ
1
0
)(
, (1)
2
2
4
exp
2
L
L
L
L
L
L
ttb
ttz
. (2)
The simulation (1) assumes the first
- neuron
involving a number of spikes. We determine the
time of each spike occurrence either
phenomenologically or as a solution of more
complex models of neuron functioning. Each spike
;;
L L L
L b t
occurs at a time moment
L
tt
, has
its own amplitude
L
b
and duration
L
. In addition
to the spikes with
L
much smaller than the time
interval between spikes, this model comprises some
bursts. Each burst has its own center
LВ
t
and its
characteristic duration
LB
(
LB
L
). Various
bursts of
- neuron do not overlap (
LB
is much
smaller than the distance between bursts), and the
number of spikes in each burst can vary. The
proposed model makes it possible to take into
account the long-term changes in the work of an
individual neuron. Various types of effects on the
neuron (medicinal and light effects) can evoke such
perturbations. We represent the signal of second
neuron
)(tZ
as a superposition
K
N
K
K
ttztZ
1
0
)(
(3)
of Gaussian peaks
K
K
ttz
characterized by a set
of parameters
KKK
tbK ;;
.
Let us consider the expression for the correlation
function,
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
202
tdttZtZtССF
, (4)
which shows the coupling between two signals
()Zt
and
)(tZ
at different time points. We can
obtain the analytical expression for the cross-
correlation function of two Gaussian signals
2
22
22
exp
4
2
KL
LK
LK
LK
LK
t t t
bb
ССF t
. (5)
It is convenient to use the normalized cross-
correlation function
()n
LK
ССF t
with the maximum
value of
()n
LK
ССF t
equal to one at
KL
t t t
.
Taking into account (1), (3), the correlation function
(4) takes the form
1
1
()
00
N
N
n
LK
LK
CCF t CCF t
(6)
We find out that function (6) does not change if
we reverse the direction of time, and replace all the
times of spikes’ and neurons’ occurrences by the
opposite values
LL
tt
,
KK
tt
.
Hereinafter, we assume that all spikes of neurons
and
are equal
LK
, where
=0.001s,
and their maximum amplitudes
2
LK
bb
are
equal to one. Suppose that for
-neuron we have
N
=4 of spikes
0 1 2 3
; ; ;
L
localized at
0.01 ;0.03;0.06;0.1
L
ts
. For
-neuron we
have
N
=4,
0 1 2 3
; ; ;
K
with
0.71;0.73;0.79;0.89
k
ts
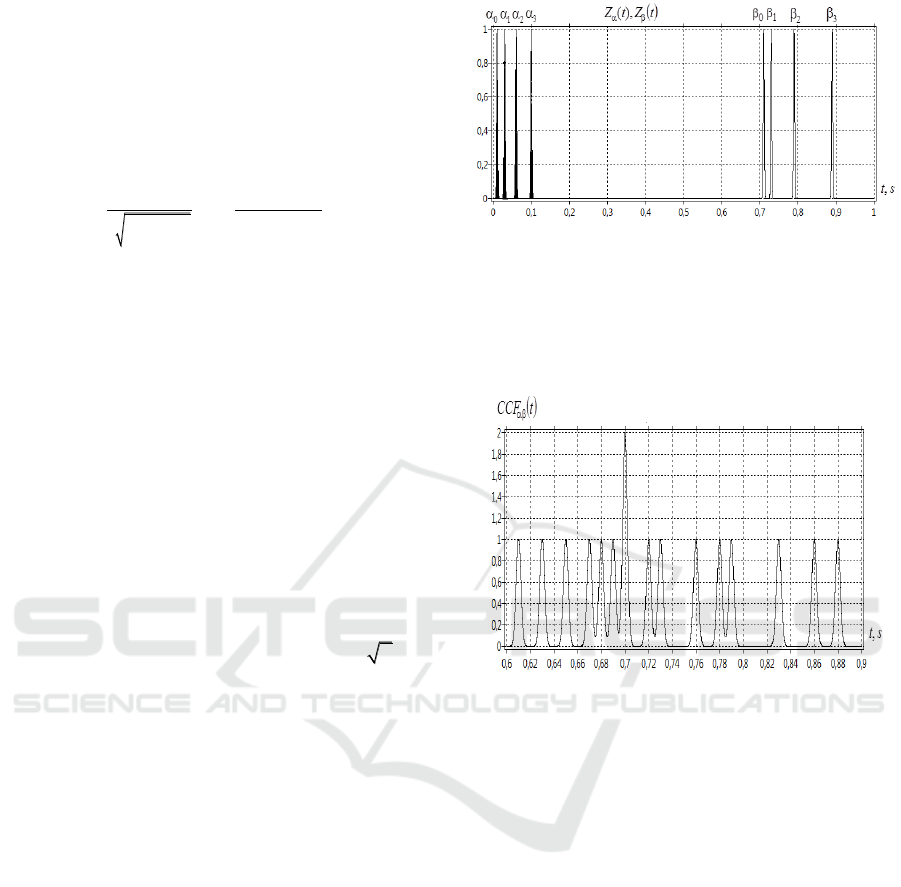
. Fig. 1 shows the signal
Zt
of the first
-neuron. We highlight in bold
four spikes of this neuron, given by the Gaussian
peaks. Four spikes forming the signal
Zt
associated with
-neuron are not highlighted.
The first peak of
CCF t
at
t
=0.61 s is due to
the coupling (correlation) of spikes
03
( ; )
. The
second peak at 0.88 s corresponds to the coupling of
spikes
30
( ; )
. The peak having a doubled
amplitude at
t
=0.70 s is due to the synchronization
of two pairs of spikes
);(
00
and
);(
11
. All
other peaks are related to the difference in
localization times of other spikes and neurons (Fig.
1).
Figure 1: The dependence of time
,ts
for
-neuron
signal
Zt
(in bold) и
-neuron signal.
Fig.2 shows instantaneous correlation function
ССF t
(4) for signals
Zt
and
Zt
.
Figure 2: The dependence of time
,ts
for
CCF t
.
2.2 Continuous Wavelet Transform of
Neural Signal
Time-frequency properties of
and
neurons
vary with time. We can successfully process such
nonstationary signals by Continuous Wavelet
Transform – CWT. This type of integral transform
maps nonstationary signal
)(tZ
to the plane of time
t
(s) and frequency
(Hz) (Bozhokin, 2010,
Bozhokin and Suslova, 2015) by the formula
tdtttZtV
*
,
, (7)
where
x
is the mother wavelet function, symbol
* means complex conjugation. We use here a new
adaptive Morlet wavelet function (AMW) with the
control parameter
m
(Bozhokin and Suslova,
2016):
Wavelet Correlation of Neural Activity Bursts Generating Spikes
203
.exp2exp
2
exp
2
2
2
mm
ix
m
x
Dx
(8)
In (8) we have the parameter
2
m
m
, and
constant
m
D
defined from the condition
.1
2
x
The properties of the mother wavelet (8) are given in
(Bozhokin and Suslova, 2016). In (Bozhokin and
Suslova, 2016) the value of
m
acts as a control
parameter of AMW. We can change temporal
resolution
x
and frequency resolution
F
of
signals under study by varying
m
. The
characteristic moments of time
t
, which make the
main contribution to the integral (7), satisfy the
relation
//
xx
t t t
. The adaptive
mother wavelet (8) acts as a varying window, which
depends on control parameter
m
. The window width
automatically becomes large for small frequencies
and small for large ones.
To calculate (8), we use the Fourier transform of
all functions in (7):
*
ˆ
ˆ
, exp 2
f
V t Z f ift df
, (9)
where
ˆ
Zf
and
*
ˆ
/f
are the Fourier
components of
Zt
and
x
. The Fourier
component
ˆ
F
equals:
2
2
2
ˆ
exp 1
1 exp 2 .
mm
m
m
D
FF
F
(10)
The application of the AMW makes it possible to
improve the results for spectral and time resolutions
of
)(tZ
in comparison with the application of the
conventional Morlet wavelet. We can illustrate the
fact by considering an infinite harmonic signal
0
( ) cos(2 )Z t f t
with frequency
0
f
. We can derive
the analytical expression for continuous wavelet
transform
,Vt
(7) using AMW (8). The maximum
of
,Vt
is located at point
0
f
. The full width
at half maximum of
,Vt
given by
0
2 2ln2 /( )
FWHM
fm
decreases with the
increase in parameter
m
.
If we present the signal
Zt
as a superposition
(1) of elementary signals (2), then
,Vt
also
should be the superposition of wavelet images
,
L
Vt
corresponding to the signals (2). The
wavelet images
,
L
Vt
for our model of neural
signals can be derived analytically:
,exp
2
exp
2
12
exp),(
2
2
2
0
22
2222
0
L
m
L
L
Lm
L
mL
L
aa
ix
am
amx
a
Db
tV
(11)
where
0 L
x t t
,
2 2 2
1 2 /
LL
am
.
3 RESULTS
3.1 Wavelet Analysis of Model Neural
Signals
Using the simulation (1), we can calculate
analytically the modulus of wavelet transform
),( tV
for signal
)(tZ
with four spikes
0.01 ;0.03;0.06;0.1
L
ts
presented in Fig.1.
Fig. 3 shows the ridges of two-dimensional surface
),( tV
.
Figure 3: Modulus of wavelet transform
),( tV
depending on frequency
, Hz and time
,ts
.
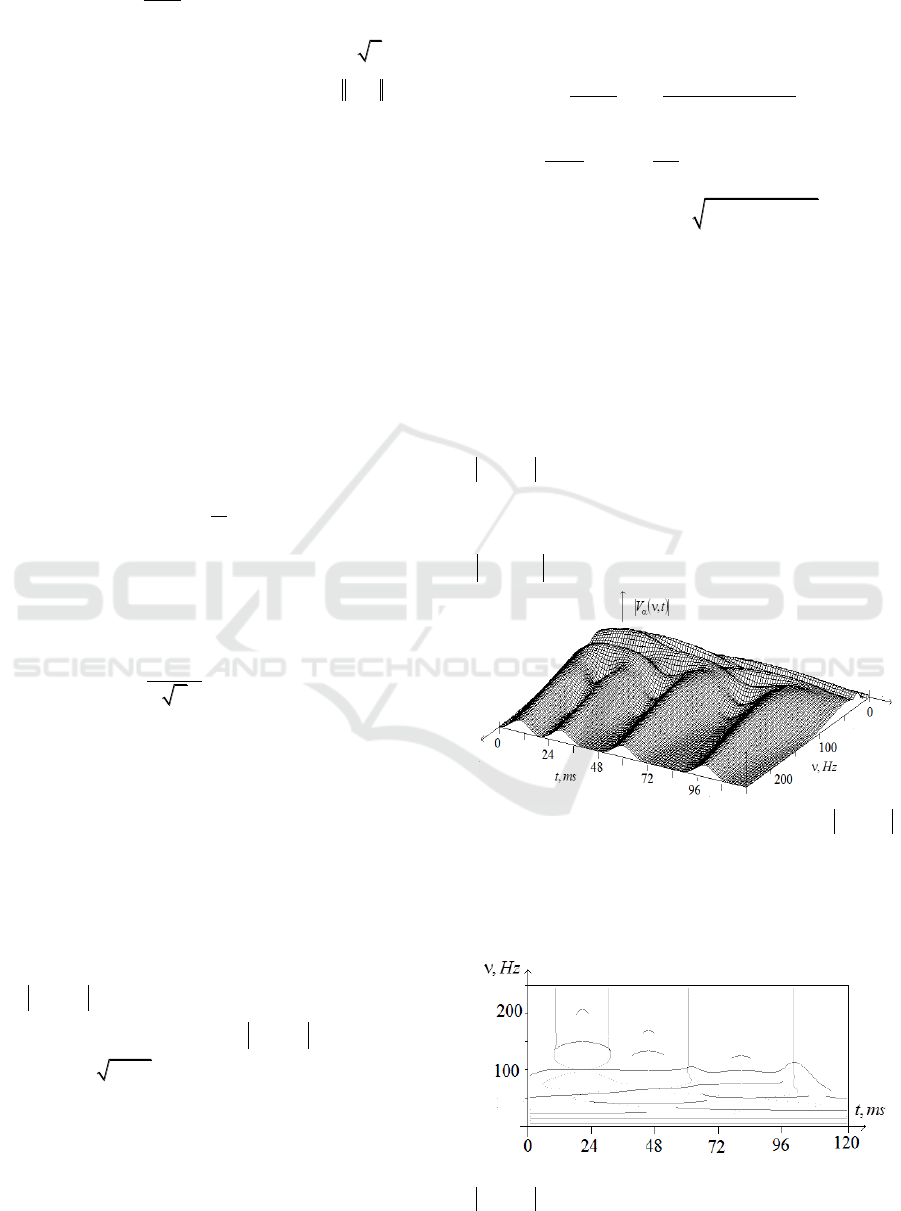
Fig. 4 displays the skeleton of the wavelet
transform, which shows the location of extremal
ridges on time-frequency plane.
Figure 4: Skeleton of Modulus of wavelet transform
),( tV
depending on frequency
,Hz and time
st,
.
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
204

3.2 Wavelet Correlation Behavior
We introduce wavelet correlation function
),( tWCF
by the formula
tdttVtVtWCF
,,),(
*
, (12)
which, in contrast to (4), shows the correlation
between CWT of two signals
),( tV
and
),( tV
taken at different time moments. According to the
principle of superposition wavelet correlation
),( tWCF
(10) can be represented as a double sum,
which includes
( , )
LK
WCF t
calculated for
elementary Gaussian signals. Note that under this
approach, we can also derive
( , )
LK
WCF t
analytically.
Hereinafter, we will need to know the
normalized function
2
( ) 2
22
22
1
, 8 exp 2
2
exp 2 2exp 1 .
2
n
LK m
mm
d
WCF t m e A
d
iB iB
dd
(13)
calculated as
( ) (max)
( , ) , /
n
LK LK LK
WCF t WCF t WCF
with
maximal value equal to unit. In (13) we have
e
2.72 and
2 2 2
2
1
KL
d
m
, (14)
2
2
22
(
4
KL
t t t
A
md
, (15)
2
KL
t t t
B
d
. (16)
Function
( , )
LK
WCF t
reaches its maximal value
(max)
LK
WCF
at
KL
t t t
. Under the condition
KL
, the value of
(max)
LK
WCF
has its
maximum at the point
22
max
1 1/ (16 /(4 )m
, which for
=
=0.001 s approximately equals to 80 Hz.
To achieve the best time resolution of spikes, we
use here the control parameter
1m
.
Fig.5 shows
),( tWCF
for two neurons
and
.
Figure 5: Dependence of
),( tWCF
on frequency
,Hz
and time
st,
.
The analysis of Fig. 5 shows that at large
frequencies
1/(4 )
(
80 Hz) the time
behaviour of wavelet correlation modulus
( , )WCF t
corresponds exactly to the classical
correlation function
ССF t
. The doubled peak at
t
=0.70 s at these frequencies also appears to be due
to the synchronization of two pairs of spikes
);(
00
and
);(
11
. The special features of low-
frequency behaviour of
),( tWCF
are associated
with the characteristic intervals of peaks sequence in
the process of neurons synchronization.
4 CONCLUSION
We propose a simple mathematical model of neural
signals, which allows us to obtain analytical
expressions for wavelet correlation functions
( , )WCF t
.The neural signal as a sequence of bursts
containing a certain number of spikes is simulated
by the superposition of elementary Gaussian signals
characterized by several parameters such as
amplitude
L
b
, duration
L
and time of occurrence
L
tt
.
The study of the maximal value of
( , )WCF t
depending on time gives the opportunity to detect
the synchronization of spikes between various
neurons at different time moments. The dependence
of
),( tWCF
on frequency
provides additional
information on the correlation of spikes. In the
limiting case
1/(4 )
, the time behavior of
),( tWCF
is identical to that of the classical
correlation function
ССF t
.
Wavelet Correlation of Neural Activity Bursts Generating Spikes
205

The task of determining neuronal correlations is
particularly important in the development of neuro-
interfaces, which are multi-electrode arrays that
exchange information between the neuronal
population and the outside world (Bursáki et al.,
2012,). Such neuro-interfaces allow both stimulation
and synchronous probing of dozens of neurons at the
cellular level. Our method can be used to determine
individual spikes of neurons in the patch-clamp
method (Suk et al., 2017), as well as in studying the
functioning of mirror neurons (Hou et al., 2017).
The wavelet-correlation function introduced in
this paper can be used as a tool to study rapidly
changing burst processes in radio-physics, plasma
physics and astrophysics, as well as the stability of
quantum frequency standards.
ACKNOWLEDGMENTS
The work has been supported by the Russian
Science Foundation (Grant of the RSF 17-12-
01085).
REFERENCES
Bozhokin S.V., 2010. Wavelet analysis of learning and
forgetting of photostimulation rhythms for a
nonstationary electroencephalogram. In Technical
Phys. V.55(9), 1248-1256.
Bozhokin S.V., Suslova I.B., 2015. Wavelet-based
analysis of spectral rearrangements of EEG patterns
and of non-stationary correlations. In Physica A:
Statistical Mechanics and its Applications.V. 421(1),
151–160, available at
http://www.sciencedirect.com/science/article/pii/S037
8437114009777 - af000010
Bozhokin S.V., Suslova I.B., 2016. Instantaneous
Correlation Of Spectral Integrals Related to Records
from Different EEG Channels. In Lecture Notes of
Computer Science.V.9719, 49-55.
Buzsáki G., Costas A., Anastassiou C.A., Koch C., 2012.
The origin of extracellular fields and currents — EEG,
ECoG, LFP and spikes. In Nature Reviews
Neuroscience. V. 13, 407-420.
Gerstner W., Werner M., Kistler W.M., 2002. Spiking
Neuron Models Single Neurons, Populations,
Plasticity,Cambridge University Press. Cambridge,
UK.
Hou J., Rajmohan R., Fang D., Kashfi K., Al-Khalil K.,
Yang J., Westney W., Grund C.M., O’Boyle W.O.,
2017. Mirror neuron activation of musicians and non-
musicians in response to motion captured piano
performances. In Brain and Cognition. V.115(7), 47-
55.
Hramov A.E., Koronovskii A.A., Makarov V.A., Pavlov
A.N., Sitnikova E., 2015. Wavelets in neuroscience,
Springer-Verlag, Berlin.
Izhikevich E.M., 2003. Simple Model of Spiking Neurons.
In IEEE Transactions of neural networks. V.14(6),
1569-1572.
Izhikevich E.M., Gally J.A., Edelman G.M., 2004. Spike-
timing dynamics of neuronal groups. In Cerebral
Cortex. V.14(8), 933–944.
Izhikevich E.M., 2006. Polychronization: Computation
with Spike. In Neural Computation.V.18, 245-282.
Kiselev M.V., 2016. Asynchronous/polychronous scheme
of information coding in spiking neural networks. In
Proceedings of the conference "Neuroinformatics-
2016". ch.3. M.: NNIU MEPI.
Lowet Е., Roberts M.J., Bonizzi P., Karel J., De Weerd
P., 2016. Quantifying Neural Oscillatory
Synchronization: A Comparison between Spectral
Coherence and Phase-Locking Value Approach. In
PLoS One. 11(1). e0146443.
Mizuno-Matsumoto Y., Ukai S., Ishil R., Date S.,
Kaishima T., Shonosaki K., Shimoyo S., Takeda M.,
Tamura S., Inouye T., 2005. Wave-Сrosscorrelation
Analysis of Neurophysiological Signals. In Brain
Topography. V.17(4), 237-252.
Nekorkin V.I., 2008. Nonlinear oscillations and waves
in neurodynamics”. In Physics-Uspekhi.V.51(3), 295-
304.
Quyen M.L., Foucher J., Lachaux J.-Ph, Rodriguez E.,
Lutz A., Martinerie J., Varela F.J., 2001. Comparison
of Hilbert transform and wavelet methods for the
analysis of neuronal synchrony. In Journal of
Neuroscience Methods.V.111, 83–98.
Suk H.J., Welie I., Kodandaramaiah S.B., Allen B., Forest
C.R, Boyden E.S., 2017. Closed-Loop Real-Time
Imaging Enables Fully Automated Cell-Targeted
Patch-Clamp Neural Recording In Vivo. In Neuron.
V.95(5), 1037-1047.
Tuchwell H.C., 1988. Introduction to Theoretical
Neurobiology, Cambridge Univ. Press. Cambridge.
Xiaojuan Sun, Jinzhi Lei, Matjaz Perc, Ju¨rgen Kurths,
and Guanrong Chen, 2011. Burst synchronization
transitions in a neuronal network of subnetworks. In
Chaos.V.21, 016110-2–016110-10.
Zhou C., Kurths J., 2003. Noise-induced synchronization
and coherence resonance of a Hodgkin–Huxley model
of thermally sensitive neurons. In Chaos. V.13(1),
401-409.
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
206
