Protein Disorder Prediction using Jumping Motifs from Torsion Angles

Dynamics in Ramachandran Plots

Jonny Alexander-Uribe

, Juli

an D. Arias-Londo

and Alexandre Perera-Lluna

Department of Systems Engineering and Computer Science, Universidad de Antioquia,

Calle 67 No. 53 - 108, 050010, Medell

ın, Colombia

Research Center for Biomedical Engineering, ESAII, Universitat Polit

ecnica de Catalunya,

Pau Gargallo 5, 08028, Barcelona, Spain

Keywords:

Intrinsically Disordered Proteins, Intrinsically Disordered Regions, Dihedral Torsion Angles, Ramachandran

Plot, Conditional Random Fields.

Abstract:

Disordered proteins are functional proteins that do not fold in a ﬁxed 3D structure. The order/disorder pre-

diction in protein sequences is an important task given the biological roles of disordered proteins. In the last

decade many computational based methods have been proposed for the disorder identiﬁcation but currently

the most accurate strategies depend on the sequence alignment of large databases of proteins, making the

methods slow and hard to apply on proteome-wide analysis. In this paper is proposed an innovative approach

for linking the amino acid sequences with transition tendencies in their dihedral torsion angles. The aim is to

characterize the dynamical angle variations along the protein chain, as a way of measuring the ﬂexibility of the

amino acids and its connection with the disorder state. The features are estimated from empirical propensities

computed from Ramachandran Plots. The classiﬁcation is performed using structural learning in the form of

CRF (Conditional Random Fields). The performance is evaluated in terms of AUC (Area Under the ROC

Curve), and three suitable performance metrics for unbalanced classiﬁcation problems. The results show that

the proposed method outperforms the most referenced alignment-free predictors and its performance is also

competitive with the slower and mature alignment-based methods.

1 INTRODUCTION

For many years it was thought that proteins had to

fold in a ﬁxed 3D structure to accomplish their bio-

logical functions. When some experiments showed

the existence of proteins in a chaotic state, which re-

mained without folding, they were initially consid-

ered as anomalies or errors in the experiment (De-

Forte and Uversky, 2016). But as these weird proteins

accumulated, they could no longer be ignored and the

paradigm of sequence → 3D structure → function,

had to be reevaluated for accepting that some proteins

are biologically relevant and must persist in a ﬂexible

conﬁguration (DeForte and Uversky, 2016).

These proteins are now called disordered proteins:

biologically active proteins, which do not have a spe-

ciﬁc 3D-structure under normal physiological con-

ditions. When the complete protein remains with-

out a ﬁxed tertiary structure and persist in a ﬂexible

state, the term intrinsically disordered protein (IDP)

is used. In contrast, when a protein is mostly struc-

tured but displays some regions of disorder, it is said

to have intrinsically disordered protein regions (ID-

PRs) (DeForte and Uversky, 2016). Prevalence of dis-

order in nature is global, all organism have IDPs or

IDPR, being estimated that 30% of eukaryotic pro-

teins have long disordered regions (gretear than 30

residues) (Ward et al., 2004). This fact reinforces the

idea that IDPs are part of a clever mechanism for ac-

complishing complex functions that completely fold

proteins could not do.

The biological importance of IDPs is high, they

participate in essential celular processes such as

molecular regulation, transport and signaling. Addi-

tionally, they were found to be associated with hu-

man diseases including cancer, diabetes, cardiovascu-

lar affection, amyloidoses and neurodegenerative dis-

eases (Uversky et al., 2008). Because of that, in recent

years the discovery and characterization of disordered

proteins has become in one of the fastest growing ar-

eas in protein science (He et al., 2009). Neverthe-

less, experimental determination of IDPs and IDPRs

Alexander-Uribe, J., Arias-Londoño, J. and Perera-Lluna, A.

Protein Disorder Prediction using Jumping Motifs from Torsion Angles Dynamics in Ramachandran Plots.

DOI: 10.5220/0006647900380048

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 3: BIOINFORMATICS, pages 38-48

ISBN: 978-989-758-280-6

poses a costly and complex challenge, requiring both,

a lot of time and an extensive human expertise (He

et al., 2009). Computational methods have become

a valuable alternative to process the large amount of

proteins sequences available and infer their disorder

states. Although several predictors of IDPs have been

proposed in the past, there is still need of faster and

accurate methods for protein disorder identiﬁcation

(Peng et al., 2015),(Varadi et al., 2015).

The use of Multiple Sequence Alignment (MSA)

algorithms is the main distinguishing characteris-

tic of the current computational methods for detect-

ing disorder. Predictors using MSA, commonly ap-

ply several iterations of PSI-BLAST (Altschul et al.,

1990)(Altschul et al., 1997) for identifying proteins

homologues in known databases. This preliminar

phase, allows the creation of tuned Position Score

Matrices (PSSM). The PSSM can capture the statis-

tical variations of every amino acid on targeted pro-

teins, and are used as inputs for the disorder pre-

dictors, improving their performance in comparison

with the use of only the raw protein sequences. Al-

though the sequence alignment can offer an advan-

tage in the accuracy of the methods, it also imposes

a set of methodological and practical issues. One of

them is the computational cost, which becomes rele-

vant when the method is used on large scale proteome

analysis (thousands to millions of proteins). A sec-

ond and more relevant drawback, is the implicit as-

sumption that the proteins under evaluation have ho-

mologous sequences into the used databases. Some

of the methods that take advantage of the MSA algo-

rithms for identifying disorder include PONDR (Xue

et al., 2010), DISOPRED (Jones and Cozzetto, 2014),

NORSnet (Schlessinger et al., 2007) and SPINE-D

(Zhang et al., 2012).

In contrast, methods that avoid sequence align-

ment can reach more modest classiﬁcation results on

known datasets, but can be applied comparatively

faster on huge databases of unlabeled proteins (De-

Forte and Uversky, 2016), and more importantly, they

do not make assumptions about the existence of ho-

mologues proteins.

Among the most used alignment-free methods for

protein disorder prediction are IUPRED and Espritz

(Dosztnyi et al., 2005), (Walsh et al., 2012). IUPRED

uses the amino acid pair interaction energy estimated

using only the amino acid compositions, to create ma-

trices of potentials between amino acids. The au-

thors concluded that when a sequence contains few

hydrophobic residues, the composition-based mutual

interaction energy will be small, indicating the lack

of potential for folding. In IUPRED the scoring ma-

trices were adjusted using a Support Vector Machine

(SVM) (Cortes and Vapnik, 1995) and independent

models were created for short and long disorder re-

gions. IUPRED is computationally fast and have

been used in proteome-wide analyses (Oates et al.,

2013) (Potenza et al., 2015). The systems that use

predictors ensembles (metapredictors) recurrently in-

cluded IUPRED as a component (Bulashevska and

Eils, 2008) (Lieutaud et al., 2008), and in many

works where new predictors are proposed, IUPRED

is used as a baseline for comparison purposes (He

et al., 2009)(Deng et al., 2012). On the other hand,

Espritz is based on a Bidirectional Recursive Neu-

ral Network whose inputs are 5 scales obtained from

the clustering of AAindex properties (Kawashima and

Kanehisa, 2000), and a one-hot enconding vector of

length 20, which identify the amino acid being mod-

eled/evaluated at a time. It means that, given an amino

acid, this property vector will have a value 1 for only

one position, and 0s for the 19 other positions. Espritz

is also a fast predictor used in similar scenarios than

IUPRED and therefore well suitable for performance

comparison.

A common strategy for improving the perfor-

mance in disorder vs order classiﬁcation, is to com-

bine the outputs of several individual predictors, cre-

ating a metapredictor. This combination is often ap-

plied at the residue level where the probability out-

puts from different methods are fusioned into a new

classiﬁcation phase. Examples of metapredictors are:

MetaPdDOS (Bulashevska and Eils, 2008), MFDp

(Mizianty et al., 2010), MeDor (Lieutaud et al., 2008)

and Metadisorder (MD) (Kozlowski and Bujnicki,

2012).

In spite of the multiple efforts for introducing

more elevorated classiﬁcation strategies, the perfor-

mance of disorder predictors still has room for im-

provement. A valid approach to increase the protein

disorder classiﬁcation accuracy, is to create new fea-

tures capable of extracting relevant information from

the sequence, that can be related to the folded or un-

folded state of proteins. A promisory idea is to link

the protein sequence with the dihedral torsion an-

gles of the amino acid chain. This could be rele-

vant because these angles contain information about

restrictions, allowed values and tendencies associated

to the ﬁnal structure of proteins (Hollingsworth and

Karplus, 2010). This idea was explored in (Baruah

et al., 2015), where the dihedral angles were used

with the aim of estimating the conformational entropy

of IDP, IDPR, and completely ordered proteins. The

proposed metric was found to be a potential mea-

sure for the discrimination of complete disordered vs

complete ordered proteins. In (Uribe et al., 2017) a

set of information theory measures derived from tor-

Protein Disorder Prediction using Jumping Motifs from Torsion Angles Dynamics in Ramachandran Plots

sion angles extracted from Ramachandran plots (RP)

were also found to be relevant in the detection of IDP

and IDPR, when they were combined with other well-

established features in the state of the art for disorder

prediction.

In this work, an innovative characterization that

links the inferred torsion angles dynamic along the

chain with the disorder state, is proposed. The

strategy uses the RP distributions for quantifying

the amino acid tendency to jump between confor-

mational regions, transforming the idea proposed in

(Hollingsworth et al., 2012), in a practical tool for

characterizing proteins. The results will show that

using only the information from RPs, it is possible

to design a valuable feature extraction phase, which

once incorporated in a classiﬁer, is able to achieve

similar performance metrics than MSA based meth-

ods, but with a methodology that can be efﬁciently

computed on millions of proteins. This characteri-

zation called the jumping Motifs, was used here for

the creation of a disorder predictor called jMotCRiF.

The proposed predictor was build using a structural

learning scheme based on Conditional Random Fields

(CRFs) (Lafferty et al., 2001). CRFs are discrimina-

tive non-parametric models able to capture the cor-

relation amongst neighboring labels in a sequence,

therefore they are well suitable for the annotation of

amino acids as ordered/disorder (Uribe et al., 2017).

CRFs were ﬁrst used in the identiﬁcation of disor-

dered residues on (Wang and Sauer, 2008), but there

authors used a completely different characterization

based on conventional chemical properties.

The rest of the papers is organized as follows:

section 2 presents the characterization proposed and

describes the learning strategies. It also refers the

dataset used and the applied validation methodology.

Section 3 presents the results obtained and ﬁnally sec-

tion 4 includes some conclusions extracted from the

work.

2 MATERIAL AND METHODS

2.1 Characterization

Proteins are linear chains of connected amino acids

that can have hundreds to thousands of elements.

Neighbor amino acids, in order to avoid atomic

clashes, must limit their possible conﬁgurations. In

the backbone structure of an amino acid, there are

mainly two angles of turn for every residue: the tor-

sion angles known as φ and ψ. For illustrating this

Figure 1 shows a small stick and ball diagram of a

short subchain of amino acids where the torsion an-

gles are depicted. In this sense, the RPs are 2D repre-

sentations of the variation of φ and ψ angles on known

proteins. The 20 amino acids have different prefer-

ence in the φ and ψ space, because differences in

the three-dimensional structure of the residues, con-

fer different ranges of ﬂexibility. For example, the

residue in Glycine is just a single atom of hydrogen

giving the molecule the highest ﬂexibility and the pos-

sibility of exploring the bigest φ and ψ space. In con-

trast, Proline has a backbone covalent link, that im-

poses strong rigidity on the molecule, reducing the

possible φ and ψ valid angles to minimum. Other

amino acids have intermediate constrains that allow

them to explore different zones in the RPs. Figure 2

shows the RPs of Proline and Glycine, along with two

other representative amino acids.

Ψi

Φi

Ψi

VAL ALA ASP GLY

Φi

Figure 1: Ball diagram of small subchain with residues

Valine (VAL), Alanine (ALa), Aspartic Acid (ASP) and

Glycine (GLY). Φ and ψ torsion angles are shown around α

carbons of ASP and GLY.

2.1.1 The Jumping Motifs

An ideal procedure for the identiﬁcation of the protein

structure conformation, would take the amino acid

sequence and will predict the torsion angle dynamic

along the chain. Such method does not exists yet but

indirect measures related with this task, can be dis-

cerned using the amino acid propensities computed

from the thousands of known folded proteins.

In (Kalmankar et al., 2014), using proteins from

PDB (Berman et al., 2007), the authors constructed

amino acid propensities for 14 differentiated regions

on the RPs. Many of these zones have direct con-

nection with the secondary structures found in folded

proteins but the sparsely populated zones, in appar-

ently disallowed regions, are also considered. Overall

these propensities capture relevant torsion angle con-

ﬁgurations and some preferences that amino acids fol-

low, quantifying the tendency of sets of amino acids

to inhabit particular RP zones.

In Figure 3 the 14 zones are depicted, along with

some of the amino acids more frequently found inside

BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms

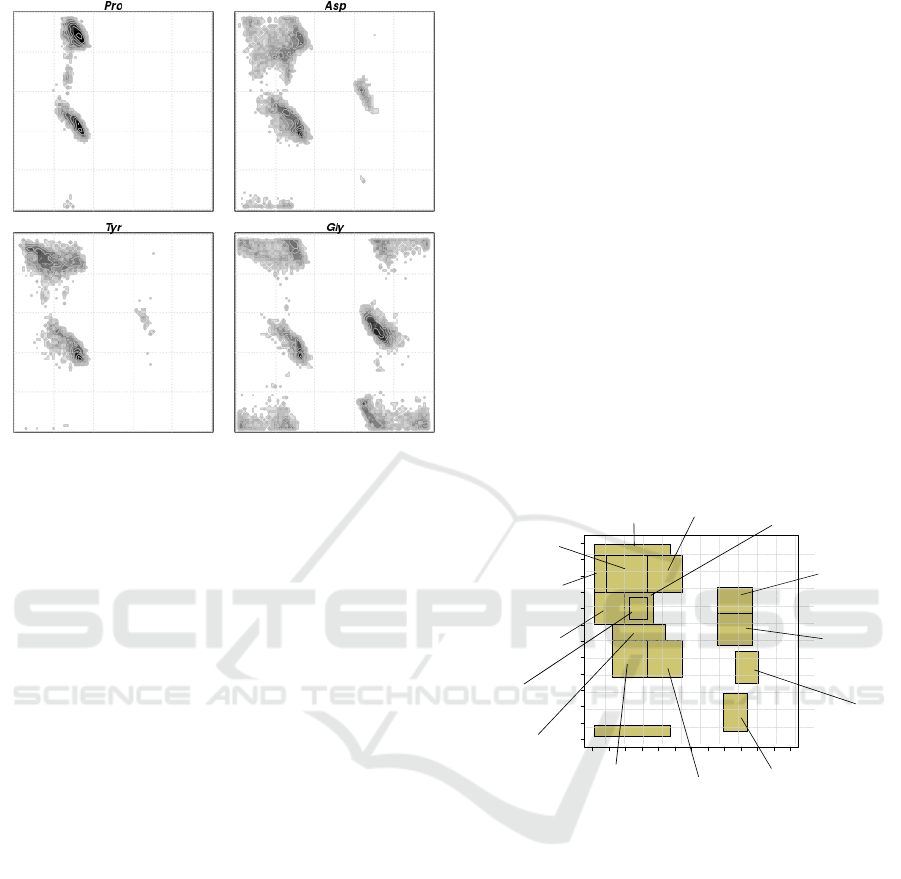
Figure 2: Ramachandran Plots of some amino acids, Pro-

line, Aspartic Acid, Tyrosine and Glycine. φ is along x-axis

and ψ is along y-axis.

these regions. Region number 8 is the most crowded

zone with around 40% of the amino acids analyzed,

inhabiting there. The primarily reason for this, is that

the most common secondary structure, the α helix,

belongs to this region. Zones 1, 2 and 9 together,

contribute with another 40% of the observations. In

region 1, resides the β sheet, the second most com-

mon secondary structure. Poliproline II is in region

number 2 and the inverted α helix is in region 11.

A remarkable contribution of the division made by

(Kalmankar et al., 2014), is that poor favored regions

are also included. For example region 12 contains the

less common structure called γ turn; inverted γ turns

are in region 5 and the type II β turns are in zone num-

ber 13. To consider the low inhabited regions, allows

to capture a more complete dynamic characterization,

covering the entire set of possible torsion angle con-

ﬁgurations.

As stated before, amino acids have different ten-

dencies to inhabit the RP regions. Propensities of

some of the residues are depicted in Figure 3. This

preferences are not deterministic, instead must be

treated as stochastic in nature, showing only the statis-

tically most common states. It is also true, that some

amino acids are rarely found in certain regions and

its appearance constitute a unexpected event. These

complementary and opposed dispositions, are con-

cretely quantiﬁed in Table 1, where the tendencies of

some amino acids to reside in the different regions

and the tendencies of some of them for avoiding the

zones, are speciﬁed numerically.

Given a short protein sequence, is possible to in-

spect their residues and identify which of the RP re-

gions are “activated” by the amino acids in consid-

eration. This activation could also be quantiﬁed by

the propensities associated to the residues, in such

way that if many amino acids coincide in the activated

zone its activation intensity would be higher.

Although the resulting activation patterns could be

useful, it would be better to capture, not only the pre-

ferred regions by the sequence, but also its transition

preferences. That is to say, a quantiﬁcation of the

dynamic change between the RPs regions, could be

of major interest, because of the fact that disordered

amino acids are presumably changing continuously

their torsion angles states, not resting in any partic-

ular spot for long but restlessly jumping between re-

gions. In this way, for identifying the IDPs, an in-

direct measure about the jumping dynamic between

regions, would be useful for inferring the transition

preferences and quantify a disorder tendency much

better.

R1 R2

R5R5A

R10

R11

R12

R13

P = 3.4

N, H, D = 1.7

N, D = 2.4

N, D, H = 2.0

H, Y, R = 1.6

S, N, D = 1.9

A, E = 1.3

T, H = 1.4

N, D = 2.2

N, H, D = 2.2

N, C, H, D = 2.0

S, A, H = 1.8

S, T = 2.2

V, I, F, Y = 1.3

−180 −120 −90 −60 −30 0 30 60 90 120 150 180

−180 −120 −60 −30 0 30 60 90 120 150 180

R5A

Figure 3: Diagram showing the 14 regions dividing the RP

as proposed by (Kalmankar et al., 2014). Also some amino

acid propensity intensities for inhabiting the RP regions are

depicted.

Using groups of four amino acids taken from cu-

rated proteins from PDB, (Hollingsworth et al., 2012)

explored the existence of recurrent transition patterns

in the RPs. They found 101 signiﬁcant transitions

between close φ and ψ angles, that represent nearby

conﬁgurations visited for many groups of consecu-

tive amino acids. They called these sets (φ, ψ)

Mo-

tifs. Figure 4 shows the relevant transitions found by

(Hollingsworth et al., 2012). Although the massive

regions contain the majority of jumps, some of the

motifs are also near to poorly inhabited regions. Un-

fortunately the authors reported that the link between

these motifs and the amino acid sequences, was not

strong enough for identifying direct mapping rules,

making difﬁcult to use the (φ,ψ)

Motifs, as a char-

Protein Disorder Prediction using Jumping Motifs from Torsion Angles Dynamics in Ramachandran Plots

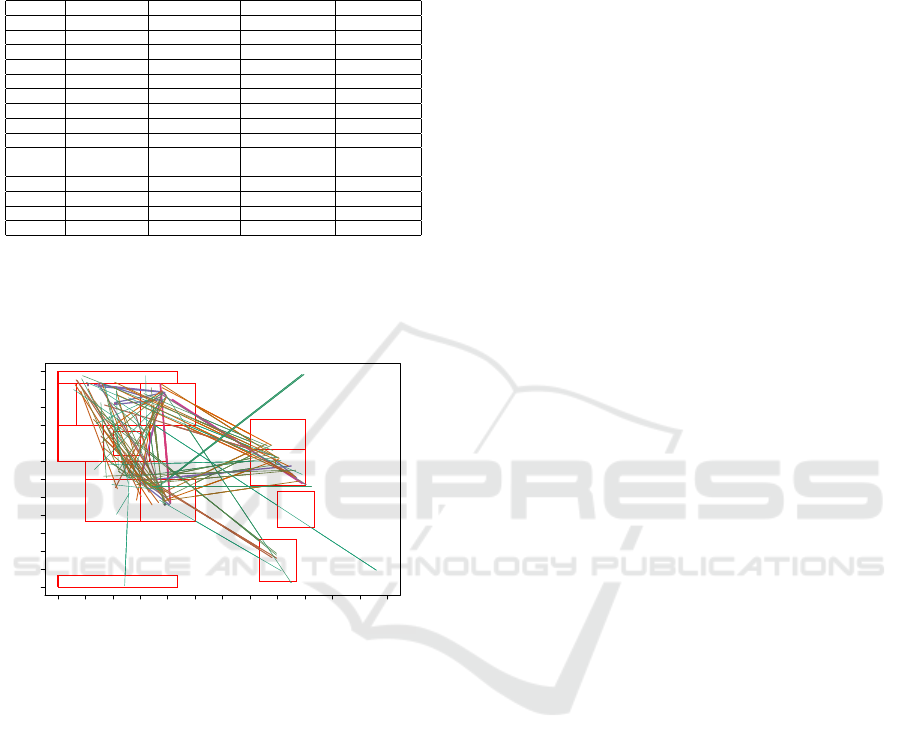
Table 1: Amino acid propensities for inhabiting the 14

zones of the RP as proposed by Kalmankar. Table was

adapted from (Kalmankar et al., 2014). The φ and ψ co-

ordinates ranges are delimiting the zones. Columns 4 and

5 list the high and low propensities of the amino acids for

inhabiting every region.

Region φ ψ High Prop. Low Prop.

1 -160 to -90 90 to 160 V,I,F,Y = 1.3 P = 0.02

2 -90 to -30 90 to 160 P = 3.4

3 -180 to -160 90 to 160 S,A,H =1.8 P,V,L,I = 0.4

4 -180 to -130 30 to 90 N,C,H,D = 2.0 P,I,V,L = 0.4

5 -130 to -80 30 to 90 N,H,D = 1.7 I,V, = 0.5

5A -120 to -90 40 to 80 N,H,D = 2.2 P,V,T = 0.4

6 -150 to -60 0 to 30 N,D = 2.2 P,I,V = 0.5

7 -150 to -90 -70 to 0 T,H = 1.4 P,A = 0.5

8 -90 to -30 -70 to 0 A,E = 1.3

9 -180 to -50 -180 to -160 y S,T = 2.2 L,I = 0.5

160 to 180

10 30 to 90 50 to 100 N,D = 2.4 I,V,L,T = 0.3

11 30 to 90 -10 to 50 N,D,H = 2.0 I,V,T = 0.2

12 60 to 100 -80 to -20 H,Y,R = 1.6 A,L,C = 0.6

13 40 to 80 -170 to -100 S,N,D = 1.9 I,V,T = 0.1

acterization tool for proteins. Therefore, a strategy for

transforming direct amino acid sequences to jumps on

the RP plane, is still missing.

−180 −150 −120 −90 −60 −30 0 30 60 90 120 150 180

−180 −120 −90 −60 −30 0 30 60 90 120 150 180

Figure 4: Graphical representation of the 101 motifs

(φ,ψ)

, over the 14 analyzed regions of the RPs. The width

and color of every line, represents the intensity of every mo-

tif. For those motifs with their coordinates lying outside of

the considered regions, the closest zone was selected. Al-

though not all regions are inhabited with the same density,

all of them have been assigned at least one motif.

The amino acid propensities found by (Kalmankar

et al., 2014) and the trajectories implicit in the (φ,ψ)

Motifs, can be combined for creating a new protein

characterization, capable of representing indirectly,

the structural transition propensities.

The procedure combines the information present

in the amino acid tendencies for region occupancy

(Table 1), with the initial and ﬁnal coordinates of the

(φ,ψ)

Motifs. Concretely the proteins are taken in

overlapping subsequences of 3 to 5 amino acids. Ev-

ery subsequence has a propensity for inhabit differ-

ent RP regions and these zones are then “activated”.

Then, every activated region, could be the initial or

ﬁnal target of different (φ,ψ)

Motifs. In this way

every subsequence is represented by the intensities of

the activated (φ, ψ)

Motifs, times the propensity of

the subchain for inhabiting the activated region. By

this simple procedure, every protein can be mapped to

202 (101 initial plus 101 ﬁnal) sparse characteristics,

each of them associated to a corresponding (φ,ψ)

Motif. We called this strategy, the Jumping Motifs

(jMotifs). The jMotifs characterization is a sparse

representation of every protein sequence, that is in-

directly capturing the dynamic torsion angle propen-

sities along the chain. As an example, Figure 5 is the

representation of a protein, using the jumping Motifs.

In the ﬁgure the real state of disorder is signaled

with the black line, when the line is in a high level the

corresponding amino acids are disordered. Is possi-

ble to observe that the disordered regions in this pro-

tein have distinctive activation patterns on the jMotifs

proﬁle. Concretely the ﬁrst and second disordered re-

gions have a high intensity variation for many jMotifs

when compared with the ordered zones. The pattern

transition is also discernible on the third peak where

the disorder ed zone induces a sustained variation on

the jMotifs intensities. Although these patterns are

not visual identiﬁable for all the disordered regions in

all the proteins, it will be shown that the jMotifs char-

acterization capture statistically, the transition prefer-

ences in the sequences, allowing the identiﬁcation of

IDPRs.

2.2 Classiﬁcation Methods

Structural learning methods are able to model differ-

ent statistical dependences among elements on a se-

quence. This is the case of the probabilistic models

known as Conditional Random Fields (CRFs), which

are able to segment and label sequence data (Lafferty

et al., 2001). The CRFs have several advantages in

comparison to more classical models for sequence

classiﬁcation such as hidden Markov models. CRFs

belong to the class of discriminative models, so they

model directly the conditional distribution of the la-

bels given the input variables, which is more suitable

for classiﬁcation purposes. Eq. 1 shows the condi-

tional probability of any particular label y given an

example x used by CRFs. The component F

(x,y)

is called a feature function. Intuitively, each feature

function is a speciﬁc measure of the compatibility of

the observation x and the label y. Every F

(·,·) func-

tion measures a different type of compatibility. The

weighting parameter w

, quantiﬁes the inﬂuence of

its corresponding feature function in relation with the

other ones. When w

> 0, a positive value for the

feature function makes y more likely as the true label

of x. When w

< 0, a positive values of the function

BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms

1 11 21 31 41 51 61 71 81 91 101 111 121 131 141 151 161 171

MARMNRP AP VE VS YK HMR F L I T HNP TNAT LS T F I EDL K KYGA T T VVRVCE VT YD KT P L E KDG I T V VDWP FDDGAP PPGK VV EDWLS L V KA K FCE APGSCVA VHCV AGL GRAPVL VA L A L I ESGMKYED A I

F I R

KRRGA I NSK

L T Y L EK YRP K

RL R FK DPH THK T RCCVM

1 11 21 31 41 51 61 71 81 91 101 111 121 131 141 151 161 171

MARMNRP AP VE VS YK HMR F L I T HNP TNAT LS T F I EDL K KYGA T T VVRVCE VT YD KT P L E KDG I T V VDWP FDDGAP PPGK VV EDWLS L V KA K FCE APGSCVA VHCV AGL GRAPVL VA L A L I ESGMKYED A I

F I R

KRRGA I NSK

L T Y L EK YRP K

RL R FK DPH THK T RCCVM

Motifs Finales

Final Motifs

Initial Motifs

Figure 5: Jumping Motifs Proﬁle representing protein DP0054 of Disprot. At the top is the activation pattern of initial jMotifs

and below the corresponding activation of ﬁnal jMotifs. Every jMotif value is along the vertical axis while the amino acid

sequence is along the horizontal axis. Activation intensity is high on the yellow zones and low on the red spots. For this

protein its disorder state is known and is signaled with the black line.

makes y less likely as true label for x. If w

= 0 then

the feature function is irrelevant as a predictor of y.

The feature functions are deﬁned in advance by the

designer, while weights are learned by the training al-

gorithm. The denominator Z(x,w) in Eq. 1 is a nor-

malizing factor that constraints the values to the range

[0,1].

P(y|x;w) =

exp

∑

j=1

(x,y)

Z(x, w)

(1)

In the case of a linear chain CRF, the feature func-

tions must link maximum two labels, while x could

represent any value in the sequence. The Figure 6 de-

picts graphically a linear chain CRF. The convex loss

function used for ﬁnding the parameters w

, is showed

in Eq. 2. It corresponds to the logarithm of the condi-

tional likelihood associated with Eq. 1. Some advan-

tages of the linear chain CRF, is that convergence to

the global optimum is guaranteed, and efﬁcient train-

ing algorithms do already exist (Lafferty et al., 2001).

LCL(x,y;w) = F

(x,y) −

∑

(x,y

)p(y

|x;w) (2)

2.3 Feature Selection

Feature selection can be done independently of the

classiﬁcation method or can be adjusted to the par-

Figure 6: The graphical structure of the linear chain CRF.

The variable y

represents the label in every sequence time-

step. The entire sequence characteristics (x

,...,x

) are

represented in a single node X.

ticular classiﬁer. In this case, we use the regular-

ization parameter of the CRF objective function for

ﬁnding a representative subset of characteristics. The

regularization is a strategy for improving model per-

formance, where the objective function that is maxi-

mized during the training phase, is modiﬁed for ﬁnd-

ing fewer or smaller parameters avoiding over-ﬁtting.

It works through the addition of a penalty term, which

castigates the selection of big or abundant parameters.

In the case of CRF, parameters are usually found

by maximizing the log-likelihood function. For exam-

ple, by adding a penalty term based on the L2 norm,

the objective function takes the form showed in Eq. 3.

max

LCL(x,y;w) −λw

w (3)

max

LCL(x,y;w) −λ

∑

(4)

Protein Disorder Prediction using Jumping Motifs from Torsion Angles Dynamics in Ramachandran Plots

In Eq. 3, the parameter λ controls the degree of

the penalty over the likelihood function: parameters

with high magnitude will lead to a higher L2 norm,

reducing the objective function value. Use of the L2-

norm keeps the objective function convex and differ-

entiable, and hence the effort to train a CRF with or

without L2 regularization, is in computationally cost,

very similar. In general, using L2 regularization, the

training procedure will ﬁnd parameters with reduced

magnitude compared with the function without the

regularization.

A complimentary regularization technique uses

the L1-norm over the parameters. In Eq. 4 the L1

penalty applied over the CRF likelihood function is

shown. In this case, the ﬁnal model will have many

parameters with exactly zero value, producing simple

and sparse models. L1 regularization applies penal-

ties proportional to parameters magnitude, and al-

though objective function in CRF remains convex, it

is no longer differentiable. This complicates some-

how the training phase when gradient methods are

used (Tsuruoka et al., 2009). The procedure for fea-

ture selection using L1 regularization on CRFs mod-

els is similar to the well known LASSO regression

(Tibshirani, 1996). A regularization path is recon-

structed using different values of λ in the regular-

ization term. The regularization path allows the in-

formed selection of a given set of characteristics, ac-

cording to the performance reached. For avoiding

over ﬁtting and ﬁnding the appropriate characteristics,

the regularization path must be found on different par-

titions of the data. That is, a hold out set is required

for allowing correct validation of the characteristics

found. Concretely the algorithm used for ﬁnding the

selected features was:

Feature Selection on CRF using L1-norm:

1. Partition of dataset in Train, Test and Valida-

tion subsets

2. Find λ

, the value of L1 regularization pa-

rameter that excludes all the properties

3. While some weight = 0

3.1. Decrease λ (this allows to include proper-

ties progressively)

3.2. Train CRF using the Train set and apply-

ing L1 regularization with λ parameter

3.3. Test the CRF using the test set

3.4. Compute performance metrics for Test

and Train samples

3.5. End while

4. Find best λ considering metrics on Test sam-

ples

5. Select only the features present when using

best Lambda on test samples

6. Train CRF model using Train + Test samples

with the features selected, and L2 Regular-

ization

7. Test CRF using Validation samples if avail-

able

2.3.1 Properties Selected

The procedure using the regularization path for select-

ing the best model characteristics, was implemented

on the 202 jMotifs. Initially, using a shallow training

(12 iterations), the value of parameter λ that excluded

all the properties was explored. This was called λ

and found to be the value 10

5.3

. Later, exploring

λ from 10

−1

to λ

, regularizations paths were com-

puted. Figure 7 shows the AUC performance, the

magnitude of weights and the number of variables in-

cluded as λ parameter varies in a logarithm progres-

sion. The point where AUC performance in training

samples reaches a plateau, is selected as the optimal

point for variable inclusion. Thus, 37 of the original

202 properties were included.

−1 0 1 2 3 4 5

0.4

0.45

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

X: 2.4

Y: 0.8382

Testing

Training

−1 0 1 2 3 4 5

Log10(Lambda)

−1 0 1 2 3 4 5

100

200

300

X: 2.4

Y: 37

NÃºmero de variables activas al Variar Factor RegularizaciÃ³n L1

Log10(Lambda)

AUC

Log(

)

Log(

)

Log(

)

Weights sum of variables included

Number of variables included

Figure 7: Regularization path with jMotif properties. AUC

metric on training and testing samples is on the left. In the

point where log(λ) = 2.4, are required only 37 character-

istics, as can be see in the right plot, with these properties

subset is enough for reaching a good performance.

Positions of the selected jMotifs appear on Fig-

ure 8. We can see that many of the 14 RPs zones are

represented for the selected jMotifs. There are four

jMotifs that conserved its initial and ﬁnal points, these

were ββ.1, PP.1, Pδ.1 and Pδ.2. Transitions in region

β and P, have the same zone as origin and destination,

it means they represent amino acids that preserve their

torsional conﬁgurations in the jump. In Figure 8 the

transitions given by jumps from P to δ

and δ

to P

are represented using arrows. It is quite notorious that

symmetrical jumps, are marked as important for the

identiﬁcation of disorder. Additionally P

is a low in-

habited region, and nevertheless it is identiﬁed as rel-

evant for the recognition of disordered amino acids.

BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms

Figure 8: a) RP coordinates of initial (blue) and ﬁnal (black) selected jMotifs with asymmetrical components. Important areas

of the RPs are covered by the selected jMotifs, even some low inhabited regions are represented. b) For some jMotifs, both

components were selected, and ﬁnal and initial coordinates are shown. Two of these transitions involves jumps in the same

area.

3 EXPERIMENTS AND RESULTS

For the sake of comparison, the proposed charac-

terization methods were evaluated on a target data

set and their result were compared with sequence

based predictors and also with MSA based methods.

The CRF models were implemented using the library

HCRF2.0b ((Morency, 2015)).

3.1 Data Sets

For training our predictor, we used the 3000 se-

quences in the database DM3000, prepared in (Zhang

et al., 2012). This dataset mainly contains proteins

took from PDB and selected with the following cri-

teria: a resolution less than 2 amstrongs, a size big-

ger than 60 residues and having X-ray structures with

missing electron densities for groups of amino acids,

which are assumed to be in disorder.

Later, the proposed predictor was evaluated on the

SL329 Data set, which was prepared in (Zhang et al.,

2012). The referenced authors created the database

selecting proteins with sequence homology less than

(25%) from the SL benchmark data set. The SL data

set (Sirota et al., 2010) is a subset of Disprot, the

most referenced and commonly used database (Sick-

meier et al., 2007). SL329 contains 329 proteins

with 51.292 ordered residues and 39.544 disordered

residues.

3.2 Model Validation

The selection of model parameters was carried out

using a 10-fold cross-validation strategy on train-

ing samples. In general data sets can include

some level of imbalance between ordered and dis-

ordered proteins, then some metrics able to quan-

tify the performance in such scenarios were included.

The set of metrics used includes: AUC, Sensitiv-

ity, Speciﬁcity, B

ACC

and MCC. AUC refers to the

area under the ROC curve, being disorder the pos-

itive class. MCC is the Matthews correlation co-

efﬁcient, which according to (Baldi et al., 2000) is

an appropriate measure of performance for unbal-

anced data sets. MCC can be estimated as MCC =

T P·TN−FP·FN

√

(T P+FP)·(T P+FN)·(T N+FP)·(T N+F N)

, where TP de-

notes True Positive, TN stands for True Negative, FP

is False Positive and FN is False Negative.

On the other hand, B

ACC

is the balanced accuracy

which can be expressed as

ACC

Sensi + Speci

(5)

where Sensi = T P/(T P + FN), and Speci =

T N/(T N + FP) are the sensitivity and the speciﬁcity

respectively.

3.3 Results

Table 2 shows evaluation results on benchmark SL329

data set. Performance of compared methods were

took from (Faraggi et al., 2012). Is possible to observe

Protein Disorder Prediction using Jumping Motifs from Torsion Angles Dynamics in Ramachandran Plots

that the method SPINE-D, who is using sequence

alignment, obtained the best performance on this

data set. The proposed jMotCRiF method achieved

the second best performance, surpassing many MSA

methods in the state-of-art. Even metapredictors as

MFdp and MD, are doing comparatively worse on this

data set than jMotCRiF. Considering that jMotCRiF

is using only information from the RPs, this per-

formance is quite impressive. We can also observe

that all the free alignment methods were surpassed.

For example jMotCRif gets an AUC 4.5% bigger

than commonly referenced IUPRED. Espritz showed

a good performance compared with many MSA-

based methods, but its metrics did not surpassed the

metapredictors or jMotCRiF. In terms of MCC and

AUC, jMotCRiF outperforms Espritz in about 2.5%

and 1.6% respectively, considering relative differ-

ences. jMotCRiF outperforms some of the state-of-

art MSA-based methods, with a considerably margin,

for example MCC metric of jMotCRiF is 63% higher

that the same value in PONDR.

The performance of SPINE-D is better, although

pretty close to the one obtained by jMotCRiF. This

result could be explained due to the fact that SPINE-

D corresponds to an adaptation of a secondary struc-

ture predictor, which was based on the prediction of

torsion angles from sequence proﬁles (Faraggi et al.,

2012). jMotCRiF is also using information of torsion

angles, but applying a more simple strategy which

is based only in the protein sequence, without us-

ing MSA algorithms and the collection of proper-

ties that SPINE-D requires, as the prediction of sec-

ondary structure, complexity, amino acid composi-

tion, physic-chemical characteristics, etc.

Table 2: Performance comparison among disorder identiﬁ-

cation methods on SL329 data set. jMotCRiF reaches the

second place in AUC value, even without using MSA algo-

rithms.

METHOD AUC SEN SPE MCC TYPE

SPINE-D 0,886 0,780 0,850 0,630 MSA

jMotCRiF 0,877 0,804 0,824 0,621 FREE

MFDp 0,873 0,880 0,620 0,510 MSA

MD 0,864 0,660 0,890 0,580 MSA

Espritz 0,863 0,728 0,868 0,606 FREE

Disopred 0,858 0,690 0,900 0,590 MSA

PONDR 0,843 0,610 0,910 0,550 MSA

IUPRED 0,839 0,758 0,598 0,504 FREE

NORSnet 0,815 0,540 0,920 0,510 MSA

PONDR 0,755 0,590 0,780 0,380 MSA

4 DISCUSSION AND

CONCLUSIONS

In this paper, a new methodology for characterizing

protein sequences that rely exclusively in the occu-

pation propensities on the Ramachandran plots was

described. The strategy aims to capture, at least in-

directly, the dynamic variations of the torsional an-

gles in the amino acid chains, for creating suitable nu-

merical descriptors that can be linked with the amino

acid disorder state. Using this fast characterization, a

classiﬁcation based on structured classiﬁers was ex-

plored and tuned. The obtained predictor, jMotCRiF,

is a fast and alignment-free tool for disorder identiﬁ-

cation, that is capable of achieving high performance

when compared with the state-of-art methods.

Even though jMotCRiF could be use as stand

alone predictor, the results obtained show that there

is still an improvement margin to be reached. An al-

ternative for attaining a better performance, could be

the combination of jMotCRiF with other complemen-

tary features available in the state of the art, or with

current high potential classiﬁcation techniques such

as different deep learning architectures. In the past,

we proposed a predictor, CRF InfoThor (Uribe et al.,

2017), also inspired in the dynamics hidden on the

RPs, which also reached a good performance in the

identiﬁcation of disordered regions, although it was

based on more complex descriptors. Either in combi-

nation with that predictor or with some of the classi-

ﬁers in the state-of-art, jMotCRiF has the potential for

obtaining a high performance and contribute with the

correct labeling of IDPRs. Additional experiments

for validating such progress must be done on bigger

datasets and with the inclusion of the different disor-

der predictors for achieving an appropriate compari-

son.

REFERENCES

Altschul, S. F., Gish, W., Miller, W., Myers, E. W., and

Lipman, D. J. (1990). Basic local alignment search

tool. Journal of molecular biology, 215(3):403–410.

Altschul, S. F., Madden, T. L., Schffer, A. A., Zhang, J.,

Zhang, Z., Miller, W., and Lipman, D. J. (1997).

Gapped BLAST and PSI-BLAST: a new generation

of protein database search programs. Nucleic acids

research, 25(17):3389–3402.

Baldi, P., Brunak, S., Chauvin, Y., Andersen, C. A., and

Nielsen, H. (2000). Assessing the accuracy of predic-

tion algorithms for classiﬁcation: an overview. Bioin-

formatics, 16(5):412–424.

Baruah, A., Rani, P., and Biswas, P. (2015). Conforma-

tional entropy of intrinsically disordered proteins from

amino acid triads. Scientiﬁc reports, 5.

Berman, H., Henrick, K., Nakamura, H., and Markley, J. L.

(2007). The worldwide Protein Data Bank (wwPDB):

ensuring a single, uniform archive of PDB data. Nu-

cleic acids research, 35(suppl 1):D301–D303.

BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms

Bulashevska, A. and Eils, R. (2008). Using Bayesian multi-

nomial classiﬁer to predict whether a given protein se-

quence is intrinsically disordered. Journal of theoret-

ical biology, 254(4):799–803.

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

Machine Learning, 20(3):273–297.

DeForte, S. and Uversky, V. N. (2016). Order, Disorder, and

Everything in Between. Molecules, 21(8):1090.

Deng, X., Eickholt, J., and Cheng, J. (2012). A compre-

hensive overview of computational protein disorder

prediction methods. Molecular BioSystems, 8(1):114–

121.

Dosztnyi, Z., Csizmok, V., Tompa, P., and Simon, I. (2005).

IUPred: web server for the prediction of intrinsically

unstructured regions of proteins based on estimated

energy content. Bioinformatics, 21(16):3433–3434.

Faraggi, E., Zhang, T., Yang, Y., Kurgan, L., and Zhou, Y.

(2012). SPINE X: improving protein secondary struc-

ture prediction by multistep learning coupled with

prediction of solvent accessible surface area and back-

bone torsion angles. Journal of computational chem-

istry, 33(3):259–267.

He, B., Wang, K., Liu, Y., Xue, B., Uversky, V. N., and

Dunker, A. K. (2009). Predicting intrinsic disorder in

proteins: an overview. Cell research, 19(8):929–949.

Hollingsworth, S. A. and Karplus, P. A. (2010). A fresh look

at the Ramachandran plot and the occurrence of stan-

dard structures in proteins. Biomolecular concepts,

1(3-4):271–283.

Hollingsworth, S. A., Lewis, M. C., Berkholz, D. S., Wong,

W.-K., and Karplus, P. A. (2012). ($\phi$, $\psi$)

2 motifs: a purely conformation-based ﬁne-grained

enumeration of protein parts at the two-residue level.

Journal of molecular biology, 416(1):78–93.

Jones, D. T. and Cozzetto, D. (2014). DISOPRED3: precise

disordered region predictions with annotated protein-

binding activity. Bioinformatics, page btu744.

Kalmankar, N. V., Ramakrishnan, C., and Balaram, P.

(2014). Sparsely populated residue conformations

in protein structures: Revisiting experimental Ra-

machandran maps. Proteins: Structure, Function, and

Bioinformatics, 82(7):1101–1112.

Kawashima, S. and Kanehisa, M. (2000). AAindex:

amino acid index database. Nucleic acids research,

28(1):374–374.

Kozlowski, L. P. and Bujnicki, J. M. (2012). MetaDisorder:

a meta-server for the prediction of intrinsic disorder in

proteins. BMC bioinformatics, 13(1):111.

Lafferty, J., McCallum, A., and Pereira, F. (2001). Con-

ditional random ﬁelds: Probabilistic models for seg-

menting and labeling sequence data. In Proceedings

of the eighteenth international conference on machine

learning, ICML, volume 1, pages 282–289.

Lieutaud, P., Canard, B., and Longhi, S. (2008). MeDor: a

metaserver for predicting protein disorder. BMC ge-

nomics, 9(Suppl 2):S25.

Mizianty, M. J., Stach, W., Chen, K., Kedarisetti, K. D.,

Disfani, F. M., and Kurgan, L. (2010). Improved

sequence-based prediction of disordered regions with

multilayer fusion of multiple information sources.

Bioinformatics, 26(18):i489–i496.

Morency, L.-P. (2015). HCRF library (including CRF and

LDCRF).

Oates, M. E., Romero, P., Ishida, T., Ghalwash, M.,

Mizianty, M. J., Xue, B., Dosztnyi, Z., Uversky, V. N.,

Obradovic, Z., Kurgan, L., and others (2013). D2p2:

database of disordered protein predictions. Nucleic

acids research, 41(D1):D508–D516.

Peng, Z., Yan, J., Fan, X., Mizianty, M. J., Xue, B., Wang,

K., Hu, G., Uversky, V. N., and Kurgan, L. (2015).

Exceptionally abundant exceptions: comprehensive

characterization of intrinsic disorder in all domains of

life. Cellular and Molecular Life Sciences, 72(1):137–

151.

Potenza, E., Di Domenico, T., Walsh, I., and Tosatto, S. C.

(2015). MobiDB 2.0: an improved database of intrin-

sically disordered and mobile proteins. Nucleic acids

research, 43(D1):D315–D320.

Schlessinger, A., Punta, M., and Rost, B. (2007). Natively

unstructured regions in proteins identiﬁed from con-

tact predictions. Bioinformatics, 23(18):2376–2384.

Sickmeier, M., Hamilton, J. A., LeGall, T., Vacic, V.,

Cortese, M. S., Tantos, A., Szabo, B., Tompa, P.,

Chen, J., Uversky, V. N., and others (2007). DisProt:

the database of disordered proteins. Nucleic acids re-

search, 35(suppl 1):D786–D793.

Sirota, F. L., Ooi, H.-S., Gattermayer, T., Schneider, G.,

Eisenhaber, F., and Maurer-Stroh, S. (2010). Parame-

terization of disorder predictors for large-scale appli-

cations requiring high speciﬁcity by using an extended

benchmark dataset. BMC genomics, 11(Suppl 1):S15.

Tibshirani, R. (1996). Regression shrinkage and selection

via the lasso. Journal of the Royal Statistical Society.

Series B (Methodological), pages 267–288.

Tsuruoka, Y., Tsujii, J., and Ananiadou, S. (2009). Stochas-

tic Gradient Descent Training for L1-regularized Log-

linear Models with Cumulative Penalty. In Pro-

ceedings of the Joint Conference of the 47th Annual

Meeting of the ACL and the 4th International Joint

Conference on Natural Language Processing of the

AFNLP: Volume 1 - Volume 1, ACL ’09, pages 477–

485, Stroudsburg, PA, USA. Association for Compu-

tational Linguistics.

Uribe, J. A., Arias-Londo

no, J. D., and Perera-Lluna, A.

(2017). Protein Disorder Prediction using Informa-

tion Theory Measures on the Distribution of the Dihe-

dral Torsion Angles from Ramachandran Plots:. pages

43–51. SCITEPRESS - Science and Technology Pub-

lications.

Uversky, V. N., Oldﬁeld, C. J., and Dunker, A. K. (2008).

Intrinsically disordered proteins in human diseases:

introducing the D2 concept. Annu. Rev. Biophys.,

37:215–246.

Varadi, M., Vranken, W., Guharoy, M., and Tompa, P.

(2015). Computational approaches for inferring the

functions of intrinsically disordered proteins. Fron-

tiers in molecular biosciences, 2.

Walsh, I., Martin, A. J., Di Domenico, T., and Tosatto, S. C.

Protein Disorder Prediction using Jumping Motifs from Torsion Angles Dynamics in Ramachandran Plots

(2012). ESpritz: accurate and fast prediction of pro-

tein disorder. Bioinformatics, 28(4):503–509.

Wang, L. and Sauer, U. H. (2008). OnD-CRF: predicting or-

der and disorder in proteins conditional random ﬁelds.

Bioinformatics, 24(11):1401–1402.

Ward, J. J., Sodhi, J. S., McGufﬁn, L. J., Buxton, B. F., and

Jones, D. T. (2004). Prediction and functional analysis

of native disorder in proteins from the three kingdoms

of life. Journal of molecular biology, 337(3):635–645.

Xue, B., Dunbrack, R. L., Williams, R. W., Dunker,

A. K., and Uversky, V. N. (2010). PONDR-FIT: a

meta-predictor of intrinsically disordered amino acids.

Biochimica et Biophysica Acta (BBA)-Proteins and

Proteomics, 1804(4):996–1010.

Zhang, T., Faraggi, E., Xue, B., Dunker, A. K., Uversky,

V. N., and Zhou, Y. (2012). SPINE-D: accurate predic-

tion of short and long disordered regions by a single

neural-network based method. Journal of Biomolecu-

lar Structure and Dynamics, 29(4):799–813.

BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms