Design, Test and Fabrication of a Droplet based Microfluidic Device

for Clinical Diagnostics

F. Jacinto, A. S. Moita and A. L. N. Moreira

IN+ - Center for Innovation, Technology and Policy Research, Instituto Superior Técnico, Universidade de Lisboa,

Av. Rovisco Pais, 1049-001, Lisboa, Portugal

Keywords: Lab-on-a-chip, Droplet based Microfluidics, Clinical Diagnostics, Chip Design and Test, Experimental and

Numerical Approaches.

Abstract: Despite the intensive research performed towards the development of biomicrofuidic devices, information

on the design, test and microfabrication of the devices is scarcely reported. Following our previous work,

this paper describes the design, microfabrication and test of an electrowetting chip to transport and

manipulate biosamples, towards the development of a microfluidic device for cancer diagnostics. As a first

approach, experiments are performed to infer on the basic chip dimensions and configuration (size and

positioning of the electrodes), allowing its best performance, evaluated based on droplet dynamics

(spreading/receding diameter and contact line velocity). Then, to scale down this section, for its proper

integration in the device, these basic dimensions are introduced as first guess values in a numerical model,

used to optimize the distance between the electrodes, the thickness of the dielectric and the electric potential

and frequency to be applied.

1 INTRODUCTION

Since their introduction by Manz (1990), lab-on-a-

chip devices have shown a fast evolution, based on

intensive research. Many applications mainly deal

with DNA manipulation and with basic biochemical

analysis (e.g. Wheeler et al., 2004) and only recent

studies have seriously focused on the development

of microfluidic devices for clinical diagnostics (e.g.

Dance, 2017).

The most popular configuration in lab-on-chip

design is based on the continuous transport of the

samples in an immiscible fluid, which flows inside

microchannels. Dance et al. (2.17) detail the

development of microchips capable of performing

blood samples separation, isolation of specific cells

for further analysis, diagnostics based, for instance,

on DNA analysis and cell sorting. These devices,

which are mostly focused on cancer diagnostics, are

nevertheless all based on microchannel flows.

Despite being effective, this configuration addresses

several issues related to clogging and maintenance

difficulties, lack of flexibility in the design and the

requirement of auxiliaries such as pumps and valves,

which have a very low efficiency at the microscale

(Geng et al., 2017). On the other hand, droplet based

digital microfluidics, in which the samples are

transported in microdroplets manipulated by

electrowetting, is an alternative which may solve

many of the limitations of the configuration based

on microchannels. In this context, closed

configuration systems, where droplets travel

between parallel plates are still most often used for

sample manipulation and for clinical diagnostics.

However, open configuration electrowetting

systems, in which the electrodes and counter

electrodes are gathered in a single plate over which

the droplet is transported, can fully take advantage

of the aforementioned positive characteristics of

digital microfluidics, but have still several technical

difficulties to overcome. The most adequate

electrodes configuration depends on the wetting

properties of the dielectric material covering the

electrodes and on the particular wetting and physico-

chemical properties of the samples (e.g. Moita et al.,

2016, Geng et al., 2017, Vieira et al., 2017).

Furthermore, the affinity of the dielectrics with the

biosamples, e.g. proteins, has been reported to

locally alter the wettability at the droplet-dielectric

surface interface, thus affecting the effectiveness of

droplet transport (e.g. Yoon and Garrell, 2003,

Moita et al., 2016).

Jacinto, F., Moita, A. and Moreira, A.

Design, Test and Fabrication of a Droplet based Microﬂuidic Device for Clinical Diagnostics.

DOI: 10.5220/0006656600880095

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 1: BIODEVICES, pages 88-95

ISBN: 978-989-758-277-6

Finally, there are numerous papers concerning

EWOD – Electrowetting on Dielectric applications

on microchips (including lab-on-chip systems),

which describe quite well the physics governing

electrowetting (from experimental evidence to

models), as recently reviewed for instance in Nelson

et al. (2012), but most of these papers are focused on

the fundamentals explaining droplet motion, rather

than on device fabrication. Relating the

fundamentals with device fabrication, however is not

always easy and erroneous relations may ultimately

preclude the development of an efficient device, as

explained for instance by Li et al. (2012).

Within this scope, the present paper addresses

the design and test of a simple lab-on-chip

configuration, towards the development of a

microfluidic device applied for cancer diagnostics,

based on cells elasto-mechanical properties and on

the particular rheology of the fluid droplets

transporting the biosamples. These properties are

then expected to be correlated with the different

stages of cell stiffness, which in turn be used for

cancer diagnostics, following the work of for

instance Gosset et al. (2010). Hence succeeding

previous work (Vieira et al., 2017), which

introduced the microfluidic device, as a whole and

focused on the effects of the properties of the

dielectrics and of the biosamples, this paper

addresses the configuration of the transport section

of this device, namely on the dimensions and

positioning of the electrodes. First, an experimental

approach is followed to infer on the basic

dimensions, allowing the best performance,

evaluated based on droplet dynamics

(spreading/receding diameter and contact line

velocity). Then, to scale down this section for a

proper integration in the device, these basic

dimensions are introduced in a numerical model,

used to optimize the distance between the electrodes,

the thickness of the dielectric and the electric

potential and frequency to be applied. The main

difficulty and novelty in this device is the proper

manipulation and transport of the droplets using the

dynamic behaviour and its relation with the physico-

chemical properties of the fluids for the diagnostics.

In the current stage of development, droplet

dynamics (contact diameters and angles) is used to

optimize the configuration of the chip namely the

size and position of the electrodes. Despite looking a

basic task, it is usually performed on a trial-and-

error basis, not considering droplet dynamics. In this

work, given that droplet dynamics, related to the

fluids rheology is useful for the diagnostics itself,

using the parameters describing droplet dynamics

(spreading diameter, spreading velocity and contact

angles) to optimize the size and position of the

electrodes is a relevant approach, as the chip is

configured, from the start, as a function of the

parameters useful for the diagnostics.

2 MANUSCRIPT PREPARATION

2.1 Experimental Method

Test chips, microfabricated at INESC-MN (Institute

for Systems Engineering and Computers –

Microsystems and Nanotechnologies) are composed

by arrays of interdigited electrodes printed on a 0.6

μm aluminium film by lithography and wet etch on a

glass substrate with 102x45 mm

and 700 μm width.

A thin film of a dielectric material (PDMS –

Polydimethylsiloxane) was deposited on the chip

assembly, without covering the contacts. The

different configurations tested only vary in the

electrodes width, w (120 ≤ w ≤ 1400 μm), being the

numerous interdigitated coplanar electrodes

displaced with a fixed distance between them, 2a=60

μm. The chips are actuated using DC current

provided by a Sorensen DCR600-.75B power

supply. The applied voltage was varied from 0 to

245 V. The frequency imposed for switching the

polarities at the electrodes is programmed using a

square wave, as in Fan et al. (2007). The imposed

frequencies were varied between 0 and 400Hz.

The performance of the chips is evaluated

looking at the dynamic response of the droplets on

the chips, which in turn is discussed based on the

measurement of several quantities such as the

spreading diameter (diameter of the droplet as it

spreads on the surface), the contact angles under

actuation and the velocity of the contact line

(derivative of the spreading diameter). These

quantities are determined from high-speed

visualization and post-processing. The high-speed

images are taken at 2200 fps using a Phantom v4.2

from Vision Research Inc., with 512x512

pixels@2100fps resolution. For the present optical

configuration, the spatial resolution is 25m/pixel

and the temporal resolution is 0.45 ms. The post-

processing is performed using a home-made routine

developed in Matlab. Temporal evolution of the

contact (spreading and receding) diameters is

presented as the average curve of at least 6 events (6

droplets), obtained under similar experimental

conditions. Each curve depicting the temporal

evolution of the spreading diameters requires nearly

500 measurements. So, 6 complete curves are

Design, Test and Fabrication of a Droplet based Microﬂuidic Device for Clinical Diagnostics

considered for each voltage, frequency, electrode

configuration, i.e. for all the parameters varied in the

study. Then, maximum/averaged vales are taken to

obtain the discrete values for the velocity and for

D/D

. Contact angle measurements are averaged

from twelve events.

All the experiments were performed in a Perspex

chamber, saturated with the working fluid and the

tests were performed under continuous monitoring

of temperature and relative humidity of the

surrounding air. The measurements were taken with

a DHT 22 Humidity & Temperature Sensor, at a

sample rate of 0.5 Hz. Relative humidity was

measured within 2-5% accuracy, while temperature

measurements were taken within ±0.5°C accuracy.

The temperature was observed to be constant within

T=20±3ºC and relative humidity was kept constant

between 75% and 78%.

Detailed description of the experimental method

and procedures used can be found in Moita et al.

(2016) and in Vieira et al. (2017).

The biofluid used here is a solution of GFP –

Green Fluorescent Protein, (produced and purified in

house) with 1.71x10

-3

mM concentration. The

solution was characterized in terms of density,

surface tension and viscosity, as summarized in

Table 1 and following the procedures described in

Moita et al. (2016) and in Vieira et al. (2017). The

GFP solution depicted a Newtonian behaviour, from

the rheological point of view. The volume of the

produced droplets is set between 1.5 and 2L.

Table 1: Physico-chemical properties of the GFP solution

used in the present work.

Solution

Density



[kg/m

]

Surface

tension 

[mN/m]

Dynamic

viscosity

[Ns/m

]

GFP

(1.71x10

-3

mM)

998

72.20.7

1x10

-3

2.2 Numerical Method

The simulations were performed using COMSOL

Multiphysics 4.3b. To evaluate the electric forces

generated, the numerical domain considered was a

0.655mm radius sphere (droplet domain) within an

air space of 3.21x1.6x3mm

. The electrostatic

boundary conditions are an electrical potential of

70V imposed to the electrode on the right (positive

x-axis) and a ground (0V) imposed the electrode on

the left (Fan et al., 2007). The model considers a

thin low permittivity gap with a 10m dielectric

layer (Mata et al., 2016). The mesh is composed of

67025 tetrahedral elements, being refined at the

liquid-solid and liquid-vapor interfaces.

For the simulation of droplet motion under

transient conditions, the electrostatic boundary

conditions are similar, but the distance between

electrodes is imposed as 2a = 10m, following the

analysis of the electric force, as a function of this

distance (as later discussed in the results). The

numerical domain is a 0.655mm radius sphere

(droplet domain) within an air space of 5X2mm

The mesh in this case is composed of 35831 free

triangular elements, being also refined at the liquid-

surface and liquid-air interfaces.

The electrostatic force actuating on the droplet is

calculated using the Maxwell stress tensor,

integrated on the droplet surface. A global

evaluation method was used to perform this integral

in COMSOL. Hence, the electrostatic force is

calculated by integrating:









 











 











 







(1)

on the surface of the droplet, where E is the electric

field, D the electric displacement, and n

the

outward normal from the object. Using the Maxwell

stress tensor for a 2D configuration, the volume

force is calculated as the first derivative of this

tensor.

Regarding the droplet flow, Phase Field User

Interface is used to track the liquid-air interface, for

a laminar flow, using the incompressible formulation

of the Navier-Stokes equations:







 



 



 



  



  





 



 



 



 

(2)

    (3)

The four forces on the right-hand side of eq. (2)

are due to gravity, surface tension, external

contribution to the free energy, and a user defined

volume force.

The phase field method adds the following

equations:





    







 (4)

   



 







 



  















(5)

where the quantity λ (SI unit: N) is the mixing

energy density and ε (SI unit: m) is a capillary width

that scales with the thickness of the interface. These

BIODEVICES 2018 - 11th International Conference on Biomedical Electronics and Devices

two parameters are related to the surface tension

coefficient, σ (SI unit: N/m), through equation:

















(6)

The volume fraction of air (fluid 2) is computed

as:

=min(max([1+f)/2],0,1) (7)

where the min and max operators are used so that

the volume fraction has a lower limit of 0 and an

upper limit of 1. The density is then computed by:

 = 

+ (

- 

(8)

and the dynamic viscosity according to

 = 

+ (

- 

(9)

where ρ

and ρ

are the densities and μ

and μ

are the dynamic viscosities of fluid 1 (biofluids) and

fluid 2 (air), respectively.

3 RESULTS AND DISCUSSION

As aforementioned in the Introduction, the entire

microfluidic device under development has three

main sections: the transport section, the diagnostics

section and the sorting section. This paper will focus

on the configuration of the first, given the paramount

role of an effective transport and manipulation of the

samples in the entire device. The motion of the

droplet requires it to be in contact with at least two

electrodes, which are actuated according to an

imposed switching frequency. The imposed duty

cycle, which acts as the switching frequency

between electrodes, was programmed to vary

between 0Hz and 400Hz, so one can infer on the

effect of this frequency on the dynamic response of

the droplet. Following the recommendations of Chen

et al. (2004) to evaluate the chip capacitance, the

distance between electrodes a should be much

smaller than their width w. So, after some

preliminary calculations, four basic configurations

were tested, namely, w = 120m, 800m, 1200m

and 1400m, with a fixed distance between

electrodes, 2a = 60m.

The chips performance is evaluated based on the

dynamic response of the droplets under actuation,

namely evaluating the spreading diameter, made

non-dimensional with the initial diameter of the

deposited droplet, the contact angles measured under

actuation and the velocity of the contact line. It is

worth reminding that the droplets are formed from

the solution of GFP (1.71x10

-3

mM). The main

objective is to set the width and distance between the

electrodes which maximizes droplet spreading

diameter and velocity for various conditions of

imposed frequency and imposed voltage. The later

should be as low as possible to avoid dielectric

breakdown.

Figure 1 shows the contact angle obtained under

electrostatic actuation, as a function of the applied

electric potential, for different imposed frequencies

and the temporal evolution of the spreading contact

diameter of a droplet on two coplanar electrodes,

with w=1400 μm, for 350 Hz, with different values

of the applied electric potential. Consistently with

the Young-Lippmann equation, the contact angle

decreases with the increment of applied tension and,

consequently, the spreading droplet diameter is

larger for increasing imposed voltages for the same

frequency, being this trend observed, regardless of

the configuration set-up.

The trend observed for the contact angles is in

line with the results expected, at the light of Young-

Lippmann equation and evidences the independence

of the contact angles with the imposed frequency.

This indicates that the spreading diameter is

independent from the imposed frequency which can

be lowered, to simplify the chip arrangement and

programming.

Figure 2 emphasizes that the droplet motion is

irreversible due to the high adhesion force of the

PDMS substrate. Hence after the spreading of the

droplet, up to its maximum diameter, this strong

adhesion due to the high contact angle hysteresis

(larger than 20º, as reported in previous work –

Vieira et al., 2017) promotes energy dissipation at

the contact line, thus restraining the spreading

motion of the droplet. The energy dissipation during

this motion precludes the recoiling, thus turning the

motion of the droplet irreversible. Consequently, it is

difficult for the droplet to be transported to the

subsequent electrodes. The dynamic behaviour of

the droplet illustrated here for 230 V, is consistently

observed for all the applied voltages, in steps of 15

V between 200 and 245 V.

Design, Test and Fabrication of a Droplet based Microﬂuidic Device for Clinical Diagnostics

(a)

/(b)

Figure 1: (a) Contact angle as a function of the applied

electric potential for different imposed frequencies and (b)

evolution of the spreading diameter for 350 Hz of a GFP

droplet, for the configuration 2a=60 μm and w=1400 μm.

The dielectric substrate is PDMS. The volume of the

liquid droplet is 1.8L.

In a more quantitative approach, the spreading

velocity and the maximum diameter of the droplet,

as a function of the imposed frequency are shown in

figure 2, for the different voltages. The current

configuration requires very high imposed voltages

(above 200 V), being limited to 245 V, as above this

value, the dielectric breakdown occurs leading to

electrolysis inside the droplet, which in turn

generates a violent droplet disintegration, in

agreement with the observations reported, for

instance by Mugele and Baret (2005) and by Cooney

et al. (2006). The difference between the green (230

V) and the blue (245 V) lines is small, which may be

indicative of contact angle saturation. On the other

hand, the minimum voltage required to observe any

droplet response to the actuation on the chips is 200

Analysis of figures 2 and 3 suggests that droplet

dynamics is nearly independent from the imposed

frequency. However, the results suggest that the

droplet has a weaker response to low frequencies (50

Hz) and a swifter response for frequencies between

100-300 Hz, although one cannot identify any

monotonic trend between the frequency and the

spreading diameter or the velocity. On the other

hand, maximum spreading diameters are observed

for the highest imposed frequency (400 Hz), but the

droplet depicts a lower response in time. This trend

is attributed to the imposed electric force that must

overcome the resistance to droplet motion associated

to the energy dissipation on the surface. The

velocities obtained here are lower than those

reported in other studies in the literature (e.g.

Cooney et al. 2006, Fan et al. 2007, Sen and Kim,

2009), as the chips configuration is not optimized

yet. Also, most of the fluids used in the

aforementioned studies are salt solutions and not

biofluids.

Figure 2: Temporal evolution of the spreading diameter of

a GFP droplet on a PDMS substrate, actuated at 230 V for

different imposed frequencies, for the configuration

2a=60 μm and w=1400 μm. The volume of the liquid

droplet is 1.8L.

To infer on the influence of the electrodes width

on the dynamic response of the droplets, four

alternative electrode configurations were tested.

Comparative results between the different

configurations are presented in figure 4, which

depicts the contact line velocity and the maximum

spreading diameter, as a function of the imposed

frequency. The results highlight that the

configuration with w=120 μm provides the worst

droplet response to the electrostatic actuation,

expressed by the low values of the spreading

velocity and of the non-dimensional spreading

diameter D/D

. The response of the droplet under

actuation on all the other configurations is very

similar, being however, overall more regular for the

BIODEVICES 2018 - 11th International Conference on Biomedical Electronics and Devices

chip with w =1200μm, mainly regarding the values

achieved for the maximum diameter.

(a)

(b)

Figure 3: (a) Spreading velocity of the contact line and (b)

maximum spreading dimensionless diameter of a GFP

droplet on PDMS, moving between coplanar electrodes for

the configuration 2a=60 μm and w=1400 μm for different

applied voltages and an imposed frequency. The volume

of the liquid droplet is 1.8L.

In agreement with figures 1 and 2, the set of

plots shown here does not identify a monotonic

trend between the spreading velocity and diameter

and the imposed frequency. Overall it mainly

indicates a slower response for very low frequencies

(50Hz) and faster response (with larger spreading

diameters) for higher imposed frequencies.

Nevertheless these plots show that regardless of the

imposed frequencies, the configurations with w

=120m and w =1400m provide a better dynamic

response which enables droplet motion.

(a)

(b)

Figure 4: (a) Spreading velocity and (b) maximum

spreading dimensionless diameter of a GFP droplet on

PDMS, moving between coplanar electrodes for the

different configurations, for an imposed frequency of

350Hz and an imposed electric potential of 230 V. The

volume of the liquid droplet is 1.8L.

For all the configurations tested and discussed in

the previous paragraphs, the dielectric material used

was PDMS, with a thickness of 30m. This

thickness was set following the values reported in

the literature and due to some limitations of the

microfabrication method, which did not allow a

deposition of a thinner dielectric layer. Vieira et al.

(2017), further showed improvements in the

transport efficiency of the droplet by coating the

PDMS with a chemical compound called Glaco®,

which is mainly a perfluoroalkyltrichlorosilane

combined with perfluoropolyether carboxylic acid

and a fluorinated solvent (Kato et al., 2008).

Glaco®, improves the dynamic response of the

droplet, turning the dielectric surface

superhydrophobic (depicting equilibrium contact

angles



=153±2º, with a hysteresis lower than 10º,

as measured by Vieira et al. 2017) and reducing the

Design, Test and Fabrication of a Droplet based Microﬂuidic Device for Clinical Diagnostics

adsorption of the biocomponents by the PDMS,

which was shown to improve the local wettability at

droplet-dielectric surface interaction. However,

Vieira et al. (2017) also show that the Glaco®

coating increases substantially the thickness of the

dielectric layer, turning difficult for the droplet to

respond to the electrical actuation, according to

Young-Lippmann equation. Consequently, despite

functional, the chips are working under very high

imposed voltages and frequencies. Hence, to scale

down the transport section, addressing smaller

dimensions and thinner dielectric layers, a model

was developed and simulations were performed

using COMSOL Multiphysics 4.3b, as described in

Section 2.2. It is worth reminding that the boundary

conditions addressing the wettability of the dielectric

surface were set to match the set PDMS+Glaco (



153º) and the biofluid droplet has the properties

depicted in Table 1 for GFP (1.71x10

-3

m). The

thickness of the film was reduced to 10m,

following the recommendations of Di Virgilio

(2015) and of Mata et al. (2016). The first important

output taken from the simulation performed was the

electric force generated by the electric field, for

different distances between electrodes 2a. The

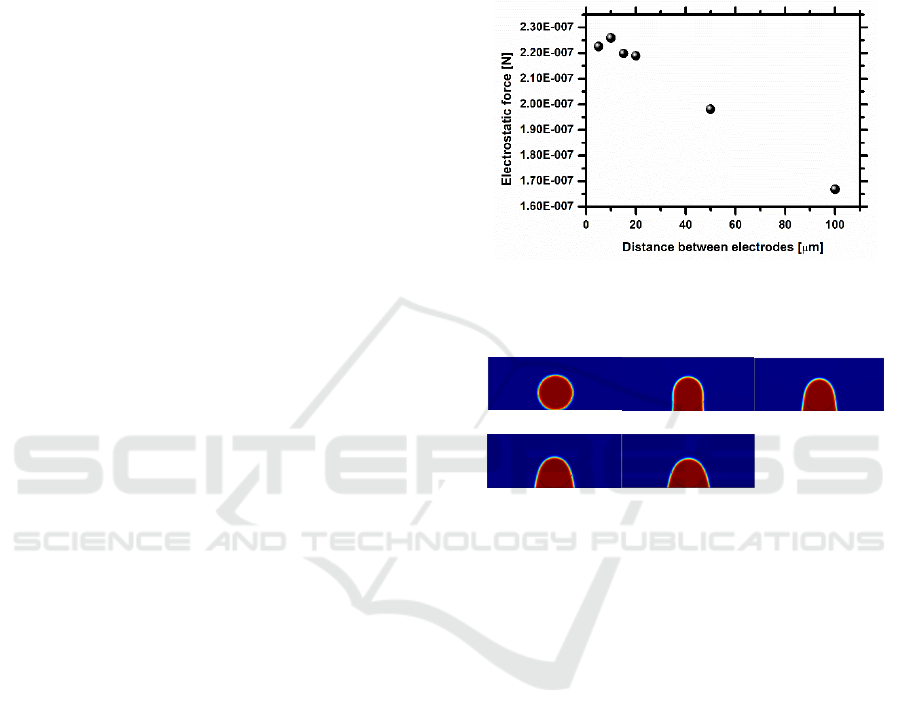
results, depicted in figure 5 show that the distance

2a considered in the experimental approach was

over dimensioned and that the optimum distance

which maximizes the electric force generated is

around 10m. The values obtained for the electric

force are in qualitative agreement with those

reported by Di Virgilio (2015), with a similar

geometry. Performing the entire simulation of the

dynamic behaviour of the droplet for the optimum

distance between electrodes 2a = 10m, as depicted

in figure 6, the droplets shows a significant motion

for an applied voltage of 70V, which is significantly

lower than the 200V required in the first tested set of

chips. Also, the imposed frequency could be lowered

down to 9Hz, matching the very low values achieved

by Fan et al. (2007). Overall the dynamic behaviour

of the droplet is in qualitative agreement with that

reported in the simulations of Di Virgilio (2015).

The nearly independent dynamic response of the

droplet with the imposed frequency, shown in the

experimental tests is well patent in the simulation

and in the results of Di Virgilio (2015): droplet

motion is not affected even at frequencies lower than

the 50Hz experimentally tested.

Despite preliminary, these results are quite

promising, considering that other parameters such as

the thickness of the dielectric layer can be further

optimized. The new patch of chips being currently

produced are following a fabrication method

allowing a more precise control of the thickness of

the dielectric layer, so that it can be quite reduced

now. This new patch of chips will now be tested

following a procedure similar to that reported here to

then be integrated in the more complex design of the

entire microdevice, towards the assembly of the final

prototype.

Figure 5: Electric force generated by the electrodes

configuration, as a function of the distance between

electrodes.

t = 0ms t = 0.75ms t = 1.50ms

t = 2.25ms t = 3ms

Figure 6: Sequence of images showing the motion of the

GFP droplet on co-planar electrodes, spaced with a

distance 2a = 10m, for an imposed electric potential of

70V and an imposed frequency of 9Hz. The volume of the

liquid droplet is 1.8L.

4 CONCLUSIONS

The present paper describes the design,

microfabrication and test of an electrowetting chip to

transport and manipulate biosamples, towards the

development of a microfluidic device for clinical

diagnostics, based on cell elasto-mechanical

properties and on the rheology of the biofluidic

droplets. Emphasis is put here in the design of the

section for sample manipulation and transport.

Experiments are performed, at an earlier stage of the

work, to determine basic chip dimensions and

configuration (size and positioning of the

electrodes), allowing its best performance, evaluated

based on droplet dynamics (spreading/receding

diameter and contact line velocity). Then, to scale

down this section, for its proper integration in the

BIODEVICES 2018 - 11th International Conference on Biomedical Electronics and Devices

device, these basic dimensions serve as input for a

numerical model, used to optimize the distance

between the electrodes, the thickness of the

dielectric and the electric potential and frequency to

be applied.

Preliminary results are promising, predicting the

satisfactory behaviour of a chip where the distance

between electrodes could be optimized to 10m, for

a dielectric thickness of 10m. Under these

conditions, the chip can transport droplets of the

order of 0.65mm diameter (thus allowing the

manipulation of biological flows containing cells)

for imposed voltages up to 70V and imposed

frequencies as low as 9Hz. These values are

significantly lower than those achieved in the

preliminary design stages, which could reach

imposed voltages of the order of 230V.

ACKNOWLEDGEMENTS

The authors are grateful to Fundação para a Ciência

e a Tecnologia (FCT) for partially financing this

research through the project UID/EEA/50009/2013,

and for supporting F. Jacinto with a fellowship.

A.S. Moita also acknowledges the contribution

of FCT for financing her contract through the IF

2015 recruitment program and for partially financing

this research through the exploratory project

associated to this contract.

Finally, the authors acknowledge the

contribution of Prof. Susana Freitas and her team

from INESC-MN for the microfabrication of the test

chips.

REFERENCES

Chen, J. Z., Darhuber, A. A., Troian, S. M., Wagner, S.,

2004. Capacitive sensing of droplets for microfluidic

devices based on thermocapillary actuation, Lab-on-a-

Chip, 4(5):473–480.

Cooney, C. G., Chen, C. Y., Emerling, M. R., Nadim, A.,

Sterling, J. D., 2006. Electrowetting droplet

microfluidics on a single planar surface. Microfluidics

and Nanofluidics, 2(5):435–446.

Dance, A., 2017. The making of a medical microchip.

Nature, 545:512-514.

Di Virgilio, V., 2015. Contactless electrowetting, PhD

Thesis, Universitat Politècnica de Catalunya,

Catalunya, Spain, 2015.

Fan, S.-K., Yang, H., Wang, T.-T., & Hsu, W., 2007.

Asymmetric electrowetting--moving droplets by a

square wave. Lab-on-a-Chip, 7(10):1330–1335.

Geng, Hongyao., Feng, J., Stabryl, L. M., Cho, S. K., 2017

Dielectroetting manipulation for digital microfluidics:

creating, transporting, splitting, and merging droplets.

Lab-on-Chip, 17:1060-1068.

Gosset, G.R., Tse, H.T.K., Lee, S.A., Ying, Y., Lidgren,

A.G., Yang, O.O., Rao, J., Clark, A.T., Di Carlo, D.,

2010. Hydrodynamic stretching of single cells for

large population mechanical phenotyping, PNAS,

109(20):7630-7635.

Kato M, Tanaka A, Sasagawa M, Adachi H, 2008.

Durable automotive windshield coating and the use

thereof. US Patent, 8043421 B2.

Li, Y., Fu, Y. Q., Brodie, S. D., Alghane, M., Walton, A.

J., 2012. Integrated microfluidics system using surface

acoustic wave and electrowetting on dielectrics

technology. Biomicrofluidics, 6:012812.

Manz, A., Widmers, H. M., Graber, N., 1990.

Miniaturized total chemical analysis systems: A novel

concept for chemical sensing, Sensors and Actuators

B: Chemical, 1(1-6):244–248.

Mata F., Moita, A.S., Kumar, R., Cardoso, S., Prazeres

D.M.F, Moreira, A.L.N., 2016. Effect of surface

wettability on the spreading and displacement of

biofluid drops in electrowetting. Proceedings of ILASS

– Europe 2016, 27th Annual Conference on Liquid

Atomization and Spray Systems, Sep. 2016, Brighton,

UK 4-7 September 2016. ISBN 978-1-910172-09-4.

Moita, A. S., Laurência, C., Ramos, J.A., Prazeres, D. M.

F., Moreira, A. L. N., 2016. Dynamics of droplets of

biological fluids on smooth superhydrophobic surfaces

under electrostatic actuation, J. Bionic Eng., 13:220-

234.

Mugele F, Baret J C., 2005. Electrowetting: From basics

to applications. Journal of Physics Condensed Matter,

17:R705–R774.

Sen, P., Kim, C.-J. C., 2009. Capillary spreading dynamics

of electrowetted sessile droplets in air. Langmuir,

25(8):4302–4305.

Vieira, D. Mata, F., Moita, A.S., Moreira, A.L.N., 2017.

Microfluidic Prototype of a Lab-on-Chip Device for

Lung Cancer Diagnostics. Proceedings of the 10th

International Joint Conference on Biomedical

Engineering Systems and Technologies - Volume 1:

BIODEVICES, 63-68, 2017, Porto, Portugal, 21-13

February 2017. DOI: 10.5220/0006252700630068,

ISBN: 978-989-758-216-5.

Wheeler A R, Moon H, Kim C J, Loo J A, Garrell R L.,

2004. Electrowetting-based microfluidics for analysis

of peptides and proteins by matrix-assisted laser

desorption/ionization mass spectrometry, Analytical

Chemistry, 76:4833–4838.

Wyatt, C. N., Kim, C.-J., 2012. Droplet actuation by

Electrowetting-on-Dielectric (EWOD): A review. J.

Adhesion Sci. Tech., 26:1747-1771.

Yoon, J Y, Garrell R L., 2003. Preventing biomolecular

adsorption in electrowetting-based biofluidic chips,

Analytical Chemistry, 75:5097–5102.

Design, Test and Fabrication of a Droplet based Microﬂuidic Device for Clinical Diagnostics