Distributed Clustering using Semi-supervised Fusion and Feature
Reduction Preprocessing
Huaying Li and Aleksandar Jeremic
∗
Department of Electrical and Computer Engineering, McMaster University, Hamilton, Ontario, Canada
Keywords:
Clustering, Information Fusion, Cluster Ensemble, Semi-supervised Learning.
Abstract:
In the recent years there has been tremendous development of data acquisition system resulting in a whole
new set of so called big data problems. In addition to other techniques data analysis of these data sets involves
significant amount of clustering and/or classification. Due to a heterogeneous nature of the data sets the perfor-
mance of these algorithms can vary significantly in different applications. In our previous work we proposed
semi-supervised information fusion system and demonstrated its performance in various applications. In this
paper we proposed to improve the performance of the proposed system by applying data preprocessing algo-
rithms using feature reduction as well as various base clustering techniques. We demonstrate the applicability
of the proposed techniques using real data sets.
1 INTRODUCTION
Thee major goal of data clustering is to find the hid-
den structure of a given data set by dividing data
points into distinct clusters based on certain criteria.
Data points in the same cluster are expected to be sim-
ilar to each other than to a data point from another
cluster. Although many clustering algorithms exist
in the literature, in practice no single algorithm can
correctly identify the underlying structure of all data
sets (Jain and Dubes, 1988), (Xu and Wunsch, 2008).
Furthermore, it is usually difficult to select a suit-
able clustering algorithm for a given data set when the
prior information about cluster shape and size is not
available. Therefore, in many applications one option
to improve the clustering results is to generate multi-
ple base clusterings and combine them into a consen-
sus clustering (Strehl and Ghosh, 2003),(Vega-Pons
and Ruiz-Shulcloper, 2011). This is often referred to
as clustering ensemble. Many existing clustering en-
semble methods consist of two major steps: genera-
tion and fusion of multiple base clusterings. Nowa-
days, there is a growing interest in utilizing additional
supervision information in the unsupervised learning
process (such as clustering) to improve the perfor-
mance. This is often referred to as semi-supervised
clustering (Chapelle et al., 2006).
Motivated by the success of both approaches, re-
searchers become interested in combining the ben-
efits of both techniques to further improve cluster-
∗
This work was supported by Natural Sciences and Engi-
neering Research Council of Canada.
ing results. The supervision information of semi-
supervised learning can be provided and utilized in
either step of clustering ensemble methods. In (Iqbal
et al., 2012), the supervision information is utilized
in the base clustering generation step, i.e., applying
semi-supervised clustering algorithms to generate the
set of base clusterings and fuse the cluster labels with-
out supervision. In this paper, we propose to utilize
the supervision information in the fusion step, i.e.,
applying unsupervised clustering algorithms to gen-
erated the set of base clusterings and fuse the cluster
labels with supervision. The remainder of this paper
is organized as follows. In Section 2, we propose the
modified semi-supervised clustering ensemble algo-
rithm using data preprocessing based on variable base
clustering generation and normalization. In Section 3,
we demonstrate the performance of our proposed al-
gorithms and the effect of normalization in clustering
ensemble. In the last section, we give the summary
of current research work and also list some future re-
search direction we will continue to work on.
2 SEMI-SUPERVISED
CLUSTERING ENSEMBLE
Clustering ensemble methods usually consists of two
major steps: the generation and fusion of base cluster-
ings, as shown in Fig. 1. In this section, we propose
four different ways to generate a set of base cluster-
ings and two different ways to combine the set into a
consensus clustering.
Li, H. and Jeremic, A.
Distributed Clustering using Semi-supervised Fusion and Feature Reduction Preprocessing.
DOI: 10.5220/0006658002330239
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 4: BIOSIGNALS, pages 233-239
ISBN: 978-989-758-279-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
233

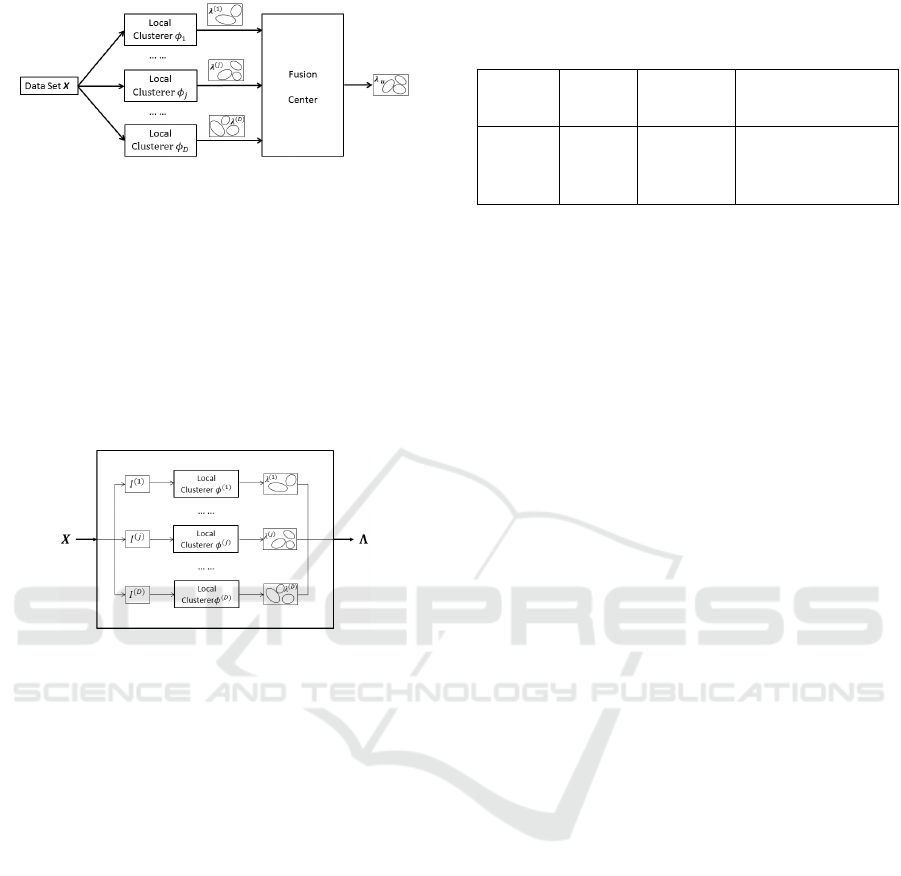
Figure 1: Distributed clustering system.
2.1 Base Clustering Generation
In this paper, the term clusterer represent the process-
ing unit that produces cluster labels for the given data
input. The set of D local clusterers (Fig. 1) is viewed
as a black box, which takes data set X as the input
and produces a set of base clusterings as the output.
We name it as the base clustering generator Φ (BCG).
The internal structure of base clustering generator is
shown in Fig. 2.
Figure 2: Base clustering generator with D local clusterers.
As a preliminary approach we apply K-means al-
gorithm in each local clusterer. In practice, different
clustering algorithms can be implemented in the local
clusterers to generate base clusterings. In order to de-
scribe the setting of base clustering generator, we first
define some necessary parameters as follow:
• φ
( j)
: j-th local clusterer
• D: total number of local clusterers in Φ
• I
( j)
: input of local clusterer φ
( j)
• λ
( j)
: output of local clusterer φ
( j)
• K
( j)
: number of clusters in λ
( j)
One possible way to design the base clustering
generator is to build D identical local clusterers and
apply the same clustering algorithm with different ini-
tializations in each local clusterer. We set D = 21
and denote this base clustering generator as Φ
1
. The
set of base clusterings generated by Φ
1
is named as
“BASE1”. The parameter settings of Φ
1
is listed
in Table 1. In this design, the clustering processes
are distributed over different local clusterers. The
advantage is that each local clusterer has the access
to the entire data matrix and generates base cluster-
ings based on all the information. In the literature,
Table 1: Base clustering generators: X represents the input
data matrix, F represents the number of features (columns)
of X, and x
( j)
represents the j-th feature (column) of X.
Base
Set Name
No. of Local Local Clusterer φ
( j)
Clustering Clusterers Input No. of Clusters
Generator (D) (I
( j)
) (K
( j)
)
Φ
1
BASE1 21 X K
( j)
= K
0
Φ
2
BASE2 F x
( j)
K
( j)
= K
0
Φ
3
BASE3 21 X K
( j)
∈ [K
0
,40]
Φ
4
BASE4 F x
( j)
K
( j)
∈ [K
0
,40]
many clustering ensemble methods are evaluated by
generating base clusterings in this way (Strehl and
Ghosh, 2003),(Fred and Jain, 2005),(Visalakshi and
Thangavel, 2009).
Another way to design the base clustering gener-
ator is to apply clustering algorithm to only one of
the data features in each local clusterer. For a data set
containing F features, there are D = F local clusterers
in the generator. We denote this base clustering gen-
erator as Φ
2
and the set of base clusterings generated
by this generator as “BASE2”. The parameter settings
of Φ
2
is listed in Table 1. In this design, data features
are distributed over different local clusterers. Each lo-
cal clusterer only has the access to one of the features
and partitions data points from a specific aspect of the
data. It is suitable for data sets whose features are
measured in diverse scales. It is also suitable for data
sets whose features are heterogeneous or categorical
when the dissimilarity measure based on all features
does not have a real meaning. Furthermore, the afore-
mentioned approach may be the only choice when the
features or attributes of the data set are not shareable
between organizations due to privacy, ownership or
other reasons.
Note that recently proposed MCLA algorithm
(Strehl and Ghosh, 2003) is also based on clustering
clusters. Similar clusters (from different clusterings)
are grouped together to form a meta-cluster, which is
finally collapsed into a consensus cluster. Intuitively,
it is easier to identify similar clusters with less num-
ber of data points. Therefore, we modify base cluster-
ing generator Φ
1
and Φ
2
by setting K
( j)
to relatively
larger integers. Due to the fact that optimal value of
K
( j)
is data dependent and to avoid the selection of
a suitable value for K
( j)
, we propose to randomly se-
lect an integer value for K
( j)
of each local clusterer.
The parameter settings of the modified base cluster-
ing generators Φ
3
and Φ
4
are also listed in Table 1.
The sets of base clusterings generated by the modified
generators are denoted as “BASE3” and “BASE4” re-
spectively.
Suppose the input data set X is the combination of
a training set X
r
and a testing set X
u
. The training set
X
r
contains data points {x
1
,. ..,x
N
r
}, for which labels
are provided in a label vector λ
r
. The testing data set
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
234

X
u
contains data points {x
N
r
+1
,. ..,x
N
}, the labels of
which are unknown. The consensus cluster label vec-
tor (output of SEA) of testing set X
u
is denoted by λ
u
.
The size of training set X
r
is measured by the number
of data points in the training set and denoted by N
r
,
i.e., |X
r
| = N
r
. Similarly, the size of testing set X
u
is measured by the number of data points in the test-
ing set and denoted by N
u
, i.e., |X
u
| = N
u
. Accord-
ing to the training and testing sets, the label matrix
F can be partitioned into two block matrices F
r
and
F
u
, each of which contains all the labels correspond-
ing to the data points in the training set X
r
and testing
set X
u
respectively. Suppose training data points be-
long to K
0
classes and all training points from the k-th
class form one cluster, denoted by C
k
r
(k = 1,...,K
0
).
Therefore, the training set X
r
consists of a set of K
0
clusters {C
1
r
,. ..,C
k
r
,. ..,C
K
0
r
}. If the size of cluster C
k
r
is denoted by N
k
r
, the total number of training points
equals to the sum of N
k
r
, i.e., N
k
r
=
∑
K
0
k=1
N
k
r
. We re-
arrange label matrix F
r
to form K
0
block matrices:
[F
1
r
,. ..,F
k
r
,. ..,F
K
0
r
]. Each block matrix F
k
r
con-
tains the base cluster labels of data points in the k-th
training cluster C
k
r
.
The SHSEA is defined as follows: (1) for a par-
ticular data point count the number of agreements be-
tween its label and the labels of training points in each
training cluster, according to an individual base clus-
tering (2) calculate the association vector between this
data point and the corresponding base clustering, (3)
compute the average association vector by averaging
the association vectors between this data point and all
base clusterings and (4) repeat for all data points and
derive the soft consensus clustering for the testing set.
Since the overall consensus cluster labels are derived
from the fuzzy(soft) label matrix, we name this ap-
proach as the soft-to-hard semi-supervised clustering
ensemble algorithm (SHSEA).
According to the j-th clustering λ
( j)
, we compute
the association vector a
( j)
i
for the i-th unlabelled data
point x
i
, where i = 1,...,N
u
and j = 1,...,D. Since
there are K
0
training clusters, the association vector
a
( j)
i
has K
0
entries. Each entry describes the asso-
ciation between data point x
i
and the corresponding
training cluster. The k-th entry of the association vec-
tor a
( j)
i
is measured as the occurrence of cluster label
of data point x
i
among the labels of reference data
points in the k-th training cluster (according to base
clustering λ
( j)
), i.e.,
a
( j)
i
(k) =
occurrence of F
u
(i, j)in F
k
r
(:, j)
N
k
r
, (1)
where F
u
(i, j) represents the cluster label of data
point x
i
and F
k
r
(:, j) represents the labels of reference
points in the k-th training category generated accord-
ing to base clustering λ
( j)
. In order to fuse the set
of base clusterings, the weighted average association
vector a
i
of data point x
i
is computed by averaging D
association vectors a
( j)
i
, i.e.,
a
i
=
D
∑
j=1
ω
j
a
( j)
i
, (2)
where ω
j
is the corresponding weight of the j-th lo-
cal clusterer. When local clusterers are equally impor-
tant, ω
j
= 1/D. Each entry of a
i
describes the overall
association between data point x
i
and the correspond-
ing training cluster. As a consequence, the summation
of all the entries of a
i
could be used to describe the
association between data point x
i
and all the training
clusters quantitatively. We define it as the association
level of data point x
i
to all training clusters and denote
it as γ
i
, i.e.,
γ
i
=
K
0
∑
k=1
a
i
(k). (3)
By computing association level for all data observa-
tions, the association level vector γ
u
for the testing set
X
u
is made up by stacking association level γ
i
for all
i = 1,...,N
u
, i.e., γ
u
= [γ
1
,γ
2
,. ..,γ
N
u
]
T
. We have two
options to present the overall consensus clustering for
testing set X
u
. One option is to produce a soft consen-
sus label matrix Λ
u
. The i-th row of Λ
u
is computed
by normalizing the average association vector a
i
, i.e.,
Λ
u
(i,:) = a
T
i
/γ
i
. (4)
The other option is to produce a hard consensus la-
bel vector λ
u
. The consensus cluster label assigned
to each data point is its most associated category la-
bels in the corresponding average association vector.
Since the overall hard cluster labels are assigned ac-
cording to the soft label matrix, we name this algo-
rithm as the soft-to-hard semi-supervised clustering
ensemble algorithm (SHSEA). The normalized soft
consensus label matrix (Λ
u
) can be used as the out-
put of the algorithm.
Following the naming convention, the other
semi-supervised ensemble method is called hard-to-
hard semi-supervised clustering algorithm (HHSEA),
since the overall cluster labels are assigned based on
hard label matrix. The HHSEA is defined as follows:
(1) for a particular data point count the number of
agreements between its label and the labels of train-
ing points in each training cluster, according to an in-
dividual base clustering, (2) calculate the association
vector between this data point and the corresponding
base clustering, (3) assign this data point to its most
associated cluster label (4) repeat for all data points
Distributed Clustering using Semi-supervised Fusion and Feature Reduction Preprocessing
235

and all base clusterings to relabel the labels in ma-
trix F
u
and (5) apply majority voting to derive hard
consensus clustering. The details of both SHSEA
and HHSEA are given in our previous work (Li and
Jeremi
´
c, 2017).
3 NUMERICAL EXAMPLES
In this section, we evaluate the performance of
the proposed distributed clustering system using the
breast cancer data cells. This data is used to study hu-
man breast cancer cells undergoing treatment of dif-
ferent drugs. The cancer cells are plated into clear-
bottom well plates and 10 types of treatments are
taken placed to the cells. Images of the untreated
and treated cells are captured using the high content
imaging system and processed by the CAFE (Clas-
sification and Feature Extraction of micro-graphs of
cells) software to extract useful information. In total
705 attributes/features per cell are recorded for further
analysis (Razeghi Jahromi, 2014).
Since the ground truth of class assignments for
each data set are available, we use micro-precision
(Modha and Spangler, 2003) as our metric to mea-
sure the accuracy of clustering result with respect to
the expected (true) labelling. Recall that data set X
contains N data points that belong to K
0
classes and
N
k
represents the number of data points in the k-th
cluster that are correctly assigned to the correspond-
ing class. Corresponding class here represents the
true class that has the largest overlap with the k-th
cluster. The micro-precision (MP) is calculated by
MP =
∑
K
0
k=1
N
k
/N. The data set that are used in this
paper are listed Table 2, including the number of data
points, features and classes. The available data points
are divided in testing and training sets (data points
with know reference labels).
Table 2: Data Information I: the number of data points, fea-
tures and classes.
Data Sets Data Points Features Classes
DataSet1 300 705 2
DataSet2 300 705 2
DataSet3 300 705 2
DataSet4 450 705 3
3.1 Data Pre-processing
Data pre-processing is a necessary step to improve the
results of cluster analysis (Liu and Motoda, 1998),
(Pyle, 1999). In practice, many data sets to be clus-
tered contain features that are measured in different
units and scales. Features measured in relatively large
scales may play a dominant role in the similarity mea-
sure and influence the accuracy of the clustering re-
sults. As a consequence, normalizing the features
is an important pre-processing procedure, especially
when the similarity measure is based on Euclidean
distances (de Souto et al., 2008). Min-max normaliza-
tion is a linear transformation of features into a spec-
ified range, which equalize the magnitude of the fea-
tures and prevents over weighting features measured
in relatively large scale over features measured in rel-
atively small scale. Suppose x
( f )
represents the f -th
feature of data set X. Let x
( f )
max
and x
( f )
min
represent the
maximum and minimum value of the f -th feature re-
spectively. Min-max normalization maps the f -th fea-
ture into range [0, 1] by
x
( f )
Norm
=
x
( f )
− x
( f )
max
x
( f )
max
− x
( f )
min
. (5)
In this paper, we demonstrate the effect of normal-
ization in clustering ensemble methods by comparing
the clustering results using original data sets (without
any pre-processing) and normalized data sets.
3.2 Original Data Sets
To study the effect of base clusterings on clustering
ensemble problem, we generate four different sets of
base clusterings (BASE1 to BASE4) for each data
set. Note that base clustering generator F
1
is de-
signed based on the common way used in the litera-
ture to generate base clusterings (Strehl and Ghosh,
2003),(Wang et al., 2011),(Dudoit and Fridlyand,
2003),(Fred and Jain, 2005). To evaluate different
clustering ensemble methods, we apply the unsuper-
vised HGPA, CSPA, MCLA (Strehl and Ghosh, 2003)
and BCE (Wang et al., 2011) in the fusion center and
compare the performance to the proposed SHSEA and
HHSEA. Recall that the ratio of number of reference
data points (N
r
) to number of testing data points (N
u
)
is denoted by P. We set P = 25% in the experiments
and repeat each experiment 100 times to calculate the
average micro-precision.
The micro-precision of K-means clustering algo-
rithm using all original features is listed in Table 3.
The maximum and minimum micro-precision of K-
means using features individually are also listed in
Table 3. Among all 11 data sets maximum MP of
K-means using single feature is higher than MP of K-
means using all features. Recall that BASE1 set of
base clusterings is generated by repetitively applying
K-means to all features together, while BASE2 is gen-
erated by applying K-means to each feature individu-
ally. Therefore, we expect the micro-precision of en-
semble methods using BASE2 to be higher than that
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
236

Table 3: Micro-precision of K-means using all features and
single feature of original data.
Data Sets
Kmeans
All Features
Single Feature
Max Min
DWALabSet1 0.5033 0.7917 0.5000
DWALabSet2 0.5033 0.7233 0.5000
DWALabSet3 0.5367 0.7933 0.5000
DWALabSet4 0.3400 0.5642 0.3333
of BASE1 since BASE2 contains a certain number
of “better” base clusterings. In addition, the perfor-
mance of SHSEA using BASE2 is expected to be bet-
ter than HHSEA, since base clusterings with higher
MP are given larger weights in the consensus fusion
step. Furthermore, recall that BASE3 (BASE4) is
generated in the same way as BASE1 (BASE2) re-
spectively expect that K
( j)
(number of clusters in each
local clusterers) are set to be greater than K
0
(ex-
pected number of clusters). Therefore, we expect the
performance of SHSEA and HHSEA using BASE3
(BASE4) to be better than BASE1 (BASE2), since
the proposed semi-supervised methods are expected
to perform better when data points are divided into
smaller groups.
The micro-precision of our proposed system
(four unsupervised and two semi-supervised ensem-
ble methods) using four sets of base clusterings
(BASE1 to BASE4) is illustrated by sub-figure (a) of
Fig. 3 to Fig. 6. The performance of SHSEA and HH-
SEA is represented by series SH(P25) and HH(P25)
respectively and P25 means the ratio of reference and
testing points is P = 25%. Among four groups of
clustering results, the bar corresponding to the high-
est average MP of the unsupervised ensemble meth-
ods and the bars corresponding to the highest MP of
SHSEA and HHSEA are labelled in each chart. It
is clear that the performance of the proposed semi-
supervised methods conforms with our expectations.
Compared to the micro-precision of K-means al-
gorithm (Table 3), the clustering results has been im-
proved by both operational modes of the proposed
system. The performance of the semi-supervised
mode is better than the unsupervised mode (except
“DataSet1”). The winning set of base clusterings is
either BASE2 or BASE4. In all the example the best
performance is achieved by utilizing SHSEA.
To study the effect of quantity of reference points
on semi-supervised clustering ensemble methods, we
repeat the experiments in semi-supervised mode by
selecting different numbers of reference points, i.e.,
by varying the value of P in N
r
= P · N
u
. Compared
to the performance of K-means (Table 3), micro-
precision of SHSEA or HHSEA increases dramati-
cally when P is relatively small. It becomes steady
and sometimes starts to decrease as P increases.
Therefore, for the purpose of improving the perfor-
mance of semi-supervised ensemble algorithms may
not be beneficial to label more data points. It is due
to the facts that more reference points do not guaran-
tee the improvement and obtaining additional labels
is time-consuming and expensive.
Recall that the number of clusters in the j-th base
clustering K
( j)
is randomly generated in the base clus-
tering generator Φ
3
and Φ
4
. To study the effect of
randomized K
( j)
on the clustering ensemble methods,
we repeat the experiments by setting the number of
clusters in each base clustering the same and varying
the value of K
( j)
. Among these data sets, the high-
est MP occurs at different K
( j)
. The performance of
the proposed system using randomized K
( j)
is either
the best of all tested values of K
( j)
or it is very closed
to best. Due to the fact that we lack the knowledge
on how to select the optimal K
( j)
, we use randomized
K
( j)
in the following experiments to avoid the selec-
tion of K
( j)
for each data set.
3.3 Normalized Data Sets
The micro-precision of K-means using all normal-
ized features and normalized features individually is
shown in Table 4. The performance of K-means using
all features has been improved significantly by nor-
malization except the first three data sets, as compared
to Table 3. As discussed earlier the performance of
distance-based clustering algorithms may be affected
when data sets to be clustered contains features mea-
sured in diverse scales. By investigating features of
each data set, we noticed that the data sets contain fea-
tures measured in quite different ranges. Moreover,
the performance of K-means using normalized fea-
tures individually is similar to the performance of K-
means using original features individually. This result
is expected since similarity measure for single feature
is based on 1-dimensional distance calculation and it
is invariant to the feature scales.
Table 4: Micro-precision of K-means using all features and
single feature or normalized data.
Data Sets
Kmeans
All Features
Single Feature
(Normalized) Max Min
DWALabSet1 0.6628 0.7920 0.5000
DWALabSet2 0.5609 0.7233 0.5000
DWALabSet3 0.6120 0.7933 0.5000
DWALabSet4 0.5058 0.5644 0.3333
To study the effect of normalization on clustering
ensemble methods, we repeat the experiments previ-
ously described in Section 3.2 using normalized data
sets. The micro-precision of the proposed system is
illustrated by sub-figures (b) of Fig. 3 to Fig. 6.
Distributed Clustering using Semi-supervised Fusion and Feature Reduction Preprocessing
237

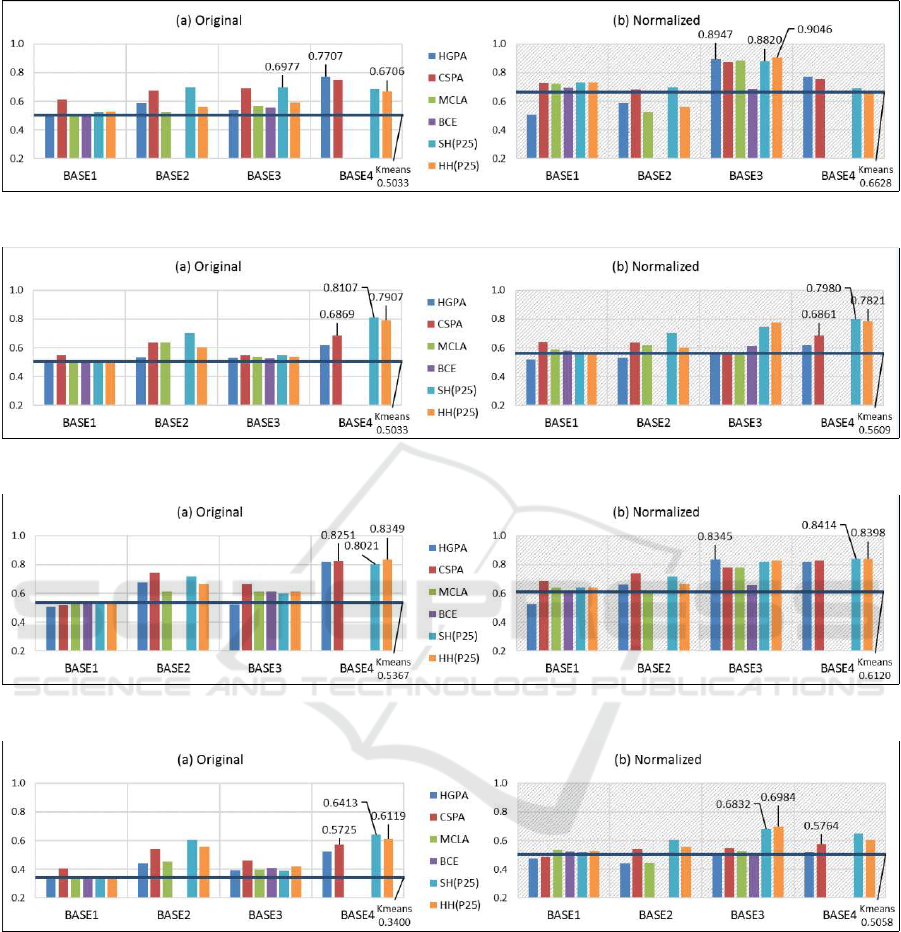
Figure 3: Data Set: DWALabSet1.
Figure 4: Data Set: DWALabSet2.
Figure 5: Data Set: DWALabSet3.
Figure 6: Data Set: DWALabSet4.
Note that the system performance using BASE1 and
BASE3 has been improved by normalization, while
the system performance using BASE2 and BASE4
stays close to the system performance using the corre-
sponding sets of base clusterings obtained by cluster-
ing original data sets. It is also expected since normal-
ization does not affect the performance of K-means
using single feature. Overall it can be observed that
the performance of SHSEA is very close to the per-
formance of HHSEA using normalized data.
4 CONCLUSIONS
In this paper we have proposed semi-supervised clus-
tering ensemble algorithms based on utilizing labelled
training data to improve the clustering results. We
designed four different ways to generate base clus-
terings and two ways to fuse them in the fusion cen-
ter with supervision. We provided numerical exam-
ples to demonstrate the effect of base clusterings on
the clustering ensemble methods and the performance
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
238

of semi-supervised clustering algorithms. We also
demonstrated the effect of normalization in the clus-
tering ensemble. In the future, we will focus on uti-
lizing the supervision information in both steps of the
clustering ensemble methods.
REFERENCES
Chapelle, O., Sch
¨
olkopf, B., Zien, A., et al. (2006). Semi-
supervised learning.
de Souto, M. C., de Araujo, D. S., Costa, I. G., Soares,
R. G., Ludermir, T. B., and Schliep, A. (2008). Com-
parative study on normalization procedures for clus-
ter analysis of gene expression datasets. In 2008
IEEE International Joint Conference on Neural Net-
works (IEEE World Congress on Computational In-
telligence), pages 2792–2798. IEEE.
Dudoit, S. and Fridlyand, J. (2003). Bagging to improve the
accuracy of a clustering procedure. Bioinformatics,
19(9):1090–1099.
Fred, A. L. and Jain, A. K. (2005). Combining multiple
clusterings using evidence accumulation. IEEE trans-
actions on pattern analysis and machine intelligence,
27(6):835–850.
Iqbal, A. M., Moh’d, A., and Khan, Z. (2012). Semi-
supervised clustering ensemble by voting. arXiv
preprint arXiv:1208.4138.
Jain, A. K. and Dubes, R. C. (1988). Algorithms for clus-
tering data. Prentice-Hall, Inc.
Li, H. and Jeremi
´
c, A. (2017). Semi-supervised distributed
clustering for bioinformatics - comparison study. In
BIOSIGNALS 2017, pages 649–652.
Liu, H. and Motoda, H. (1998). Feature extraction, con-
struction and selection: A data mining perspective.
Springer Science & Business Media.
Modha, D. S. and Spangler, W. S. (2003). Feature weighting
in k-means clustering. Machine learning, 52(3):217–
237.
Pyle, D. (1999). Data preparation for data mining, vol-
ume 1. Morgan Kaufmann.
Razeghi Jahromi, M. (2014). FRECHET MEANS OF RIE-
MANNIAN DISTANCES: EVALUATIONS AND AP-
PLICATIONS. PhD thesis.
Strehl, A. and Ghosh, J. (2003). Cluster ensembles—
a knowledge reuse framework for combining multi-
ple partitions. The Journal of Machine Learning Re-
search, 3:583–617.
Vega-Pons, S. and Ruiz-Shulcloper, J. (2011). A survey of
clustering ensemble algorithms. International Jour-
nal of Pattern Recognition and Artificial Intelligence,
25(03):337–372.
Visalakshi, N. K. and Thangavel, K. (2009). Impact of nor-
malization in distributed k-means clustering. Interna-
tional Journal of Soft Computing, 4(4):168–172.
Wang, H., Shan, H., and Banerjee, A. (2011). Bayesian
cluster ensembles. Statistical Analysis and Data Min-
ing, 4(1):54–70.
Xu, R. and Wunsch, D. (2008). Clustering, volume 10. John
Wiley & Sons.
Distributed Clustering using Semi-supervised Fusion and Feature Reduction Preprocessing
239