
Removing Monte Carlo Noise with Compressed Sensing and Feature
Information
Changwen Zheng
1
and Yu Liu
1,2
1
Institute of Software, Chinese Academy of Sciences, Beijing, China
2
University of Chinese Academy of Sciences, Beijing, China
Keywords:
Adaptive Rendering, Compressed Sensing, Ray Tracing, Cross-bilateral Filter.
Abstract:
Monte Carlo renderings suffer noise artifacts at low sampling rates. In this paper, a novel rendering algorithm
that combines compressed sensing (CS) and feature buffers is proposed to remove the noise. First, in the
sampling stage, the image is divided into patches that each one corresponds to a fixed resolution. Second, each
pixel value in the patch is reconstructed by calculating the related coefficients in a transform domain, which is
achieved by a CS-based algorithm. Then in the reconstruction stage, each pixel is filtered over a set of filters
that use a combination of colors and features. The difference between the reconstructed value and the filtered
value is used as the estimated reconstruction error. Finally, a weighted average of two filters that return the
smallest error is computed to minimize output error. The experimental results show that the new algorithm
outperforms previous methods both in visual image quality and numerical error.
1 INTRODUCTION
Monte Carlo renderings produce photorealistic im-
ages through the distributed samples that correspond
to light paths in multidimensional space. Pixel value
is then computed by integrating light paths that reach
it. However, a large number of samples are typically
required to converge to the actual value of the integral,
otherwise considerable noise, i.e., variance, is gener-
ated. While a vast body of variance reduction tech-
niques have been proposed, adaptive sampling and re-
construction are two effective techniques to remove
noise.
Adaptive sampling refers to techniques that con-
centrate more samples on difficult regions. Typi-
cally, a robust metric is needed to measure the per-
pixel error. Reconstruction algorithms, in contrast,
use suitable filters to denoise from the obtained sam-
ples. These two techniques are usually coupled under
an iterative framework, where the reconstruction error
determines the sampling rates. The key issue is how
to select a suitable filter kernel for each pixel, as the
optimal reconstruction kernels are usually spatially-
varying. Recently, the use of feature buffers facilitates
the computation of filter weights. Novel features such
as surface normal, albedo color, depth, and visibil-
ity are typically less noisy than the output of Monte
Carlo renderer, and they often contain rich informa-
tion about the scene details. With these feature infor-
mation, many approaches have been developed to im-
prove image quality. Li et al. (Li et al., 2012), for in-
stance, calculate the reconstruction error through the
Steins unbiased risk estimator (SURE), and then se-
lect the optimal kernel among a discrete set of filters.
Rousselle et al. (Rousselle et al., 2013) carefully de-
sign three filters with different parameters to make a
trade-off between noise reduction and detail fidelity.
They compute a weighted average of the candidate
filters for output. However, these feature-based meth-
ods typically need sophisticated error analyses such
as SURE estimator, which are unreliable at low sam-
pling rates. In addition, they are prone to blurring
structure details that are not well represented by the
features.
Most recently, there has been a growing interest in
Compressed Sensing (CS), which states that a signal
can be well reconstructed if the signal is sparse in a
transform domain. The main advantage of CS over
conventional Nyquist-Shannon sampling theorem is
that its sampling rate only depends on the sparsity of
the signal in the transform basis, rather than on its
band-limit. A novel approach that employs the CS is
proposed by Sen et al. (Sen and Darabi, 2011). They
first render only a subset of pixels and then estimate
the missing ones by leveraging CS solvers such as
Regularized Orthogonal Matching Pursuit (ROMP).
Zheng, C. and Liu, Y.
Removing Monte Carlo Noise with Compressed Sensing and Feature Information.
DOI: 10.5220/0006671601450153
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 1: GRAPP, pages
145-153
ISBN: 978-989-758-287-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
145

Although their impressive performance at accelerat-
ing the renderings, the image quality is not compet-
itive with those feature-based methods. Meanwhile,
fine details such as textures are hard to be preserved
since the rendered pixels can also be noisy.
In this paper, a novel rendering algorithm that
combines CS and feature information is proposed. By
assuming that the image is sparse in a transform do-
main, we divide the image into patches with a fixed
resolution, and use an advanced CS solver to recon-
struct the pixel values in each patch. Each pixel
is then filtered over a set of discrete filters, where
the difference between the filtered value and recon-
structed value is used as pixel error. Especially, un-
like previous methods that select one single filter for
output, two filters with the smallest errors are care-
fully chosen and a weighted average value is com-
puted to minimize the output error. Finally, a heuris-
tic metric is directed to allocate more samples in re-
gions with higher error. Experiments show that the
new method produces visually pleasing results over
previous methods.
2 RELATED WORK
To obtain high-quality images with sparse samples,
many types of adaptive sampling and reconstruction
algorithms have been proposed. Typically, there are
two efficient categories to address these methods:
image and multidimensional space rendering.
Image Space Rendering. Image space rendering
has been a popular approach since it is simple while
effective. As the rich information of details are easy
to save from most rendering systems, image space
methods estimate per-pixel error with various criteria.
Many approaches achieved significant improvements
by using multi-scale filters. Rousselle et al. (Rous-
selle et al., 2011), for instance, used several Gaussian
filters to form a filter bank, and then performed an
error minimization framework to select the optimal
one. However, it was limited to symmetric kernels.
A similar work was proposed by Chen et al. (Lehti-
nen et al., 2011). Based on the depth buffer, they se-
lected appropriate Gaussian filter to improve the ef-
fect of depth-of-field. By applying features that are
less noisy than pixel colors, many novel filters yield
impressive results. Li et al. (Li et al., 2012) com-
puted the Steins Unbiased Risk Estimator (SURE) to
estimate the errors of filtered values, where the sin-
gle filter that returned the smallest error was selected.
Rousselle et al. (Rousselle et al., 2013) designed three
candidate filters to make a trade-off between detail fi-
delity and noise reduction. They also used the SURE
estimator to compute a weighted average of candidate
filters to minimize pixel error. However, some fine
details tend to be over smoothed. Sen et al. (Sen and
Darabi, 2012) analyzed the functional relationships
between inputs and outputs, and then used this infor-
mation to reduce the importance of samples affected
by noise. Rousselle et al. (Rousselle et al., 2012)
adopted the Non-local means filter to spilt samples
into two buffers, where the difference between these
two buffers was treated as an error estimate. Moon
et al. (Moon et al., 2014) applied local weighted re-
gression to derive an error analysis. Besides, they also
built multiple linear models (Moon et al., 2015) to es-
timate the reconstruction errors. Noticing that there
is a complex relationship between the ideal parame-
ters and the noisy scene data, Kalantari et al. (Kalan-
tari et al., 2015) proposed to train a neural network to
drive suitable filters. In addition, they also enabled the
use of any spatially-invariant image denoising tech-
niques in Monte Carlo rendering (Kalantari and Sen,
2013). Moon et al. (Moon et al., 2013) constructed
an edge-stopping function with a virtual flash image,
which enabled that only statistically equivalent pix-
els were considered together. Most recently, Bako et
al. (Bako et al., 2017) further used a convolutional
neural network to improve image details. Readers are
encouraged to read Zwicker et al. (Zwicker et al.,
2015) work, which gave a detailed description for re-
cent image-space methods.
Multidimensional Space Rendering. Multidimen-
sional approaches typically consider the information
in a high dimensional space, which is not accessi-
ble for most image space methods. Hachisuka et al.
(Hachisuka et al., 2008) designed the structure ten-
sors to reconstruct samples anisotropically. By work-
ing in wavelets rather than pixels, Overbeck et al.
(Overbeck et al., 2009) proposed to sample features
that have high variance in other dimensions. Lehtinen
et al. (Lehtinen et al., 2011) introduced a visibility-
aware reconstruction process to support indirect illu-
mination. However, these approaches are less effi-
cient as the number of dimensions increases. Based
on the work of Durand et al. (Durand et al., 2005),
many approaches have been developed to focus on
specific distributed effects such as motion blur (Egan
et al., 2009) and depth of field (Soler et al., 2009).
Compressed Sensing in Monte Carlo Rendering.
In general, Compressed Sensing is related to the ap-
proaches that explore the sparsity in a transform do-
main. Egan et al. (Egan et al., 2009) revealed that
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
146

Figure 1: The framework of our algorithm.
motion lead to a shear in the transform domain, and
they introduced a sheared reconstruction filter to re-
duce the sampling rates. Sen et al. (Sen and Darabi,
2011) first introduced the idea of accelerating Monte
Carlo renderings with CS. They ray-traced only a sub-
set of pixels selected by a Poisson-disk distribution,
which provided a speedup over conventional tech-
niques. The missing pixels were then estimated by
a CS solver. Besides, they noticed that the sparsity
of signal goes up as the dimensionality of signal in-
creases. In these cases, high dimensional effects such
as motion blur and depth of field are improved by inte-
grating down to obtain the final image. However, this
method has difficulty in simulating scenes with very
complex details, and is not competitive with those ap-
proaches using feature buffers. Most recently, CS is
also employed to reduce noise artifacts in direct PET
image reconstruction (Vaquer et al., 2016) and the
memory footprint for the scalar flux (Dominik et al.,
2014).
3 COMPRESSED SENSING
Although compressed sensing is not new to computer
graphics, it is rarely applied to improve the quality of
Monte Carlo Renderings. The key idea of compressed
sensing is that a signal can be perfectly reconstructed
if it is sparse in a transform domain. Assuming that
there is a N-dimensional signal x which is to be re-
constructed from M-dimensional sampling signal y,
the CS states that the sampling process is written as:
y = Φx (1)
Where Φ is a M ×N sampling matrix (M < N). In this
paper, the image is divided into patches with a fixed
resolution of
√
N ×
√
N, and each patch performs a
single process of calculating the reconstructed values.
In other words, the local statistics of N pixels is esti-
mated by M pixels.
Typically, it is impossible to reconstruct x from y
with the previous Nyquist-Shannon theorem, because
the band-limit is not met. However, since the CS as-
sumes that x is K-sparse in a transform domain, the
coefficients of x in a transform domain are written as:
θ = Ψ
−1
x (2)
Where Ψ is the N ×N transform basis (or compres-
sion basis). In this case, θ has at most K non-zero
values, which is called the sparsity of the signal in the
compressed basis. Consequently, it is able to elimi-
nate many elements that do not have sparse proper-
ties, and the sampling equation is written as:
y = Φx = ΦΨθ = Aθ (3)
Where A = ΦΨ is a M × N measurement matrix.
Given y and A, θ should be reconstructed if the above
linear system could be solved. Unfortunately, previ-
ous methods such as least squares failed to do this
because M < N and thus the system is undetermined.
In this case, CS algorithms solve the system correctly
as long as some constraints are met. One is that the
sampling number M is twice larger than the sparsity of
the signal (M > 2K). Another one is that the measure-
ment matrix A meets the Restricted Isometry Condi-
tion (RIC), which requires that the sampling matrix
and compressed basis should be incoherent. As K is
usually much smaller than N, less efforts are taken for
CS to reconstruct the original signal. Pay attention to
the formation of x. As the original patch is composed
of
√
N ×
√
N pixels, we keep track of them with a col-
umn vector of size N ×1, and solve the linear system
for each patch uniquely.
The main challenge is how to select a suitable
sampling matrix Φ and a compressed basis Ψ. There
are many choices such as Gaussian sampling ma-
trix and Bernoulli sampling matrix. Here, since
the Gaussian matrix is uncorrelated with most com-
pressed bases, it is adopted to construct Φ, where
each element of Φ accords with a normal distribution
N(0,
1
M
). Besides, Gaussian sampling matrix avoids
the extra sharpening procedure, which is used by Sen
et al. (Sen and Darabi, 2012) as they used a Poisson-
disk distribution to produce y. For the compressed
basis, Discrete Cosine Transform (DCT) is adopted
Removing Monte Carlo Noise with Compressed Sensing and Feature Information
147

in this paper as it outperforms in image processing ar-
eas.
To solve Equation 3, many fast CS algorithms
have been proposed to find an approximate solution.
Herein, we employed the Orthogonal Matching Pur-
suit (OMP) since it is simple while effective. The
key idea of OMP is to find the representative columns
(atoms) of A that are most related with the sampling
signal y. In this paper, we do not explain OMP details
since it has been widely used, and we just use it to
solve Eq. (3). Readers are encouraged to read related
works for further information about OMP.
Once the linear system is solved, the reconstructed
values can be computed through an inverse transform.
For our method, the reconstructed values are further
used to estimate per-pixel error, which finally directs
the selection of suitable filters.
4 ALGORITHM OVERVIEW
Adaptive rendering algorithms that use feature buffers
are extremely effective at removing noise, especially
for scenes that contain very complex details. How-
ever, previous methods usually perform sophisticated
error analyses such as SURE estimator to select an
appropriate filter, which is unreliable at low sampling
rates. In these cases, many fine details may be lost.
In this paper, the CS is applied to reconstruct pixel
values, which are then used to perform a robust error
analysis.
Our framework is illustrated in Fig. 1. An ini-
tial image x is first generated with a small number of
samples. The initial image is divide into patches with
a fixed resolution, and each patch constructs its sam-
pling signal y = Φx. Given the sampling signal y and
measurement matrix A, we calculate the coefficients
θ in the compressed basis through OMP algorithm,
and then take an inverse transform to reconstruct pixel
vales x = Ψθ. Intuitively, the reconstructed values re-
duce the coherence between pixels, and thus they are
less influenced by neighbors that have a different na-
ture.
After computing the reconstruct pixel values x
with OMP, each pixel is filtered over a discrete set of
filters with varying parameters to produce the candi-
date filtered value F (Sec.5). The difference between
x and the F is estimated as the pixel error. In gen-
eral, the potential filter bank is rather large that it is
intractable to find the optimal one. In this case, we
carefully choose two filters with the smallest errors,
and then compute a weighted average of them for out-
put. In particularly, the reconstructed values are pre-
filtered, which allows for producing smooth details.
Finally, if more sample budget is available, a heuristic
metric is proposed to allocate more samples in regions
with larger errors.
5 FILTER SELECTION
To combine pixel colors with feature buffers, the
Cross-bilateral weight is computed for each pixel, and
the filtered value of pixel p is computed as:
F(p) =
1
N(p)
∑
q∈w(p)
W (p,q)I(q) (4)
Where N(p) =
∑
q∈w(p)
W (p,q) is a normalization
factor. W (p,q) is the contribution of q contributes to
p. I(q) is the input pixel color for pixel q.
5.1 Feature Distance
In this paper, the surface normals, albedo colors and
depths are used to form the feature buffers, and the
feature weight between pixel p and q is computed as:
f
i
(p,q) = exp
−
D( f
ip
−f
iq
)
2
2σ
2
i
(5)
Where σ
i
denotes the standard deviation of the i fea-
ture and D( f
ip
− f
iq
) is the feature distance between
these two pixels. Since the distributed effects such as
motion blur may lead to noisy features, using the sam-
ple means of feature directly can result in inaccurate
results. Thus, a normalized distance is computed as:
D( f
ip
− f
iq
) =
s
|f
ip
− f
iq
|
2
−(var
ip
+ var
ipq
)
τ(var
ip
+ var
iq
)
(6)
Where f
ip
and var
ip
are the sample mean and vari-
ance of the i feature for pixel p, respectively. var
ipq
=
min(var
ip
,var
iq
) and τ is a user parameter that con-
trols the sensitivity of feature differences. Intuitively,
larger τ causes a more aggressive filtering. In particu-
larly, varying values of τ are designed for different fil-
ters in the filter bank, which make a balance between
sensitivity to noise and detail fidelity.
The advantages of our normalized distance are
twofolds: First, for a pixel with strong motion blur
or depth of field effects, large variances tend to be
generated. Thus D( f
ip
− f
iq
) is relatively small and
the filtering weight increases even when the fea-
tures are far apart. Second, a variance cancellation
term (var
ip
+ var
ipq
) is subtracted to remove the bias
caused by noisy features. Finally, the filter weight is
computed as:
W (p,q) = exp
−
|p−q|
2
2σ
2
s
exp
−
|I(p)−I(q)|
2
2σ
2
r
3
∏
i=1
f
i
(p,q) (7)
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
148

Figure 2: Feature buffer and the scale selection map. Our
approach make a nice trade-off between robustness to noise
and fidelity to image detail.
Where σ
s
and σ
r
are the stand deviation parameters
of the spatial and range kernels, respectively.
5.2 Filters Averaging
Previous methods typically choose a single filter from
the pre-defined filter bank for output. However, as
the potential size of the ground truth is very large, it
is intractable to select the optimal one. Furthermore,
choosing the appropriate parameters of filter bank for
different scenes is challenging. In this paper, this
problem is addressed by evaluating the errors of the
filtered colors on a per-pixel basis, which allows us to
obtain a better choice.
Assuming the reconstructed value using CS solver
at pixel p is interpreted as x
p
, the filtered error of the
i filter is estimated as:
Err
i
= 2
|x
p
−F
i
(p)|
F
i
(p) + ε
+ σ
2
p
(8)
Where F
i
(p) denotes the filtered value of pixel p using
the i filter in the filter bank. σ
2
p
is the sample variance
and ε is a small number to prevent division by zero.
Eq. 8 focuses on two issues. First, the difference be-
tween the filtered value F
i
(p) and reconstructed value
x
p
is estimated to measure the size of the optimal fil-
ter. Second, the variance term is considered to obtain
a more smooth result. For pixels with complex geom-
etry details, large scale filters produce a large differ-
ence term, and thus they lead to large errors. For sim-
ple pixels, however, the reconstructed values tend to
be smoother. In these situations, large scale filters re-
sult in small errors. In practice, we use the Y channel
of CIE1934(XYZ) color space to compute the filtered
error.
After calculating the filtered error of each candi-
date filter, a weighted average of two filters is com-
puted. For each pair of consecutive filters, the sum of
their cumulative error Err
i
+Err
i+1
is computed. The
single pair that returns the smallest value is selected.
Then, the weighted average is computed as:
F(p) =
∑
i+1
j=i
exp
−
Err
j
2
F
j
(p)
∑
i+1
j=i
exp
−
Err
j
2
(9)
Figure 3: Sampling density map.
Where i = arg min
i=1,2,...L−1
{Err
i
+ Err
i+1
} and L is
the size of filter bank. Finally, F(p) is used to update
pixel.
Fig. 2 demonstrates our scale selection map,
which is denoted by the i filter for each pixel. It is
obviously that our approach make a nice trade-off be-
tween robustness to noise and fidelity to image detail,
where small scale filters concentrate on complex re-
gions and large ones tend to be used in simple regions.
5.3 Adaptive Sampling
To perform the adaptive sampling process, the esti-
mated error is chosen as a feedback to direct the sam-
pling function:
S
p
=
1
2
(Err
i
+ Err
i+1
) + σ
2
p
F(p)
2
+ n
p
(10)
Where F(p)
2
is the squared luminance of the
weighted average value, and n
p
is the number of sam-
ples that have already been distributed in pixel p.
Thus, pixel p obtain kS
p
/(
∑
j
S
j
) samples if there are
k samples available. The sampling density map is
shown in Fig. 3. It shows that samples concentrate
on regions with complex details and more noise.
6 ANALYSES
Fig. 4 compares our method with global filters of
each scale. For small scale filters (scale = 0,1),
noise is hard to be removed. For large scale filters
(scale = 4,8), however, edge details on the window
are over smoothed. It is obviously that our method
make a nice trade-off between robustness to noise and
fidelity to image details.
Removing Monte Carlo Noise with Compressed Sensing and Feature Information
149
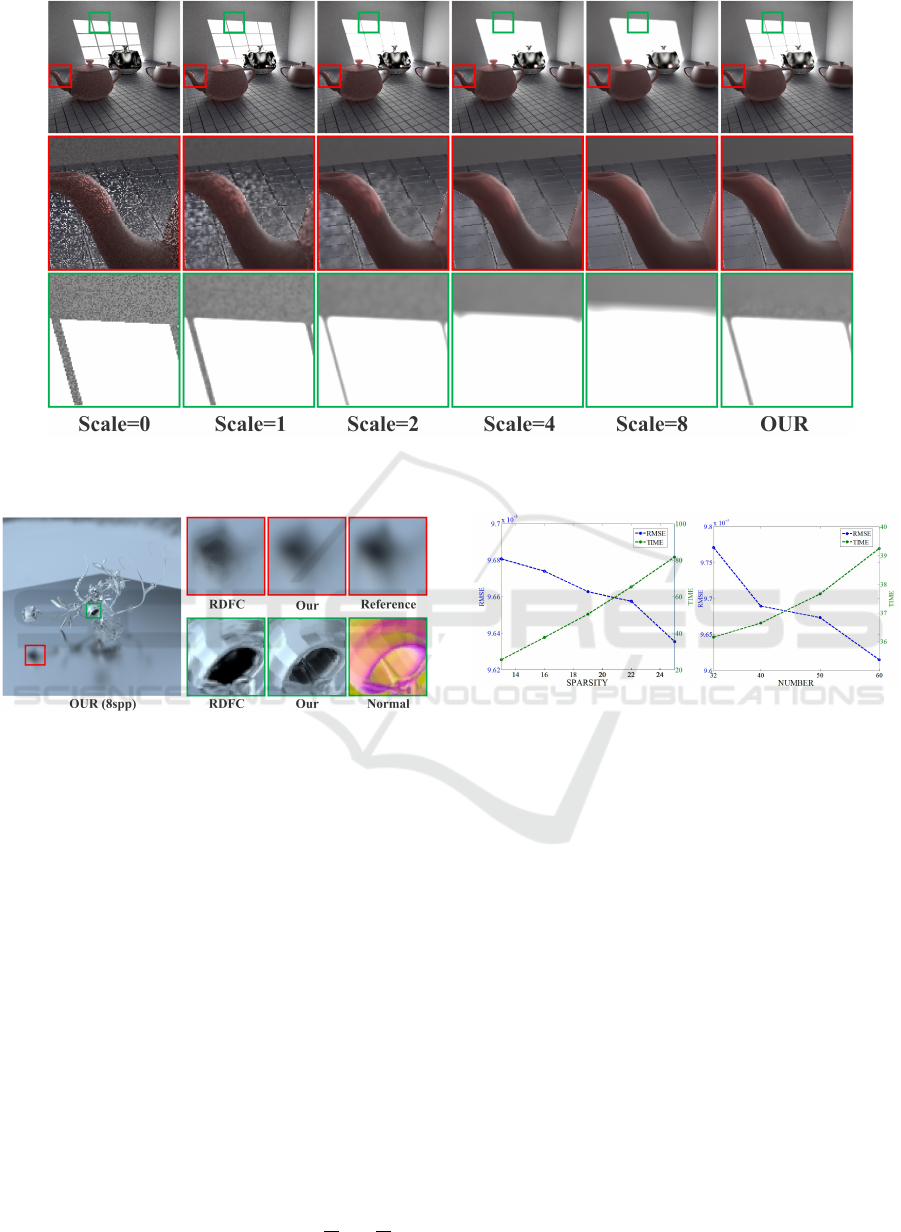
Figure 4: The comparison between our method and global filters. Our method adjusts filter scales in a consecutive manner
and removes noise while preserving details.
Figure 5: The comparison between our method and RDFC
method. RDFC does not estimate filter errors accurately at
low sampling rates and thus over blurs image details. Our
method returns a better result.
One key advantage of the new approach is the ro-
bustness of error analysis at low sampling rates. For
previous error estimators such as SURE, excessive
variance tends to be generated in the color buffer, and
thus they are unreliable at low sampling rates. In such
situations, edge details are hard to be preserved. Fig.
5 shows a scene with glossy materials. It is obvi-
ously that RDFC frequently shows ringing artifacts
caused by its inaccurate error estimation. The second
row of insets further highlights the contribution of our
CS framework. As the image is sparse in the trans-
form domain, the reconstructed values reduce the co-
herence between pixels greatly. Thus, the difference
between the filtered value and reconstructed value re-
turns a more reliable error estimation. Pay attention to
the structure edges, RDFC over blurs the details while
our method keeps the fidelity.
For the proposed approach, the image is divided
into patches with a fixed resolution of
√
N ×
√
N pix-
Figure 6: Visualizations of different sparsity values and
sampling numbers. Larger values lead to smaller errors,
however, more time is also needed.
els, and there are two key parameters to be deter-
mined: sparsity K and sampling number M. For the
current implementation, N is set to 64. The visual-
izations of these two parameters are shown in Fig. 6,
which uses the scene in Fig. 5. As shown in the figure,
large values for both parameters lead to smaller errors,
however, the time also increases greatly. For our cur-
rent implementation, K and M are set to 20 and 50
respectively, and the experimental results show that
they outperforms in most cases.
7 RESULTS
The proposed approach was implemented on the top
of PBRT-V2 (Pharr and Humphreys, 2010). The CS
framework was implemented in MATLAB2013 using
the paralleling computing toolbox and then integrated
into PBRT. All the images were rendered by an Intel
Core 2.4 GHz CPU with 8 GB of memory. In addi-
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
150

Figure 7: Comparisons between our method and previous methods. MC typically produces considerable noise. GEM removes
noise effectively, however, it tends to over blur images. RDFC presents visually pleasing results. Nonetheless, some fine
details may be lost at low sampling rates.
tion, we wrote a GPU-based Cross-bilateral filter to
accelerate the algorithm. For our method, the filter
bank was constructed with spatial-varying parameters
σ
s
= 0,1, 2,4,8 and τ = 0.125, 0.5,1,2, 5. The pa-
rameters of features were set as for σ
1
= 0.2 albedo,
σ
2
= 0.3 for depth and σ
3
= 0.4 for normal.
7.1 Scenes
We compared our method with three previous meth-
ods. The first one is the naive Monte Carlo method
(MC) that is available from PBRT render (Pharr and
Humphreys, 2010). The second method is the greedy
error minimization algorithm (GEM) proposed by
Rousselle et al. (Rousselle et al., 2011), and the
gamma parameter was set to 0.2 as suggested in the
Removing Monte Carlo Noise with Compressed Sensing and Feature Information
151
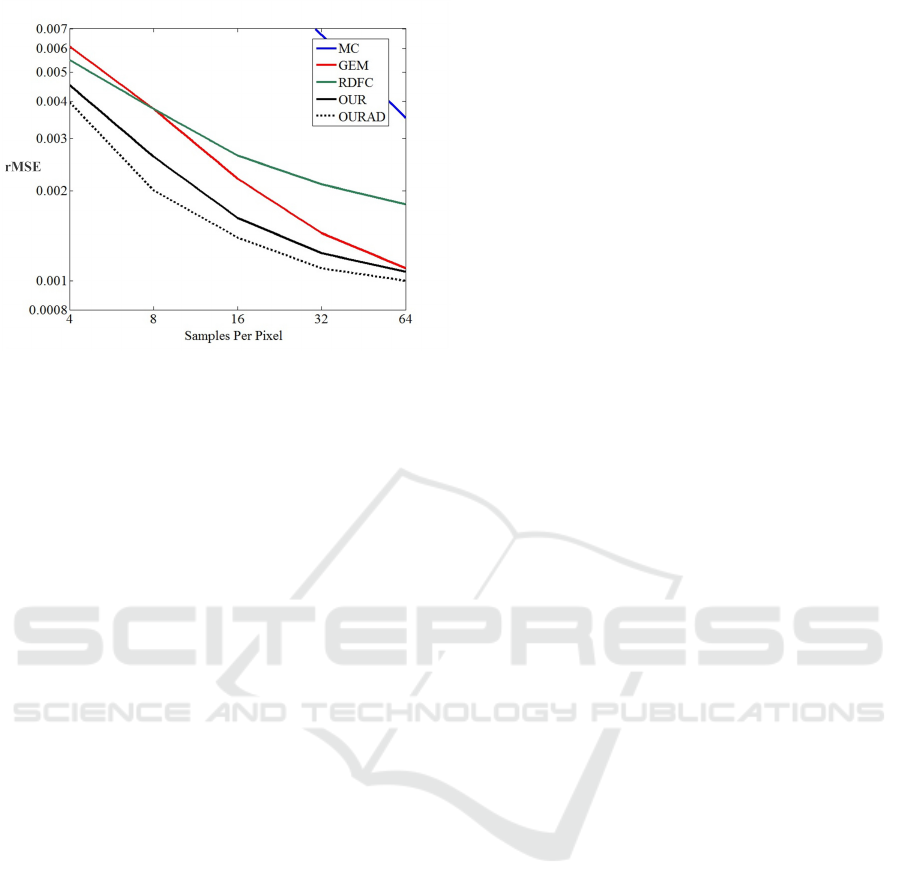
Figure 8: Convergence plots for different methods.
original paper. The last method is a feature-based
method (RDFC) (Rousselle et al., 2013). The win-
dow size was set to 10 and all the other parameters
were default values. For all of the tested scenes, both
visual image quality and relative MSE (rMSE) were
tested with the same sample number. We adopted the
rMSE proposed by Rousselle et al. (Rousselle et al.,
2011): (img −re f )
2
/(re f
2
+ε). re f is the pixel color
in the reference image, and ε = 0.01 is a small number
to prevent division by zero.
In Fig. 7, three scenes are compared and all the
images were rendered at a resolution of 800 ×800
pixels. The first ROOM-IGI scene is a challeng-
ing scene rendered by instant global illumination al-
gorithm, where most of the illumination is indirect.
The image produced by MC contains considerable
noise both on the wall and spout of the teapot. GEM
removes noise greatly on the wall, however, it fre-
quently presents splotches. RDFC returns clearer de-
tails, but it over blurs the edges on the floor. Besides,
RDFC also introduces visible artifacts on the window.
Compared with these methods, our method generates
a relatively noise-free image while faithfully preserv-
ing details.
The SANMIGUEL is a path-traced scene with
very complex geometries. Again, MC presents severe
noise, and GEM over blurs the textures because of the
symmetric kernels. Compared with MC and GEM,
RDFC preserves the structure details and removes the
noise. However, as the SURE-error estimation is in-
accurate at low sampling rates, some fine details are
lost. Meanwhile, the features are not weighted ap-
propriately by RDFC and thus it fails to keep the fine
details, while our method yields a smoother result and
preserves foliage details very well.
The DRAGONFOG scene includes many partic-
ipating media, and is rendered using PBRTs photon
mapper. GEM removes most noise on the smooth
regions, but it generates ambiguous details on the
mouth. Although RDFC and our method present the
visually equal results, we found that RDFC tends to
produce darker details for this scene and thus results
in a larger rMSE. Meanwhile, our result is closer to
the ground truth.
Fig. 8 presents the log-log convergence plots for
the dragonfog scene. We demonstrate the results
for naive Monte Carlo method (MC in blue), GEM
method (Rousselle et al., 2011) (GEM in red), RDFC
method (RDFC in green), our work using uniform
sampling (OUR in black), and our work with adap-
tive sampling (OURAD in dotted black). RDFC out-
performs GEM at low sampling rates. However, it
performs worse at high sampling rates since it tends
to produce darker details. Although higher sam-
pling number and sparsity could reduce the errors,
experimental results demonstrate that our current set-
tings are able to handle most cases. This figure
demonstrates that our CS-based weighted averaging
of candidate filters consistently returns pleasing re-
sults. Moreover, our adaptive sampling process fur-
ther reduces the rMSE.
7.2 Limitations
There are some limitations for the proposed algo-
rithm. First, the initial image is divided into patches
that each one corresponds to a fixed resolution. It lim-
its the quality of rendering results, where patches with
varying sizes are more suitable. Second, similar to
previous methods, filters based on features are prone
to blurring structure details that are not well repre-
sented by these features. Novel features such as caus-
tics, visibility and feature gradient help to further re-
move noise. Feature gradient, for instance, prevents
restrictive filter weights and preserves edge details.
For our current implementation, we only use surface
normal, albedo color and depth since they outperform
in most cases. Finally, little theoretically sound con-
tributions are presented for the compressed sensing.
Improvements on the sampling basis and compressed
basis can further improve the rendering quality.
8 CONCLUSIONS AND FUTURE
WORKS
A novel rendering algorithm has been presented to
address the noise artifacts of Monte Carlo rendering.
A robust error estimation procedure is proposed by
exploring the sparsity with compressed sensing theo-
rem. Pixel values are reconstructed in a transform do-
main, which returns a sparse nature and facilitates the
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
152

estimation of filter errors. We use a normalized dis-
tance to measure the difference between features and
then return more reasonable filter weights. To obtain
the optimal filter scale, two candidate filters are se-
lected to determine a weighted average value on a per-
pixel basis. Meanwhile, an iterative sampling process
is also adopted to distribute more samples in regions
with higher estimated errors. Through combining CS
results with feature information, our method provides
significant improvements both in visual and numeri-
cal quality.
This paper raises several interesting issues for our
future work. First, the sparsity of the image goes up as
the number of considered dimensions increases. This
allows us to explore the improvements of specific dis-
tributed effects such as depth of field and motion blur.
For example, by integrating samples along the dimen-
sion of time, motion blur is improved with pixel val-
ues reconstructed in the transform domain. Second, a
better transform basis that is more suitable for Monte
Carlo renderings should be directed through combin-
ing with recent advances in Compressed Sensing. In
addition, we intend to apply this work to related areas
such as wave rendering.
REFERENCES
Bako, S., Vogels, T., Mcwilliams, B., Meyer, M., Nov
´
aK,
J., Harvill, A., Sen, P., Derose, T., and Rousselle,
F. (2017). Kernel-predicting convolutional networks
for denoising monte carlo renderings. ACM Trans.
Graph., 36(4):97:1–97:14.
Dominik, R., Thomas C., B.-L., Thomas, K., and Andr, F.
(2014). Compressed sensing for reduction of noise
and artefacts in direct pet image reconstruction. Z.
Med. Phys, 24(1):16–26.
Durand, F., Holzschuch, N., Soler, C., Chan, E., and Sillion,
F. X. (2005). A frequency analysis of light transport.
ACM Trans. Graph., 24(3):1115–1126.
Egan, K., Tseng, Y.-T., Holzschuch, N., Durand, F.,
and Ramamoorthi, R. (2009). Frequency analysis
and sheared reconstruction for rendering motion blur.
ACM Transactions on Graphics (SIGGRAPH 09),
28(3).
Hachisuka, T., Jarosz, W., Weistroffer, R. P., Dale, K.,
Humphreys, G., Zwicker, M., and Jensen, H. W.
(2008). Multidimensional adaptive sampling and re-
construction for ray tracing. ACM Trans. Graph.,
27(3):33:1–33:10.
Kalantari, N. K., Bako, S., and Sen, P. (2015). A machine
learning approach for filtering monte carlo noise.
ACM Trans. Graph., 34(4):122:1–122:12.
Kalantari, N. K. and Sen, P. (2013). Removing the
noise in monte carlo rendering with general image
denoising algorithms. Computer Graphics Forum,
32(2pt1):93102.
Lehtinen, J., Aila, T., Chen, J., Laine, S., and Durand,
F. (2011). Temporal light field reconstruction for
rendering distribution effects. ACM Trans. Graph.,
30(4):55:1–55:12.
Li, T.-M., Wu, Y.-T., and Chuang, Y.-Y. (2012). Sure-
based optimization for adaptive sampling and recon-
struction. ACM Trans. Graph., 31(6):194:1–194:9.
Moon, B., Carr, N., and Yoon, S.-E. (2014). Adaptive
rendering based on weighted local regression. ACM
Trans. Graph., 33(5):170:1–170:14.
Moon, B., Iglesias-Guitian, J. A., Yoon, S.-E., and Mitchell,
K. (2015). Adaptive rendering with linear predictions.
ACM Trans. Graph., 34(4):121:1–121:11.
Moon, B., Jun, J. Y., Lee, J., Kim, K., Hachisuka, T., and
Yoon, S. (2013). Robust image denoising using a vir-
tual flash image for Monte Carlo ray tracing. Comput.
Graph. Forum, 32(1):139–151.
Overbeck, R. S., Donner, C., and Ramamoorthi, R. (2009).
Adaptive wavelet rendering. ACM Trans. Graph.,
28(5):140:1–140:12.
Pharr, M. and Humphreys, G. (2010). Physically Based
Rendering: From Theory to Implementation. Morgan
Kaufmann Publishers Inc., San Francisco.
Rousselle, F., Knaus, C., and Zwicker, M. (2011). Adaptive
sampling and reconstruction using greedy error mini-
mization. ACM Trans. Graph., 30(6):159:1–159:12.
Rousselle, F., Knaus, C., and Zwicker, M. (2012). Adaptive
rendering with non-local means filtering. ACM Trans.
Graph., 31(6):195:1–195:11.
Rousselle, F., Manzi, M., and Zwicker, M. (2013). Robust
Denoising using Feature and Color Information. Com-
puter Graphics Forum.
Sen, P. and Darabi, S. (2011). Compressive rendering: A
rendering application of compressed sensing. IEEE
Transactions on Visualization & Computer Graphics,
17(4):487–499.
Sen, P. and Darabi, S. (2012). On filtering the noise from
the random parameters in monte carlo rendering. ACM
Trans. Graph., 31(3):18:1–18:15.
Soler, C., Subr, K., Durand, F., Holzschuch, N., and Sillion,
F. (2009). Fourier depth of field. ACM Trans. Graph.,
28(2):18:1–18:12.
Vaquer, P. A., McClarren, R. G., and McClarren, R. G.
(2016). A compressed sensing framework for monte
carlo transport simulations using random disjoint tal-
lies. Journal of Computational and Theoretical Trans-
port, 45(3):219–229.
Zwicker, M., Jarosz, W., Lehtinen, J., Moon, B., Ra-
mamoorthi, R., Rousselle, F., Sen, P., Soler, C., and
Yoon, S.-E. (2015). Recent advances in adaptive sam-
pling and reconstruction for Monte Carlo rendering.
Comput. Graph. Forum, 34(2):667–681.
Removing Monte Carlo Noise with Compressed Sensing and Feature Information
153
