
Approximate Epipolar Geometry from Six Rotation Invariant
Correspondences
D
´
aniel Bar
´
ath
MTA SZTAKI, Kende u. 13-17, Budapest H-1111, Hungary
ELTE IK, P
´
azm
´
any P
´
eter s
´
et
´
any 1/C, H-1117 Budapest, Hungary
Keywords:
Fundamental Matrix, Epipolar Geometry, Rotation Invariant Features, Approximation.
Abstract:
We propose a method for estimating an approximate fundamental matrix from six rotation invariant feature
correspondences exploiting their rotation components, e.g. provided by SIFT or ORB detectors. The cameras
are not calibrated. First, a linear sub-space is calculated from the point coordinates, then the rotations are used
assuming orthographic projection. It is demonstrated that combining the proposed method with Graph-cut
RANSAC makes it superior to the state-of-the-art in terms of accuracy for tasks requiring a strict time limit.
These tasks are practically the ones which need to be done real time. We tested the method on 203 publicly
available real image pairs.
1 INTRODUCTION
In this paper, we aim to approximate the epipolar ge-
ometry between two non-calibrated cameras exploi-
ting six rotation invariant feature correspondences in
general position (see Fig. 1). The approximated fun-
damental matrix F ∈ R
3×3
is then used in a recent
variant of locally optimized RANSAC (Chum et al.,
2003) making it faster than the state-of-the-art due
to the reduced number of the required points. This
speedup is beneficial in online applications, i.e. when
real time processing is needed, and leads to results
superior to the state-of-the-art in terms of accuracy.
The common techniques to estimate the funda-
mental matrix when no camera parameters are known,
i.e. the non-calibrated case, are the eight- and seven-
point methods (Hartley and Zisserman, 2003). Both
of them are widely-used in computer vision applicati-
ons and have thousands of citations year-by-year. The
eight-point algorithm is based on estimating the direct
linear transformation which the epipolar constraint in-
duces. The method is fast and the stability issues had
already been solved by the normalization technique of
Hartley (Hartley, 1997) making the technique accu-
rate despite the noise. The seven-point algorithm en-
forces the rank-two constraint, i.e. the determinant of
F must be zero, by solving the cubic polynomial equa-
tion which it implies.
Getting more information using exclusively point
correspondences is not possible. Nevertheless, se-
C
1
C
2
P
4
P
1
P
2
P
3
P
5
P
6
Figure 1: The projections on cameras C
1
and C
2
of six 3D
points P
i
(i ∈[1,6]) in general position.
veral approaches had been proposed to reduce the
number of unknowns. As an example, knowing
the intrinsic parameters of the cameras (focal length,
pixel ratio or the principal point) makes the so-called
trace constraint applicable. The problem becomes
solvable using six (Li, 2006; Kukelova et al., 2008;
Stew
´
enius et al., 2008; Torii et al., 2010) correspon-
dences in the semi-calibrated case – when all intrinsic
parameters are known but a common focal length. For
fully calibrated cameras, five (Nist
´
er, 2004; Li and
Hartley, 2006; Batra et al., ; Kukelova et al., 2008;
Hartley and Li, 2012) point pairs are enough for esti-
mating the relative motion. One can also restrict the
camera movement, e.g. the one point method propo-
sed by Davide Scaramuzza (Scaramuzza, 2011) assu-
mes the cameras to move on a plane and the so-called
non-holonomic constraint to hold.
464
Baráth, D.
Approximate Epipolar Geometry from Six Rotation Invariant Correspondences.
DOI: 10.5220/0006678304640471
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages
464-471
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Approaching the problem from a different di-
rection, it is very rare nowadays to have solely the
point coordinates obtained by the feature detector. For
example, SIFT (Lowe, 1999) features contain a rota-
tion and a scale or ORB (Rublee et al., 2011) features
provide a rotation. This plus information is usually
not used in recent geometric model estimators. It is
just thrown away at the very beginning. In this paper,
we involve an additional affine parameter, i.e. rotation
of the feature, into the fundamental matrix estimation
process to reduce the size of the minimal sample re-
quired for fundamental matrix estimation.
Of course, using full affine correspondences
(point pair together with rotation, shear and scales
along the image axes) for epipolar geometry estima-
tion is not a new idea. Perdoch et al. (Perdoch et al.,
2006) proposed techniques for approximating the es-
sential and fundamental matrix exploiting two and
three correspondences, respectively. Barath et al. (Ba-
rath et al., 2017) showed that using two affine corre-
spondences, the fundamental matrix and a common
focal length can be estimated simultaneously. Raposo
et al. (Raposo and Barreto, 2016) proposed a solution
for essential matrix estimation using two correspon-
dences. Bentolila et al. (Bentolila and Francos, 2014)
proposed a method to estimate the F from three cor-
respondences proposing conic constraints.
Exploiting only a part of an affine correspondence,
e.g. exclusively the rotation component, is a well-
known technique for example in wide-baseline fea-
ture matching (Matas et al., 2004). To the best of our
knowledge, the sole work involving them into geo-
metric model estimation is (Barath, 2017). It assu-
mes that F is known a priori and a technique is pro-
posed for estimating a homography using two SIFT
correspondences using their scale and rotation com-
ponents. Nevertheless, they consider that the scales
along axes u and v equal to that of the SIFT features –
which is practically not true. Thus the method obtains
an approximation of the homography.
The contributions of this paper: (i) the relations-
hip of affine correspondences and epipolar geometry
proposed in (Barath et al., 2017) are reformulated ma-
king it separable to orientation and scale components.
(ii) Using the proposed formulas, we assume that the
orientation constraint can be satisfied by the rotation
of the feature, thus making the fundamental matrix
estimable from six correspondences. It is demonstra-
ted on 203 real image pairs that the proposed method
combined with a recent variant of locally optimized
RANSAC outperforms the state-of-the-art if real time
performance is required.
2 THEORETICAL BACKGROUND
Affine Correspondences. In this paper, we con-
sider an affine correspondence (AC) as a triplet:
(p
1
,p
2
,A), where p
1
= [u
1
v
1
1]
T
and p
2
=
[u
2
v
2
1]
T
are a corresponding homogeneous point
pair in the two images, and
A =
a
1
a
2
a
3
a
4
is a 2 ×2 linear transformation which we call local
affine transformation. To define A, we use the defi-
nition provided in (Moln
´
ar and Chetverikov, 2014) as
it is given as the first-order Taylor-approximation of
the 3D → 2D projection functions. Note that, for per-
spective cameras, A is the first-order approximation
of the related homography matrix
H =
h
1
h
2
h
3
h
4
h
5
h
6
h
7
h
8
h
9
as follows:
a
1
=
∂u
2
∂u
1
=
h
1
−h
7
u
2
s
, a
2
=
∂u
2
∂v
1
=
h
2
−h
8
u
2
s
,
a
3
=
∂v
2
∂u
1
=
h
4
−h
7
v
2
s
, a
4
=
∂v
2
∂v
1
=
h
5
−h
8
v
2
s
,
(1)
where u
i
and v
i
are the directions in the ith image
(i ∈{1,2}) and s = u
1
h
7
+ v
1
h
8
+ h
9
is the projective
depth.
Fundamental Matrix
F =
f
1
f
2
f
3
f
4
f
5
f
6
f
7
f
8
f
9
is a 3×3 transformation matrix ensuring the so-called
epipolar constraint p
T
2
Fp
1
= 0 for rigid scenes. Since
its scale is arbitrary and det(F) = 0, F has seven
degrees-of-freedom (DoF).
The relationship of affine correspondences and
epipolar geometry is defined in (Barath et al., 2017)
as follows:
A
−T
(F
T
p
2
)
(1:2)
= (Fp
1
)
(1:2)
, (2)
where operator v
(i: j)
selects a sub-vector consisting of
the elements of vector v from the ith to the jth. Vector
F
T
p
2
is basically the normal of the epipolar line on
which point p
1
lies in the first image, and Fp
1
is the
same for p
2
. Expanding this formula leads to a system
of two linear, homogeneous equations as follows:
(u
2
+ a
1
u
1
) f
1
+ a
1
v
1
f
2
+ a
1
f
3
+ (v
2
+ a
3
u
2
) f
4
+
a
3
v
1
f
5
+ a
3
f
6
+ f
7
= 0, (3)
a
2
u
1
f
1
+ (u
2
+ a
2
v
1
) f
2
+ a
2
f
3
+ a
4
u
1
f
4
+
(v
2
+ a
4
v
1
) f
5
+ a
4
f
6
+ f
8
= 0. (4)
Approximate Epipolar Geometry from Six Rotation Invariant Correspondences
465

Thus each affine correspondence reduces the degrees-
of-freedom by three. Having three of them are enough
for the estimation. These properties will help us to
recover an approximate fundamental matrix from six
rotation invariant feature correspondences.
3 FUNDAMENTAL MATRIX
ESTIMATION
In this section, we first propose two constraints refor-
mulating the one given in (Barath et al., 2017). Com-
paring to the original one, the proposed constraints are
separable into two, geometrically interpretable (rota-
tion and scaling), transformations. We simplify the
affine transformation model using the given rotations
and this simplified model is then used to approximate
the fundamental matrix.
3.1 Geometric Constraints
As it was shown before, an affine correspondence
yields three linear equations. However, in our case,
not a full affine correspondence is given but a part
of it: the point coordinates and a rotation. There-
fore, assume point pair p
1
, p
2
and the related angle,
α ∈ [0,2π), to be known in two images.
To exploit solely the rotation from the local affine
transformation Eqs. 2 have to be reformulated. First
replace F
T
p
2
and Fp
1
by the related normals as
A
−T
n
1
= −n
2
.
It means that the coordinates of the line normal in the
first image n
1
= [n
u,1
n
v,1
]
T
must be mapped to its
coordinates n
2
= [n
u,2
n
v,2
]
T
in the second one by
A
−T
. This relationship can be separated into orienta-
tion and scale components.
The orientation constraint states that A
−T
must
rotate the direction of n
1
into that of n
2
as follows:
A
−T
n
1
k n
2
,
This can be written as
(A
−T
n
1
)
T
n
2
|An
1
||n
2
|
= cos(0) = 1.
In order to eliminate the length calculation (|A
−T
n
1
|
and |n
2
|), it is beneficial to require perpendicularity
instead of parallelity. Thus the original equations are
formulated equivalently in the following way:
(A
−T
n
1
)
T
R
π/2
n
2
|An
1
||R
π/2
n
2
|
= cos(π/2) = 0, (5)
where R
π/2
is an orthonormal 2D rotation matrix rota-
ting by π/2 radians and R
π/2
n
2
(= v
2
= [v
u,2
v
v,2
]
T
)
is basically the tangent direction of the epipolar line
in the second image. R
π/2
is as follows:
R
π/2
=
cos(
π
2
) −sin(
π
2
)
sin(
π
2
) cos(
π
2
)
=
0 −1
1 0
.
Since for requiring Eq. 5 to be zero, the lengths do not
have to be estimated. Thus Eq. 5 becomes
(A
−T
n
1
)
T
R
π/2
n
2
= 0.
To avoid inversion this can be written as follows:
(R
π/2
n
1
)
T
(A
T
n
2
) = 0.
This formula leads to the following equation
(a
1
n
u,2
+ a
2
n
v,2
)v
u,1
+ (a
3
n
u,2
+ a
4
n
v,2
)v
v,1
= 0.
Remember that n
2
and v
1
are computed from the fun-
damental matrix. They are as
v
1
= R
π/2
n
1
= R
π/2
(F
T
p
2
)
(1:2)
=
R
π/2
f
1
u
2
+ f
4
v
2
+ f
7
f
2
u
2
+ f
5
v
2
+ f
8
=
f
2
u
2
+ f
5
v
2
+ f
8
−f
1
u
2
− f
4
v
2
− f
7
,
and
n
2
= (Fp
1
)
(1:2)
=
f
1
u
1
+ f
2
v
1
+ f
3
f
4
u
1
+ f
5
v
1
+ f
6
.
The final formula encapsulating the orientation con-
straint is the following:
(−u
2
f
2
−v
2
f
5
− f
8
)(a
1
(u
1
f
1
+ v
1
f
2
+ f
3
)+
(u
2
f
1
+ v
2
f
4
+ f
7
)(a
2
(u
1
f
1
+ v
1
f
2
+ f
3
)+
a
3
(u
1
f
4
+ v
1
f
5
+ f
6
)) + a
4
(u
1
f
4
+ v
1
f
5
+ f
6
)) = 0
(6)
The scale constraint states that the length of the
transformed normal in the first image must be the in-
verse of that in the second one. Due to A
−T
n
1
= −n
2
,
|n
1
| equals to |A
T
n
2
|. Therefore,
n
2
u,1
+ n
2
v,1
= (a
1
n
u,2
+ a
2
n
v,2
)
2
+ (a
3
n
u,2
+ a
4
n
v,2
)
2
.
(7)
The final formula for the scale constraint (after re-
arranging Eq. 7 and substituting the elements of the
fundamental matrix) is as follows:
( f
1
u
2
+ f
4
v
2
+ f
7
)
2
+ ( f
2
u
2
+ f
5
v
2
+ f
8
)
2
−
(a
1
( f
1
u
1
+ f
2
v
1
+ f
3
) + a
2
( f
4
u
1
+ f
5
v
1
+ f
6
))
2
−
(a
3
( f
1
u
1
+ f
2
v
1
+ f
3
) + a
4
( f
4
u
1
+ f
5
v
1
+ f
6
))
2
= 0
(8)
3.2 Fundamental Matrix Estimation
Suppose that six point pairs p
1,i
= [u
1,i
v
1,i
1]
T
,
p
2,i
= [u
2,i
v
2,i
1]
T
, (i ∈ [1,6]) in their homogene-
ous form and the corresponding rotations α
i
are gi-
ven. The task is to estimate fundamental matrix F
which is compatible with both the point coordina-
tes and the given rotations. In order to reduce the
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
466

number of unknowns we first form a linear homoge-
neous equation system Cx = 0 from the point coor-
dinates via the well-known formula, p
T
2,i
Fp
1,i
= 0.
Vector x = [ f
1
f
2
f
3
f
4
f
5
f
6
f
7
f
8
f
9
]
T
consists of the unknown variables and coefficient ma-
trix C ∈ R
6×9
is as follows:
C =
u
1,1
u
2,1
v
1,1
u
2,1
u
2,1
u
1,1
v
2,1
v
1,1
v
2,1
v
2,1
u
1,1
v
1,1
1
...
u
1,6
u
2,6
v
1,6
u
2,6
u
2,6
u
1,6
v
2,6
v
1,6
v
2,6
v
2,6
u
1,6
v
1,6
1
.
Since the null-space of C is three-dimensional, F can
be calculated as their linear combination as
F = βe + γg + δh, (9)
where β, γ and δ are unknown scalars, e = [e
1
... e
9
]
T
,
g = [g
1
... g
9
]
T
and h = [h
1
... h
9
]
T
are the null-vectors.
Due to the scale ambiguity of F one scale can be cho-
sen to an arbitrary value, thus δ = 1 in our algorithm.
In order to exploit the given rotations we approx-
imate the affine transformation model assuming that
the orientation constraint (Eq. 8) can be satisfied by
purely a rotation. Note that, without proof, this as-
sumption holds for orthogonal projection. However,
for perspective projection, the shear also affects Eq. 8.
This approximation means that A
i
≈ R
α
i
, where R
α
i
is a 2D rotation matrix rotating by α
i
radians. We do
not exploit the scale constraint, since no information
is available about how A scales the normal of the re-
lated epipolar line.
Replacing each f
i
with βe
i
+ γg
i
+ h
i
in
Eq. 8 leads to a multivariate polynomial equa-
tion (see Appendix 5 for details) with monomials
[β
2
γ
2
βγ β γ 1]
T
. Since we are given
six rotations, it yields six polynomial equations.
Considering each monomial as an independent
variable the obtained inhomogeneous linear system
Dh = d becomes solvable, where D is the coefficient
matrix, h = [β
2
γ
2
βγ β γ]
T
consists of the
unknown variables and d is the vector containing
the inhomogeneous part of the equations. The final
solution is obtained as h = D
†
d, where D
†
is the
Moore-Penrose pseudo-inverse of matrix D. The
final fundamental matrix is calculated by substituting
the obtained β and γ into Eq. 9. Note that it is
beneficial to get the final scalars as β =
√
h
1
+h
4
2
and
γ =
√
h
2
+h
5
2
. Due to the approximation we made, F
is not the exact fundamental matrix. However, it is
good starting point for numerical optimization or, as
we will demonstrate it later, for locally optimized
robust estimators like LO-RANSAC (Chum et al.,
2003).
Robustness: is achieved by normalizing the coeffi-
cients of each polynomial equation making their sum
one. It is also beneficial to apply the normalization
technique of Hartley (Hartley, 1997) which is as fol-
lows: given a set {(p
1, j
,p
2, j
)}
n
j=1
of n point corre-
spondences in their homogeneous forms. Normali-
zing transformation T
i
in the ith image (i ∈ {1,2}) is
as follows:
T
i
=
√
2/d
i
0 0
0
√
2/d
i
0
0 0 1
1 0 −¯u
i
0 1 −¯v
i
0 0 1
where
¯
p
i
= [ ¯u
i
, ¯v
i
,1]
T
is the mean of the point set in
the ith image and
d
i
=
1
n
n
∑
j=1
q
(p
i
−
¯
p)
T
(p
i
−
¯
p) (10)
is its average distance from the mean. Applying
the normalizing transformations, the normalized cor-
respondence set is as follows: {(
ˆ
p
1, j
,
ˆ
p
2, j
)}
n
j=1
=
{(T
1
p
1, j
,T
2
p
2, j
)}
n
j=1
. After the estimation, F is cal-
culated from the normalized fundamental matrix
ˆ
F
as follows: F = T
−T
2
ˆ
FT
−1
1
. Note that the normali-
zing transformations consist of a scale and a transla-
tion, therefore, the rotations of the features remain the
same, they do not have to be modified.
3.3 Processing Time
The proposed method consists of two main steps: (i)
the null-space computation of a matrix of size 6 ×9.
(ii) Using the estimated null-vectors and the rotation
components, a coefficient matrix of size 6 ×5 is built
and its null-space is computed. The average proces-
sing time of 100 runs of our C++ implementation
using OpenCV was 0.03 milliseconds.
Combining hypothesize-and-verify robust estima-
tors, like RANSAC (Fischler and Bolles, 1981), with
the proposed method is beneficial since their proces-
sing time highly depends on the size of the minimal
sample required for the estimation. Table 1 shows
the theoretically needed iteration number of RAN-
SAC combined with minimal methods (columns) on
different outlier levels (rows). The confidence value
was set to 95%. It can be seen that using the proposed
6-point algorithm leads to significant improvement in
the processing time.
4 EXPERIMENTAL RESULTS
In this section, we will compare the proposed method
with the eight- and seven-point algorithms on publicly
available real datasets.
Approximate Epipolar Geometry from Six Rotation Invariant Correspondences
467

Table 1: Required theoretical iteration number of RAN-
SAC (Fischler and Bolles, 1981) combined with minimal
methods (columns) with confidence set to 95% on different
outlier levels (rows).
Confidence 95%
Outl. 6 7 8
50% 190 382 765
80% ∼ 10
4
∼ 10
5
∼ 10
6
95% ∼ 10
8
∼ 10
9
∼ 10
10
99% ∼ 10
12
∼ 10
14
∼ 10
16
In order to overcame the approximative nature of
the proposed approximating six-point technique we
combined it with a recent variant of locally optimized
RANSAC (Chum et al., 2003). We chose Graph-Cut
RANSAC (Barath and Matas, 2017) (GC-RANSAC)
as robust estimator since it can be considered as state-
of-the-art and its source code is publicly available
1
.
Briefly, it replaces the local optimization step of LO-
RANSAC with graph-cut applied to the current best
model. In the local optimization step, we used the
normalized eight-point algorithm. Thus the approxi-
mated fundamental matrix is used only as an initial es-
timate to determine a set of inliers, then the obtained F
is refined iteratively exploiting a set of corresponden-
ces, i.e. the inliers. We used the same parameters as
the authors proposed: the inlier-outlier threshold was
set to 0.31, the iteration limit to 5000 and the weight
of the spatial coherence term was 0.14.
We used the AdelaideRMF, Kusvod2, Multi-H,
and Strecha datasets (see Fig. 2) to evaluate the propo-
sed method on real world data. AdelaideRMF, Kus-
vod2 and Multi-H contains image pairs of size from
455 × 341 to 2592 ×1944 and manually annotated
point correspondences (assigned to the outlier or in-
lier classes) for each pair. Since the reference points
do not contain rotation components we detected and
matched points applying ORB feature detector (Ru-
blee et al., 2011). ORB features contain the orienta-
tion and the point coordinates.
Strecha dataset contains image sequences toget-
her with projection matrices. Each image is of resolu-
tion 3072 ×2048. The fundamental matrices are esti-
mated for all possible image pairs in every sequence.
Correspondences were obtained by ORB detector and
the ground truth fundamental matrices were calcula-
ted from the given projection matrices (Hartley and
Zisserman, 2003). All detected point pairs were con-
sidered as reference points for which the symmetric
epipolar distance (Hartley and Zisserman, 2003) from
the ground truth F was smaller than 1.0 pixels. To dis-
card not stable image pairs, the minimum reference
point number was set to 10. Thus every image pair
1
https://github.com/danini/graph-cut-ransac
for which less than 10 correspondences were closer
to the ground truth F than one pixels was not used in
the evaluation.
We used the reference point sets to validate the
estimated fundamental matrices. The reported geo-
metric errors were computed as the mean symmetric
epipolar distance as
1
2
∑
(p
1
,p
2
)∈P
R
Fp
1
q
(Fp
1
)
2
1
+ (Fp
1
)
2
2
+
p
T
2
F
q
(p
T
2
F)
2
1
+ (p
T
2
F)
2
2
,
(11)
where P
R
is the set consisting of the reference point
correspondences.
The competitor methods, i.e. the minimal sol-
vers combined with GC-RANSAC, were the normali-
zed eight- and seven-point algorithms
2
. In the least-
squares model re-fitting step of GC-RANSAC, the
normalized eight-point method was applied using the
current inlier set.
Table 3 reports the mean result of 100 runs on
every pair from the Strecha dataset. The first column
denotes the name of the sequence, the second one is
the number of the image pairs used – the ones for
which more than 10 reference points were kept. The
next two blocks, each consisting of three columns,
shows the results of the methods if the confidence
of GC-RANSAC is set to 99% (first block) and for a
strict time limit (60 FPS; second block). The reported
properties are the mean and median geometric errors
of the estimated fundamental matrices (Eq. 11) w.r.t.
the reference point sets, and the number of the sam-
ples, i.e. iterations, drawn by GC-RANSAC. It can
be seen that for no time limit (first three columns),
the seven-point algorithm obtains the most accurate
results on average. This is not surprising since it is
a consistent estimator (for no noise the error is zero)
and “inifite” time is given to get the most accurate re-
sult. It can also be seen that if there is a strict time
limit to achieve real time performance (last three co-
lumns), the proposed method yields the most accurate
results.
Table 2 shows the mean results on AdelaideRMF,
Kusvod2 and Multi-H datasets (first column) if the
confidence is set to 99% (third – sixth column). The
last three columns report the results if there is a strict
60 frames-per-seconds (FPS) time limit. The same
property can be seen as for the Strecha dataset: (i) for
no time limit, the best is the seven-point algorithm.
(ii) For 1/60 FPS, the proposed approximating six-
point method combined with GC-RANSAC leads to
the most accurate fundamental matrix estimates.
2
The implementation provided in OpenCV is used for
the eight- and seven-point algorithms.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
468
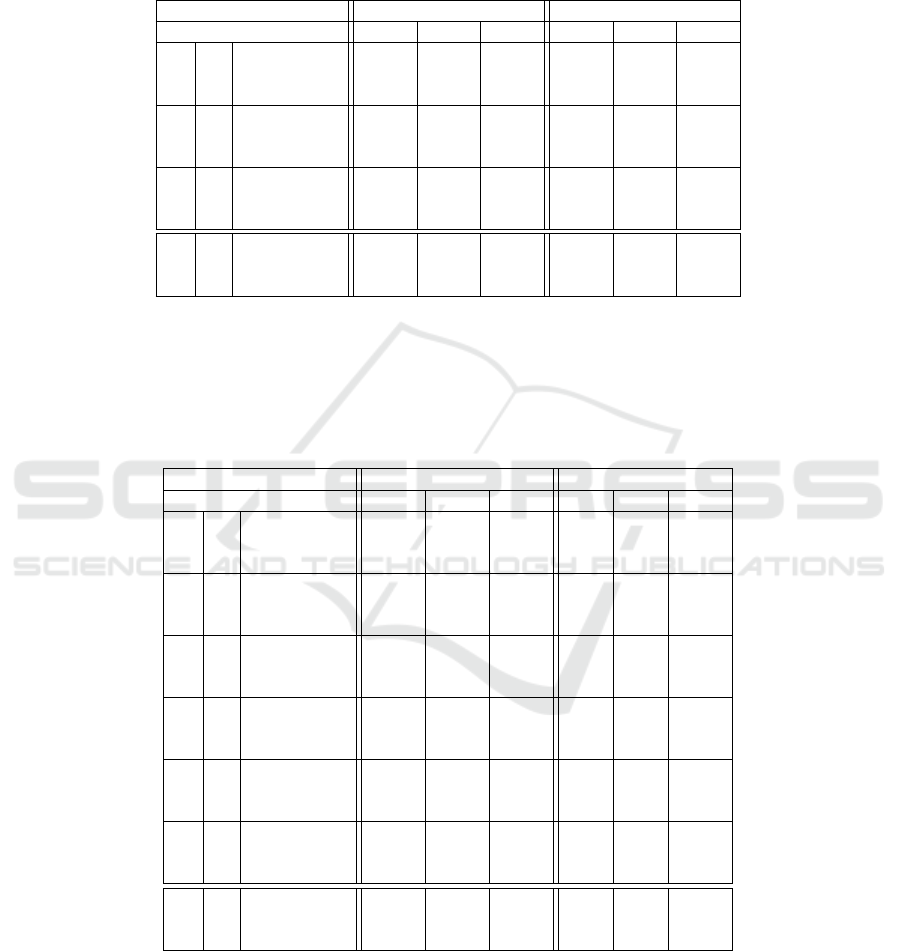
Table 2: Fundamental matrix estimation on the (a) Kusvod2, (b) AdelaideRMF, and (c) Multi-H datasets applying GC-
RANSAC (Barath and Matas, 2017) combined with minimal methods (second row). The number of the image pairs and the
properties are written into the second and third columns. The results at 99% confidence are reported in the next three. The last
three columns contain the results for a time limit set to 60 FPS, i.e. the run is interrupted after 1/60 secs. Values are computed
as the means of 100 runs on each test pair. The mean and median errors (in pixels) of the estimated model w.r.t. the manually
annotated inliers are written in each first and second rows; the required number of samples are reported in every third row.
Confidence 99% 60 FPS
Minimal methods 6 7 8 6 7 8
(a)
24
Avg Err (px) 21.67 23.78 47.67 16.62 20.18 45.38
Med Err (px) 22.45 24.72 43.50 13.88 21.81 44.06
Samples 4992 5000 5000 74 119 380
(b)
18
Avg Err (px) 4.63 3.04 6.72 4.00 3.67 7.63
Med Err (px) 3.63 2.33 4.05 3.56 2.82 4.87
Samples 4982 5000 5000 74 136 292
(c)
4
Avg Err (px) 4.17 4.45 11.26 4.52 4.59 12.18
Med Err (px) 4.46 4.91 11.41 4.15 4.54 11.55
Samples 5000 5000 5000 51 83 403
(all)
Avg Err (px) 13.48 13.98 28.48 10.63 12.36 27.72
Med Err (px) 10.18 10.65 19.65 7.20 9.72 20.16
Samples 5000 5000 5000 72 122 349
Table 3: Fundamental matrix estimation on the Strecha dataset applying GC-RANSAC (Barath and Matas, 2017) combined
with minimal methods (second row). The first column contains the names of the sequences: (a) fountain-p11, (b) entry-p10,
(c) castle-p19, (d) castle-p30, (e) herzjesus-p8, and (f) herzjesus-p25. The number of the image pairs and the properties are
written into the second and third columns. The results at 99% confidence are reported in the next three. The last three columns
contain the results for a time limit set to 60 FPS, i.e. the run is interrupted after 1/60 secs. Values are computed as the means
of 100 runs on each test pair. The mean and median errors (in pixels) of the estimated model w.r.t. the manually annotated
inliers are written in each first and second rows; the required number of samples are reported in every third row.
Confidence 99% 60 FPS
Minimal methods 6 7 8 6 7 8
(a)
19
Avg Err (px) 1.93 9.75 7.19 1.84 5.71 6.26
Med Err (px) 0.99 3.42 2.78 0.98 1.64 3.12
Samples 4 394 5 748 5 721 279 352 447
(b)
5
Avg Err (px) 30.15 7.83 13.67 5.71 7.04 41.90
Med Err (px) 4.64 1.74 3.08 1.56 2.27 39.71
Samples 4 981 5 121 5 004 134 183 284
(c)
21
Avg Err (px) 2.43 3.98 12.62 5.42 7.16 20.00
Med Err (px) 1.77 2.90 4.62 1.69 5.46 9.87
Samples 4 575 5 355 5 613 210 348 436
(d)
51
Avg Err (px) 9.24 5.11 10.73 3.33 6.29 9.82
Med Err (px) 2.92 1.89 4.24 1.32 2.11 4.49
Samples 5 669 6 306 6 339 200 311 392
(e)
16
Avg Err (px) 2.34 1.77 16.51 2.85 3.11 8.50
Med Err (px) 0.81 1.50 4.75 2.05 1.73 2.65
Samples 6 492 6 708 6 757 199 249 382
(f)
45
Avg Err (px) 5.47 4.31 10.50 1.24 2.27 6.46
Med Err (px) 1.71 1.84 2.57 1.24 1.32 2.71
Samples 6 305 6 708 6 758 179 240 361
(all)
157
Avg Err (px) 6.33 5.04 11.17 3.62 4.80 12.95
Med Err (px) 1.93 1.87 3.49 1.36 2.11 3.96
Samples 5 613 6 199 6 252 200 280 387
Fig. 2 shows example image pairs from each da-
taset with the epipolar lines of 50 random inliers. It
can be seen, that the results seem good: the epipolar
lines go through the same pixels in the first (left) and
second (right) images.
5 CONCLUSION
In this paper, we proposed a method for approx-
imating the fundamental matrix between two non-
calibrated views from six rotation invariant feature
Approximate Epipolar Geometry from Six Rotation Invariant Correspondences
469

(a) AdelaideRMF
(b) Multi-H
(c) Kusvod2
(d) Strecha
Figure 2: The results of the proposed method combined
with Graph-Cut RANSAC. An image pair from each dataset
with the corresponding epipolar lines of 50 random inliers
drawn by colors.
correspondences. The method is solved through the
null-space computation of two matrices of sizes 6×9
and 6 ×5, thus achieving fast calculation, i.e. around
0.03 milliseconds in C++. Due to the reduced number
of required samples, the approximating six-point al-
gorithm combined with locally optimized RANSAC
obtains results superior to the state-of-the-art if a strict
time limit is given.
ACKNOWLEDGEMENTS
This research was supported by the Hungarian Scien-
tific Research Fund (No. OTKA/NKFIH 120499),
the Hungarian National Research, Development and
Innovation Office under the grant VKSZ 14-1-2015-
0072, and the European Union, co-financed by
the European Social Fund (EFOP-3.6.3-VEKOP-16-
2017-00001).
REFERENCES
Barath, D. (2017). P-HAF: Homography estimation using
partial local affine frames. In VISAPP.
Barath, D. and Matas, J. (2017). Graph-cut ransac. ArXiv
preprint arXiv:1706.00984.
Barath, D., Toth, T., and Hajder, L. (2017). A minimal so-
lution for two-view focal-length estimation using two
affine correspondences. In Conference on Computer
Vision and Pattern Recognition.
Batra, D., Nabbe, B., and Hebert, M. An alternative formu-
lation for five point relative pose problem. In Works-
hop onMotion and Video Computing.
Bentolila, J. and Francos, J. M. (2014). Conic epipolar con-
straints from affine correspondences. Computer Vision
and Image Understanding.
Chum, O., Matas, J., and Kittler, J. (2003). Locally optimi-
zed ransac. In Joint Pattern Recognition Symposium.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: a paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM.
Hartley, R. and Li, H. (2012). An efficient hidden variable
approach to minimal-case camera motion estimation.
Pattern Analysis and Machine Intelligence.
Hartley, R. and Zisserman, A. (2003). Multiple view geome-
try in computer vision. Cambridge University Press.
Hartley, R. I. (1997). In defense of the eight-point algo-
rithm. Pattern Analysis and Machine Intelligence.
Kukelova, Z., Bujnak, M., and Pajdla, T. (2008). Polyno-
mial eigenvalue solutions to the 5-pt and 6-pt relative
pose problems. In British Machine Vision Conference.
Li, H. (2006). A simple solution to the six-point two-view
focal-length problem. In European Conference on
Computer Vision.
Li, H. and Hartley, R. (2006). Five-point motion estimation
made easy. In International Conference on Pattern
Recognition.
Lowe, D. G. (1999). Object recognition from local scale-
invariant features. In International Conference on
Computer vision.
Matas, J., Chum, O., Urban, M., and Pajdla, T. (2004). Ro-
bust wide-baseline stereo from maximally stable ex-
tremal regions. Image and vision computing.
Moln
´
ar, J. and Chetverikov, D. (2014). Quadratic transfor-
mation for planar mapping of implicit surfaces. Jour-
nal of Mathematical Imaging and Vision.
Nist
´
er, D. (2004). An efficient solution to the five-point
relative pose problem. Pattern Analysis and Machine
Intelligence.
Perdoch, M., Matas, J., and Chum, O. (2006). Epipolar
geometry from two correspondences. In International
Conference on Pattern Recognition.
Raposo, C. and Barreto, J. P. (2016). Theory and practice
of structure-from-motion using affine corresponden-
ces. In Computer Vision and Pattern Recognition.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
470

Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.
(2011). ORB: An efficient alternative to sift or surf.
In Computer Vision (ICCV), 2011 IEEE international
conference on, pages 2564–2571. IEEE.
Scaramuzza, D. (2011). 1-point-ransac structure from mo-
tion for vehicle-mounted cameras by exploiting non-
holonomic constraints. International Journal of Com-
puter Vision.
Stew
´
enius, H., Nist
´
er, D., Kahl, F., and Schaffalitzky, F.
(2008). A minimal solution for relative pose with
unknown focal length. Image Vision Computing.
Torii, A., Kukelova, Z., Bujnak, M., and Pajdla, T. (2010).
The six point algorithm revisited. In Asian Conference
on Computer Vision.
APPENDIX
Formulas for the Orientation Constraint
Replacing each f
i
with βe
i
+ γg
i
+ h
i
in Eq. 8 leads to
a multivariate polynomial equation with monomials
[β
2
γ
2
βγ β γ 1]
T
. The coefficients regarding
to each monomial are shown in Figure 3.
β
2
: −a
3
b
2
5
v
1
v
2
+ a
4
b
4
b
5
v
1
v
2
−a
1
b
2
b
5
v
1
v
2
+ a
2
b
2
b
4
v
1
v
2
−a
3
b
4
b
5
u
1
v
2
−a
1
b
1
b
5
u
1
v
2
+ a
4
b
2
4
u
1
v
2
+ a
2
b
1
b
4
u
1
v
2
−a
3
b
5
b
6
v
2
+
a
4
b
4
b
6
v
2
−a
1
b
3
b
5
v
2
+ a
2
b
3
b
4
v
2
−a
3
b
2
b
5
u
2
v
1
+ a
4
b
1
b
5
u
2
v
1
−a
1
b
2
2
u
2
v
1
+ a
2
b
1
b
2
u
2
v
1
−a
3
b
5
b
8
v
1
−a
1
b
2
b
8
v
1
+ a
3
b
2
b
6
u
2
+
a
4
b
1
b
6
u
2
−a
1
b
2
b
3
u
2
+ a
4
b
5
b
7
v
1
+ a
2
b
2
b
7
v
1
−a
3
b
2
b
4
u
1
u
2
+ a
4
b
1
b
4
u
1
u
2
−a
1
b
1
b
2
u
1
u
2
+ a
2
b
2
1
u
1
u
2
−a
2
b
1
b
3
u
2
−a
3
b
4
b
8
u
1
−
a
1
b
1
b
8
u
1
+ a
4
b
4
b
7
u
1
+ a
2
b
1
b
7
u
1
−a
3
b
6
b
8
−a
1
b
3
b
8
+ a
4
b
6
b
7
+ a
2
b
3
b
7
γ
2
: −a
3
c
2
5
v
1
v
2
+ a
4
c
4
c
5
v
1
v
2
−a
1
c
2
c
5
v
1
v
2
+ a
2
c
2
c
4
v
1
v
2
−a
3
c
4
c
5
u
1
v
2
−a
1
c
1
c
5
u
1
v
2
+ a
4
c
2
4
u
1
v
2
+ a
2
c
1
c
4
u
1
v
2
−a
3
c
5
c
6
v
2
+
a
4
c
4
c
6
v
2
−a
1
c
3
c
5
v
2
+ a
2
c
3
c
4
v
2
−a
3
c
2
c
5
u
2
v
1
+ a
4
c
1
c
5
u
2
v
1
−a
1
c
2
2
u
2
v
1
+ a
2
c
1
c
2
u
2
v
1
−a
3
c
5
c
8
v
1
−a
1
c
2
c
8
v
1
+
a
4
c
5
c
7
v
1
+ a
2
c
2
c
7
v
1
−a
3
c
2
c
4
u
1
u
2
+ a
4
c
1
c
4
u
1
u
2
−a
1
c
1
c
2
u
1
u
2
+ a
2
c
2
1
u
1
u
2
−a
3
c
2
c
6
u
2
+ a
4
c
1
c
6
u
2
−a
1
c
2
c
3
u
2
+
a
2
c
1
c
3
u
2
−a
3
c
4
c
8
u
1
−a
1
c
1
c
8
u
1
+ a
4
c
4
c
7
u
1
+ a
2
c
1
c
7
u
1
−a
3
c
6
c
8
−a
1
c
3
c
8
+ a
4
c
6
c
7
+ a
2
c
3
c
7
βγ : −2a
3
b
5
c
5
v
1
v
2
+ a
4
b
4
c
5
v
1
v
2
−a
1
b
2
c
5
v
1
v
2
+ a
4
b
5
c
4
v
1
v
2
+ a
2
b
2
c
4
v
1
v
2
−a
1
b
5
c
2
v
1
v
2
+ a
2
b
4
c
2
v
1
v
2
−a
3
b
4
c
5
u
1
v
2
−a
1
b
1
c
5
u
1
v
2
−
a
3
b
5
c
4
u
1
v
2
+ 2a
4
b
4
c
4
u
1
v
2
+ a
2
b
1
c
4
u
1
v
2
−a
1
b
5
c
1
u
1
v
2
+ a
2
b
4
c
1
u
1
v
2
−a
3
b
5
c
6
v
2
+ a
4
b
4
c
6
v
2
−a
3
b
6
c
5
v
2
−a
1
b
3
c
5
v
2
+
a
4
b
6
c
4
v
2
+ a
2
b
3
c
4
v
2
−a
1
b
5
c
3
v
2
+ a
2
b
4
c
3
v
2
−a
3
b
2
c
5
u
2
v
1
+ a
4
b
1
c
5
u
2
v
1
−a
3
b
5
c
2
u
2
v
1
−2a
1
b
2
c
2
u
2
v
1
+
a
2
b
1
c
2
u
2
v
1
+ a
4
b
5
c
1
u
2
v
1
+ a
2
b
2
c
1
u
2
v
1
−a
3
b
5
c
8
v
1
−a
1
b
2
c
8
v
1
+ a
4
b
5
c
7
v
1
+ a
2
b
2
c
7
v
1
−a
3
b
8
c
5
v
1
+ a
4
b
7
c
5
v
1
−a
1
b
8
c
2
v
1
+
a
2
b
7
c
2
v
1
−a
3
b
2
c
4
u
1
u
2
+ a
4
b
1
c
4
u
1
u
2
−a
3
b
4
c
2
u
1
u
2
−a
1
b
1
c
2
u
1
u
2
+ a
4
b
4
c
1
u
1
u
2
−a
1
b
2
c
1
u
1
u
2
+ 2a
2
b
1
c
1
u
1
u
2
−a
3
b
2
c
6
u
2
+
a
4
b
1
c
6
u
2
−a
1
b
2
c
3
u
2
+ a
2
b
1
c
3
u
2
−a
3
b
6
c
2
u
2
−a
1
b
3
c
2
u
2
+ a
4
b
6
c
1
u
2
+ a
2
b
3
c
1
u
2
−a
3
b
4
c
8
u
1
−a
1
b
1
c
8
u
1
+ a
4
b
4
c
7
u
1
+ a
2
b
1
c
7
u
1
−
a
3
b
8
c
4
u
1
+ a
4
b
7
c
4
u
1
−a
1
b
8
c
1
u
1
+ a
2
b
7
c
1
u
1
−a
3
b
6
c
8
−a
1
b
3
c
8
+ a
4
b
6
c
7
+ a
2
b
3
c
7
−a
3
b
8
c
6
+ a
4
b
7
c
6
−a
1
b
8
c
3
+ a
2
b
7
c
3
β : −2a
3
b
5
d
5
v
1
v
2
+ a
4
b
4
d
5
v
1
v
2
−a
1
b
2
d
5
v
1
v
2
+ a
4
b
5
d
4
v
1
v
2
+ a
2
b
2
d
4
v
1
v
2
−a
1
b
5
d
2
v
1
v
2
+ a
2
b
4
d
2
v
1
v
2
−a
3
b
4
d
5
u
1
v
2
−a
1
b
1
d
5
u
1
v
2
−
a
3
b
5
d
4
u
1
v
2
+ 2a
4
b
4
d
4
u
1
v
2
+ a
2
b
1
d
4
u
1
v
2
−a
1
b
5
d
1
u
1
v
2
+ a
2
b
4
d
1
u
1
v
2
−a
3
b
5
d
6
v
2
+ a
4
b
4
d
6
v
2
−a
3
b
6
d
5
v
2
−a
1
b
3
d
5
v
2
+ a
4
b
6
d
4
v
2
+
a
2
b
1
d
2
u
2
v
1
+ a
4
b
5
d
1
u
2
v
1
+ a
2
b
3
d
4
v
2
−a
1
b
5
d
3
v
2
+ a
2
b
4
d
3
v
2
−a
3
b
2
d
5
u
2
v
1
+ a
4
b
1
d
5
u
2
v
1
−a
3
b
5
d
2
u
2
v
1
−2a
1
b
2
d
2
u
2
v
1
+
a
2
b
2
d
1
u
2
v
1
−a
3
b
5
d
8
v
1
−a
1
b
2
d
8
v
1
+ a
4
b
5
d
7
v
1
+ a
2
b
2
d
7
v
1
−a
3
b
8
d
5
v
1
+ a
4
b
7
d
5
v
1
−a
1
b
8
d
2
v
1
+ a
2
b
7
d
2
v
1
−a
3
b
2
d
4
u
1
u
2
+
a
4
b
1
d
4
u
1
u
2
−a
3
b
4
d
2
u
1
u
2
−a
1
b
1
d
2
u
1
u
2
+ a
4
b
4
d
1
u
1
u
2
−a
1
b
2
d
1
u
1
u
2
+ 2a
2
b
1
d
1
u
1
u
2
−a
3
b
2
d
6
u
2
+ a
4
b
1
d
6
u
2
−a
1
b
2
d
3
u
2
+
a
2
b
1
d
3
u
2
−a
3
b
6
d
2
u
2
−a
1
b
3
d
2
u
2
+ a
4
b
6
d
1
u
2
+ a
2
b
3
d
1
u
2
−a
3
b
4
d
8
u
1
−a
1
b
1
d
8
u
1
+ a
4
b
4
d
7
u
1
+ a
2
b
1
d
7
u
1
−a
3
b
8
d
4
u
1
+ a
4
b
7
d
4
u
1
−
a
1
b
8
d
1
u
1
+ a
2
b
7
d
1
u
1
−a
3
b
6
d
8
−a
1
b
3
d
8
+ a
4
b
6
d
7
+ a
2
b
3
d
7
−a
3
b
8
d
6
+ a
4
b
7
d
6
−a
1
b
8
d
3
+ a
2
b
7
d
3
γ : −2a
3
c
5
d
5
v
1
v
2
+ a
4
c
4
d
5
v
1
v
2
−a
1
c
2
d
5
v
1
v
2
+ a
4
c
5
d
4
v
1
v
2
+ a
2
c
2
d
4
v
1
v
2
−a
1
c
5
d
2
v
1
v
2
+ a
2
c
4
d
2
v
1
v
2
−a
3
c
4
d
5
u
1
v
2
−a
1
c
1
d
5
u
1
v
2
−
a
3
c
5
d
4
u
1
v
2
+ 2a
4
c
4
d
4
u
1
v
2
+ a
2
c
1
d
4
u
1
v
2
−a
1
c
5
d
1
u
1
v
2
+ a
2
c
4
d
1
u
1
v
2
−a
3
c
5
d
6
v
2
+ a
4
c
4
d
6
v
2
−a
3
c
6
d
5
v
2
−a
1
c
3
d
5
v
2
+ a
4
c
6
d
4
v
2
+
a
2
c
3
d
4
v
2
−a
1
c
5
d
3
v
2
+ a
2
c
4
d
3
v
2
−a
3
c
2
d
5
u
2
v
1
+ a
4
c
1
d
5
u
2
v
1
−a
3
c
5
d
2
u
2
v
1
−2a
1
c
2
d
2
u
2
v
1
+ a
2
c
1
d
2
u
2
v
1
+ a
4
c
5
d
1
u
2
v
1
+
a
2
c
2
d
1
u
2
v
1
−a
3
c
5
d
8
v
1
−a
1
c
2
d
8
v
1
+ a
4
c
5
d
7
v
1
+ a
2
c
2
d
7
v
1
−a
3
c
8
d
5
v
1
+ a
4
c
7
d
5
v
1
−a
1
c
8
d
2
v
1
+ a
2
c
7
d
2
v
1
−a
3
c
2
d
4
u
1
u
2
+
a
4
c
1
d
4
u
1
u
2
−a
3
c
4
d
2
u
1
u
2
−a
1
c
1
d
2
u
1
u
2
+ a
4
c
4
d
1
u
1
u
2
−a
1
c
2
d
1
u
1
u
2
+ 2a
2
c
1
d
1
u
1
u
2
−a
3
c
2
d
6
u
2
+ a
4
c
1
d
6
u
2
−a
1
c
2
d
3
u
2
+
a
2
c
1
d
3
u
2
−a
3
c
6
d
2
u
2
−a
1
c
3
d
2
u
2
+ a
4
c
6
d
1
u
2
+ a
2
c
3
d
1
u
2
−a
3
c
4
d
8
u
1
−a
1
c
1
d
8
u
1
+ a
4
c
4
d
7
u
1
+ a
2
c
1
d
7
u
1
−a
3
c
8
d
4
u
1
+
a
4
c
7
d
4
u
1
−a
1
c
8
d
1
u
1
+ a
2
c
7
d
1
u
1
−a
3
c
6
d
8
−a
1
c
3
d
8
+ a
4
c
6
d
7
+ a
2
c
3
d
7
−a
3
c
8
d
6
+ a
4
c
7
d
6
−a
1
c
8
d
3
+ a
2
c
7
d
3
1 : −a
3
d
2
5
v
1
v
2
+ a
4
d
4
d
5
v
1
v
2
−a
1
d
2
d
5
v
1
v
2
+ a
2
d
2
d
4
v
1
v
2
−a
3
d
4
d
5
u
1
v
2
−a
1
d
1
d
5
u
1
v
2
+ a
4
d
2
4
u
1
v
2
+ a
2
d
1
d
4
u
1
v
2
−a
3
d
5
d
6
v
2
+
a
4
d
4
d
6
v
2
−a
1
d
3
d
5
v
2
+ a
2
d
3
d
4
v
2
−a
3
d
2
d
5
u
2
v
1
+ a
4
d
1
d
5
u
2
v
1
−a
1
d
2
2
u
2
v
1
+ a
2
d
1
d
2
u
2
v
1
−a
3
d
5
d
8
v
1
−a
1
d
2
d
8
v
1
+ a
4
d
5
d
7
v
1
+
a
2
d
2
d
7
v
1
−a
3
d
2
d
4
u
1
u
2
+ a
4
d
1
d
4
u
1
u
2
−a
1
d
1
d
2
u
1
u
2
+ a
2
d
2
1
u
1
u
2
−a
3
d
2
d
6
u
2
+ a
4
d
1
d
6
u
2
−a
1
d
2
d
3
u
2
+ a
2
d
1
d
3
u
2
−a
3
d
4
d
8
u
1
−
a
1
d
1
d
8
u
1
+ a
4
d
4
d
7
u
1
+ a
2
d
1
d
7
u
1
−a
3
d
6
d
8
−a
1
d
3
d
8
+ a
4
d
6
d
7
+ a
2
d
3
d
7
Figure 3: The coefficient for each monomial in the polynomial equation to which the orientation constraint lead (Eq. 8).
Approximate Epipolar Geometry from Six Rotation Invariant Correspondences
471
