Bicluster Detection by Hyperplane Projection and Evolutionary
Optimization
Maryam Golchin and Alan Wee-Chung Liew
School of Information and Communication Technology, Griffith University, Southport, QLD, 4215, Australia
Keywords: Geometric Biclustering, Linear Pattern Bicluster, Multi-Objective Evolutionary Algorithm.
Abstract: Biclustering is a powerful unsupervised learning technique that has different applications in many fields
especially in gene expression analysis. This technique tries to group rows and columns in a dataset
simultaneously, which is an NP-hard problem. In this paper, a multi-objective evolutionary algorithm is
proposed with a heuristic search to solve the biclustering problem. To do so, rows are projected into the
column space. Projection decreases the computational cost of geometric biclustering. The heuristic search is
done by sample Pearson correlation coefficient over the rows and columns of a dataset to prune unwanted
rows and columns. The experimental results on both synthetic and real datasets show the effectiveness of
our proposed method.
1 INTRODUCTION
Finding relation among the elements of a dataset can
lead to valuable information (Liew, 2016). One way
to find patterns in a dataset is by clustering
techniques. Clustering is an unsupervised technique
that groups data into meaningful categories such that
the data in each category are similar to each other
and dis-similar to the data of other categories. In
clustering, in order to find the similarity of patterns
the entire set of attributes (i.e. features) is used.
However, in most of the situations patterns only
exhibit similar behaviour under a subset of
attributes. This kind of methods is called
biclustering. Biclustering is a powerful technique to
group similar rows and columns of a dataset
simultaneously. The difference between clustering
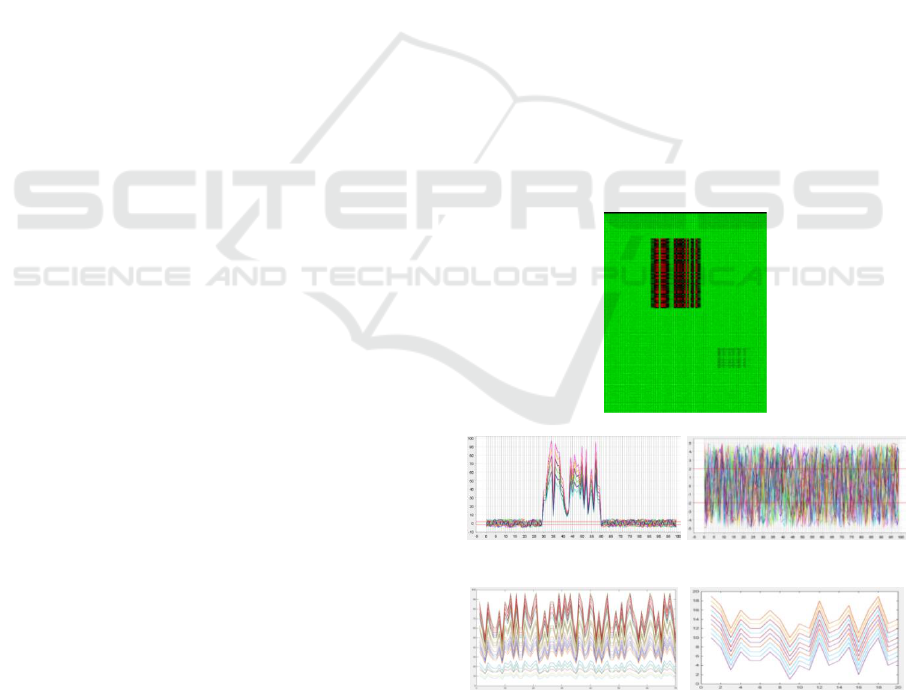
and biclustering is visualised in Figure 1. The
original dataset with 200 rows and 100 columns is
shown in Figure 1 (a) with two biclusters. Figure 1
(b, c) are the clusters by a clustering technique and
Figure 1 (d, e) are the detected biclusters by a
biclustering technique. Figure 1 (b, d), and Figure 1
(c, e) refer to a same set of samples with different
subset of features (Figure 1 (b, c) include all features
in the dataset). As it is clear, information that is
more valuable can be obtained from biclustering
technique (Figure 1 (d, e)). Biclustering has found
many applications in different fields e.g. disease
detection (Maulik et al., 2013); social networks
clustering (Shafiq et al., 2013) and gene expression
analysis (Ben-Dor et al., 2003; Cheng and Church,
2000; Divina and Aguilar, 2006; Gan et al., 2005;
Gan et al., 2008; Ihmels et al., 2004; Golchin and
Liew, 2017; Cheng et al. 2008).
(a)
(b)
(c)
(d)
(e)
Figure 1: The difference between a clustering method (b
and c) and a biclustering method (d and e). The x-axis is
the feature indices and the y-axis is the expression values;
the original dataset with 200 rows and 100 columns is
shown in (a) with two biclusters.
Golchin, M. and Liew, A.
Bicluster Detection by Hyperplane Projection and Evolutionary Optimization.
DOI: 10.5220/0006710000610068
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 3: BIOINFORMATICS, pages 61-68
ISBN: 978-989-758-280-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
61

One way to detect biclusters with linear coherent
structure in datasets is via geometric biclustering. In
geometric biclustering, each bicluster is described
with a linear equation. In computer vision, an
effective way to detect linear structures in an image
is the Hough Transform (HT) (Hough, 1962). HT
identifies lines in the dataset by a voting procedure,
which is performed in Hough space. It maps the x-y
coordinates into ρ-θ parameter space where ρ is the
distance of the line to the origin and θ is the angle of
the normal vector. HT parametrizes pattern space
then projects all points into the parameter space,
from which the local maxima in an accumulator
space imply the line candidates. Gan et al. (2005,
2008) propose to detect a bundle of hyperplanes
representing biclusters within a dataset using HT
method. However, HT is computationally expensive
and the storage memory requirement is high. This
makes HT un-scalable for high dimensional data. In
order to overcome the large memory and
computational time, Zhao et al. (2008) proposed to
apply HT in column-pair space. In order to combine
the coherent sub-biclusters B
1
= (r
1
, c
1
) and B
2
= (r
2
, c
2
), they used the operation B
1
B
2
= (r
1
∩ r
2
, c
1
c
2
). Liu et al. (2014) and Wang et al. (2012) also
used the same method to combine column pair sub-
biclusters. Wang and Yan (2013) used a graph
spectrum algorithm to combine sub-biclusters. All
these efforts in using HT show the effectiveness of
HT in detecting biclusters. However, the heuristic
combination strategies may fail with regard to detect
and combine sub-biclusters to generate bigger
biclusters and may converge to local maxima.
In order to overcome the space usage and
complexity of Hough transform, evolutionary
algorithms and heuristic search are introduced to
biclustering. In evolutionary algorithms, the merit
functions are very important to obtain good results.
However, the objectives that are applicable in
biclustering are often in conflict with each other.
Therefore, the single objective merit function is not
very useful for this kind of problem. Instead, multi-
objective evolutionary algorithms (Błażej et al.
2017; Winterhalter et al. 2014) are desired.
In this paper, we propose a multi-objective
strength Pareto front evolutionary algorithm based
on SPEA2 (Zitzler et al., 2001) for biclustering. Our
method uses a new heuristic search based on sample
Pearson correlation coefficient. We present
experimental results showing that our algorithm can
detect biclusters with linear coherent patterns well
compared to many state-of-the-arts.
2 METHODOLOGY
We consider a dataset as an m × n matrix of real
numbers. Let R = {r
1
, r
2
, …, r
m
} represents the rows
in the dataset and C = {c
1
, c
2
, …, c
n
} represents the
columns in the dataset. A bicluster is a set of rows
and columns with elements e
ij
that follow a certain
pattern, where i {1 .. m} and j {1 .. n}. For
linear coherent patterns, we consider biclusters that
satisfy a linear relationship given by c
l
= Ac
k
+ B,
where c
l
,
c
k
C, A is the coefficient matrix and B is
the constant vector. Linear relationship has been
used extensively in pattern recognition and machine
learning (Bishop, 2006) and linear coherent patterns
cover many biclusters of interest in many
applications (Gan et al., 2005, Gan et al., 2008,
Liew, 2016).
The general steps of the proposed method are
summarized in Pseudocode 1. Each step of the
algorithm is explained in details in the remaining of
this paper.
Pseudocode 1: The proposed framework
1:
For maximum number of biclusters
do
2:
Generate initial populations
3:
For maximum number of iterations
do
4:
Apply heuristic search for
each individual
5:
Calculate the fitness
function for each individual
6:
Generate Pareto front
7:
Apply crossover and mutation
8:
Apply the k-means algorithm to
the Pareto front
2.1 Population
In our method, we have two populations, i.e. a
normal population and an archive population,
hereinafter referred as population and archive,
respectively.
We encode each bicluster as an individual with a
fixed size m + n bit string where one indicates that
the corresponding row or column belongs to the
bicluster and zero otherwise. Figure 2 illustrates an
encoded bicluster. This bicluster is generated from a
dataset with 8 rows and 6 columns. In this bicluster
row indices {2, 3, 5, 8} and column indices {1, 2, 6}
are selected.
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
62

Figure 2: The presentation of biclusters as an individual.
All the individuals are kept in the population and
only the best non-dominated individuals are added to
the archive. This helps to keep the best individuals
for the next steps and make a good mating pool
including the best non-dominated and dominated
individuals.
The size of the archive is fixed, so if the number
of non-dominated individuals is bigger than the size
of the archive, only individuals with small fitness
value and non-duplicated individuals from the
previous archive and the present population are
added to the archive. On the other hand, if the
number of non-dominated individuals is smaller than
the archive size, then dominated individuals with
higher fitness value from the present population are
added to the archive.
2.2 Heuristic Search
Due to the nature of the evolutionary algorithms, the
probability of having unwanted rows and columns in
a bicluster is high. A greedy heuristic search is
designed to remove these uncorrelated columns and
rows and to add correlated columns and rows to the
bicluster. In order to find correlated rows and
columns, sample Pearson correlation coefficient
(SPCC) is used. SPCC measures the linear
dependence between two variables and it is
calculated as in Equation (1)
(1)
The value of τ can be from -1 to 1 with -1 and 1
show highest correlation and 0 shows no correlation.
The steps of the proposed heuristic search are
summarized in Pseudocode 2.
Pseudocode 2: Heuristic search
For each individual:
// Rows deletion
1:
For all rows in a bicluster do
2:
Calculate τ between a random row
r
j
in the bicluster and the
remaining rowsin the bicluster
3:
If τ ≤ α
rr
then count = count + 1
4:
If counter ≥ 2/3 × n
r
then remove r
i
// Columns deletion
5:
For all columns in the bicluster do
6:
Calculate τ between a random
column c
j
in the bicluster and the
remaining columns in the bicluster
7:
If τ ≤ α
cr
then counter = counter
+ 1
8:
If counter ≥ 2/3 * n
c
then remove c
j
// Rows addition
9:
For a number of selected rows from
the dataset excluding the bicluster
do
10:
Calculate τ between a random row
r
i
from the selected rows and the
rows in the bicluster
11:
If τ ≥ α
ra
then counter = counter
+ 1
12:
If counter ≥ 2/3 * n
r
then add r
i
to
the bicluster
// Columns addition
13:
For a number of selected columns
from the dataset excluding the
bicluster do
14:
Calculate τ between a random
column c
j
from the selected
columns and the columns in the
bicluster
15:
If τ ≥ α
ca
then counter = counter
+ 1
16:
If counter ≥ 2/3 * n
c
then remove c
j
In this algorithm, α
rr
, α
cr
, α
ra
, and α
ca
are the
user-defined thresholds to control the rate of row
deletion, column deletion, row addition, and column
addition, respectively. These values are determined
experimentally and are set to 0.98 in our
experiments.
2.3 Fitness Function
Biclustering has been shown to be NP-Hard (Cheng
and Church, 2000). In order to overcome this
problem, EA based biclustering algorithms have
been proposed. Divina and Ruiz (2006) used EA to
find biclusters in gene expression data. In their
method, they used three objectives plus a penalty
value for their evolutionary search and they
combined these objectives additively in a merit
function. However, the objectives i.e. size,
coherence, and row variance are in conflict with
each other by nature. So, multi-objective
evolutionary algorithms are introduced to overcome
this problem (Maulik et al., 2009; Seridi et al., 2015;
Golchin and Liew, 2017).
In this paper, a strength Pareto front multi-
objective evolutionary algorithm is used. The
conflicting objectives in our algorithm include the
size of a bicluster (S
b
) which we try to maximize and
Bicluster Detection by Hyperplane Projection and Evolutionary Optimization
63
the coherence of the bicluster (e
r
) which we try to
minimize. These two objectives are in conflict since
maximizing the size would increase the incoherence
of the bicluster.
2.3.1 Bicluster Size
In order to calculate the size of a bicluster, rows and
columns are considered separately and they are
added together by a weighted sum as in Equation (2)
(2)
where w
r
and w
c
are weights that are assigned to
rows and columns, respectively; m and n are the
number of rows and columns in the dataset; m
b
and
n
b
are the number of rows and columns in the
bicluster, respectively.
2.3.2 The Coherence of Patterns
In order to calculate the coherence of patterns, each
row in a data matrix is considered as a data point in
a high dimensional space where each column defines
a dimension and each element specifies a coordinate
value in the high dimensional space. The linear
pattern among the elements of the dataset makes a
hyperplane in the high dimensional space. In order
to find the hyperplane, the normal vector of the
hyperplane is computed. To do so, singular value
decomposition (SVD) is used. The SVD
decomposition of a matrix includes left singular
matrix U R
m×m
, right singular matrix V R
n×n
and
singular values S R
m×n
in a way that
1
≥
2
≥ … ≥
r
≥ 0, r = min (m, n). The SVD of matrix M is
calculated as MV = US. According to Tomasi (2013)
the r
th
row of the left singular matrix represents the
normal vector of the hyperplane. The coherence of a
bicluster is calculated as how close the rows in a
bicluster are to the detected hyperplane. To find this
value, the root mean square error (RMSE) are
calculated by
(3)
Here, r
b
is the number of rows in the bicluster, n
is the normal vector of the hyperplane, c is the
constant value of the hyperplane, p
i
represents each
row in the bicluster, ǁ•ǁ denotes the norm value of a
vector and • is the inner product of two vectors.
2.4 Pareto Front
In a single objective minimization problem, we try
to find min[f(x)] where f is a scalar fitness function,
x S and S = {x R
m
: h(x) = 0, g(x) ≥ 0} (objective
space). The multi-objective optimization problem is
denoted as min[f
1
(x), …, f
n
(x)], x S and n > 1. In
multi-objective optimization, there is no unique
solution. Rather, there exists a set of solutions that
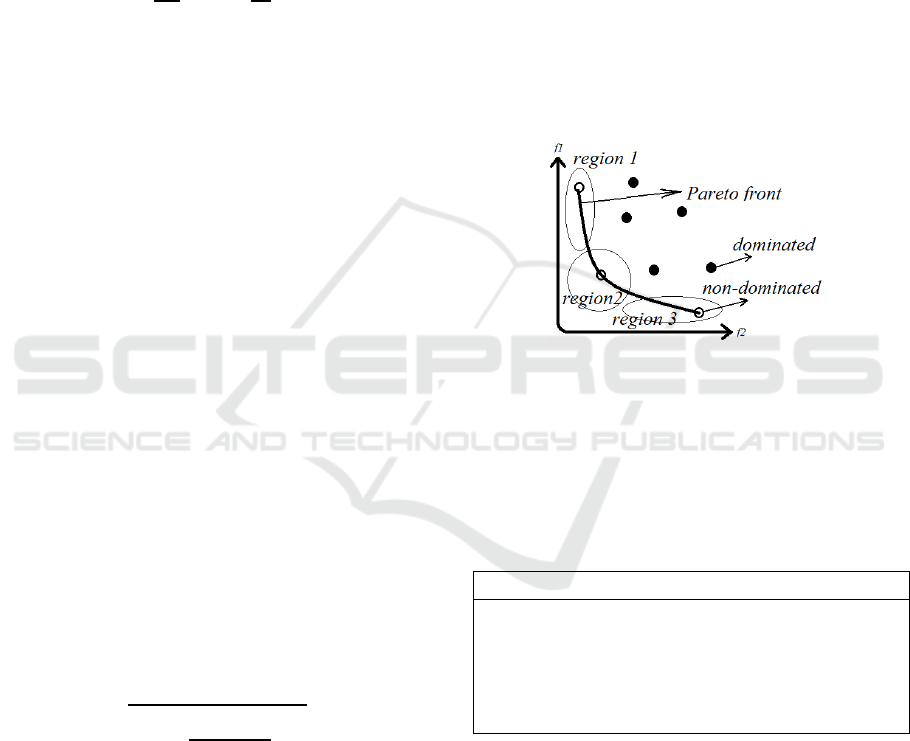
constitute the Pareto front solutions (Deb, 2014).
The Pareto front is defined by x* S, if f
i
(x*) ≤ f
i
(x)
for all i {1, …, n} (n is the number of objectives)
and at least one f
i
(x*) < f
i
(x). in this case, x* S
dominates x S (x* x). x* is called a non-
dominated individual and x is called a dominated
individual. These definitions are illustrated in Figure
3.
Figure 3: The objective space with two objectives f
1
and f
2
;
hollow dots represent non-dominated individuals and
filled dots represent dominated individuals; Pareto front is
clustered using the k-means algorithm to detect the final
individual.
In order to constitute the Pareto front in the
proposed method, several values are calculated for
each individual.
Pseudocode 3: The Pareto front constitution
1:
For each individual x in the
population p and the archive a do
2:
S(x)=|{x* | x* ap ˄ xx*}|
3:
R(x)=
x*
a
p ˄ x*
x
S(x*)
4:
D(x)=1/(d
xk
+ 2)
5:
F(x)=R(x)+D(x)
S(x) is the strength value of each individual and
it shows the number of individuals it dominates. R(x)
is the raw fitness value and it is the sum of the
strength values of the individuals that dominates
individual x. Non-dominated individuals are not
dominated by any individuals, so their raw fitness
value should equal to zero. Density value D(x) is a
small value (< 1) to differentiate between the
individuals with similar raw fitness and it is
calculated as the inverse of Euclidean distance
between individual x and the k
th
individual. Finally,
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
64
F(x) is the sum of raw fitness and density value and
it is the final value that is assigned to each
individual.
2.5 Crossover and Mutation
Single point crossover and bit string mutation are
applied to generate the next population. Rows and
columns undergo the crossover and mutation
separately.
The parents are selected based on binary
tournament selection by replacement from
individuals in the archive.
In crossover, a row or column index is randomly
selected. Then all the values in rows or columns
beyond that index are swapped between the two
parents. In mutation, a row or column index is
randomly selected and the value of that bit is
flipped.
2.6 Final Individual Selection
The last step of the proposed method is to find the
final individual among the Pareto front individuals.
The k-means algorithm is applied for this purpose.
The number of k is set to three in this study to
convert Pareto front to three separate regions and the
final individual is selected from region 2 as shown in
Figure 3. In this figure, f
1
denotes the size of the
bicluster and f
2
denotes RMSE.
3 RESULTS AND DISCUSSION
In order to qualify the performance of the proposed
method, we performed experiments on synthetic and
real gene expression datasets. We designed several
experiments with synthetic datasets to study
different aspects of the proposed algorithm. The
generated datasets include linear pattern biclusters
with different noise levels and different degree of
overlaps. In order to evaluate the performance of the
proposed algorithm, Jaccard index J is calculated for
each bicluster as in Equation (4):
(4)
where r
B
and c
B
are the rows and columns of the
detected bicluster, respectively, r
g
and c
g
are the
rows and columns of the ground truth, and |•|
represents the number of elements.
Jaccard index calculates the ratio of similar rows
and columns over the total number of rows and
columns in the detected bicluster and the ground
truth. The value of Jaccard index differs from 0 to 1
where 1 indicates 100% similarity and 0 indicates no
similarity.
The proposed method is also compared with
several methods such as CC (Cheng and Church,
2000), xMotifs (Murali and Kasif, 2003), ISA
(Ihmels et al., 2004) and OPSM (Ben-Dor et al.,
2003). The results of CC, xMotifs, ISA and OPSM
are obtained using BicAT toolbox (Barkow et al.,
2006). The default parameters are used to generate
their results.
3.1 Synthetic Datasets
In the first experiment, the noise tolerance of the
proposed method in noisy datasets is considered.
The dataset consists of 50 rows and 50 columns with
a noisy background generated by a uniform
distribution U(-5,5). There are five hidden biclusters
in the dataset. The size of each bicluster is 10×10
and their values are generated randomly in a way
that the element values vary over the range from 6 to
30 and contain a linear pattern. Gaussian noise with
variance from zero to one degraded the biclusters.
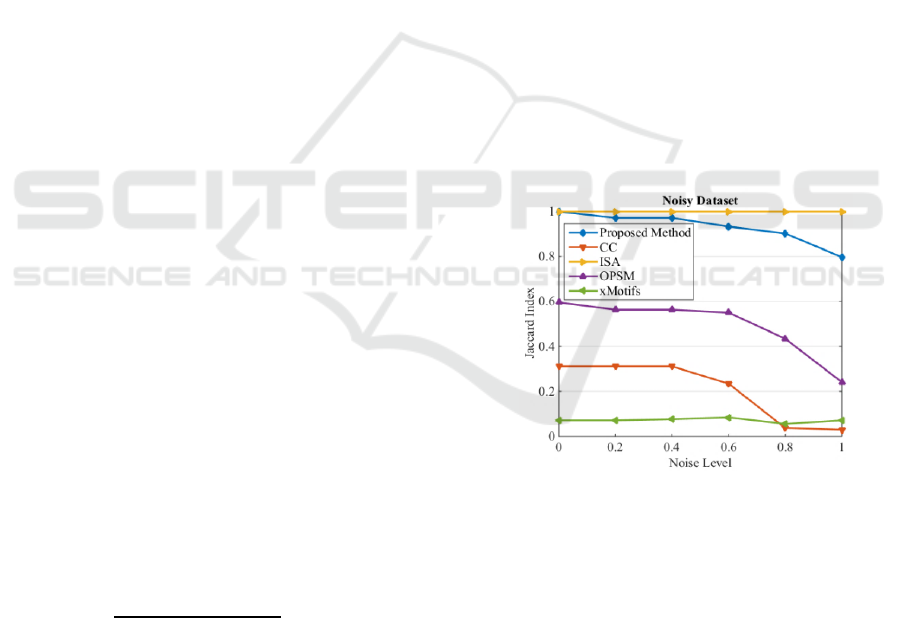
The results are visualized in Figure 4. The average
value of Jaccard index for all the detected biclusters
are used to plot the results.
Figure 4: Jaccard index of noisy dataset.
As it is clear ISA exhibits a robust behaviour
with respect to noise. The proposed method is still
relatively robust, but exhibited sensitivity and
dropped performance at higher noise levels. This is
caused by the use of sample Pearson correlation
coefficient, i.e. as the noise increases the tendency of
rows mismatch also increase. The xMotifs algorithm
performs the worst by detecting partially 2 biclusters
out of 5 biclusters. CC is able to detect only 3
biclusters which dropped to 2 when the noise level
increases. OPSM is able to detect all 5 biclusters
when the noise level is from 0 to 0.6 and it drops to
detect only 2 biclusters when the noise level is 0.8
Bicluster Detection by Hyperplane Projection and Evolutionary Optimization
65
and 1. The proposed method and ISA are able to
detect all five biclusters with different noise levels.
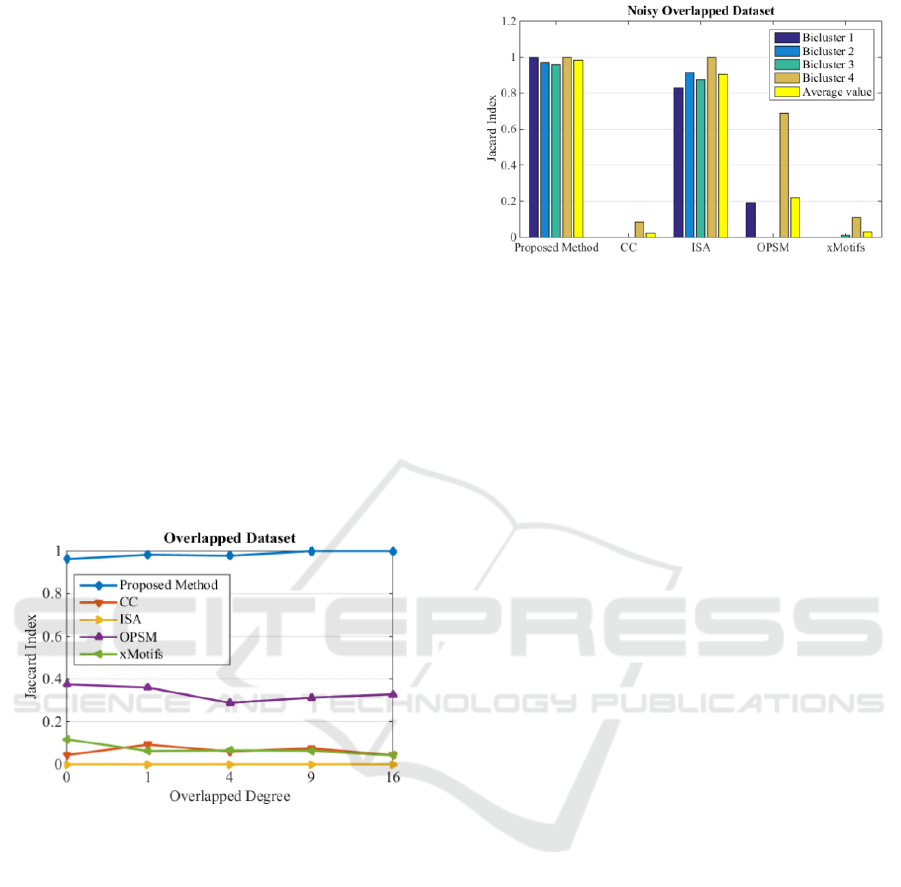
In the second experiment, the ability of the
algorithm in detecting overlapped biclusters is
studied. A dataset with the above property is
designed with 60 rows and 35 columns for the
background matrix with 2 biclusters of size 20×10
and 15×7. The results are visualized in Figure 5. The
average value of Jaccard index for the two biclusters
is used to plot the results. The y-axis shows the
overlapped degree, which is the number of
overlapped elements as in rows and columns e.g. 16
means 4 rows and 4 columns (4 degree).
In the noise level experiment, ISA performs very
poorly in this experiment and this algorithm is not
able to detect any bicluster at all. xMotifs and
OPSM are able to detect only one bicluster at any
overlapped degree. CC is able to detect only a few
rows and columns of both biclusters, as it is clear by
the value of its Jaccard index. The proposed method
out performed other methods in this experiment by
detecting almost 100% of all biclusters at different
overlapped degree.
Figure 5: Jaccard index of overlapped dataset.
The last experiment evaluates the performance of
the proposed method in detecting differing size of
biclusters in a dataset including both noisy and
overlapped biclusters. The background matrix
includes 200 rows and 60 columns with 4 biclusters.
The sizes of biclusters are 40×7, 25×10, 40×8 and
19×9. The biclusters are degraded by Gaussian noise
of variance 0.3 and the first two biclusters are
overlapped by degree of three (nine elements are
similar). The results are illustrated in Figure 6.
In this experiment, the proposed method
achieved the highest Jaccard index in all four
biclusters. The ISA algorithm is also able to detect
over 80% of the biclusters, especially when there is
no overlap in the biclusters.
Figure 6: Jaccard index of noisy overlapped dataset.
3.2 Real Dataset
Gene expression dataset is the expression level of
genes (rows) under several biological conditions
(columns). The purpose of biclustering is to discover
subgroups of genes, which are active in a subset of
conditions such that these groups show considerable
homogeneity from microarray data. In order to
assess the quality of detected biclusters in real
datasets, we performed an experiment on the yeast
Saccharomyces cerevisiae gene expression dataset
(Cho et al., 1998). The expression matrix of this data
set consists of 2884 genes (rows) and 17 conditions
(columns). In order to verify the functional
enrichment of detected genes in biclusters,
GenCodis (Tabas Madrid et al., 2012, Carmona Saez
et al., 2007, Nogales Cadenas et al., 2009) is used,
which has ten annotations for Saccharomyces
cerevisiae: GO Biological Process (BP); GO
Molecular Function (MF); GO Cellular Component
(CC); GOSlim Process (GP); GOSlim Function
(GF); GOSlim Component (GC); KEGG Pathways;
InterPro Motifs (IPM); Panther Pathways (PP); and
Transcription Factors (TF). From the 100 detected
biclusters, 100% achieved singular enrichment of
InterPro motifs, 95% achieved singular enrichment
of GOSlim Process, 93% achieved singular
enrichment of Panther Pathways, 80% achieved
singular enrichment of Go Biological Process, and
77% achieved singular enrichment of GO Cellular
Component. The remaining annotations had the
enrichment smaller than 10%. The graphical view of
co-occurrence annotation result for a detected
bicluster with 27 genes and 4 conditions is shown in
Figure 7.
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
66
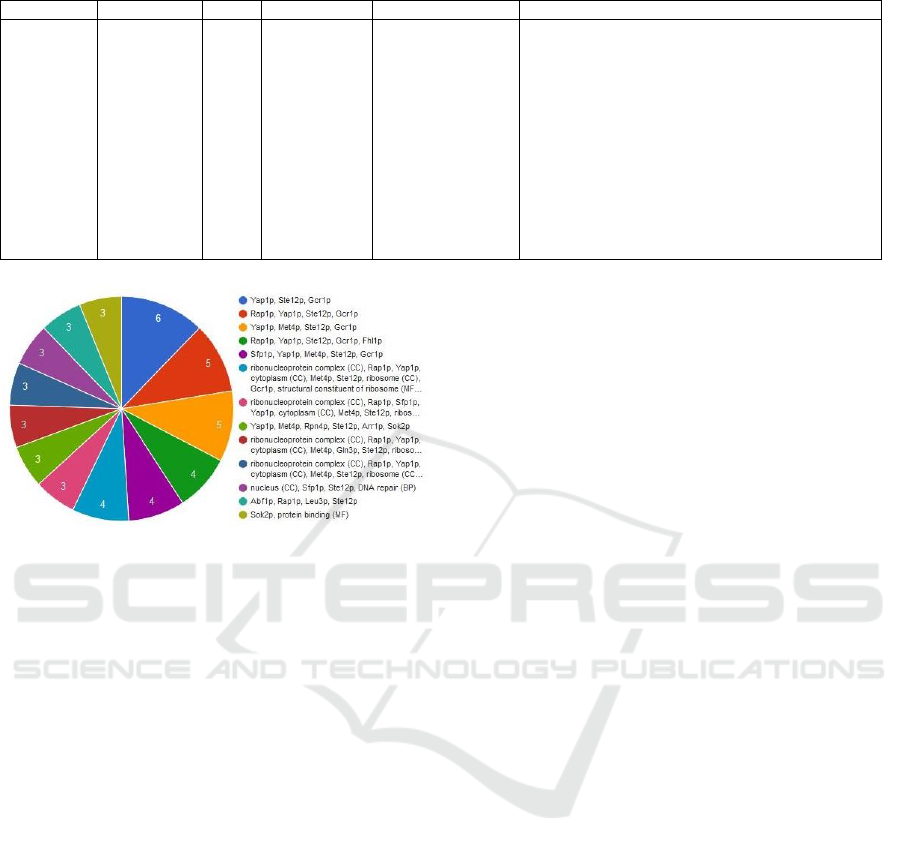
Table 1: Modular enrichment analysis of all annotations.
Genes
# Reference
# List
p-value
Corrected p-value
Annotations
YHL001W,
YDL081C,
YOL127W,
YKR094C
20 (7109)
4 (27)
6.54701e-07
4.97573e-05
GO:0030529: ribonucleoprotein complex (CC)
(Transcription factor) Rap1p
(Transcription factor) Yap1p
GO:0005737: cytoplasm (CC)
(Transcription factor) Met4p
(Transcription factor) Ste12p
GO:0005840: ribosome (CC)
(Transcription factor) Gcr1p
GO:0003735: structural constituent of ribosome (MF)
GO:0022625: cytosolic large ribosomal subunit (CC)
(KEGG) 03010: Ribosome
(Transcription factor) Ifh1p
GO:0002181: cytoplasmic translation (BP)
Figure 7: Number of genes per concurrent annotations.
Modular enrichment analysis (MEA) integrates
heterogeneous annotations from different sources,
which are BP, MF, CC, GP, GF, GC, KEGG, IPM,
PP, and TF, to find significant and enriched
combination of annotations in the list of detected
genes (Nogales Cadenas et al., 2009).
MEA of the smallest p-value for the same
bicluster as in Figure 8 is also presented in Table 1.
In this table, # reference shows the number of
annotated genes in the reference list. # list is the
number of annotated genes in the list of genes. From
27 detected genes in this bicluster, 4 genes have
modular enrichment of all annotations with a p-value
4.97573e-05. This indicates that the detected
bicluster is highly enriched.
4 CONCLUSIONS
In this paper, a new multi-objective evolutionary
based biclustering algorithm is introduced to
uncover hidden linear patterns in data. Our novel
contributions are as follows. First, our algorithm
takes advantage of the dimension information of the
hyperplane to reduce the time and space complexity
of the geometric biclustering. Secondly, our method
is able to detect different types of bicluster patterns
such as additive or multiplicative patterns without
pre-processing the dataset. Several synthetic
experiments are provided to validate the
performance of the algorithm. The results are also
compared with several well-known biclustering
methods, which show the superior performance of
the proposed method in different situations, i.e.,
noise and overlapping biclusters. Furthermore, a real
gene expression dataset is used to demonstrate the
accuracy of our method.
In the proposed method, only one bicluster is
detected at a time. For our future work, we want to
find multiple biclusters concurrently during the
optimization process.
ACKNOWLEDGEMENTS
Maryam Golchin is supported by the Australian
Government Research Training Program
Scholarship.
REFERENCES
Barkow, S., Bleuler, S., Prelić, A., Zimmermann, P. &
Zitzler, E. 2006. BicAT: A Biclustering Analysis
Toolbox. Bioinformatics, 22, 1282-1283.
Ben-Dor, A., Chor, B., Karp, R. & Yakhini, Z. 2003.
Discovering Local Structure in Gene Expression Data:
The Order-Preserving Submatrix Problem. Journal of
Computational Biology: A Journal of Computational
Molecular Cell Biology, 10, 373-384.
BISHOP, C. M. 2006. Pattern Recognition and Machine
Learning, New York, Springer.
Błażej, P., Mackiewicz, D., Grabińska, M., Wnętrzak, M.
& Mackiewicz, P. 2017. Optimization of Amino Acid
Replacement Costs by Mutational Pressure in
Bacterial Genomes. Scientific Reports, 7, 1061.
Carmona Saez, P., Chagoyen, M., Tirado, F., Carazo, J.
M. & Pascual Montano, A. 2007. GENECODIS: A
Web-Based Tool for Finding Significant Concurrent
Annotations in Gene Lists. Genome Biology, 8, R3.
Bicluster Detection by Hyperplane Projection and Evolutionary Optimization
67

Cheng, K.O., Law, N.F., Siu, W.C. & Liew, A. W. C.
2008. Identification of Coherent Patterns in Gene
Expression Data using an Efficient Biclustering
Algorithm and Parallel Coordinate Visualization.
BMC Bioinformatics, 9:210.
Cheng, Y. & Church, G. M. Biclustering of Expression
Data. Proceeding of Intelligent Systems for Molecular
Biology (ISMB), 2000. American Association for
Artificial Intelligence (AAAI), 93-103.
Cho, R. J., Campbell, M. J., Winzeler, E. A., Steinmetz,
L., Conway, A., Wodicka, L., Wolfsberg, T. G.,
Gabrielian, A. E., Landsman, D. & Lockhart, D. J.
1998. A Genome-Wide Transcriptional Analysis of the
Mitotic Cell Cycle. Molecular Cell, 2, 65-73.
Deb, K. 2014. Multi-Objective Optimization in Search
Methodologies. In: Burke, E. & Kendall, G. (eds.)
Search Methodologies. New York: Springer.
Divina, F. & Aguilar Ruiz, J. S. 2006. Biclustering of
Expression Data with Evolutionary Computation.
IEEE Transactions on Knowledge and Data
Engineering, 18, 590-602.
Gan, X. C., Liew, A. W. C. & Yan, H. Biclustering Gene
Expression Data Based on a High Dimensional
Geometric Method. Proceedings of 2005 International
Conference on Machine Learning and Cybernetics,
2005. IEEE, 3388-3393.
Gan, X. C., Liew, A. W. C. & Yan, H. 2008. Discovering
Biclusters in Gene Expression Data based on High-
Dimensional Linear Geometries. BMC Bioinformatics,
9:209.
Golchin, M. & Liew, A. W. C. 2017. Parallel Biclustering
Detection using Strength Pareto Front Evolutionary
Algorithm. Information Sciences, 415-416, 283-297.
Hough, P. V. 1962. Method and Means for Recognizing
Complex Patterns. United States patent application.
Ihmels, J., Bergmann, S. & Barkai, N. 2004. Defining
Transcription Modules using Large-Scale Gene
Expression Data. Bioinformatics, 20, 1993-2003.
Liew, A. W. C. 2016. Biclustering Analysis of Gene
Expression Data using Evolutionary Algorithms In:
IBA, H. & NOMAN, N. (eds.) Evolutionary
Computation in Gene Regulatory Network Research.
Hoboken, NJ, USA: John Wiley & Sons Inc.
Liu, B., Yu, C. W., Wang, D. Z., Cheung, R. C. & YAN,
H. 2014. Design Exploration of Geometric
Biclustering for Microarray Data Analysis in Data
Mining. IEEE Transaction on Parallel and Distributed
Systems, 25, 2540 - 2550.
Maulik, U., Mukhopadhyay, A. & Bandyopadhyay, S.
2009. Finding Multiple Coherent Biclusters in
Microarray Data using Variable String Length
Multiobjective Genetic Algorithm. IEEE Transactions
on Information Technology in Biomedicine, 13, 969-
975.
Maulik, U., Mukhopadhyay, A., Bhattacharyya, M.,
Kaderali, L., BRORS, B., Bandyopadhyay, S. & Eils,
R. 2013. Mining Quasi-Bicliques from HIV-1-Human
Protein Interaction Network: A Multiobjective
Biclustering Approach. IEEE/ACM Transactions on
Computational Biology and Bioinformatics, 10, 423-
435.
Murali, T. & Kasif, S. Extracting Conserved Gene
Expression Motifs from Gene Expression Data.
Proceedings of the Pacific Symposium on
Biocomputing, 2003. 77-88.
Nogales Cadenas, R., Carmona Saez, P., Vazquez, M.,
Vicente, C., Yang, X., Tirado, F., Carazo, J. M. &
Pascual Montano, A. 2009. GeneCodis: Interpreting
Gene Lists through Enrichment Analysis and
Integration of Diverse Biological Information. Nucleic
Acids Research, 37, W317-W322.
Seridi, K., Jourdan, L. & Talbi, E. G. 2015. Using
Multiobjective Optimization for Biclustering
Microarray Data. Applied Soft Computing, 33, 239-
249.
Shafiq, M. Z., Ilyas, M. U., Liu, A. X. & Radha, H. 2013.
Identifying Leaders and Followers in Online Social
Networks. IEEE Journal on Selected Areas in
Communications, 31, 618-628.
Tabas Madrid, D., Nogales Cadenas, R. & Pascual
Montano, A. 2012. GeneCodis3: A Non-Redundant
and Modular Enrichment Analysis Tool for Functional
Genomics. Nucleic Acids Research, 40, W478-W483.
Tomasi, C. 2013. Orthogonal Matrices and the Singular
Value Decomposition. Available:
https://www.cs.duke.edu/courses/fall13/compsci527/n
otes/svd.pdf [Accessed 17/01/2017].
Wang, D. Z. & Yan, H. 2013. A Graph Spectrum Based
Geometric Biclustering Algorithm. Journal of
Theoretical Biology, 317, 200-211.
Winterhalter, C., Nicolle, R., Louis, A., TO, C., Radvanyi,
F. & Elati, M. 2014. Pepper: Cytoscape App for
Protein Complex Expansion using Protein–protein
Interaction Networks. Bioinformatics, 30, 3419-3420.
Zhao, H., Liew, A. W. C., Xie, X. & Yan, H. 2008. A New
Geometric Biclustering Algorithm Based on the
Hough Transform for Analysis of Large-Scale
Microarray Data. Journal of Theoretical Biology, 251,
264-274.
Zitzler, E., Laumanns, M. & Thiele, L. SPEA2: Improving
the Strength Pareto Evolutionary Algorithm.
Proceedings of the Evolutionary Methods for Design,
Optimization and Control with Applications to
Industrial Problems (EUROGEN'01), 2001 Athens.
Greece. Eidgenössische Technische Hochschule
Zürich (ETH), Institut für Technische Informatik und
Kommunikationsnetze (TIK).
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
68
