PRACTICAL CHARACTERIZATION OF CELL-ELECTRODE

ELECTRICAL MODELS IN BIO-IMPEDANCE ASSAYS

Juan A. Serrano

1

, Pablo Pérez

1

, Andrés Maldonado

1

, María Martín

2

, Alberto Olmo

1

, Paula Daza

2

,

Gloria Huertas

1

and Alberto Yúfera

1

Instituto de Microelectrónica de Sevilla (IMSE), Universidad de Sevilla, Av Americo Vespuccio, S/N Sevilla, Spain

2

Departamento de Biología Celular, Facultad de Biología, Universidad de Sevilla, Av. Reina Mercedes, S/N, Sevilla

Keywords: Biomedical circuits; Impedance spectroscopy; Bioimpedance; Electrode-model; Oscillation Based Test

circuits (OBT); ECIS.

Abstract: This paper presents the fitting process followed to adjust the parameters of the electrical model associated to

a cell-electrode system in Electrical Cell-substrate Impedance Spectroscopy (ECIS) technique, to the

experimental results from cell-culture assays. A new parameter matching procedure is proposed, under the

basis of both, mismatching between electrodes and time-evolution observed in the system response, as

consequence of electrode fabrication processes and electrochemical performance of electrode-solution

interface, respectively. The obtained results agree with experimental performance, and enable the evaluation

of the cell number in a culture, by using the electrical measurements observed at the oscillation parameters

in the test circuits employed.

1 INTRODUCTION

Many research efforts have been devoted to find a

reliable and robust non-invasive technique to

estimate and study cell growth on a cell-culture

assays (Khalil, 2014; Lu, 2009; Lei, 2014;

Borkholder, 1998; Giaever, 1986) from several

viewpoint. It can be found: toxicology assays (Daza,

2013), cancer characterization (Pradham, 2014;

abdolahad, 2014) biochemical (Lourenco, 2016),

immune-assays (Dibao-Dina, 2015), stem cells

differentiation protocols (Reitingen, 2012), etc., that

look to quantify the number of cells for

characterizing a diversity of research objectives.

Bioimpedance based (BioZ) measurements

technique as ECIS, senses the electrical response

generated on a biological sample, the cell-culture,

when is excited with an AC electrical source,

voltage or current, at several frequencies, as

consequence of its conductivity properties. To obtain

confident results, ECIS technique requires precise

electronic circuits for picking-up the signals of

interest (Grimmes, 2008), and accurate electrical

models for the electrodes and cell-electrode-solution

systems, mandatory for decoding the electrical

measurements done by the circuits, and to express

them in terms of cell number.

Several works on BioZ modelling and monitoring

have been reported (Borkholder, 1998; Giaever,

1986; Huang, 2004), based on complex analytical

approaches or Finite Element (FE) simulations of the

whole cell-electrode-solution system. The obtained

results are applied to mono-layer cell-culture

configurations, fitting the proposed parameters

and/or electrical circuits, to model the cell-electrode-

solution. This article proposes a method to

characterize an electric model for the cell-electrode

interface in (Huang, 2004), using experimental data

gathered from several experiments carried out in our

research group. Our motivation is mainly derived

from analysis of the parameter evolution observed

on experiments, from the beginning of a cell growth

assays, and before to win the confluent or mono-

layer phase. These parameters associated to

electrode models change from one electrode to

100

Serrano, J., Pérez, P., Maldonado, A., Martín, M., Olmo, A., Daza, P., Huertas, G. and Yúfera, A.

Practical Characterization of Cell-Electrode Electrical Models in Bio-Impedance Assays.

DOI: 10.5220/0006712601000108

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 1: BIODEVICES, pages 100-108

ISBN: 978-989-758-277-6

another, and also in time, as consequence of

electrochemical processes in electrode-solution-cell

interfaces. The Fig. 1 shows the oscillation

frequencies measured with our technique (Huertas,

2015) for eight different cell cultures in a growth

curve assay. Each curve shows the oscillation

frequency measured as a function of the time. The

number of cell in the culture increases in time,

depending of the cycle division of the cell line.

Cell-cultures are done with commercial electrodes

(Applied Biophysics), for several number of initial

cells seeded: W1, W3: 2500 cells, W4, W5: 5000

cells; W7, W8: 10000 cells. From these responses, it

can be concluded that:

1) Equal or similar oscillation frequencies were

expected at the beginning of the assays,

because cell density is very low. However, a

wide frequency dispersion can be observed at t

= 0 h, for example.

2) It will be expected a constant frequency

response in cultures with only medium (W2

and W6). However, frequency response

decreases in time from 790 Hz to 760 Hz, after

one week (W2 and W6).

3) Responses of cultures with the same initial

cells (W8-W7, W4-W5, W1-W3) should lead

us to similar oscillation frequencies also. This

is no true: measured frequencies (see W4 and

W5 seeded with 5000 cells, for example) at the

same times, are quite different.

4) The frequency dynamic range of the resulting

frequencies changes between cultures, both for

the same initial and different number of cells.

This experimental performance observed it is also

detected for the amplitude of the oscillations (Fig.

1b). In all cases, measures were done with the same

circuit, so measuring mismatching was not due to

difference on circuit implementation. Considering

these data, the electrical model for electrode-cell-

solution system seems to change from electrode

sample-to-sample, and in time, for the same

electrode sample. This make not possible to consider

a “static” model for the parameter values of the

electrical model defining the performance of this

system, in the sense that these parameters (resistance

and capacitance values linked) will change for each

sample, and also progress in time. It is proposed in

this paper, on that basis of experimental result

analysed, a “dynamic” matching of these

parameters, once each experiment is finished. It is

true that this approach does not allow full prediction

of growth curves, but it will be demonstrated that

errors in measured parameters (frequency and

amplitude of the oscillations) are reduced by the

matching method proposed in the following.

Figure 1: Measured time evolution of the oscillation frequency (a)

and amplitude (b) of voltage signal Vcell. Curves corresponds to

2.500 cells (W1, W3), 5.000 cells (W4, W5) and 10.000 cells

(W7, W8), seeded at t = 0, into separate well pairs. Wells W2 and

W6 contain only medium.

The measurement system is described on section 2

with the sensing principle based on Oscillation

Based Test (OBT) (Huertas, 2015). A method to

solve the system equations is needed to obtain the

oscillation amplitude (a

osc

) and frequency (f

osc

)

(Huertas, 2015, Maldonado, 2016). Also, equations

proposed to match experimental results are derived

to put forward an electrical cell-electrode-solution

model. Section 3 will describe the followed fitting

process. Experimental results are described in

section 4, and finally, conclusions are summarized in

section 5.

2. MATERIALS AND METHODS

2.1 Cell-culture assay

Several experiments were carried out within one

week. The electrodes employed for our tests are

commercial electrodes from Applied Biophysics.

These electrodes contain 8 separated wells with ten

Practical Characterization of Cell-Electrode Electrical Models in Bio-Impedance Assays

101

circular biocompatible gold microelectrodes of 250

m diameter. The biological sample under test is

formed by Chinese hamster ovarian fibroblasts. This

cell line is identified as AA8 (American Type

Culture Collection). This sample is immersed in

McCoy’s medium supplemented with 10 % (v/v)

foetal calf serum; 2mM L-glutamine, 50 μg/ml

streptomycin and 50 U/ml penicilin. The growing

environment is set at 37oC and 5% CO2 in a humid

atmosphere. Different initial number of cells was

planned for our experiments, either 2500, 5000 or

10000.

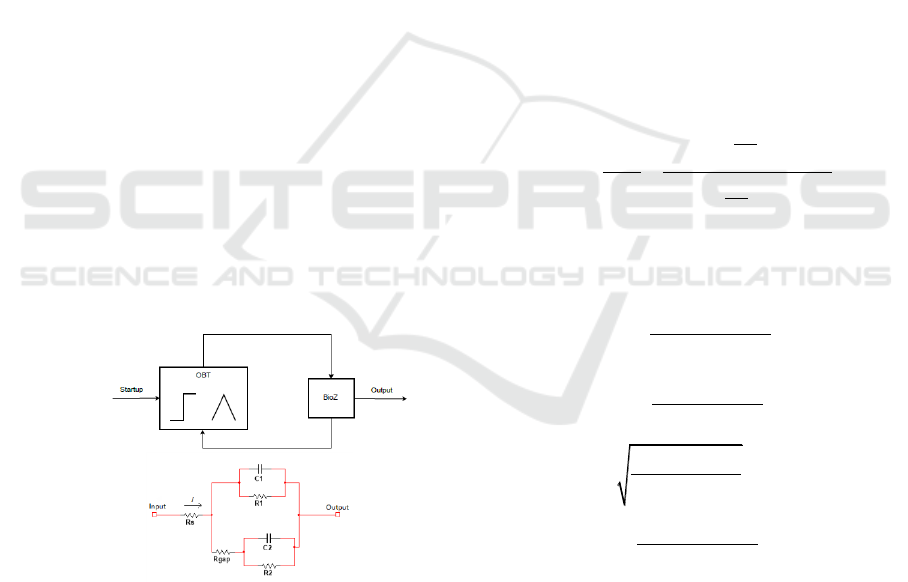
2.2 Cell-electrode electrical model

The biological sample under test is located on a

two electrode system. The first one acts as a

reference electrode and the second one is the

measurement electrode. Cells are deployed on the

electrodes alongside with medium solution. The

electrical model describing this cell-electrode

interface is presented on Fig 2a. This model has

been explored on the literature in (Borkholder, 1998;

Huang, 2004; Huertas, 2015). The sample is the

connected to the oscillator as shown in Fig 2b, to

build the biological sensor. A start-up signal is

provided to the OBT to provide faster measurements

and assure the optimal oscillation point for the

system thus avoiding nonlinear behaviours of the

electrical model. As it was mentioned in the

previous section, the variation of the BioZ implies a

change on the oscillator values, which is directly

relate to the fill-factor, ff, on the cell culture, thus

allowing us to measure cell population and growth.

Figure 2. (a) Electric model of cell-electrode (BioZ). (b)

Measuring circuit diagram.

The BioZ main electrical-model parameters are C,

the double-layer capacitance arising from the cell

electrode complex and R, the transfer resistance that

represents biological sample resistance. Both

elements are placed in parallel (Huang, 2004;

Huertas, 2015). Fill-factor is presented as the cell

covered area ratio in the electrodes (if there are not

cells, is 0, and it is 1 when electrode is fully

covered).

1

2

/ (1 )

.(1 )

/

.

R R ff

C C ff

R R ff

C C f





(1)

where C

1

and R

1

account for the empty

microelectrodes contribution to the electrical

response of the biological sample, and C

2

and R

2

depict the electrical response generated by the

electrodes covered by cells. The R

s

models the

resistance which current must overtake to arrive at

reference electrode. Finally, R

gap

represents the

resistance shaped at the gap or interface region

between cell and electrode.

The model fitting process requires further

knowledge on the circuit transfer function. Having

analyzed the electrical model, next step is to define

the transfer functions for the measuring system

(Huertas, 2015; Maldonado 2016; Pérez, 2017). The

analysis is presented below and summarized in eq.

(2).

22

2 1 0

22

()

o

k s k s k

Vs

Q

Zs

Is

ss

Q









(2)

where,

2 s

kR

(3)

1

12

.

2

gap

s

gap

RR

kR

R R R





(4)

12

0

12

()

gap

s

gap

R R R

kR

R R R







(5)

12

0

2

()

gap

R R R

R RC







(6)

12

.

2

gap

o

gap

R RC

Q

R R R







(7)

During the modelling adjustment process, three

challenges were identified:

• Fill-factor: This is the measurement we aim to

find out. This work is part of the process to

obtain a reliable ff measurement out of the a

osc

and f

osc

acquired from the implemented sensor.

To fit the model, we need to use a reliable

reference for ff other than the measurements

itself. This ff reference may be obtained from the

microscopic analysis of the cell cultures under

(a)

(b)

BIODEVICES 2018 - 11th International Conference on Biomedical Electronics and Devices

102

test, but it can be the final solution because the

ultimate goal is getting a sensing robust system

to measure the number of cells without touch the

cell-culture assay until the end of experiment.

• Non-constant value of the BioZ parameters along

ff: The following Bode diagrams acquired from

biological samples under test (Fig. 3) shows that

magnitude at high frequencies can be used to

determine R

s

. However it is important to remark

the differences among different days (cells are

growing, hence increasing ff), which implies also

variations on the R

s

obtained values.

Figure 3: Bode diagram, magnitude and phase, for a single well

during the experiment.

• Each well starts at different values of f

osc

and

a

osc

: Fig. 4 illustrates small differences on each

well in magnitude and phase during the

experiment starting period. Experiment begins at

several hundred Hertz, below 1 kHz, at this

operation point each well has different frequency

and amplitude values. The sample contains eight

wells, each of them contain only either medium

or cells with medium. These one start in an initial

value of f

osc

and a

osc

which does not match with

expected theoretical values for low ff.

Experimental measurements tend to fit the

expected values around 20 hours periods,

corresponding to the cell division cycle.

Figure 4: Bode diagram for each well on the first day.

2.3 Oscillator

Complete closed-loop system (circuit with BioZ)

behaves like an oscillator (Fig 2 (b)). This is due to

the circuit containing a non-linear element, a

comparator in the feedback loop. Non-Linear system

can present oscillations with a constant amplitude

and frequency without external stimulation (limit-

circles). According to describing-function method,

non-linear component of the system can be

linearized like it is presented in equation,

( , )

Y

NA

X





(8)

where N(A, ) is an approximate linear form of

the non-linear element, X is the sine input

amplitude, Y is the amplitude of output fundamental

harmonic component, and  is phase difference of

output fundamental harmonic component. In this

case, describing function of comparator is shown in

eq. (9).

4

( ) .( cos( ) sin( ))

ref

hh

osc

V

NA

a





  

(9)

where V

ref

is the reference voltage for the

comparator and 

h

is defined in eq. (10),

sin( )

h

osc

h

a





(10)

being h the comparator hysteresis. The shape of

describing-function has been defined. Additionally,

the behaviour of the system is determined by the

characteristic equation (11). If a solution exists for

the given system, with a specific amplitude and

frequency, means that the system is oscillating at

that frequency with given amplitude.

1 ( ) ( ) 0G j N A





(11)

where G(j) is the transfer function for the linear

component of the system, which is the measurement

circuit without the comparator and with BioZ. This is

fulfilled when the following conditions are met:

1. A non-linear component must be part of the

system. In this case non-linear part is the

comparator.

2. Non-linear component does not depend on time.

3. Linear parts behave like a low-pass filter to

guarantee that high frequency harmonics do not

affect non-linear part. The system contains a

band-pass filter, which avoid the input of non-

fundamental harmonic components of the signal

in the comparator.

Practical Characterization of Cell-Electrode Electrical Models in Bio-Impedance Assays

103

4. Non-linearity is symmetrical, so there is not any

DC component in the output signal when input

signal is a sine.

With this method, theoretical a

osc

and f

osc

can be

obtained depending on system parameters. Therefore,

it is necessary to characterize a system model to

compare theoretical and experimental results.

2.4 Sensitivity

To characterize an empirical model it is necessary

to understand how changes in model parameters

affect amplitude and frequency of the oscillation

signal.

2.4.1 Fill-factor

It is important to understand the effects of fill-

factor in the model of BioZ. Considering ff →0, we

can conclude that R

2

→∞ and C

2

→0. Transfer

function for BioZ is presented in eq. (12).

0

( ) ( || )

ff s

Z s R C R





(11)

0

1

.( )

( || )

()

1

s

ff

Rs

R R C

Zs

s

RC









(12)

where Z

ff→0

(s) is the impedance of cells for ff→0.

Considering ff→1 we can conclude that R

1

→∞ and

C

1

→0. Transfer function for BioZ is presented in eq.

(14).

1

( ) ( || )

ff s gap

Z s R C R R



  

(13)

1

()

( ) ( )

1

s gap

ff s gap

R R R

s

RC R R

Z s R R

s

RC











(14)

where Z

ff→1

(s) is the impedance of cells having ff→1.

From equations (13) and (14), the following

statements are deduced. Low ff (experiment

beginning) implies that Rgap does not affect model

behavior. However, high ff implies greater effect on

system model.

2.4.2 Poles and zeros location

It is necessary to identify the position of pole and

zero in transfer function in eq. (14). These are

defined on eq. (15) and eq. (16).

11

( 0)

2 ( | ) 2

z

ss

f ff

C R R CR



  

(15)

1

( 0)

2

p

f ff

RC





(16)

It is possible now to calculate R

S

and R using eqs.

(17) and (18),

0

lim( )( ))

ff s

f

Z s R R





(17)

1

lim( )( ))

ff s

f

Z s R







(18)

by knowing the Bode diagram of the real system

when the experiment starts and finishes. This task

has been performed in three different experiments.

Fig. 4 shows Bode diagrams for well number one

during each day of the experiment. First approach

was to try to fit the model using such Bode diagrams

but it was very difficult to find a suitable fit, as it is

illustrated on Fig. 5.

Firstly, the model of BioZ is far from perfect, so that

it is not possible to get a Bode diagram of the model

similar to experimental Bode diagram. Secondly, it

is difficult to reproduce similar magnitude and phase

at the same frequency in model and experiment.

Thus, it is necessary to find another way to fit the

model. However, it is important to remark that zero

is approximately at 15 kHz in every well and

considered ff. To prove the use of 15 kHz as the zero

value it is compared to another experiment, this is

shown in Fig. 6. This experiment was performed in

one day. Different cells concentrations were put on

all wells, in ascending order, from well one

(medium) until well eight (upper cells

concentrations). Objective of this experiment is to

obtain the Bode diagram of the system for each cell

concentration without medium degradation.

Figure 5: First approach fitting.

BIODEVICES 2018 - 11th International Conference on Biomedical Electronics and Devices

104

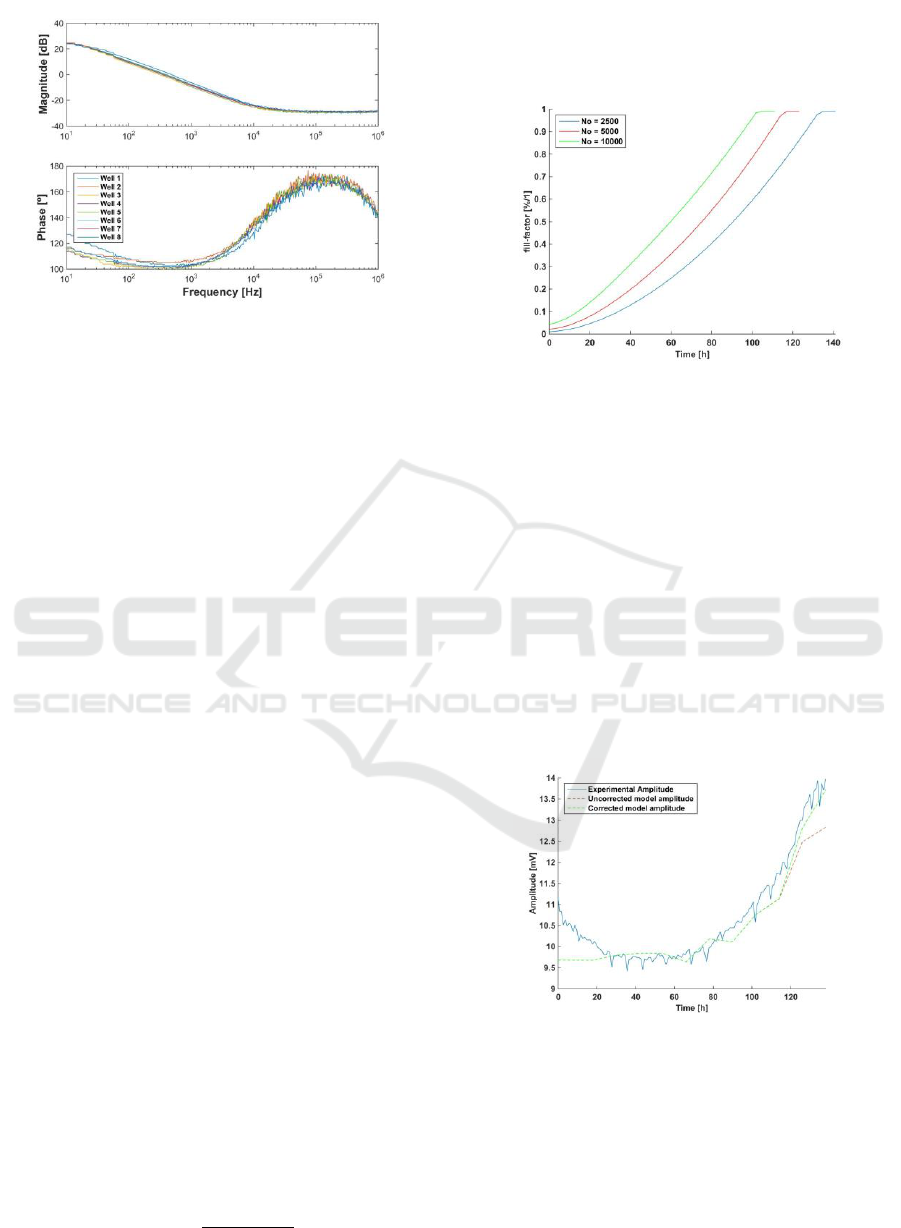
Figure 6: One day experiment

2.4.3: Other parameters

There are some parameters which are yet not

characterized. It is important to consider the effect of

these parameters in frequency and amplitude of the

oscillator. Thank to electric simulator Multisim (and

comparing with theoretical results of Matlab), the

effects can be estimated using parametric sweeping.

Some conclusions are provided below:

• ff→0 (beginning of the experiment):

o Initial frequency can be selected only with

position of the pole fp.

o Initial amplitude can be selected using R

s

and f

p

.

The R

s

effect is significantly higher.

• ff→1 (end of the experiment). Frequency can be

selected using R

gap

, however it is important to

remark that R

gap

affect final amplitude as well.

It is possible to characterize the model parameters

using this conclusions and eqs. (15) and (16).

2.5 Estimation of ff

During first experiment, which Bode diagrams

were measured, wells were also photographed to

estimate ff once a day until the end of the

experiment. However, estimation of ff using photos

was not accurate enough. On the following, a math

temporal evolution estimation method for ff is

presented.

Considering the area of the well is A

w

=0.8 cm

2

,

approximate radio of cells is r

cell

= 10 μm

2

. Knowing

the number of cells at the beginning of experiment

as N

o

and the division time of cells as t

r

= 18 hours,

it is possible to define a growth curve for (ff) in time.

( ) 2

k

o

N k N

(19)

2

()

cell

k

w

N k r

ff

A





(20)

Using eqs. (19) and (20), it is possible to calculate

the number of cells and ff at a given moment, k, as is

shown in Fig. 7.

Figure 7: Estimated evolution of ff with No = 2.500, 5.000 and

10.000 cells.

3. Fitting model

There is enough information to fit the experiment

model. Keeping in mind that f

z

= 15 kHz, the

algorithm to obtain the model:

Step 1: Select f

p

using experiment initial frequency.

Step 2: Select R

s

using experiment initial amplitude.

Step 3: Select R

gap

using experiment final frequency.

Following this three steps, it is possible to fit a

model which behaves similar to the experimental

results. Even so, there is an amplitude error that

increases with ff, observed in Fig. 8.

Figure 8: Comparison between experimental amplitude,

uncorrected and corrected model amplitudes.

To solve this problem, first approach is to use the

work presented in (Huang, 2004), but performing an

alternative correction of R

s

with ff. Moreover, it is

decided that parameter R

s

, which is calculated for ff

→0, is an initial value of R

s

, named R

si

. R

s

grows

with ff during the whole experiment. R

s

must match

Practical Characterization of Cell-Electrode Electrical Models in Bio-Impedance Assays

105

the amplitude in ff → 1. This is represented on eq.

(21).

( ) . ( )

n

s si s

R k R R ff k  

(21)

where R

si

is the initial value for R

s

, R

s

is the range

of R

s

from ff = 0 to ff = 1, and n decided the growth

rate of R

s

until the maximum value (n=4 in this

case). The eq. (21), represents R

s

variation, allowing

R

s

to reach its final value when well is full (R

s

(ff

→1) = R

si

+R

s

). Finally, it is necessary to complete

the fitting model selecting R

s

.

Step 4: Select R

s

using experiment final amplitude.

The Fig. 7 shows the effect of the evolution of R

s

,

with good agreement for amplitude estimation.

4. RESULTS

This section presents the results of the fitting

method proposed before. Results are shown from

Figures 9 to 11 (each figure shows one well with

cells), and start from three different values of initial

number of cells: 2500, 5000 and 10.000 cells. For

each initial number of seeded cells, the time

evolution of the ff is calculated according to eq. (20),

and then, electrical simulations are performed in

Multisim, considering the proposed parameters

evaluated for the electrical model. The oscillation

parameters, f

osc

and a

osc

, are measured and compared

with the experimental ones.

In all cases, the amplitude and frequency errors

are reduced, being possible to make the cell number

estimation, at every time of the experiment. Errors

observed at amplitudes are lower than frequencies.

One of the main problems to fit the models of each

well of the experiments is the small range of a

osc

and

f

osc

found on the available data. Using this method,

theoretical results are similar to experimental results.

5. CONCLUSIONS

It has been presented a fitting procedure to

assign values to proposed parameters of the

electrical-model in cell cultures assays. The proposal

is useful in ECIS experiments to define the number

of cells in a culture, giving a general solution, not

only for cell monolayer configurations. For several

initial

values of cell seeded, results show that fitting

models

provide low error estimations for ff values.

Thanks

to ff estimation and R

s

modification, it is

possible

to fit a model for each well knowing only

a

osc

y

f

osc

values at beginning and end of the

experiment.

A Matlab script has been developed to do

this

work automatically when experiment ends,

either

using theoretical equations of the system or

using the

software Multisim software to execute

electrical simulations.

Figure 9: Comparison of frequencies and amplitudes between

model and experiment for No = 2500 cells.

BIODEVICES 2018 - 11th International Conference on Biomedical Electronics and Devices

106

Figure 10: Comparison of frequencies and amplitudes between

model and experiment for N

o

= 5.000 cells.

Figure 11: Comparison of frequencies between model and

experiment for N

o

= 10.000 cells.

ACKNOWLEDGMENT

This work was supported in part by the Spanish

founded Project: Integrated Microsystems for cell

culture test (TEC2013-46242-C3-1-P), co-financed

with FEDER program.

REFERENCES

Abdolahad, M., Shashaani, H., Janmaleki, M., Mohajerzadeh, S.,

2014. “Silicon nano grass based impedance biosensor for

label free detection of rare metastatic cells among primary

cancerous colon cells, suitable for more accurate cancer

staging,”. Biosensors and Bioelectronics, 59, 151-159.

Applied Biophysics (http://www.biophysics.com/).

Borkholder, D. A., 1998. ”Cell based biosensors using

microelectrode”. Ph D. Thesis.

Daza, P., Olmo, A., Cañete, D., Yúfera, A., 2013. “Monitoring

living cell assays with bio-impedance sensors”. Sensors and

Actuators B: Chemical. 176, 605-610.

Dibao-Dina, A., Follet, J., Ibrahim. M., Vlandas, A., Senez, V.,

2015.“Electrical impedances sensor for quantitative

monitoring of infection processes on HCT-8 cells by the

water borne parasite Cryptosporidium,” at Biosensors and

Bioelectronics, 66, 69-76.

Grimnes, S. and Martinsen, O., 2008. Bio-impedance and

Bioelectricity Basics. 2nd edition. Academic Press, Elsevier.

Giaever, I. and Keese, C. R., 1986. “Use of Electric Fields to

Monitor the Dynamical Aspect of Cell Behaviour in Tissue

Cultures”. IEEE Transactions on Biomedical Engineering,

vol. BME-33, nº 2, 242-247.

Huang, X., Nguyen, D., Greve, D. W. And Domach, M. M., 2004.

”Simulation of Microelectrode Impedance Changes Due to

Cell Growth” IEEE Sensors Journal, vol. 4, n

o

. 5.

Huertas, G., Maldonado-Jacobi, A., Yúfera, A., Rueda, Huertas,

J- L., 2015. “The Bio-Oscillator: A Circuit for Cell-Culture

Assays,” IEEE Trans on CAS-II. 62, 164-168.

Khalil, S. F., Mohktar, M. S. and Ibrahim, F., 2014. ”The Theory

and Fundamentals of Bioimpedance Analysis in Clinical

Status Monitoring and Diagnosis of Diseases” Sensors,

14(6): 10895 – 10928.

Lei, K. F., 2014. ”Review on Impedance Detection of Cellular

Responses in Micro/Nano Environment” Micromachines.

Lourenco, F., Ledoa, C. A., Laranjinhaa, J., Gerhardtc, G. A.,

Barbosa, R. M., 2016. “Microelectrode array biosensor for

high-resolution measurements of extracellular glucose in the

brain,”. Sensors and Actuators B: Chemical. 237, 298-307.

Lu, Y-Y., Huang, J-J. and Cheng, K-S., 2009. ”The design of

electrode-array for monitoring the cellular bioimpedance”

Industrial Electronics and Applications.

Maldonado, A., Huertas, G., Rueda, A., Huertas, J. L., Pérez, P.

and Yúfera, A., 2016. ”Cell-culture measurements using

voltage oscillations” IEEE 7

th

Latin American Symposium

on CAS (LASCAS).

Pérez, P., Maldonado-Jacobi, A., López, A., Martínez, C., Olmo,

A., Huertas, G. and Yúfera, A., 2017. “Remote Sensing of

Cell Culture Assays. Cell Culture,” Chap 4: New Insights

in Cell Culture Technology. 135-155. InTech Europe.

Pradham, R., Mandal, M., Mitra, A., Das, S., 2014. “Monitoring

cellular activities of cancer cells using impedance sensing

devices”. Sensors and Actuator B: Chemical, 193, 478-483.

Reitinger, S., Wissenwasser. J., Kapferera, W., Heer, R.,

Lepperdinger, G., 2012. “Electric impedance sensing in cell

substrates for rapid and selective multipotential

differentiation capacity monitoring of human mesenchymal

stem cells,”. Biosensors and Bioelectronics, 34, 63-69.

Practical Characterization of Cell-Electrode Electrical Models in Bio-Impedance Assays

107