
Orthogonal Compaction using Additional Bends
Michael J
¨
unger
1
, Petra Mutzel
2
and Christiane Spisla
2
1
University of Cologne, Cologne, Germany
2
TU Dortmund, Dortmund, Germany
Keywords:
Orthogonal Compaction, Graph Drawing, Total Edge Length, Bends, Flow-based Compaction.
Abstract:
Compacting orthogonal drawings is a challenging task. Usually algorithms try to compute drawings with small
area or total edge length while preserving the underlying orthogonal shape. We suggest a moderate relaxation
of the orthogonal compaction problem, namely the one-dimensional monotone flexible edge compaction prob-
lem with fixed vertex star geometry. We further show that this problem can be solved in polynomial time using
a network flow model. An experimental evaluation shows that by allowing additional bends we were able to
reduce the total edge length and the drawing area.
1 INTRODUCTION
The compaction problem in orthogonal graph draw-
ing deals with constructing an area-efficient draw-
ing on the orthogonal grid. Every edge is drawn
as a sequence of horizontal and vertical segments,
where the vertices and bends are placed on grid
points. Compaction has been studied in the context
of the topology-shape-metrics approach (Batini et al.,
1986). Here, in a first phase a combinatorial embed-
ding is computed that determines the topology of the
layout with the goal to minimize the number of cross-
ings. In the second phase, a dimensionless orthogo-
nal shape of the graph is determined by fixing the an-
gles between adjacent edges and the bends along the
edges. The goal is to minimize the number of bends,
which can be done in polynomial time for a fixed em-
bedding (Tamassia, 1987). In the third phase, metrics
are added to the orthogonal shape. In this context, first
the coordinates of vertices and bends are assigned to
grid points so that the given orthogonal shape is main-
tained. Finally, the (orthogonal) compaction problem
asks for a drawing minimizing geometric aestetic cri-
teria, such as the area of the drawing or the total edge
length. The shape is not allowed to change.
Since the orthogonal compaction problem is NP-
hard (Patrignani, 1999), in practice heuristics are used
that fix the x- (or y-, resp.) coordinates and solve
the resulting compaction problem in one dimension.
Given an initial drawing, the one-dimensional com-
paction problem with the goal of minimizing the
height (or width, resp.) of the layout can be trans-
formed to the longest path problem in a directed
acyclic graph. If in addition the total edge length shall
be minimized, the problem can be solved by comput-
ing a minimum cost flow.
The topology-shape-metrics approach aims at
drawings with a small number of crossings, a small
number of bends, and a small drawing area. These
goals are addressed in this order. And indeed, com-
pared with other drawing methods, the number of
crossings and bends is relatively small (Di Battista
et al., 1997). However, the layouts often contain large
areas of white space. It seems that the goal of get-
ting a small drawing area has not been achieved so
far. Consider the drawing in Fig. 1(a) which contains
large areas of white space due to shape restrictions.
By introducing two bends on one of the edges the
drawing area can be reduced drastically. This moti-
vates us to study a compaction problem in which the
shape conditions are relaxed.
This brings us back to the origin of the or-
thogonal compaction problem in VLSI-design (see,
e.g., Lengauer (1990)). In contrast to the compaction
problem considered in graph drawing, even the per-
mutation of wires along the boundary of a component
(and hence, changing the embedding) is allowed.
We suggest a moderate relaxation of the orthogo-
nal compaction problem. More precisely, we suggest
to study the one-dimensional monotone flexible edge
compaction problem with fixed vertex star geometry,
henceforth the Fled-Five compaction problem, which
asks for the minimization of the vertical (horizontal,
resp.) edge length and allows changing the orthogonal
shape of edges, but preserves the x-monotonicity (y-
144
Jünger, M., Mutzel, P. and Spisla, C.
Orthogonal Compaction using Additional Bends.
DOI: 10.5220/0006713301440155
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages
144-155
ISBN: 978-989-758-289-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

monotonicity, resp.) of edge segments and prohibits
changing the directions of the initial edge segments
around the vertices (vertex star geometry). We present
a polynomial-time algorithm based on a network flow
model that solves the Fled-Five compaction problem
to optimality. Our computational results show that re-
peated application of Fled-Five compaction in x- and
y-direction is able to reduce the total edge length and
the drawing area at the expense of additional bends.
This paper is organized as follows. We recall the
state of the art in Sect. 2 and some basic definition
about orthogonal graph drawing and especially the
compaction phase in Sect. 3. We present our new al-
gorithm in Sect. 4 and evaluate it experimentally in
Sect. 5.
(a) (b)
Figure 1: (a) A drawing with large areas of white space due
to shape restrictions. (b) Introducing two additional bends
to one edge of the drawing leads to a smaller drawing.
2 STATE-OF-THE-ART
Patrignani (1999) has shown that planar orthogonal
compaction is in general NP-hard and Bannister et al.
(2012) have given inapproximability results for the
nonplanar case. But for some special cases there ex-
ist polynomial-time algorithms, e.g., if all faces are
of rectangular shape (Di Battista et al., 1999) or if
all faces are so-called turn-regular (Bridgeman et al.,
2000) or have a unique completion (Klau and Mutzel,
1999). Klau and Mutzel (1999) suggested a branch-
and-cut approach to solve an integer linear program
based on extending a pair of constraint graphs.
However, in practice, heuristics are used which it-
eratively fix the x-, and then the y-coordinates, and
solve the resulting one-dimensional compaction prob-
lem. This process is repeated until no further progress
is made. One-dimensional compaction algorithms of-
ten use either network flow techniques or a longest
path method in order to assign integer coordinates to
the vertices, see, e.g., Kaufmann and Wagner (2001)
for an overview. An experimental comparison of pla-
nar compaction algorithms was presented by Klau
et al. (2001).
There has been some work to improve the qual-
ity of a drawing by changing its shape, e.g., F
¨
oßmeier
et al. (1998) or Six et al. (1998). The former uses
shifting and resizing vertices and modifies the shape
of the edges in order to save area and bends, and the
latter may additionally change the topology to im-
prove the drawing. But most compaction algorithms
for planar 4-graphs take as input an orthogonal repre-
sentation and try to produce compact drawings with
respect to that representation. This can lead to an un-
necessarily large drawing area with unused space. Of-
ten better results in terms of area and edge length can
be achieved if the orthogonal shape can be altered, as
we have seen in Fig. 1. On the other hand, it might
be desirable to not change a given drawing too much
in order to preserve the mental map. In some applica-
tions, like layouting data flow diagrams, edges should
start and end at specific points or sides of the ver-
tices (Sp
¨
onemann et al., 2010). These so-called port
constraints would correspond to fixing the initial edge
segments around vertices (vertex star geometry) in an
orthogonal representation while leaving flexibility to
the edges.
3 NOTATION AND
PRELIMINARY RESULTS
In this section we give basic definitions and nota-
tions. For more details on orthogonal drawings and
graph drawing in general see, e.g., Di Battista et al.
(1999), Kaufmann and Wagner (2001) or Tamassia
(2013).
3.1 Orthogonal Graph Drawing
For the rest of this paper we restrict ourselves to undi-
rected 4-graphs, i.e. graphs whose vertices have at
most four incident edges. A graph G = (V,E) with
|V | = n and |E| = m is called planar if it admits a
drawing Γ in the plane without edge crossings. Such
a planar drawing of G induces a (planar) embedding,
which is represented by a circular ordered list of bor-
dering edges for every face. The unbounded region of
a planar drawing is called external face.
An orthogonal representation H is an extension
of a planar embedding that gives combinatorial infor-
mation about the orthogonal shape of a drawing. For
every edge we provide information about the bends
encountered while traversing the edge and the angle
formed at vertices by two consecutive edges. If one
of these angles is 270
◦
or 360
◦
we associate with v a
reflex corner. An orthogonal representation is called
normalized if it has no bends. An orthogonal grid
Orthogonal Compaction using Additional Bends
145
drawing Γ of G is a drawing in which every edge is
drawn as a sequence of horizontal and vertical edge
segments and every vertex and bend has integer coor-
dinates. Such a drawing induces an orthogonal rep-
resentation H
Γ
and a star geometry for every vertex
fixing the directions of the initial line segments of its
incident edges. If an edge first turns to the right and
then to the left, or vice versa, we call this a double
bend and the edge segment between these two bends
a middle segment. Every orthogonal representation
can be normalized by replacing all bends in H
Γ
with
dummy vertices of degree two, thus adding vertices to
G and Γ.
Since our new approach is based on a network
flow model for one-dimensional compaction, we will
give a brief introduction to minimum cost flows here.
For more information about network flows, see Ahuja
et al. (1993). Let N = (V
N
,E
N
) be a directed graph.
Whenever we talk about flows we will call N a net-
work, the members of V
N
nodes and the members
of E
N
arcs (in contrast to vertices and edges in an
undirected graph). Every arc a has a lower bound
l(a) ∈ R
≥0
, an upper bound u(a) ∈ R
≥0
∪ {∞}
and a nonnegative cost c(a). A demand b(n) ∈ R
is associated with every node. We call a func-
tion x : A → R
≥0
a flow if x satisfies the following
conditions:
capacity constraint:
l(a) ≤ x(a) ≤ u(a) ∀ a ∈ E
N
(1)
flow conservation:
∑
a=(k,l)
x(a) −
∑
a=( j,k)
x(a) = b(k) ∀ k ∈ V
N
(2)
A minimum cost flow is a flow x with minimum to-
tal cost c
x
=
∑
a∈E
N
x(a)c(a) under all feasible flows.
The minimum cost flows we are interested in can be
computed in O (|V
N
|
3/2
log|V
N
|) time (Cornelsen and
Karrenbauer, 2012).
3.2 Compaction of Orthogonal
Drawings
We focus on the vertical (orthogonal) compaction
problem that receives as input a planar grid drawing Γ
of a graph G with an orthogonal representation H
Γ
,
and asks for another planar orthogonal drawing Γ
0
of G realizing H
Γ
so that the vertical edge length is
minimized subject to fixed x-coordinates. In the fol-
lowing we describe a flow-based method for vertical
compaction similar to the coordinate assignment al-
gorithm in Di Battista et al. (1999).
Assume we have an initial grid drawing Γ. In
a first step we normalize H
Γ
resulting in
Γ and H
Γ
.
Then we add vertical visibility edges (so-called dis-
secting edges). We insert a vertical edge connect-
ing each reflex corner with the vertex or edge that
is visible in vertical direction, possibly introducing
dummy vertices. This gives us
e
Γ and
e
H
Γ
. This way
we eliminate all reflex corners and have a represen-
tation with rectangular faces. Now we are ready to
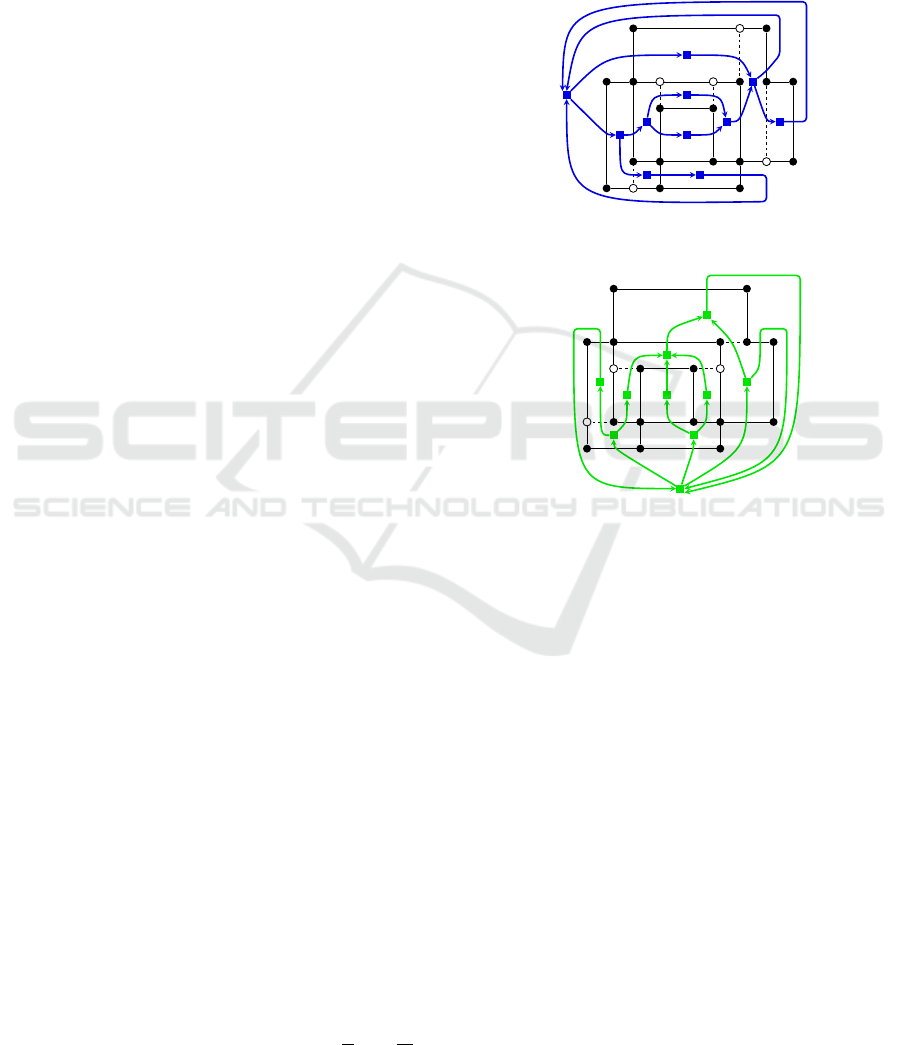
(a)
(b)
Figure 2: The flow networks (a) N
y
for vertical compaction
and (b) N
x
for horizontal compaction. White vertices are
dummy vertices and dashed edges are dummy edges.
construct the network N
y
for vertical compaction. For
each face f in representation
e
H
Γ
we add a node n
f
to N
y
with demand b(n
f
) = 0 and for every vertical
edge e with left face f
l
and right face f
r
we insert an
arc a
e
= (n
f
l
,n
f
r
) with lower bound l(a
e
) = 1 and up-
per bound u(a
e
) = ∞. If e is a dummy edge a
e
gets
zero cost, otherwise a cost of one. See Fig. 2 for an
example.
Suppose we have computed a feasible flow. Now
a unit of flow corresponds to one unit of vertical edge
length. The x-coordinates remain unchanged. The ca-
pacity constraint assures that every edge gets a min-
imum length of one and the flow conservation con-
straint guarantees that every face is drawn as a proper
rectangle. Finally, the visibility edges and dummy
vertices can be removed.
Lemma 1. The above algorithm solves the vertical
compaction problem to optimality.
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
146

Proof. In the vertical compaction problem we have
to preserve the vertical visibility properties of Γ in
order to avoid overlapping graph elements. This is
achieved by the newly added visibility edges. Be-
cause of the one-to-one correspondence of vertical
length of an edge segment in the resulting drawing Γ
0
and the amount of flow carried by a non-zero-cost arc
a
e
∈ N
y
, the result of the minimum cost flow gives
us a minimal vertical length assignment.
4 THE FLED-FIVE COMPACTION
APPROACH
In this section we study the following relaxation
of the one-dimensional compaction problem called
the monotone flexible edge compaction problem with
fixed vertex star geometry (Fled-Five compaction
problem). For vertical compaction it is defined as fol-
lows: Given a planar grid drawing Γ of a 4-graph G
with an orthogonal representation H
Γ
, compute an-
other planar grid drawing of G that minimizes the
vertical edge length subject to fixed x-coordinates in
which all horizontal edge segments of Γ are drawn
x-monotonically and the vertex star geometry for all
vertices as well as the planar embedding is main-
tained.
In contrast to the classical compaction problem,
it is not required here to realize the entire orthogonal
representation, but only the local geometric surround-
ing of each vertex. The fixed x-coordinates and the
x-monotonicity prohibits the lengthening of the total
horizontal edge length (see Fig. 3).
(a) (b)
(c) (d)
Figure 3: Modifications in Fled-Five. (a) The original edge
of length three. (b) Modification allowed in Fled-Five.
(c) Not allowed because of changed x-coordinates and
(d) not allowed, because x-monotonicity is violated.
We adapt the network flow approach described in
Sect. 3.2. But now we are able to introduce or remove
double bends of certain edges in order to improve the
vertical edge length. We illustrate the concept by the
following example. Figure 4(a) shows an optimally
compacted drawing with respect to its orthogonal rep-
(a) (b) (c)
Figure 4: A graph and the arcs of the corresponding flow
network (a,b) of the traditional algorithm and (c) in our al-
gorithm.
resentation. The blue arcs show the arcs of the verti-
cal compaction network (compare Fig. 2). For better
readability we omitted the network nodes belonging
to the faces. In Fig. 4(b), the same graph is shown,
but with a different orthogonal representation. The
new double bend in the middle edge leads to a smaller
drawing. In this drawing it is possible to send flow be-
tween the two internal faces, since they are separated
by a vertical edge segment. In the corresponding flow
network there is a new network arc (red, dashed) con-
necting the upper and the lower face. This leads to
the key idea of our approach. Introducing arcs in the
vertical flow network between horizontally separated
face nodes enables us to shift flow between them and
therefore exchange vertical edge length at the expense
of a double bend (see Fig. 4(c)). We can also reverse
this thought. If there is an unnecessary double bend
we can get rid of it by not sending flow over the arc
corresponding to its middle segment and thus remov-
ing the middle segment from the drawing.
But we have to be careful here. First, we are com-
pacting in vertical direction, so we cannot change the
x-coordinates. If an edge has a double bend, it needs
to have a horizontal expansion of at least two. Thus
we will not consider edges of length one as possible
candidates for getting a double bend. Second, adding
a double bend to e introduces two reflex corners, one
in both adjacent faces of e. Two double bends may
even cause an edge overlap, see Fig. 5(a). We need to
ensure that the computed flow corresponds to a feasi-
ble drawing. Therefore we will treat each grid point
along an edge that could be part of a double bend
as a potential reflex corner, which we will eliminate
by dissecting. We will now describe the algorithm
in detail.
Our algorithm works in three phases: dissection,
computation of a minimum cost flow and transform-
ing the flow into a new drawing. First we normalize
H
Γ
to H
Γ
. For dissection we split the horizontal edges
of Γ by placing an artificial bend vertex on every in-
ner grid point of an horizontal edge. The bend ver-
tices may later be transformed to double bends. Then
we dissect Γ as described in Sect. 3 and treat every
Orthogonal Compaction using Additional Bends
147

2
2 2
(a)
2 2 2 2
2
2
1 1
(b)
Figure 5: Input graph with modified flow network and a
minimum cost flow (all unlabeled arcs carry one unit of
flow) with the resulting drawing (a) without additional dis-
secting edges and (b) including them. The bold edge in (a)
indicates an edge overlap and the grey vertices result from
normalization, the white vertices in (b) are bend vertices.
Dissecting edges are indicated in (b).
bend vertex as a reflex corner in its adjacent faces (see
Fig. 5(b)). That means, we may dissect the drawing
in vertical stripes of unit length. Doing so, we solve
both of the problems mentioned above. Since we con-
sider only edges of length at least two, we guarantee
that the edge will be long enough for a double bend
and by inserting the visibility edges we keep the ver-
tical separation of graph elements intact. This results
in the extensions
e
Γ and
e
H
Γ
and
e
G.
Observation 1. After this dissection method the num-
ber of vertices and edges in
e
G is O(A), where
A = h
Γ
· w
Γ
and h
Γ
(w
Γ
) is the height (width) of Γ.
Next we construct the network from Sect. 3.2. Ad-
ditionally to the already introduced arcs (straight blue
arcs in Fig. 5) we add two arcs a
↑
v
and a
↓
v
for every
bend vertex (curved, red arcs in Fig. 5). Notice that
every such bend vertex v has four adjacent faces, one
at the lower and upper left and right. If it lies on the
external face, two of the adjacent faces may coincide.
Arc a
↑
v
goes from the lower left face of v to its up-
per right face and a
↓
v
goes from the upper left to the
lower right face. Flow on one of these arcs will lead
to a double bend in the edge segment of G that is split
by v. The lower bound of these arcs is zero, the upper
bound is set to infinity and the cost is one. For every
edge e ∈
e
G that is a middle segment in G we decrease
the lower bound of its arc a
e
to zero, since this is a
vertical edge segment, that we may delete (dashed,
orange arc in Fig. 5).
After computing a minimum cost flow in this net-
work, we interpret the result in the following way: For
every vertical edge e of
e
G we translate the amount of
flow on the arc a
e
of N
y
to the length of e. Let a
↑
v
be an arc corresponding to a bend vertex v carrying k
units of flow. Let e be the split horizontal edge and
x
v
the x-coordinate of v. Then e will start at its left
endpoint in horizontal direction, bend downwards at
x-coordinate x
v
, proceed for k units in y-direction and
then continue to the right to its other endpoint. If we
deal with an arc of the form a
↓
v
the corresponding edge
will do an upward bend at x
v
. Let e
0
∈
e
G be an edge
that corresponds to a middle segment and let a
e
0
be the
corresponding arc. If a
e
0
carries no flow we do not as-
sign any vertical length to e
0
, hence the double bend to
which e
0
belongs collapses. Notice that flow on every
non-zero-cost arc corresponds to vertical edge length.
Theoretically, it is possible that both a
↑
v
and a
↓
v
carry
flow in a feasible, but not optimal, solution. In this
case we can always augment the flow in a way that
at most one of a
↑
v
or a
↓
v
carries flow. Finally, we re-
move all dummy edges and vertices. See Fig. 5 for an
example and Algorithm 1 for pseudocode.
Let us assume that the width and height of Γ are
bounded by the number of its vertices and bends. Oth-
erwise there would be a grid line without any vertex
or bend on it. We can delete such grid lines iteratively
until we reach our bound.
Theorem 1. Let Γ be a planar grid drawing of a 4-
graph G with an orthogonal representation H
Γ
. Let ¯n
be the number of vertices and bends of Γ. Then the
above described extended network-based compaction
algorithm takes O ( ¯n
3
log ¯n) time and solves the verti-
cal Fled-Five compaction problem to optimality.
Proof. Because of the visibility edges we will main-
tain visibility properties of Γ. Every vertical edge seg-
ment of G that is not a middle segment gets a mini-
mum length of one due to the lower bound of the cor-
responding arc in N
y
. Every bend vertex can safely be
turned to a double bend if its corresponding arc carries
flow, since we add visibility edges to the top and bot-
tom of it. By this modification we do not change the
vertex star geometry of Γ, because bend vertices are
not part of G. Every middle segment can be removed
if there is no flow on the corresponding arc. Because
its edge e ∈ Γ has a horizontal expansion of at least
two, e will still have a proper length and due to the
dissection phase visibility properties are maintained.
This modification also does not affect the vertex star
geometry of Γ, since a middle segment is not adjacent
to a vertex of G. So every face will have a rectangu-
lar shape, no matter what modification we apply, and
due to flow conservation every face and thus the entire
graph is drawn consistently. Similar to Lemma 3.2 the
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
148

Input : orthogonal drawing Γ
Output: optimal solution Γ
0
to the Fled-Five
compaction problem
Γ ← normalize(Γ);
e
Γ ← addBendVerticesAndVertVisEdges(Γ);
// construct network N
for every face f do
N ← node n
f
;
demand[n
f
]=0;
for every vertical edge e do
node n1 = leftFaceNode(e);
node n2 = rightFaceNode(e);
if isMidSegment(e) then
lowerBound[a
e
]=0;
else lowerBound[a
e
]=1;
upperBound[a
e
]=∞;
if isVisEdge(e) then cost[a
e
] = 0;
else cost[a
e
]=1;
for every bend vertex v do
node n1 = lowerLeftFaceNode(v);
node n2 = upperRightFaceNode(v);
N ← arc a
↑
= (n1,n2);
lowerBound[a
↑
]=0; upperBound[a
↑
]=∞;
cost[a
↑
]=1;
node n3 = upperLeftFaceNode(v);
node n4 = lowerRightFaceNode(v);
N ← arc a
↓
= (n3,n4);
lowerBound[a
↓
]=0; upperBound[a
↓
]=∞;
cost[a
↓
]=1;
// compute length assignment
x ← computeMinimumCostFlow(N);
for every vertical edge e do
length(e) ← x(networkArc(e));
for every bend vertex v do
edge e ← horizontalEdge(v);
int xc ← xCoordinate(v);
if x(a
↑
v
) 6= 0 then
addDownwardMidSegment(e,xc,x(a
↑
v
));
if x(a
↓
v
) 6= 0 then
addUpwardMidSegment(e, xc,x(a
↓
v
));
Γ
0
← RemoveBendVerticesAndVisEdges(
e
Γ);
Algorithm 1: verticalFledFive.
length of vertical segments of Γ
0
is equal to the cost
of the computed minimum cost flow. Since the initial
drawing can be interpreted as a feasible flow, we get a
drawing Γ
0
with total edge length less or equal to that
of Γ. The horizontal edge segments maintain their x-
monotonicity, because we only add vertical segments
to the drawing. Hence the horizontal edge lengths and
the x-coordinates of the vertices in Γ stay the same.
Because the minimum cost flow gives us a minimal
vertical length assignment we have an optimal solu-
tion for the vertical Fled-Five compaction problem.
For the running time we first consider the dissec-
tion phase. By Observation 1 we end up with O(¯n
2
)
vertices. For inserting dummy edges based on visibil-
ity properties we can use a sweep-line algorithm that
runs in O ( ¯n
2
log ¯n) time in our case. The construc-
tion of the flow network runs in linear time in the size
of
e
G. The network is planar and has O( ¯n
2
) nodes.
For planar flow networks with n nodes and O(n) arcs
there exists a O(n
3/2
logn) time algorithm for com-
puting a minimum cost flow (Cornelsen and Karren-
bauer, 2012). Therefore we have a total running time
of O( ¯n
3
log ¯n).
4.1 Short Remarks
Running Time. The cubic part of the running time
comes from the possibly quadratic number of bend
vertices and dissecting edges. So if we restrict the
number of bend vertices to be linear, we can decrease
the running time to O( ¯n
3/2
log ¯n).
Controlling the Number of New Bends. Although
the above compaction approach may reduce the to-
tal edge length, the number of bends in the resulting
drawing may increase. A possible approach to control
the number of new bends could be to bound the num-
ber of specific arcs used by a feasible flow. This is
known as the binary case of the budget-constrained
minimum cost flow problem for which Holzhauser
et al. (2016) showed strong NP-completeness. In fact,
in this model we have no other control over the num-
ber of additional bends than restricting the number of
bend vertices. Each such vertex can generate two new
bends. By assigning higher cost to arcs a
↑
v
and a
↓
v
it
becomes more unlikely for these arcs to carry much
flow, but it does not limit its number used by the flow.
It makes no difference in terms of total cost if we
send, e.g., 10 units of flow over a
↑
v
or one unit of
flow over 10 such arcs, while the former produces two
bends and the latter 20 bends.
Extensions to Other Models. While in a drawing
model for 4-graphs a node occupies exactly one grid
point, there are other models for drawing graphs with
maximum degree greater four, e.g., the Kandinsky
model (F
¨
oßmeier and Kaufmann, 1995), where es-
sentially nodes spread over several grid points (big
nodes) or the quasi-orthogonal model (J
¨
unger et al.,
2004), where edges are allowed to leave the grid
around vertices. Our approach can be extented to
Orthogonal Compaction using Additional Bends
149
0
5
10
15
20
25
30
35
10-50 51-100 101-150 151-200 200-314
decrease in %
nodes
total
max
area
0
100
200
300
400
500
600
700
800
10-50 51-100 101-150 151-200 200-314
increase in %
nodes
bends
time per iteration
time
vis. edges
(a)
-15
-10
-5
0
5
10
15
20
40-100 101-200 201-300 301-400 401-500
decrease in %
nodes
total
max
area
0
20
40
60
80
100
120
140
160
40-100 101-200 201-300 301-400 401-500
increase in %
nodes
bends
time per iteration
time
vis. edges
(b)
0
5
10
15
20
25
30
35
40
45
50
40-100 101-200 201-300 301-400 401-500
decrease in %
nodes
total
max
area
0
50
100
150
200
250
300
40-100 101-200 201-300 301-400 401-500
increase in %
nodes
bends
time per iteration
time
vis. edges
(c)
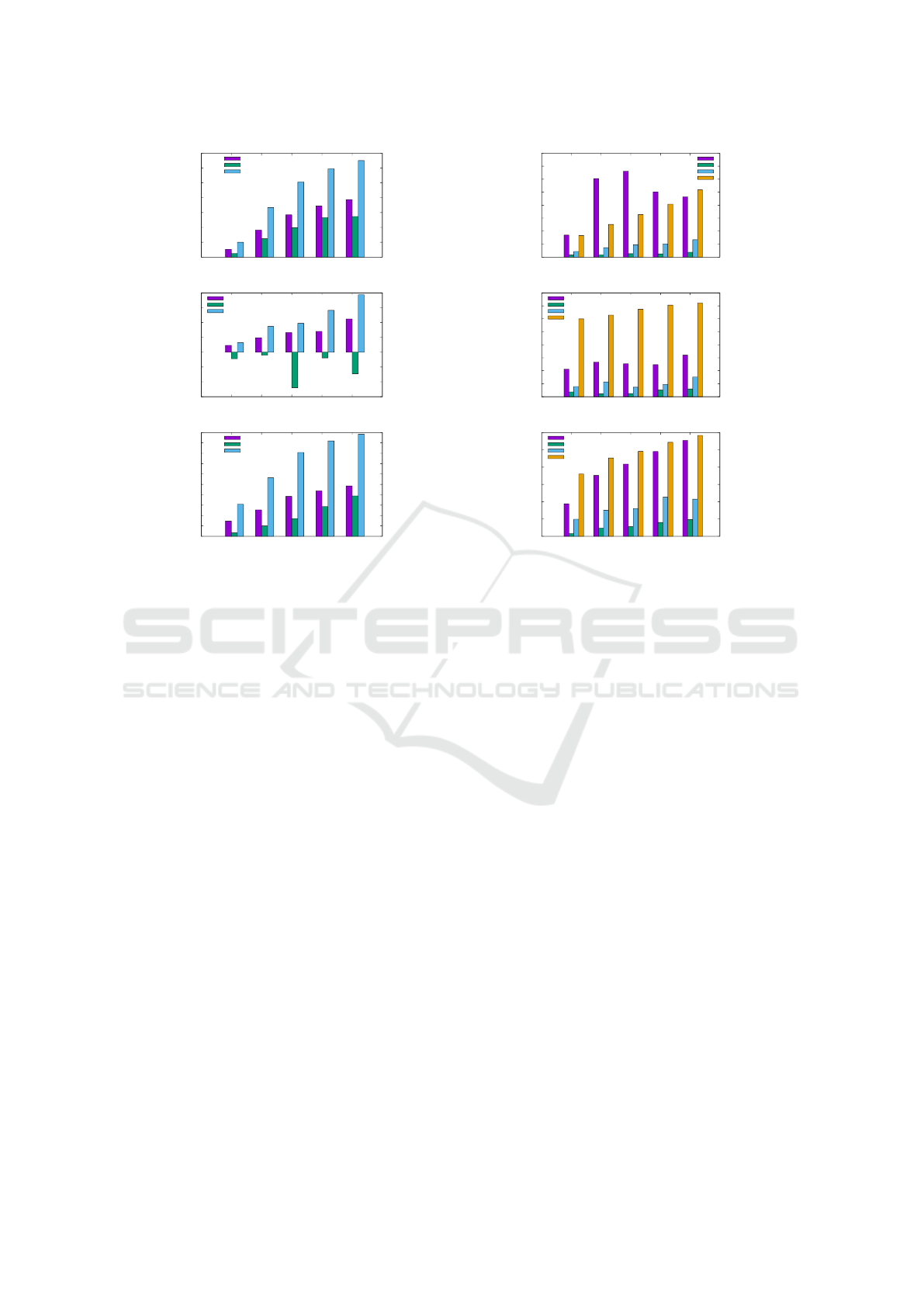
Figure 6: Average change of the total edge length, the maximum edge length, the area, the number of bends, the time per
iteration, the total running time and the number of visibility edges from TRAD to FF in percent for (a) the Rome graphs, (b)
the quasi trees, and (c) the biconnected graphs.
these models in a straightforward way by modeling
big nodes as rectangular faces of suitable size for all
the incident edges and prohibit changing the shape of
the dummy edges that participate in these faces. Since
in the quasi-orthogonal model, until the last step of
actual drawing, high-degree nodes are also handled
as faces, the extension works for this model as well.
5 EXPERIMENTAL EVALUATION
In this section we evaluate our algorithm FF focusing
on the total edge length and area improvement. Klau
et al. (2001) compared 12 compaction heuristics that
maintain the orthogonal representation and we chose
the best of these traditional heuristics (T2FL in Klau
et al. (2001)), which we call TRAD, for comparison
in order to demonstrate the benefit of slightly chang-
ing the orthogonal shape. This method was within
one percent of the optimal value for practical in-
stances. We refrain from comparing to improvement
algorithms like the 4M algorithm (F
¨
oßmeier et al.,
1998) or the refinement method from Six et al. (1998)
since they change the vertex star geometry, the topol-
ogy and even vertex sizes. The moving operation of
the 4M algorithm is the only operation that fits our
model, but would not change any layout generated by
a flow-based compaction algorithm. The only appli-
cable modification from Six et al. (1998) (superflu-
ous bends) does not have an impact on bend minimal
drawings that we use as input.
The algorithms were implemented in C++ using
the OGDF library (Chimani et al., 2013). For both
algorithms we start with a bend minimal orthogonal
representation. For TRAD we apply a constructive
compaction method, that transforms the orthogonal
representation into a turn-regular one and then runs
a flow-based coordinate assignment in order to get
a feasible planar grid drawing. Then we repeatedly
apply horizontal and vertical compaction steps with
a flow-based improvement heuristic until no further
improvement can be achieved, see heuristic T2FL in
Klau et al. (2001). For FF we use the same con-
structive heuristic and then apply the modified flow
technique from Sect. 4 with a cost of one for the net-
work arcs causing double bends to achieve best possi-
ble shortening, also repeatedly in horizontal and ver-
tical direction. Recall that although both approaches
are optimal for the one-dimensional compaction prob-
lems, repeated application of horizontal and verti-
cal compaction steps does in general not lead to
drawings with optimal total edge length for the two-
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
150
0
200
400
600
800
1000
1200
1400
1600
1800
2000
0 100 200 300 400 500
total edge length
nodes
TRAD
FF
(a)
0
1000
2000
3000
4000
5000
6000
0 100 200 300 400 500
area
nodes
TRAD
FF
(b)
0
10
20
30
40
50
60
70
80
90
100
0 100 200 300 400 500
maximum edge length
nodes
TRAD
FF
(c)
0
20
40
60
80
100
120
140
160
180
200
0 100 200 300 400 500
bends
nodes
TRAD
FF
(d)
0
0.5
1
1.5
2
2.5
3
0 100 200 300 400 500
time per iteration in seconds
nodes
TRAD
FF
(e)
0
2
4
6
8
10
12
0 100 200 300 400 500
total running time in sec.
nodes
TRAD
FF
(f)
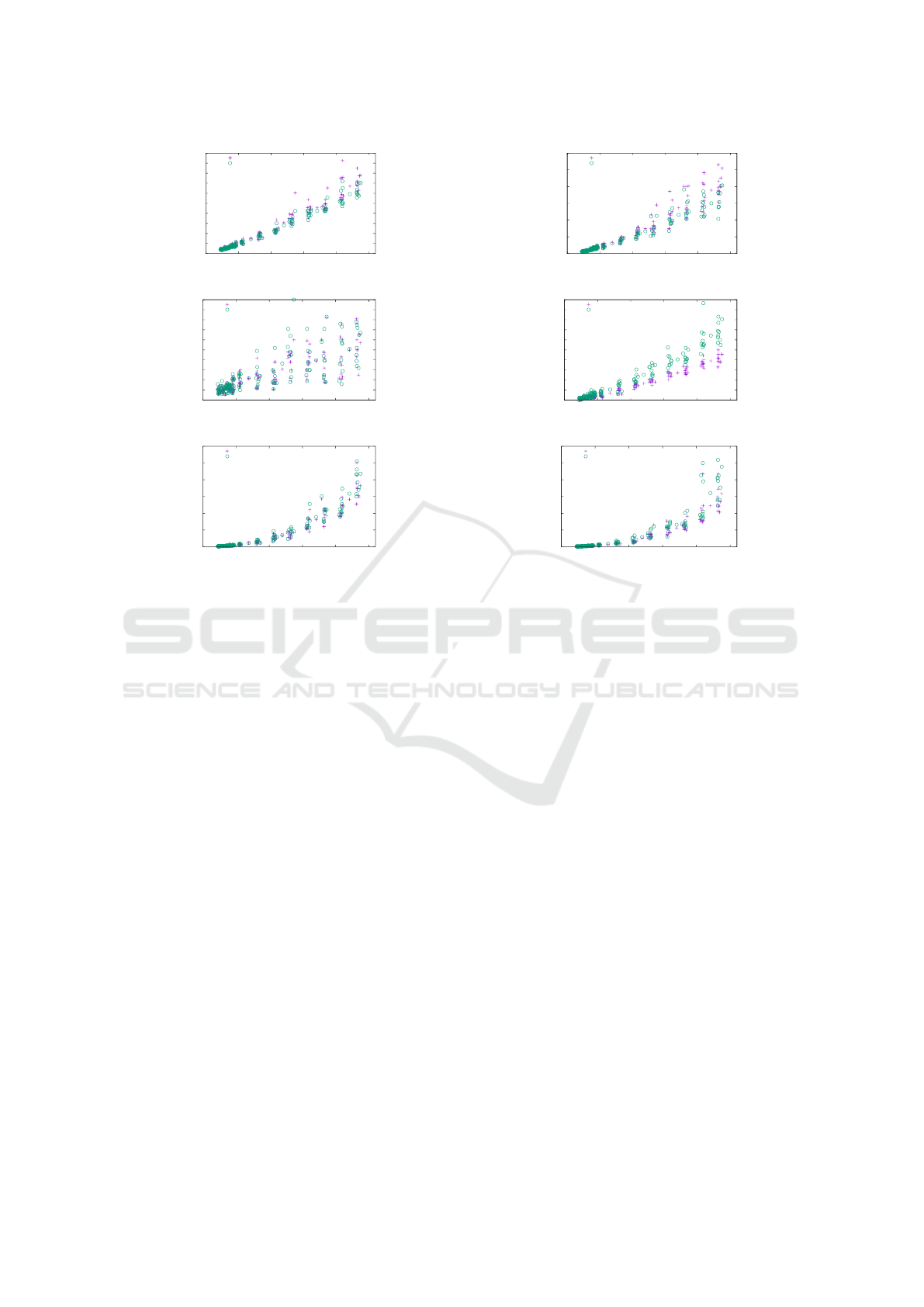
Figure 7: Absolute results of TRAD and FF for the quasi-trees: (a) total edge length, (b) area, (c) maximum edge length, (d)
number of bends, (e) time per iteration, (f) total running time.
dimensional compaction problems. Notice also that
due to the alternating repetitions in FF the monotonic-
ity of edge segments may no longer be maintained.
We state the following hypotheses regarding the
results of our new approach FF compared to those of
TRAD:
(H1) The total edge length and therefore the area
of the drawings will decrease. We will also
examine the change of the maximum edge
length. It is hard to predict the behaviour, be-
cause on the one hand adding a double bend
lengthens an edge, but it could also lead to
shorter edges in other places.
(H2) The number of bends will rise significantly.
(H3) Although there will be many more dissecting
edges, the running time will not increase dras-
tically.
We tested our algorithm on three test suites. The
standard benchmark set called Rome graphs intro-
duced in Di Battista et al. (1997) consists of about
11,000 real-world and real-world like graphs with
10 to 100 vertices. The second set of graphs are
quasi-trees which are known to be hard to compact.
They have already been used in the compaction liter-
ature (e.g., Klau et al. (2001), Klau (2002)). From
this, we selected a subset of 155 graphs with 40
to 450 vertices. The last set consists of 240 ran-
domly generated biconnected planar 4-graphs with
40 to 500 vertices. All used graphs were, if neces-
sary, initially turned into planar 4-graphs by planariz-
ing them with methods of OGDF and replacing ver-
tices with k > 4 outgoing edges with faces of size k.
This results in graph sizes of up to 314 vertices for
the Rome test suite and up to 475 vertices for the
quasi-trees before the orthogonalization step. The in-
put instances are available on https://ls11-www.cs.tu-
dortmund.de/mutzel/compaction. All tests were run
on an Intel Xeon E5-2640v3 2.6GHz CPU with 128
GB RAM.
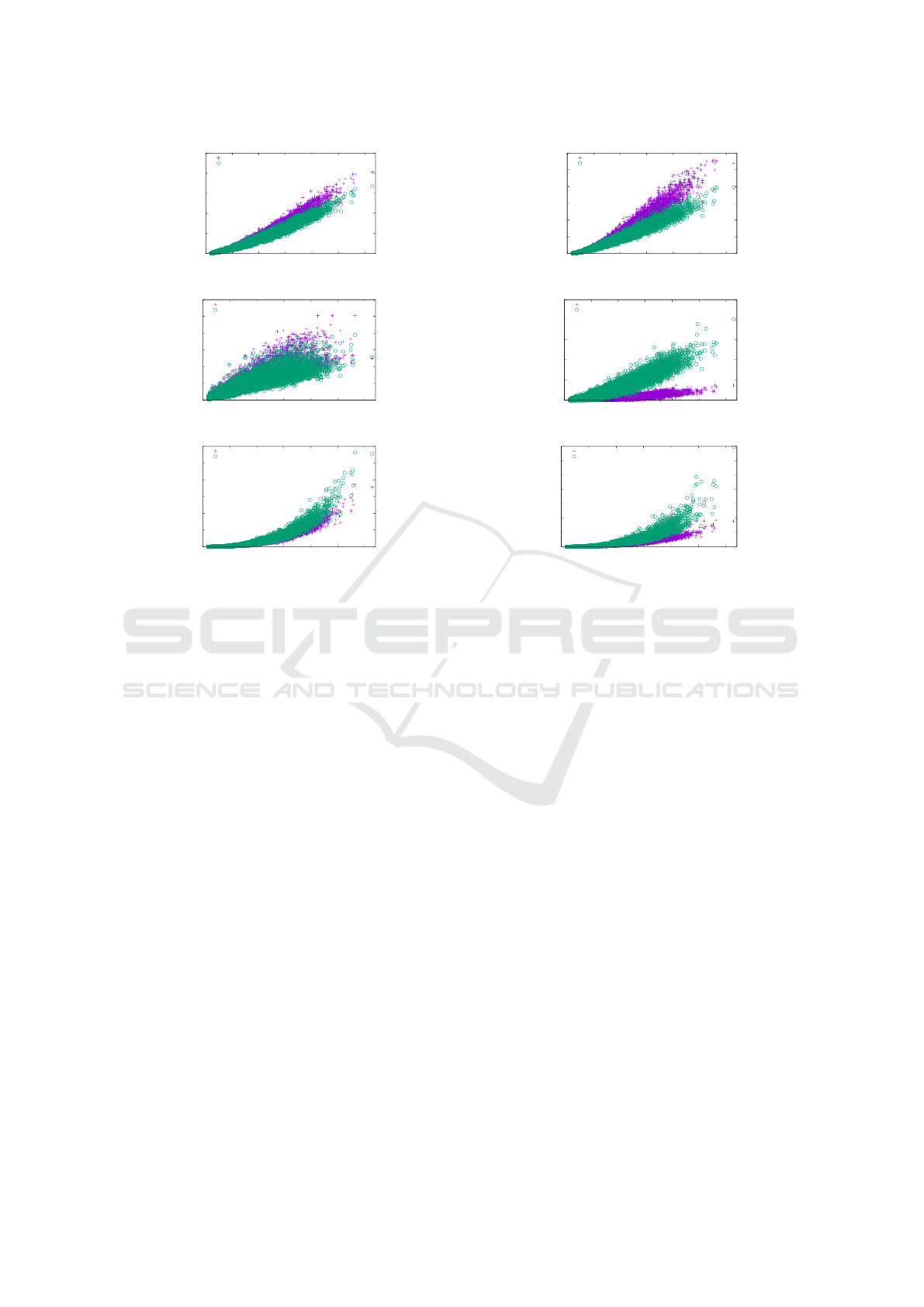
(H1) Figure 6 shows the average decrease of the to-
tal and maximum edge length as well as of the area in
percent. In all three graph classes the total edge length
as well as the area has improved. We were able to de-
crease the total edge length by up to 36.1% and the
area by up to 68.7%. In general, larger graphs allow a
larger improvement. It turned out that for the majority
of the instances we were also able to reduce the maxi-
mum edge length. Only for the quasi-trees the longest
edges produced by FF are longer on average. But in
general the results are mixed, reaching from a length-
ening by 87.5% to a shortening by 58.1%. Figures 7,
Orthogonal Compaction using Additional Bends
151
0
500
1000
1500
2000
2500
0 50 100 150 200 250 300
total edge length
nodes
TRAD
FF
(a)
0
500
1000
1500
2000
2500
3000
0 50 100 150 200 250 300
area
nodes
TRAD
FF
(b)
0
20
40
60
80
100
120
0 50 100 150 200 250 300
maximum edge length
nodes
TRAD
FF
(c)
0
50
100
150
200
250
0 50 100 150 200 250 300
bends
nodes
TRAD
FF
(d)
0
0.5
1
1.5
2
2.5
3
0 50 100 150 200 250 300
time per iteration in seconds
nodes
TRAD
FF
(e)
0
2
4
6
8
10
12
14
0 50 100 150 200 250 300
total running time in sec.
nodes
TRAD
FF
(f)
Figure 8: Absolute results of TRAD and FF for the Rome graphs: (a) total edge length, (b) area, (c) maximum edge length,
(d) number of bends, (e) time per iteration, (f) total running time.
8 and 9 (a) - (c) show absolute values for the total
edge length, the area and the maximum edge length
measured for the three graph classes.
(H2) Figure 6 displays the average increase of the
number of bends. If an instance had no bends af-
ter TRAD, we use the number of bends after FF as
relative increase to take also these instances into ac-
count for computing the average increase of bends.
As expected the drawings produced by FF have many
more bends, especially for the Rome graphs. In one
of the worst cases the number of bends went up from
zero to 72. Although the relative increase of bends
is very high, the average number of bends per edge
in the drawings produced by FF is 0.18 for the Rome
graphs, 0.13 for the quasi trees and 0.30 for the bi-
connected graph, respectively. The highest ratio over
all instances is 0.52. Recall, that we started with
bend minimal orthogonal representations. Figures 7,
8 and 9 (d) show the absolute values for the number
of bends measured for the test graphs. Figure 10 gives
the relation between the number of invested bends
and the improvement in terms of area and total edge
length for the biconnected graphs. The data for the
other two graph classes can be found in J
¨
unger et al.
(2017). Figure 11 plots the relation between the num-
ber of bends and the number of edges.
As mentioned before, we cannot limit the num-
ber of bends added by FF, but we decrease the like-
lyhood to send flow over an arc of the form a
↑
v
or a
↓
v
by assigning higher costs to these arcs. We evalu-
ated the number of additional bends, the area and to-
tal edge length for different arc costs on the subset
of the Rome graphs with 100 to 150 vertices. These
instances showed the greatest increase regarding the
number of bends. Since we focus on the impact of
the arc cost here, we apply only one compaction step
in each direction. As expected the number of new
bends as well as the achieved improvement in terms
of area and total edge length compared to TRAD de-
creases with increasing arc costs, see Fig. 12. With a
slightly higher arc cost we can reduce the number of
additional bends without drastically affecting the area
and total edge length improvement. The average rela-
tive increase of bends went down from 663.7% for an
arc cost of one to 324.6% for an arc cost of two and
234.3% for an arc cost of three. The average improve-
ment of area (total edge length) is 24.7% (13.8%),
22.5% (11.4%) and 20.5% (10.2%), respectively. The
differences between higher arc costs in terms of addi-
tional bends become smaller. The data regarding the
number of bends scatter over a wide range (notice the
different scale on the right in Fig. 12 for the change
of bends), especially for low arc cost, therefore it is
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
152
0
1000
2000
3000
4000
5000
6000
0 100 200 300 400 500
total edge length
nodes
TRAD
FF
(a)
0
2000
4000
6000
8000
10000
12000
14000
0 100 200 300 400 500
area
nodes
TRAD
FF
(b)
0
20
40
60
80
100
120
140
160
180
200
0 100 200 300 400 500
maximum edge length
nodes
TRAD
FF
(c)
0
50
100
150
200
250
300
350
0 100 200 300 400 500
bends
nodes
TRAD
FF
(d)
0
5
10
15
20
25
30
0 100 200 300 400 500
time per iteration in seconds
nodes
TRAD
FF
(e)
0
20
40
60
80
100
120
0 100 200 300 400 500
total running time in sec.
nodes
TRAD
FF
(f)
Figure 9: Absolute results of TRAD and FF for the biconnected graphs: (a) total edge length, (b) area, (c) maximum edge
length, (d) number of bends, (e) time per iteration, (f) total running time.
0
10
20
30
40
50
60
70
0 100 200 300 400 500 600
decrease of area in %
increase of bends in %
(a)
0
5
10
15
20
25
30
35
40
0 100 200 300 400 500 600
decrease of tot. edge length in %
increase of bends in %
(b)
Figure 10: Relation between additional bends and (a) improvement of area and (b) total edge length for the biconnected
graphs.
hard to determine which arc cost is suitable to keep
the number of additional bends low, but still yields
good geometric results.
(H3) We measured the total running time and the
number of performed compaction iterations. For bet-
ter comparison we also display the running time per
iteration, because FF tends to do more iterations. The
reason for that is that a compaction step of FF changes
the drawing and therefore the flow network of the next
step more significantly, leading to more new possibil-
ities in compacting. The right side of Figure 6 dis-
plays the average increase of the running time and the
number of visibility edges. In all cases the number
of additional dissecting edges has increased signifi-
cantly. The running time per iteration has also in-
creased, but not more than 50% on average. Only
for 252 instances of the Rome graphs and one bicon-
nected graph the running time per iteration has more
than doubled.
The results support the hypotheses. Our new ap-
proach is able to improve the drawing area and the to-
tal edge length by introducing additional bends. Fig-
ure 13 shows two examples drawn with TRAD and FF,
respectively.
6 CONCLUSION
We have presented a new compaction heuristic for or-
thogonal graph drawing that alters the orthogonal rep-
Orthogonal Compaction using Additional Bends
153
0
50
100
150
200
250
300
350
0 100 20 0 300 400 5 00 600
bends
edges
f(x)=x
(a)
0
50
100
150
200
250
300
350
0 100 200 300 400 50 0 600 700
bends
edges
f(x)=x
(b)
0
50
100
150
200
250
300
350
0 100 200 300 400 500 600 700 800
bends
edges
f(x)=x
(c)
Figure 11: Number of bends in the drawings produced by FF for (a) the Rome graphs, (b) the quasi trees and (c) the bicon-
nected graphs.
0
5
10
15
20
25
30
35
40
1 2 3 4 5 6 7 8 9 10
0
200
400
600
800
1000
decrease of area
and edge length in %
increase of bends in %
arc cost
bends
area
edge length
Figure 12: Relative change of the number of bends, area
and total edge length with increasing arc costs for a subset
of the Rome graphs. The whiskers cover 90% of the data,
no outliers are depicted for better readability.
resentation. We were able to reduce the total edge
length and drawing area, but at the expense of addi-
tional bends. Unfortunately, in our model we have no
control over the number of bends added, but if the fo-
cus of interest lies on area and edge length, the results
show a very positive effect. Future research could fo-
cus on studying the trade-off between bends and area
or bends and total edge length as a bicriteria optimiza-
tion problem.
ACKNOWLEDGEMENTS
This work was supported by the DFG under the
project Compact Graph Drawing with Port Con-
straints (DFG MU 1129/10-1). We would like to
thank Gunnar Klau for providing us with most of our
test instances and anonymous reviewers for helpful
remarks on a previous version of this paper. We also
gratefully acknowledge helpful discussions with Mar-
tin Gronemann, Sven Mallach, and Daniel Schmidt.
REFERENCES
Ahuja, R. K., Magnanti, T. L., and Orlin, J. B. (1993). Net-
work Flows: Theory, Algorithms, and Applications.
Prentice-Hall, Inc., Upper Saddle River, NJ, USA.
Bannister, M. J., Eppstein, D., and Simons, J. A. (2012). In-
approximability of orthogonal compaction. J. Graph
Algorithms Appl., 16(3):651–673.
(a)
(b)
(c)
(d)
Figure 13: Biconnected graph with 220 vertices and 304
edges and Rome graph with 55 vertices and 66 edges (af-
ter planarization and expanding high degree vertices): (a)
TRAD: total edge length 1459, area 3060, bends 31 (b) FF:
total edge length 1107, area 1320, bends 133 (c) TRAD: total
edge length 168, area 240, bends 1 (d) FF: total edge length
140, area 140, bends 13. Edges with additional bends are
red.
Batini, C., Nardelli, E., and Tamassia, R. (1986). A layout
algorithm for data flow diagrams. IEEE Transactions
on Software Engineering, SE-12(4):538–546.
Bridgeman, S. S., Di Battista, G., Didimo, W., Liotta, G.,
Tamassia, R., and Vismara, L. (2000). Turn-regularity
and optimal area drawings of orthogonal representa-
tions. Comput. Geom., 16(1):53–93.
Chimani, M., Gutwenger, C., J
¨
unger, M., Klau, G. W.,
Klein, K., and Mutzel, P. (2013). The Open Graph
Drawing Framework (OGDF). In Tamassia, R., edi-
tor, Handbook of Graph Drawing and Visualization,
chapter 17, pages 543–569. CRC Press.
Cornelsen, S. and Karrenbauer, A. (2012). Acceler-
ated bend minimization. J. Graph Algorithms Appl.,
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
154

16(3):635–650.
Di Battista, G., Eades, P., Tamassia, R., and Tollis, I. G.
(1999). Graph Drawing: Algorithms for the Visual-
ization of Graphs. Prentice-Hall, Upper Saddle River,
NJ, USA.
Di Battista, G., Garg, A., Liotta, G., Tamassia, R., Tassi-
nari, E., and Vargiu, F. (1997). An experimental com-
parison of four graph drawing algorithms. Comput.
Geom., 7:303–325.
F
¨
oßmeier, U., Heß, C., and Kaufmann, M. (1998). On im-
proving orthogonal drawings: The 4m-algorithm. In
Whitesides, S., editor, Graph Drawing, 6th Interna-
tional Symposium, GD’98, Proceedings, volume 1547
of LNCS, pages 125–137. Springer.
F
¨
oßmeier, U. and Kaufmann, M. (1995). Drawing high
degree graphs with low bend numbers. In Bran-
denburg, F., editor, Graph Drawing, Symposium on
Graph Drawing, GD ’95, Proceedings, volume 1027
of LNCS, pages 254–266. Springer.
Holzhauser, M., Krumke, S. O., and Thielen, C. (2016).
Budget-constrained minimum cost flows. J. Comb.
Optim., 31(4):1720–1745.
J
¨
unger, M., Klau, G. W., Mutzel, P., and Weiskircher, R.
(2004). AGD - A library of algorithms for graph draw-
ing. In Graph Drawing Software, pages 149–172.
J
¨
unger, M., Mutzel, P., and Spisla, C. (2017). Orthog-
onal compaction using additional bends. CoRR,
abs/1706.06514.
Kaufmann, M. and Wagner, D., editors (2001). Drawing
Graphs, Methods and Models, volume 2025 of LNCS.
Springer.
Klau, G. W. (2002). A combinatorial approach to orthog-
onal placement problems. PhD thesis, Saarland Uni-
versity, Saarbr
¨
ucken, Germany.
Klau, G. W., Klein, K., and Mutzel, P. (2001). An exper-
imental comparison of orthogonal compaction algo-
rithms. In Marks, J., editor, Graph Drawing, 8th Inter-
national Symposium, GD 2000, Proceedings, volume
1984 of LNCS, pages 37–51. Springer.
Klau, G. W. and Mutzel, P. (1999). Optimal compaction of
orthogonal grid drawings. In Cornu
´
ejols, G., Burkard,
R. E., and Woeginger, G. J., editors, Integer Program-
ming and Combinatorial Optimization, 7th Interna-
tional IPCO Conference, 1999, Proceedings, volume
1610 of LNCS, pages 304–319. Springer.
Lengauer, T. (1990). Combinatorial Algorithms for Inte-
grated Circuit Layout. John Wiley & Sons, Inc., New
York, NY, USA.
Patrignani, M. (1999). On the complexity of orthogonal
compaction. In Algorithms and Data Structures, 6th
International Workshop, WADS ’99, Proceedings, vol-
ume 1663 of LNCS, pages 56–61. Springer.
Six, J. M., Kakoulis, K. G., and Tollis, I. G. (1998). Refine-
ment of orthogonal graph drawings. In Whitesides, S.,
editor, Graph Drawing, 6th International Symposium,
GD’98, Proceedings, volume 1547 of LNCS, pages
302–315. Springer.
Sp
¨
onemann, M., Fuhrmann, H., von Hanxleden, R., and
Mutzel, P. (2010). Port constraints in hierarchical
layout of data flow diagrams. In Eppstein, D. and
Gansner, E. R., editors, Graph Drawing, 17th Interna-
tional Symposium, GD 2009. Revised Papers, volume
5849 of LNCS, pages 135–146. Springer.
Tamassia, R. (1987). On embedding a graph in the grid
with the minimum number of bends. SIAM J. Com-
put., 16(3):421–444.
Tamassia, R., editor (2013). Handbook on Graph Drawing
and Visualization. Chapman and Hall/CRC.
Orthogonal Compaction using Additional Bends
155
