
Generic Caching Library and Its Use for VTK-based Real-time
Simulation and Visualization Systems
Luk
´
a
ˇ
s Hruda
1
and Josef Kohout
2
1
Department of Computer Science and Engineering, Faculty of Applied Sciences, University of West Bohemia,
Univerzitn
´
ı 8, Pilsen, Czech Republic
2
NTIS - New Technologies for the Information Society, Faculty of Applied Sciences, University of West Bohemia,
Univerzitn
´
ı 8, Pilsen, Czech Republic
Keywords:
Cache, Memoization, VTK, Visualization.
Abstract:
In many visualization applications, physics-based simulations are so time consuming that desired real-time
manipulation with the visual content is not possible. Very often this time consumption can be prevented by
using some kind of caching since many of the processes in these simulations repeat with the same inputs pro-
ducing the same output. Creating a simple caching mechanism for cases where the order of the data repetition
is known in advance is not a very difficult task. But in reality, the data repetition is often unpredictable and in
such cases some more sophisticated caching mechanism has to be used. This paper presents a novel generic
caching library for C++ language that is suitable for such situations. It also presents a wrapper that simplifies
the usage of this library in the applications based on the popular VTK visualization tool. Our experiments
show that the developed library can speed up VTK based visualizations significantly with a minimal effort.
1 INTRODUCTION
The VTK (Visualization Toolkit) (Schroeder et al.,
2004) is a very popular tool for visualizing various
types of data and information, usually scientific. It
is written in C++ and has found its use in many
existing visualization systems like ParaView (Ahrens
et al., 2005), MayaVi (Ramachandran and Varoquaux,
2011), 3D Slicer (Pieper et al., 2004), OsiriX (Rosset
et al., 2004) or MVE-2 (Frank et al., 2006).
The data of today tends to be very complex and its
analysis is usually only possible through visual ana-
lytics. This means that in the background of the visu-
alization system data-acquisition and further process-
ing of this data take place and the result is visualized
for the user who can then interact with the data, filter
it or change the way it is acquired. This also means
that the visualization has to be updated in an interac-
tive time (at least 15 frames per second). Since so-
phisticated data-acquisition techniques are producing
datasets of continually increasing size, even on a very
powerful computer with parallel processing, this is
usually not possible. It seems obvious that any unnec-
essarily repeated processes or calculations in such vi-
sualization system are very undesirable and prevent-
ing this repetition would in many cases increase the
speed of the visualization rapidly. If such unneces-
sary repetition occurs, some form of caching can be
used to prevent it, at least partially.
Although the VTK has been under development
for many years, its caching possibilities still seem to
be quite limited. This is why, in this paper, we present
a caching library, written in C++ and build on the fea-
tures of C++11, which can be used to prevent unnec-
essary repeating of time consuming processes not just
in VTK but, since the library was written as generi-
cally as possible, in quite any C++ application.
The rest of the paper is organized as follows. Sec-
tion 2 describes the VTK pipeline and its problems
which raise the need for caching. Section 3 shows ex-
isting approaches for caching results of time consum-
ing processes. The proposed strategy and presented
caching library are described in Section 4. The results
achieved using this library are presented in Section 5
and Section 6 concludes the paper.
2 VTK
The VTK is based on the data-flow paradigm. It con-
tains modules that can be connected by the user to
form a pipeline. Each module may have various con-
figuration parameters that define how the module be-
154
Hruda, L. and Kohout, J.
Generic Caching Library and Its Use for VTK-based Real-time Simulation and Visualization Systems.
DOI: 10.5220/0006714501540164
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 1: GRAPP, pages
154-164
ISBN: 978-989-758-287-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

haves. There are three types of modules in VTK. The
data sources, which are modules that create new data
(by loading it from a file, generating it, etc.), have
only outputs and no inputs (except for their configura-
tion parameters). The filters are modules, which per-
form various processes with a given data, have both
inputs and outputs. The sinks are always in the end of
the pipeline and do the final operations with the data
(writing it into a file, showing it on the screen, etc.).
Diagram of a simple VTK pipeline is depicted in
Figure 1. There are two data sources, A and B, three
filters, C, D and E, and two sinks, F and G. The ar-
rows show the connections between the modules. For
example, filter C receives two inputs, one from data
source A and one from data source B, and has two out-
puts, one connected to filter E and the other to sink F.
Figure 1: Example of a VTK pipeline.
2.1 Problem with the Pipeline
The VTK pipeline is demand-driven by default. This
means that every module provides the data on its out-
put only when it is needed on the input of the mod-
ule which it is connected to. Let us again consider
the example from Figure 1. When, for example, sink
F needs to perform the final operation with the data
(e.g. render in onto the screen), it sends a request for
the data to filter C which then sends the request to
sources A and B. Sources A and B create (e.g. read
from given files) their output data and send it to fil-
ter C which uses the data to create its output which is
then sent to sink F. Sink F now can use the data to
perform the final operation (render it).
This is the basic principle of the demand-driven
pipeline. In VTK, the pipeline is actually enriched by
a feature which partially prevents unnecessary repe-
tition of processes performed by the modules in the
pipeline. It uses timestamps to recognize whether
a module’s input or any of its configuration param-
eters have changed. Every module has an attribute,
let MT (modification time) denote it, and another at-
tribute, let ET (execution time) denote it. The MT
attribute of a module is set to the current timestamp
every time the module’s input or any of its parame-
ters are changed. The ET attribute of a module is set
to the current timestamp every time the module exe-
cutes the process to create its output. When data is
requested from a module and its ET is greater than
its MT , instead of executing the process to create the
output data (including sending requests for data to the
preceding modules), it provides the data which is still
in the module from the last execution.
Although this mechanism increases the perfor-
mance of the entire visualization significantly, espe-
cially, when some of the processes performed by the
modules in the pipeline takes lot of time, in many
cases this is not sufficient. Let us imagine a case
where we have a module which executes its process
for output creation with certain input values and cer-
tain parameter values. After this, one of its parame-
ters is changed to a different value, which updates the
module’s MT attribute, and then the parameter gets
reset to its original value, which updates the module’s
MT attribute again. At this point all the module’s in-
puts and parameters have the same values as they had
at the time the last output creation process was ex-
ecuted. However, as the module’s MT attribute has
been updated since then, when the next request for
the module’s output comes, the process will be exe-
cuted, although the output will be exactly the same as
the last time.
Let us imagine another case where we have a mod-
ule which can only be in two certain configurations
of its inputs and parameters. Let us call them con f
1
and con f
2
. The configuration of the module changes
after every request for its output, so it starts with
con f
1
, then the request comes and its configuration
is changed to con f
2
. When another request comes it
gets changed back to con f
1
and this repeats in a loop.
Obviously each change of the module’s configuration
also updates its MT attribute, so every time the re-
quest comes the output creation process will be exe-
cuted. This creates a lot of unnecessary computation
though it could be quite easily prevented by storing
the two outputs somewhere and reuse them.
Note that these two cases are only simple exam-
ples. In reality the situation is typically more com-
plex. Different inputs and parameter configurations
can occur in an unpredictable order, whereas many of
them can repeat whilst many others occur only once.
Also the configurations of the pipeline modules can
be quite complex and can contain ON/OFF switches
that can cause some of the module’s parameters to
be ignored. But even if such ignored parameter gets
changed, it updates the module’s MT attribute despite
the fact that the change has no effect on the module’s
output. These cases are what raises the need for some
more advanced caching mechanism like the one pre-
sented in this paper.
Generic Caching Library and Its Use for VTK-based Real-time Simulation and Visualization Systems
155

3 RELATED WORK
Seemingly there has not been much work done in the
area of caching results of time consuming processes.
But there are at least some existing caching mecha-
nisms worth mentioning.
The Visualization Toolkit itself contains a class
called vtkTemporalDataSetCache
1
. Instances of
this class allow to store data associated with times-
tamps. When a data for a given timestamp is re-
quested and this timestamp is present in the given in-
stance then the data can be found in the cache and
used directly without the need to recompute or reload
it. This mechanism can be efficiently used for caching
animation data since we can precompute the anima-
tion or its part and then store each frame associated
with a timestamp. Afterwards we can access all the
stored frames through their timestamps without re-
computing them. But in general, not all the possible
data are known in advance and cannot all be associ-
ated with timestamps, which makes this mechanism
insufficient in many cases.
A little different approach is the memoization
(Hall and McNamee, 1997). Memoization is an op-
timization technique used to speed up programs by
storing results of function calls associated with given
argument values and returning the stored results when
the same combination of arguments occurs. For ex-
ample the latest (2017) version of Matlab has its own
built in memoize function
2
. The memoize function
takes a function, let f denote it, as its argument and
returns a function, let mf denote it, which is a mem-
oized version of the original function. The function
mf calls the function f internally and stores its return
value. When the mf function is called again with the
same combination of argument values it returns the
stored value instead of calling the f function again.
In most programming languages, when only in-
put arguments and return value of built-in data types
are considered, the memoization can be quite easily
implemented. When it comes to more complicated
data types like classes and structures, and in some
languages (C++ included) even arrays, the problem
of memoization becomes a lot more complex since
in many languages (again C++ included) there is no
general way to compare two objects and tell whether
or not they are the same. Similarly there is usually
no general way to define how to copy an object into
the cache or how to copy the resulting object from
the cache to where the user expects it. Also in many
1
http://www.vtk.org/doc/nightly/html/
classvtkTemporalDataSetCache.html#details
2
https://www.mathworks.com/help/matlab/ref/
memoize.html
languages the result does not have to be given back
by the return value but it can be passed using the so
called output arguments. An output argument is an
address in the memory, passed to the function by its
argument, into which the called function stores the
result. Output arguments are quite commonly used in
VTK.
For C++ a few recently developed small memo-
ization libraries exist
3 4 5
but they mostly seem to
only support primitive data types and in some cases
the memoized function can even have only one argu-
ment. Also none of these libraries seems to cover out-
put arguments.
The C++ library presented in this paper is based
on the memoization approach and extends it onto a
higher level of genericity covering many of the issues
described above.
4 OUR CACHING LIBRARY
As mentioned before, the caching library we present
is based on the memoization approach and is written
in C++11, which is nowadays standard. We decided
to design the library in C++ because this language is
used in most visualization applications, those based
on VTK included. Variadic templates, introduced in
C++11, which take a variable number of arguments,
were exploited to support memoization of virtually
any function with a minimal overhead associated with
the caching.
The developed library, which is publicly avail-
able to download from https://github.com/kivzcu/
HrdDataCacheSystem, consists of many classes most
important of which are the CachedFunction class
and the CachedFuctionManager class. An instance
of the CachedFunction class represents the caching
object which simulates calls of a given function and
is responsible for storing data into the cache and
for searching data in the cache. An instance of the
CachedFunctionManager class represents the cache
manager which serves as a factory for the caching ob-
jects. Since all caching objects created by the same
cache manager share the same cache, the cache man-
ager also takes care of evicting data from the cache
when its capacity gets exceeded. The relationship be-
tween instances of these classes is shown in Figure 2.
3
https://github.com/giacomodrago/cppmemo/blob/
master/cppmemo.hpp
4
https://github.com/jimporter/memo/blob/master/
include/memoizer.hpp
5
https://github.com/xNephe/MemoizationLibCpp
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
156

CachedFunctionManager
CachedFunction
CachedFunction
CachedFunction
CachedFunction
CachedFunction
CachedFunction
CachedFunctionManager
CachedFunction
CachedFunction
CachedFunction
CachedFunction
CachedFunction
CachedFunction
Figure 2: Relationship between instances of the
CachedFunction class and the CachedFunctionManager
class.
For the sake of clarity, we first describe our
caching library from the user perspective and only af-
ter that we give the details regarding its design (see
Sections 4.5 and 4.6).
4.1 Creating the Cache Manager
The cache manager can be created simply by decla-
ration or by dynamic creation using the new opera-
tor. The cache manager’s constructor takes one argu-
ment, which is its configuration object that determines
the cache’s capacity and contains information about
the data eviction policy which is used to remove data
from the cache when its capacity gets exceeded (see
Section 4.5). For example, the cache manager can be
created as shown in this snippet:
CacheManagerConfiguration managerConf;
managerConf.setCacheCapacity(100000000);
CachedFunctionManager manager(managerConf);
4.2 Creating the Caching Object
For the sake of simplicity, let us suppose we have a
function performing some time consuming operation
whose declaration is:
double func(int in1, int in2, int* out);
The arguments in1 and in2 are input arguments
of type int. One part of the operation result is passed
to the caller by the output argument out, the other, of
type double, is passed to the caller by the function’s
return value. If we want to cache the results of this
function using our library, we have to create a caching
object using a cache manager. The caching object
creation can be done as shown in this snippet:
CacheConfiguration conf;
...
CachedFunction<double, int, int, int*>* cf =
manager.createCachedFunction(conf, func);
The cf object represents the caching object,
manager is the cache manager which creates the
caching object, func is the previously described func-
tion which performs the time consuming operation
and conf contains the caching object’s configuration
which will be described later. The three dots are
where the configuration setting occurs. The caching
object cf is actually something of a memoized ver-
sion of the function func. It can be noticed that the
CachedFunction is a template class. Specifically it
is a variadic template which means it has a variable
number of arguments. The first argument is the type
of the return value of the function whose results are
supposed to be cached and the other arguments are the
types of the function’s arguments. There is also a spe-
cialization for functions with no return value (void).
4.3 Using the Caching Object
The caching object cf can be used to simulate calls of
the function func. This can be done using the call
method which can be used in the following way:
int result1;
double result2 = cf->call(1547, 325, &result1);
If the call method is called with the given combi-
nation of input arguments (in the considered example,
in1 = 1547 and in2 = 325) for the first time, the func-
tion func is called internally and its results (in this ex-
ample, return value and out) are stored into the cache
under the key formed by the input arguments. If the
call method is called with a combination of input ar-
guments that is present in the cache as a key together
with the corresponding result values, the func func-
tion is not called at all, instead the stored results are
used. In this case, after calling the call method, the
variables result1 and result2 contain the results of
the function call. The results should be the same as
when using the following code:
int result1;
double result2 = func(1547, 325, &result1);
For this to work, the func function’s results must de-
pend only on the input arguments, which has to be
ensured by the user of our library.
4.4 Configuring the Caching Object
As already mentioned, when creating the caching ob-
ject, its configuration must be defined first using the
CacheConfiguration class. An instance of this class
contains information about all of the cached func-
tion’s arguments and its return value. For each ar-
gument, it defines whether it is an input or output
argument (or ignored, which can be useful in some
Generic Caching Library and Its Use for VTK-based Real-time Simulation and Visualization Systems
157

cases), and it contains pointers to data manipulation
functions. These are functions that define how to copy
the argument to the cache, how to compare two in-
stances of the argument, how to copy the stored value
into the argument, etc. Similar functions must be de-
fined for the return value. These functions are usually
up to the user do define but for the primitive types we
have defined them implicitly.
Setting the information for the first argument from
our considered example might look as:
CacheConfiguration conf;
conf.setParamInfo(0, TypedParameterInfo<int>(
ParameterType::InputParam,
param0EqualFunction,
param0InitFunction,
nullptr,
param0DestroyFunction,
param0HashFunction,
param0GetSizeFunction
));
The first argument of the setParamInfo method is
the index of the cached function’s argument for which
the information is supposed to be set. The second ar-
gument is an instance of the TypedParameterInfo
class which contains all the information and can be
created using its constructor. The constructor’s first
argument states whether the given cached function’s
argument is an input or output argument or ignored.
The other arguments are pointers to the data manipu-
lation functions described above. The nullptr value
in this case corresponds with a function which should
define how to copy the corresponding stored value
from the cache to the argument but this function is
useless in case of an input argument. Information for
the return value can be configured similarly.
4.5 Eviction Policy
Given the fact that the cache’s capacity is typically
limited, a behaviour for cases the capacity gets ex-
ceeded must be defined. This behaviour is called
cache eviction policy and defines how to choose
which data should be removed from the cache in case
new data is up to be stored and there is not enough
space for it. There are many existing eviction policies
like LRU, LFU (B
ˇ
zoch et al., 2012), LRD (Effelsberg
and Haerder, 1984) or LRFU (Lee et al., 2001) but
all these policies only take reference count or refer-
ence recency of the data into account. In our case,
we need to also consider the data size and its cre-
ation time. For this purpose, an eviction policy was
designed based on the LRD policy and extended by
data size and creation time information. Our policy
uses a priority function to estimate the value of data
in the cache and in case an eviction is needed, the data
with the lowest priority is removed from the cache.
The function we use is given in Equation 1.
P
i
= k
R
·R
i
+6k
S
·(1 −
3
p
S
i
)+k
T
·(2
log
10
(T
i
)
−2) (1)
The priority of data with index i is denoted P
i
, R
i
is
the data’s priority according to the LRD policy, S
i
is the data’s size mapped to h0; 1i, T
i
is the data’s
creation time in milliseconds and k
R
≥ 0, k
S
≥ 0,
k
T
≥ 0 are constant parameters set by the user so that
k
R
+k
S
+k
T
= 1. The default (and recommended) val-
ues are k
R
= k
S
= k
T
=
1
3
. Details of how this priority
function was derived are beyond the scope of this pa-
per.
Although this policy is the default eviction policy
in our caching library, there is indeed a possibility for
the user to define his own policy.
4.6 Design Details
The data stored in the cache are contained in data
items. Each data item contains a single unique con-
figuration of input values and a corresponding con-
figuration of output values and is stored in the cache
under a non-unique hash value.
When the Call method is called with given ar-
gument values on an arbitrary caching object, which
simulates calls of a function denoted f, first all in-
put arguments are identified and their hash values are
computed using the user defined hash functions. All
these hashes are combined into a single hash value by
the approach used in the popular boost library
6
that is
known to provide a decent hash, unless some of the
hashes to combine is indecent. The combination for-
mula of this approach is following:
single_hash = hash1 ˆ (hash2 + 0x9e3779b9
+ (hash1 << 6) + (hash1 >> 2))
After that all the data items stored in the cache
under this hash value are acquired. These data items
are iterated one by one and for each of them, the in-
put arguments, passed to the Call method, are com-
pared with corresponding input values stored in the
given data item using the user defined comparison
functions. If any of these comparisons indicates a
mismatch between the given argument and the corre-
sponding stored input value then the given data item
is rejected. The iteration continues until there are no
more data items to iterate or until a data item is found
for which all the comparisons indicate matching in-
put values, such data item is then labelled a matching
data item.
If the matching data item is found in the cache, the
output values are acquired from it and copied into the
6
http://www.open-std.org/jtc1/sc22/wg21/docs/papers/
2014/n3876.pdf
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
158

corresponding output arguments of the Call method
using the user defined copy functions. If one of the
output values is the return value the Call method
terminates by returning it, either directly or using
the user defined return function, depending on the
caching object’s configuration. Otherwise the Call
method terminates by returning nothing (this occurs
when the return type is void).
When no matching data item is found the situa-
tion is a little more complicated. In such case a new
empty data item is created and the Call method’s in-
put arguments are copied into it using the user defined
initialization functions. Afterwards the f function is
called with all the Call method’s arguments to cre-
ate the output values. These output values are copied
into the new data item, again using the user defined
initialization functions. Also the sizes in bytes of all
input and output values stored in the new data item
are computed, using the user defined size computa-
tion functions, and summed together to get the data
item’s size. If there is not enough space in the cache
for the new data item, the eviction policy (see Sec-
tion 4.5) is used to remove some data from it making
the space. Finally the new data item is stored into
the cache under the combined hash value computed
at the beginning. Also, of course, the output values
are copied into the corresponding output arguments
of the Call method and the method terminates by re-
turning the correct return value or nothing in case of
void return type. Figure 3 shows the flowchart of the
Call method which briefly describes the method’s be-
haviour.
In some cases, the performance of our library
strongly depends on the quality of hash functions pro-
vided for the input arguments. If the hash functions
produce the same hashes for different values too of-
ten, it can result in higher number of comparisons
made when searching the cache for the matching data
item. For the primitive and standard data types (such
as std::string) decent hashes can be obtained using
the Standard Template Library’s std::hash
7
. For
user defined data types, the hash functions must be
defined manually. In the case of arrays or collec-
tions, there is usually no need to use all their items
to compute the hash, in most cases only a few deter-
ministically selected items can be used. The hash of
a more complex object can be computed by combin-
ing hashes of its attributes using the boost library ap-
proach we use for combining the hashes of the input
arguments (as described above).
7
http://en.cppreference.com/w/cpp/utility/hash
Figure 3: Flowchart of the Call method (created using
https://www.draw.io/).
4.7 Use in VTK
Since the presented library is very generic, there is no
problem using it in the VTK as it is. But to make the
usage in VTK easier for developers, we have created
a wrapper for it, specifically for VTK7. The wrapper
consists of a few classes but the most important one is
the CachingFilter class. Using this class any VTK
filter can be made to use our caching library through
inheritance. Filters in VTK7 contain a method named
RequestData which performs the filter’s operation.
The user who wants to create his own filter overrides
this method and defines it as he wishes. The method’s
declaration looks like this:
virtual int RequestData(
vtkInformation* request,
vtkInformationVector** inputVector,
vtkInformationVector* outputVector
);
Generic Caching Library and Its Use for VTK-based Real-time Simulation and Visualization Systems
159

It has two important arguments, inputVector, which
contains all the filter’s inputs, and outputVector,
which is an output argument into which the filter’s
output is supposed to be stored. The argument
request in some cases contains some additional in-
formation for the filter’s operation and in such cases
has to be considered an input argument as well, al-
though in many cases it is unused. The method’s re-
turn value only indicates whether the operation has
finished successfully. There is one more hidden in-
put argument which is the filter itself (meaning the
instance of the filter class on which the RequestData
method is called) since the filter’s configuration also
has impact on its output.
To create a caching version of an existing fil-
ter new class must be created inheriting from the
CachingFilter class. Creation of such class can be
similar to this example:
class CachingDecimator :
public CachingFilter<CachingDecimator,
vtkDecimatePro>
{ ... };
In this case, we have created a new filter which will
be a caching version of the vtkDecimatePro
8
filter
whose task is to perform a triangle mesh simplifica-
tion. We note that this task is crucial for an interac-
tive visualization of big data sets, multi-resolution hi-
erarchies for efficient geometry processing, and many
other computer graphics applications.
The CachingFilter class internally creates a
caching object which simulates calls of the original
filter’s RequestData method, in our case the origi-
nal filter is vtkDecimatePro, therefore it simulates
calls of vtkDecimatePro::RequestData. It also in-
herits from the original filter (vtkDecimatePro in
our case), therefore it is a valid VTK filter, and
it overrides the RequestData method to use the
caching object to perform the original filter’s op-
eration instead of performing it directly. Inherit-
ing from such class gives us the caching version of
the original filter (vtkDecimatePro), in our case the
CachingDecimator.
For all this to work, the data manipulation func-
tions must be defined, which can be done through
several methods declared in CachingFilter that the
user can override in the inheriting class. For example,
in the case of the CachingDecimator, the compar-
ison function for the input parameter inputVector
can be overridden to look like this:
bool inputEqualsFunction(
vtkInformationVector** a,
vtkInformationVector** b)
8
http://www.vtk.org/doc/nightly/html/
classvtkDecimatePro.html#details
{
vtkPolyData* inputPoly1 =
vtkPolyData::GetData(a[0]);
vtkPolyData* inputPoly2 =
vtkPolyData::GetData(b[0]);
return CacheUtils::CacheEquals(
inputPoly1, inputPoly2);
}
The static function CacheEquals is a predefined
data manipulation function that compares two in-
stances of the class vtkPolyData. The data manipu-
lation functions for the most used data types in VTK
are predefined in the CacheUtils class so that the de-
velopers do not have to create them on their own.
Actually, for the two most important argu-
ments of the RequestData method, inputVector
and outputVector, the data manipulation func-
tions are already defined in a usable way in the
CachingFilter class so that in most cases the user
does not have to override and redefine them at all. The
data manipulation functions, however, should always
be overridden and redefined for the filter object, in our
case the CachingDecimator, since the filter’s output
usually depends on its configuration and it is virtually
impossible to create generic data manipulation func-
tions for filters. This is due to the fact that C++ lacks
any advanced reflection features (such as in, e.g., C#)
and, therefore, it is impossible to identify all the filter
parameters in runtime.
Nevertheless, even if the runtime parameter iden-
tification was possible, it would still be impossi-
ble to detect mutual interdependencies between the
parameters. For example, the vtkDecimatePro
class has a parameter named Splitting, which is
an ON/OFF switch, and also a parameter named
SplitAngle that is completely ignored by the filter,
when Splitting parameter is set to OFF. The VTK,
by default, does not take such dependencies into ac-
count and, therefore, without our library, just chang-
ing the SplitAngle (and nothing else including the
input data) would lead to a new execution of the fil-
ter’s operation even when the Splitting parameter is
set to OFF creating exactly the same output as when
executed the last time (see also Section 2.1). Us-
ing our caching library such unnecessary executions
can be prevented by defining the filter’s data manip-
ulation functions correctly, especially the comparison
function which in our case could be overridden and
defined for example like this:
bool filterEqualsFunction(
CachingDecimator* filter1,
CachingDecimator* filter2)
{
if ((filter1->GetSplitting() !=
filter2->GetSplitting()) ||
(filter1->GetSplitting() &&
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
160
filter1->GetSplitAngle() !=
filter2->GetSplitAngle())
)
return false;
...
return true;
}
For a complex filter, we also recommend defin-
ing its hash function (filterHashFunction) to in-
clude only the parameters that are most typically
changed. For example, in various simplification sce-
narios, only the TargetReduction parameter of the
vtkDecimatePro class is typically being modified
while all other parameters retain their default val-
ues. Hence, implementing the hash function to re-
turn the hash of the TargetReduction parameter is
an optimal solution to improve the performance of the
caching in a vast majority of cases.
5 RESULTS
The developed library was tested on a computer with
CPU Intel Pentium Processor N3540 (clock rate 2.16
GHz, 4 cores, L1 cache 224 kB, L2 cache 2 MB),
graphics card NVIDIA GeForce 920M and 4GB of
memory with clock rate of 666MHz.
To gather the results presented in this section, two
test cases were created. The first test case was created
artificially, the second test case represents real appli-
cation where our library was used on real data.
In both test cases, the default eviction policy
briefly described in Section 4.5 was used with the pa-
rameters k
R
, k
S
, k
T
set to their default values k
R
=
k
S
= k
T
=
1
3
unless stated otherwise.
5.1 Artificial Case
In this test case, we used the CachingDecimator
class (see Section 4.7) which uses functionality of the
vtkDecimatePro class to simplify triangle meshes of
scaled spheres. The results of the mesh simplification
were cached.
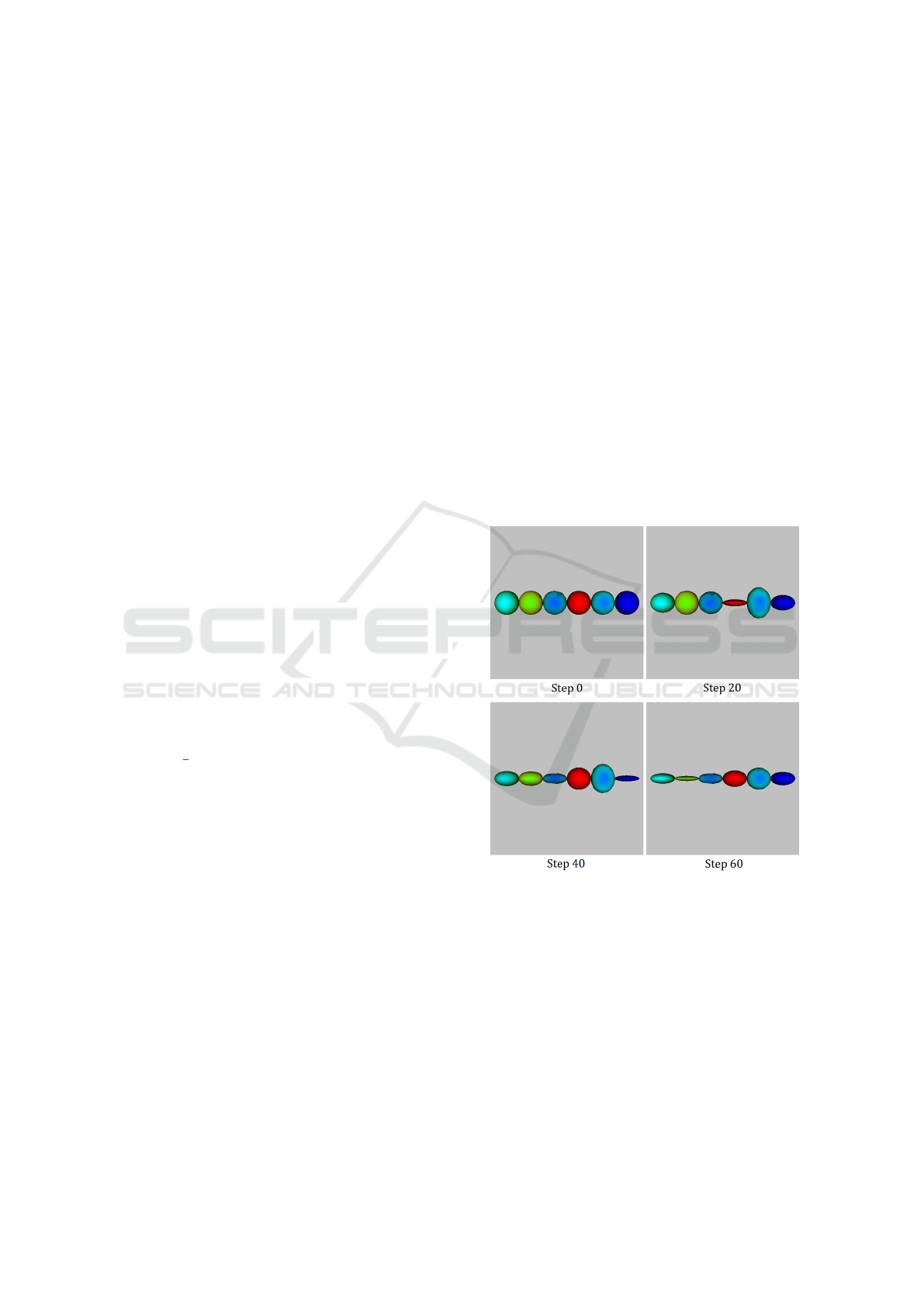
To demonstrate the functionality simple animation
was created containing six spheres represented by tri-
angle meshes, each with different vertex count. The
first frame of the animation is just the six spheres
placed next to each other. With every animation step
each sphere’s height (size along the y axis) is increas-
ing linearly using scaling until it gets to a threshold
h
max
and then it starts to decrease linearly until it gets
to a threshold h
min
. This repeats infinitely and each
sphere’s height changes at different speed.
While the h
min
value is constant (but different for
each sphere), the h
max
value increases a bit whenever
the sphere’s height gets to h
max
until some threshold
H
max
(different for each sphere) is reached. After that
the h
max
value starts to decrease in the same fashion
until the threshold H
min
is reached. This also repeats
infinitely. As a result, the animation has a very long
repeat period though there is some repetition within a
single period.
Before rendering each sphere at the end of the an-
imation step, the simplification of its triangle mesh is
performed to lower its vertex count to approximately
10% of its original vertex count. At the beginning
of each animation step new unsimplified spheres are
generated. Since the simplification is quite time con-
suming, its results are cached using our library. The
input of the cached function is the sphere triangle
mesh after being scaled to the given height and the
output is the simplified mesh (of a scaled sphere). The
simplified spheres are rendered at the end of each ani-
mation step. Figure 4 shows the scene at four different
steps of the animation.
Figure 4: Four different animation steps of the artificial test
case.
The testing itself was done by running the first
3 000 steps of the animation (with 6 spheres, this rep-
resents 18 000 simplifications) and the total time and
the cache hit count were measured. In this test case,
the total of 74.6 MB of different data are generated
and can be stored into the cache. We ran the test with
three different cache capacities, unlimited capacity,
60 MB and 30 MB. The results are shown in Table 1.
It can be seen that the acceleration is quite signif-
icant in all three cases. Better results can be achieved
by changing the eviction policy parameters k
R
, k
S
, and
Generic Caching Library and Its Use for VTK-based Real-time Simulation and Visualization Systems
161
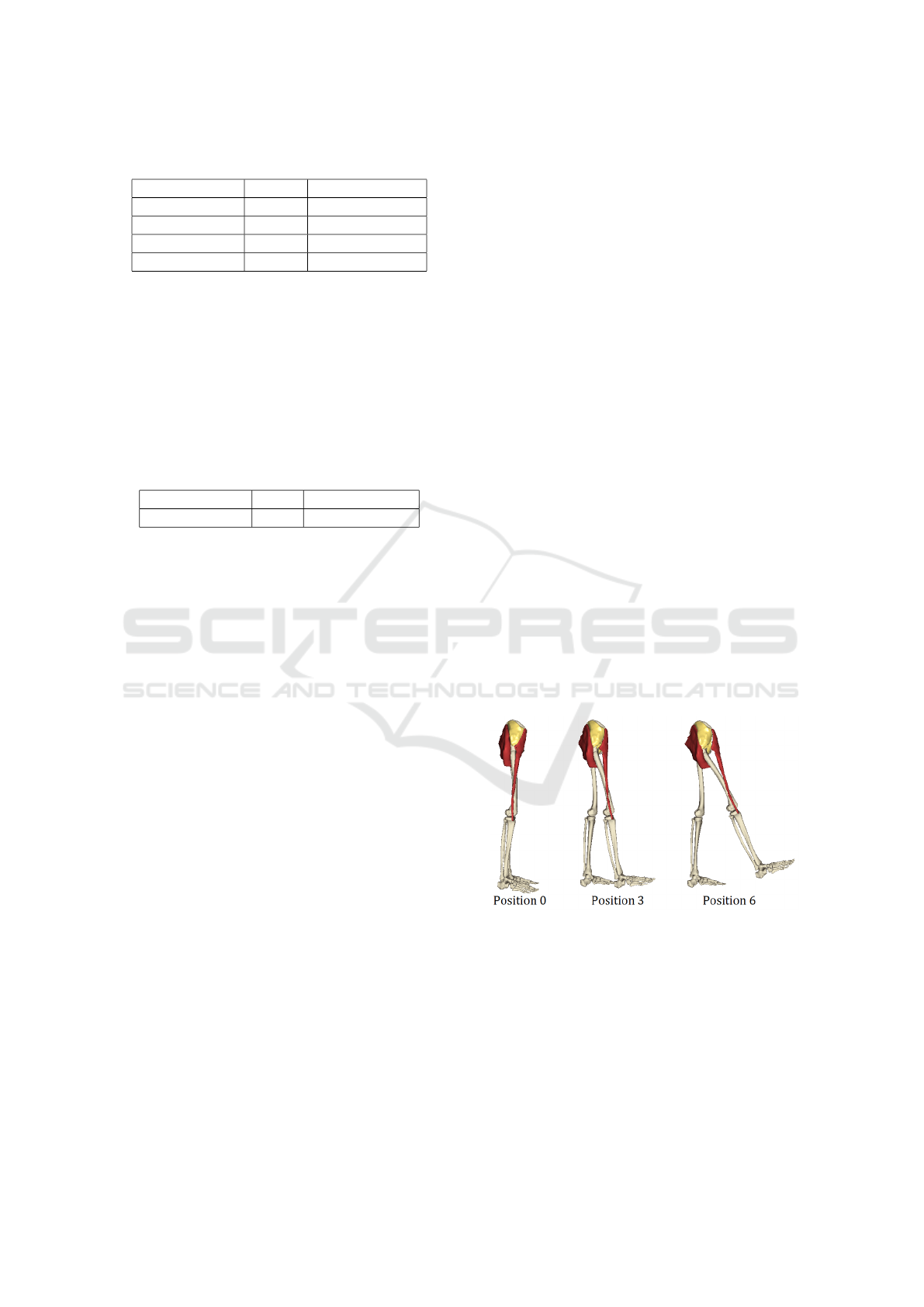
Table 1: Results of the artificial test case.
Cache capacity Time Cache hit count
No cache 1 302 s N/A
Unlimited 125 s 17 587 (97.7 %)
60 MB 167 s 16 886 (93.8 %)
30 MB 745 s 8 854 (49.2 %)
k
T
to the values different from defaults. Especially,
if the cache capacity is small, increasing the param-
eter k
T
, i.e., making the impact of the data time cre-
ation more important, often helps. In the case of the
cache capacity set to 30 MB, the best result, which is
shown in Table 2, was achieved for the configuration
k
R
= 0.05, k
S
= 0, k
T
= 0.95.
Table 2: Result of the artificial test case with k
R
= 0.05,
k
S
= 0, k
T
= 0.95.
Cache capacity Time Cache hit count
30 MB 614 s 8 161 (45.3 %)
It can be seen that, in comparison to the default
configuration, the cache hit count has dropped but the
time has improved (from 745 to 614 s). Given the fact
that 30 MB is only 40.2 % of the total 74.6 MB, the
time 614 s is a very good result since it is not even a
half of the time achieved with no cache (1 302 s).
Despite the fact, we are dealing with an an-
imation in this experiment, its handling using
vtkTemporalDataSetCache concept, which is de-
signed for time-varying data sets, does not bring any
acceleration because the period of the entire anima-
tion is larger than 3 000 steps. In order to achieve
a comparable acceleration, one can implement a fil-
ter that would associate the simplified sphere with the
timestamp derived from the height of the sphere and
another one that would convert the number of anima-
tion step into the timestamp. However, this seems to
be a quite complex process, and, furthermore, possi-
ble to do only, if the animation is known in the design
time, while replacing vtkDecimatePro by its caching
version, using our caching library, is simple and with-
out any restrictions.
5.2 Real Application
In this test case, our caching library was integrated
into lhpBuilder, a VTK based virtual human simula-
tion and visualization application. One of its features
is muscle fibre wrapping that allows clinical experts to
study subject-specific skeletal loading in various po-
sitions of the subject movement (e.g., walking, stair
climbing, etc.) using various simulation settings (e.g.,
the requested number of lines of action, impenetra-
bility tolerance, etc.). Typically, the experts visual-
ize the movement step by step until they find some-
thing suspicious or interesting, then they tend to re-
peatedly switch between several positions to compare
them while trying to change some of the settings pa-
rameters to get a bit different results and visualize
these results from various viewpoints. As the most
time-consuming part of the whole process, which is
the deformation of 3D models of muscles (for the de-
tails, see, e.g., (Kohout et al., 2013)), takes easily sec-
onds or even tens of seconds per one step, employing
some caching mechanism is desirable.
Obviously, the vtkTemporalDataSetCache con-
cept is well suitable for this case: the position index
serves as a timestamp and, if the settings changes,
the cache is cleared. Even better acceleration can
be achieved with our library due to reusing some of
the deformation results for one position/settings in an-
other. In this case, the inputs of the cached function
are the original muscle model, bones, and the settings
and other deformation parameters, not the position in-
dex.
In our test case, the right hip flexion is performed,
whereas five muscles of the right leg and pelvic re-
gion are, after their deformation to fit the current posi-
tion, visualized together with the bones – see Figure 5.
During our testing, the positions were chosen to be: 0,
3, 9, 3, 9, 3, 9, 6, 9, 6, 3, 0, 3, 6, 9. For the sake of
simplicity, no other settings were changed. The total
time and cache hit count were measured.
Figure 5: The muscles of the right leg in three different
positions.
During the experiment, the total of 24.8 MB of
different data were successively generated by the
muscle wrapping process that could be stored into the
cache. We ran the test with three different cache ca-
pacities, unlimited capacity, 20 MB and 10 MB. The
results are shown in Table 3.
It can be seen that even in this test case, the ac-
celeration is quite significant, especially, if the cache
capacity is large. It should be noted that in this test
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
162

Table 3: Results of the muscle deformation test case.
Cache capacity Time Cache hit count
No cache 779 s N/A
Unlimited 200 s 55 (73.3%)
20 MB 274 s 45 (60.0%)
10 MB 545 s 13 (17.3%)
case there is not that much data repetition as it was
in the artificial test case. For a longer sequence of
positions, the results would be naturally even better.
Similarly, with more detailed models of the muscles
or a more complex muscle wrapping algorithm, using
our caching library would be even more beneficial.
In case of the 10 MB capacity, better results can
be ensured by using k
R
= 0, k
S
= 0.7, k
T
= 0.3 as
values of the eviction policy’s parameters. The result
achieved with this configuration is shown in Table 4.
Even though after this change the cache hit rate is only
Table 4: Result of the muscle deformation test case with
k
R
= 0, k
S
= 0.7, k
T
= 0.3.
Cache capacity Time Cache hit count
10 MB 463 s 18 (24.0%)
24%, more than 40% time is saved in comparison with
the case where no cache is used.
5.3 Performance of the Caching Library
In computer graphics, there are many algorithms that
perform a simplification of the input surface mesh in
the first step to reduce their time or memory con-
sumption, or to increase robustness of the solvers they
employ (e.g., (Huang et al., 2006)). To investigate
performance of our library, we, therefore, compared
the times needed to simplify a single sphere using
the original vtkDecimatePro class with the times
achieved by CachingDecimator class when the com-
parison function (see Section 4.7), which is used to
determine whether the data is in the cache, returned,
after doing the comparison, false in k% of its calls. In
both cases, only the modification time (MT attribute)
of the module producing the input data changed, i.e.,
the input actually remained the same, and the sim-
plification was repeated 1000 times. The experiments
ran on a computer with Intel Core i7-4930K CPU (3.4
GHz, 6 cores), 64 GB RAM, Windows 10 64-bit.
Figure 6 shows that the speed-up achieved by the
caching library exhibits an exponential character. It
can be seen that even with a very low cache hit rate,
there is some interesting acceleration in comparison
with the original application that does not use any
data caching. For example, for a mesh of medium
size (ca. 20K triangles), cache hit rate about 1%
is needed to counterbalance the overhead associated
with the library. With larger meshes this threshold is
even lower. Hence, using our caching library can be
recommended in almost all scenarios since extremes
such as 100% cache miss rates are very rare in prac-
tice and even if they occur, the overhead is very small
– it is less than 3.5 milliseconds per call.
Figure 6: The dependence of the speed-up on the cache hit
count in the experiment with simplification of single sphere
of various sizes: XS = 1 680, S = 4 800, M = 19 600, L =
79 200, XL = 498 000 triangles.
6 CONCLUSION
We have presented a caching library, written in
C++11 and based on the memoization approach, that
can be used to speed up applications where some rep-
etition of time consuming processes is occurring. The
library is very generic so it can be used in quite any
C++ application but the original motivation for de-
veloping such library came from the VTK (see Sec-
tion 2) and its problems with unnecessary computa-
tion repetition. To make the usage in VTK7 easier,
a wrapper was created (see Section 4.7) which al-
lows the user to simply create a caching version of
an existing VTK filter by inheritance and by defining
a few predeclared methods. Due to the fact that the
library was implemented in C++ and exploits vari-
adic templates, its overhead is minimal, which makes
Generic Caching Library and Its Use for VTK-based Real-time Simulation and Visualization Systems
163

it typically useful even in scenarios with a very low
expected cache hit rate. The library was tested on
three visualization applications, all based on the VTK,
and in all these cases our library was able to speed up
the processing significantly (see Section 5). Our im-
plementation of the library together with the wrapper
for VTK users is publicly available to download from
https://github.com/kivzcu/HrdDataCacheSystem.
In the future, we would like to simplify the usage
of our library in VTK as much as possible by creat-
ing a software tool that could generate the code of the
inherited class of a caching filter using the VTK wrap-
per automatically. Using such a tool, the user would
have to write very little code or even none at all in or-
der to use our library in VTK. Furthermore, we would
like to add the possibility to use hard drive to store
the cached data, not just to extend the possible cache
capacity but also for data persistence.
ACKNOWLEDGEMENTS
This work was supported by the project PUNTIS
(LO1506) of the Ministry of Education, Youth and
Sports of the Czech Republic and also by the Uni-
versity specific research project SGS-2016-013 Ad-
vanced Graphical and Computing Systems.
REFERENCES
Ahrens, J., Geveci, B., and Law, C. (2005). Paraview: An
end-user tool for large data visualization. The Visual-
ization Handbook, 717.
B
ˇ
zoch, P., Mat
ˇ
ejka, L., Pe
ˇ
si
ˇ
cka, L., and
ˇ
Safa
ˇ
r
´
ık, J.
(2012). Towards caching algorithm applicable to mo-
bile clients. In Computer Science and Information
Systems (FedCSIS), 2012 Federated Conference on,
pages 607–614. IEEE.
Effelsberg, W. and Haerder, T. (1984). Principles of
database buffer management. ACM Transactions on
Database Systems (TODS), 9(4):560–595.
Frank, M., V
´
a
ˇ
sa, L., and Skala, V. (2006). Mve-2 applied in
education process. Proceedings of NET technologies,
pages 39–45.
Hall, M. and McNamee, J. P. (1997). Improving soft-
ware performance with automatic memoization. Johns
Hopkins APL Technical Digest, 18(2):255.
Huang, J., Shi, X., Liu, X., Zhou, K., Wei, L.-Y., Teng,
S.-H., Bao, H., Guo, B., and Shum, H.-Y. (2006).
Subspace gradient domain mesh deformation. ACM
Transactions on Graphics, 25(3):1126–1134.
Kohout, J., Clapworthy, G. J., Zhao, Y., Tao, Y., Gonzalez-
Garcia, G., Dong, F., Wei, H., and Kohoutova, E.
(2013). Patient-specific fibre-based models of muscle
wrapping. INTERFACE FOCUS, 3(2, SI).
Lee, D., Choi, J., Kim, J.-H., Noh, S. H., Min, S. L., Cho,
Y., and Kim, C. S. (2001). Lrfu: A spectrum of poli-
cies that subsumes the least recently used and least
frequently used policies. IEEE transactions on Com-
puters, 50(12):1352–1361.
Pieper, S., Halle, M., and Kikinis, R. (2004). 3d slicer. In
Biomedical Imaging: Nano to Macro, 2004. IEEE In-
ternational Symposium on, pages 632–635. IEEE.
Ramachandran, P. and Varoquaux, G. (2011). Mayavi: 3d
visualization of scientific data. Computing in Science
& Engineering, 13(2):40–51.
Rosset, A., Spadola, L., and Ratib, O. (2004). Osirix: an
open-source software for navigating in multidimen-
sional dicom images. Journal of digital imaging,
17(3):205–216.
Schroeder, W. J., Lorensen, B., and Martin, K. (2004). The
visualization toolkit: an object-oriented approach to
3D graphics. Kitware.
GRAPP 2018 - International Conference on Computer Graphics Theory and Applications
164
