Countering Bias in Tracking Evaluations

Gustav H

ager, Michael Felsberg and Fahad Khan

Computer Vision Lab, Link

oping University, Sweden

Keywords:

Tracking, Evaluation.

Abstract:

Recent years have witnessed a signiﬁcant leap in visual object tracking performance mainly due to powerful

features, sophisticated learning methods and the introduction of benchmark datasets. Despite this signiﬁcant

improvement, the evaluation of state-of-the-art object trackers still relies on the classical intersection over

union (IoU) score. In this work, we argue that the object tracking evaluations based on classical IoU score are

sub-optimal. As our ﬁrst contribution, we theoretically prove that the IoU score is biased in the case of large

target objects and favors over-estimated target prediction sizes. As our second contribution, we propose a new

score that is unbiased with respect to target prediction size. We systematically evaluate our proposed approach

on benchmark tracking data with variations in relative target size. Our empirical results clearly suggest that

the proposed score is unbiased in general.

1 INTRODUCTION

A signiﬁcant progress has been made in challenging

computer vision problems, including object detection

and tracking during the last few years (Kristan et al.,

2016), (Russakovsky et al., 2015). In object detection,

the task is to simultaneously classify and localize an

object category instance in an image whereas visual

tracking is the task of estimating the trajectory and

size of a target in a video. Generally, the evaluation

methodologies employed to validate the performance

of both object detectors and trackers are based on the

intersection over union score (IoU). The IoU provi-

des an overlap score for comparing the outputs of

detection/tracking methods with the given annotated

ground-truth. Despite its widespread use, little rese-

arch has been done on the implications of IoU score

during object detection and tracking performance eva-

luations.

Recent years have seen a signiﬁcant boost in

tracking performance both in terms of accuracy and

robustness. This signiﬁcant jump in tracking perfor-

mance is mainly attributed to the introduction of ben-

chmark datasets, including the visual object tracking

(VOT) benchmark (Kristan et al., 2016). In the VOT

benchmark, object trackers are ranked according to

their accuracy and robustness. The accuracy is deri-

ved from the IoU score (Jaccard, 1912),(Everingham

et al., 2008), while the robustness is related to how

often a particular tracker loses the object. Different

to VOT, the online tracking benchmark (Wu et al.,

2015) (OTB) only takes accuracy into account by

again using evaluation methodologies based on IoU

criteria. Both the VOT and OTB benchmarks contain

target objects of sizes ranging from less than one per-

cent to approximately 15% of the total image area.

The lack of larger objects in object tracking bench-

marks is surprising, as it directly corresponds to situ-

ations where the tracked object is close to the camera.

However, in such cases, the de facto tracking evalu-

ation criteria based on IoU score will be sub-optimal

due to its bias towards over-estimated size prediction

of targets. In this work, we theoretically show that

the standard IoU is biased since it only considers the

ground-truth and target prediction area, while igno-

ring the remaining image area (see ﬁgure 1).

When dealing with large size target objects, a

naive strategy is to over-estimate the target size by

simply outputting the entire image area as a pre-

dicted target region (see ﬁgure 1). Ideally, such a

naive strategy is expected to be penalized by the stan-

dard tracking evaluation measure based on the IoU

score. Surprisingly, this is not the case (Felsberg

et al., 2016). The IoU based standard evaluation met-

hodology fails to signiﬁcantly penalize such an over-

estimated target prediction case, thereby highlighting

the bias within the IoU score.

In this paper, we provide a theoretical proof that

the standard IoU score is biased in case of large target

objects. To counter this problem, we propose an unbi-

Häger, G., Felsberg, M. and Khan, F.

Countering Bias in Tracking Evaluations.

DOI: 10.5220/0006714805810587

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

581-587

ISBN: 978-989-758-290-5

581

Figure 1: An example image, where the target (red) covers

a large area of the image. The tracker outputs a target pre-

diction (blue) covering the entire image. The standard IoU

score will be equal to the ratio between the size of the target

and the total image size, assigning an overlap score of 0.36.

Our proposed unbiased score assigns a signiﬁcantly lower

score of 0.11, as it penalizes the severe over-estimation of

the target size.

ased approach that accounts for the total image area.

Our new score is symmetric with respect to errors in

target prediction size. We further validate our propo-

sed score with a series of systematic experiments si-

mulating a wide range of target sizes in tracking sce-

narios. Our results clearly demonstrate that the pro-

posed score is unbiased and is more reliable than the

standard IoU score when performing tracking evalua-

tions on videos with a wide range of target sizes.

2 RELATED WORK

A signiﬁcant leap in performance has been witnes-

sed in recent years for both object detection and

tracking (Kristan et al., 2014),(Everingham et al.,

2008). Among other factors, this dramatic impro-

vement in tracking detection performance is attribu-

ted to the availability of benchmark datasets (Kristan

et al., 2014),(Russakovsky et al., 2015). These ben-

chmark datasets enable the construction of new met-

hods by providing a mechanism for systematic per-

formance evaluation with existing approaches. The-

refore, it is imperative to have a robust and accurate

performance evaluation score that is consistent over

different scenarios. Within the areas of object de-

tection and tracking (Everingham et al., 2008), (Wu

et al., 2013),(Russakovsky et al., 2015), standard eva-

luation methodologies are based on the classical in-

tersection over union (IoU) score. The IoU score,

also known as Jaccard overlap (Jaccard, 1912), ta-

kes into account both the intersection and the union

between the ground-truth and target prediction. The

score compares the distance between a pair of binary

feature vectors. Despite its widespread use, the IoU

score struggles with large size target objects.

Other than the IoU score, the F1 score is com-

monly employed in medical imaging and text proces-

sing. The F1 score is computed as the geometric mean

of the precision and recall scores and can be viewed

as analogous to the IoU score. However, a drawback

of F1 score measure is its inability to deal with highly

skewed datasets, as it does not sufﬁciently account the

true negatives obtained during the evaluation (Powers,

2011). Most tracking benchmarks are highly skewed,

as they contain signiﬁcantly more pixels annotated as

background than the target object. Surprisingly, this

problem has not been investigated in the context of

object detection and visual tracking.

In the context of object detection, the issue of

skewed data is less apparent since the overlap bet-

ween the target prediction and ground-truth is only

required to be greater than a certain threshold (ty-

pically 0.5). Different to object detection, the eva-

luation criteria in object tracking is not limited to a

single threshold value. Instead, the tracking perfor-

mance is evaluated over a range of different threshold

values. Further, the ﬁnal tracking accuracy is com-

puted as an average overlap between target prediction

and the ground-truth over all frames in a video. In this

work, we investigate the consequences of employing

IoU metric in visual object tracking performance eva-

luation.

3 OVERLAP SCORES

Here we analyze the traditional intersection over

union (IoU) O. We prove that it is biased with re-

gard to the prediction size. The reasoning is built on

the notion of four different regions of the image given

by the annotation bounding box, S

, and the detection

bounding box, S

. These areas are: A

= |S

∩ S

(true positive), A

d ¯a

= |S

∩

| (false positive), A

∩S

| (false negative), and A

d ¯a

= |

∩

| (true ne-

gative).

3.1 Bias Analysis for Intersection over

Union

The classical IoU, O measures the overlap as the ratio

of the intersection area between detection and ground

truth, and union area:

O =

+ A

¯ad

+ A

(1)

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

582

Figure 2: One dimensional image (black) with the annota-

tion (red) and the bounding box (green). Image coordinates

range from 0 to 1.

While the IoU behaves satisfactorily for objects

of smaller size, it does not function well when ob-

jects are larger enough to cover a signiﬁcant portion

of the image. For an annotation of covering most of

the image area it is possible for the tracker to set the

prediction size to cover the full image, and still main-

tain good overlap.

We will now show that the IoU is biased with re-

spect to the size of the prediction. To simplify the

derivation, we consider without loss of generality a

one dimensional image. As the IoU only considers

areas of prediction and ground truth, extending the

reasoning to two dimensional images can be done tri-

vially. A visualization of the one dimensional image,

with the annotated bounding interval in red and the

detection interval in green can be seen in ﬁgure 2.

In one dimension the annotation is an interval star-

ting at A

, and ending in A

. The prediction interval

starts at D

and ends at D

. A small perturbation of

or D

, will change the overlap interval I

, or the

false positive interval I

¯ad

respectively. As we will now

show the IoU is not the optimal choice for overlap

comparison as it does not treat errors in position and

size equally.

We assume that the overlap is non-empty, i.e.,

< A

∧ D

> A

. We then get four different ca-

ses of imperfect alignment (I

∩ I

= I

and I

∪ I

+ I

¯ad

+ I

; ﬁgure 2 shows case 4.):

case boundaries I

∩ I

∪ I

1. D

< A

∧ D

> A

− A

− D

2. D

< A

∧ D

< A

− A

− D

3. D

> A

∧ D

< A

− D

− A

4. D

> A

∧ D

> A

− D

− A

By considering a change in position of the boun-

ding box ε

, [D

] 7→ [D

+ε

], and a small

change in size ε

, [D

] 7→ [D

− ε

+ ε

], we

compute the effect they will have on the resulting IoU,

respectively. Starting with the size change, the IoU

for case 4 becomes:

O =

− (D

− ε

)

+ ε

− A

− D

+ ε

− A

+ ε

. (2)

Taking the derivative with respect to ε

yields

∂O

∂ε

− A

+ ε

) − (A

− D

+ ε

)

− A

+ ε

)

(3)

At the stationary solution, i.e., ε

= 0, we thus obtain

lim

→0

∂O

∂ε

− A

) − (A

− D

)

− A

)

+ I

¯ad

+ I

) − I

+ I

¯ad

+ I

)

> 0

(4)

Where we have used the fact that: A

− D

= I

, and

− A

= I

+ I

¯ad

+ I

Following the same procedure for the case of a

change in position we get for ε

O =

− (D

+ ε

)

+ ε

− A

− D

− ε

− A

+ ε

. (5)

lim

→0

∂O

∂ε

= −

− A

) + (A

− D

)

− A

)

−

+ I

¯ad

+ I

) + I

+ I

¯ad

+ I

)

< 0

(6)

Computing both derivatives for all cases 1.-4. re-

sults in the following table:

case ε

1. −

¯ad

)

< 0 0

¯ad

)−I

¯ad

)

> 0

¯ad

)+I

¯ad

)

> 0

2(I

¯ad

)

¯ad

)

> 0 0

¯ad

)−I

¯ad

)

> 0 −

¯ad

)+I

¯ad

)

< 0

The zero entries above imply that if the annotation

lies completely inside the detection (case 1.) or the

detection lies completely inside the annotation (case

3.), an incremental shift does not change the IoU me-

asure. The negative/positive derivatives of ε

in case

1. and 3. lead to a compensation of a too large/too

small detection. The positive/negative derivatives of

in case 2. and 4. lead to a compensation of a

detection-displacement to the left/right. The proble-

matic cases are the positive derivatives of ε

in case

2. and 4.: In the case of a displacement error, the IoU

measure is always improved by increasing the size of

the detection. For the majority of cases a slight in-

crease in detection size will improve the overlap, only

for the ﬁrst case when the detection is overlapping on

both sides will it decrease the overlap score. This is in

contrast to the change in position where it is equally

likely to decrease the overlap depending on the di-

rection selected. This results in a biased estimate of

the object size.

3.2 Unbiased Intersection over Union

In order to remove this bias we also account for the

true negatives, that is the parts of the image that is

Countering Bias in Tracking Evaluations

583

neither annotated as belonging to the target, or con-

sidered to be part of the object by the tracker. We do

this by computing an IoU score for the object as usual,

but also the inverse IoU, that is IoU with respect to the

background. We then weight these two together using

the relative weights w

and w

, derived from the size

of the object in the image. The new unbiased overlap

metric is:

O =

+ A

¯ad

+ A

¯a

+ A

¯ad

(7)

It is now no longer possible to simply increase the

bounding box size and obtain a better IoU, since ex-

cessive background will be penalized by the second

term. The severity of the penalty is balanced by the

factor. All that remains is then to set the cor-

responding weights in a principled manner. A naive

approach would be to set the weighting based on the

relative size of the object in the image. However since

we wish to equalize the impact of estimating the size

wrongly in the case of displacement errors, we can

use this to calculate a better weighting. We do this by

returning to the one dimensional case used before, but

with our new measure that includes the background:

¯a

+ I

¯ad

+ I

1 − D

+ A

1 − A

+ D

(8)

The overlap with the background is calculated as the

size of the image, minus the size of the annotated area.

As in ﬁgure 2 the size of our image is 1. For the

IoU with background, we repeat all derivatives from

above. The most interesting two cases 2./4. result in

case ε

2. −

¯a

¯ad

)−I

¯a

¯ad

)

< 0

4. −

¯a

¯ad

)−I

¯a

¯ad

)

< 0

(9)

Combining this with the size-derivative for the

IoU in case 2. and 4., we obtain a the following requi-

rement for the weights w

and w

= 1 − w

0 = w

+ I

¯ad

+ I

) − I

+ I

¯ad

+ I

)

−

(1 − w

)

¯a

+ I

¯ad

+ I

) − I

¯a

+ I

¯ad

+ I

)

(10)

Simplifying this expression with some algebraic

manipulation gives the weight for the annotation as:

+ I

¯ad

)

+ I

¯ad

)

+ (I

¯a

+ I

¯ad

+ I

)

(11)

This gives an unbiased overlap estimate for an

image of ﬁnite size according to (7) when using the

derived weights for foreground and background.

0.0 0.2 0.4 0.6 0.8 1.0

image area / object area

5000

10000

15000

20000

25000

30000

35000

40000

Object / image size ratio for tracking datasets

Figure 3: Histogram over ratio of image covered by the

image for common tracking datasets (OTB100 (Wu et al.,

2015), VOT 2015 (Kristan et al., 2015), VOT-TIR 2015

(Felsberg et al., 2015), VOT 2016 (Kristan et al., 2016))

. The vast majority of frames in all datasets have objects

covering less than a few percent of the image. In close to

100k frames from 4 different datasets, none contains an ob-

ject covering more than 50% of the image area.

4 EXPERIMENTAL EVALUATION

First we investigate the statistics of current tracking

datasets with respect to object size, and conclude that

the distribution of relative object sizes is signiﬁcantly

skewed towards smaller objects.

Surprisingly current tracking benchmark datasets

(Wu et al., 2015), (Kristan et al., 2015), (Kristan et al.,

2016) contain almost no frames where the tracked ob-

ject covers a signiﬁcant portion of the image, a histo-

gram over the ratio of image covered by the annotated

object can be seen in ﬁgure 3. Construing an entire

new dataset from scratch is out of the scope of this

work, instead we derive a new dataset by cropping

parts of the image around the object. This effectively

increases the relative size of the object in each video.

We experimentally validate our unbiased inter-

section over union score in two ways. First we ge-

nerate a large number of synthetic scenarios where

the tracker prediction has the correct center coordi-

nate, with varying size. We investigate by comparing

the performance of well known state of the art tracker

CCOT (Danelljan et al., 2016) with a naive method

that always outputs the entire image on a set of se-

quences with a wide range of object sizes.

In order to demonstrate the bias inherent in the tra-

ditional IoU, we compare the overlap given by it with

that of our new overlap score. From ﬁgure 4 it is appa-

rent that the penalty for an excessively large bounding

box decreases with increased size of the box, until the

size of the box itself is saturated at an IoU overlap of

0.6. For our unbiased overlap score the penalty for in-

creasing the size decreases far more rapidly, at a simi-

lar rate as to decreasing the size of the bounding box,

until it saturates at a lower point. The bounding box

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

584

0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6

Scale Factor

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

Overlap

Eﬀect of scale change with no oﬀset

IoU

Our

Figure 4: Scale factor plotted against overlap for a correctly

centered bounding box. The right side of the curve clearly

shows that the IoU score (blue) is not symmetric. While

over-estimating the size of the object is penalized, it is not

as harsh as over-estimation. Our unbiased score (red), while

not perfectly symmetric is still signiﬁcantly better, particu-

larly for larger objects.

size saturates as the edge hits the edge of the image

and is truncated. Truncating the bounding box is rea-

sonable since the size of the image is known, and no

annotations exist outside the image. For the IoU this

means that the lowest possible score is the ratio bet-

ween the object area and the total image area. For our

proposed overlap score the saturation point is much

lower as the minimal value is scaled by the size of the

object relative to the image.

In order to show the impact of the bias in IoU in

a more realistic situation we generate a number of se-

quences with varying object size. The sequences are

generated from the BlurCar1 sequence by cropping a

part of the image around the tracked object, effecti-

vely zooming in on the tracked object. We compare

the performance of the state-of-the art CCOT (Danel-

ljan et al., 2016), (the vot2016 winner (Kristan et al.,

2016)) with a naive baseline tracker. The naive ba-

seline tracker always outputs the full image as pre-

diction, except for the ﬁrst row and column of pixels.

The average overlap for the Frame tracker and the

CCOT is shown in ﬁgure 5, the same plot but using

our unbiased score is shown in ﬁgure 6. An example

of a generated frame can be seen in ﬁgure 1.

While the CCOT obtains near-perfect results on

the sequence, it does not track every frame exactly

correct. For an object covering the entire frame, this

leads to an overlap slightly below 1. For a ratio be-

tween image and object close to 1 the naive method

1.0 1.2 1.4 1.6 1.8 2.0

Image / object ratio

0.0

0.2

0.4

0.6

0.8

1.0

Average overlap

CCOT vs naive (IoU score)

CCOT

Naive

Figure 5: Performance of the CCOT and the full frame trac-

ker with respect to relative object size using the standard

IoU score. For large objects covering most of the image, the

naive frame tracker outperforms the state-of-the-art CCOT.

Once the objects are approximately 80% of the image, the

CCOT approach begins to outperform the naive frame trac-

ker. However, the naive frame tracker still obtains a re-

spectable overlap until the object is smaller than 50% of

the image.

outperforms the CCOT, regardless of score used, as is

reasonable as the object covers the entire image. Ho-

wever it continues to outperform the CCOT until the

ratio is slightly below 1.2 when using the traditional

IoU score (ﬁgure 5). With an object covering 70% of

the image the IoU is still at 0.7, only 0.1 less than that

of the CCOT, despite not performing any tracking at

all. As the size of the object decreases so does the

IoU, however it remains quite good even for smaller

objects, when the object covers only half the image

by area the IoU is still 0.3 despite covering twice as

many pixels as the ground truth.

When performing the same experiment using our

proposed overlap score, the naive tracker is severely

penalized for over-estimating the object size. The cor-

responding plot to 5, can be seen in 6. Here the over-

lap score for the naive method is only higher than the

CCOT for those cases where the object is covering

practically the entire frame (image-to-object ratio less

than 1.05). In such situations even a minor mistake in

positioning is penalized more harshly. Once the ob-

ject becomes relatively smaller the CCOT tracker be-

gins to signiﬁcantly outperform the naive method. Fi-

nally the penalty for the naive method is far more sig-

niﬁcant, making the performance difference far more

obvious than when using the IoU metric.

In ﬁgure 7 we show some qualitative examples of

Countering Bias in Tracking Evaluations

585

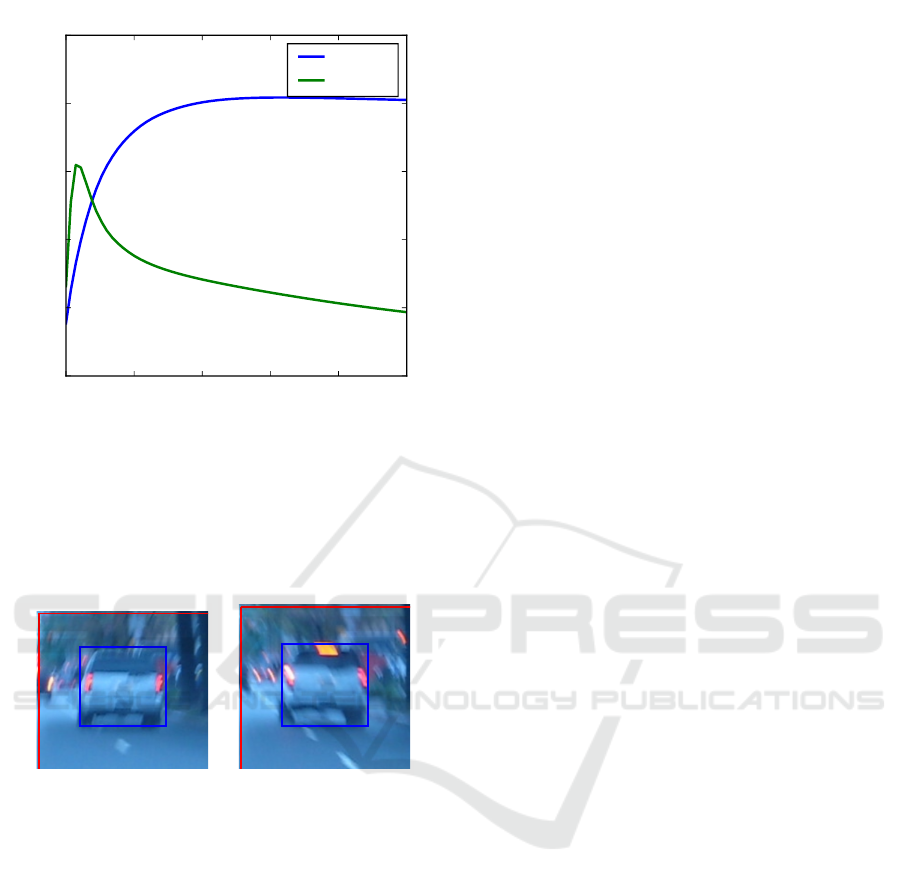
1.0 1.2 1.4 1.6 1.8 2.0

Image / Object ratio

0.0

0.2

0.4

0.6

0.8

1.0

Average overlap

CCOT vs naive (Our score)

CCOT

Naive

Figure 6: Performance of the CCOT and the full frame trac-

ker for relative object sizes using our proposed score. At

lower relative size (larger object), the naive frame tracker

outperforms the state-of-the-art CCOT approach as it is gua-

ranteed to cover the entire object, while the CCOT typically

has some offset error. At smaller object sizes, our proposed

score heavily penalizes the naive frame tracker.

Figure 7: Example frames from the CarBlur sequence, with

a naive method that outputs close to the entire image as each

detection (red box). The ground truth annotation is the blue

box. Due to severe motion blur and highly irregular mo-

vements in the sequence tracking is difﬁcult. The traditi-

onal IoU score for this frame is 0.26 (left), while our new

unbiased metric provides a far lower score of 0.11 for both

the left and right images. This suggests that using the IoU

is not optimal in many cases.

frames from the cropped CarBlur sequence. As the vi-

deo is extremely unstable tracking is difﬁcult, due to

motion blur and sudden movements. Here a predicted

bounding box generated by the naive tracker provides

a decent score of 0.22, despite always outputting the

entire frame. When instead using our unbiased score

the penalty for for over estimation of object size is

severe enough that the overlap score is more than hal-

ved. Here the IoU gives close to twice the overlap

score compared to our own approach.

5 CONCLUSIONS AND FURTHER

WORK

We have proven that the traditionally used IoU score

is biased with respect to over estimation of object si-

zes. We demonstrate this bias exists theoretically, and

derive a new unbiased overlap score. We note that

most tracking datasets are heavily biased in favor of

smaller objects, and construct a new dataset by crop-

ping parts of images at varying sizes. This demonstra-

tes a major issue with current tracking benchmarks as

situations with large objects directly correspond to si-

tuations when the tracked objects are close. We de-

monstrate the effect of using a biased metric in situa-

tions where the tracked object covers the majority of

the image, and compare to our new unbiased score.

Finally we have demonstrated the effect of introdu-

cing larger objects into tracking sequences by genera-

ting such a sequence, and comparing the performance

of a stationary tracker with that of a state of the art

method. While the CCOT signiﬁcantly outperforms

the stationary tracker for smaller objects (as is ex-

pected), for larger objects the naive approach simply

outputting the entire image is quite successful. In the

future we aim to investigate the effect of this bias in

object detection scenarios. It would also be relevant

to construct a new tracking dataset where the tracked

objects size is more evenly distributed than what is

currently typical. Acknowledgements: This work was

supported by VR starting Grant (2016-05543), Veten-

skapsr

adet through the framework grant EMC

, and

the Wallenberg Autonomous Systems and Software

program (WASP).

REFERENCES

Danelljan, M., Robinson, A., Khan, F. S., and Felsberg, M.

(2016). Beyond correlation ﬁlters: Learning continu-

ous convolution operators for visual tracking. In Euro-

pean Conference on Computer Vision, pages 472–488.

Springer.

Everingham, M., Van Gool, L., Williams, C. K., Winn, J.,

and Zisserman, A. (2008). The pascal visual object

classes challenge 2007 (voc 2007) results (2007).

Felsberg, M., Berg, A., Hager, G., Ahlberg, J., Kristan, M.,

Matas, J., Leonardis, A., Cehovin, L., Fernandez, G.,

Vojir, T., et al. (2015). The thermal infrared visual ob-

ject tracking vot-tir2015 challenge results. In Procee-

dings of the IEEE International Conference on Com-

puter Vision Workshops, pages 76–88.

Felsberg, M., Kristan, M., Matas, J., Leonardis, A., Pﬂug-

felder, R., Hager, G., Berg, A., Eldesokey, A., Ahl-

berg, J., ehovin, L., Vojr, T., Lukei, A., and Fernndez,

G. (2016). The thermal infrared visual object tracking

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

586

vot-tir2016 challenge results. In Proceedings, Euro-

pean Conference on Computer Vision (ECCV) works-

hops, pages 824–849.

Jaccard, P. (1912). The distribution of the ﬂora in the alpine

zone. New phytologist, 11(2):37–50.

Kristan, M., Leonardis, A., Matas, J., Felsberg, M., Pﬂug-

felder, R., ehovin, L., Vojr, T., Hager, G., Lukei, A.,

and Fernndez, G. (2016). The visual object tracking

vot2016 challenge results. In Proceedings, European

Conference on Computer Vision (ECCV) workshops.

Kristan, M., Matas, J., Leonardis, A., Felsberg, M., Ce-

hovin, L., Fern

andez, G., Vojir, T., Hager, G., Nebe-

hay, G., and Pﬂugfelder, R. (2015). The visual object

tracking vot2015 challenge results. In Proceedings of

the IEEE international conference on computer vision

workshops, pages 1–23.

Kristan, M., Pﬂugfelder, R., Leonardis, A., Matas, J., Ceho-

vin, L., Nebehay, G., Vojir, T., Fernandez, G., and Lu-

kezic, A. (2014). The visual object tracking vot2014

challenge results. In Proceedings, European Con-

ference on Computer Vision (ECCV) Visual Object

Tracking Challenge Workshop, Zurich, Switzerland.

Powers, D. M. W. (2011). Evaluation: from precision, re-

call and f-measure to roc, informedness, markedness

and correlation. International Journal of Machine Le-

arning Technology, 2(1):37–63.

Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh,

S., Ma, S., Huang, Z., Karpathy, A., Khosla, A.,

Bernstein, M., Berg, A. C., and Fei-Fei, L. (2015).

ImageNet Large Scale Visual Recognition Challenge.

International Journal of Computer Vision (IJCV),

115(3):211–252.

Wu, Y., Lim, J., and Yang, M.-H. (2013). Online object

tracking: A benchmark. In Proceedings of the IEEE

conference on computer vision and pattern recogni-

tion, pages 2411–2418.

Wu, Y., Lim, J., and Yang, M.-H. (2015). Object tracking

benchmark. PAMI.

Countering Bias in Tracking Evaluations

587