
Dense 3D Reconstruction of Endoscopic Polyp
Ankur Deka
1
, Yuji Iwahori
2
, M. K. Bhuyan
1
, Pradipta Sasmal
1
and Kunio Kasugai
3
1
Department of Electronics and Electrical Engineering, Indian Institute of Technology Guwahati, India
2
Department of Computer Science, Chubu University, Aichi, Japan
3
Department of Gastroenterology, Aichi Medical University, Aichi, Japan
Keywords: MIS, SfM, SLAM, Specularity, Malignant, ORB.
Abstract: This paper proposes a model for 3D reconstruction of polyp in endoscopic scene. 3D shape of polyp enables
better understanding of the medical condition and can help predict abnormalities like cancer. While there
has been significant progress in monocular shape recovery, the same hasn’t been the case with endoscopic
images due to challenges like specular regions. We take advantage of the advances in shape recovery and
suitably apply these with modifications to the scenario of endoscopic images. The model operates on 2
nearby video frames. ORB features are detected and tracked for computing camera motion and initial rough
depth estimation. This is followed by a dense pixelwise operation which gives a dense depth map of the
scene. Our method shows positive results and strong correspondence with the ground truth.
1 INTRODUCTION
Endoscopy is a Minimally Invasive Surgery (MIS)
for examining and operating on the medical
condition. It benefits patients through smaller
trauma, shorter hospitalization, lesser pain and lower
risk of infection than traditional open cavity
surgeries. A device called endoscope is inserted into
the body through a natural orifice.
In colonoscopy, the colon and the large intestine
is examined. One of the major benefits is the
detection of malignant (cancerous) polyp in
endoscopy through properties such as shape, texture
and size of the polyp. Shape cannot be judged
directly from 2D images of a monocular endoscope.
Specialized endoscopes with a laser light beam head
(Nakatani et al., 2007; Hayashibe et al., 2005) or
with two cameras mounted on the head for stereo
vision (Chang et al., 2014; Stoyanov et al., 2010;
Mourgues et al., 2001) are available. However, the
sizes of such endoscopes are large. A 3D scanner is
developed by Schmalz et al. (2012). Here, we
consider a general purpose endoscope, of the sort
still most widely used in medical practice. Shape
from shading approach using single monocular
endoscope has been explored (Iwahori et al., 1990;
Wang et al., 2009). Wu et al., (2010) used Multi-
view Shape from Shading.
We explore the possibility of using multiple
images or video for shape recovery. Shape recovery
from multiple images constitute the SfM (Structure
from Motion) or SLAM (Simultaneous Localization
And Mapping) problem. Both the scene’s structure
and the camera’s ego-motion are unknown, and the
challenge is to simultaneous solve them. EKF
(Extended Kalman Filter) based Monocular SLAM
is used by Grace et al. (2009). Mahmoud et al.
(2016) used ORB SLAM. Grace et al. and Mahmoud
et al. give real time performance but produce sparse
or semi-dense reconstruction which may not be
sufficient for the medical practitioner to understand
the medical condition.
There has been significant progress in monocular
SLAM in terms of both camera tracking and shape
recovery. Newcombe et al. (2011) made a dense
reconstruction of the scene (non-medical) from an
input video. We take some ideas from this paper for
our approach.
We propose a simple method for dense 3D shape
reconstruction. We use feature based method for
tracking the camera and creating an initial sparse
depth map. We then use the estimated camera
motion to obtain a dense depth map of the scene by
minimizing a cost function. Section 3 discusses the
proposed method in detail. In many cases, validating
a 3D reconstruction algorithm for endoscopy images
/ video is difficult as ground truth data is not
available. We use the Tsukuba dataset for validating
Deka, A., Iwahori, Y., Bhuyan, M., Sasmal, P. and Kasugai, K.
Dense 3D Reconstruction of Endoscopic Polyp.
DOI: 10.5220/0006720701590166
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 2: BIOIMAGING, pages 159-166
ISBN: 978-989-758-278-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
159

the algorithm (Peris et al., 2012; Martull et al.,
2012). Final test is performed on real endoscope
images that we obtained from Aichi Medical
University, Japan.
2 NOTATIONS
1) T: Rigid Body Transformation matrix in
homogeneous coordinate
T =
Where θ
1
, θ
2
and θ
3
are the translation angles along
the 3 axes and c
0
, c
1
and c
2
and the translation values
along the 3 axes.
Multiplication by T converts from converts from
coordinate system of one camera frame to another.
2) Ω R
2
: image domain
Any image point u=(u,v)
T
Ω
3) I: Ω → R
3
RGB value at pixel point
4) Ƹ(u): Ω → R
Inverse Depth Map: The range of values the
reciprocal of depth can take.
d= Ƹ(u) gives 1/depth
5) K: Camera intrinsic matrix
K =
=
f
x
, f
y
are focal lengths of the camera in the x and y
axes respectively. We use K
ij
’s to refer to the terms
in the camera intrinsic matrix. All elements in these
matrices are in units of pixels.
6)
where ů=(u,v,1)
T
7) Π(x) : Dehomogenization function
Π(x) = (x/z, y/z)
8) K* =
=
9) K
-1
=
1) K
-1
* =
2) ¥ =
T
Where c
0
, c
1
and c
2
denote the translations in the 3
axes respectively and d1 to dn denote the inverse
depth values at each of the n feature points in the
view of image 1.
A point u
1
in image 1 (Im
1
) corresponds to a
point u
2
in image 2 (Im
2
), which can be found as:
u
2
= Π (KT
21
)
We can represent this operation using only
matrix multiplications in homogeneous coordinates:
= (K*) x (T
21
) x (1/d) x (K
-1
*) x
= (1/d) x (K*) x (T
21
) x (K
-1
*) x
= (1/d) x ϒ
Where ϒ = (K*) x (T
21
) x (K
-1
*) x
=
ϒ
ϒ
ϒ
3 PROPOSED METHOD
The outline of the algorithm is shown in Fig.1. Two
nearby frames from a video are taken as input. These
two images are of the same scene with a slight
movement of the camera (3DOF translation).
Specularity is removed using method of [17]. The
endoscope camera is calibrated using a 3
rd
party
software.
The algorithm can be divided into 2 parts. These
two parts deal with the feature points and remaining
points respectively. The idea is that a few number of
number of good and distinct feature points are
generally available in endoscope scene. So we use
those to track the camera and obtain depth at those
points. For the remaining points we use the obtained
camera tracking information to obtain depth.
3.1 Feature Points
Feature points are detected and matched in the 2
images. We randomly initialize the camera
transformation matrix. Thereafter, we keep changing
the transformation matrix till the pairs of
corresponding feature points are correctly mapped
BIOIMAGING 2018 - 5th International Conference on Bioimaging
160

Figure 1: Block diagram of the proposed approach.
from one image to the other. The value of camera
transformation when the mapping aligns with direct
matching of feature points is supposed to be the
correct camera transformation.
a) Mask is applied to the specular region and ORB
(Oriented FAST and rotated BRIEF) Features are
extracted from both the images (Im1 and Im2) in
regions where specularity is absent. n best matching
pairs of points are taken (Fig.1).
b) ¥ is initialized to:
T
(1)
(¥ is (n+3)x1 dimensional)
That is, we initialized with no translation between
the two images and uniform inverse depth of d at all
n feature points.
c) At every feature point u1 in Im1, we can compute
u2 in Im2 using (1). We also have u2_true, which is
obtained by matching ORB feature points.
Thus we can define IE (Individual Error) at each
(i
th
) point as:
IE(i) = ½(|u2-u2_true|2)2
Total Error (TE) is defined as:
TE =
We wish to minimize TE by varying the entries in ¥.
d) We use gradient descent for m steps to minimize
¥.
e) The iteration step of gradient descent is:
¥n+1 = ¥n -
(2)
Where, µ is vector storing the gradient descent rates
for each of the entries in ¥.
denotes dot product operation.
f)
=
(3)
g)
=
(4)
Where:
=
ϒ
ϒ
ϒ
(5)
=
ϒ
ϒ
ϒ
(6)
h)
=
(7)
Where:
=
ϒ
ϒ
ϒ
(8)
=
ϒ
ϒ
ϒ
i)
=
(9)
j) We use µ of dimension (n+3)x1 as:
µ=
T
(10)
There is several order of magnitude difference in
gradient descent rates: µT and µd for c
i
’s and d
i
’s
respectively. This is because of c
i
’s are roughly near
to 0 (Camera is not moved much in two nearby
frames). However, initial values of d
i
’s are assigned
randomly to a constant d
0
and they can vary a lot
from it.
3.2 Remaining Points
Photometric error at every pixel u
1
in Im
1
is defined
as:
ρ(Im
1
,
u1
,d) = | Im
1
(u
1
)-Im
2
(Π(KTmrΠ
-1
(u
1
,d))) |
An exhaustive search is performed between d
min
and
d
max
for every pixel and d
optimal
is chosen as the d that
given minimum error.
Dense 3D Reconstruction of Endoscopic Polyp
161

(d)
d
min
is chosen as smaller than all d
i
’s among the
feature points. Similarly, d
max
is chosen as larger
than all d
i
’s among the feature points.
DTAM (Newcombe et al., 2011) uses pixel
intensity values for both tracking and reconstruction.
We chose to use feature points for tracking as pixel
intensity values can give ambiguous tracking results
in case of our target medical images where several
similar intensity pixels can be found in the
neighbourhood of each pixel.
4 PARAMETERS
We choose the parameters as follows:
n (number of feature points used) = 30
d
0
(initial inverse depth value, Eq.1) = 50
µ
T
(gradient descent rate for translation, Eq.10)
= 9x10
-14
µ
d
(gradient descent rate for inverse depth, Eq.10)
= 9x10
1
m (number of gradient descent steps) = 100
The number of feature points n is considered low as
in endoscopic image very less number of good
distinct feature points can be found. A large number
of feature points would lead to wrong matches and
result in error in camera motion estimation. µT and
µd have an order of 10
15
difference. This is because
translation value need not change much but the
inverse depth value is initialized randomly. The
number of gradient steps is considered sufficiently
high at 100.
5 EVALUATION
We use Tsukuba dataset’s [14, [15] stereo image
pair to validate our approach. Though the images are
taken from a stereo camera (1 DOF translation), our
approach is designed to handle 3DOF translation.
The images taken are from stereo vision dataset.
Thus we can verify results with Stereo vision
formula for this particular dataset.
Depth = (Bxf)/Disparity
Where,
Baseline is the distance between optical centres of
the two cameras in stereo vision. Disparity is the
distance between the pixels of the same point in the
two images.
Depth x Disparity = Bxf
= constant
In our case,
Depth = 1/d
Disparity/d = constant
We used disparity values from Tsukuba Ground
Truth and inverse depth from the implementation.
Disparity/d for the n (30) feature points are
computed. The normalised standard deviation (ratio
of standard deviation to mean) of the data is found to
be 0.043<<1 implying the data is almost constant.
Thus, the results are consistent with the stereo vision
formula.
Matched feature points are shown in Fig.2.
Linear interpolation of the obtained inverse depth
map is shown Fig.3. The final dense inverse depth
map is shown in Fig.4. Fig.5 shows the final inverse
depth map (with median filter) alongside the ground
truth disparity. The black strip on the left part of the
reconstruction is because of the absence of the
corresponding points in the 2
nd
image.
Figure 2: ORB features matched in the 2 input images.
BIOIMAGING 2018 - 5th International Conference on Bioimaging
162
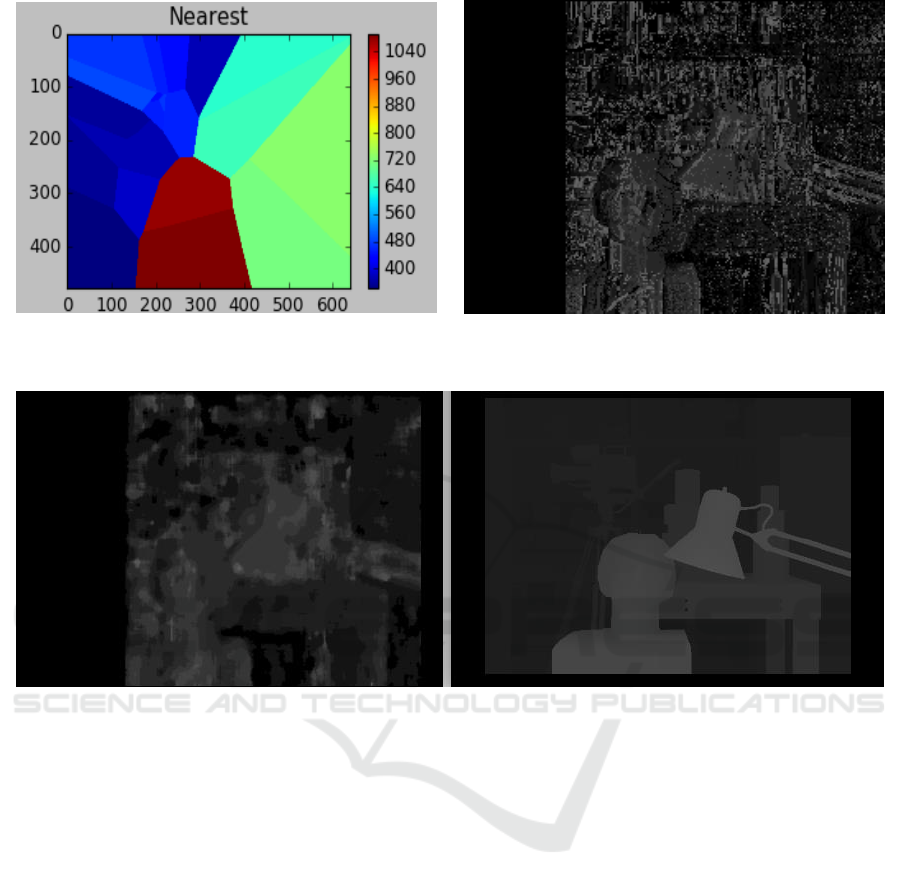
Figure 3: Nearest neighbour interpolation of inverse depth
at feature points.
Figure 4: Final dense inverse depth map.
Figure 5: Left- Median filter applied to dense inverse depth reconstruction, Right- Ground Truth disparity. In stereo vision
disparity is proportional to inverse depth.
6 RESULTS
We tested the algorithm on endoscopic video which
we collected from Aichi Medical University. We
carefully selected two nearby video frames which
had translation only motion. The feature tracking
fails without specularity removal leads to matching
points in specular region (Fig.6). This would result
in erroneous camera tracking as specular regions are
not static. Specularity removal is done using 2
methods of separately as shown in Fig.7 (Bertalmio et
al., 2001; Telea, 2004). We finally use the method
proposed by Telea which gave better result. Even
after specularity removal the matching gives poor
results (Fig.8) This is because specularity removal is
not perfect. Moreover, there is information loss
wherever specularity is removed. We, therefore, use
a mask to extract feature points only in regions
where there was no specularity in the original image.
This results in almost perfect matching (Fig.9). The
final dense reconstruction is shown in Fig.10.
7 CONCLUSIONS
Our approach effectively applies feature matching
for camera motion estimation and performs
pixelwise operations to compute dense
reconstruction. Even though ground truth 3D
structure is not available for the endoscope images,
we performed a check on our method using the
Tsukuba dataset. The tracking results are highly
accurate, and the dense reconstruction closely
resembles the ground truth.
Further developments could be to include
rotation into the model. There is also the possibility
to improve reconstruction by imposing smoothness
constraint. Computational efficiency can also be
improved.
Dense 3D Reconstruction of Endoscopic Polyp
163
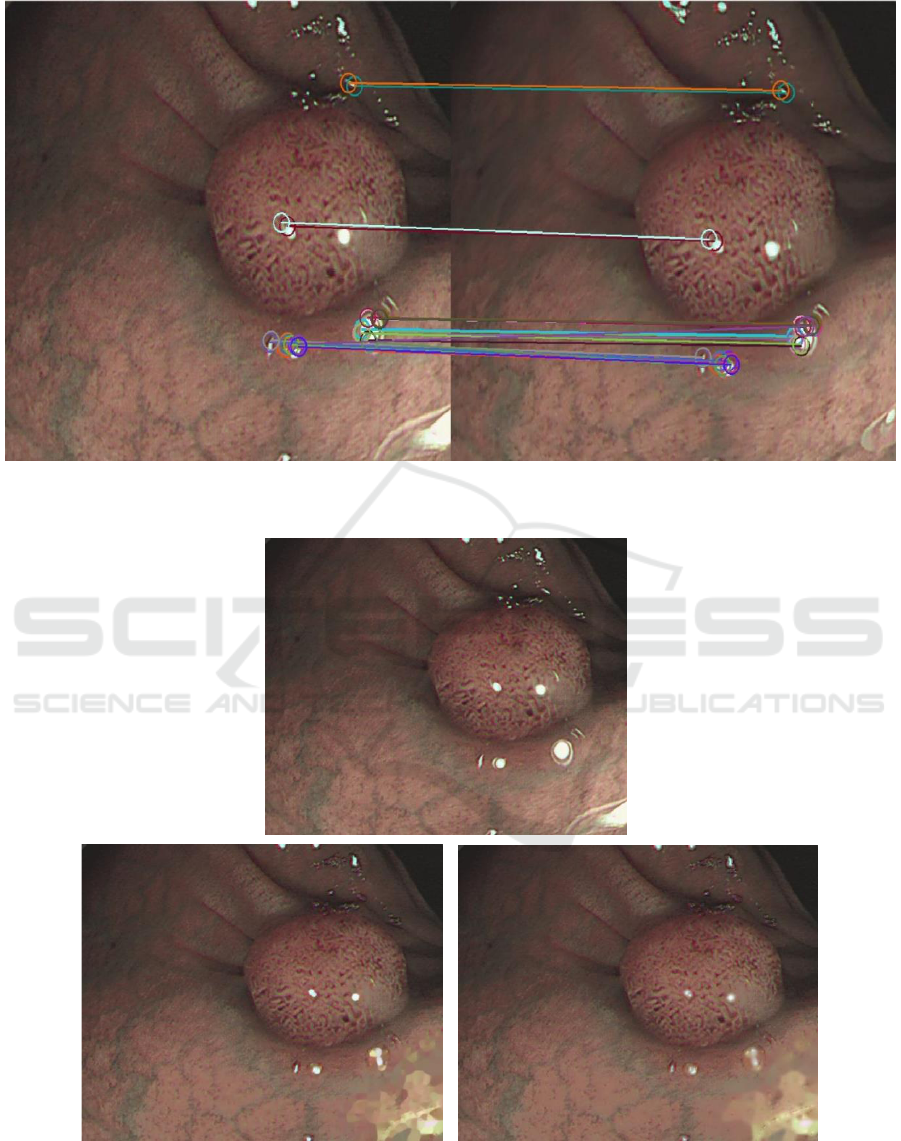
Figure 6: Matching feature points without specularity removal. Feature points are selected in specular region which would
result in wrong estimation of tracking.
Figure 7: Top- Original Image. Bottom Left- Specularity Removal using method of Bertalmio et al., 2001. Bottom Right-
Specularity removal using method of Telea, 2004.
BIOIMAGING 2018 - 5th International Conference on Bioimaging
164
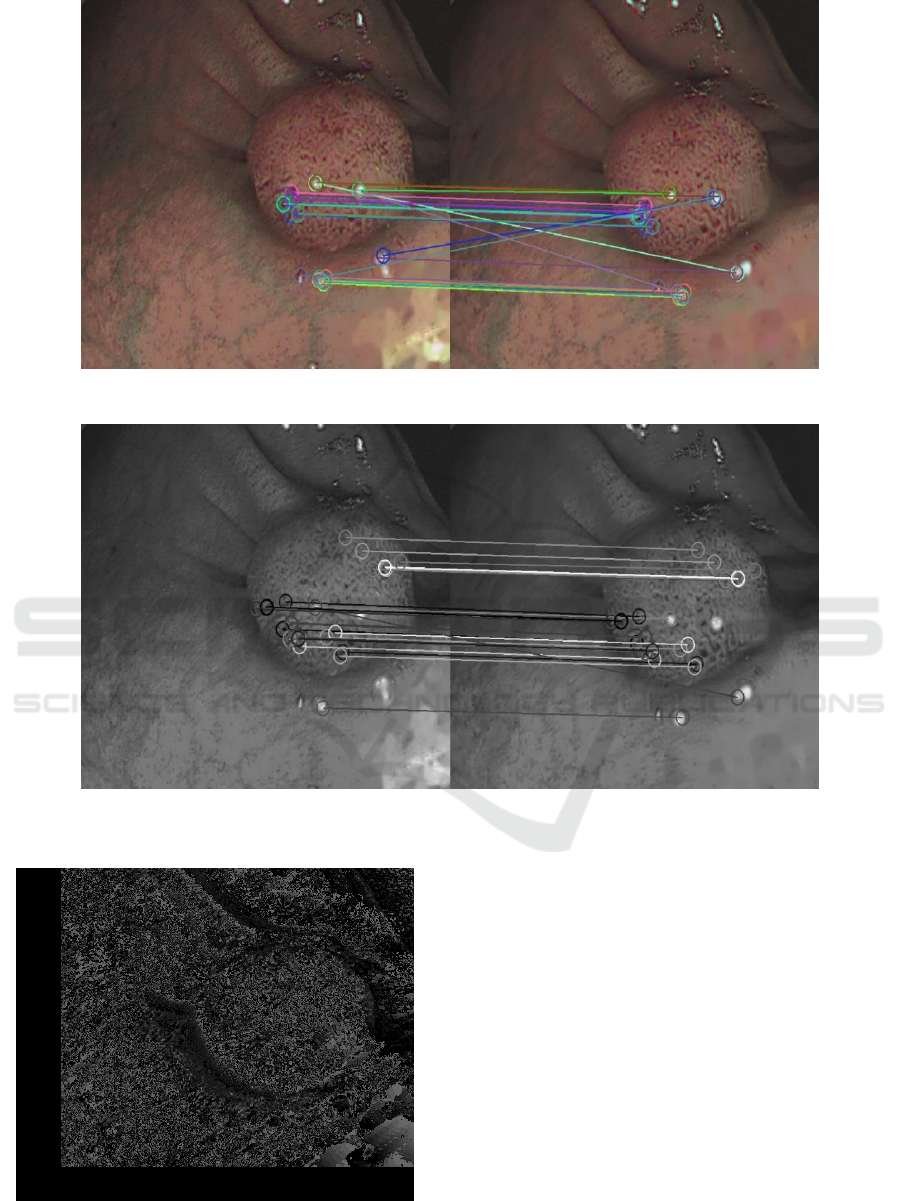
Figure 8: Matched feature points after removing specularity using method Proposed by Telea (2004).
Figure 9: Matched feature points after removing specularity and applying mask to specular region.
Figure 10: Final dense reconstruction of endoscopic
image.
ACKNOWLEDGEMENTS
Iwahori's research is supported by JSPS Grant-in-
Aid for Scientific Research (C) (17K00252) and
Chubu University Grant. The authors would like to
thank Iwahori Lab. member for their useful
discussions.
REFERENCES
Nakatani, H., Abe, K., Miyakawa, A., and Terakawa, S.
(2007). Three-dimensional measurement endoscope
system with virtual rulers. Journal of Biomedical
Optics, vol. 12, no. 5, Article ID 051803-1.
Hayashibe, Mitsuhiro, Suzuki, Naoki, and Nakamura,
Dense 3D Reconstruction of Endoscopic Polyp
165

Yoshihiko (2005). Laser-scan endoscope system for
intraoperative geometry acquisition and surgical robot
safety management. Special Issue on Functional
Imaging and Modelling of the Heart (FIMH 2005),
Volume 10, Issue 4, August 2006, Pages 509-519.
Chang, PL., Handa, A., Davison, A.J., Stoyanov, D.,
Edwards, P.. (2014). Robust Real-Time Visual
Odometry for Stereo Endoscopy Using Dense
Quadrifocal Tracking. International Conference on
Information Processing in Computer-Assisted
Interventions (IPCAI 2014), pp 11-20.
Stoyanov, Danail, Scarzanella, Marco Visentini, Pratt,
Philip, Yang, Guang-Zhong (2010). Real-Time Stereo
Reconstruction in Robotically Assisted Minimally
Invasive Surgery. Medical Image Computing and
Computer-Assisted Intervention – MICCAI 2010, pp
275-282.
Mourgues, F., Devemay, F., and Coste-Maniere, E.
(2001). 3D reconstruction of the operating field for
image overlay in 3D-endoscopic surgery. In
Proceedings of the IEEE and ACM International
Symposium on Augmented Reality (ISAR '01), pp.
191–192, New York, NY, USA.
Schmalz, Christoph, Forster, Frank, Schick, Anton,
Angelopoulou, Elli (2012). An endoscopic 3D
scanner based on structured light. Medical Image
Analysis, Volume 16, Issue 5, July 2012, Pages 1063-
1072.
Iwahori, Yuji, Sugie, Hidezumi, Ishii, Naohiro (1990).
Reconstructing shape from shading images under
point light source illumination. International
Conference on Pattern Recognition (ICPR), i. 83 - 87
vol.1. 10.1109/ICPR.1990.118069.
Wang, Guo-hui, Han, Jiu-qiang and Zhang, Xin-man
(2009). Three-dimensional reconstruction of
endoscope images by a fast shape from shading
method. Measurement Science and Technology,
Volume 20, Number 12.
Wu, Chenyu, Narasimhan, Srinivasa G., Jaramaz,
Branislav (2010). A Multi-Image Shape-from-Shading
Framework for Near-Lighting Perspective
Endoscopes. International Journal of Computer
Vision, January 2010, Volume 86, Issue 2–3, pp 211–
228.
Grasa, O.G., Civera, J., Guemes, A., Munoz, V. and
Montiel, J.M.M. (2009). EKF monocular SLAM 3D
modeling, measuring and augmented reality from
endoscope image sequences. Medical image
computing and computer-assisted intervention
(MICCAI) (Vol. 2).
Mahmoud, N., Cirauqui, I., Hostettler, A., Doignon, C.,
Soler, L., Marescaux, J. and Montiel, J.M.M. (2016).
Orbslam-based endoscope tracking and 3d
reconstruction. International Workshop on Computer-
Assisted and Robotic Endoscopy (pp. 72-83). Springer,
Cham.
Newcombe, R.A., Lovegrove, S.J. and Davison, A.J.,
2011, November. DTAM: Dense tracking and
mapping in real-time. Computer Vision (ICCV), 2011
IEEE International Conference (pp. 2320-2327).
IEEE.
Peris, M., Martull, S., Maki, A., Ohkawa, Y. and Fukui, K.
(2012). Towards a simulation driven stereo vision
system. In Pattern Recognition (ICPR), 2012 21st
International Conference on (pp. 1038-1042). IEEE.
Martull, S., Peris, M. and Fukui, K. (2012). Realistic CG
stereo image dataset with ground truth disparity maps.
In ICPR workshop TrakMark2012 (Vol. 111, No. 430,
pp. 117-118).
Bertalmio, M., Bertozzi, A.L. and Sapiro, G. (2001).
Navier-stokes, fluid dynamics, and image and video
inpainting. In Computer Vision and Pattern
Recognition, 2001. CVPR 2001. Proceedings of the
2001 IEEE Computer Society Conference on (Vol. 1,
pp. I-I). IEEE.
Telea, A. (2004). An image inpainting technique based on
the fast marching method. Journal of graphics tools,
9(1), pp.23-34.
BIOIMAGING 2018 - 5th International Conference on Bioimaging
166
