An in Silico Approach for Understanding the Complex Intercellular

Interaction Patterns in Cancer Cells

Maura Cárdenas-García

and Pedro Pablo González-Pérez

Facultad de Medicina, Benemérita Universidad Autónoma de Puebla, 13 Sur 2702, Puebla, Mexico

Departamento de Matemáticas Aplicadas y Sistemas, Universidad Autónoma Metropolitana,

Unidad Cuajimalpa, Ciudad de México, Mexico

Keywords: In Silico Approach, Modelling and Simulation, Intercellular Interaction, Cancer Cells, Signalling Pathways.

Abstract: Intercellular interaction allows cancer cells to preserve their malignance and through cell junctions to induce

malignance in neighbouring cells and receive nutrients from them. The Wnt (wingless-related integration

site) signalling pathway plays an important role in the formation of intercellular communications. In this

work, we explore the complex interactions patterns of intercellular communication in cancer cells using an

in silico modelling and simulation methodology developed by us. The proposed cellular signalling model,

characterized by a multicompartmental nature, provides symbolic abstractions and accurate algorithms to

model both intracellular and intercellular behaviours. In particular, in this work, we propose an in silico

model and simulation of the formation of different communication channels, involving the Wnt signalling

pathway. The final purpose of this study is to propose target molecules leading to break the communication

between a cancer cell and surrounding normal cells. In this way, it is not necessary to carry out long series

of different in vitro experiments, but only a few, because the focus should be only on the key molecules,

which saves time and money. We observed, using in silico experiments, how the inhibition of Wnt

signalling pathway prevents that the cells surrounding a cancerous cell are transformed.

1 INTRODUCTION

Intercellular communication allows the transfer of

information from one cell to another. This type of

interaction takes place by physical unions between

the cells or through signalling molecules, released in

the extracellular space by one cell and received by

another cell through its receptors. By means of

intercellular communication, the cells work in

coordination, facilitating their survival. In the case

of cancer cells, this communication allows them to

continue growing, as well as inducing malignancy in

neighbouring cells (Brücher and Jamall, 2014).

Surrounding normal cells also send signals to cancer

cells, thus these are destroyed, but not always

successfully. The formation of junctions between

normal and malignant cells plays an important role

in the control of a cellular focus that will result in a

tumour (Lum and Chen, 2015). The Wnt signalling

pathway plays an important role in the formation of

intercellular communications and regulates cell

proliferation. The Wnt protein family includes a

large number of cysteine-rich glycoproteins. Wnt

proteins activate different signal transduction

pathways. In this work, we model and simulate the

canonical Wnt signalling pathway because this

pathway is related to other signalling pathways in

cancer.

The modelling and simulation of cellular

signalling systems has found valuable support in a

wide range of modelling approaches, which cover a

wide spectrum ranging from mathematical models,

e.g., ordinary differential equation systems,

statistical methods and numerical methods, to

computational models, e.g., cellular automata,

Boolean networks, Petri nets, neural networks and

multi-agent systems. Based on these models,

different simulation tools have been developed from

mathematical ones to computational ones (Alves et

al., 2006). However, the majority of these former

tools are based on abstractions to model only

intracellular behaviour. Thus, they are not suitable to

model intercellular communication. Consequently,

in recent years, other major requirements in the

simulation of cellular communication systems –such

as multiple levels of compartmentalization, topology

188

Cárdenas-García, M. and Pérez, P.

An in Silico Approach for Understanding the Complex Intercellular Interaction Patterns in Cancer Cells.

DOI: 10.5220/0006722601880195

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 3: BIOINFORMATICS, pages 188-195

ISBN: 978-989-758-280-6

and locality– have emerged, guiding the

development of new computational models and

tools. Notable examples of computational simulation

tools supporting such features are Bio-PEPA

(Ciocchetta et al., 2009), MCell (Kerr et al., 2008),

COPASI (Hoops et al., 2006), Virtual Cell (Cowan,

2012) and CompuCell 3D (Swat et al., 2012).

In this work, we simulate and explore the

complex interaction patterns of intercellular

communication in cancer cells using an in silico

modelling and simulation approach developed by us,

and motivated by two key elements: 1) a tuple

space-based model (Gelernter, 1985) for the

representation of the signalling elements (i.e.,

reactions with their own kinetic parameters, and

reactants with their concentrations) and 2) a control

mechanism for the selection and execution of

reactions based on the Gillespie’s algorithm

(Gillespie, 1971) –a stochastic simulation algorithm

typically used to mimic systems of

chemical/biochemical reactions in an efficient and

accurate way. A significant characteristic of this in

silico approach is its multicompartmental nature.

Specifically, it is suitable to model cells in their

“social context”, along with all those biological

mechanisms that involve two or more cells, that is

essential in the scenario discussed in this work. The

main idea behind of this in silico modelling and

simulation approach is to provide a computational

experimentation environment that complements and

guides in vitro experimentation in intra and

intercellular signalling networks.

In this work, we showed and discussed how this

in silico modelling and simulation approach can be

used successfully to understand and explore the

intercellular communication between a cancer cell

and normal cells and, consequently, to propose key

molecules, which can be targeted to allow us to

break the communication between cancer cells and

surrounding normal cells.

2 MATERIALS AND METHODS

2.1 The Multicompartmental

Intercellular Signalling Model

Here we introduce the key elements of the intra and

intercellular signalling model, characterized by its

multicompartmental nature. The proposed model

provides the logical abstractions for the

representation and manipulation of the signalling

elements, i.e., reactions, reactants and products. As

mentioned earlier, the logical abstractions for the

representation of the signalling elements are

conceived from the notion of tuple and tuple spaces

(Gelernter, 1985; González-Pérez et al, 2013),

although the control mechanism for the selection and

execution of the reactions is based in Gillespie's

algorithm.

2.1.1 Tuple Space-based Model for

Representation of Signalling Elements

Denote by C

, 1 ≤ i ≤ m, the i-th cell belonging to the

cellular group G, which is represented by a set of n

tuple spaces (TS) such that:

(1)

Each tuple space TS

, 1 ≤ j ≤n, is a set of tuples,

where each individual tuple (t) represents a

signalling element. Denote by cr a reaction, by r a

reactant, and by p a product, therefore we have:

(2)

From (1) and (2) we have that any tuple t in any

tuple space TS

, 1 ≤ j ≤n, and therefore in cell C

represents either a reaction (cr), a reactant (r) or a

product (p). Note that each TS

, 1 ≤ j ≤n, represents

a cell compartment, e.g., nucleus, mitochondria,

cytoplasm, cell membrane, or even extracellular

space, which guarantees the multicompartmental

nature of the cell signalling model.

In order to simplify the notation, the subscripts

corresponding to cr, r and p have not been

considered in expression (2). However, it should be

clear that each of these identifiers is accompanied by

three sub-indices, the first refers to the set of spaces

of tuples (cell), the second refers to the space of

tuples (cellular compartment), and the third refers to

the element itself (particular reaction, reactant o

product).

Regarding representation of reactions,

expression (3) provides the symbolic abstraction that

allows to represent, and therefore manipulate,

chemical reaction schemes commonly required when

modelling cellular signalling systems, such as

synthesis, decomposition, and standard equation for

enzymatic reactions, as referred in expression (4) to

(6), respectively.

(3)

where: r

, r

are reactants and reqMol

, reqMol

are

the number of molecules involved of reactants r

, r

respectively; K is the reaction rate constant; p

, p

are products and pm

, pm

are the number of

molecules formed of products p

, p

, respectively.

An in Silico Approach for Understanding the Complex Intercellular Interaction Patterns in Cancer Cells

189

(4)

(5)

(6)

Let TS

and TS

be two neighbouring tuple

spaces, which we represent by the tuple:

(7)

Consider also that a tuple space can have at most

two neighbours, given the type of biological system

that we are modelling. As already established, a

tuple space (TS

) models a particular cellular

compartment. Thus, an example of tuple space with

more than one neighbour is given by the “cellular

membrane” tuple space, which has as neighbours the

“extracellular space” and the “cytosol” tuple spaces.

The notion of neighbouring tuple spaces

(expression (7)) plays a key role in our signalling

model, since it allows us to establish that the

products formed by a reaction cr belonging to a

tuple space TS

, are translocated to another tuple

space TS

, if and only if TS

and TS

are neighbours.

In this way, the continuity of the signal transduction

is guaranteed through all tuple spaces (cell

compartments) that make up the cell C

Then, returning to expression (3), if we require

that one of the products formed, for example p

, be

translocated to the tuple space TS

, being TS

and

neighbours, then the tuple (p

, pm

), located in

the right part of the expression (3) will be replaced

by the tuple (translocate(p

, pm

), TS

With regard to reactants and products involved

in the reactions, both are also represented as tuples

in the tuple space, through the symbolic abstraction

provided in the expression (8).

(8)

where r

is the reactant and Mol

is the number of

available molecules.

2.1.2 The Algorithm for the Selection and

Execution of Reactions

Once all the reactions and the reactants are

modelled, then every reaction is explicitly simulated

on the basis of the Gillespie algorithm. In detail, the

main steps performed by the algorithm for the

selection and execution of reactions, i.e., for starting

and continuing cellular signal transduction, are

summarized below:

1. Calculate the rate for each eligible reaction

(cr) –see expression (3)– according to the

expression:

(9)

where K is the reaction rate constant, Mol

is the

number of available molecules of reactant r

, and

reqMol

is the number of molecules required of

reactant r

The rate with which the reaction will be selected

is equal to the rate of this reaction (K) –where K can

be estimated as a measure of affinity or calculated

from the maximum rate (V

max

) and the Michaelis

constant (K

)– multiplied by the product of the

binomial coefficients of the available moles of each

reactant involved in the reaction and the number of

moles of this required by the reaction. If a reaction is

not eligible for lack of any of the required reactants,

then the rate (Rate) of this reactions will be zero.

2. Calculate the summation of the rates (Rate) of

all eligible reactions, the resulting value is RTot.

3. Sort all eligible reactions by rate in a

descending order.

4. Generate a random number ψ between 0 and 1.

5. From sorted list of eligible reactions, the k-th

reaction is chosen if:

(10)

Note, that the value of the summation is equal to 1

for the last reaction in the sorted list. So, if there are

eligible reactions, then one of them will always be

executed.

6. Generate a random number τ between 0 and 1.

Stop the execution of the reactions for a time

given by:

(11)

The simulation proceeds choosing the next

reaction to occur on the basis of a random number

and its propensity function that is calculated based

on the reaction rate and on the number of reactants.

The time interval to update the simulation time is

also computed step by step depending on a random

number and on the sum of propensity functions of all

reactions. The iteration of these steps (involving

expressions (9), (10) and (11)) constitutes the

simulation. The simulation concludes when there are

no eligible reactions.

BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms

190

2.2 The Computational Simulation

Tool Associated with the Proposed

Model

The modelling approach proposed was integrated in

Cellulat, an already existing computational

simulation tool for signal transduction systems,

developed by us (González-Pérez et al., 2013;

Cárdenas-García et al., 2016). Cellulat establishes in

itself an integrated virtual environment for in silico

experimentation on cellular signalling pathways and

networks, strongly dependent on characteristics such

as multi-compartmentalization, location and

topology.

As a highly interactive application, Cellulat

provides the user with a wide range of visual and

interactive tools, to follow and feedback at every

moment the signal transduction that takes place in

the simulated signalling network.

It is important to note that all the elements

required by the simulation –cellular structures and

compartments, reactions with their kinetic

parameters, and reactants with their concentration or

number of available molecules– are written or

recorded in the same written language used when

describing these elements; it is the simulation tool

itself that will translate them into logical abstractions

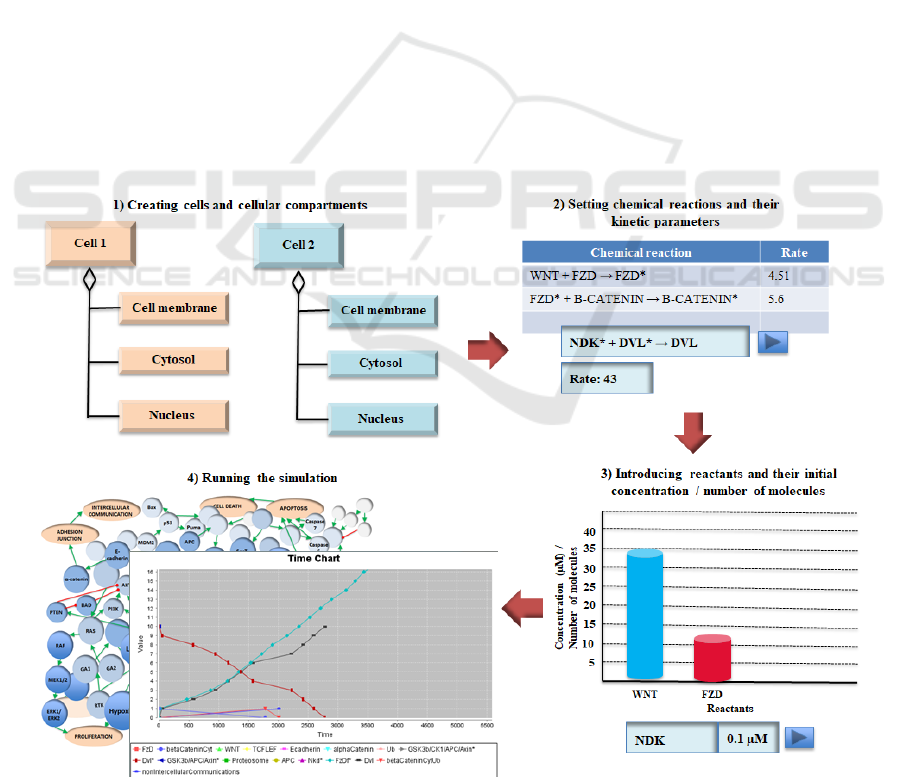
based on tuple spaces, previously introduced. Figure

1 shows the key phases in the creation and execution

of a simulation using Cellulat.

Cellulat (in its Executable Jar File version) can

be either executed or downloaded from the

bioinformatics website of our research group at

http://bioinformatics.cua.uam.mx/node/10. The

instructions required for the download can be

consulted on this website.

2.3 The Methodological Approach

The methodology followed in this work is based on

a continuous bidirectional feedback between the in

silico modelling and simulation approach and

theoretical and experimental knowledge. That is, the

proposed multicompartmental intercellular signal-

ling model and the results of its associated

computational simulation should provide valuable

support to guide in vitro experimentation; while the

results of theoretical and experimental research

should lead to both the improvement of the model

and the design of the most appropriate in silico

experiments.

Figure 1: Sequence of the major activities carried out during the creation and execution of a cell signalling simulation using

Cellulat.

An in Silico Approach for Understanding the Complex Intercellular Interaction Patterns in Cancer Cells

191

The main phases involved in this methodology are

summarized below:

Modelling phases:

1. Modelling the integrated Wnt signalling

pathways.

2. Taking into account the model developed in

phase 1, define the cellular structures and

compartments involved in the signalling and,

for each of these, the list of reactions and

reactants located there.

Simulation phases:

3. Creating cellular compartments.

4. Setting reactions and their kinetic parameters.

5. Introducing reactants and their available

concentration o number of molecules.

6. Design the in silico experiments.

7. Running the simulation.

8. Visualize simulation execution.

Analysis phases:

9. Analysis of simulation execution.

10. Feedback between the in silico modelling and

simulation approach and theoretical and

experimental knowledge.

3 RESULTS

3.1 The Integrated Model of Wnt

Signalling Pathways

Figure 2 shows, as first result, a simplified version

of Wnt signalling pathway model proposed by us, to

be simulated using the in silico approach previously

presented and following the methodology described

above. As can be seen in Figure 2, β-catenin is the

central part in this pathway, interacting with E-

cadherin and α-catenin proteins. We have integrated

into the model the canonical and non-canonical

pathways as well as Notch (Borggrefe et al., 2016),

Hedgehog (Shimizu and Nakagawa, 2015), and

Hypoxias (Grunsven and Vlierberghe, 2014) ones.

On the other hand, we will also consider, as the

background of the model illustrated in Figure 2,

other previously modelled signalling pathways with

which the Wnt signalling path intersects, such as

EGF/MAPK/JAK-STAT (González-Pérez et al.,

2003), PI3K (González-Pérez et al., 2013) and

caspases (Cárdenas-García and González-Pérez,

2013). In Table 1 can be observed some examples of

signalling elements –reactions and reactants–

defined as part of the integrated model of Wnt

signalling pathways. Note that both types of cells

(normal and cancer cells) exhibit the same signalling

elements to form communication channels.

Figure 2: A simplified version of Wnt signalling pathway

modelled in this study. Red arrows indicate inhibition

relationships and green arrows indicate activation

relationships.

3.2 The Simulation of the Wnt

Signalling Pathways

As can be seen in Figure 3, the simulation is ready

for execution. That is, cellular compartments,

reactions and reactants have been created from the

Wnt signalling pathway model, which has been

conceived and verified as initial phase of our

methodological approach.

The simulated Wnt signalling network is made

up of 146 nodes representing reactants, 12 nodes

representing cell processes, such as adhesion

junction, proliferation, apoptosis and cell death, and

204 arcs representing reactions between the involved

nodes. Table 1 shows some reaction examples. The

overall signalling network extends across 5 cell

compartments (i.e., extracellular space, cell

membrane, cytosol, mitochondria and nucleus)

comprising key cellular signalling pathways

involved in growth and metabolism leading to

survival, proliferation, tumour progression and cell

death, as well as integration with the formation of

intercellular interactions (i.e., EGF/MAPK/JAK-

STAT, PI3K/AKT and caspases signalling

pathways).

BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms

192

Table 1: Examples of signalling elements –reactions and reactants– defined as part of the integrated model of Wnt

signalling pathways.

Cellular

compartment

Reaction

Vmax

Reactant

Conc. (µM)

Reference

Extracellular

space / membrane

WNT + FZD -> FZD

4.51

FZD

WNT

(Lee et al., 2003)

Cytosol

FZD

+ β-CATENIN ->

β-CATENIN

5.6

β-CATENIN

0.001

(Hernández et al.,

2012)

Cytosol

NDK

+ DVL

-> DVL

NDK

DVL

0.1

0.01

(Blaheta et al. 2005)

Cytosol

APC

+ β-CATENIN

β-CATENIN

APC

0.4

(Blaheta et al. 2005)

Cytosol

β-CATENIN

+ TCF-LEF ->

β-CATENIN

/ TCF-LEF

TCF-LEF

(Hernández et al.,

2012)

Figure 3: Cells, cell compartments, reactions and reactants have been created as the initial components required by the

simulation of Wnt signalling pathways. Signalling elements, e.g., proteins and enzymes, are represented by solid blue

spheres. Each signalling element is identified by its name (acronym). Red arrows indicate inhibition relationships and green

arrows indicate activation relationships.

3.3 An Overview of the in Silico

Experiments

The simulated intercellular communication scenario

consisted of two cells: a cancer cell and a normal

cell. The simulated cell junctions in cancer cell are

used to share information with the normal cell. The

goal of the designed in silico experiments was to

find proteins that prevent the formation of gap

junctions and leave the cancer cell uncommunicated.

The early in silico experiments carried out

consisted of running the simulation through a series

of combinations among the concentrations of several

target proteins. e.g., FZD, NDK, DVL, DSH and

APC. After a series of possible arrangements, i.e.,

increasing or decreasing the concentration, or even

removing the protein, we selected two proteins, APC

and NDK.

To determine the necessary concentration of

APC or NKD to prevent the formation of

intercellular junctions, experiments were designed

using concentrations of APC or NDK with the

lowest concentration of 0.001 μM and the highest

concentration of 1000 μM, i.e., 0.001, 0.1, 1, 10, 100

and1000 μM.

We observed that the increase in the

concentration of APC or NKD leads to degradation

of β-catenin in early stages of simulated signal

An in Silico Approach for Understanding the Complex Intercellular Interaction Patterns in Cancer Cells

193

transduction, thus preventing the formation of

intercellular junctions. Regarding APC, at a

concentration of 0.01 μM, it was observed that β-

Catenin disappears at 1,000 milliseconds (ms) and

DVL at 3,000 ms (see Figure 4). Concerning NKD,

at a concentration of 0.001 μM, the disappearance of

β-catenin and DVL is observed at 1000 ms, although

their disappearance is even faster (500 ms) when

using a concentration of 0.01 μM.

4 CONCLUSIONS

The in silico modelling and simulation approach

allowed us to observe, that increasing the

concentration of APC and NKD inhibits the Wnt

signalling pathway, preventing the formation of

intercellular junctions, since the β-CateninCyt is

destroyed and disappears. In silico experimentation

help us to determine the appropriate concentration of

these target molecules.

To carry out the experiments in cancer cells, we

use concentrations of 0.1 μM for both NKD2 and

APC. Using this concentration, β-CateninCyt

quickly disappears, and thus the formation of gap

junctions is avoided. Thanks to in silico experiments

we found two target proteins involved in the

intercellular communication channels and we

observed that their inhibition can stop cancer

development. The next step is to use this result to

guide the in vitro experiments, which in turn will

feedback the in silico modelling and simulation

approach proposed here.

The model of intercellular communication in cancer

cells evolved meaningfully, from the first versions to

later version, after multiple theoretical/experimental

feedbacks which allowed to solve the following

problems that emerged during the execution of the

associated simulation:

1) the earliest models of intercellular

communication in cancer cells did not include all the

required reactions, particularly negative feedback (or

balancing feedback), and 2) the estimated reaction

rate constant of some reactions did not meet the

required value, avoiding that such reactions were

executed at the appropriate time by Gillespie’s

algorithm, resulting that some slower reactions were

executed before the faster reactions.

As part of our future work, 1) we will increase

the size and complexity of the Wnt signalling

network, including other Wnt cross talk pathways,

since if we are able to understand, explore and

control this cellular signalling network, then tissue

invasion and metastasis can be avoided, 2) larger

intercellular communication systems (i.e., 3 o more

cells) will be simulated for verifying how the

proposed approach scales with the system size, and

3) we will use other related simulation tools, such as

MCell (Kerr et al., 2008) and Virtual Cell (Cowan et

al., 2012) for comparison with Cellulat.

Figure 4: APC at a concentration of 0.01 µM. After a series of possible arrangements, we selected two proteins: APC and

NKD. The APC protein is part of the complex that favors the ubiquitination of β-catenin, and therefore its destruction. If

there is no β-catenin, there is no union formation. This is still observed using an APC concentration of 0.001 µM, β -catenin

and DVL disappear around 2500 milliseconds. At this point only the Wnt receptor remains present. On the chart, the x-axis

represents the time in millisecond, and the y-axis represents the concentration of reactants (scaled by 10) in micromolar.

BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms

194

ACKNOWLEDGEMENTS

The authors would like to thank A. Boccacci and O.

Sánchez-Cortés for making a valuable contribution

to this Project.

REFERENCES

Alves, R., Antunes, F., Salvador, A., 2006. Tools for

kinetic modeling of biochemical networks. Nat

Biotechnol. 24(6), 667–72.

Blaheta, R.A., Michaelis, M., Driever, P. H. Cinatl, J. Jr.,

2005. Envolving anticancer drug valproic acid:

Insights into the mechanism and clinical studies. Med

Res Reviews 25(4), 383-397.

Borggrefe, T., Lauth, M., Zwijsen, A., Huylebroeck, D.,

Oswald, F., Giaimo, B.D., 2016. The Notch

intracellular domain integrates signals from Wnt,

Hedgehog, TGFβ/BMP and hypoxia pathways.

Biochim Biophys Acta 1863(2), 303–13.

Brücher, B. L. D. M., Jamall, I.S., 2014. Cell-cell

communication in the tumor microenvironment,

carcinogenesis, and anticancer treatment. Cell Physiol

Biochem. 34, 213–43.

Cárdenas-García, M., González-Pérez, P.P., 2013.

Applying the tuple space-based approach to the

simulation of the caspases, an essential signalling

pathway. J Integr Bioinform. 10(1), 225–34.

Cárdenas-García, M., González-Pérez, P. P., Montagna,

S., Cortés Sánchez, O., Caballero, E. H., 2016.

Modeling Intercellular Communication as a Survival

Strategy of Cancer Cells: An In Silico Approach on a

Flexible Bioinformatics Framework. Bioinformatics

and Biology Insights 10, 5-18.

Ciocchetta, F., Duguid, A., Guerriero, M. L., 2009. A

compartmental model of the cAMP/PKA/MAPK

pathway in bio-PEPA. Proceedings Third Workshop

on Membrane Computing and Biologically Inspired

Process Calculi, MeCBIC 2009, Bologna, Italy,

http://dx.doi.org/10.4204/EPTCS.11.5.

Cowan, A. E., Moraru. I. I, Schaff, J. C., Slepchenko, B.

M., Loew, L. M., 2012. Spatial modeling of cell

signaling networks. Methods Cell Biol. 110, 195–221.

Gelernter, D., 1985. Generative communication in Linda.

ACM Transactions on Programming Languages and

Systems 7(1), 80–112.

Gillespie, D. T., 1977. Exact stochastic simulation of

coupled chemical reactions, The Journal of Physical

Chemistry 81(8), 2340-2361.

González-Pérez, P. P., Cárdenas, M., Camacho, D.,

Franyuti, A., Rosas, O., Lagúnez-Otero, J., 2003.

Cellulat: an agent-based intracellular signalling model.

Biosystems 68(2–3),171–85.

González-Pérez, P. P., Omicini, A., Sbaraglia, M., 2013.

A biochemically inspired coordination-based model

for simulating intracellular signalling pathway. J

Simul. 7(3), 216–26.

González-Pérez, P. P., Cárdenas-García, M., Montagna,

S., 2013. Understanding the PI3K/AKT anti-apoptotic

signalling pathway: a tuple space-based computational

framework for simulating the signal transduction. J

Comput Model. 3(2), 35–65.

Grunsven, V., Vlierberghe, V., 2014. The roles of

transforming growth factor-β, Wnt, Notch and hypoxia

on liver progenitor cells in primary liver tumours

(review). Int J Oncol. 44(4), 1015–22.

Hernández, A. R., Klein, A. M., Kischner, M. W., 2013.

Kinetic responses of b-catenin specify the sites of Wnt

control. Science (338), 1337-1340.

Hoops, S., Sahle, S., Gauges, R., et al., 2006. COPASI: a

complex pathway simulator. Bioinformatics 22(30),

67–74.

Kerr, R. A., Bartol, T. M., Kaminsky, B., et al., 2008. Fast

Monte Carlo simulation methods for biological

reaction-diffusion systems in solution and on surfaces.

SIAM J Sci Comput. 30(31), 26–49.

Lee, E., Salic, A., Kruger, R., Heinrich, R., Kirschner, M.

W., 2003. The roles of APC and Axin derived from

experimental and theoretical analysis of the Wnt

pathways. PLoS Biology 1(1), 116-132.

Lum, L., Chen, C., 2015. Chemical disruption of WNT-

dependent cell fate decision-making mechanisms in

cancer and regenerative medicine. Curr Med Chem.

22(35), 4091–103.

Shimizu, T., Nakagawa, K., 2015. Novel signal

transduction pathways: the molecular basis for

targeted cancer therapies in Hedgehog/Notch/Wnt

pathway. Nihon Rinsho. 73(8), 1342–8.

Swat, M., Thomas, G. L., Belmonte, J. M., Shirinifard, A.,

Hmeljak, D., Glazier, J.A., 2012. Multi-scale

modeling of tissues using CompuCell3D. Methods

Cell Biol. 110, 325–66.

An in Silico Approach for Understanding the Complex Intercellular Interaction Patterns in Cancer Cells

195