White Blood Cells Counting Via

Vector Field Convolution Nuclei Segmentation

Simone Porcu, Andrea Loddo, Lorenzo Putzu and Cecilia Di Ruberto

University of Cagliari, Italy

Keywords:

WBC Count, Detection, Segmentation, Vector Field Convolution, Mathematical Morphology.

Abstract:

Haematological procedures like analysis, counting and classiﬁcation of White Blood Cells (WBCs) are very

helpful in the medical ﬁeld, in order to recognize a pathology, e.g., WBCs analysis leukaemia correlation.

Expert technicians manually perform these procedures, therefore, they are inﬂuenced by their tiredness and

subjectivity. Their automation is still an open issue. Our proposal aims to replicate every single step of

the haematologists’ job with a semi-automatic system. The main targets of this work are to decrease the

time needed for an analysis and to improve the efﬁciency of the procedure. It is based on the Vector Field

Convolution (VFC) to describe cells edges, going beyond more classic methods like the active contour model.

This approach is crucial to face the WBCs clumps and overlaps segmentation issue. To sum up, we deﬁned

a system that is able to recognise the leukocytes, to differentiate them from the other blood cells and, ﬁnally,

to divide the overlapping leukocytes. Experimental results obtained on three public datasets showed that the

method is accurate and robust, outperforming the state of the art methods for cells clumps identiﬁcation and

cells counting.

1 INTRODUCTION

Blood is a body ﬂuid deliver. It contains and trans-

ports many of the nutrients substances that humans

need to live. Blood is mainly composed of two ele-

ments: cells and plasma. The blood cells are the red

blood cells (RBCs) and white blood cells (WBCs).

Haematology is the ﬁeld related to the study of blood

conditions in order to measure the health status of the

patients. Nowadays the analysis work ﬂow is a ma-

nual process. Every single blood slide is analysed by

an expert haematologist that counts and extracts the

needed information for the requested analysis. Ho-

wever it is a very delicate procedure and it is error-

prone. For this reason, having an automatic or semi-

automatic system would be useful to avoid issues.

The main contribute of this work is a semi-automated

method that can extract all the WBCs from the pe-

ripheral blood smear images and count every single

WBC in order to obtain their exact count. The pro-

posed system is based on a segmentation algorithm

especially designed for this purpose. No machine le-

arning approach has been used in our method, either

to increase the performances in detection and to avoid

the learning phase, that is slow and focused on a parti-

cular training set. Thus the proposed algorithm is not

tuned to a speciﬁc training set and it could be used

for whichever dataset of peripheral blood images. In

the literature there are a lot of methodologies devoted

to the identiﬁcation and counting of single cells, but

only few works addressed clumped cells separation

and counting issues. For this reasons, this work is fo-

cused on the clumped cells separation issue. The rest

of the paper is organized as follows. Section 2 pre-

sents the related works about peripheral blood image

analysis. Section 3 illustrates the proposed method.

Section 4 presents the obtained results on the consi-

dered datasets. Discussions, conclusions and future

aspects are ﬁnally given in Section 5.

2 STATE OF THE ART

Commonly, blood cells images segmentation can be

performed with two different approaches: the ﬁrst one

works at a cell level and the last one aims to do an

intra-cell segmentation. The purpose of the ﬁrst one

is to discriminate foreground from background, while

the second one has the target to divide the different

components contained inside the cells, such as nu-

cleus from cytoplasm or intracellular parasites. For

example, Madhloom (Madhloom et al., 2010) imple-

Porcu, S., Loddo, A., Putzu, L. and Ruberto, C.

White Blood Cells Counting Via Vector Field Convolution Nuclei Segmentation.

DOI: 10.5220/0006723202270234

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theor y and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages

227-234

ISBN: 978-989-758-290-5

227

mented an automated system to localise and segment

WBC nuclei based on arithmetical and threshold ope-

rations. Sinha (Sinha and Ramakrishnan, 2003) and

Kovalev (Kovalev et al., 1996) tried to differentiate

the leukocytes types typically contained in cell ima-

ges. Sinha used k-means clustering based on the HSV

colour space for WBCs segmentation. Kovalev ﬁrstly

identiﬁed the nuclei and then detected the entire mem-

brane by means of region growing techniques. A low-

pass ﬁlter has been employed (Scotti, 2006) in order

to remove background and, after that, WBCs segmen-

tation is approached with different threshold opera-

tions and image clustering. Piuri’s approach (Scotti

and Piuri, 2004) is based on edge detection for WBCs

segmentation. Halim (Halim et al., 2011) proposed

an automated blast counting method to detect acute

leukaemia in blood microscopic images that identiﬁes

WBCs through a thresholding operation performed

on the S component of the HSV colour space, fol-

lowed by morphological erosion for image segmen-

tation. Mohapatra (Mohapatra et al., 2013) investi-

gated the early diagnosis of ALL in blood microsco-

pic images. The identiﬁcation and segmentation of

WBCs is realised through image clustering followed

by the extraction of different types of features, such

as shape, contour, fractal, texture, colour and Fourier

descriptors, from the sub-image. Moving to the pro-

blem of clumped cells separation, some methods are

included in the process of segmentation, while others

are speciﬁcally dedicated to overlapping cells separa-

tion.The Watershed transform is certainly one of the

most common methods. Putzu (Putzu et al., 2014)

used the distance transform and the watershed algo-

rithm to separate cells agglomerates. The separation

is less inﬂuenced by cells shape, but it works only

for small or simple cells agglomerates. On the other

hand, Ghane (Ghane et al., 2017) used K-means al-

gorithm for nuclei segmentation and morphological

operators to remove small objects, obtaining an en-

hancement of the segmentation results. Finally, he

used the Watershed transform to split touching cells

and nuclei. Mahmood and Alomari (Mahmood et al.,

2013), (Alomari et al., 2014), differently from the pre-

vious, proposed two WBCs count methods based on

the circular Hough transform (CHT). Mahmood ap-

plied the CHT on binary images obtained from the

Lab colour space, while Alomari modiﬁed the CHT

in order to reduce the number of cells candidates by

choosing the one with the highest probability of being

a circle. A different approach has been proposed by

Alilou (Alilou and Kovalev, 2013), where a detection

phase using grey level co-occurrence matrix has been

applied directly on the original images without a pre-

vious segmentation. As it can be guessed, it produces

a signiﬁcant amount of false positives since it works

without restrictions on the area of interest. Finally, Di

Ruberto (Di Ruberto et al., 2016) and Loddo (Loddo

et al., 2016) applied the CHT to recognize circular

shapes inside the clumped cells obtained in the seg-

mentation phase. To sum up, every non-classiﬁer ba-

sed method typically works with the following stra-

tegy: ﬁrst a threshold methodology is used to extract

the cells and then the clumped cells separation is re-

alized by using another method, e.g., the Watershed

transform. Our work aims to use a different appro-

ach. It performs the clumped cells separation along

with the segmentation step so that every identiﬁed re-

gion is obtained in only one computational step.

3 PROPOSED METHOD

The main target of our proposed method is to segment

all the WBCs nuclei by using Vector Field Convolu-

tion (VFC) strategy and to divide potential clumps

by using an analysis of the real cells boundaries,

overcoming the use of Watershed transform. The

system is composed of the following phases: pre-

processing, binary edge map generation, VFC (Bing

and Scott, 2007) application, grades transformation,

external energy computation, black and white dis-

tance calculation and, ﬁnally, skeletonizing and re-

gion merging application. Figure 1 shows the of pro-

posed method ﬂow diagram. It starts with a contrast

stretching on the RGB colour space’s G channel. The

regions boundaries are extracted by means of a gra-

dient operator which permits to obtain a binary edge

map. Subsequently the VFC is computed with the

initialization of the kernel vector ﬁeld and the edge

map creation. A ﬁrst WBCs detection has been so far

obtained with the previous steps and a ﬁrst nuclei seg-

mentation can be consequently obtained by applying

the skeleton function on the overlap between the ex-

ternal force and the binary distance transform ima-

ges. The ﬁnal segmentation result is described in de-

tail further on.

3.1 Pre-processing

It is the ﬁrst step of the proposed technique and it is

needed to extract all the information for WBCs areas

detection. WBCs nuclei has been highlighted by stret-

ching the histogram of RGB colour space’s G channel

(Figure2). The purpose is to obtain only the cells of

interest in order to create the best possible edge map.

The high spacial frequency regions, correspon-

ding to the edges, have been highlighted thanks to

the Sobel operator. It is a kind of orthogonal gradient

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

228

Figure 1: Diagram of WBC image recognizer.

operator and it has the advantage to produce a smoo-

thing effect to the image’s random noise (Gao et al.,

2010). Gradient corresponds to ﬁrst derivative, there-

fore gradient operators are derivative. For a continu-

ous function f (x, y), in the position (x, y), its gradient

can be expressed as a vector:

∇ f (x,y) =







δ f

δx

δ f

δy



(1)

This operator applies two kernels in the two prin-

cipal directions. Calling G

and G

the horizontal and

vertical derivative approximations and I the image,

the computation is described as follows:





+1 0 −1

+2 0 −2

+1 0 −1





× I (2)





+1 +2 +1

0 0 0

−1 −2 −1





× I (3)

Figure 2: RBC image’s G channel extraction. The WBCs

are highlighted with respect to the other regions.

where the × operator indicates the convolution ope-

ration.

3.2 VFC Segmentation

An external force, namely the VFC, can be obtained

by convolving a vector ﬁeld with the edge map de-

rived from the image (Bing and Scott, 2007). Active

contours using the VFC external force are called VFC

snakes. Differently from the GVF (Xu and Prince,

1998) snakes, that are formulated using the stan-

dard energy minimization framework, VFC snakes

are constructed from a state of equilibrium between

the forces. Furthermore, VFC snakes have a lot of ad-

vantages, e.g., a wide capture range, they are able to

grab the concavities, they are better resistant to noise

images, they have the ability to adapt the force ﬁeld

and to reduce drastically the computational cost. Be-

fore going into detail, it is useful to deﬁne the Vector

Field Kernel (VFK). It is computed using the follo-

wing equation:

k(x, y) = m(x,y)n(x,y) (4)

where n is the unit vector that points to the origin of

the kernel

n(x,y) = [

−x

−y

] (5)

and m is the magnitude of the vector. Potentially,

every single pixel in an image may be attracted to the

edge of its region (Bing and Scott, 2007). This fact

could be compared to the gravity effect on every sin-

gle object in Earth: it is attracted to the Earth surface.

Consequently, if we consider the origin as the point

of interest, VFK has the desirable property that a free

particle placed in the vectorial ﬁeld is able to move to

a point of interest. The external force that works in

the VFC is deﬁned in this way:

v f c

(x,y) = u

v f c

(x,y),v

v f c

(x,y) (6)

Since the edge map is non-negative and wider near

the edges of the image, the VFC acts more on the

edges than to homogeneous regions. Therefore, the

free particles of homogeneous regions will be attrac-

ted to the edges. If we use a complex-valued range,

the VFC acts as a ﬁlter on the edge map, which does

not depend on the origin of the kernel. The VFC ﬁeld

highly depends on the magnitude of the VFK in such

a way that it is directly proportional to the VFK(x, y).

The farther is the ﬁgure of interest (FOI) (Bing and

Scott, 2007), the less powerful is the force and, the-

refore, the magnitude must be expressed as a positive

function that decreases with respect to the distance of

the origin. Two types of magnitude functions are de-

ﬁned as follows:

White Blood Cells Counting Via Vector Field Convolution Nuclei Segmentation

229

Figure 3: VFC right and left component.

(x,y) = (r + ε)

−γ

(7)

(x,y) = exp(−r

) (8)

where γ and ζ are positive parameters to control the

decrease rate, ε is a small positive constant which pre-

vents division by zero at the origin, while m

(x,y) is

inspired by Newton’s universal gravitation law. Furt-

hermore, the pixels in the edge map can be considered

as objects of mass proportional to the strength of the

edges and the VFC would be the gravitational ﬁeld

generated by all objects. m

(x,y) is a Gaussian shape

function, and ζ can be viewed as the standard devia-

tion. The inﬂuence of FOI is strongly dependent from

γ and ζ because it increases if the ﬁrst one decreases or

the second one increases. In general, the inﬂuence of

FOI should be increased (or decrease) as the signal-

to-noise ratio is decreased (or increased) (Bing and

Scott, 2007).

The VFC uses the two components of the external

force u

v f c

(x,y),v

v f c

(x,y) to describe the ﬁeld of the

image and its magnitude. These two components are

very useful to describe all the edges, both from single

leukocytes and from cell clumps. VFC’s right and left

components can be computed as follows:

v f c

= ExtF(x)/

ExtF(x)

+ ExtF(y)

(9)

v f c

= ExtF(y)/

ExtF(x)

+ ExtF(y)

(10)

where ExtF is the External force of the Field. u and

v are two intensity images with values range in −pi

and +pi. They need to be combined and converted in

degrees values so that the orientation of every image

pixel can be described, as shown in Fig. 3.

VFC application typically generates some arte-

facts. In order to delete them all, this method applies

the distance transform. It assigns a number that is the

distance between each pixel and the nearest non-zero

pixel of the image. As a result, the entropy of the

image is reduced as well as the noise even though it

does not distinguishes if the edge is a RBC’s edge or

Figure 4: Distance transform image.

a WBC’s edge. As a consequence, the application of

the External Energy is needed to overcome this pro-

blem.

For an image I(x,y) the general formulation of the

image Energy is:

image

= w

line

+ w

edge

+ w

term

(11)

where w

line

edge

term

are weights of the features.

Line Functional: the line functional, also known as

the image intensity, is the attracted value of the dark

lines to the light lines. It is possible to choose this

value by selecting a positive or negative value of the

force

line

= f ilter(I(x,y)) (12)

Edge Functional: The edge functional bases its work

on the image gradient.

edge

= −

∇I(x,y)

(13)

This formula deﬁnes the strategy by which the met-

hod gets rid of the local minima that are not object

of interest. The energy functional using scale space

continuation is

edge

= −



× ∇



(14)

where G

is a Gaussian with standard deviation σ.

Termination Functional: The lines curvature in an

image is used to detect corners and terminations. Put

C(x, y) = G

× I(x,y) (15)

we derive a gradient angle

θ = arctan

, (16)

the unit vectors that move along the gradient direction

n = (cos θ,sin θ), (17)

and the unit vectors perpendicular to the gradient di-

rection.

⊥

= (−sin θ,cos θ). (18)

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

230

Figure 5: External energy image.

Figure 6: Overlay image.

Having deﬁned the previous four formulas, the termi-

nation functional of energy can be deﬁned as follows:

term

∂θ

∂n

⊥

∂

C/∂

⊥

∂C/∂n

⇒

− 2C

)

3/2

(19)

External Energy Result: As stated before, a median

ﬁlter has been employed in order to delete all the uni-

form part of the ﬁgure and to highlight the edges. It

searches the 13

element of the 5 × 5 mask (Figure

5).

Once the median ﬁlter has been applied over the

degrees image we apply and AND operation between

it and the edges regions image so that we can highlight

the points which result to be in overlay (Figure 6).

3.3 Post-processing

The image obtained from the previous steps present

only the WBCs edges that, in some regions of the

image, are far from being a connected boundary.

Thus, a further step is needed to link the edges pre-

serving the original boundary of the objects. Actu-

ally, this phase includes different steps. The ﬁrst one

Figure 7: Opened image.

consists in connecting every single white point to the

nearest in order to produce a connected objects boun-

dary. A dilation with a 6 pixels size diamond structu-

ral element is applied in order to dilate all white dots.

Secondly, the opening of the closing is applied with

a 4 and 3 pixels size disks, respectively. Then, the

skeleton function is performed. It produces an image

that contains some spurious branches which are re-

dundant for our purposes and, consequently, we reali-

zed the following strategy in order to get rid of them.

To solve this problem we used a path analyser that

checks for the presence of open paths. Indeed, a con-

nected border is a closed path in which a pixel of that

border is at the same time a starting and ending point.

So, each pixel that does not belong to a closed path is

removed. At this moment, every pure edge belonging

to the cells is available but over-segmentation could

occur so that we need to perform an arithmetical ope-

ration which ﬁlls all the WBCs edges and removes the

others. This operation uses a mask obtained from the

external force image. Finally, the application of an

opening on the edge map with a 6 pixels radius disk

structural element and its addition to WBCs image

in foreground, all connected components, ﬁtting into

a speciﬁc area range, are successfully extracted, as

shown in ﬁg. 7. It is the ﬁrst WBC segmented image

obtained with the proposed method. It needs some

improvements, following deﬁned.

Once the cleaned binary mask has been obtained,

we should be able to perform the count of the cells

inside the image. Unfortunately, as it can be obser-

ved in Figure 8, using the proposed method also some

WBCs have been separated in two or more regions,

hampering a correct cell counting.

Thus, it is necessary a further step that merges all

the image regions that belongs to the same cells. In

order to understand which are the regions that should

be part of a single cell we performed a check based

on the area value. All the regions that have an area

smaller than the half of the biggest region inside the

White Blood Cells Counting Via Vector Field Convolution Nuclei Segmentation

231

Figure 8: Oversegmented image.

Figure 9: Final result.

image are considered part of a single cell, while the

other regions are considered complete cells. Keeping

in mind that smaller area regions belong to larger area

regions, we need to identify which of the ﬁrst ones

belongs to the latter. The threshold area used to cre-

ate these two different images is exactly half of the

image’s biggest region area. Labelling each area and

computing all the centroids, we can know which areas

need to be joined together, using the Euclidean dis-

tance formula. Finally, it is possible to isolate the two

areas and merge them using a closing procedure with

a 7 pixels radius disk element. The ﬁnal result is gi-

ven by an overlay of this step to the over-segmented

image by means of the union operator (ﬁgure 9).

4 DATASETS AND

EXPERIMENTAL RESULTS

This section present the experimental result of the

proposed white blood cells nuclei segmentation

technique. The system has been tested on three diffe-

rent dataset, that is ALL-IDB, IUMS-IDB and SMC-

IDB. First one is composed of images captured with

an optical laboratory microscope coupled with a Ca-

non PowerShot G5 camera. All the images are in

JPG format with 24-bit colour depth. The ﬁrst 33

have 1712 × 1368 resolution, while the remaining

have 2592 × 1944 resolution. The images are taken

with different magniﬁcations of the microscope ran-

ging from 300 to 500 which brings the colour dif-

ferences that we managed grouping the images with

same brightness characteristics together. It is com-

posed of two versions: ALL-IDB1 and ALL-IDB2.

ALL-IDB1 can be used for testing the segmentation

capability of the algorithms. This dataset is compo-

sed of 108 images collected during September, 2005.

It contains about 39000 blood elements, where the

lymphocytes have been labelled by expert oncologists

(Unimi, 2005). ALL-IDB2 has been designed for tes-

ting the performances of classiﬁcation systems. The

ALL-IDB2 version is a collection of cropped area of

interest of healthy and blast cells that belong to the

ALL-IDB1 dataset. They have similar grey level pro-

perties to ALL-IDB1 images, except from their di-

mensions (Unimi, 2005). In order to understand if the

algorithm can obtain the best result with every kind of

luminance or noise, it has been tested over two more

datasets. IUMS-IDB is provided by Iran University of

Medical Science (Sarrafzadeh et al., 2014) and con-

tains 100 microscopic images of size 732 ×572, taken

from peripheral blood of 8 healthy subjects. They are

really different from those of ALL-IDB, since the mi-

croscope slides have been smeared and stained with a

different staining technique. The third dataset, pro-

posed in (Mohamed et al., 2012), has been acquired

from slides stained with the same staining technique

as ALL-IDB, even though the images are really dif-

ferent, since they have been acquired with a different

combination of microscope and camera. It has a total

of 367 peripheral blood images of size 640 × 480.

A visual result for each dataset is reported in ﬁg.

10. A quantitative experimentation has been con-

ducted by considering every single image for a WBCs

analysis and relative count. Three metrics have been

adopted to evaluate our study: False Negative Rate

(FNR), Precision and Recall. The obtained results are

reported in table 1. It is evident that our approach cor-

rectly identiﬁes 100% of the leukocytes inside ALL-

IDB, IUMS-IDB and SMC-IDB datasets. The ma-

jority of clumped cells has been found in ALL-IDB,

which presents a lot of complex images, with lots

of leukocytes per image and different agglomerates,

while IUMS-IDB and SMC-IDB contain simpler ima-

ges composed of fewer leukocytes and only few, sim-

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

232

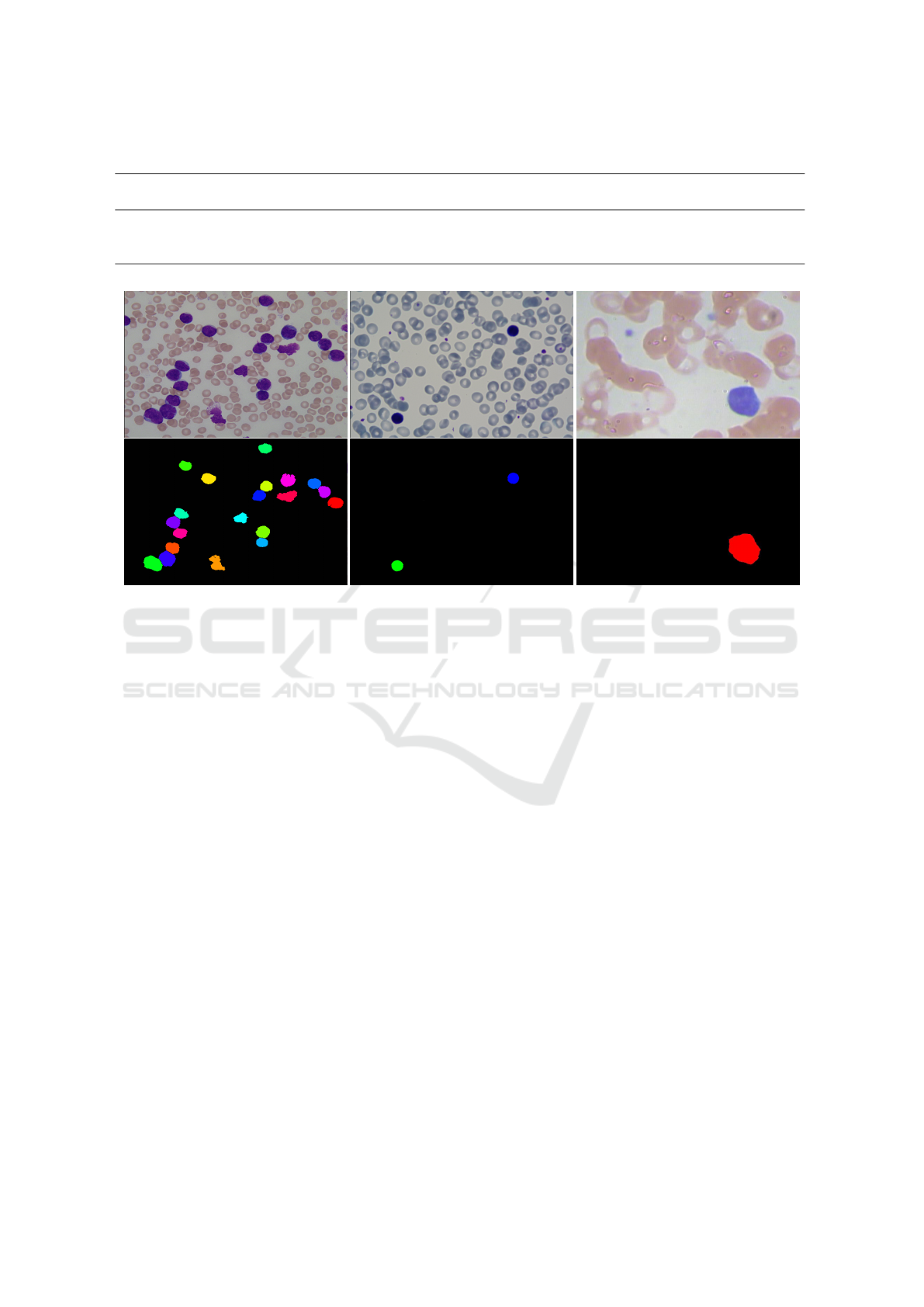
Table 1: Detection performances compared with the state-of-the-art.

Mahmood, 2013 Alilou, 2013 Putzu, 2014 Alomari, 2014 Di Ruberto, 2016 Our Approach

ALL ALL ALL ALL ALL IUMS SMC ALL IUMS SMC

FNR - - - 1.5% 0.7% 0% 0% 0% 0% 0%

Precision - - - 90% 100% 100% 100% 100% 100% 100%

Recall 81% 88% 92% 98% 99.2% 100% 100% 100% 100% 100%

Figure 10: Top: from left to right, images extracted from ALL-IDB, IUSMS-IDB and SMC-IDDB, respectively. Bottom:

from left to right, the ﬁnal segmentation results for each image on top.

pler, agglomerates. They also have a poorer quality

than the ALL-IDB images. The proposed approach

produces no false positives, being able to exclude all

other image regions before the detection phase, and

thus considering only the portions of image contai-

ning leukocytes. Some other state of the art methods

used the aforementioned datasets for their segmenta-

tion clumped cells separation experiments, e.g. (Lata

et al., 2016) and (Di Ruberto et al., 2015) use ALL-

IDB. The ﬁrst authors perform a WBCs count by

counting the number of connected components even

though it is not present a method to divide the clum-

ped cells, while the second ones perform a separation

of clumped and overlapped cells although they state

some errors in the procedure. Our proposed approach

outperforms both.

5 CONCLUSIONS

A new semi-automated WBCs recognition system has

been investigated and proposed in this work. It can

be used to support some existing medical methods,

like the white blood cells counting. Its novelty in the

state of the art is related to the clumped cells sepa-

ration strategy, realised using a Vector Field Convo-

lution model. It works by following only their na-

tural shape even if they are hard to distinguish. Its

strength lies in the invariance to cells shapes and, by

using the gradients movement, it can ﬁnd the edge

shape even if this is not immediately visible. Moreo-

ver, the proposed algorithm is not tuned to a speciﬁc

training set and it could be used for whichever pe-

ripheral blood images dataset. Experimental results

demonstrate that this new approach is very accurate

and robust for detection, if compared to some tra-

ditional methods, being able to obtain excellent re-

sults with the three public tested datasets, even though

some improvements could be implemented. Firstly,

the post-processing phase could be afforded with an

edge-linking algorithm referred the same region ed-

ges, in order to reduce the computational cost of this

step. Secondly, the pre-processing step could be im-

proved so as to consider both WBCs nuclei and cyto-

plasm.

REFERENCES

Alilou, M. and Kovalev, V. (2013). Automatic object de-

tection and segmentation of the histocytology images

using reshapable agents. Image Analysis and Stereo-

logy, 32(2):89–99.

Alomari, Y. M., Huda, S. A. S. N., Raja, Z. A., and Khairud-

White Blood Cells Counting Via Vector Field Convolution Nuclei Segmentation

233

din, O. (2014). Automatic detection and quantiﬁcation

of wbcs and rbcs using iterative structured circle de-

tection algorithm. Computational and mathematical

methods in medicine, 2014.

Bing, L. and Scott, T. (2007). Active contour external force

using vector ﬁeld convolution for image segmentation.

Acton, vol. 16, pp. 2096 - 2106.

Di Ruberto, C., Loddo, A., and Putzu, L. (2015). a multiple

classiﬁer learning by sampling system for white blood

cells segmentation. proceedings in CAIP, vol. 9257,

pp. 415 - 425.

Di Ruberto, C., Loddo, A., and Putzu, L. (2016). A leucocy-

tes count system from blood smear images. Machine

Vision and Applications, vol. 27, pp. 1151 - 1160.

Gao, W., Yang, L., Zhang, X., and Liu, H. (2010). An

improved sobel edge detection. 2010 3rd Internatio-

nal Conference on Computer Science and Information

Technology, pp. 67 - 71.

Ghane, N., Vard, A., Talebi, A., and Nematollahy, P. (2017).

Segmentation of white blood cells from microscopic

images using a novel combination of k-means cluste-

ring and modiﬁed watershed algorithm. ournal of Me-

dical Signals and Sensors. vol. 7, no. 2, pp. 92-101.

Halim, N. H. A., Mashor, M. Y., and Hassan, R. (2011).

Automatic blasts counting for acute leukemia based

on blood samples. International Journal of Research

and Reviews in Computer Science, vol. 2, no. 4.

Kovalev, V. A., Y.Grigoriev, A., and H.Ahn (1996). Robust

recognition of white blood cell images. IEEE Publis-

her, pp. 371-375.

Lata, A., Udesang, K. B., and Joshi, J. J. M. (2016). seg-

mentation and counting of wbcs and rbcs from mi-

croscopic blood sample images. proceedings in MECS

(http://www.mecs-press.org/), vol. 11, pp. 32 - 40.

Loddo, A., Putzu, L., Ruberto, C. D., and Fenu, G. (2016).

A computer-aided system for differential count from

peripheral blood cell images. In 2016 12th Internatio-

nal Conference on Signal-Image Technology Internet-

Based Systems (SITIS), pages 112–118.

Madhloom, H. T., Kareem, S. A., Arifﬁn, H., Zaidan, A. A.,

Alanazi, H. O., and Zaidan, B. B. (2010). An automa-

ted white blood cell nucleus localization and segmen-

tation using image arithmetic and automated thres-

hold. Journal of Applied Sciences, vol. 10, no. 11,

pp. 959-966.

Mahmood, N. H., Lim, P. C., Mazalan, S. M., and Razak,

M. A. A. (2013). Blood cells extraction using color

based segmentation technique. International Journal

of Life Sciences Biotechnology and Pharma Research,

2(2).

Mohamed, M., Far, B., and Guaily, A. (2012). An efﬁ-

cient technique for white blood cells nuclei automatic

segmentation. IEEE International Conference on Sy-

stems, Man, and Cybernetics (SMC), pp. 220225.

Mohapatra, S., Patra, D., and Satpathy, S. (2013). An en-

semble classiﬁer system for early diagnosis of acute

lymphoblastic leukemia in blood microscopic images.

Journal of Neural Computing and Applications, Arti-

cle in Press,.

Putzu, L., Caocci, G., and Di Ruberto, C. (2014). Leu-

cocyte classiﬁcation for leukaemia detection using

image processing techniques. Artiﬁcial Intelligence

in Medicine, vol. 62 , pp. 179 - 191.

Sarrafzadeh, O., Rabbani, H., Talebi, A., and Banaem, H.

(2014). Selection of the best features for leukocy-

tes classiﬁcation in blood smear microscopic images.

SPIE Medical Imaging, pp. 90410P 90410P.

Scotti, F. (2006). Robust segmentation and measurements

techniques of white cells in blood microscope images.

IEEE Publisher, pp. 43-48.

Scotti, F. and Piuri, V. (2004). Morphological classiﬁca-

tion of blood leucocytes by microscope images. IEEE

Publisher pp. 103-108.

Sinha, N. and Ramakrishnan, A. G. (2003). Automation of

differential blood count. in proceedings of the confe-

rence on convergent technologies for the asia-paciﬁc

region. IEEE Publisher, vol. 2, pp. 547-551, Taj Resi-

dency, Bangalore.

Unimi (2005). All-idb acute lymphoblastic leukemia image

database for image processing.

Xu, C. and Prince, J. L. (1998). Generalized gradient vector

ﬂow external forces for active contours. Signal Pro-

cess., vol. 71, pp. 131 - 139.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

234