Development of the Decision Support System in Treatment of Arterial

Hypertension

Application of Artificial Neural Networks for Evaluation of Heart Rate Variability

Signals

Anton Dolganov

, Vladimir Kublanov

, David Belo

and Hugo Gamboa

Ural Federal University, Mira 19, 620002, Yekaterinburg, Russian Federation

Laboratório de Instrumentação, Engenharia Biomédica e Física da Radiação (LIBPhys-UNL),

Departamento de Física, Faculdade de Ciências e Tecnologia da Universidade Nova de Lisboa,

Monte da Caparica, 2892-516 Caparica, Portugal

Keywords: Heart Rate Variability, Artificial Neural Networks, Classification, Arterial Hypertension.

Abstract: The article presents first step of the decision support system development in treatment of arterial hypertension.

Results of arterial hypertension diagnostic task by short-term signals of heart rate variability are presented.

The tilt test study was used as the functional load. The peculiarity of this work is application of neural

networks for this task. The different number of hidden layers in the neural networks and different number of

neurons in hidden layers were tested in this study. The classification accuracy of the neural networks was

compared with those of simple machine learning classifiers. The following steps of the decision support

system development are declared.

1 INTRODUCTION

According to the WHO experts the arterial hyper-

tension is the most frequent pathology of cardio-

vascular system. It is occurring among 15-25% of

adult population. Hypertension is one of the most

important factors of such diseases as coronary heart

disease, stroke and heart failure. The arterial hyper-

tension has a multi-factor origin and for a long time

is asymptomatic. However, fairly soon it might lead

to acute events. Therefore the task of early preclini-

cal diagnostic is relevant (Feng et al., 2014; Mancia

et al., 2013; Mendis et al., 2010).

The arterial hypertension emerges as a result of

regulatory mechanisms disorders of the vascular tone.

The most important indicator of the vascular tone is

the arterial pressure. It is well known that arterial

pressure is supported by the several regulatory

mechanisms, including neuronal and humoral. Here

is the exceptional role of the autonomic nervous

system (ANS).

Often, in accordance with recommendations of

the medical societies, arterial hypertension treatment

consists of several medications. These may lead to

polypragmasy and several side effect (Mancia et al.,

2013). The alternative to the pharmacological

approach is application of the physiotherapy

equipment dedicated to improvement of the

cardiovascular system. The ‘SYMPATHOCOR-01’

neuro-electrostimulator is one of such devices. The

device provides correction of the sympathetic

department of the ANS. Through the sympathetic

department the device has constricted control of the

vascular tone (Kublanov et al., 2010). Thereby it is

appropriate to apply in the development of the decision

support system in treatment of arterial hypertension

such methods that allow monitoring current state of the

ANS.

One of the indirect ways to access functioning of

the ANS is the heart rate variability (HRV). (Kseneva

et al., 2016). Non-invasiveness and easy derivation of

the HRV measurement make it widely studied and

practical tool to monitor ANS function (Zadeh et al.,

2010). The R-R intervals of the ECG signals forms

the Heart Rate Variability (HRV) signals. The digital

HRV signal processing has a long history and

methodological recommendation for practical usage

were reflected in work of various scientific groups in

many countries around the globe (Malik, 1996;

Tarvainen et al., 2014; Ushakov et al., 2013).

Dolganov, A., Kublanov, V., Belo, D. and Gamboa, H.

Development of the Decision Support System in Treatment of Arterial Hypertension - Application of Artiﬁcial Neural Networks for Evaluation of Heart Rate Variability Signals.

DOI: 10.5220/0006728903250331

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 4: BIOSIGNALS, pages 325-331

ISBN: 978-989-758-279-0

325

In some works authors suggest that common

features of HRV have low sensitivity. However, joint

application of common features with non-linear

estimations could be of great benefit for more

practical identification of patients at risk

(Chattipakorn et al., 2007)

The Artificial Neural Networks (ANN) Artificial

neural networks is a computing approach, which was

inspired by the functioning of the biological neural

networks. Such approach have proven to be

successful in solving different task on variety of

data(Belova et al., 2007; Lee et al., 2005; Tkacz and

Kostka, 2000). There are several works in which

ANN is applied for HRV signals computing (Patel et

al., 2011; Rajendra Acharya et al., 2003). However,

in that works a limited number of HRV features were

used.

On the other hand, there are works that apply

ANN for classification of arterial hypertension

among people suffering from obesity (Pytel et al.,

2015). There, anthropometric measures were used as

the hypertension indicators. However such approach

does not allows to evaluate dynamic reaction of the

organism on the functional load.

To our knowledge this study is the first attempt to

apply ANN for diagnostic of the arterial hypertension

using big vector of the HRV features. The goal of the

present work is first stage in the development of the

decision support system in treatment of arterial

hypertension. For this in present work classification

accuracy of ANN was evaluated for two groups –

relatively healthy volunteers and patients suffering

from arterial hypertension. Additionally, obtained

results were compared with evaluations of other

machine learning classifiers.

2 MATERIALS AND METHODS

2.1 Clinical Data

The clinical data was recorded at the Sverdlovsk

Clinical Hospital of Mental Diseases for Military

Veterans (Yekaterinburg, Russian Federation). This

pilot study had an approval of the local Ethics

Committee (Ural State Medical University,

Yekaterinburg, Russian Federation). The dataset

itself includes the recorded data of 28 healthy people

and 40 patients. All the patients were diagnosed with

the II/III degree of arterial hypertension. All

participants were volunteers and had signed the

participation consent.

The exclusion criteria were: liver failure, kidney

failure, diabetes of I type, diffusion collagen disease,

heart failure of III-IV class (NYHA classification),

respiratory failure, acute impairment of cerebral

circulation (6 month prior to the study), unstable

angina or myocardial infarction (6 month prior to the

study), permanent atrial fibrillation, women during

pregnancy and lactation period.

Electrocardiography (ECG) signals were recorded

by the electroencephalograph-analyzer “Encephalan-

131-03” (“Medicom-MTD”, Taganrog, Russian

Federation) in the first limb lead (Kleiger et al.,

2005). After the ECG signal recording the

“Encephalan-131-03” software automatically derive

the HRV signals.

The clinical data was recorded in three functional

states involving the rotating table Lojer (Vammalan

Konepaja DY, Finland). During the first state the

participant calmly lies on the exanimating table (state

F). At the second state the so-called tilt-test is

performed – the head end of the table is lifted up to

from the horizontal position (state O). At the final

state the participant returns to the horizontal position

(state K). The functional load was supervised by the

physician. The duration of the signal record in each

state was 300 seconds. In this study only features of

state O were used, as this state was the most efficient

classification accuracy wise (Kublanov et al., 2017).

2.2 Heart Rate Variability Features

Usually in state-of-art works that involve HRV signal

processing the Kubios software package is used to

extract HRV-related features (Tarvainen et al., 2014).

Tables 1-6 present summary of the features used in

this study. That list of features consist of time-domain

(tables 1 and 2) and frequency-domain features (table

3) established by the European Society of Cardiology

(Malik, 1996) as well as relevant non-linear features

(table 4) (Sivanantham and Shenbaga Devi, 2014). In

our study, in addition to commonly used features, the

wavelet transform features were used (tables 5 and 6)

(Egorova et al., 2014). Overall, a comprehensive list

of 64 features was considered.

Before features calculation, the outliers were

removed from the original R-R time series. By

outliers in this study, we have considered values of R-

R time series that differed from the mean of time-

series by more than three times of the standard

deviation. Across the entire signal samples less than

1.7 % of data were removed. This processed version

of the signal will be referred as a NN (Normal-to-

Normal) time series.

NENT 2018 - Special Session on Neuro-electrostimulation in Neurorehabilitation Tasks

326

Table 1: HRV statistical features.

Feature

Description

Mean value of the NN time-series

Heart Rate

SDNN

Standard Deviation of the NN time-series

skewness

Skewness of the NN time-series

kurtosis

Kurtosis of the NN time-series

the Coefficient of Variation

RMSSD

Square Root of the Mean of Squares of the

NN time-series

NN50

Variation higher than 50ms in the NN time-

series

pNN50

Normalized NN50 by the length of NN time-

series

SDSD

Standard Deviation of Differences between

Successive elements in NN time-series

ZCR

Zero Crossing Rate

Statistical features included general estimation,

like mean and standard deviation. Moreover, there

were HRV-specific ones, which concern interaction

between consequent intervals (Malik, 1996). In table

1 the ZCR feature is evaluated in relation to the mean

value of the NN time series.

Table 2: HRV geometric features.

Feature

Description

Mode of the NN time-series

Variation Range

AM0

Amplitude of the Mode

Stress Index

IAB

Index of Autonomic Balance

ARI

Autonomic Rhythm Index

IARP

Index of Adequate Regulation

Processes

St. George Index

The triangular Index

In table 2 the standard features are the mode,

amplitude of the mode, variation range and St.

George Index (Malik, 1996). Remaining features are

calculated using the standard ones, in accordance

with recommendations (Baevskiy, 2001).

In the case of the Fourier and wavelet transform

evaluation, the original R-R intervals were

interpolated, for a corresponding sampling frequency

of 10Hz, using cubic splines before the spectral

analysis (De Boor, 1978). For the wavelet transform

computation the Gaussian wavelet of the 8-th order

was used (Mallat, 2009). Main frequency components

of HRV are: high frequency (HF), from 0.15 to 0.4

Hz; low frequency (LF), from 0.04 to 0.15 Hz; very

low frequency (VLF), from 0.003 to 0.04 Hz.

Table 3: HRV Fourier spectral features.

Feature

Description

HF(Fr)

High Frequency Fourier Spectral Power

LF(Fr)

Low Frequency Fourier Spectral Power

VLF(Fr)

Very Low Frequency Fourier Spectral

Power

TP(Fr)

Total Power of the Fourier Spectrum

LF/HF(Fr)

Autonomic Balance Exponent Power of

the Fourier Spectrum

HFmax(Fr)

Maximum power of the HF

HFn(Fr)

Normalized Power of the HF Fourier

Spectrum

LFn(Fr)

Normalized Power of the LF Fourier

Spectrum

VLFn(Fr)

Normalized Power of the VLF Fourier

Spectrum

Index of Centralization

IAS

Index of the Subcortical Nervous Center’s

Activation

HFmax

the maximal power of the HF spectral

component

Respiration Frequency

LFmax

the maximal power of the LF spectral

component

f(LFmax)

the frequency that corresponds to the

LFmax

VLFmax

the maximal power of the VLF spectral

component

f(VLFmax)

the frequency that corresponds to the

VLFmax

In table 4 the SD1 and SD2 values are evaluated

for the Poincare plot – graph of the NN time-series,

when each interval is plotted against the following

interval. The Entropy indexes are indicators of the

time series complexity and regularity (Yentes et al.,

2013).

Table 4: HRV non-linear features.

Feature

Description

Shannon entropy

EnInterp

Shannon entropy of the interpolated time-

series

ApEn

Approximate Entropy

SamEn

Sample Entropy

SD1

Standard Deviation perpendicular the line-

of-identity

SD2

Standard Deviation along the line-of-identity

SD1/SD2

Ratio of Poincare Plot’s Standard Deviations

In table 5, in addition to the common HRV

spectral features, the Standard Deviations and

Shannon entropies of the time series, obtained by the

wavelet transform are presented.

Development of the Decision Support System in Treatment of Arterial Hypertension - Application of Artiﬁcial Neural Networks for

Evaluation of Heart Rate Variability Signals

327

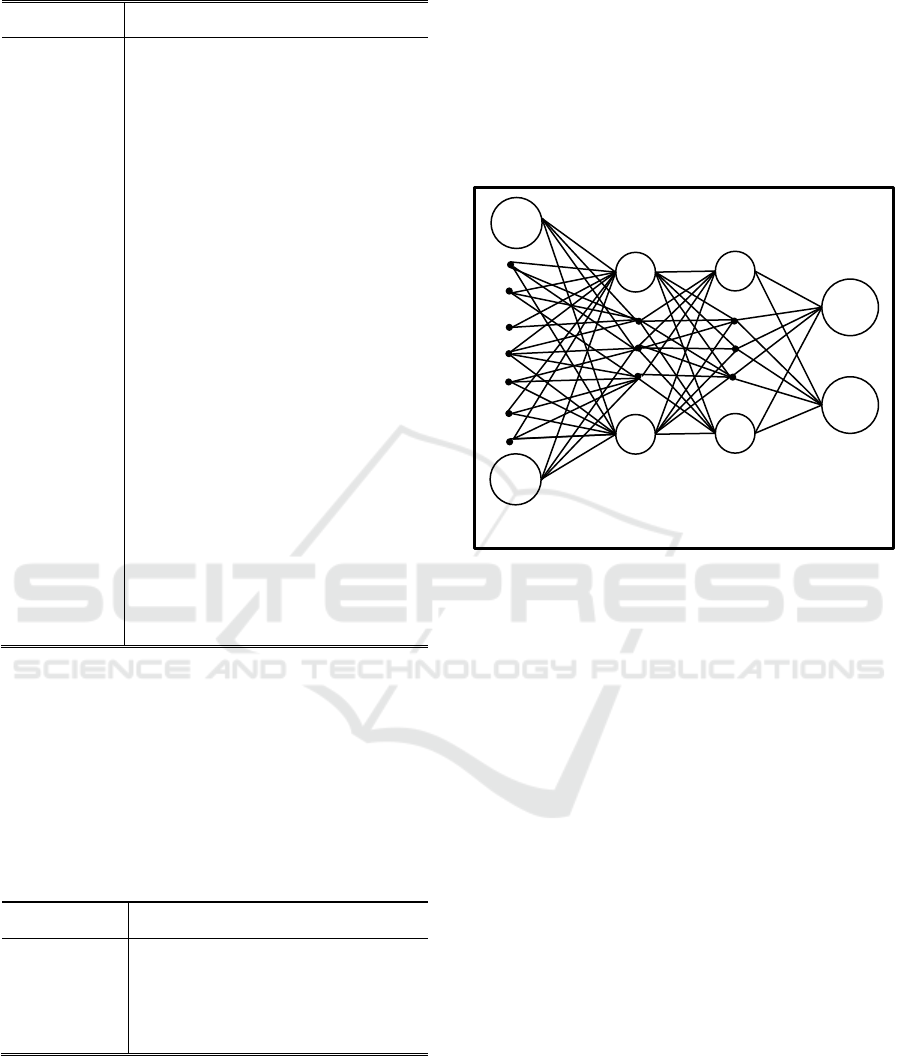
Table 5: HRV wavelet spectral features.

Feature

Description

HF(wt)

High Frequency Wavelet Spectral Power

LF(wt)

Low Frequency Wavelet Spectral Power

VLF(wt)

Very Low Frequency Wavelet Spectral

Power

TP(wt)

Total Power of the Wavelet Spectrum

HFn(wt)

Normalized Power of the HF Wavelet

Spectrum

LFn(wt)

Normalized Power of the LF Wavelet

Spectrum

VLFn(wt)

Normalized Power of the VLF Wavelet

Spectrum

LF/HF(wt)

Autonomic Balance Exponent Power of

the Wavelet Spectrum

mHF(wt)

Mean High Frequency Wavelet Spectral

Power

mLF(wt)

Mean Low Frequency Wavelet Spectral

Power

mVLF(wt)

Mean Very Low Frequency Wavelet

Spectral Power

SDHF(wt)

Standard deviation of the HF(t) Wavelet

time series

SDLF(wt)

Standard deviation of the LF(t) Wavelet

time series

SDVLF(wt)

Standard deviation of the VLF(t) Wavelet

time series

EnHF(wt)

Shannon entropy of the HF(t) Wavelet

time series

EnLF(wt)

Shannon entropy of the LF(t) Wavelet

time series

EnVLF(wt)

Shannon entropy of the VLF(t) Wavelet

time series

Table 6 presents features of the (LF/HF)[t]

informational characteristics. (LF/HF)[t] is the

continuous function of the LF/HF ratio, obtained by

means of the wavelet analysis. Local dysfunctions of

this function represent relevant information of the

functional changes during the loads. The

effectiveness of such features was shown previously

in (Egorova et al., 2014).

Table 6: HRV wavelet dysfunctions features.

Feature

Description

(LF/HF)max

Maximal value of dysfunctions

(LF/HF)int

Intensity of dysfunctions

Number of dysfunctions

pNd

the number of dysfunctions divided by

the length of the (LF/HF)[t].

All 64 features for all 68 subjects have formed

single matrix of features X (matrix size 68x64). In

addition, the class matrix was created (matrix size

68x2): for relatively healthy volunteers the line in

matrix is (1,0); for patients suffering from arterial

hypertension is (0,1).

2.3 Artificial Neural Networks

The ANN learn a set of parameters that are adjusted

to the input data, while comparing the their prediction

with the output in the training phase. In current work,

several Multilayer Perceptrons (MLP) with different

number of hidden layers and neurons were

considered. The general view of the used neural

networks structure is presented on figure 1.

Figure 1: Neural networks schematic.

Neural networks were used as the classifier: based

on the input matrix X the network is expected to

define affiliation to either group of healthy volunteers

or patients suffering from arterial hypertension. Input

layer consists of 64 nodes – neurons. Each node

represents one of the considered heart rate variability

features. Prior to feeding the features to the network,

the feature vector was normalized to have a zero mean

value and uniform standard deviation (Sola and

Sevilla, 1997).

Output layer consisted of 2 neurons; one neuron is

responsible for defining affiliation to group of healthy

volunteers, second is responsible for defining

affiliation to the group of patients. Therefore, the

network is expected to give an answer (1,0) if the

subject belongs to the group of healthy volunteers,

and to give an answer (0,1) if the subject belongs to

the group of patients suffering from the arterial

hypertension. The number of neurons in the hidden

layers varied. Two types of neural networks were

analyzed: with one hidden layer, and with two hidden

layers. In addition number of neurons in each layer

varied from 1 to 64.

In order to define weights and biases the back

propagation method was used. The learning method

was set to be 0.1. As the stopping criteria the maximal

error level was used, which should not suppress 0.01.

Input Layer

Output Layer

Hidden Layers

NENT 2018 - Special Session on Neuro-electrostimulation in Neurorehabilitation Tasks

328

Maximal number of iterations was set to be 10000.

However, all networks configuration converged

prior. As the activation function the logistic function

was used. One of the features of this function is

relative easiness of prime evaluation (Demuth et al.,

2014; Hornik et al., 1989; Schmidhuber, 2015) .

In order to evaluate efficacy of the network

configuration, the leave-one-out cross-validation

(LOOCV) technique was used. LOOCV is the so-

called exhaustive cross-validation type which uses

one of the observations in the dataset as the test set,

while remaining data is used as the training set. This

procedure is repeated for all the observations in the

dataset (Refaeilzadeh et al., 2009). The total accuracy

(ACC) is evaluated as the number of correctly

predicted test set during whole LOOCV application.

Using the LOOCV approach allows one to prevent

overfitting on the training set while evaluating

classification efficacy on the external data.

3 RESULTS

In our previous works (Kublanov et al., 2017) we

have analyzed the following machine learning

classifiers – linear and quadratic discriminant

analysis (LDA and QDA); k-nearest neighbors (k-

NN), for k = 3,4,5; Decision Tree (DT) and Naïve

Bayes (NB). The table presents results of the

classification using all features for different

classifiers.

Table 7: Classifiers accuracy, %.

LDA

QDA

3-NN

4-NN

5-NN

66.2

58.8

75.0

72.1

75.0

73.5

66.2

Data in table show that application of all features

gives unsatisfactory results for all tested classifiers.

Therefore it is appropriate to search for way to

improve classification accuracy.

Firstly, the ANN classification accuracy was

evaluated for single hidden neuron configuration.

Results of the single layer configurations evaluation

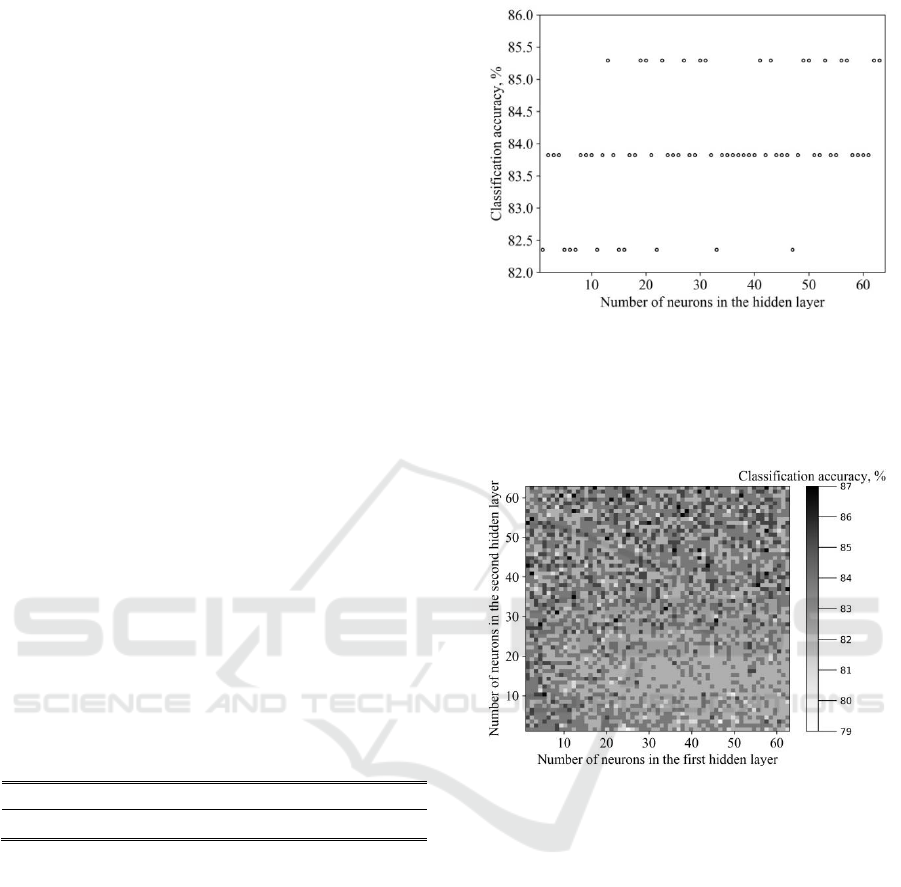
accuracy are summarized on figure 2.

The minimal accuracy among all 64

configurations was 82.4; maximal – 85.3; average –

83.96. The maximal accuracy was achieved by 16

different configurations and includes (13, 19, 20, 23,

27, 30, 31, 41, 43, 49, 50, 53, 56, 57, 62, 63) neurons

in hidden layer. Overall the single hidden layer

configuration has consistent results.

Figure 2: Single hidden layer classification accuracy.

Then, the possibilities of the two hidden layers

configuration was evaluated. Results of the two layer

configurations evaluation accuracy are summarized

on figure 3.

Figure 3: Two hidden layer classification accuracy.

The minimal accuracy among all 4096

configurations was 79.4; maximal – 86.8; average –

83.26. The maximal accuracy was achieved by 38

different configurations.

It is worthy to point out that, all configurations,

studied in this work have shown result higher than

simple classifiers while using all features. Obtained

in this work accuracy is comparable with those

presented in (Pytel et al., 2015). However, in men-

tioned work, the anthropometric features were used.

This reduce application for the dynamic reaction

evaluation to the neuro-electrostimulation.

It is worthy to point out that the highest accura-cy,

when using only features in state F, was 72.1 %. This

furthermore highlights the importance of the tilt-test

in the arterial hypertension diagnosing.

However the overall accuracy can be still

improved. One of the possible solutions is prior

application of the efficient features selection.

Development of the Decision Support System in Treatment of Arterial Hypertension - Application of Artiﬁcial Neural Networks for

Evaluation of Heart Rate Variability Signals

329

4 DISCUSSIONS AND

CONCLUSIONS

The present works shows results of the artificial

neural networks application in task of the arterial

hypertension diagnostics. The distinctive feature of

the present work is application of the heart rate

variability signals data recorded during tilt-test study.

The vector of 64 time-domain, frequency-domain and

non-linear features was used. The results, obtained in

this work will become foundation of the decision

support system in treatment of arterial hypertension.

Results of this study showed, that application of

Artificial Neural Networks reaches higher

classification accuracy results than such machine

learning classifiers as discriminant analysis, Naïve

Bayes, Decision Tree, Nearest Neighbors. Relatively

high values of accuracy were obtained – 86.8. We

want to point out that this work was the first step in

the neural networks application study. In the

following we are interested in continuing more

complex networks that could perform prior features

selection for accuracy improvement. One of the

possible ways of the future development is usage of

different networks architectures, like auto-encoding,

for dimension reduction (Hinton and Salakhutdinov,

2006).

The next step in the development of the decision

support system in treatment of arterial hypertension is

evaluation of the treatment efficiency. We are

planning to evaluate efficiency of the standard

pharmacological therapy and neuro-

electrostimulation by the ‘SYMPATHOCOR-01’

device. Such study will allow to estimate possibility

of the proposed system application for evaluation of

the treatment efficiency and prognosis of the

treatment process.

ACKNOWLEDGEMENTS

The work was supported by Act 211 Government of

the Russian Federation, contract № 02.A03.21.0006.

REFERENCES

Baevskiy, R.M., 2001. Аnaliz variabelnosti serdechnogo

ritma pri ispolzovanii razlichnykh

ehlektrokardiograficheskikh sistem (metodicheskie

rekomendatsii) [Analysis of heart rate variability using

different electrocardiographic systems (guidelines)].

Vestn. Aritmologii Her. Arhythmology 65–87.

Belova, N.Y., Mihaylov, S.V., Piryova, B.G., 2007.

Wavelet transform: A better approach for the evaluation

of instantaneous changes in heart rate variability.

Auton. Neurosci. 131, 107–122.

Chattipakorn, N., Incharoen, T., Kanlop, N., Chattipakorn,

S., 2007. Heart rate variability in myocardial infarction

and heart failure. Int. J. Cardiol. 120, 289–296.

De Boor, C.A., 1978. Practical Guide to Splines. Springer-

Verlag.

Demuth, H.B., Beale, M.H., De Jess, O., Hagan, M.T.,

2014. Neural network design. Martin Hagan.

Egorova, D.D., Kazakov, Y.E., Kublanov, V.S., 2014.

Principal Components Method for Heart Rate

Variability Analysis. Biomed. Eng. 48, 37–41.

Feng, X.L., Pang, M., Beard, J., 2014. Health system

strengthening and hypertension awareness, treatment

and control: Data from the China health and retirement

longitudinal study. Bull. World Health Organ. 92, 29–

41.

Hinton, G.E., Salakhutdinov, R.R., 2006. Reducing the

dimensionality of data with neural networks. science

313, 504–507.

Hornik, K., Stinchcombe, M., White, H., 1989. Multilayer

feedforward networks are universal approximators.

Neural Netw. 2, 359–366.

Kleiger, R.E., Stein, P.K., Bigger, J.T., 2005. Heart rate

variability: measurement and clinical utility. Ann.

Noninvasive Electrocardiol. 10, 88–101.

Kseneva, S.I., Borodulina, E.V., Trifonova, O.Y., Udut,

V.V., 2016. Cardiac Autonomic Drive during Arterial

Hypertension and Metabolic Disturbances. Bull. Exp.

Biol. Med. 161, 237–240.

Kublanov, V.S., Dolganov, A.Y., Belo, D., Gamboa, H.,

2017. Comparison of Machine Learning Methods for

the Arterial Hypertension Diagnostics. Appl. Bionics

Biomech. 2017.

Kublanov, V.S., Shmirev, V.I., Shershever, A.S., Kazakov,

J.E., 2010. About Innovative Possibilities of Device

“SIMPATOCOR-01” in Management of Functional

Disorders of Vegetative and Central Nervous System in

Neurology, Kremljovskaya Medicine. Clin. Vestn. 4,

60–64.

Lee, C.K., Yoo, S.K., Park, Y., Kim, N., Jeong, K., Lee, B.,

2005. Using Neural Network to Recognize Human

Emotions from Heart Rate Variability and Skin

Resistance. In: 2005 IEEE Engineering in Medicine and

Biology 27th Annual Conference. Presented at the 2005

IEEE Engineering in Medicine and Biology 27th

Annual Conference, pp. 5523–5525.

Malik, M., 1996. Heart rate variability: Standards of

measurement, physiological interpretation, and clinical

use. Circulation 93, 1043–1065.

Mallat, S., 2009. A Wavelet Tour of Signal Processing, A

Wavelet Tour of Signal Processing.

Mancia, G., Fagard, R., Narkiewicz, K., Redon, J.,

Zanchetti, A., Böhm, M., Christiaens, T., Cifkova, R.,

Backer, G.D., Dominiczak, A., Galderisi, M., Grobbee,

D.E., Jaarsma, T., Kirchhof, P., Kjeldsen, S.E., Laurent,

S., Manolis, A.J., Nilsson, P.M., Ruilope, L.M.,

Schmieder, R.E., Sirnes, P.A., Sleight, P., Viigimaa,

NENT 2018 - Special Session on Neuro-electrostimulation in Neurorehabilitation Tasks

330

M., Waeber, B., Zannad, F., 2013. 2013 ESH/ESC

Guidelines for the management of arterial hypertension.

Eur. Heart J. 34, 2159–2219.

Mendis, S., Johnston, S.C., Fan, W., Oladapo, O., Cameron,

A., Faramawi, M.F., 2010. Cardiovascular risk

management and its impact on hypertension control in

primary care in low-resource settings: A cluster-

randomized trial. Bull. World Health Organ. 88, 412–

419.

Patel, M., Lal, S.K.L., Kavanagh, D., Rossiter, P., 2011.

Applying neural network analysis on heart rate

variability data to assess driver fatigue. Expert Syst.

Appl. 38, 7235–7242.

Pytel, K., Nawarycz, T., Ostrowska-Nawarycz, L., Drygas,

W., 2015. Anthropometric predictors and Artificial

Neural Networks in the diagnosis of hypertension. In:

2015 Federated Conference on Computer Science and

Information Systems (FedCSIS). Presented at the 2015

Federated Conference on Computer Science and

Information Systems (FedCSIS), pp. 287–290.

Rajendra Acharya, U., Subbanna Bhat, P., Iyengar, S.S.,

Rao, A., Dua, S., 2003. Classification of heart rate data

using artificial neural network and fuzzy equivalence

relation. Pattern Recognit. 36, 61–68.

Refaeilzadeh, P., Tang, L., Liu, H., 2009. Cross-validation.

In: Encyclopedia of Database Systems. Springer, pp.

532–538.

Schmidhuber, J., 2015. Deep learning in neural networks:

An overview. Neural Netw. 61, 85–117.

Sivanantham, A., Shenbaga Devi, S., 2014. Cardiac

arrhythmia detection using linear and non-linear

features of HRV signal. In: 2014 International

Conference on Advanced Communication Control and

Computing Technologies (ICACCCT). pp. 795–799.

Sola, J., Sevilla, J., 1997. Importance of input data

normalization for the application of neural networks to

complex industrial problems. IEEE Trans. Nucl. Sci.

44, 1464–1468.

Tarvainen, M.P., Niskanen, J.-P., Lipponen, J.A., Ranta-

Aho, P.O., Karjalainen, P.A., 2014. Kubios HRV–heart

rate variability analysis software. Comput. Methods

Programs Biomed. 113, 210–220.

Tkacz, E.J., Kostka, P., 2000. An application of wavelet

neural network for classification of patients with

coronary artery disease based on HRV analysis. In:

Proceedings of the 22nd Annual International

Conference of the IEEE Engineering in Medicine and

Biology Society (Cat. No.00CH37143). Presented at

the Proceedings of the 22nd Annual International

Conference of the IEEE Engineering in Medicine and

Biology Society (Cat. No.00CH37143), pp. 1391–1393

vol.2.

Ushakov, I.B., Orlov, O.I., Baevskii, R.M., Bersenev, E.Y.,

Chernikova, A.G., 2013. Conception of health: Space-

Earth. Hum. Physiol. 39, 115–118.

Yentes, J.M., Hunt, N., Schmid, K.K., Kaipust, J.P.,

McGrath, D., Stergiou, N., 2013. The Appropriate Use

of Approximate Entropy and Sample Entropy with

Short Data Sets. Ann. Biomed. Eng. 41, 349–365.

Zadeh, A.E., Khazaee, A., Ranaee, V., 2010. Classification

of the electrocardiogram signals using supervised

classifiers and efficient features. Comput. Methods

Programs Biomed. 99, 179–194.

Development of the Decision Support System in Treatment of Arterial Hypertension - Application of Artiﬁcial Neural Networks for

Evaluation of Heart Rate Variability Signals

331