
Localization of Neuron Nucleuses in Microscopy Images with
Convolutional Neural Networks
Arkadiusz Tomczyk
1
, Bartłomiej Stasiak
1
, Paweł Tarasiuk
1
,
Anna Gorzkiewicz
2
, Anna Walczewska
2
and Piotr S. Szczepaniak
1
1
Institute of Information Technology, Lodz University of Technology,
Wolczanska 215, 90-924 Lodz, Poland
2
Department of Cell-to-Cell Communication, Medical University of Lodz,
Keywords:
Convolutional Neural Networks, Machine Learning, Fluorescent Microscope, Nucleus Localization.
Abstract:
In this paper, an automatic method of neuron nucleuses localization in the images, taken with the fluorescent
microscope, is presented. The proposed approach has two phases. During the first phase, a properly trained
convolutional neural network acts as a non-linear filter which indicates regions of interest. The network
architecture and specific method of its training are original concepts of the authors of this work. In the second
phase, analysis of these regions allows to identify points representing positions of the nucleuses. To illustrate
the method, images of neurons isolated from neonatal rat cerebral cortex were used. These images were
inspected by a domain expert and all the visible nucleuses were manually annotated. This allowed not only to
objectively assess the obtained detection results but it enabled the application of machine learning as well.
1 INTRODUCTION
Automatic analysis of images becomes a crucial task
in a world where there are more and more image
sources. To design proper algorithms, machine learn-
ing techniques can be used, where both models and
parameters of these models can be selected automat-
ically during the training phase. Application of ma-
chine learning requires, however, access to the do-
main knowledge, which usually is expressed in form
of a train set which contains inputs and correspond-
ing expected outputs. The gathering of this knowl-
edge constitutes a separate, difficult task, which is
even harder in the case of specialized images where
the number of qualified domain experts is usually rel-
atively small.
In this paper, neuron images, acquired with fluo-
rescent microscope, are analyzed to localize all neu-
ron nucleuses. For this purpose a two-stage approach
is proposed, which in its first phase uses a convo-
lutional neural network (CNN) (LeCun and Bengio,
1995) to find regions of interest. Since it is not a typ-
ical application of such networks, the proposed archi-
tecture can be considered as a main contribution of
this paper. It should be emphasized that the conducted
research was possible only thanks to the manually in-
dicated nucleuses provided by a domain expert.
The paper is organized as follows: section 2 de-
scribes the similar works briefly, in section 3 the
used data are characterized, in sections 4 and 5 the
proposed approach and the obtained results are dis-
cussed, respectively and finally, the last section con-
tains a short summary of the conducted research.
2 RELATED WORK
Application of convolutional neural networks to ana-
lyze microscopy images is a relatively new idea. In
the literature some existing approaches can be found,
which differ in: analyzed image type, the goal of
image analysis, CNN application method, etc. All
of them have, however, one common problem which
needs to be overcome – availability of training data.
Localization and segmentation tasks are not areas
of typical CNN applications. CNN is usually used as
a part of a classifier which may assign labels to the
whole image or to some of its regions when a mov-
ing window procedure is applied. For segmentation
and localization tasks, this classic architecture is usu-
188
Tomczyk, A., Stasiak, B., Tarasiuk, P., Gorzkiewicz, A., Walczewska, A. and Szczepaniak, P.
Localization of Neuron Nucleuses in Microscopy Images with Convolutional Neural Networks.
DOI: 10.5220/0006753601880196
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 2: BIOIMAGING, pages 188-196
ISBN: 978-989-758-278-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ally modified, because at the output there should be
an image of the same size as at the input. To achieve
that goal, some up-scaling layers are added after some
number of classic convolutional and pooling layers.
Such approach was used in the works presented be-
low:
• In (Sadanandan et al., 2017) the problem of cul-
tured cell segmentation was considered. To over-
come a problem with limited number of training
samples, a method of automated train set gener-
ation was proposed. After normal image acqui-
sition, cells were stained with fluorescent markers
allowing to identify nucleuses and cytoplasmic re-
gions. Then, images were used again, but this
time simple segmentation techniques allowed to
detect their positions and prepare the correspond-
ing expected output masks for CNN training.
• In (Ho et al., 2017) 3D fluorescent microscopy
images of rat kidney cells were segmented and
the data was processed by a properly trained 3D
CNN. In the case of 3D images, however, the dif-
ficulty of manual image annotation is even big-
ger than in 2D case, so to obtain sufficiently nu-
merous train set, data augmentation procedures
were used. These included modifications of im-
age brightness and contrast as well as elastic de-
formations warping images locally.
• In (Quan et al., 2016), as a part of an approach
similar to works mentioned above, the training
data generation procedures were used (rotations,
reflections, random noise) to increase the size of
the train set. This time, however, 2D electron mi-
croscopy images were analyzed and the goal was
cell membrane segmentation.
• In (Xie et al., 2016), the problem of cell counting
was presented. In this work, CNN was trained to
regress a cell spatial density distribution. To avoid
problems with training data, both inputs and out-
puts were synthesized automatically. An interest-
ing element of the method presented there is that
two parallel regression networks were trained si-
multaneously and their results were combined to
get the final response.
The solution presented in this work differs mainly in
the type of the analyzed images and in the specific
method of CNN application. Here, while the image
processing is performed, the image size is not re-
duced. Consequently, all the feature maps have the
same size and no up-scaling is required.
3 DATA
The images analyzed in this work contain neurons
that were isolated from neonatal rat cerebral cor-
tex. The cells were divided into four groups. The
first is the control group where the cells were incu-
bated in standard neuronal medium for 3 days. In
three other groups, the standard neuronal medium was
changed for the third day: the second group was incu-
bated with medium collected from astrocytes culture,
whereas the groups three and four were incubated
with medium collected from the culture of astrocytes,
that were earlier modified with two different polyun-
saturated omega-3 fatty acids, DHA and EPA, respec-
tively. After the time of incubation, the neurons were
fixed and immunostained with primary monoclonal
anti-β-Tubulin antibody and secondary antibody con-
jugated with fluorescent molecules. The fixed slides
were analyzed and the pictures were taken using a flu-
orescent microscope.
The further aim of this research is to measure how
the factors released to medium by the modified as-
trocytes influence neuronal wiring. The formation of
neuronal projections and connections during develop-
ment is crucial for the proper functioning of the ner-
vous system. The recognition of neuronal nucleuses
will help to determine localizations of the cell bodies
on the picture, in order to further define the number,
lengths and widths of the neuronal projections in pro-
portion to the number of cells.
The set of available data contained 16 images
which size is 1024 × 1024 pixels. An example im-
age is shown in Fig. 1. In every image, the position of
every neuron nucleus was manually indicated by a do-
main expert (Fig. 2), constituting a set of expected
localization points O
e
= {o
e
i
: i = 1,..., N
e
} where
o
e
i
∈ {0,...,1023} × {0,. .. ,1023}. This set was fur-
ther split into train, validation and test set which con-
tained 8, 4 and 4 images, respectively. The initial
analysis of the reference points revealed that the min-
imum pixel distance d between these points is equal
to 8. This value will be used later in the presented
experiments.
4 METHOD
The method of neuron nucleuses localization is com-
posed of two, separately trained, phases. In the first
phase, the specially designed fully convolutional neu-
ral network tries to approximately indicate image re-
gions that are similar to nucleuses. It is a kind of
a non-linear filter which should have a high response
in the potentially interesting regions and low response
Localization of Neuron Nucleuses in Microscopy Images with Convolutional Neural Networks
189

Figure 1: Representative fluorescence image of neurons stained with antibodies against beta-tubulin, class III conjugated with
Alexa Fluor 488 acquired using a Zeiss microscope. The squares indicates the image regions, which, for better visibility, will
be used further to illustrate the presented concepts (the original image size – 1024 × 1024 pixels, the region size – 300 × 300
pixels).
(a) (b)
Figure 2: Sample regions with manually indicated nucleuses. For better visibility the points given by an expert are surrounded
with circles (circle radius – 20 pixels).
in the other places. In the second phase, the result of
the filtration is analyzed to give a set of points that are
suspected to be located within neuron nucleus area
(one point per nucleus). Obviously, the found points
do not need to precisely correspond with the reference
points given by a domain expert. That is why a ded-
icated evaluation procedure is required to objectively
measure the quality of the results. It can be used both
to summarize the final results and to find the optimal
parameters while training. All those elements are de-
scribed in the further sections in details.
4.1 Convolutional Neural Network
Architecture and Training
Convolutional neural networks are biologically in-
spired neural networks that succeeded in many tasks
connected with image analysis (Cires¸an et al., 2011;
Krizhevsky et al., 2012). In typical applications,
where they are used as image classifiers, they have
a common general architecture in which after some
number of convolutional layers, the resulting feature
maps are processed by fully connected layers to give
a final response (which is a form of predicted label en-
coding). The feature maps produced by the successive
layers usually have decreasing sizes, which is caused
both by the convolution itself (no additional padding
is used) and by the pooling (e.g. max-pooling) layers.
In this work, the approach described above is not
acceptable, since the CNN is supposed to work like
a non-linear filter which, given an image, is able to
produce the image of the same size after the filtra-
tion. That is why the architecture, firstly proposed in
(Stasiak et al., 2017), will be used here instead. In
this architecture fully connected layers are removed,
in every convolutional layer the appropriate padding
is added and no pooling layers are involved at all. The
non-linearity of such a network is guaranteed by the
non-linear activation functions (Fig. 3).
To train such a network, the output should be
KALSIMIS 2018 - Special Session on Knowledge Acquisition and Learning in Semantic Interpretation of Medical Image Structures
190

given in a form of the expected, filtered image. In
our case it must be prepared with usage of the refer-
ence points O
e
given by an expert. The simplest solu-
tion could be generation of the whole black outputs,
with only given points set to be white. After initial
experiments it appeared, however, that this approach
is not acceptable, as the network in the training pro-
cess favors those combinations of weights that lead to
the whole black output (the number of white pixels is
very small in comparison with the size of the image
and such a solution will constitute an attractive local
minimum of a training loss function). The other solu-
tion could be to draw filled, white circles around the
expected points with the radius big enough to avoid
the problem mentioned above. This would, however,
lead to another difficulty. Sufficiently big radius may
cause that after the filtration, pairs of nucleuses that
are very close to each other will be indistinguishable.
That is why, further in this work, a different approach
was proposed. The Gaussian function was used to de-
scribe the expected response around reference points.
Such a response was generated in some area around
every reference point and if some points were close to
each other, the maximum response was selected (Fig.
4). The Gaussian function parameters were selected
according to the visual field of the CNN (at the border
of that field, Gaussian function value should decrease
to 0.5). Such an expected output allows to train CNN
using a classic Euclidean loss function L (regression
problem).
The interesting property of the used architecture
is the fact that it can be trained using smaller im-
ages (that refers to cutting, but not scaling) and after
training it can be applied for full-size inputs (Stasiak
et al., 2017). This property was also used in this work,
where training images had size of 51 × 51 pixels (Fig.
4). Of course, to train the network properly. the set
of these images had to be representative. That is why
two groups of such images were generated. In the
first group, there were images taken from the neigh-
borhood of the reference points (positive samples). In
the second group, 200 randomly located images were
cut (negative samples) in such a way to not overlap
with positive samples. Since the number of nucle-
uses is smaller than 200, this procedure gave unbal-
anced positive and negative sets. To avoid problems
with training, the number of positive samples was in-
creased by taking into account all the rotations of the
positive images and by oversampling (the same im-
age was repeated multiple times in the generated set).
Positive and negative samples were generated from
every full-size image and the corresponding expected
output images in the train and validation sets were
used to produce train (2312 positive and 1600 neg-
ative) and validation (1140 positive and 800 negative)
sets of smaller images for network training.
In the further experiments, two architecture types
were considered as presented in Fig. 3. The second
model M
+
(K) differs from the first one M
−
(K) only
with additional dropout layer (Srivastava et al., 2014)
which was added before the final convolutional layer
(K defines the number of kernels). Since the dropout
probability is set to 50%, the number of filters in the
last but one layer was doubled in M
+
(K). The propor-
tion between the number of filters in successive layers
and the size of the filters were selected based on the
existing hints from the literature. In the initial layers
filters are smaller, but their number is bigger. Both ar-
chitectures have a visual field of size 23 × 23 pixels,
which should be enough to cover single nucleus in the
analyzed images.
4.2 Neuron Nucleuses Localization
The positions of the nucleuses cannot be extracted di-
rectly from the network output since, which is a con-
sequence of the expected output type used for CNN
training, the pixel values in filtered images change
smoothly in the areas were nucleuses can be ex-
pected. To find them, a dedicated procedure was pro-
posed where connected regions of pixels with inten-
sity above the threshold t are searched for using re-
gion growing algorithm. The regions of area greater
than a are rejected as overly general. The centers of
gravity (expressed in image coordinates) of the re-
gions found in this way constitute a preliminary set of
the result points. The proper values of threshold t and
area a can be selected automatically using full-sized
training images.
To find a final set of points O
r
= {o
r
j
: j =
1,. .. ,N
r
} where o
r
j
∈ {0,.. ., 1023} × {0,. .. ,1023},
additional post-processing needs to be performed, as
the filtration output is not perfect. First, all the du-
plicates are removed. Next, if the distance between
points is smaller than an expected minimum distance
between nucleuses d, those points are merged to-
gether (their coordinates are averaged). To avoid
a chain effect, this procedure is performed starting
from points with the biggest number of such overly
close neighbors. Merging is performed as long as
there are points that could be merged.
4.3 Result Evaluation Procedure
To evaluate the results of nucleuses localization, two
sets of points O
e
and O
r
must be compared. As
it was already mentioned, since the nucleuses have
some non-zero size, it cannot be expected that coor-
Localization of Neuron Nucleuses in Microscopy Images with Convolutional Neural Networks
191
Input
data
Conv1:
2K kernels,
3 3 filters,×
1 1 padding,×
PReLU
Conv2:
2K kernels,
5 5 filters,×
2 2 padding,×
PReLU
Conv3:
K kernels,
5 5 filters,×
2 2 padding,×
PReLU
Conv4:
K kernels,
5 5 filters,×
2 2 padding,×
PReLU
Conv5:
K kernels,
7 7 filters,×
3 3 padding,×
PReLU
Conv6:
1 kernel,
7 7 filters,×
3 3 padding,×
Sigmoid
Output
data
(a)
Input
data
Conv1:
2K kernels,
3 3 filters,×
1 1 padding,×
PReLU
Conv2:
2K kernels,
5 5 filters,×
2 2 padding,×
PReLU
Conv3:
K kernels,
5 5 filters,×
2 2 padding,×
PReLU
Conv4:
K kernels,
5 5 filters,×
2 2 padding,×
PReLU
Conv5:
2K kernels,
7 7 filters,×
3 3 padding,×
PReLU
Conv6:
1 kernel,
7 7 filters,×
3 3 padding,×
Sigmoid
Dropout
with
p=50%
Output
data
Input
data
(b)
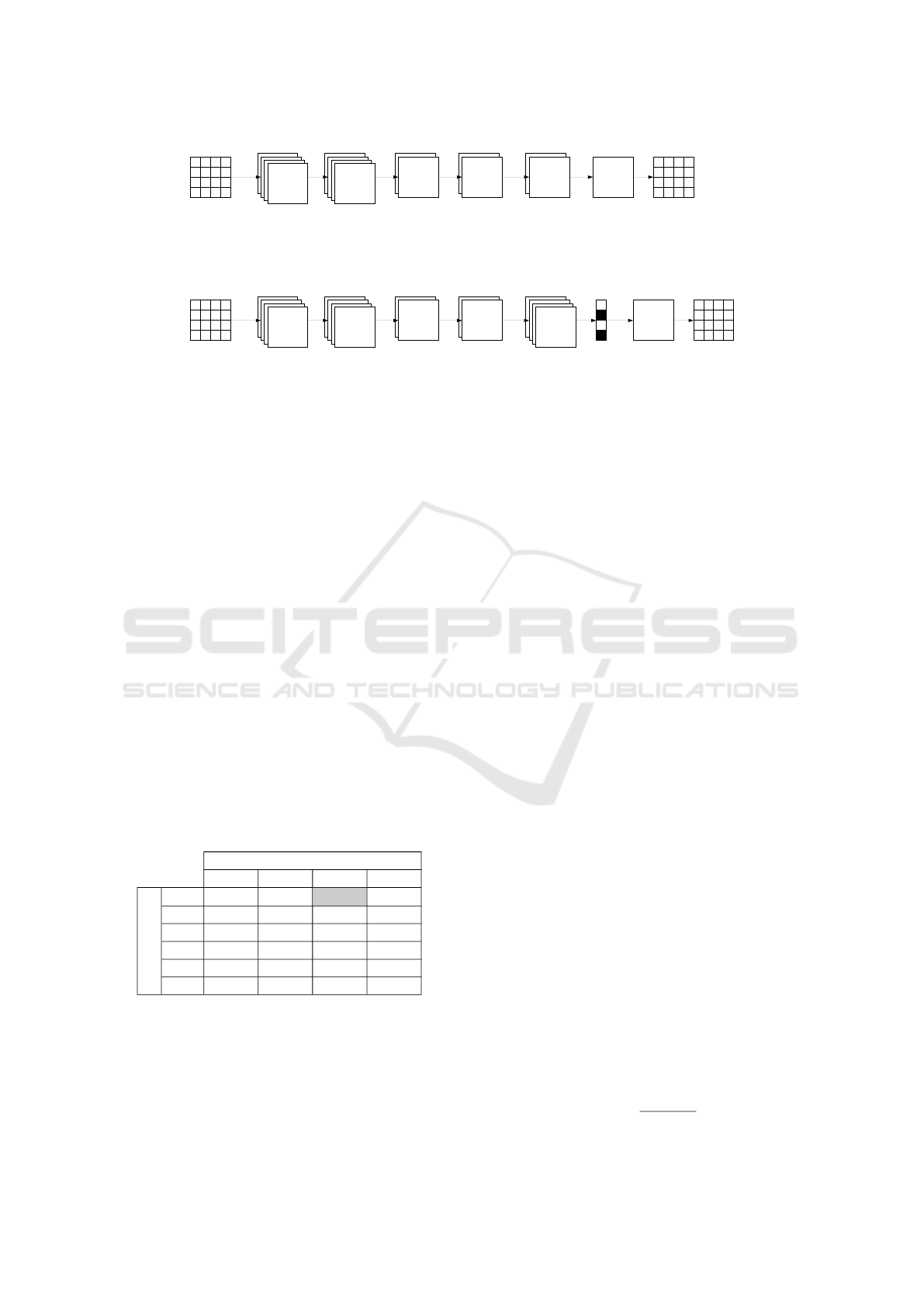
Figure 3: Architecture of the considered convolutional networks (K is equal to either 10 or 20): (a) - network without droput
layer M
−
(K), (b) - network with dropout layer M
+
(K). All except the last convolutional layers use PReLU (parametrized
rectified linear unit) and in the last layer sigmoid function is used to obtain values from [0,1] interval. The last convolutional
layer has only one kernel to generate one output image.
dinates of the expected and the found points will be
the exactly the same. Consequently, some reasonable
distance tolerance D should be assumed. If the dis-
tance between the expected point and the found point
is smaller than this value, the corresponding nucleus
can be considered to be found. Further the following
notation will be used:
• S
e
i
= { j = 1,. .. ,N
r
: ρ(o
e
i
,o
r
j
) < D} – a set of in-
dexes of those result points that lie closer than D
to the expected point o
e
i
• S
r
j
= {i = 1, .. ., N
e
: ρ(o
r
j
,o
e
i
) < D} – a set of in-
dexes of those expected points that lie closer than
D to the result point o
r
j
where ρ denotes the Euclidean metric.
Table 1: Selection of the best combination of parameters
t and a for optimal network M
+
(20). Every cell contains
averaged F
1
value calculated for 8 images in a train set. The
highlighted cell indicates the optimal combination.
a
100 150 200 250
t
200 0.492 0.570 0.593 0.592
210 0.509 0.564 0.572 0.572
220 0.522 0.556 0.555 0.555
230 0.473 0.485 0.485 0.485
240 0.382 0.381 0.381 0.381
250 0.170 0.170 0.170 0.170
To compare the expected and the found points,
two error types need to be considered. The first one
checks false positives, i.e. the number of found points
that do not correspond with any nucleus:
FP =
N
r
∑
j=1
I(S
r
j
=
/
0). (1)
The second one checks false negatives, i.e. the num-
ber of nucleuses that do not have corresponding de-
tected point:
FN =
N
e
∑
i=1
I(S
e
i
=
/
0). (2)
In the notation presented in this paper, I is an indicator
function which value is equal 1 if the given condition
is true and 0 otherwise.
The above measures do not allow to fully evaluate
the quality of the results, because those values need to
be compared with the number of correctly identified
nucleuses. Their number can be found, however, in
two different ways as:
• a number of nucleuses that have at least one cor-
responding result point
T P
e
=
N
e
∑
i=1
I(S
e
i
6=
/
0), (3)
• a number of result points that have at least one
corresponding nucleus
T P
r
=
N
r
∑
j=1
I(S
r
j
6=
/
0). (4)
Those numbers may differ if |S
e
i
| > 1 or |S
r
j
| > 1
(Fig. 5). Fortunately, this situation will not occur if
D = d/2. Then T P = T P
e
= T P
r
and the localization
results can be evaluated using typical measures such
as:
• precision – the percentage of correctly localized
points
P =
T P
T P + FP
, (5)
KALSIMIS 2018 - Special Session on Knowledge Acquisition and Learning in Semantic Interpretation of Medical Image Structures
192

(a) (b) (c) (d)
(e) (f)
(g) (h) (i) (j) (k) (l) (m) (n)
(o) (p) (q) (r) (s) (t) (u) (v)
Figure 4: Convolutional training data (regions size – 51 ×51 pixels): (a), (b) - positions of positive samples generated around
the reference points, (c), (d) - positions of positive samples selected randomly – they do not overlap with positive samples,
(e), (f) - expected output with Gaussian functions generated around the reference points, (g) - (n) - examples of network inputs
(4 positive samples and 4 negative samples), (o) - (v) - examples of the corresponding expected network outputs (4 positive
samples and 4 negative samples).
Table 2: Comparison of the trained solutions. Average F
1
value on a validation set should allow to select solution with the
greatest chance for generalization abilities. The highlighted row indicates the optimal solution.
solution
final L avarage F
1
train validation train validation test
M
−
(10), t = 220, a = 150 17.89 20.10 0.49 0.35 0.51
M
+
(10), t = 210, a = 200 18.75 20.02 0.51 0.39 0.51
M
−
(20), t = 220, a = 200 13.07 12.49 0.55 0.42 0.50
M
+
(20), t = 200, a = 200 12.91 12.79 0.59 0.44 0.45
• recall – the percentage of the correctly localized
nucleuses
R =
T P
T P + FN
. (6)
For a perfect solution, both these values should be
close to 1. To obtain a single value, they are usually
combined using harmonic mean:
F
1
=
2PR
P + R
. (7)
Such a single averaged value will be further used to
select a proper solution and to find proper values of
the parameters t and a.
5 RESULTS
The results presented in this work required CNN
training and usage of the trained CNN. It would not be
Localization of Neuron Nucleuses in Microscopy Images with Convolutional Neural Networks
193

Figure 5: For evaluation purposes, the reference points
(dark gray) needed to be compared with the found points
(light gray) – the distances between points are bigger than in
real cases for better visibility. The following situations are
possible: 3, 6 – detections unrelated to the expected points,
2 – missing detection, 5 – good detection, 1 – one point de-
tected twice, 4 – merged points. Detections are considered
with some distance tolerance.
possible to perform with an acceptable performance if
a proper hardware with GPU units were not available.
For the experiments described further, NVIDIA Tesla
P100 card and Caffe faramework (Jia et al., 2014)
were used.
Table 3: Results of application of optimal network M
+
(20)
for all available images. In the second and third column the
numbers of the expected nucleuses and numbers of local-
ized nucleuses are presented, respectively. The highlighted
row indicates a case which was used in figures presented in
this work.
image |O
e
| |O
r
| P R F
1
train set
1 20 20 0.50 0.50 0.50
2 10 12 0.75 0.90 0.82
3 51 45 0.58 0.51 0.54
4 29 23 0.43 0.34 0.38
5 28 26 0.58 0.54 0.56
6 26 27 0.67 0.69 0.68
7 33 35 0.74 0.79 0.76
8 92 116 0.45 0.57 0.50
validation set
9 41 34 0.44 0.37 0.40
10 11 13 0.62 0.73 0.67
11 15 16 0.19 0.20 0.19
12 28 24 0.54 0.46 0.50
test set
13 33 33 0.61 0.61 0.61
15 37 34 0.29 0.27 0.28
16 43 47 0.47 0.51 0.49
17 33 29 0.45 0.39 0.42
5.1 Experiments
In the presented experiments, two variants (K = 10
and K = 20) of both convolutional neural network ar-
chitectures (without and with the dropout layer) were
considered. Consequently, 4 neural networks were
trained using 3912 images of size 51 × 51. In the
beginning, the learning rate was equal to 0.00001
and was decreased every 100 iterations with factor
0.995. The momentum was equal to 0.95 and max-
imum number of iterations was set to 100000. For
these parameters, the training process took from 2 to
5 hours depending on the network architecture. In
Fig. 6, an example of changes of Eculidean loss can
be observed both on the train set and on the validation
set (1940 images of size 51× 51). The similar charac-
teristic of the training process was observed for all 4
networks. Since the validation error did not increase,
no evident overfitting problem was noticed and the fi-
nal network obtained from the training was used for
the further computations. In Fig. 8, sample filtration
results of the trained network are presented.
The next step was selection of the parameters t
and a required in the second phase of the proposed
approach. For that purpose, selected combinations of
these parameters were tested for all 4 networks. Every
combination was evaluated using the train set with 8
images of size 1024 ×1024. To sum up the evaluation
procedure with a single numerical value, the average
F
1
value was calculated. Results are presented in Tab.
1. It allowed to select optimal parameter combination
for every network which can be found in Tab. 2.
When the network is trained and above parameters
are found, the solutions are ready for nucleus localiza-
tion. There are, however, 4 solutions, and one must
be selected as the final one. In order to do that, solu-
tions were evaluated using average F
1
on the valida-
tion set with 4 images of size 1024 ×1024. Again, the
obtained values can be found in Tab. 2. This proce-
dure allowed to select as a final solution – the network
M
+
(20). Sample results generated by this solution are
depicted in Fig. 7. The summary of the results for all
16 available images is presented in Tab. 3.
5.2 Analysis
Analyzing results presented in Tab. 2, the first conclu-
sion is that networks with bigger number of kernels K
allowed to get a better averaged F
1
measure both for
the training and the validation set. This observation
is quite intuitive, since more complex network should
have bigger flexibility, allowing it to learn to perform
more complex filtering. There is no significant differ-
ence of final Euclidean loss L values between the ar-
chitectures with and without dropout. It could be ex-
pected, however, that for dropout-enabled networks,
the overfitting problem will not be observed too early
and, in consequence, for these architectures the dif-
KALSIMIS 2018 - Special Session on Knowledge Acquisition and Learning in Semantic Interpretation of Medical Image Structures
194

Figure 6: The value of loss function L during the training process of optimal network M
+
(20). This value is calculated both
on train set (dark gray) and validation set (light gray). No evident overfitting problem can be observed.
(a) (b) (c) (d)
Figure 7: Sample localization results for optimal network M
+
(20) after its training and selection of corresponding t and
a parameters: (a), (c) - comparison of expected points (dark gray) and detected points (light gray), (b), (d) - the predicted
localization of nucleuses within the original image.
(a) (b)
Figure 8: Sample outputs of the optimal neural network M
+
(20) after its training (result of filtration). Higher response can
be observed in the regions where nucleuses are expected.
ference between train and validation errors should be
a smaller than int the case of architectures without
dropout. But since, as it was already mentioned, an
overfitting was not observed at all in Fig. 6, this ex-
pected trend is not visible in the presented results.
Interesting are, however, the averaged F
1
values
obtained for the test set (presented in Tab. 2), where
a tendency is quite opposite to the trend observed for
the train set and the validation set. The only explana-
tion of such an observation is a small number of the
available images. As it was decribed in Sec. 3, the im-
ages come from 4 different groups. In the presented
work, the possible differences between those groups
were not taken into account and, as it was checked
after the experiments, the pseudo-random assignment
of images to the train, validation and test sets caused
that one group was overrepresented in the test set.
Further analysis of the obtained results depicted in
Fig. 8 and Fig. 7 reveals what are the other problems
of the proposed solution:
• Nucleuses and their surrounding areas can have
a very different characteristics.
• There are structures in the images similar to the
nucleuses, that should not be detected (region on
the left of the top nucleus in Fig. 7b).
• There are very dark (almost invisible) nucleuses
(nucleus at the top of Fig. 7d).
Localization of Neuron Nucleuses in Microscopy Images with Convolutional Neural Networks
195

Most of these problems could be overcome, as it is of-
ten with machine learning based techniques, if more
samples of the training data were available. Addition-
ally, some image pre-processing could be helpful here
to increase local contrast in dark areas. Nevertheless,
the obtained preliminary results are undoubtedly en-
couraging.
6 SUMMARY
In this work, we present a method of automatic local-
ization of the neuron nucleuses in the images acquired
with fluorescent microscope. This method is based on
the convolutional neural network which is trained to
act as a non-linear filter. These filtration results are
analyzed further to indicate possible localizations of
nucleuses. An original element of the presented work
is the way a CNN concept was used for the filtration
task. Also the result evaluation technique can be con-
sidered as an interesting idea for similar works. This
approach allowed not only to objectively measure the
quality of the proposed solution, but to find the op-
timal parameters used in the second phase of the de-
scribed approach as well.
The obtained results leave a lot of space for fur-
ther improvement. Some of the possible ideas were
already mentioned in the previous section. To im-
prove the filtration results, maybe the number of pos-
itive and negative samples could be increased. There
is no problem with the second group, but for obvi-
ous reasons the number of positive samples is lim-
ited. The main attempt to overcome this problem was
taking into account all 4 rotations of these samples.
This, however, may not cover the whole variety of
visible structures, since CNN is not invariant to input
rotation. To solve this problem, CNN modification
described in (Tarasiuk and Pryczek, 2016) may be of
use. Data augmentation methods, such as brightness
and contrast modifications or local elastic deforma-
tions, can be of use here as well. Also a bigger visual
field could allow the filter to take more information
about the pixel surrounding into account. All those
aspects are under further investigation.
ACKNOWLEDGEMENTS
This project has been partly funded with support from
National Science Centre, Republic of Poland, deci-
sion number DEC-2012/05/D/ST6/03091.
REFERENCES
Cires¸an, D. C., Meier, U., Masci, J., Gambardella, L. M.,
and Schmidhuber, J. (2011). Flexible, high perfor-
mance convolutional neural networks for image clas-
sification. In Proceedings of the Twenty-Second In-
ternational Joint Conference on Artificial Intelligence
- Volume Volume Two, IJCAI’11, pages 1237–1242.
AAAI Press.
Ho, D. J., Ch., F., Salama, P., Dunn, K. W., and Delp,
E. J. (2017). Nuclei Segmentation of Fluorescence
Microscopy Images Using Three Dimensional Con-
volutional Neural Networks. In IEEE Conference on
Computer Vision and Pattern Recognition Workshops
(CVPRW) 2017, pages 834–842.
Jia, Y., Shelhamer, E., Donahue, J., Karayev, S., Long, J.,
Girshick, R., Guadarrama, S., and Darrell, T. (2014).
Caffe: Convolutional Architecture for Fast Feature
Embedding. arXiv preprint arXiv:1408.5093.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012).
Imagenet classification with deep convolutional neu-
ral networks. In Pereira, F., Burges, C. J. C., Bottou,
L., and Weinberger, K. Q., editors, Advances in Neu-
ral Information Processing Systems 25, pages 1097–
1105. Curran Associates, Inc.
LeCun, Y. and Bengio, Y. (1995). Convolutional networks
for images, speech, and time-series. In Arbib, M. A.,
editor, The Handbook of Brain Theory and Neural
Networks. MIT Press.
Quan, T. M., Hildebrand, D. G. C., and Jeong, W. (2016).
FusionNet: A deep fully residual convolutional neu-
ral network for image segmentation in connectomics.
CoRR, abs/1612.05360.
Sadanandan, S. K., Ranefall, P., Le Guyader, S., and Whlby,
C. (2017). Automated Training of Deep Convolutional
Neural Networks for Cell Segmentation. Scientific Re-
ports, 7(1).
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. (2014). Dropout: A Simple
Way to Prevent Neural Networks from Overfitting. J.
Mach. Learn. Res., 15(1):1929–1958.
Stasiak, B., Tarasiuk, P., Michalska, I., Tomczyk, A., and
Szczepaniak, P. (2017). Localization of Demyeli-
nating Plaques in MRI using Convolutional Neural
Networks. In Proceedings of the 10th International
Joint Conference on Biomedical Engineering Sys-
tems and Technologies (BIOSTEC 2017) - Volume 2:
BIOIMAGING, pages 55–64. SCITEPRESS.
Tarasiuk, P. and Pryczek, M. (2016). Geometric Trans-
formations Embedded into Convolutional Neural Net-
works. Journal of Applied Computer Science,
24(3):33–48.
Xie, W., Noble, J., and Zisserman, A. (2016). Microscopy
cell counting and detection with fully convolutional
regression networks. Computer Methods in Biome-
chanics and Biomedical Engineering: Imaging & Vi-
sualization, pages 1–10.
KALSIMIS 2018 - Special Session on Knowledge Acquisition and Learning in Semantic Interpretation of Medical Image Structures
196
