
Stability Analysis for Adaptive Behavior
(Position Paper)
Emil Vassev and Mike Hinchey
Lero – The Irish Software Research Centre, University of Limerick, Limerick, Ireland
Keywords: Stability Analysis, Lyapunov Stability, Autonomous Systems, Adaptive Systems, KnowLang.
Abstract: One of the biggest challenges related to the research and development of autonomous systems is to prove
the correctness of their autonomy. Nowadays, autonomous and adaptive systems are the roadmap to AI and
the verification of such systems needs to set boundaries that will provide the highest possible guarantees
that AI will be safe and sound, so trust can be established in its innocuous operation. In this paper, the
authors draw upon their work on integrating stabilization science as part of a mechanism for verification of
adaptive behavior. Stability analysis is studied to find an approach that helps to determine stable states of
the behavior of an autonomous system. These states are further analyzed to determine behavior trajectories
and equilibrium orbits. KnowLang, a formal method for knowledge representation and reasoning of
adaptive systems, is used as a platform for stability analysis of autonomous systems.
1 INTRODUCTION
In today’s technologies, the terms autonomous and
adaptive started to progressively underline the new
trends of research and development of software-
intensive systems. Autonomous systems, such as
automatic lawn mowers, smart home equipment,
driverless train systems, or autonomous cars,
perform their tasks without human intervention.
Eventually, the most challenging question which
comes up when following the life cycle of the terms
“autonomy“ and "adaptation" is the potential to
construct a system that behaves and operates
similarly to, or even better than, a human being.
Obviously, this is the roadmap to AI, and proving
the correctness of autonomous and adaptive systems
becomes extremely important. The point is that the
verification of an autonomous system needs to set
the boundaries of such AI and provide autonomic
operations at least in a certain context with highest
safety guarantees, and finally establish trust in its
innocuous operation.
This paper draws upon the authors' work on a
special approach to Adaptive Behavior Verification
(ABV) (Vassev and Hinchey, 2014) where stability
analysis is performed to identify unstable behavior
that will eventually require autonomy and adaptation
to restore the stability of the system.
2 VERIFICATION OF ADAPTIVE
BEHAVIOR
The ABV approach consists of the following parts
(see Figure 1):
1) a stability analysis capability that identifies
instabilities given a system model and
partitions the system model into stable and
unstable component models;
2) a state-space reduction capability that
prunes the state space of an unstable
component model without loss of critical
fidelity;
3) high performance computing (HPC)
simulations to explore component behavior
over a wide range of an unstable
component’s reduced state space and
produce a statistical verification for the
component;
4) a compositional verification capability that
integrates individual component
verifications;
Vassev, E. and Hinchey, M.
Stability Analysis for Adaptive Behavior.
DOI: 10.5220/0006782204810487
In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2018), pages 481-487
ISBN: 978-989-758-293-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
481
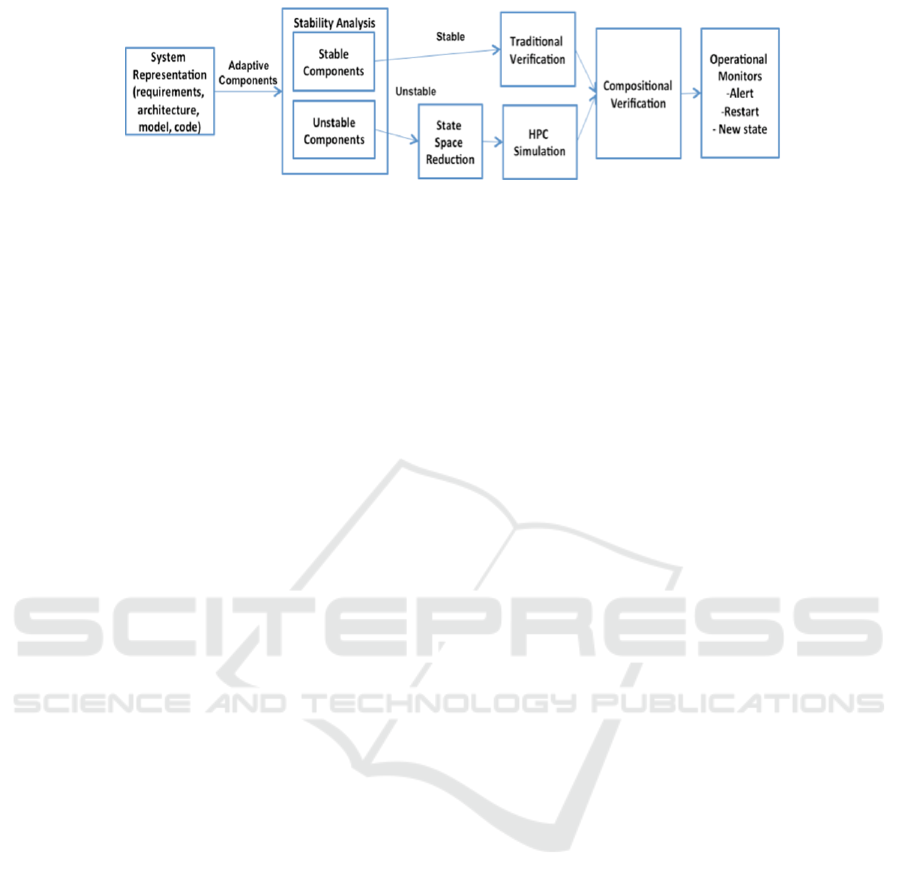
Figure 1: Adaptive Behavior Verification (Vassev and Hinchey, 2014).
5) operational monitors to detect and take
action to correct undesired unstable
behavior of the system during operation.
This work is based on the principles of stabilization
science (Arora, 2000). In our approach, stability
analysis is performed over a model built with the
KnowLang framework (Vassev and Hinchey, 2015a;
Vassev and Hinchey, 2015b) (see Section 4) where
the model is partitioned into system elements
providing the overall behavior as a collection of
stable (deterministic) and unstable
(nondeterministic) components. The stable parts (or
components) can then be verified with traditional
verification methods, e.g., model checking. To
verify the unstable parts we reduce their state space
first and then use HPC simulation (see Figure 1) and
testing. Finally, a compositional verification
approach integrates the verification results of both
stable and unstable parts by using special behavior
invariants as approximation of safe states along with
interaction invariants as interaction states.
3 STABILITY
In this work, the term “stable” informally means
resistant to change in behavior. Stabilization science
(Arora, 2000) provides a common approach to
studying system stability where a system behavior is
linearized around an operating point to determine a
small-signal linearized model of that operating point.
The stability of the system is then determined using
linear system stability analysis criterions such as:
Circle criterion (Shiriaev et al., 2003), Routh-
Hurwitz criterion (Gantmacher, 1959), Nyquist
stability criterion (Pippard, 1985), etc.
In this work, the mathematical model for stability
means differential equations used for the simulation
of a self-adaptive system. In general, we deal with a
semi-discrete model, which is discrete in space and
continuous in time. The mathematical model for
stability is based on the Lyapunov Stability Theory
(Lyapunov, 1892). Here, the stability of a system is
modeled for behaviors near to a point of equilibrium
and where a behavior orbit around that point is
defined stable if the forward orbit of any point is in a
small enough neighborhood or it stays in a small
(but perhaps, larger) neighborhood. In simple terms,
if a behavior
determined by a sequence of
actions that starts out near an equilibrium point
stays near
forever, then
is Lyapunov stable
near
.
The theory behind the stability analysis is based
on the qualitative theory of differential equations
and dynamical systems, and deals with asymptotic
properties of a system and the trajectories describing
what happens with that system after a long period of
time. A simple stable behavior
is exhibited by
equilibrium points (or fixed points) and by periodic
orbits.
We adapted the Lyapunov stability theory to
address the following three questions:
1) Will a nearby behavior orbit indefinitely
stay close to an equilibrium orbit?
2) Will a nearby behavior orbit converge to
an equilibrium orbit?
3) Will a nearby behavior orbit depart away
from an equilibrium orbit?
In the first case, the behavior is called stable, in
the second case, it is called asymptotically stable,
and in the third case, the behavior is said to be
unstable.
An equilibrium solution
(where all the
evaluated behaviors are stable) to an autonomous
system is called:
stable if for every small depart from the
equilibrium orbit , there exists a
such that every solution having
initial conditions within distance , i.e.,
of the equilibrium
remains within distance , i.e.,
for all
;
asymptotically stable if it is stable and, in
addition, there exists
such that
whenever
then
as .
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
482
In this model stability means that the behavior
trajectories do not change too much under small
perturbations, e.g., changes in the environment. In
this case, we can consider the behavior
deterministic and verifiable with the methods of
model checking.
Figure 2: Stable and Unstable Behavior.
In contrary, when a nearby behavior orbit is
getting repelled from the given orbit of stability
(stability point) (see Figure 2), we may consider
such a behavior unstable and non-deterministic.
Such a behavior cannot be verified with the
traditional model checking, but through simulation
and/or probabilistic model checking. In general,
unstable behaviors may be perturbing in a trajectory
asymptotically approaching the stable one or in a
trajectory getting away from the stability point (see
Figure 2). There may also be directions for which
the behavior of the perturbed orbit is more
complicated. e.g., neither converging nor escaping
completely.
Various criteria have been developed to prove
stability or instability of a behavior orbit (or
trajectory). Under favorable circumstances, the
question may be reduced to a well-studied problem
involving eigenvalues of matrices. A more general
method involves Lyapunov functions. In practice,
any one of a number of different stability criteria are
applied.
One of the key ideas in stability theory, and
pursued in this approach, is that the qualitative
behavior of a behavior orbit under perturbations can
be analyzed using the linearization of the system
near the equilibrium point. In particular, at each
equilibrium of a self-adaptive system with an n-
dimensional phase space, there is a certain
matrix whose eigenvalues characterize the
behavior of the nearby points (Hartman–Grobman
theorem) (Arrowsmith and Place, 1992). More
precisely, if all eigenvalues are negative real
numbers or complex numbers with negative real
parts then the point is a stable equilibrium point
(Lyapunov stability) and the nearby points converge
to it at an exponential rate form a zone of
asymptotical stability. If none of the eigenvalues are
purely imaginary (or zero) then the attracting and
repelling directions are related to the eigenspaces of
the matrix with eigenvalues whose real part is
negative and, respectively, positive, i.e.,
corresponding to unstable behavior.
4 KnowLang
KnowLang (Vassev and Hinchey, 2015a; Vassev
and Hinchey, 2015b; Vassev and Hinchey, 2015c) is
a framework for KR&R that aims at efficient and
comprehensive knowledge structuring and
awareness (Vassev and Hinchey, 2012) based on
logical and statistical reasoning. Knowledge
specified with KnowLang takes the form of a
Knowledge Base (KB) that outlines a Knowledge
Representation (KR) context. A key feature of
KnowLang is a formal language with a multi-tier
knowledge specification model (see Figure 3)
allowing integration of ontologies together with
rules and Bayesian networks (Neapolitan, 2013).
Figure 3: KnowLang Specification Model.
The language aims at efficient and comprehensive
knowledge structuring and awareness. It helps us
tackle (Vassev and Hinchey, 2015b): 1) explicit
representation of domain concepts and relationships;
2) explicit representation of particular and general
factual knowledge, in terms of predicates, names,
connectives, quantifiers and identity; and 3)
uncertain knowledge in which additive probabilities
are used to represent degrees of belief. Other
remarkable features are related to knowledge
cleaning (allowing for efficient reasoning) and
knowledge representation for autonomic behavior.
Stability Analysis for Adaptive Behavior
483

KnowLang employs special knowledge
structures and a reasoning mechanism for modeling
autonomic self-adaptive behavior (Vassev and
Hinchey, 2015a; Vassev and Hinchey, 2015b). Such
a behavior can be expressed via KnowLang policies,
events, actions, situations and relations between
policies and situations (see Definitions 1 through
10). Policies () are at the core of autonomic
behavior. A policy has a goal (), policy situations
(
), policy-situation relations (
), and policy
conditions (
) mapped to policy actions (
)
where the evaluation of
may eventually (with
some degree of probability) imply the evaluation of
actions (denoted
) (see Definition 6). A
condition () is a Boolean expression over an
ontology (see Definition 2), e.g., the occurrence of a
certain event. Policy situations
are situations
(see Definition 7) that may trigger (or imply) a
policy , in compliance with the policy-situations
relations
(denoted by
), thus implying
the evaluation of the policy conditions
(denoted
by
)(see Definition 6). Therefore, the
optional policy-situation relations (
) justify the
relationships between a policy and the associated
situations (see Definition 10).
(
policies
) (1)
(
Boolean expression over ontology
) (2)
() (3)
(
state
) (4)
(
goal
) (5)
(
policy
) (6)
(
situations
) (7)
(
situation
) (8)
(
relations
) (9)
(
relation
) (10)
,
Note that in order to allow for self-adaptive
behavior, relations must be specified to connect
policies with situations over an optional probability
distribution () where a policy might be related to
multiple situations and vice versa. Probability
distribution () is provided to support probabilistic
reasoning and to help the reasoner to choose the
most probable situation-policy "pair". Thus, we may
specify a few relations connecting a specific
situation to different policies to be undertaken when
the system is in that particular situation and the
probability distribution over these relations
(involving the same situation) should help the
reasoner decide which policy to choose (denoted by
) (see Definition 10). Hence, the presence of
probabilistic beliefs () in both mappings and policy
relations justifies the probability of policy execution,
which may vary with time.
Ideally, KnowLang policies are specified to
handle specific situations, which may trigger the
application of policies. A policy exhibits a behavior
via actions generated in the environment or in the
system itself. Specific conditions determine which
specific actions (among the actions associated with
that policy (see Definition 6) shall be executed.
These conditions are often generic and may differ
from the situations triggering the policy. Thus, the
behavior not only depends on the specific situations
a policy is specified to handle, but also depends on
additional conditions. Such conditions might be
organized in a way allowing for synchronization of
different situations on the same policy. When a
policy is applied, it checks what particular
conditions
are met and performs the mapped
actions
(
) (see Definition 6).
An optional probability distribution may
additionally restrict the action execution. Although
specified initially, the probability distribution at both
mapping and relation levels is recomputed after the
execution of any involved action. The re-
computation is based on the consequences of the
action execution, which allows for reinforcement
learning.
States and goals drive the specification of any
system modeled with KnowLang. States are used to
specify goals (see Definition 5) and situations (see
Definition 8), which on other side are used to
specify policies (see Definition 6) often intended to
provide self-adaptive behavior. The following is an
example of a Boolean expression defining a state in
KnowLang.
STATE ArrivedOnTime {
carSafety.eCars.CONCEPT_TREES.Journey.STATES.Arrived
AND
(carSafety.eCars.CONCEPT_TREES.JourneyTime <=
carSafety.eCars.CONCEPT_TREES.Journey.PROPS.journeyTime)}
As shown, the logical expression above needs to
be evaluated as true in order to consider the
ArrivedOnTime state as active.
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
484
5 STABILITY POINTS WITH
KnowLang
In this work, stability analysis works on states,
goals, situations, and policies to determine behavior
trajectories under perturbations in the execution
environment. Here, the first task is to determine the
stable equilibrium points (representing Lyapunov
stability) and then the nearby points forming zones
of asymptotical stability (see Section 3). The
following elements are considered to be equilibrium
points of stability in KnowLang specifications:
1) departing states (or expression of states)
used in goal definitions;
2) arriving states (or expression of states)
used in goal definitions (achieved goals);
3) policies handling situations to support goal
achievement.
Note that policies are originally intended to
handle situations that are considered to be critical for
achieving a goal. Because these policies are part of
the expected (deterministic) behavior, we consider
as stable points both the execution of the policies'
actions and handled situations. Here, the
asymptotical stability of an autonomous system
modeled with KnowLang is a set of areas of
asymptotical stability (see Definition 11). Here, each
area of asymptotical stability is determined by zones
defined by (see Definition 12):
the goal through its goal states (zone
-
see Definition 13) ;
the goal-supporting policies through the
execution of their actions (zones
- see
definitions 14 and 15) ;
the critical situations (through their
associated states) addressing that area of
asymptotical stability, because they are
deterministic (zones
- see definitions 16
and 17).
(
asymptotical stability
) (11)
(area of
asymptotical stability
) (12)
(zone of goal
stability
) (13)
(zones of policy
stab.
) (14)
(zone of policy
stability
) (15)
(zones of situat.
stab.
) (16)
(zone of situation
stability
) (17)
Here, the areas of asymptotical stability are
determined by the defined goals through their
departing and arriving states. Note that in each area
the zone of goal stability (see Definition 13) is
determined by a specific goal and the zones of
policy stability
(see Definition 14) are basically
formed by policies
supporting that goal (see
Definition 15). Finally, the zones of situation
stability
are formed by situations associated with
the policies forming the zones of policy stability. In
this stability model, defines a space of
asymptotical stability and the continuous in time
system is considered stable if at any time its
behavior stays in that space or in a close proximity
to that space. Here, if we consider that the system
behavior is determined by a sequence of actions
that starts out in the space of asymptotical stability
and stays in that space (or in a close proximity)
forever, then
is Lyapunov stable near .
Figure 4: KnowLang Asymptotical Stability.
Figure 4 demonstrate a Lyapunov stable
behavior determined by a sequence of actions that
form the state trajectory
. As shown, the
exemplar space of asymptotical stability is formed
by six areas of asymptotical stability (each driven by
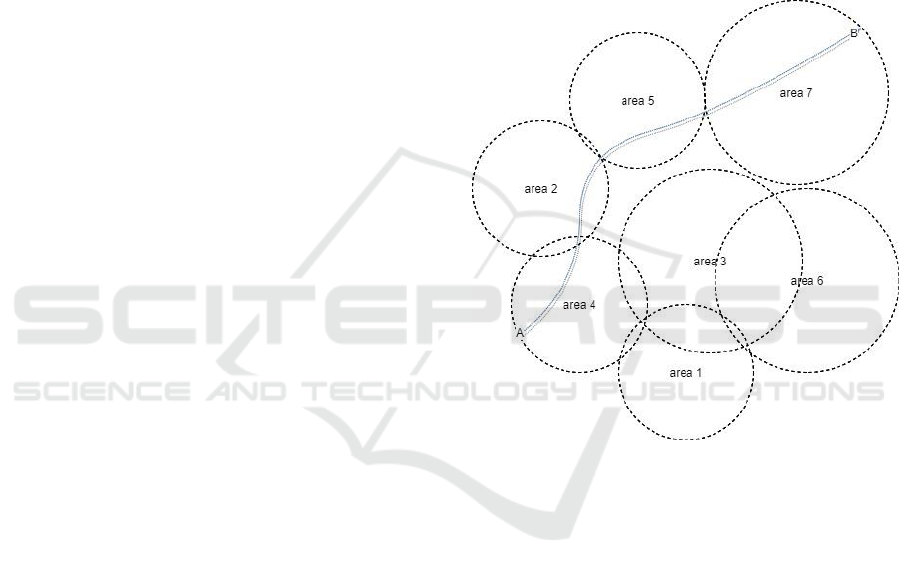
a distinct system goal ). Figure 5 depicts a possible
area of asymptotical stability driven by a goal
that defines the zone of goal stability
(a trajectory
from a departing state to an arriving state), a zone of
policy stability
presented as a set of policy
trajectories each determined by a sequence of policy
actions, and a zone of situation stability presented as
a set of situation states.
Stability Analysis for Adaptive Behavior
485

Figure 5: KnowLang Area of Asymptotical Stability.
Note that when a state trajectory
goes
through an area of asymptotical stability (see Figure
4), the presented behavior is considered stable if at
any time it stays in one of the zones of asymptotical
stability or stays in a close proximity to one of those
zones. Here, the definitions for stability can be
adapted to the KnowLang specifics as following:
An equilibrium solution
(where all the
evaluated behaviors are stable) to an autonomous
system modeled with KnowLang is called:
stable if for every small depart from
the space of stability , there exists a
such that every solution having
initial conditions within distance , i.e.,
of the equilibrium
remains within distance , i.e.,
for all
;
asymptotically stable if it is stable and, in
addition, there exists
such that
whenever
then
as .
Here, one of the challenges in this solution that
we still need to overcome is to determine the
trajectory from a departing point to an arriving point
(e.g., state transitions in goals). Further, we need to
determine the borderline distances from stable states
and deviations from stable trajectories , and
.
In this case, we need to break the state expressions
down to atomic Boolean sub-expressions and
determine sub-expressions that may vary in
expression components without changing the overall
expression evaluation.
Moreover, state-reduction techniques need to be
developed to target the partitioning of the Boolean
state expressions into sub-state expressions to
determine parts that are irrelevant to the final result
(TRUE or FALSE) and therefore can be excluded
from the expression (replaced by TRUE or FALSE).
Finally, a methodology for impact analysis to
exclude low-impact partitions need to be developed,
so the state space can be reduced.
6 CONCLUSION
An autonomous system is loaded with AI and
operates in a potentially nondeterministic
environment. Therefore, the verification of such
systems needs to set boundaries that will provide the
highest possible guarantees that the autonomy
behavior will be safe and sound, so trust can be
established in its innocuous operation. In this paper,
we have presented our work on stability analysis for
systems modeled with KnowLang. In this approach,
a space of asymptotical stability is determined by
analyzing the system goals along with the associated
supportive policies and involved situations. The
stable states and trajectories of action executions and
state transitions form zones of asymptotical stability.
Zones driven by a single system goal are grouped
into areas of asymptotical stability and then these
areas form a space of asymptotical stability. Here, if
a system behavior determined by a sequence of
actions that starts out in the space of asymptotical
stability and stays in that space (or in a close
proximity) forever, then that behavior is Lyapunov
stable near that space of asymptotical stability.
Future work is considered with further
development of this approach in terms of stability
analysis automation, state trajectory definition and
deviation borderlines. Moreover, state-reduction
techniques need to be developed along with state
impact analysis.
ACKNOWLEDGEMENTS
This work was supported with the financial support
of the Science Foundation Ireland grant 13/RC/2094
and co-funded under the European Regional
Development Fund through the Southern & Eastern
Regional Operational Programme to Lero—the Irish
Software Research Centre (www.lero.ie).
REFERENCES
Arora, A., 2000. Stabilization. In: Encyclopedia of
Distributed Computing. Kluwer Academic Publishers.
Arrowsmith, D. K., Place, C. M., 1992. The Linearization
Theorem. In Dynamical Systems: Differential
Equations, Maps, and Chaotic Behavior. 77–81.
London: Chapman & Hall.
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
486

Gantmacher, F. R., 1959. Applications of the Theory of
Matrices. Wiley, New York.
Lyapunov, A. M., 1892. The General Problem of the
Stability of Motion (in Russian), Doctoral dissertation,
Univ. Kharkov. English translation: Lyapunov, A. M.,
1966. Stability of Motion, Academic Press, New-York
& London, 1966
Neapolitan, R., 2013. Learning Bayesian Networks.
Prentice Hall.
Pippard, A.B., 1985. Response & Stability. Cambridge
University Press.
Shiriaev, A., Johansson, R., Robertsson, A., 2003.
Sufficient conditions for dynamical output feedback
stabilization via the circle criterion. In 42nd IEEE
International Conference on Decision and Control,
4682-4687, Vol.5.
Vassev, E., Hinchey, M., 2012. Awareness in Software-
Intensive Systems. In IEEE Computer 45(12), 84–87.
Vassev, E., Hinchey, M., 2014. Autonomy Requirements
Engineering for Space Missions. In NASA
Monographs in Systems and Software Engineering.
Springer.
Vassev, E., Hinchey, M., 2015a. Knowledge
Representation for Adaptive and Self-aware Systems.
In Software Engineering for Collective Autonomic
Systems, Volume 8998 of LNCS. Springer.
Vassev, E., Hinchey, M., 2015b. Knowledge
Representation for Adaptive and Self-Aware Systems.
In: Wirsing, M., H•olzl, M., Koch, N., Mayer, P.
(eds.) Software Engineering for Collective Autonomic
Systems: Results of the ASCENS Project, Lecture
Notes in Computer Science, vol. 8998. Springer
Verlag.
Vassev, E., Hinchey, M., 2015c. KnowLang: Knowledge
Representation for Self-Adaptive Systems. In IEEE
Computer 48 (2), 81–84.
Yerramalla, S., Fuller, E., Mladenovski, M., Cukic, B.,
2003. Lyapunov Analysis of Neural Network Stability
in an Adaptive Flight Control System. In Self-
Stabilizing Systems, 77–91.
Stability Analysis for Adaptive Behavior
487
