
Data Clustering using Homomorphic Encryption and Secure Chain
Distance Matrices
Nawal Almutairi
1,2
, Frans Coenen
1
and Keith Dures
1
1
Department of Computer Science, University of Liverpool, U.K.
2
Information Technology Department, College of Computer and Information Sciences,
King Saud University, Riyadh, Saudi Arabia
Keywords:
Privacy Preserving Data Mining, Secure Clustering, Homomorphic Encryption, Order Preserving Encryption,
Secure Chain Distance Matrices.
Abstract:
Secure data mining has emerged as an essential requirement for exchanging confidential data in terms of
third party (outsourced) data analytics. An emerging form of encryption, Homomorphic Encryption, allows
a limited amount of data manipulation and, when coupled with additional information, can facilitate secure
third party data analytics. However, the resource required is substantial which leads to scalability issues.
Moreover, in many cases, data owner participation can still be significant, thus not providing a full realisation
of the vision of third party data analytics. The focus of this paper is therefore scalable and secure third
party data clustering with only very limited data owner participation. To this end, the concept of Secure Chain
Distance Matrices is proposed. The mechanism is fully described and analysed in the context of three different
clustering algorithms. Excellent evaluation results were obtained.
1 INTRODUCTION
Data mining is a well established research field that
has been effectively employed in many disciplines.
However, the exponential growth in data availability
has lead to the involvement of third parties for the
purpose of storing and processing data on behalf of
data owners; for example third party data mining or
collaborative data mining. The involvement of third
parties has clear security risks associated with it, such
as unauthorised data access (data leakage) and issues
concerning data privacy preservation. One current
solution is Privacy Preserving Data Mining (PPDM)
(Agrawal and Srikant, 2000; Lindell and Pinkas,
2002). The typical approach is to conceal sensitive
data attributes by applying some form of data trans-
formation to generate “sanitised” counterpartattribute
values that can be safely disclosed to (untrusted) third
parties (Chhinkaniwala and Garg, 2011). Well known
transformation techniques include value perturbation
and data anonymisation (Chhinkaniwala and Garg,
2011). Such techniques tend to operate by introduc-
ing “statistical noise” to either the entire dataset or to
selected sensitive attributes. An issue with these tech-
niques is that they cannot guarantee data confidential-
ity; it might still be possible to “reverse engineer” the
original data (Vaidya et al., 2006; Berinato, 2015).
Data confidentiality, and protection against leak-
age, can be assured using data encryption. However,
standard forms of encryption do not support data min-
ing activities, which typically require data manipula-
tion and record comparison. A potential solution is
the use of Homomorphic Encryption (HE) schemes
that provide malleability properties that permit lim-
ited calculation over cyphertexts without compromis-
ing security. Although HE schemes support primitive
operations that go some way to supporting data min-
ing, they do not provide an entire solution. For exam-
ple they do not support record comparison; a require-
ment with respect to many data mining algorithms.
One mechanism whereby this can be addressed is to
involve data owners so that the operations that a given
HE scheme does not support can be performed by
the data owners (Erkin et al., 2009; Liu et al., 2014).
For example, in the context of data clustering, record
similarity checking can be conducted in this manner.
However, the degree of data owner involvement can
be substantial given any kind of sophisticated data
analysis task, which in turn detracts from the vision
of third party data mining.
There has been some work that seeks to diminish
data owner participation with respect to third party
Almutairi, N., Coenen, F. and Dures, K.
Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices.
DOI: 10.5220/0006890800410050
In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 1: KDIR, pages 41-50
ISBN: 978-989-758-330-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
41

data clustering. Of note is the 3-D Updatable Dis-
tance Matrix (UDM) introduced in (Almutairi et al.,
2017). However, use of the UDM featured two disad-
vantages: (i) a substantial memory requirement, be-
cause the first two dimensions of the matrix were cor-
related to the number of records in the given dataset
thus limiting the scalability and (ii) the potential for
reverse engineer given that a UDM is essentially a
(very large) set of linear equations.
Given the above, this paper proposes the idea of
the Secure Chain Distance Matrix (SCDM) which
provides for secure third party data mining us-
ing a proposed Order Preserving Encryption (OPE)
scheme, which can limit recourse to data owners dur-
ing the processing of the data (depending on the na-
ture of clustering) and features none of the mem-
ory requirement and security disadvantages associ-
ated with the UDM concept proposed in (Almutairi
et al., 2017). The novel elements of the SCDM con-
cept are firstly the chaining mechanism used, which
means that the storage requirement, compared with
UDMs, is reduced by a factor equivalent to the num-
ber of input data records (−1). Secondly, the pro-
posed Order Preserving Encryption (OPE) scheme
with which the matrix is encoded, thus allowing for
third party record comparison without the risk of po-
tential reverse engineering as in the case of UDM.
The SCDM concept is fully described and evaluated.
The evaluation is conducted in the context of three
different clustering algorithms (Nearest Neighbour,
DBSCAN and k-Means), however, the SCDM idea
clearly has wider application.
The rest of this paper is structured as follows. Sec-
tion 2 provides a review of related research. Sec-
tion 3 presents the data encryption schemes used to
provide for proposed secure clustering methods. The
proposed Secure Chain Distance Matrix (SCDM) idea
is then detailed in Section 4. The utilisation of the
SCDM concept, in the context of secure data cluster-
ing, is presented in Section 5. Section 6 then reports
on the experiments conducted to evaluate the SCDM
concept and the results obtained (in the context of se-
cure data clustering). The paper is concluded in Sec-
tion 7, with a summary of the main findings and sug-
gestion for future work.
2 PREVIOUS WORK
This section presents a review of previous work on
secure data clustering that uses HE schemes as a data
confidentiality preservation method. The main chal-
lenge of HE-based privacy preserving data clustering
(and other forms of data mining), is that HE schemes
support only a limited number of operations. Sev-
eral solutions havebeen proposed to address this chal-
lenge, mostly in the context of collaborative data clus-
tering whereas the work presented in this paper is
directed at third party data clustering, which can be
broadly categorised into: (i) involving data owners
when unsupported operations are required, and (ii)
utilising the concept of “secret sharing” to delegate a
key and operations to semi-honest and non-colluding
parties that collaboratively perform operations on the
data owners’ behalf. Both have limitations in term of
communication complexity and security threats.
The main feature of the first category is the main-
tenance of data confidentiality by allowing a third
party to only manipulate cyphertexts using HE prop-
erties (no access to any secret key). In this case, in
the context of data clustering, data owner participa-
tion becomes a necessity. In some cases, the majority
of the work is done by data owners. For example,
a number of authors have proposed mechanisms for
k-means clustering using Secure Multi-Party Compu-
tation (SMPC), where data owners repeatedly cluster
their own data and only share encrypted data centroids
so that an eventual global clustering can be arrived at
(Jha et al., 2005; Mittal et al., 2014). A similar idea
is used in (Tong et al., 2018) to implement DBSCAN
where data owners independently apply DBSCAN on
their local data. The resulting boundary records and
their labels are then shared (in plaintext) with the third
party who then determines global boundary records
which are returned to the individualdata owner so that
they can update their local clusters. However, shar-
ing boundary data records in plaintext form presents
a security threat. Secure nearest neighbour clustering
is presented in (Shaneck et al., 2009) using SMPC
primitives; secure product for distance calculation
and Yao’s millionaires’ protocol for data comparison.
A significant drawback of these proposed solutions
is that they introduce a computation/communication
overhead because of the amount of data owner partic-
ipation required.
In (Erkin et al., 2009; Liu et al., 2014; Almutairi
et al., 2017; Rahman et al., 2017) the basic idea was
for the third party to do as much of the clustering as
possible (centroid calculation, data aggregation and
so), using the properties of a selected HE scheme, and
involve data owners only when the properties of the
particular HE scheme used do not support the desired
analysis. For example, in the case of (Erkin et al.,
2009), in the context of collaborative clustering, the
adopted HE scheme does not support record similar-
ity checking, thus this is done by a randomly selected
data owner. The number of data owner participation
instances is given by n × |C| × i, where n is the num-
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
42

ber of records, |C| the number of centroids and i the
number of clustering iterations; thus the amount of
data owner participation is considerable. The con-
cept of “trapdoors” are used to minimise the num-
ber of data owner participation in (Liu et al., 2014).
“Static” and “dynamic” trapdoors were therefore cal-
culated by the data owners so as to convert cypher-
texts to order cyphertexts; consequently off-line com-
parison (without data owner participation) was sup-
ported. However, the main issue with this approach
was that it was very inefficient, particularly when con-
sidering large datasets; in addition data owner partici-
pation could still be high (depending on the nature of
the clustering) because of the need to recalculate the
dynamic trapdoors on each iteration. An alternative is
the UDM concept presented in (Almutairi et al., 2017)
that dramatically reduces the data owner participation
overhead to |C| × i, however this also has limitations;
firstly in terms of security in that a UDM represents
a set of linear equations that might be reverse engi-
neered (although the set of linear equations is very
large), and secondly in terms of memory requirement
and communication complexity cost in that the size
of a UDM increases exponentially with the number
of records in the input dataset. The third party collab-
orative DBSCAN mechanism described in (Rahman
et al., 2017) uses HE properties to calculate the re-
quired distances. However, as noted previously, the
generated cyphers do not preserve the data ordering,
thus data owner participation was still required to de-
termine whether the distances were below or above
the DBSCAN threshold ε value.
The second category comprises more recent work
that uses “secret sharing” to eliminate data owner par-
ticipation. The basic idea is to use a scheme, as
in (Hazay et al., 2012), that mathematically splits
a secret key among multiple semi-honest and non-
colluding parties that collaboratively manipulate data
on behalf of data owners. In (Rao et al., 2015; Saman-
thula et al., 2015), the concept of secret sharing was
used to design secure computation protocols that se-
curely execute mathematical operations by third par-
ties without involving data owners in the data min-
ing process. The limitation of this approach is that
it tends to be inefficient and not practical for large
datasets. In addition, the requirement for at least two
semi-honest and none-colluding parties is of concern,
and for many data owners a security risk. Moreover,
the secret key that has been generated to encrypt a
given dataset cannot be revoked by data owners, thus
a version of the data needs to be stored locally by each
individual data owners.
3 DATA ENCRYPTION
The proposed Secure Chain Distance Matrix (SCDM)
based clustering approaches utilised two encryption
schemes: (i) Liu’s HE scheme (Liu, 2013) and (ii)
a proposed Order Preserving Encryption (OPE). The
first is used to encrypt the data to be outsourced, the
second to encrypt the CDM. Both are discussed in
further detail in the following two sub-sections, Sub-
sections 3.1 and 3.2 respectively.
3.1 Liu’s Homomorphic Encryption
Scheme
In Liu’s scheme each data attribute v is encrypted
into m sub-cyphers, C = {c
1
,c
2
,... ,c
m
} where m ≥
3. Algorithm 1 shows the pseudo code for the
Encrypt(v,K(m)) where K(m) is a list of secret keys.
K(m) = [(k
1
,s
1
,t
1
),..., (k
m
,s
m
,t
m
)] and k
i
, s
i
and t
i
are real numbers. Given a set of sub-cyphers C =
c
1
,..., c
m
and the key K(m) Algorithm 2 gives the
pseudo code for the Decrypt(C,K(m)) decryption
function to return the value v.
Algorithm 1: Encrypt(v, K(m)).
1: procedure ENCRYPT(v, K(m))
2: generate m arbitrarily real random numbers
r
1
,.... .,r
m
3: Declare C as a real value array of m elements
4: c
1
= k
1
∗t
1
∗ v+ s
1
∗ r
m
+ k
1
∗ (r
1
− r
m−1
)
5: for i = 2 to m− 1 do
6: c
i
= k
i
∗t
i
∗ v+ s
i
∗ r
m
+ k
i
∗ (r
i
− r
i−1
)
7: c
m
= (k
m
+ s
m
+t
m
) ∗r
m
8: Exit with C
Algorithm 2: Decrypt(C, K(m)).
1: procedure DECRYPT(C, K(m))
2: T =
∑
m−1
i=1
t
i
3: S = c
m
/(k
m
+ s
m
+t
m
)
4: v = (
∑
m−1
i=1
(c
i
− S∗s
i
)/ki)/T
5: Exit with v
The scheme has both security and homomorphic
properties. The scheme is semantically secure in that
it produces different cyphertexts for the same plain-
text on each occasion, even when the same secret key
is used. Further detail regarding the security of Liu’s
scheme is given in Section 6. In terms of its homo-
morphic properties the scheme supports: the addition
of cyphertexts ⊕ and multiplication of a cyphertext
with a real value ⊗ as shown in Equation 1. Hence
the subtraction ⊖ of cyphertexts and the division ⊘
of a cyphertexts by a real value are implemented
Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices
43

as given in Equation 2.
C⊕C
′
= {c
1
⊕ c
′
1
,.. .,c
m
⊕ c
′
m
} = v+v
′
r⊗C = {r⊗ c
1
,.. .,r ⊗ c
m
} = r× v
(1)
C⊖C
′
= C⊕ (−1⊗C
′
)
C⊘ r =
1
r
⊗C
(2)
3.2 Order Preserving Encryption
A Chain Distance Matrix (CDM) holds distances be-
tween every attribute value in each consecutive data
record according to whatever ordering is featured in
the data; further detail regarding the generation of
CDMs is given in Section 4. As in the case of the
UDM, the content of a CDM can be used to de-
fine a set of linear equations that might allow for
re-engineering. To prevent such re-engineering the
idea is to encode the CDM, to give a Secure CDM
(SCDM), by using an Order Preserving Encryption
(OPE) scheme, a form of encryption where the order-
ing of the values is maintained so as to allow (secure)
comparison.
c
1
= [l
′
1
,r
′
1
)
Cypher Space
l
′
c
n
= [l
′
n
,r
′
n
)
r
′
c
2
= [l
′
2
,r
′
2
)
.. .. ..
m
1
= [l
1
,r
1
)
l
m
n
= [l
n
,r
n
)
r
Message Space
.. .
Enc
2
(x
2
)Enc
1
(x
1
) Enc
n
(x
n
)
Figure 1: Message and extended cypher space splitting.
The proposed scheme is an amalgamation of two
existing OPE schemes, that of (Liu et al., 2016)
and (Liu and Wang, 2013). Using the proposed
scheme the expected message space M and the ex-
panded cypher space C is known in advance as in the
case of most OPE schemes. The expanded cypher
space should be much larger than the message space,
|C| ≫ |M|. Using the proposed scheme M = [l,r) and
C = [l
′
,r
′
) where l and l
′
are the minimum bound-
ary values and r and r
′
are the maximum boundary
values (as demonstrated in Figure 1). The key fea-
ture of the proposed OPE scheme is that it obscures
any data distribution that might be included in the
generated cyphertexts using the concept of message
space splitting and non-linear cypher space expan-
sion. To generate the desired cypher space the first
step is to randomly split the message space M into
n successive intervals M = {m
1
,m
2
,. .. ,m
n
} where
m
i
= [l
i
,r
i
) ∀(i = 1,2,. .. ,n). The process of splitting
satisfies the following: M = ∪
i=n
i=1
m
i
= ∪
i=n
i=1
[l
i
,r
i
) =
[l, r) and [l
i
,r
i
) ∩ [l
j
,r
j
) = φ ∀ i 6= j. Next, the cypher
space C was also split into n successive intervals C =
{c
1
,c
2
,. .. ,c
n
}. The length of the cypher space inter-
vals are determined by the density of the correspond-
ing message space interval, so that for a dense inter-
val, containing high frequency data, its corresponding
cypher space interval will result in a longer cypher in-
terval range.
Each interval has associated with it an encryption
function that maps data from the message space m
i
to cyphertext in the corresponding extended cypher
space c
i
. In context of the work presented in this
paper, the encryption function of the ith interval is
shown in Algorithm 3; the algorithm encrypts a plain-
text value x ∈ m
i
to an encrypted value x
′
∈ c
i
. Range
and Range
′
(lines 2 and 3) return the maximal and
minimal value for the message space interval m
i
and
the corresponding cypher space c
i
respectively. In
line 4 the Scale
i
value is calculated as a division of
the cypher space size over the corresponding message
space size. The values of the minimal cypher space,
minimal message space and the scale are used to gen-
erate a cypher x
′
(line 5). To obfuscate the occurrence
frequency of a data value a random value δ
i
is applied
to x
′
(lines 6 and 7). The value of δ
i
is sampled from
the range [0,Sens∗ Scale
i
) where Sens represents the
data sensitivity as proposed in (Liu and Wang, 2013);
the minimum distance between plaintext values.
Algorithm 3: Order Preserving Encryption algorithm.
1: procedure ENC
i
(x,Sens)
2: l
i
,r
i
← Range(i)
3: l
′
i
,r
′
i
← Range
′
(i)
4: Scale
i
=
(l
′
i
−r
′
i
)
(l
i
−r
i
)
5: x
′
= l
′
i
+ Scale
i
× (x− l
i
)
6: δ
i
= Random(0,Sens×Scale
i
)
7: x
′
= x
′
+ δ
i
8: Exit with x
′
4 THE SECURE CHAIN
DISTANCE MATRIX (SCDM)
Regardless of whether standard or HE encryption is
used, data encryption randomly transfers plaintexts
values in a dataset D to cyphertexts in such a way
that any ordering is not preserved. Therefore, data
comparisons cannot be directly applied to the cypher-
texts, and hence clustering algorithms cannot be di-
rectly applied. The proposed idea is to support third
party secure clustering over encrypted data using the
concept of a Secure Chain Distance Matrix (SCDM)
that holds the distance between every attribute in ev-
ery consecutive data records in D. An SCDM is a 2D
matrix whose first dimension is n − 1 where n is the
number of records in D and whose second dimension
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
44

is |A| (the size of the attribute set A). An SCDM is
generated in two steps: (i) CDM calculation and (ii)
CDM encryption. Algorithm 4 gives the CDM cal-
culation process. Instead of calculating distances be-
tween attribute values in records with the correspond-
ing attribute values in every other record, as in the
case of UDMs, a CDM holds only distances between
n − 1 records. This small set of distances allows a
third party to calculate the “order” of similarity be-
tween any two data records r
x
and r
y
(where x < y) in
D as per equation 3. In the case of x = y the distance
will clearly be 0.
Algorithm 4: Chain Distance Matrix Calculation.
1: procedure CDMCALCULATION(D)
2: CDM =
/
0 array of n− 1 rows and |A| column
3: for i = 1 to i = n− 1 do
4: for j = 1 to j = |A| do
5: CDM
[i, j]
= D
[i, j]
− D
[i+1, j]
6: Exit with CDM
Sim(CDM, r
x
,r
y
) =
j=|A|
∑
j=1
i=(y−1)
∑
i=x
CDM
[i, j]
(3)
Although the CDM reduces the memory require-
ment, compared to UDM, it still essentially com-
prises a set of linear equations that may support re-
engineering. Therefore, the second step is to encrypt
the matrix so that the distance ordering is preserved
to give an SCDM. To this end, the OPE described in
Sub-section 3.2 above was used. The key feature of
the encrypted CDM, the SCDM, is that a third party
now has access to the distance value ordering, not
the original distance values, between the data records.
The order of similarity is determined as per Equation
3 but with the CDM replaced by the SCDM.
5 SECURE DATA CLUSTERING
This section presents a number of examples secure
clustering algorithms that operate over HE data and
utilise the SCDM concept, two of these achieve the
ideal solution (require no data owner participation
whilst the third party processing is taking place), the
third only requires minimal data owner participation.
Whatever the case the clustering process has two
parts, data preparation (Sub-section 5.1) and the data
clustering (Sub-sections 5.2, 5.3 and 5.4), conducted
by a data owner and the third party data miner respec-
tively.
5.1 Data Preparation
The initial step in the preparation process is to trans-
late a given dataset D into a suitable format that al-
lows distance calculation and data comparison. In the
context of the work presented in this paper, casting
is used to transfer categorical values to discrete inte-
ger equivalents. The next step is to encrypt the data
attribute values to produce an encrypted dataset D
′
using Liu’s HE scheme and m = 4 (see Sub-section
3.1). The CDM is then calculated using Algorithm 4
and encoded using the proposed OPE scheme (Sub-
Section 3.2). The output from the preparation process
is the encrypted dataset D
′
and the SCDM ready to be
sent to the third party data miner.
5.2 Secure Nearest Neighbour
Clustering (SNNC)
The proposed SCDM concept was combined with
three popular clustering schemes: (i) Nearest Neigh-
bour Clustering, (ii) DBSCAN and (iii) k-Means. The
first is discussed in this section, and the remaining two
in the followingtwo sections. The pseudo code for the
proposed SNNC approach is presented in Algorithm
5, it operates in a similar manner to the standard NNC
algorithm (Cover and Hart, 1967). The main differ-
ences are that the data and threshold values σ
′
is en-
crypted and that the similarity between data records
is determined using the SCDM. The algorithm com-
mences by adding the first encrypted record r
′
1
to the
first cluster (lines 2 and 3) and then iteratively cluster-
ing the remaining records (lines 5 to 11). As in case of
standard NNC, a record r
′
i
will be assigned to a clus-
ter if there exists some record r
′
m
whose distance from
r
′
i
is less than or equal to σ
′
(lines 5 to 8). If there is
no such record, r
′
i
is assigned to a new cluster (lines
10 and 11). The similarity between records r
′
i
and r
′
m
is determined using Equation 3 (and the SCDM). The
algorithm will exit with a cluster configuration C.
5.3 Secure DBSCAN (SDBSCAN)
The SDBSCAN algorithm is presented in Algorithm
6. The inputs are the encrypted dataset D
′
and SCDM
previously provided by the data owner and the desired
density parameters (MinPts, ε
′
). Similar to the stan-
dard DBSCAN (Ester et al., 1996), density is defined
as the minimum number of points, MinPts, within a
certain distance ε. Note that, in case of SDBSCAN
the ε value is encrypted using the OPE scheme to give
ε
′
that allows secure comparison and hides the corre-
lation (distance) between data records when the third
party data miner executes SDBSCAN.
Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices
45

Algorithm 5: Secure NN clustering algorithm.
1: procedure SNNC(D
′
,SCDM,σ
′
)
2: C
1
= {r
′
1
}
3: C = {C
1
}
4: k = 1
5: for i = 2 to i = |D
′
| do
6: Find r
′
m
in some cluster inC where
Sim(SCDM,r
′
i
,r
′
m
) is minimised
7: if Sim(SCDM, r
′
i
,r
′
m
) ≤ σ
′
then ⊲ (Eq. 3)
8: C
m
= C
m
∪ r
′
i
9: else
10: k+ +
11: C
k
= {r
′
i
}
12: Exit with C
The algorithm commences by initialising the
global variables MinPts, ε
′
, SCDM and D
′
by the val-
ues received from the data owner (line 5). In line 6,
an empty set of clusters C is created and the number
of clusters so far is set to 0. For each record r
′
i
in D
′
that has not been previously assigned to a cluster, “un-
clustered”, the set S is determined. The set S is the ε-
neighbourhood of r
′
i
and comprises the set of records
in D
′
whose distance from r
′
i
is less than or equals to
ε
′
. The set is determined by calling the regionQuery
procedure (line 9) where the SCDM is used to deter-
mine the overall distances between records (see Equa-
tion 3). If the number of records in S is greater than or
equals to MinPts the density requirement is satisfied
thus r
′
i
is marked as “clustered” and considered to rep-
resent a new cluster C
k
(lines 11 to 13). This cluster is
then expanded by considering the records in S using
the expandCluster procedure called in line 14. The
input to the expandCluster procedure is: the cluster
C
k
so far and the set S. The expandCluster procedure
is a recursive procedure. For each record in S which
has not been previously clustered we add the record
to C
k
and then determine the ε-neighbourhood S
2
for
this record (line 22). If the size of S
2
is greater than
or equals to MinPts we call the expandCluster pro-
cedure again and so on until all the records in D
′
are
processed at which point the algorithm will exist with
the cluster configuration C.
5.4 Secure k-Means (Sk-Means)
The secure k-Means process is again very similar to
the standard k-Means algorithm (MacQueen et al.,
1967). However, the mathematical operations are re-
placed with equivalent secure operations using the
HE properties as presented in Sub-section 3.1. The
pseudo code is given in Algorithm 7. The inputs
are the encrypted dataset D
′
, the SCDM and number
of desired clusters k. The algorithm commences by:
initialising the global variables (line 5), dimensioning
Algorithm 6: Secure DBSCAN clustering algorithm.
1: global variables
2: MinPts, ε
′
, SCDM, D
′
3: end global variables
4: procedure SDBSCAN(D
′
, SCDM, MinPts, ε
′
)
5: Initialized global variables with received values
6: C =
/
0, k = 0
7: for i = 1 to i = |D
′
| do
8: if r
′
i
is Unclustered then
9: S = regionQuery(r
i
)
10: if |S| > MinPts then
11: mark r
′
i
as clustered
12: k = k+ 1
13: C
k
= r
′
i
14: C
k
= expandCluster(C
k
,S)
15: C = C ∪C
k
16: Exit with C
17: procedure EXPANDCLUSTER(C,S)
18: for ∀ r
′
i
∈ S do
19: if r
′
i
is Unclustered then
20: mark r
′
i
as clustered
21: C = C∪ r
′
i
22: S
2
= regionQuery(r
i
)
23: if |S
2
| > MinPts then
24: C = expandCluster(C,S
2
)
25: Exit with C
26: procedure REGIONQUERY(r
′
Index
)
27: N
ε
= empty set
28: for ∀ r
′
j
∈ D do
29: distance = Sim(SCDM, r
′
Index
,r
′
j
) ⊲ (Eq. 3)
30: if distance ≤ ε
′
then
31: N
ε
.add(r
′
j
)
32: Exit with N
ε
the cluster array C = {C
1
,C
2
,. .. ,C
k
} and assigning
the first k encrypted records to it (lines 6 and 7). A
centroid set Cent = {cent
1
,cent
2
,. .. ,cent
k
} is thus
defined to hold the current centroids (lines 8 and 9).
The remaining encrypted data records are then as-
signed to a cluster according to their similarity with
respect to the cluster centroids using the populate-
Clusters procedure (called from line 10) and given at
the end of algorithm. In populateClusters the order of
similarity is calculated using the SCDM as shown in
Equation 3. A set of new centroids (Cent
′
) are then
calculated (line 11) using the HE properties of Liu’s
scheme. An iterative loop is then entered (lines 12 to
19) that repeats until stable centroids are arrived at.
The first step of each k-Means iteration is to calcu-
late the Shift matrix S (line 13) that represents the dis-
tances between the previous iteration centroids (Cent)
and the newly calculated centroids (Cent
′
). Note that
S, is calculated using the HE properties, over the HE
data ,therefore, the next step requires recourse to the
data owner (lines 14) to decrypt matrix (S) and re-
encrypt it using OPE to give S
′
so that it can be used
to update the SCDM (line 15). The algorithm will use
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
46

Algorithm 7: Secure k-Means clustering algorithm.
1: global variables
2: D
′
, SCDM
3: end global variables
4: procedure SK-MEANS(D
′
, SCDM, k)
5: Initialized global variables with received values
6: C = Set of k empty clusters
7: Assign first k records in D
′
to C (one per cluster)
8: Cent = Set of k cluster centroids
9: Assign first K records in D
′
to Cent
10: C = PopulateClusters(k+ 1,C,Cent)
11: Cent
′
= CalculateCentroids(C)
12: while Cent 6= Cent
′
do
13: S = Cent ⊖Cent
′
14: S
′
= S decrypted and encrypt result using OPE
15: SCDM = SCDM +S
′
16: C = Set of k empty clusters
17: C = PopulateClusters(1,C,Cent
′
)
18: Cent = Cent
′
19: Cent
′
= CalculateCentroids(C)
20: Exit with C
21: procedure POPULATECLUSTERS(x,C,Cent)
22: id = null
23: for x = x to x = |D
′
| do
24: for y = 1 to y = |C| do
25: sim = Sim(SCDM, r
x
,c
y
) ⊲ (Eq. 3)
26: id = cluster identifier with lowest sim
value so far
27: C
id
= C
id
∪ r
x
(C
id
∈ C)
28: Exit with C
S
′
to update the SCDM by concatenating the k el-
ements in S
′
to SCDM (line 15). In the follow-
ing iteration S
′
is used to update the first k elements
in the SCDM. Using the newly calculated centroids
all records are again assigned to each cluster, using
the populateClusters procedure, in the same manner
as before; and so on until a fixed configuration is
reached.
6 EVALUATION
The evaluation of the proposed clustering approaches
is presented in this section. For the purpose of the
evaluation fifteen datasets from the UCI data repos-
itory (Lichman, 2013) were selected in a manner so
that datasets of a variety of sizes and different num-
bers of classes could be considered (these are listed in
columns 2 and 3 of Table 1). The number of classes
in each case was used as the value for k in the case of
k-Means clustering. The proposed approaches were
implemented using the Java programming language.
The overall objective was to evaluate the proposed
algorithms in term of: (i) data owner participation,
(ii) scalability, (iii) clustering efficiency, (iv) cluster-
ing accuracy and (v) security.
Data owner participation was measured in terms
of the runtime required for data preparation and
SCDM generation, and the amount of data owner in-
volvement during the clustering process. Preparation
time results are presented in Table 1 where columns
4, 7 and 8 give the preparation times for: data en-
cryption, CDM calculation and CDM encryption re-
spectively. From the table, it can be seen that negli-
gible time was required for the data preparation; even
with respect to the largest dataset, Arrhythmia. For
SDBSCAN and SNNC no further data owner par-
ticipation was required, whereas in the case of Sk-
Means the participation was limited to the decryption
and re-encryption of the shift matrix, S, on each it-
eration; thus data owner participation was limited to
O(|C| × i), where |C| is the number of centroids and
i is the number of k-Means iterations, the same as in
the case of the UDM approach from (Almutairi et al.,
2017).
The chain feature in SCDM reduces the required
memory resources compared to the UDM concept in
(Almutairi et al., 2017). The number of elements in
a UDM grows exponentially with the data volume;
more formally it equals to (
n(n+1)
2
× |A|)) (Column
6 in Table 1 gives the number of UDM elements for
each experimental dataset). The SCDM is more com-
pact and hence requires significant lower resource
(Column 9 in Table 1) which makes it more appro-
priate for big data. This small number of elements
means that the time required to calculate an SCDM is
less than the UDM (as shown in Columns 5 and 7 in
Table 1).
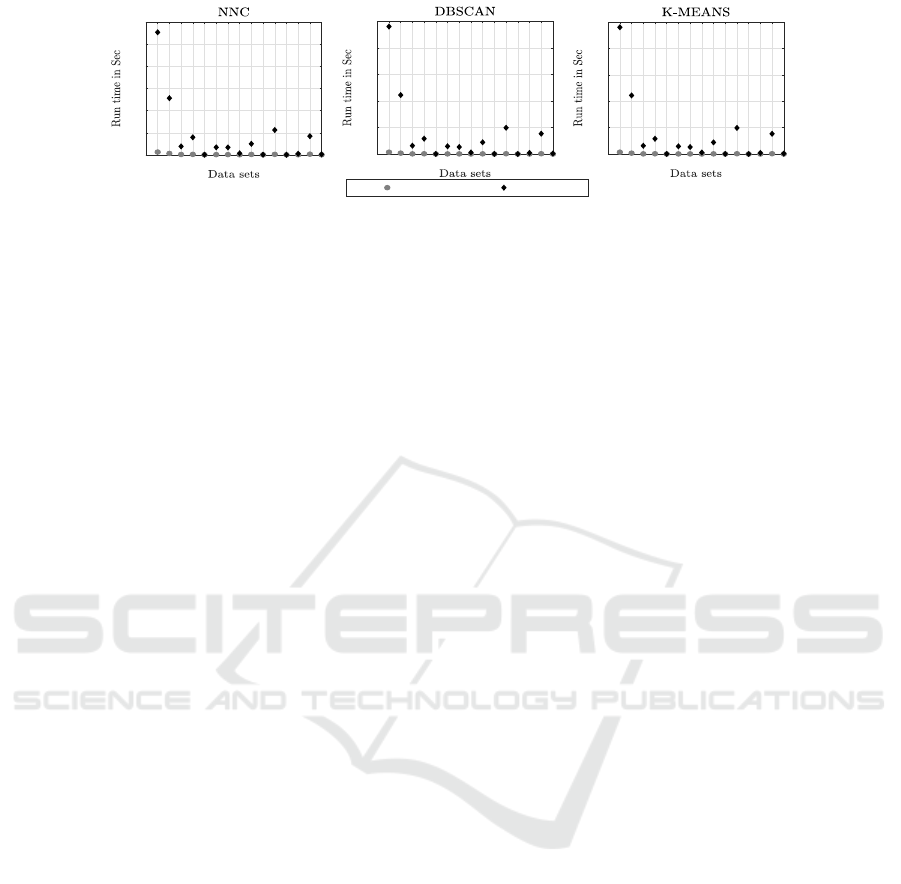
In terms of clustering efficiency, the runtime to
cluster the data using the proposed secure clustering
mechanisms was compared with the standard equiv-
alent processes. The runtime results are presented
in Figure 2. From the figure, it can be seen that the
overall runtimes required for the secure clustering ap-
proaches, as expected, were longer than in the case
of standard approaches, however, inspection of the
recorded results indicates that this did not present a
significant overhead. Of course, the bigger the dataset
the larger the SCDM, and consequently the greater
the time required to interact with the SCDM to clus-
ter data.
In terms of accuracy, cluster configuration “cor-
rectness” was measured by comparing the results
obtained with those obtained using standard (unen-
crypted) clustering algorithm equivalents. The pa-
rameters used (in practice selected by the data owner)
are given in columns 10 to 13 of Table 1. The accu-
racy metric used was the Silhouette Coefficient (Sil.
Coef.) (Rousseeuw, 1987), a real number value be-
tween −1 and +1, the closer the value is to 1 the bet-
Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices
47
Table 1: Run times for data owner data preparation and algorithm operating statistics.
Num Data UDM UDM CDM CDM CDM σ k Min ε
No. Dataset
R × C Class Encrypt. Cal. Size Cal. Encrypt. Size Pts
Labels (MSec) (MSec) (MSec) (MSec)
1. Arrhythmia 452×279 16 11.08 218.5 28563462 3.33 136.09 125829 1 16 2 600
2. Banknote Authent.
1372×4 2 1.24 81.5 3767512 0.2 32.08 5484 5 2 2 3
3. Blood transfusion
748×4 2 0.73 28.2 1120504 0.13 20.17 2988 68 2 2 10
4. Brest Cancer
699×9 2 1.64 31.6 2201850 0.19 27.36 6282 10 2 2 5
5. Breast Tissue
106×9 6 0.36 2.1 51039 0.03 23.73 945 1 6 2 100
6. Chronic Kidney Dis.
400×24 2 1.56 20.2 1924800 0.28 37.38 9576 100 2 2 70
7. Dermatology
366×34 6 1.88 22.9 2283474 0.43 31.77 12410 18 6 2 10
8. Ecoli
336×7 8 0.98 7.8 396312 0.09 31.54 2345 1 8 3 60
9. Ind. Liver Patient
583×10 2 0.99 23.3 1702360 0.15 39.39 5820 99 2 3 40
10. Iris
150× 4 3 0.24 2.9 45300 0.04 17.87 596 1 3 5 2
11. Libras Movement
360×90 15 4.01 50.3 5848200 1.26 92.07 32310 4 15 5 5
12. Lung cancer
32×56 3 0.61 1 29568 0.05 13.34 1736 1 3 2 20
13. Parkinsons
195×22 2 1.01 6.1 420420 0.13 36 4268 73 2 3 10
14. Pima Ind. Diabetes
768×8 2 1.18 36.6 2362368 0.18 37.18 6136 100 2 5 20
15. Seeds
210×7 3 0.51 4.8 155085 0.06 26.77 1463 1 3 5 1
Table 2: Cluster configuration comparison using standard and secure algorithms (differing results highlighted in bold font).
No.
Standard DBSCAN SDBSCAN Standard NNC SNNC Standard k-Means Sk-Means
Num. Sil. Num. Sil. Num. Sil. Num. Sil. Iter. Sil. Iter. Sil.
Clus. Coef Clus. Coef Clus. Coef Clus. Coef Coef Coef
1. 6 0.472 6 0.472 452 1.00 452 1 .00 10 0.536 10 0.536
2.
7 0.922 7 0.922 21 0.895 21 0.895 16 0.407 16 0.407
3.
27 0.971 33 0.976 34 0.999 35 0.999 12 0.595 12 0.595
4.
4 0.678 1 0.485 108 0.903 135 0.926 3 0.515 3 0.515
5.
3 0.628 3 0.628 105 1.00 105 1.00 18 0.984 18 0.984
6.
19 0.970 19 0.970 243 0.999 243 0.999 8 0.723 8 0.723
7.
16 0.853 15 0.881 32 0.919 37 0.915 15 0.744 9 0.713
8.
1 -1 .000 1 -1 .000 2 0.353 2 0.353 23 0.628 14 0.631
9.
7 0.789 7 0.789 100 0.997 100 0.997 13 0.569 13 0.569
10.
2 0.722 2 0.722 15 0.922 16 0.927 14 0.789 14 0.789
11.
11 0.715 11 0.715 224 0.969 224 0.969 18 0.557 18 0.557
12.
1 0.053 1 0.053 32 1.00 32 1.00 8 0.146 3 0.076
13.
5 0.829 5 0.829 11 0.953 11 0.953 7 0.406 7 0.406
14.
4 0.691 4 0.691 22 0.956 22 0.956 8 0.485 8 0.485
15.
7 0.852 7 0.852 103 0.979 103 0.979 6 0.681 6 0.681
ter the clustering. The results obtained are presented
in Table 2. From the table, it can be seen that the clus-
ter configurations produced using the proposed secure
algorithms were the same in 35 of the 45 cases (same
number of clusters). Where the configurations were
different, in one case the Sil. Coef. value was the
same, in the remaining nine cases the Sil. Coef. value
using the secure clustering was better in five of the
nine occasions. The reason for the different configu-
rations sometimes obtained was the nature of the pro-
posed OPE scheme; although ensuring that the CDM
was secure against Statistical Attacks and Cypher-
text Only Attacks by producing different cyphertext
for the same plaintext, usage of the OPE scheme did
sometimes affect the nature of the clustering because
equality is not preserved. Consequently different Sil.
Coef. values were sometimes produced in these cases,
although in most cases these differences were not sig-
nificant.
The security of the proposed clustering relies on
the security of: (i) Liu’s scheme used to encrypt the
raw data and (ii) the proposed OPE scheme used to
encrypt the CDM. Liu’s scheme has been shown to
be semantically secure (Liu, 2013); given any cypher-
text C within a message m the ability of an adversary
to determine any partial information concerning the
message will be negligible in terms of the input, hence
the scheme is “probably secure”. In other words, it
will be computationally expensive to derive informa-
tion concerning the encrypted plaintext given only the
cyphertexts and the corresponding encryption public
key. This feature makes the proposed method se-
cure against Chosen-Plaintext Attack (CPA) and con-
sequently secure against Knowing Plaintext Attack
(KPA) and Cyphertext Only Attack (COA). More-
over, once the data is encrypted and outsourced to a
third party data miner, using the proposed approaches,
no decryption takes place at the third party side which
implies even more security. In terms of the pro-
posed OPE scheme, preserving the order of gener-
ated cyphertexts raises a threat of Cyphertext Only
Attacks (COAs) that use statistical features, assum-
ing that the data distribution is known. Therefore, the
adopted OPE mechanism utilises the conceptof “mes-
sage space splitting” and “non-linear cypher space ex-
pansion” to obscure the data distribution in the gener-
ated cyphertexts, thus protecting against COAs. Fur-
thermore, the encryption function has a one-to-many
mapping feature that produces different cyphertexts
for the same plaintext value even when the same keys
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
48
0 1 2 3 4 5 6 7 8 9 1011 1213 1415
0
50
100
150
200
250
300
0 1 2 3 4 5 6 7 8 9 1011 1213 1415
0
100
200
300
400
500
0 1 2 3 4 5 6 7 8 9 1011 1213 1415
0
100
200
300
400
500
Standard Secure
Figure 2: Comparison of run times using standard and secure clustering algorithms (NNC, DBSCAN and k-means).
are used; this makes it harder to derive any informa-
tion from inspecting the cyphertexts.
7 CONCLUSION
In this paper a secure clustering mechanisms has been
proposed using the idea of an SCDM. The usage of
the SCDM was illustrated in the context of three clus-
tering approaches: (i) Secure DBSCAN, (ii) Secure
Nearest Neighbour and (iii) Secure k-Means. The ad-
vantages offered by the SCDM are firstly that it is
compact and thus appropriate for large datasets; the
SCDM requires significantly lower resource in terms
of memory and user interaction overhead, compared
to (say) the UDM concept presented in (Almutairi
et al., 2017). Secondly, the proposed OPE encryption
provides an adequate level of security against COA.
Thirdly, compared to other proposed secure clustering
approaches, data owner participation during the clus-
tering process is zero with respect to SDBSCAN and
SNNC, and limited with respect to Sk-Means. Eval-
uation was conducted, using fifteen UCI datasets, by
comparing the operation of the secure clustering al-
gorithms with their standard counterparts. The eval-
uation demonstrated that the quality of the cluster-
ing was similar although not always identical (some-
times better). The reason for the differences was the
random parameter δ added to OPE cyphertext which
made equality comparison impossible. The runtime,
as was to be expected, was greater with respect to se-
cure clustering, but not significantly so. For future
work, the authors intend to develop a “Super CDM”
where the represented data belongs to two or more
data owners who do not wish to share their data in an
unencrypted form.
REFERENCES
Agrawal, R. and Srikant, R. (2000). Privacy-preserving data
mining. In ACM Sigmod Record, volume 29, pages
439–450. ACM.
Almutairi, N., Coenen, F., and Dures, K. (2017). K-means
clustering using homomorphic encryption and an up-
datable distance matrix: Secure third party data clus-
tering with limited data owner interaction. In 19th
International Conference on Big Data Analytics and
Knowledge Discovery.
Berinato, S. (2015). There
˜
Os no such thing as anonymous
data. Harvard Business Review, February.
Chhinkaniwala, H. and Garg, S. (2011). Privacy preserv-
ing data mining techniques: Challenges and issues.
In Proceedings of International Conference on Com-
puter Science & Information Technology, CSlT, page
609.
Cover, T. and Hart, P. (1967). Nearest neighbor pattern clas-
sification. IEEE transactions on information theory,
13(1):21–27.
Erkin, Z., Veugen, T., Toft, T., and Lagendijk, R. L. (2009).
Privacy-preserving user clustering in a social network.
In 2009 First IEEE International Workshop on Infor-
mation Forensics and Security (WIFS), pages 96–100.
IEEE.
Ester, M., Kriegel, H.-P., Sander, J., Xu, X., et al. (1996).
A density-based algorithm for discovering clusters in
large spatial databases with noise. In Kdd, volume 96,
pages 226–231.
Hazay, C., Mikkelsen, G. L., Rabin, T., and Toft, T. (2012).
Efficient RSA key generation and Threshold Paillier
in the two-party setting. In CT-RSA, pages 313–331.
Springer.
Jha, S., Kruger, L., and McDaniel, P. (2005). Pri-
vacy preserving clustering. In European Symposium
on Research in Computer Security, pages 397–417.
Springer.
Lichman, M. (2013). UCI machine learning repository.
Lindell, Y. and Pinkas, B. (2002). Privacy preserving data
mining. Journal of cryptology, 15(3):177–206.
Liu, D. (2013). Homomorphic encrypton for database
querying.
Liu, D., Bertino, E., and Yi, X. (2014). Privacy of out-
sourced k-means clustering. In Proceedings of the 9th
ACM symposium on Information, computer and com-
munications security, pages 123–134. ACM.
Liu, D. and Wang, S. (2013). Nonlinear order preserving
index for encrypted database query in service cloud
environments. Concurrency and Computation: Prac-
tice and Experience, 25(13):1967–1984.
Liu, Z., Chen, X., Yang, J., Jia, C., and You, I. (2016). New
order preserving encryption model for outsourced
Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices
49

databases in cloud environments. Journal of Network
and Computer Applications, 59:198–207.
MacQueen, J. et al. (1967). Some methods for classification
and analysis of multivariate observations. In Proceed-
ings of the fifth Berkeley symposium on mathematical
statistics and probability, volume 1, pages 281–297.
Oakland, CA, USA.
Mittal, D., Kaur, D., and Aggarwal, A. (2014). Secure
data mining in cloud using homomorphic encryption.
In Cloud Computing in Emerging Markets (CCEM),
2014 IEEE International Conference on, pages 1–7.
IEEE.
Rahman, M. S., Basu, A., and Kiyomoto, S. (2017). To-
wards outsourced privacy-preserving multiparty DB-
SCAN. In Dependable Computing (PRDC), 2017
IEEE 22nd Pacific Rim International Symposium on,
pages 225–226. IEEE.
Rao, F.-Y., Samanthula, B. K., Bertino, E., Yi, X., and Liu,
D. (2015). Privacy-preserving and outsourced multi-
user k-means clustering. In Collaboration and In-
ternet Computing (CIC), 2015 IEEE Conference on,
pages 80–89. IEEE.
Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to
the interpretation and validation of cluster analysis.
Journal of computational and applied mathematics,
20:53–65.
Samanthula, B. K., Elmehdwi, Y., and Jiang, W. (2015). K-
nearest neighbor classification over semantically se-
cure encrypted relational data. IEEE transactions on
Knowledge and data engineering, 27(5):1261–1273.
Shaneck, M., Kim, Y., and Kumar, V. (2009). Privacy pre-
serving nearest neighbor search. In Machine Learning
in Cyber Trust, pages 247–276. Springer.
Tong, Q., Li, X., and Yuan, B. (2018). Efficient distributed
clustering using boundary information. Neurocomput-
ing, 275:2355 – 2366.
Vaidya, J., Clifton, C. W., and Zhu, Y. M. (2006). Privacy
preserving data mining, volume 19. Springer Science
& Business Media.
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
50
