
Sentiment Classification using N-ary Tree-Structured Gated Recurrent
Unit Networks
Vasileios Tsakalos and Roberto Henriques
NOVA IMS Information Management School, Universidade Nova de Lisboa, 1070-312, Lisboa, Portugal
Keywords:
Recursive Neural Network, Gated Recurrent Units, Natural Language Processing, Sentiment Classification.
Abstract:
Recurrent Neural Networks(RNN) is a good way of modeling sequences. However this type of Artificial
Neural Networks(ANN) has two major drawbacks, it is not good at capturing long range connections and it is
not robust at the vanishing gradient problem(Hochreiter, 1998). Luckily, there have been invented RNNs that
can deal with these problems. Namely, Gated Recurrent Units(GRU) networks(Chung et al., 2014)(G
¨
ulc¸ehre
et al., 2013) and Long Short Term Memory(LSTM) networks(Hochreiter and Schmidhuber, 1997). Many
problems in Natural Language Processing can be approximated with a sequence model. But, it is known that
the syntactic rules of natural language have a recursive structure(Socher et al., 2011b). Therefore a Recursive
Neural Network(Goller and Kuchler, 1996) can be a great alternative. Kai Sheng Tai (Tai et al., 2015) has
come up with an architecture that gives the good properties of LSTM in a Recursive Neural Network. In this
report, we will present another alternative of Recursive Neural Networks combined with GRU which performs
very similar on binary and fine-grained Sentiment Classification (on Stanford Sentiment Treebank dataset)
with N-ary Tree-Structured LSTM but is trained faster.
1 INTRODUCTION
Since the beginning of Deep Learning era, many
things have changed in Natural Language Proces-
sing(NLP). The academic community keeps on re-
defining the state-of-art performance for various NLP
tasks. One of the most important contributions
to the advancement of NLP is due to the use of
word vectors (Mikolov et al., 2013b)(Mikolov et al.,
2013a)(Pennington et al., 2014)(Luong et al., 2013).
Another family of tools that were improved with Deep
Learning and boosts the performance of NLP models
by helping in disambiguation, are the syntactic par-
sers (Charniak and Johnson, 2005) (Chen and Man-
ning, 2014)(McDonald et al., 2006) that understand
the structure of sentences. Having defined the syn-
tactic structure of the sentences, the next step is to
understand the meaning of sentences. Before the era
of Deep Learning, the semantic expressions were for-
med by lambda calculus (Hofmann, 1999) which is
a very time consuming method and does not provide
any notion of similarity. With Deep Learning the
words and word phrases are represented as vectors, a
neural network takes those vectors as inputs to a soft-
max classifier that predicts the relationship between
those two sentences(Bowman et al., 2014). Beyond
the pre-processing steps, Deep Learning is also invol-
ved in the modeling process of NLP tasks. Artificial
Neural Networks have achieved state-of-art perfor-
mance at Question-Answering tasks (Berant and Li-
ang, 2014), Dialogue agents(Chat-bots)(Young et al.,
2013)(Dhingra et al., 2016), Machine Translation
(Sutskever et al., 2014)(Bahdanau et al., 2014)(See
et al., 2016), Speech Recognition (Graves et al., 2013)
and Sentiment Classification. In this paper we will fo-
cus on Sentiment Classification. There are three ways
of modeling a Sentiment Classification problem. The
first one is a bag-of-words approach which consults
a list of ”positive” and ”negative” words to deter-
mine the sentiment of sentence without considering
the order of words. The second approach is a se-
quence model that construct the sentence representa-
tion taking into account the order of words. The third
approach, which is a superset of the second appro-
ach, is a tree-structured model that considers the syn-
tactic structure of the sentence(Socher et al., 2011a),
not just the order of the words. It was proven that
tree-structure models have state-of-art of performance
for fine-grained classification tasks and close to state-
of-art performance for binary classification(Tai et al.,
2015). The goal of this paper is to introduce a new
architecture, named N-ary tree-structured GRU, and
Tsakalos, V. and Henriques, R.
Sentiment Classification using N-ary Tree-Structured Gated Recurrent Unit Networks.
DOI: 10.5220/0006894201490154
In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 1: KDIR, pages 149-154
ISBN: 978-989-758-330-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
149

compare it with N-ary tree-structured LSTM.
2 GATED RECURRENT UNIT
Gated recurrent unit is a variant of RNN proposed by
KyungHyun Cho(Chung et al., 2014). It is closely re-
lated Long-Short Term Memory. The GRU also con-
trols the flow of information like the LSTM, but wit-
hout using a memory unit. It exposes the full hidden
content without any control.
A GRU has two gates, a reset gate (r), and an up-
date gate (z). The reset gate indicates how to combine
the new input with the previous memory. The update
gate defines how much of the previous state to keep.
The basic idea of using a gating mechanism to learn
long-term dependencies is the same as in a LSTM,
but there are a few differences in terms of architec-
ture. First of all, it doesn’t have an output gate so
it has fewer parameters (two gates, instead of three).
Secondly the input and forget gates are substituted by
an update gate z and the reset gate r is applied directly
to the previous hidden state. Thus, the responsibility
of the reset gate in a LSTM is really split up into both
r and z. Finally we don’t apply a second nonlinearity
when we compute the output.
Figure 1: Gated Recurrent Unit.
In more detail, GRU has a variable h, as all re-
current units, but with only difference that it upda-
tes that variable selectively. At every time-step we
calculate a candidate hidden state
˜
h
t
(3) using the re-
set gate which determines how useful in the new in-
put (1). Having calculated the candidate hidden state,
we recalculate the current hidden state (h
t
) (4) as the
weighted sum of the candidate hidden state (
˜
h
t
) and
the last time-step’s hidden state (dispplaystyleh
t−1
)
using the update gate (2) value as weight.
r
t
= σ(W
(r)
x
t
+U
(r)
h
t−1
) (1)
z
t
= σ(W
(z)
x
t
+U
(z)
h
t−1
) (2)
˜
h
t
= tanh(W
(h)
x
t
+U
(h)
(h
t−1
r
t
)) (3)
h
t
= (1 −z)
˜
h
t
+ z h
t−1
(4)
3 N-ARY TREE-STRUCTURED
GATED RECURRENT UNITS
N-ary Tree-structured Gated Recurrent Unit is a natu-
ral extension of standard GRU. Standard GRU can be
considered as a special case of N-ary Tree-structured
GRU that has only one child at every node and that
child is not selected based on semantic plausibility but
on its location in the sentence. N-ary Tree-structured
GRU’s recursive structure ,unlike standard GRU’s li-
near structure, helps it incorporate information from
multiple children and its gating units help it select the
meaningful children.
N-ary Tree-structured Gated Recurrent Unit net-
works can be thought as a standard Recursive Neu-
ral Network but when it comes to the calculation of
the parent node it applies the Gated Recurrent Unit
principles and it only keeps the information from the
children nodes that are semantically important.
Just like the standard GRU, N-ary Tree-structured
Gated Recurrent Unit incorporates information using
reset(r
ik
) and update(z
i
) gates. The major difference
between the two architectures is that at the sequential
model (GRU) we only have one previous state (child),
while in the N-ary Tree-GRU we have k children. In
the proposed architecture, we use k reset gates and
one update gate.
Let’s assume we want to calculate the i
th
parent
that is composed by k children nodes, each children
will have its own reset gate (r
ik
) that decide the im-
pact of every child node to the candidate parent node
(
˜
h
i
)7. Having calculated the candidate parent node,
we calculate the parent node 8 using the weighted sum
of candidate parent node (h
i
), and the children nodes
using update gate (z
i
) 6 as weight.
r
ik
= σ(W
r
x
i
+
N
∑
l=1
U
r
kl
h
il
+ b
r
) (5)
z
i
= σ(W
z
x
i
+
N
∑
l=1
U
z
l
h
jl
+ b
z
) (6)
˜
h
i
= tanh(W
h
x
i
+
N
∑
l=1
U
h
l
(h
il
r
il
) + b
h
) (7)
h
i
= (1 −z
i
)
˜
h
i
+
N
∑
l=1
z
i
N
hil (8)
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
150

Figure 2: N-ary Tree-Structured Gated Recurrent Unit.
4 METHODOLOGY
This section is dedicated to the practical comparison
between the Constituent LSTM, with the N-ary Tree-
Structured GRU.
4.1 Data Pre-processing
It is important to notice that the experiments have
been conducted 5 times and the results are the product
of the averaged results of all the trials. We use the
Stanford Sentiment Treebank (SST), and we use the
standard train/validation/test splits of 6920/872/1821
for the binary classification task and 8544/1101/2210
for the fine-grained classification task (there are fewer
examples for the binary task since the neutral instan-
ces have been excluded). Moreover, the SST have
each sentence structured as constituent parse trees,
so we will use the N-ary Tree Structured LSTM(Tai
et al., 2015) as a comparison to our model.
4.2 Classification Model
The goal of the paper is to compare the performance
of N-ary Tree-GRU architecture against the N-ary
Tree-LSTM architecture on sentiment classification
tasks. In practice, the model predicts a label ˆy from
a set of classes (2 for binary, 5 for fine grained) for
some subset of nodes in a tree. The classifier and the
objective function are exactly the same for both archi-
tectures. Let {x}
i
be the inputs observed at nodes in
the subtree with root the node i.
ˆp
θ
(y | {x}
i
) = so f tmax(W
p
h
i
+ b
p
), (9)
ˆy
i
= argmax
y
ˆp
θ
(y | {x}
i
). (10)
Let m be the number of labeled nodes in the trai-
ning set and the superscript k be the k
th
labeled node,
the cost function is:
J(θ) = −
1
m
m
∑
k=1
log ˆp
θ
(y
(k)
| {x}
(k)
) +
λ
2
kθk
2
2
(11)
4.3 Binary Classification
The binary classification is a problem that classifies
whether the sentiment of the sentence is positive or
negative. The process of the training can be seen at
the Figures 3 , 4, and 5. All the plots have as their
x-axis the number of epochs.
In more detail, at Figure 3 it is clear that N-
ary Tree-structured GRU is being trained faster than
N-ary Tree-structured LSTM. With regards to the
training loss, we can see that N-ary Tree-structured
GRU’s training loss curve is steeper at the begin-
ning but it seems to keep decreasing when the trai-
ning loss curve for N-ary Tree-structured LSTM gets
steep. Finally, we can see the training process at Fi-
gure 5 where the performance of validation set of N-
ary Tree-structured LSTM seems to be better than N-
ary Tree-structured GRU but at the end of training
process they perform similar.
4.4 Fine-grained Classification
The Fine-grained classification is a 5-class senti-
ment classification (1-Very Negative, 2-Negative, 3-
Neutral, 4-Positive, 5-Very Positive). The experiment
for the Fine-grained classification is under the same
circumstances.
The average training time can be illustrated
at Figure 6 where it is clear that N-ary Tree-
Structured GRU is being trained faster than N-ary
Tree-structured LSTM. Regarding the average loss
(Figure 7), the N-ary Tree-structured GRU’s trai-
ning loss curve is slightly steeper than N-ary Tree-
structured LSTM’s training loss curve. Finally, the
training process is illustrated at Figure 8 where we can
see that the two architectures perform similar even
though N-ary Tree-structured GRU starts overfitting
early on the training process.
All the plots have as their x-axis the number of
epochs. The metrics that we plot are computed up
until the 13
th
epoch and in cases of early stopping
1
we wouldn’t take into account the 0 or ”Non Assig-
ned Number” of the trial that its training stopped ear-
lier but we would just skip it and calculate the results
based on the rest trials that had a full training process.
1
Early stopping: when the validation error increases for
a specified number of iterations, the training process stops
Sentiment Classification using N-ary Tree-Structured Gated Recurrent Unit Networks
151
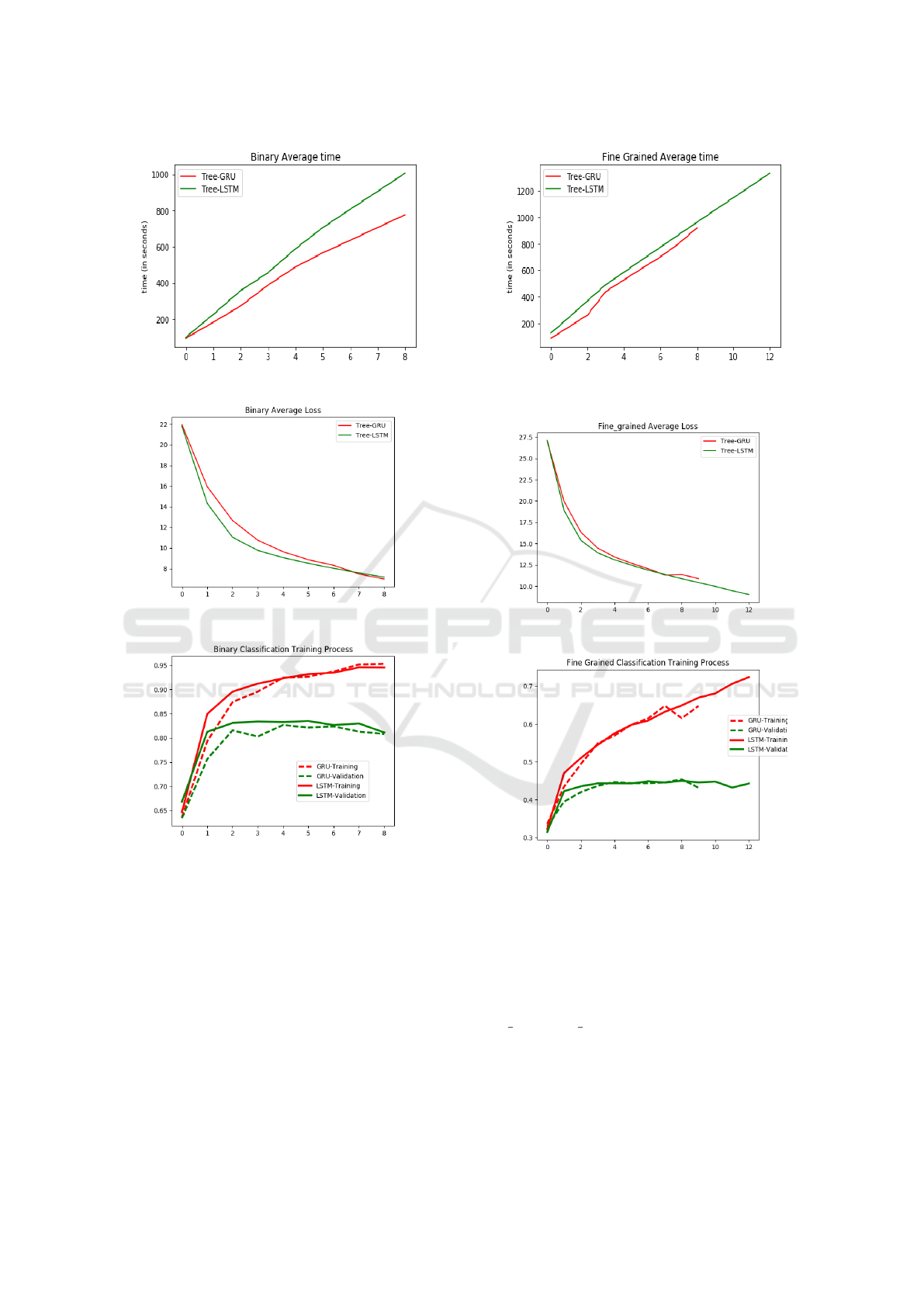
Figure 3: Binary Classification Average Training Time.
Figure 4: Binary Classification Average Training Loss.
Figure 5: Binary Classification Training Process.
4.5 Experimental Settings
We have initialized the word representations
using the pre-trained 300-dimensional GloVe vec-
tors(Pennington et al., 2014).The training of the
model was done with AdaGrad(Duchi et al., 2011)
using learning rate of 0.05 and mini-batch gradient
descent algorithm with batch size of 25. The model
parameters were regularized with L2 regularization
strength of 0.0001 and dropout rate of 0.5. For the
training process we have applied the early stopping
technique in order to avoid overfitting.
The goal of this paper is not to achieve a state-
Figure 6: Fine Grained ClassificationAverage Training
Time.
Figure 7: Fine Grained Classification Average Loss.
Figure 8: Fine Grained Classification Training Process.
of-art accuracy but to make a critical comparison be-
tween the two models therefore we won’t update the
word representations during the training which boosts
the accuracy approximately 0.05 (the accuracy boost
gave to the N-ary Tree-LSTM).
Please find the code necessary for running
those experiments at https://github.com/VasTsak/
Tree Structured GRU.
4.6 Results
The results of both the binary and fine grained classi-
fication can be seen in Table 1 we can see that N-ary
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
152

Tree-Structured GRU has on average slightly better
performance than N-ary Tree-structured LSTM, but it
is important to notice from Table 2 the standard de-
viation of the individual predictions from N-ary Tree-
GRU seem to fluctuate more than the ones from N-ary
Tree-LSTM therefore it is possible that this difference
of performance can be random.
Something important to notice about the training
process of fine grained classification is that N-ary
Tree-Structured GRU would stop at the 9
th
iteration
while N-ary Tree-Structured LSTM would go all the
way till the 13
th
iteration. Moreover another im-
portant point is that the N-ary Tree-LSTM for fine-
grained classification seems like it has some more
training to do before it overfits, in contrast with N-ary
Tree-GRU which would overfit before having execu-
ted twelve iterations, which can be observed above
(Figures 8). This may have to do with the hyperpa-
rameters that we have chosen. We have set the early
stopping at 2 iterations (as the authors of N-ary Tree-
Structured LSTM paper had), if we would set it to 3
the N-ary Tree-GRU may keep on training till the 12
th
iteration.
Moreover N-ary Tree-GRU’s training and valida-
tion scores seem to fluctuate more in the fine-grained
classification 8 which may underlies unstable pre-
diction and the need to train more.
Table 1: Sentiment Classification Accuracy.
Model Binary Fine-grained
N-ary Tree-LSTM 84.43 45.71
N-ary Tree-GRU 85.61 46.43
Table 2: Sentiment Classification Standard Deviation.
Model Binary Fine-grained
N-ary Tree-LSTM 0.93 0.35
N-ary Tree-GRU 0.98 0.55
5 CONCLUSION AND FUTURE
DIRECTIONS
We can conclude that there is a difference in terms
of performance, not that significant though, between
the tree-structured LSTM and tree-structured GRU.
Moreover, tree-structured GRUs are trained faster -
computationally- since they have fewer parameters.
Therefore it is a good alternative, if not a substi-
tute. The area of Natural Language Processing is very
active area of research, tree-structured architectures
proved to be very powerful for Natural Language Pro-
cessing tasks, mostly because of their capability of
handling negations. Many potential projects can be
developed around Tree-Based GRUs, namely a Child-
Sum approach,or the of use unique reset and update
gate for each child, or even try different GRU archi-
tectures (Dosovitskiy and Brox, 2015).
REFERENCES
Bahdanau, D., Cho, K., and Bengio, Y. (2014). Neural ma-
chine translation by jointly learning to align and trans-
late. CoRR, abs/1409.0473.
Berant, J. and Liang, P. (2014). Semantic parsing via para-
phrasing. In Association for Computational Linguis-
tics (ACL).
Bowman, S. R., Potts, C., and Manning, C. D. (2014). Re-
cursive neural networks for learning logical seman-
tics. CoRR, abs/1406.1827.
Charniak, E. and Johnson, M. (2005). Coarse-to-fine n-best
parsing and maxent discriminative reranking. In Pro-
ceedings of the 43rd Annual Meeting on Association
for Computational Linguistics, ACL ’05, pages 173–
180, Stroudsburg, PA, USA. Association for Compu-
tational Linguistics.
Chen, D. and Manning, C. (2014). A Fast and Accurate De-
pendency Parser using Neural Networks. Proceedings
of the 2014 Conference on Empirical Methods in Na-
tural Language Processing (EMNLP), (i):740–750.
Chung, J., G
¨
ulc¸ehre, C¸ ., Cho, K., and Bengio, Y. (2014).
Empirical evaluation of gated recurrent neural net-
works on sequence modeling. CoRR, abs/1412.3555.
Dhingra, B., Li, L., Li, X., Gao, J., Chen, Y., Ahmed, F.,
and Deng, L. (2016). End-to-end reinforcement lear-
ning of dialogue agents for information access. CoRR,
abs/1609.00777.
Dosovitskiy, A. and Brox, T. (2015). Inverting convoluti-
onal networks with convolutional networks. CoRR,
abs/1506.02753.
Duchi, J., Hazan, E., and Singer, Y. (2011). Adaptive
Subgradient Methods for Online Learning and Sto-
chastic Optimization. Journal of Machine Learning
Research, 12:2121–2159.
Goller, C. and Kuchler, A. (1996). Learning task-
dependent distributed representations by backpropa-
gation through structure. In Neural Networks, 1996.,
IEEE International Conference on, volume 1, pages
347–352 vol.1.
Graves, A., Jaitly, N., and rahman Mohamed, A. (2013).
Hybrid speech recognition with deep bidirectional
lstm. In In IEEE Workshop on Automatic Speech Re-
cognition and Understanding (ASRU.
G
¨
ulc¸ehre, C¸ ., Cho, K., Pascanu, R., and Bengio, Y.
(2013). Learned-norm pooling for deep neural net-
works. CoRR, abs/1311.1780.
Hochreiter, S. (1998). The vanishing gradient problem du-
ring learning recurrent neural nets and problem soluti-
ons. Int. J. Uncertain. Fuzziness Knowl.-Based Syst.,
6(2):107–116.
Sentiment Classification using N-ary Tree-Structured Gated Recurrent Unit Networks
153

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural Comput., 9(8):1735–1780.
Hofmann, M. (1999). Semantics of linear/modal
lambda calculus. J. Funct. Program., 9(3):247–277.
Luong, M.-T., Socher, R., and Manning, C. D. (2013). Bet-
ter Word Representations with Recursive Neural Net-
works for Morphology. CoNLL-2013, pages 104–113.
McDonald, R., Lerman, K., and Pereira, F. (2006). Multilin-
gual dependency analysis with a two-stage discrimi-
native parser. Proceedings of the Tenth Conference on
Computational Natural Language Learning - CoNLL-
X ’06, page 216.
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a).
Efficient estimation of word representations in vector
space. CoRR, abs/1301.3781.
Mikolov, T., Sutskever, I., Chen, K., Corrado, G., and Dean,
J. (2013b). Distributed Representations of Words and
Phrases and their Compositionality. pages 1–9.
Pennington, J., Socher, R., and Manning, C. D. (2014).
Glove: Global vectors for word representation. In
Empirical Methods in Natural Language Processing
(EMNLP), pages 1532–1543.
See, A., Luong, M., and Manning, C. D. (2016). Compres-
sion of neural machine translation models via pruning.
CoRR, abs/1606.09274.
Socher, R., Lin, C. C., Ng, A. Y., and Manning, C. D.
(2011a). Parsing Natural Scenes and Natural Lan-
guage with Recursive Neural Networks. In Procee-
dings of the 26th International Conference on Ma-
chine Learning (ICML).
Socher, R., Lin, C. C.-Y., Ng, A. Y., and Manning, C. D.
(2011b). Parsing natural scenes and natural language
with recursive neural networks. In Proceedings of the
28th International Conference on International Con-
ference on Machine Learning, ICML’11, pages 129–
136, USA. Omnipress.
Socher, R., Perelygin, A., and Wu, J. (2013). Recursive
deep models for semantic compositionality over a sen-
timent treebank. Proceedings of the . . . , pages 1631–
1642.
Sutskever, I., Vinyals, O., and Le, Q. V. (2014). Sequence
to sequence learning with neural networks. CoRR,
abs/1409.3215.
Tai, K. S., Socher, R., and Manning, C. D. (2015). Improved
semantic representations from tree-structured long
short-term memory networks. CoRR, abs/1503.00075.
Young, S., Ga
ˇ
si
´
c, M., Thomson, B., and Williams, J. D.
(2013). POMDP-based statistical spoken dialog
systems: A review. Proceedings of the IEEE,
101(5):1160–1179.
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
154
