Many-Objective Nurse Scheduling using NSGA-II based on

Pareto Partial Dominance with Linear Subset-size Scheduling

Makoto Ohki

Department of Information and Electronics, Graduate School of Tottori University,

4, 101 Koyama-Minami, Tottori, Tottori 680-8552 Japan

Keywords:

Many-objective Optimization, Combinatorial Optimization, Nurse Scheduling, Evolutionary Algorithm,

NSGA-II, Pareto Partial Dominance, Sub-set Size Scheduling.

Abstract:

This paper describes a nurse scheduling in Japanese standard general hospitals. In the standard general hospital

in Japan basically three shift system is adopted for nurses working in there. We have compiled evaluations of

the monthly nurse schedule into twelve penalty functions in the past work. These twelve penalty functions are

translated to twelve objective functions in this paper. The nurse scheduling with twelve objective functions

is solved as a multi-objective optimization problem by means of NSGA-II. The optimization is insufﬁcient

when NSGA-II is applied to such an optimization problem with four or more objective functions, known as a

many-objective optimization problem. One method for reducing this problem is a technique based on Pareto

partial dominance. In this technique, the partial non-dominated sorting is executed by using a subset selected

from all objective functions. In the conventional technique, the schedule of subset size over optimization has

to be prepared beforehand in the form of a list. Moreover, the selection list brings a great inﬂuence on the

result of optimization. Creating such a selection list is a heavy burden for the user. This paper proposes a

technique of NSGA-II based on Pareto partial dominance with a linear subset-size scheduling. By embedding

the subset-size scheduling into the algorithm, the user, namely the chief nurse, is released from the designing

of the selection list.

1 INTRODUCTION

General hospitals consist of several sections such as

the internal medicine department and the pediatrics

department. Each section is organized by about ﬁfty

to thirty nursing staffs. A section manager constitutes

a roster, or a shift schedule, of all nurses of her/his

section every month. In our interviewing research to

the actual hospitals (Ohki et al., 2006; Uneme et al.,

2008) , we found that the manager considers more

than ﬁfteen requirements for the scheduling. Such

the schedule arrangement, in other words, the nurse

scheduling, is a very complex task. In the interview,

even a veteran manager usually spends 1 or 2 weeks

to complete nurse scheduling. Moreover, the schedule

obtained after such hardships is not always satisfac-

tory. This means a great loss of work force. There-

fore, computer software for the nurse scheduling has

been recently come to require in the general hospi-

tals (Goto et al., 1993; Berrada et al., 1996; Ikegami,

2001; Burke et al., 2001a; Burke et al., 2001b; Kawa-

naka et al., 2002; Itoga et al., 2003; Ohki et al., 2006;

Uneme et al., 2008; Ohki, 2012).

In fact, the nurse schedule is still made by the hand

of a manager or a chief nurse in many general hospi-

tals. In our survey (Ohki et al., 2006; Ohki, 2012),

many general hospitals does not do the nurse sche-

duling using a commercial software, even when they

have purchased it at high price. This is because the

purchased software gives unsatisfactory optimization

results and that it is very complicated to set and dif-

ﬁcult to use. So that many interactions to correct the

schedule are also very complex for the user.

As a result of interviewing at many general hospi-

tals, twelve evaluation functions are deﬁned for the

nurse scheduling. That is, the nurse scheduling is

a multi-objective optimization problem (MOP). This

paper discusses a creation of the nurse schedule and

an optimization of it by means of multi-objective

evolutionary algorithm (MOEA). When creating the

nurse schedule, the only one constraint condition for

this problem is the degree of satisfaction of the num-

ber of nurses in each work shift. This constraint is

invalidated by restricting a crossover operator and a

mutation operator proposed in this paper. Thus, the

118

Ohki, M.

Many-Objective Nurse Scheduling using NSGA-II based on Pareto Partial Dominance with Linear Subset-size Scheduling.

DOI: 10.5220/0006894501180125

In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 118-125

ISBN: 978-989-758-327-8

nurse scheduling is deﬁned as an unconstrained multi-

objective optimization problem.

Although NSGA-II is well-known as one of ef-

fective optimizing frameworks for MOP, it is also

known that the ability of optimization signiﬁcantly

decreases for the problem with 4 or more ob-

jective functions (Aguirre and Tanaka, 2007; Tsu-

chida et al., 2009; Sato et al., 2006), in ot-

her words, many-objective optimization problem

(MaOP)(Hughes, 2005). This paper focuses NSGA-

II based on Pareto partial dominance (Brockhoff and

Zitzler, 2006; Sato et al., 2010) for MaOP. Since

NSGA-II based on Pareto partial dominance requires

a scheduling list of the size of the target subset se-

lected from all objective functions beforehand. Since

the selection list for Pareto partial dominance largely

affects the quality of the optimization, it is very difﬁ-

cult to prepare by the user. Therefore, this paper pro-

poses a technique to automatically schedule the sub-

set size for Pareto partial dominance. By means of

the proposed technique the user is not only released

from creation of the selection list, but also obtain an

effectively optimized nurse schedule.

2 MANY OBJECTIVE NURSE

SCHEDULING

Many nurse organizations of the general hospitals in

Japan are operated according to the three shift system,

including a day shift, an evening shift and night shift.

About twenty to thirty nurses belong to each depart-

ment of the general hospital. The chief of each de-

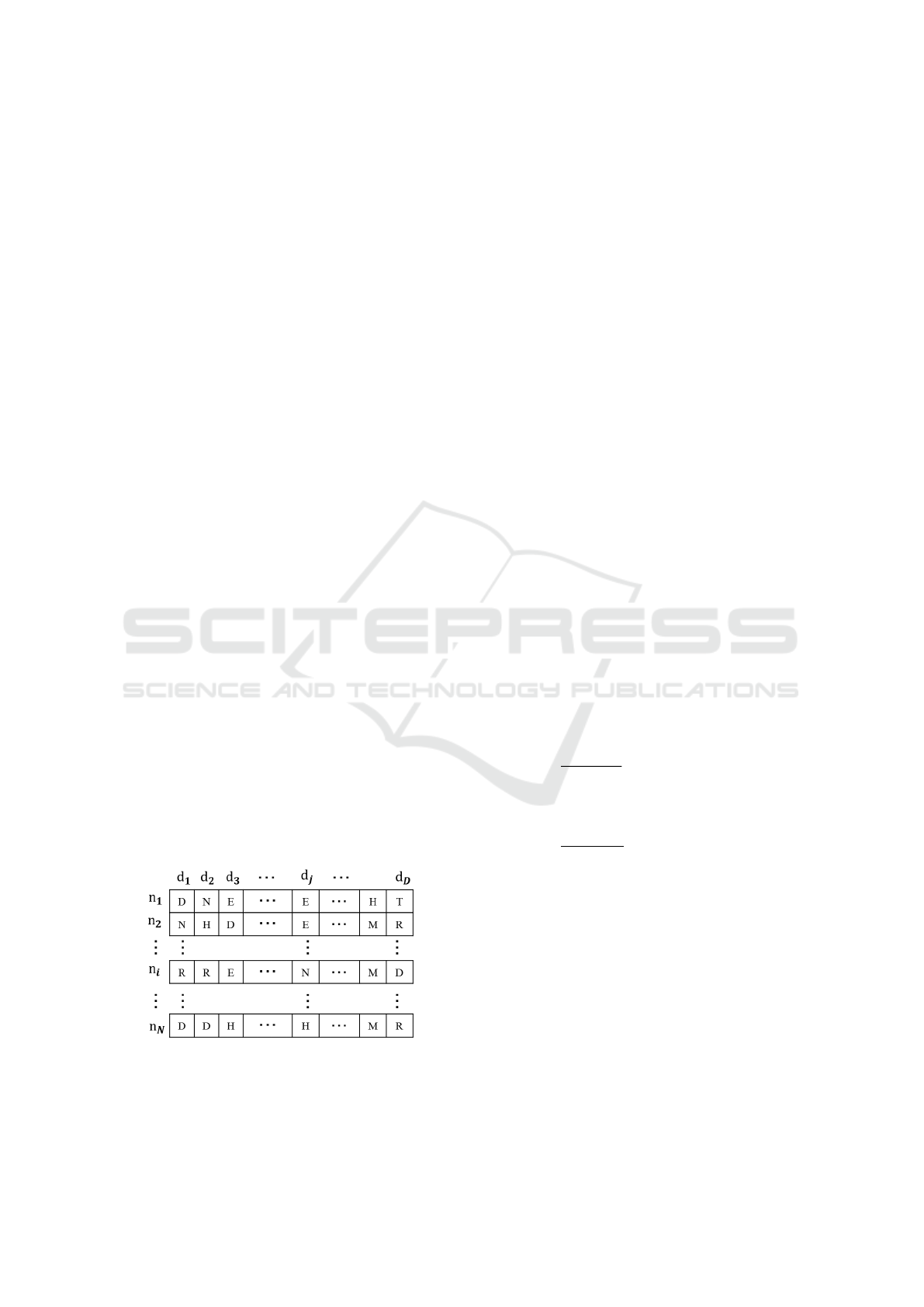
partment creates a monthly nurse schedule as shown

in Fig1. The schedule shown in Fig1 is treated as an

individual to be optimized with NSGA-II in this pa-

per. The training, the meeting and the requested ho-

liday is called a ﬁxed work and treated as a shift that

can not be modiﬁed.

Figure 1: A monthly nurse schedule, where n

denotes the i-

th nurse, d

denotes the j-th day, and D, E, N, T, M, H and R

denotes the daytime shift, the evening shift, the night shift,

a training, a meeting, a holiday and a requested holiday.

The schedule, in other words, the individual

of NSGA-II, is evaluated by the following penalty

functions.

: work load to the nurse i given by evaluation of

each consecutive three shifts

: concentration to the nurse i of the evening shift

and the night shift.

: appearance of speciﬁc prohibited shift patterns

for the nurse i.

: excess or shortage of the holiday number of the

nurse i.

: excess or shortage of the evening shift and the

night shift for the nurse i.

: excess number of days of consecutive shifts for

the nurse i.

7 j

: nursing level in the day shift of the day j.

8 j

: nursing level in the evening shift of the day j.

9 j

: nursing level in the night shift of the day j.

10 j

: compatibility among nurses during the night

shift of the day j.

11 j

: the number of new nurses at the night shift of

day j.

12 j

: absence of more than veteran at the day shift

and the night shift of day j.

These penalty functions are detailed in (Ohki, 2012) .

Objective functions for MOP are deﬁned by the follo-

wing equation by using these penalty functions.











1 +

∑

i=1

, k = 1,2,··· ,6

1 +

∑

i=1

k j

, k = 7,8,··· ,12

(1)

In general, MOP is a problem which ﬁnds solu-

tions that maximizes the objective function vector,

where the solution x satisﬁes constraint conditions, S,

as follows.



maximize f(x) = [ f

(x), f

(x),··· , f

(x)]

subject to x ∈ S

(2)

Satisfaction of the number of necessary nurses for

each shift on each day is the only constraint condi-

tion in the nurse scheduling treated in this paper. By

performing initial population generation and mating

operators as described below, the number of nurses

Many-Objective Nurse Scheduling using NSGA-II based on Pareto Partial Dominance with Linear Subset-size Scheduling

119

assigned to each shift on each day is unchanged du-

ring the optimization. Therefor, the constraint condi-

tion is invalidated, and the nurse scheduling problem

is deﬁned as the following unconstrained MOP.

maximize f(x) = [ f

(x), f

(x),··· , f

(x)]

(3)

where m = 12.

First of all in the initialization, the ﬁxed works are

placed onto the schedule. When the individuals of the

initial population is generated, the meeting and the

training is transformed to the day shift, and the reque-

sted holiday is transformed to the holiday. Taking a

look each day, in consideration of these ﬁxed work

arrangements, one of the day shift, the evening shift

nor the night shift is randomly assigned to the nur-

ses unassigned with the ﬁxed work so as to satisfy the

number of nurses assigned for each shift.

In the mating, a crossover operator and a muta-

tion operator are performed as shown in Figs.2 and

3. For each day, the crossover operator decides which

parent to extract the shift from. Since the ﬁxed works

are assigned to the same place in either parent, they

are copied to a child. Then the shift of the nurse who

is not assigned ﬁxed work is selected from a decided

parent and copied to a child. On the other hand, the

mutation operator selects two nurses and a day. Now,

Figure 2: Crossover operator.

Figure 3: Mutation operator.

two shifts have been selected. If one of them or both

have the ﬁxed work, two nurses and a day is selected

again. If both are not ﬁxed work, both are exchan-

ged. In the mating, few child individuals are gene-

rated with a low probability using only the mutation

operator, and remaining most child individuals are ge-

nerated using the crossover operator. Furthermore,

the mutation operator is applied with a low probability

to child individuals generated by the crossover opera-

tor. These mating operators always generate the indi-

vidual satisfying the number of necessary nurses for

each shift on each day. Therefor, the nurse scheduling

shown in this paper has no constraint condition.

Now, we are facing to the nurse scheduling pro-

blem (NSP), which is a multi-objective symbol matrix

optimization problem, with twelve objective functi-

ons. First, we consider applying NSGA-II as shown

in Fig.4 to this MOP. NSGA-II applies non-dominated

sorting (ND sorting) to the population Q, and the

individuals are classiﬁed to several ranked subsets,

,···. While not exceeding the size of the

parent set P, the individuals of each subset are moved

to the parent set in order. Individuals of the subset

that exceeds the size of the parent set is sorted using

crowding distance (CD sorting) and moved to the pa-

rent set. The individuals not selected are culled. The

mating operators generates the child set C from the

parent set P by using the crossover and mutation ope-

rators.

3 SUB-SET SIZE SCHEDULING

FOR PARETO PARTIAL

DOMINANCE

Although NSGA-II, shown in Fig.ﬁg:NSGA-II,

successfully solves the multi-objective optimization

problem with three or fewer objective functions, as

the objective functions increases to four or more, the

performance of the optimization gradually decreases.

When NSGA-II is applied to the optimization pro-

blem having many objective functions, since the num-

ber of the objective functions is large, the superiority

/ inferiority relationship is difﬁcult to decide among

the individuals of the population. As a result, most

individuals belong to the 1st front set, F

. Then, the

individuals are ranked only by CD sorting, not ND

sorting, and the selection pressure drops remarkably.

In this paper, NSGA-II based on Pareto partial do-

minance (Sato et al., 2010) (PPD-NSGA-II) is app-

lied to the nurse scheduling having twelve objective

functions. PPD-NSGA-II takes out from all m ob-

jective functions and performs ND sorting only with

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

120

Figure 4: NSGA-II, where g denotes a generation cycle.

Figure 5: NSGA-II based on Pareto partial dominance.

these r objective functions as shown in Fig.5. PPD-

NSGA-II takes r objective functions out from all m

objective functions and performs ND sorting only

with these r objective functions. This is an

sorting in Fig.5. In contrast, ND sorting using all m

objective functions is shown as

ND sorting. The

ND sorting is performed in I

generation cycle.

PPD-NSGA-II requires a selection list for se-

lecting r objective functions. The contents of the se-

lection list greatly inﬂuence the optimization result.

On the other hand, the creation of the selection list is

a very troublesome and difﬁcult task for the user, na-

mely the chief nurse. In order to solve this difﬁculty,

we propose a technique to simply schedule the para-

meter r, the subset size. PPD-NSGA-II treated in this

paper does not use the selection list for each I

ge-

neration cycle, randomly selects the subset using the

parameter r given by the following equations.

g · m

+ rand int(2B + 1) − B

r =







B , r

< B

, B 5 r

< m

m , m 5 r

(4)

where rand int(·) denotes a function returns a random

integer less than the argument, B denotes an integer

Figure 6: A simple subset-size scheduling for PPD-NSGA-

II. The possible value of the subset size r, which takes a

value in the colored range according to the generation g.

parameter less than m/2, and G denotes the ﬁnal ge-

neration. Therefore, the parameter r is decided as

shown in Fig.6.

In PPD-NSGA-II, individuals having the same

contents as an individual already existing in the child-

ren, C

, or the archive set, A, are generated and stored

by the mating, so that duplicates of individuals given

good evaluation increases within the population. If

the problem is relatively simple, individuals with the

same content frequently appear during the optimiza-

tion. The second improvement is killing such the in-

dividuals having the same contents of an individual

already existing in the children and the archive set af-

ter the mating. By setting the value of all objective

functions of such the individual to 0, the individual

are killed.

4 NURSE SCHEDULING IN

ACTUAL HOSPITAL

In order to verify the effectiveness of the proposed

technique, the nurse schedule is created and optimi-

zed based on the same information as the actual hos-

pital. This information represents the standard hos-

pital nurse organization in our country among the in-

formation obtained by our survey (Ohki et al., 2006;

Uneme et al., 2008) . In the nurse scheduling, the

number of nurses is 23, the number of days is 28. The

nurse schedule is optimized for 1,000,000 generati-

ons by NSGA-II. In this paper, we try to apply two

techniques, the conventional NSGA-II and the impro-

ved PPD-NSGA-II, to the nurse scheduling.

In this NSP handled in this paper, several objective

functions has saturated to a maximum number of 1.

These objective functions do not always saturate.

Fig.7 shows individual distribution on the f

—

plane at the ﬁnal generation. This ﬁgure shows

an example where PPD-NSGA-II has given dominant

Many-Objective Nurse Scheduling using NSGA-II based on Pareto Partial Dominance with Linear Subset-size Scheduling

121

results compared to the conventional NSGA-II. This

means that focusing on these two objective functions

shows that PPD-NSGA-II has given dominant result.

The same results are obtained also in Figs.8 and 9.

Fig.10 shows individual distribution on the f

—

plane at the ﬁnal generation. In this ﬁgure, several

advantageous points overlap. In other words, when

focusing on these two objective functions, the conven-

tional NSGA-II and PPD-NSGA-II have given nearly

equivalent results. The same results are obtained also

in Figs.11 and 12.

Fig.13 shows individual distribution on the f

—

plane at the ﬁnal generation. This ﬁgure shows an

example where the conventional NSGA-II has given

dominant results compared to PPD-NSGA-II. This

means that focusing on these two objective functions

shows that the conventional NSGA-II has given do-

minant result. The same results are obtained also in

Fig.14.

Fig.15 shows individual distribution on the f

—

plane at the ﬁnal generation. In this ﬁgure, the

conventional NSGA-II is advantageous for the ob-

jective function f

while PPD-NSGA-II is advanta-

geous for the objective function f

. Thus, we could

ﬁnd many cases that superiority or inferiority can not

be distinguished by the objective function of interest.

Since 12 objective functions are deﬁned in NSP

handled in this paper, as shown above, 2 objective

functions are necessary to select from 12 in order to

visualize the individual distribution . These 12 ob-

jective functions can be classiﬁed into 6 objective

functions related to the shift of each nurse and 6 ob-

jective functions based on evaluation on each work

day. Therefore, partial sums of the objective functi-

ons are deﬁned as follows.

∑

i=1

(5)

∑

i=7

(6)

By using these partial sums, the transition of the indi-

vidual distribution is observed on the s

—s

plane as

shown in Figs.16—24. In the optimization up to the

600 thousand generation, we can observe that the po-

pulation given by the both techniques gradually mo-

ves in the upper right direction. Especially in PPD-

NSGA-II, the population converges to the upper right

direction more quickly. After that, both populations

concentrate on the upper right part in the generation

of about 700 thousand. The reason for concentrating

like this is unknown. Although the population given

by the conventional NSGA-II then spreads again to

a wide range, the population given by PPD-NSGA-

II remains relatively dense afterwards. In the case of

using the conventional NSGA-II, no signiﬁcant pro-

gress is observed in the optimization after the 800

thousand generation. On the other hand, in the case

of using PPD-NSGA-II, the optimization progressed

thereafter, and gives several excellent solutions in the

900 thousand generation. However, in the ﬁnal gene-

ration of PPD-NSGA-II, each solution of the popula-

tion has been deteriorated. As one of the reason for

this result, it can be considered that the value of r of

PPD-NSGA-II is almost equal to m at the end of the

optimization.

Finally, in order to numerically compare the per-

formance of both, we consider on Norm (Sato et al.,

2006) value and Maximum Spread (MS) (Zitzler,

1999) value. These values are obtained by the fol-

lowing equations.

Norm(P OS) =

P OS

∑

j=1

∑

i=1

)

P OS

, (7)

MS(P OS) =

∑

i=1



max

P OS

j=1

) − min

P OS

j=1

)



, (8)

where P OS denotes the individuals of the ﬁrst front

set at the ﬁnal generation. These values obtained

by both are summarized in Table.1. PPD-NSGA-II

dominates to the conventional NSGA-II in terms of

the convergence property of the population to POS,

or Norm value. On the other hand, the conventional

NSGA-II is somewhat predominat with regard to the

diversity of the population at the ﬁnal generation, or

MS value.

Table 1: Comparison of Norm value and MS value of the

population at the ﬁnal generation.

NSGA-II PPD-NSGA-II

Norm 1.5589 2.1795

MS 2.9126 2.3970

5 CONCLUSION

This paper has treated the nurse scheduling in Ja-

panese standard general hospitals. Twelve objective

functions have been deﬁned for the nurse scheduling.

The nurse scheduling problem is solved as a multi-

objective optimization problem by means of NSGA-

II in this paper. It is known that optimization is insuf-

ﬁcient when NSGA-II is applied to an optimization

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

122

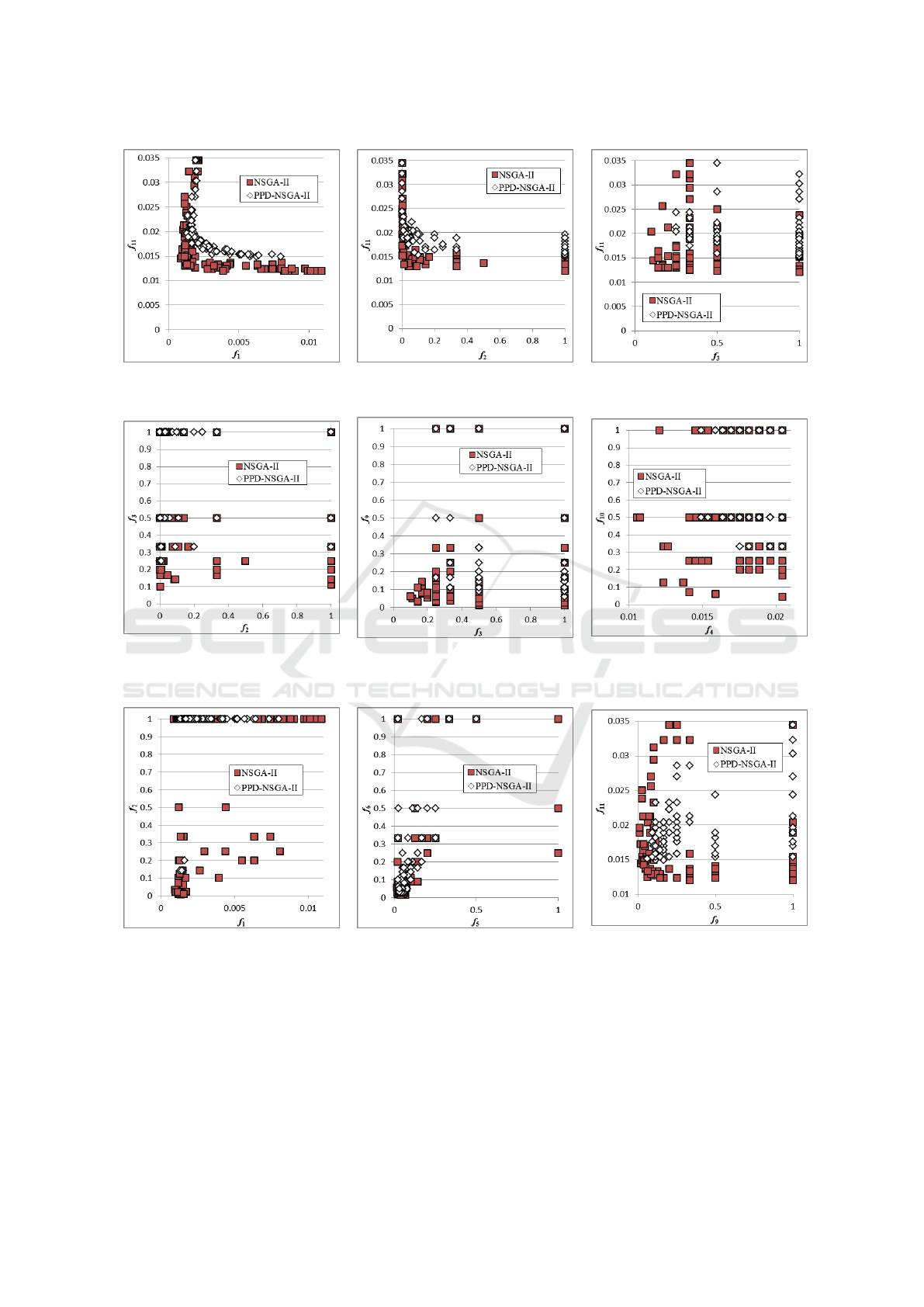
Figure 7: Individual distribution on the

— f

plane at the ﬁnal generation.

Figure 8: Individual distribution on the

— f

plane at the ﬁnal generation.

Figure 9: Individual distribution on the

— f

plane at the ﬁnal generation.

Figure 10: Individual distribution on

the f

— f

plane at the ﬁnal genera-

tion.

Figure 11: Individual distribution on

the f

— f

plane at the ﬁnal genera-

tion.

Figure 12: Individual distribution on

the f

— f

plane at the ﬁnal genera-

tion.

Figure 13: Individual distribution on

the f

— f

plane at the ﬁnal genera-

tion.

Figure 14: Individual distribution on

the f

— f

plane at the ﬁnal genera-

tion.

Figure 15: Individual distribution on

the f

— f

plane at the ﬁnal genera-

tion.

problem with four or more objective functions. One

method for reducing this problem is a technique ba-

sed on Pareto partial dominance. PPD-NSGA-II is

applied to the nurse scheduling treated in this paper.

PPD-NSGA-II requires to receive the number r of

objective functions, or the subset size, to be selected

from all m objective functions in the form of a list in

advance. Moreover, this selection list has a great in-

ﬂuence on the result of optimization. Creating such

a selection list is a heavy burden for the user and is

also substantially impossible. This paper has propo-

sed a technique of PPD-NSGA-II with linear subset-

size scheduling. By embedding the subset-size sche-

duling into the algorithm, the user, namely the chief

Many-Objective Nurse Scheduling using NSGA-II based on Pareto Partial Dominance with Linear Subset-size Scheduling

123

Figure 16: Individual distribution on

the s

—s

plane at the 100k-th gene-

ration.

Figure 17: Individual distribution on

the s

—s

plane at the 200k-th gene-

ration.

Figure 18: Individual distribution on

the s

—s

plane at the 400k-th gene-

ration.

Figure 19: Individual distribution on

the s

—s

plane at the 500k-th gene-

ration.

Figure 20: Individual distribution on

the s

—s

plane at the 600k-th gene-

ration.

Figure 21: Individual distribution on

the s

—s

plane at the 700k-th gene-

ration.

Figure 22: Individual distribution on

the s

—s

plane at the 800k-th gene-

ration.

Figure 23: Individual distribution on

the s

—s

plane at the 900k-th gene-

ration.

Figure 24: Individual distribution on

the s

—s

plane at the ﬁnal generation.

nurse, is released from the designing of the selection

list.

In order to verify the effectiveness, the proposed

technique and the conventional NSGA-II have been

applied to the nurse scheduling problem. Although

the proposed method is somewhat inferior on the di-

versity of the population as compared with the con-

ventional NSGA-II, it is signiﬁcantly effective on the

convergency of the population to the Pareto optimal

solution set.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

124

ACKNOWLEDGEMENTS

This research work has been supported by JSPS KA-

KENHI Grant Number JP17K00339.

The author would like to thank to her families, the

late Miss Blackin’, Miss Blanc, Miss Caramel, Mr.

Civita, Miss Marron, Miss Markin’, Mr. Yukichi and

Mr. Ojarumaru, for bringing her daily healing and

good research environment.

REFERENCES

Aguirre, H. E. and Tanaka, K. (2007). Working princi-

ples, behavior, and performance of moeas on mnk-

landscapes. European Journal of Operational Rese-

arch, 181(3):1670–1690.

Berrada, I., Ferland, J. A., and Michelon, P. (1996). A

multi-objective approach to nurse scheduling with

both hard and soft constraints. Socio-Economic Plan-

ning Sciences, 30(3):183–193.

Brockhoff, D. and Zitzler, E. (2006). Dimensionality re-

duction in multiobjective optimization with (partial)

dominance structure preservation: Generalized mini-

mum objective subset problems. TIK Report, 247.

Burke, E., Cowling, P., De Causmaecker, P., and Berghe,

G. V. (2001a). A memetic approach to the nurse ros-

tering problem. Applied intelligence, 15(3):199–214.

Burke, E. K., De Causmaecker, P., Petrovic, S., and Berghe,

G. V. (2001b). Fitness evaluation for nurse scheduling

problems. In Evolutionary Computation, 2001. Pro-

ceedings of the 2001 Congress on, volume 2, pages

1139–1146. IEEE.

Goto, T., Aze, H., Yamagishi, M., Hirota, M., and Fujii, S.

(1993). Application of ga, neural network and ai to

planning problems. NHK Technical report, (144):78–

85.

Hughes, E. J. (2005). Evolutionary many-objective opti-

misation: many once or one many? In Evolutionary

Computation, 2005. The 2005 IEEE Congress on, vo-

lume 1, pages 222–227. IEEE.

Ikegami, A. (2001). Algorithms for nurse scheduling. In

Proc. of 11th Intelligent System Symposium, pages

477–480.

Itoga, T., Taniguchi, N., Hoshino, Y., and Kamei, K. (2003).

An improvement on search efﬁciency of cooperative

ga and application on nurse scheduling problem. In

Proc. of 12th Intelligent System Symposium, pages

146–149.

Kawanaka, H., Yamamoto, K., Yoshikawa, T., Shinogi, T.,

and Tsuruoka, S. (2002). Automatic generation of

nurse scheduling table using genetic algorithm. IEEJ

Transactions on Electronics, Information and Sys-

tems, 122(6):1023–1032.

Ohki, M. (2012). Nurse scheduling by cooperative ga with

effective mutation operator. IEICE TRANSACTIONS

on Information and Systems, 95(7):1830–1838.

Ohki, M., Morimoto, A., and Miyake, K. (2006). Nurse

scheduling by using cooperative ga with efﬁcient mu-

tation and mountain-climbing operators. In Intelligent

Systems, 2006 3rd International IEEE Conference on,

pages 164–169. IEEE.

Sato, H., Aguirre, H. E., and Kiyoshi, T. (2010). Effects of

moea temporally switching pareto partial dominance

on many-objective 0/1 knapsack problems. Transacti-

ons of the Japanese Society for Artiﬁcial Intelligence,

25:320–331.

Sato, M., Aguirre, H. E., and Tanaka, K. (2006). Effects

of δ-similar elimination and controlled elitism in the

nsga-ii multiobjective evolutionary algorithm. In Evo-

lutionary Computation, 2006. CEC 2006. IEEE Con-

gress on, pages 1164–1171. IEEE.

Tsuchida, K., Sato, H., Aguirre, H. E., and Tanaka, K.

(2009). Analysis of nsga-ii and nsga-ii with cdas,

and proposal of an enhanced cdas mechanism. JACIII,

13(4):470–480.

Uneme, S.-y., Kawano, H., and Ohki, M. (2008). Nurse

scheduling by cooperative ga with variable mutation

operator. In ICEIS (2), pages 249–252.

Zitzler, E. (1999). Evolutionary algorithms for multiob-

jective optimization: Methods and applications.

Many-Objective Nurse Scheduling using NSGA-II based on Pareto Partial Dominance with Linear Subset-size Scheduling

125