Operator-dependent Modiﬁers in Nilpotent Logical Systems

J. Dombi

and O. Csisz

2,3

University of Szeged, Institute of Informatics, Szeged, Hungary

Hochschule Esslingen, University of Applied Sciences, Faculty of Basic Sciences, Esslingen, Germany

Obuda University, Institute of Applied Mathematics, Budapest, Hungary

Keywords:

Linguistic Modiﬁer, Modality, Hedge, Unary Operator, Nilpotent Logic, Bounded System, Possibility,

Necessity, Sharpness.

Abstract:

The purpose of the current study is to consider the main unary operators of a nilpotent logical system in an

integral framework and to reveal the underlying general structure of all the previously examined operators

in nilpotent logical systems. The unary operators are obtained by repeating the argument in multivariable

operators. This enables us to provide a widely applicable system, where all the operators are connected to

each other, and where the modalities and hedges are operator-dependent. It becomes possible to describe all

the operators by using a generator function and a few parameters. The possibility, necessity and sharpness

operators are thoroughly examined and it is also shown how the multivariable operators can be derived from

the unary ones.

1 INTRODUCTION

Among other preferable properties, the fulﬁllment of

the law of contradiction and the excluded middle, and

the coincidence of the residual and the S-implication

(Trillas and L. Valverde, 1981) make the application

of nilpotent operators in logical systems feasible. In

their pioneer work (Dombi and Csisz

ar, 2015), Dombi

and Csisz

ar examined connective systems instead of

operators themselves. It was shown that a consis-

tent connective system generated by nilpotent opera-

tors is not necessarily isomorphic to the Łukasiewicz-

system. Using more than one generator function, con-

sistent nilpotent connective systems (so-called boun-

ded systems) can be obtained in a signiﬁcantly dif-

ferent way with three naturally derived negation ope-

rators. Due to the fact that all continuous Archime-

dean (i.e. representable) nilpotent t-norms are isomor-

phic to the Łukasiewicz t-norm (Grabisch et al., 2009;

Klement et al., 2000), the previously studied nilpo-

tent systems were all isomorphic to the well-known

Łukasiewicz-logic.

In the last few years, the most important multivari-

able operators of general nilpotent systems have been

thoroughly examined. In (Dombi and Csisz

ar, 2014)

and in (Dombi and Csisz

ar, 2016), Dombi and Csisz

examined the implications and equivalence operators

in bounded systems. In (Dombi and Csisz

ar, 2017),

a parametric form of the generated operator o

was

given by using a shifting transformation of the ge-

nerator function. Here, the parameter can be inter-

preted semantically as a threshold of expectancy (de-

cision level). This means that nilpotent conjunctive,

disjunctive, aggregative (where a high input can com-

pensate for a lower one) and negation operators can

be obtained by changing this parameter.

Negation operators were also studied thoroughly

in (Dombi and Csisz

ar, 2015), as they play a signi-

ﬁcant role in logical systems by building connecti-

ons between the main operators (De Morgan law) and

characterising their basic properties. Despite their

signiﬁcance, about other unary operators (compared

to the multivariable ones) there are only limited litera-

ture available. In fuzzy theory, modalities (like possi-

bly, necessarily, ...) and hedges (like very, quite, extre-

mely, ...) are the most studied unary operators, which

modify the linguistic variables (Zadeh, 1975c; Zadeh,

1975a; Zadeh, 1975b; Huynh et al., 2002; T

urken,

2004; Banks, 1994; Jang et al., 1997; De Cock et al.,

2000). In this study, the focus is on the unary opera-

tors of a nilpotent logical system. They perform vari-

ous operations such as incrementing or decrementing

a value and they can be widely used for expressing

modalities and hedges in human thinking (Liu et al.,

2001).

In this paper, our main purpose is to consider the

main unary operators of a nilpotent logical system in

an integral framework and to reveal the underlying ge-

126

Dombi, J. and Csiszár, O.

Operator-dependent Modiﬁers in Nilpotent Logical Systems.

DOI: 10.5220/0006894701260134

In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 126-134

ISBN: 978-989-758-327-8

neral structure of all the operators considered so far.

This enables to provide a widely applicable system,

where all operators are connected to each other, and

the modalities and hedges are operator-dependent. In

such a system, only a few parameters are to be gi-

ven. By ﬁtting the parameter values, the system can

be used to model real life problems.

The article is organized as follows. After recalling

some basic preliminaries in Section 2, unary operators

in nilpotent logical systems are examined in Section

3. First, in Section 3.1, a possible way of constructing

unary operators is considered: repeating the argument

in multivariable operators; i.e. by choosing x

= x

(∀i, j) for the arguments of the many-variable opera-

tors. This is how it can be ensured that the opera-

tors are connected. In Section 3.2, our focus is on the

drastic unary operators, in Section 3.3 on the compo-

sition rules and then in Section 3.4, it is shown how

the multivariable operators can be derived from unary

ones. This result underlines the importance of the

unary operators in a logical system. In Section 3.5,

a general framework is given for all the operators dis-

cussed so far.

In Section 4, a future research direction is sugge-

sted that could provide the next steps along the path to

a practical and widely applicable system (e.g. in neu-

ral networks). The main disadvantage of the nilpotent

operator family, namely the lack of differentiability

can be eliminated by using a continuously differenti-

able approximation of the cutting function.

Finally, in Section 5, the main results are summa-

rized.

2 PRELIMINARIES

To construct a logical system, we need to deﬁne

the appropriate logical operators. As in (Dombi

and Csisz

ar, 2015), we consider connective systems

where the conjunction and disjunction operators are

special types of t-norms and t-conorms, respectively.

A triangular norm (t-norm for short) T is a bi-

nary operation on the closed unit interval [0, 1] such

that ([0, 1], T ) is an abelian semigroup with neutral

element 1 which is totally ordered, i.e., for all x

, y

∈ [0, 1] with x

≤ x

and y

≤ y

we have

T (x

, y

) ≤ T (x

, y

), where ≤ is the natural order on

[0, 1].

Standard examples of t-norms are the minimum

, the product T

, the Łukasiewicz t-norm T

given

by T

(x, y) = max(x + y − 1, 0), and the drastic pro-

duct T

with T

(1, x) = T

(x, 1) = x, and T

(x, y) = 0

otherwise.

A triangular conorm (t-conorm for short) S is a bi-

nary operation on the closed unit interval [0, 1] such

that ([0, 1], S) is an abelian semigroup with neutral

element 0 which is totally ordered. Standard exam-

ples of t-conorms are the maximum S

, the probabi-

listic sum S

, the Łukasiewicz t-conorm S

given by

(x, y) = min(x + y, 1), and the drastic sum S

with

(0, x) = S

(x, 0) = x, and S

(x, y) = 1 otherwise.

A continuous t-norm T is said to be Archimedean

if T (x, x) < x holds for all x ∈ (0, 1). A continuous

Archimedean T is called strict if T is strictly mono-

tone; i.e. T (x, y) < T (x, z) whenever x ∈ (0, 1] and

y < z , and nilpotent if there exist x, y ∈ (0, 1) such

that T (x, y) = 0.

From the duality between t-norms and t-conorms,

we can easily derive the similar properties for t-

conorms as well.

As it is well-known, t-norms and t-conorms can be

expressed by means of a single real generator function

with the following speciﬁc properties.

Proposition 1. (Baczy

nski, (Baczy

nski and Jayaram,

2009), Ling, (C. Ling, 1965)) A function T : [0, 1]

→

[0, 1] is a continuous Archimedean t-norm if and only

if it has a continuous additive generator, i.e. there

exists a continuous strictly decreasing function t :

[0, 1] → [0, ∞) with t(1) = 0, which is uniquely deter-

mined up to a positive multiplicative constant, such

that

T (x, y) = t

−1

(min(t(x) + t(y), t(0)), x, y ∈ [0, 1].

(1)

Proposition 2. (Grabisch et al., 2009)

A t-norm T is strict if and only if t(0) = ∞ holds for

each continuous additive generator t of T.

A t-norm T is nilpotent if and only if t(0) < ∞ holds

for each continuous additive generator t of T.

Due to the duality, additive generators of t-

conorms (s(x)) can be obtained from the additive ge-

nerators of their dual t-norms.

Since the generator functions of nilpotent t-norms

and t-conorms are bounded and determined up to

a multiplicative constant, they can be normalized

(Dombi and Csisz

ar, 2015). Let us use the following

notations for the uniquely deﬁned normalized genera-

tor functions:

(x) :=

t(x)

t(0)

, f

(x) :=

s(x)

s(1)

. (2)

In order to simplify the notations, we recall the

deﬁnition of the so-called cutting function.

Deﬁnition 1. (Dombi and Csisz

ar, 2015; Sabo and

Strezo, 2005) Let us deﬁne the cutting operation [ ]

[x] =







0 i f x < 0

x i f 0 ≤ x ≤ 1

1 i f 1 < x

(3)

Operator-dependent Modiﬁers in Nilpotent Logical Systems

127

and let the notation [ ] also act as brackets when wri-

ting the argument of an operator. Then we can write

f [x] instead of f ([x]).

Deﬁnition 2. (Dombi and Gera, 2005) Let a, b ∈

[0, 1], a < b and let us deﬁne the generalized cutting

operation [ ]

[x]







0 i f x < a

x−a

b−a

i f a ≤ x ≤ b

1 i f b < x

(4)

and let the notation [ ] also act as brackets when wri-

ting the argument of an operator. Then we can write

f [x] instead of f ([x]).

Proposition 3. (Dombi and Csisz

ar, 2015) With the

help of the cutting operator, we can write the con-

junction and disjunction operators in the following

form, where f

(x) and f

(x) are decreasing and incre-

asing normalized generator functions, respectively.

c(x, y) = f

−1

[ f

(x) + f

(y)], (5)

d(x, y) = f

−1

[ f

(x) + f

(y)]. (6)

From now on, the notations c(x, y) and d(x, y)

above will be used for the conjunction and disjunction

to emphasize the use of the normalized generator

functions.

Next, we recall the deﬁnition of a nilpotent logical

system.

Deﬁnition 3. (Dombi and Csisz

ar, 2015) The triple

(c, d, n), where c is a continuous Archimedean t-norm,

d is a continuous Archimedean t-conorm and n is a

strong negation, is called a connective system.

Deﬁnition 4. (Dombi and Csisz

ar, 2015) A con-

nective system is nilpotent if the conjunction c is a

nilpotent t-norm, and the disjunction d is a nilpotent

t-conorm.

It was shown in (Dombi and Csisz

ar, 2015) that

to construct a logical system, more than one genera-

tor functions can be used without losing consistency.

In these systems, n

(x) and n

(x), the negations ge-

nerated by f

and f

respectively (also called as the

natural negations) do not coincide with the negation

operator; i.e. n

(x) 6= n

(x) 6= n(x).

Deﬁnition 5. A nilpotent connective system is called

a bounded system if f

(x)+ f

(x) > 1, or equivalently

(x) < n(x) < n

(x) holds for all x ∈ (0, 1), where f

and f

are the normalized generator functions of the

conjunction and disjunction, and n

, n

are the natu-

ral negations.

The associativity of t-norms and t-conorms per-

mits us to consider their extensions to the multivari-

able case. Dombi and Csisz

ar (Dombi and Csisz

ar,

2017) examined a general parametric operator o

(x)

of nilpotent systems, where the parameter has an im-

portant semantic meaning as the threshold of expec-

tation. Nilpotent conjunctive, disjunctive, aggregative

and negation operators can be obtained by changing

the parameter value.

Deﬁnition 6. Let f : [0, 1] → [0, 1] be an increasing

bijection, ν ∈ [0, 1], and x = (x

, . . ., x

), where x

∈

[0, 1] and let us deﬁne the general operator by

(x) = f

−1

∑

i=1

( f (x

) − f (ν)) + f (ν)

= f

−1

∑

i=1

f (x

) − (n − 1) f (ν)

(7)

Remark 1. Note that the general operator for ν = 1

is conjunctive, for ν = 0 it is disjunctive and for ν =

∗

= f

−1





it is self-dual.

On the basis of Remark 1, the conjunction, the dis-

junction and the aggregative operator can be deﬁned

in the following way.

Deﬁnition 7. Let f : [0, 1] → [0, 1] be an increa-

sing bijection. Let us deﬁne the conjunction, the dis-

junction and the aggregative operator by

c(x) := o

(x) = f

−1

∑

i=1

f (x

) − (n − 1)

, (8)

d(x) := o

(x) = f

−1

∑

i=1

f (x

)

, (9)

a(x) := o

∗

(x) = f

−1

∑

i=1

f (x

) −

(n − 1)

, (10)

respectively, where ν

∗

= f

−1





Remark 2. A conjunction, a disjunction and an ag-

gregative operator differ only in one parameter of the

general operator in (7). The parameter ν has the se-

mantic meaning of the level of expectation: maximal

for the conjunction, neutral for the aggregation and

minimal for the disjunction.

Deﬁnition 8. Let w = (w

, . . ., w

) and w

> 0 be real

parameters, f : [0, 1] → [0, 1] an increasing bijection

with ν ∈ [0, 1]. The weighted general operator is deﬁ-

ned by

ν,w

(x) := f

−1

∑

i=1

( f (x

) − f (ν)) + f (ν)

. (11)

Deﬁnition 9. The operator

(x) = f

−1

∑

i=1

f (x

) −

, (12)

where w > 0, is called the weighted aggregative ope-

rator.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

128

Proposition 4. The weighted general operator

ν,w

(x) satisﬁes

1. The boundary condition a

ν,w

(0) = 0, if and only if

ν = 0 or

∑

i=1

≥ 1 (for a commutative operator:

w ≥

);

2. The boundary condition a

ν,w

(1, . . ., 1) = 1, if and

only if ν = 1 or

∑

i=1

≥ 1 (for a commutative ope-

rator: w ≥

);

3. Both of the above-mentioned boundary conditi-

ons, if and only if

∑

i=1

≥ 1 (for a commutative

operator: w ≥

);

4. a

ν,w

(ν, . . ., ν) = ν.

3 UNARY OPERATORS IN

NILPOTENT LOGICAL

SYSTEMS

In the early 1970’s, Zadeh (L. A. Zadeh, 1972) intro-

duced a class of powering modiﬁers, which deﬁned

the concept of linguistic variables and hedges (like

very, quite, extremely, ...). He proposed computing

with words as an extension of fuzzy sets and logic the-

ory and introduced modiﬁer functions of fuzzy sets

called linguistic hedges, which change the meaning

of the primary terms. As pointed out by Zadeh, lin-

guistic variables and terms are closer to human thin-

king and therefore, words and linguistic terms can be

used to model human thinking systems (L. A. Zadeh,

1971). Hedges and also modalities (like possibly, ne-

cessarily, ...) are the most examined unary operators.

From a semantic viewpoint, these unary operators can

also be viewed as a part of a logical system. In this

section, two possible ways of extending a nilpotent

logical system by deﬁning the necessity and possibi-

lity operators are examined. The novelty of these two

methods lies in the fact that they provide a logical sy-

stem, where all the operators are connected to each

other.

The possibility and neccessity operators have to

satisfy the following equations.

impossible(x) = necessity(not(x)) (13)

and

possible(x) = not(impossible(x)). (14)

3.1 Possibility and Necessity as Unary

Operators Derived from

Multivariable Operators

A possible way of obtaining unary operators is by

choosing x

= x

(∀i, j) for the arguments of the many-

variable operators. Based on the De Morgan property

of the conjunction and the disjunction, the unary ope-

rators derived from them satisfy the equations above.

Deﬁnition 10. Let k ∈ N, λ ∈ R

, λ > 1, f : [0, 1] →

[0, 1] be an increasing bijection and let us deﬁne the

so-called necessity operator, τ

(k)

(x) : [0,1] → [0, 1] in

the following way:

(k)

(x) := c[x, x, ...x

| {z }

k−times

] = f

−1

[k( f (x) − 1) + 1], (15)

and the generalized necessity operator τ

(λ)

(x) :

[0, 1] → [0, 1] as

(λ)

(x) := f

−1

[λ( f (x) − 1) + 1] =

= f

−1

[λ f (x) − (λ − 1)],

(16)

where c is the conjunction generated by f

(x) = 1 −

f (x).

Similarly, the so-called possibility operator can

also be deﬁned by means of the disjunction operator.

Deﬁnition 11. Let k ∈ N, λ ∈ R

, λ > 1, f : [0, 1] →

[0, 1] be an increasing bijection and let us deﬁne the

so-called possibility operator, τ

(k)

(x) : [0, 1] → [0, 1]

in the following way:

(k)

(x) := d[x, x, ...x

| {z }

k−times

] = f

−1

[k f (x)], (17)

and the generalized possibility operator τ

(λ)

(x) :

[0, 1] → [0, 1] as

(λ)

(x) := f

−1

[λ f (x)], (18)

where d is the disjunction generated by f (x).

Next, the so-called sharpness operator is deﬁned,

based on the self-duality of the aggregative operator.

Deﬁnition 12. Let k ∈ N, λ ∈ R

, λ > 1, f : [0, 1] →

[0, 1] be an increasing bijection and let us deﬁne the

so-called sharpness operator, τ

(k)

(x) : [0, 1] → [0, 1]

in the following way:

(k)

(x) := a[x, x, ...x

| {z }

k−times

] = f

−1



k f (x) −

k − 1



, (19)

and the generalized sharpness operator τ

(λ)

(x) :

[0, 1] → [0, 1] as

(λ)

(x) := f

−1



λ f (x) −

λ − 1



, (20)

Operator-dependent Modiﬁers in Nilpotent Logical Systems

129

where a is the aggregative operator generated by

f (x).

The three deﬁnitions above can be summarized in

a uniﬁed formula.

Deﬁnition 13. Let λ ∈ R

, λ > 1, ν ∈ [0, 1], f :

[0, 1] → [0, 1] be an increasing bijection. Let us de-

ﬁne the unary operator τ

(λ)

(x) in the following way.

(λ)

(x) := f

−1

[λ( f (x) − f (ν)) + f (ν)]. (21)

Remark 3. For ν = 1, ν = 0 and ν = ν

∗

(i.e. f (ν) =

), we get the necessity, the possibility and the sharp-

ness operators, respectively.

The above-deﬁned unary operators fulﬁll the fol-

lowing De Morgan identities (see equations 13 and

14).

Proposition 5. Let f : [0,1] → [0, 1] be an increasing

bijection and let n(x) be the negation generated by

f (x).



(λ)

(x)



= τ

(λ)

(n(x)), (22)



(λ)

(x)



= τ

(λ)

(n(x)), (23)



(λ)

(x)



= τ

(λ)

(n(x)). (24)

Proof. The proof is similar in all three cases. Let us

prove the ﬁrst statement.

Taking into account the fact that 1 − [x] = [1 − x],



(λ)

(x)



= f

−1

[1 − [λ f (x) − (λ − 1)]] =

−1

[λ(1 − f (x))] = τ

(λ)

(n(x)).

Proposition 6. τ

(λ)

(x) is for ∀ν ∈ [0, 1] increasing.

Let x = x

be the greatest value, for which τ

(λ)

(x) = 0,

and let x = x

be the lowest value, for which τ

(λ)

(x) =

1. In this case

= f



λ − 1

f (ν)



(25)

and

= f



λ − 1

f (ν) +



. (26)

Proof. The monotonicity follows from the monoto-

nicity of f (x). To ﬁnd x

and x

, the following two

equations need to be solved:

λ( f (x) − f (ν)) + f (ν) = 0,

and

λ( f (x) − f (ν)) + f (ν) = 1.

The solution follows from a direct calculation.

The values x

and x

in Proposition 6 for ν =

1, ν = 0 and ν = ν

∗

can be found in Table 1.

Table 1: x

and x

values for ν = 1, ν = 0 and ν = ν

∗

ν x

(λ)

(x) 1 f

−1



1 −



(λ)

(x) 0 0 f

−1





(λ)

(x) ν

∗

−1



λ−1

2λ



−1



λ+1

2λ



Table 2: x

and x

values for f (x) = x.

ν x

(λ)

(x) 1 1 −

(λ)

(x) 0 0

(λ)

(x) ν

∗

λ−1

2λ

λ+1

2λ

Proposition 7. Let ν

∗

= f

−1





(λ)

(ν

∗

) = f

−1



1 −



, (27)

(λ)

(ν

∗

) = f

−1





(28)

and

(λ)

(ν

∗

) = ν

∗

. (29)

Proof. The statements follow from direct calculati-

ons.

Remark 4. Note that ν

∗

is a ﬁxpoint of the sharpness

operator τ

(λ)

(x).

Next, let us consider the case f (x) = x.

Remark 5. In particular for f (x) = x,

(λ)

(x) = min (1, max (0, λx − (λ − 1))) , (30)

(λ)

(x) = min (1, max (0, λx)), (31)

(λ)

(x) = min



1, max



0, λx −

λ − 1



. (32)

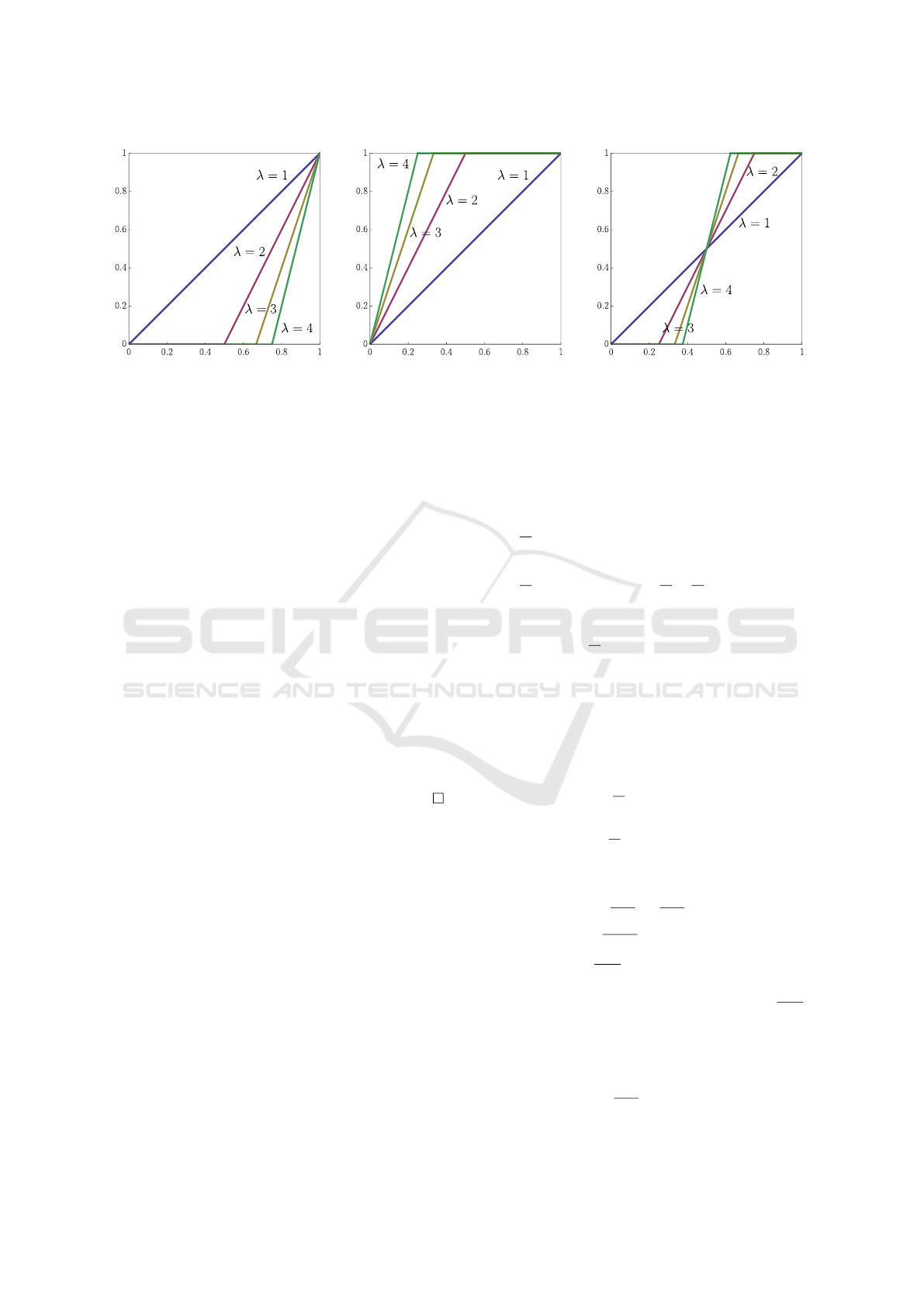
In Figure 1, unary operators generated by f (x) = x

are shown. For the values x

and x

, see Table 2.

Remark 6. As can be seen, for f (x) = x, the unary

operators τ

(λ)

(x) (I ∈ {N, P, S}), have a value in (0, 1)

if and only if x ∈ (x

, x

). Note that the length of this

interval, x

− x

3.2 Drastic Unary Operators

Let us now deﬁne the so-called drastic unary opera-

tors in the following way.

Deﬁnition 14. Let f : [0, 1] → [0, 1] be an increasing

bijection. Let

(∞)

(x) := lim

λ→∞

(λ)

(x), (33)

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

130

(a) Necessity operators τ

(λ)

for λ =

1, 2,3, 4

(b) Possibility operators τ

(λ)

for λ =

1, 2,3, 4

(λ)

for λ =

1, 2,3, 4

Figure 1: Unary operators generated by f (x) = x.

(∞)

(x) := lim

λ→∞

(λ)

(x), (34)

and

(∞)

(x) := lim

λ→∞

(λ)

(x). (35)

(∞)

(x), τ

(∞)

(x) and τ

(∞)

(x) are called drastic unary

operators.

Proposition 8.

(∞)

(x) =



0 i f x < 0

1 i f x = 1,

(36)

and

(∞)

(x) =



0 i f x = 0

1 i f x > 0,

(37)

and

(∞)

(x) =







0 i f x < ν

ν i f x = ν

1 i f x > ν.

(38)

Proof. The statement follows from a direct calcula-

tion.

3.3 Composition Rules

In human thinking and languages, emphasis is often

expressed by repeating modalities and hedges, such

as ”very-very”. The following proposition shows that

the necessity, possibility and sharpness operators are

all closed under composition. The parameter of the

compositon is the product of the input parameters.

Proposition 9. Let f : [0,1] → [0, 1] be an increasing

bijection and let n(x) be the negation generated by

f (x).

(λ

)



(λ

)

(x)



= τ

(λ

)

(x), (39)

(λ

)



(λ

)

(x)



= τ

(λ

)

(x), (40)

(λ

)



(λ

)

(x)



= τ

(λ

)

(x). (41)

Proof. 1. It has to be shown that τ

(λ

)



(λ

)

(x)



−1





−1

[λ

f (x) − (λ

− 1)]



− (λ

− 1)



−1

[λ

f (x) − (λ

− 1)] − (λ

− 1)] .

(a) For λ

f (x) − (λ

− 1) ≤ 0; i.e. for f (x) ≤ 1 −

, we obtain τ

(λ

)



(λ

)

(x)



= 0. In this case,

(λ

)

(x) = 0 as well, since from f (x) ≤ 1 −

follows f (x) ≤ 1 −

−

; i.e. λ

f (x) −

((λ

− 1)(λ

− 1) − 1) ≤ 0.

(b) For 0 < λ

f (x) − (λ

− 1) ≤ 0 < 1; i.e. for

f (x) > 1 −

, the cutting function can be omit-

ted and the statement follows from a direct cal-

culation.

> 1 and 0 ≤

f (x) ≤ 1, λ

f (x) − (λ

− 1) > 1 is impossible.

2. It has to be shown that τ

(λ

)



(λ

)

(x)



−1

[λ

f (x)]] = f

−1

[λ

f (x)].

(a) If f (x) ≥

, then f

−1

[λ

f (x)]] =

−1

[λ

f (x)] = 1.

(b) If 0 < f (x) <

, then the cutting function can

be omitted and the statement is trivial.

3. It has to be shown that τ

(λ

)



(λ

)

(x)



−1

f (x) −

−1

−

−1

f (x) −

−1

(a) If λ

f (x) −

−1

≤ 0, then taking into account

the fact that λ

> 1, the left hand side of the

equation is 0. Since in this case f (x) ≤

−1

2λ

f (x) ≤ λ

− 1 ≤ λ

− 1. Therefore,

the value in the cutting function on the right

hand side is less than or equal to 0, which me-

ans that the equation holds.

(b) If 0 ≤ λ

f (x) −

−1

≤ 1, then the cutting func-

tion can be omitted and the statement is trivial.

Operator-dependent Modiﬁers in Nilpotent Logical Systems

131

f (x) −

−1

> 1, then f (x) >

2λ

> 1,

which means that the left hand side of the equa-

tion is 1. Since in this case

1+λ

+λ

f (x), the value in the cutting function on

the right hand side is greater than 1, which me-

ans that the equation is valid.

Proposition 10. 1. For the drastic operators

(∞)



(∞)

(x)



= τ

(∞)

(x), (42)

where I, J ∈ {N, P, S}.

Proof. This statement follows from a direct calcula-

tion.

3.4 Multivariable Operators Derived

from Unary Operators

Proposition 11 tells us how the conjunction and the

disjunction can be expressed in terms of the unary

operators and the arithmetic mean operator.

First, let us recall the deﬁnition of the arithmetic

mean operator.

Deﬁnition 15.

m(x) := f

−1

∑

i=1

( f (x

))

, (43)

where f : [0, 1] → [0, 1] is an increasing bijection.

Proposition 11. The unary operators satisfy the fol-

lowing equation:

(k)

(m(x)) = o

(x). (44)

In particular,

1. τ

(k)

(m(x)) = d(x),

2. τ

(k)

(m(x)) = c(x),

3. τ

(k)

(m(x)) = a(x).

Proof. The statements follow from a direct calcula-

tion.

Proposition 12. The necessity and the possibility

operator have the following property:

1. d



(k)

), τ

(k)

), ...τ

(k)

)



= τ

(k)

(d(x)) .

2. c



(k)

), τ

(k)

), ...τ

(k)

)



= τ

(k)

(c(x)),

Proof. 1. The following statement has to be pro-

ven: f

−1



∑

i=1

[λ f (x

)]



= f

−1



∑

i=1

[ f (x

)]



. If

λ f (x

) ≤ 1 for ∀i, then the statement is trivial. If

∃i, for which λ f (x

) > 1, then both sides of the

equations have the same value (i.e. a value of 1).

2. This follows from the ﬁrst statement by applying

the De Morgen law.

3.5 A General Framework: The α, β, γ-

Model

All basic operators discussed so far can be handled in

a common framework, since they all can be described

by the following parametric form.

Deﬁnition 16. Let x, y ∈ [0, 1], α, β, γ ∈ R and let f :

[0, 1] → [0, 1] be a strictly increasing bijection. Let

the general parametric operator be

α,β,γ

(x, y) := f

−1

[α f (x) + β f (y) + γ]. (45)

The most commonly used operators for special va-

lues of α, β and γ are listed in Table 3.

Now let us focus on the unary (1-place) case.

Deﬁnition 17. Let x ∈ [0, 1], α, γ ∈ R and let f :

[0, 1] → [0, 1], a strictly increasing bijection. Then

α,γ

(x) := f

−1

[α f (x) + γ]. (46)

For special γ values, see Table 4.

In this framework it becomes possible to deﬁne all

the operators by a single generator function and a few

parameters.

4 FUTURE WORK AND

APPLICATION

The main disadvantage of the Łukasiewicz operator

family is the lack of differentiability, which would be

necessary for numerous practical applications. Alt-

hough most fuzzy applications (e.g. embedded fuzzy

control) use piecewise linear membership functions

owing to their easy handling, there are areas where

the parameters are learned by a gradient-based opti-

mization method. In this case, the lack of continuous

derivatives makes the application impossible. For ex-

ample, the membership functions have to be differen-

tiable for each input in order to ﬁne-tune a fuzzy cont-

rol system by a simple gradient-based technique. This

problem could be easily solved by using the so-called

squashing function (see Dombi and Gera (Dombi and

Gera, 2005)), which provides a solution to the above-

mentioned problem by a continuously differentiable

approximation of the cut function. This approxima-

tion could be the next step to realizing a practical and

widely applicable system.

The squashing function deﬁned below is a conti-

nuously differentiable approximation of the generali-

zed cutting function (see Deﬁnition 2) by means of

sigmoid functions (see Figure 2).

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

132

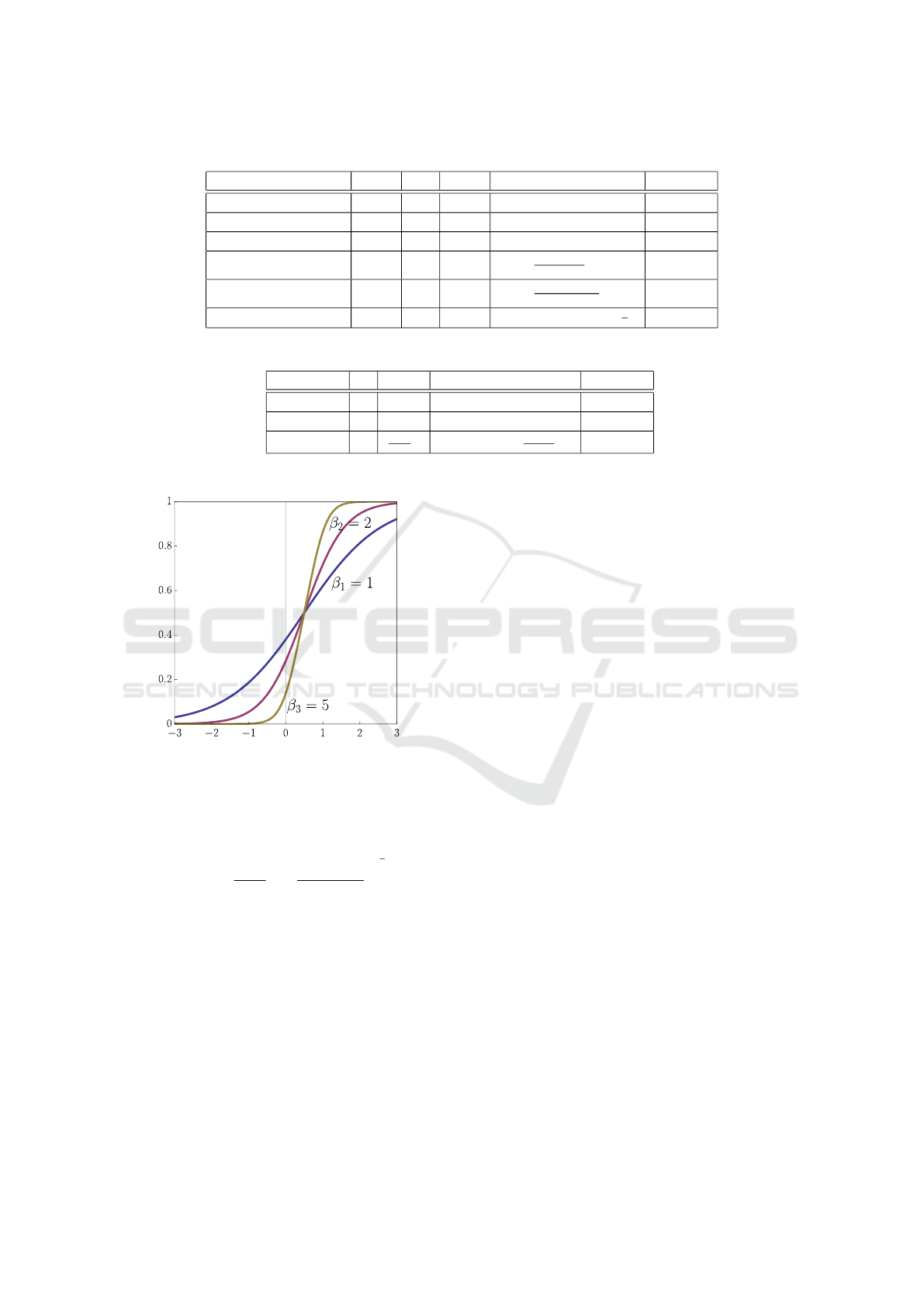
Table 3: Special values for α, β and γ.

α β γ o

α,β,γ

(x, y) Notation

disjunction 1 1 0 f

−1

[ f (x) + f (y)] d(x, y)

conjunction 1 1 −1 f

−1

[ f (x) + f (y) − 1] c(x, y)

implication −1 1 1 f

−1

[ f (y) − f (x) + 1] i(x, y)

arithmetic mean 0.5 0.5 0 f

−1

f (x)+ f (y)

m(x, y)

preference −0.5 0.5 0.5 f

−1

f (y)− f (x)+1

p(x, y)

aggregative operator 1 1 −0.5 f

−1



f (x) + f (y) −



a(x, y)

Table 4: Special values for γ.

α γ o

α,γ

(x, y) Notation

possibility α 0 f

−1

[α f (x)] τ

(x)

necessity α 1 − α f

−1

[α f (x) − (α − 1)] τ

(x)

sharpness α

α−1

−1

[α f (x) −

(α−1)

] τ

(x)

Figure 2: Squashing functions for b = 1, a = 0, for different

β values (β

= 1, β

= 2 and β

= 5).

Deﬁnition 18. (Dombi and Gera, 2005) Let the

squashing function over the interval [a, b] be

a,b

(x) =

b − a

1 + e

β(x−a)

1 + e

β(x−b)

(47)

where a, b ∈ R, a < b, β ∈ R

The parameters a and b affect the placement of the

squashing function, while the parameter β drives the

precision of the approximation.

The reason for choosing the sigmoid function is its

signiﬁcant role in applications such as artiﬁcial neural

networks, optimization methods, economic and biolo-

gical models.

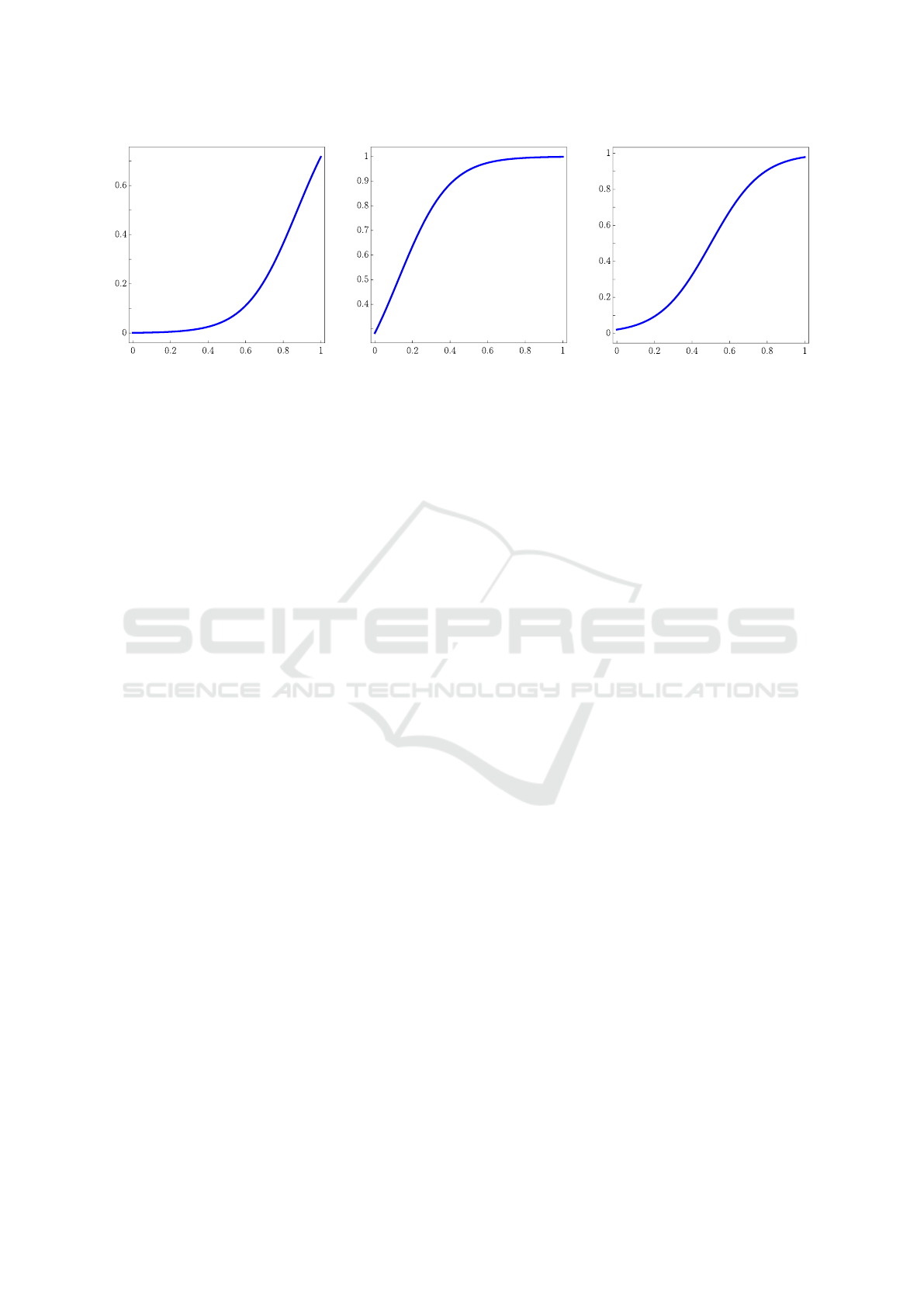
In Figure 3, ”squashed” unary operators are il-

lustrated; i.e. unary operators, in which the cutting

function is approximated with a squashing function.

5 CONCLUSIONS

The main purpose of this paper was to examine the

main unary operators of a nilpotent logical system.

An integral framework was introduced to reveal the

underlying structure of all the operators considered

so far. As a result, a nilpotent logical system can be

obtained, in which all operators are connected to each

other, and the modalities and hedges are operator-

dependent. This is how it becomes possible to deﬁne

all the operators via a single generator function and a

few parameters. By ﬁtting the parameter values, the

system can be used to model real-life problems.

ACKNOWLEDGEMENTS

The research was supported by GINOP-2.1.7-15-

2016-01782. The authors also gratefully acknow-

ledge the ﬁnancial support by the Faculty of Basic

Sciences, Hochschule Esslingen, University of App-

lied Sciences.

REFERENCES

Baczy

nski, M. and Jayaram, B. (2009). On the distributivity

of fuzzy implications over nilpotent or strict triangu-

lar conorms. IEEE Transactions on Fuzzy Systems,

17(3):590–603.

Banks, W. (1994). Mixing crisp and fuzzy logic in appli-

cations. Idea/Microelectronics, WESCON/94, pages

94–97.

C. Ling (1965). Representation of associative functions.

Operator-dependent Modiﬁers in Nilpotent Logical Systems

133

(a) necessity (b) possibility (c) sharpness

Figure 3: Unary operators approximated with the squashing function, a = 4, β = 2.

Publicationes Mathematicae, Debrecen, 12:189—-

212.

De Cock, M., Bodenhofer, U., and Kerre, E. E. (2000). Mo-

delling linguistic expressions using fuzzy relations.

Proc. 6th Int. Conf. on Soft Computing (IIZUKA2000),

2(Iizuka 2000):353–360.

Dombi, J. and Csisz

ar, O. (2014). Implications in bounded

systems. Information Sciences, 283:229–240.

Dombi, J. and Csisz

ar, O. (2015). The general nilpotent

operator system. Fuzzy Sets and Systems, 261:1–19.

Dombi, J. and Csisz

ar, O. (2016). Equivalence operators in

nilpotent systems. Fuzzy Sets and Systems, 299:113–

129.

Dombi, J. and Csisz

ar, O. (2017). Self-dual operators and

a general framework for weighted nilpotent opera-

tors. International Journal of Approximate Reasoning,

81:115–127.

Dombi, J. and Gera, Z. (2005). The approximation of pie-

cewise linear membership functions and Lukasiewicz

operators. Fuzzy Sets and Systems, 154:275–286.

Grabisch, M., Marichal, J. L., Mesiar, R., and Pap, E.

(2009). Aggregation Functions.

Huynh, V. N., Ho, T. B., and Nakamori, Y. (2002). A pa-

rametric representation of linguistic hedges in Zadeh’s

fuzzy logic. International Journal of Approximate Re-

asoning, 30(3):203–223.

Jang, J., Sun, C., and Mizutani, E. (1997). Neuro-Fuzzy and

Soft Computing-A Computational Approach to Lear-

ning and Machine Intelligence [Book Review].

Klement, E. P., Mesiar, R., and Pap, E. (2000). Triangular

norms.

L. A. Zadeh (1971). Quantitative fuzzy semantics. Infor-

mation Sciences, 3:159–176.

L. A. Zadeh (1972). A fuzzy-set-theoretic interpretation of

linguistic hedges. Journal of Cybernetics, 2(3):4–34.

Liu, B.-d., Member, S., Chen, C.-y., Member, S., and Tsao,

J.-y. (2001). Design of Adaptive Fuzzy Logic Control-

ler Based on Linguistic-Hedge Concepts and Genetic

Algorithms. 31(1):32–53.

Sabo, M. and Strezo, P. (2005). On Reverses of Some Bi-

nary Operations. Kybernetika, 41:425–434.

Trillas, E. and L. Valverde (1981). On some functionally

expressable implications for fuzzy set theory. pages

173–190.

urken, I. B. (2004). A foundation for CWW: Meta-

linguistic axioms. Annual Conference of the North

American Fuzzy Information Processing Society - NA-

FIPS, 1:395–400.

Zadeh, L. (1975a). The concept of a linguistic variable and

its applications to approximate reasoning II. Informa-

tion Sciences, 8(4):199–249.

Zadeh, L. (1975b). The concept of a linguistic variable and

its applications to approximate reasoning III. Infor-

mation Sciences, 8(4):199–249.

Zadeh, L. A. (1975c). The concept of a linguistic variable

and its application to approximate reasoning I. Infor-

mation Sciences, 8(3):199–249.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

134