Aided OWL Notation (AOWLN): Conceptual Modelling and

Visualisation of Advanced SWRL Rules

Johannes Nguyen, Jannik Geyer, Thomas Farrenkopf and Michael Guckert

KITE - Technische Hochschule Mittelhessen, Wilhelm-Leuschner-Straße 13 , Friedberg, Germany

Keywords:

Graphical Rule Representation, SWRL, OWL, Rule Visualisation.

Abstract:

Ontologies are a common and generally accepted instrument for the documentation of knowledge in a forma-

lised machine readable form. This paper focuses on ontologies encoded in Web Ontology Language (OWL).

OWL is description-logic based and can be extended by using Semantic Web Rule Language (SWRL) to express

Horn clause like rules that allow the ontology to go beyond the scope of the more object-centric description

logic propositions. The combination of OWL and SWRL has proved to be highly useful in practical appli-

cations. However, SWR L rules soon become complex and confusing in mere textual representations. This

particular issue becomes obvious w hen ontologies grow in size and the number of rules increases. A solution

for this problem can be an appropriate graphical representation of the rules. This paper proposes a graphical

visualisation concept for SWRL rules that we call Aided OWL Notation (AOWLN). Additionally, we present a

prototypical Prot´eg´e plugin that automatically visualises rules.

1 INTRODUCTION

Gruber described ontologies to be an explicit speci-

ﬁcation of a conceptualisa tion which was later re-

formu late d by Borst to also be shared (see (Guarino

et al., 2009) for a discussion). Ontologies deﬁne con-

cepts together with their properties a nd interrelations

in a formal and machine readable form. They have

become a common instrument for consistently docu-

menting knowledge to be sha red among humans and

machines. Having the idea of supporting interopera-

bility as a major purpose, standardisation is an im-

portant issue. W3C has standardised OWL. Being an

object-centric language OWL has limitations in ex-

press rather simple if-then constructions, e.g. for as-

serting data or object prope rties. Therefore, the com-

bination of OWL together with Semantic Web Ru le

Language (SWRL) is a frequ e ntly used set of tools.

1.1 Motivation

SWRL extend s OWL with the ability to use Horn

clause like if-then rules. SWRL is a proposed W3C

standard that has gained pop ularity in re c ent years.

With a growing developer base, the lack of options to

visualise rules becom e s more and more relevant. In

February 2017 Martin O’Connor (cre a tor of Prot´eg´e)

and other developers addressed this topic in a web fo-

rum, resulting in an open call for an appropriate vi-

sualisation tool.

Although this is not a new de bate,

most existing solutions have limitations, making the

development o f an easy to u se visualisation too l for

SWRL a necessity.

1.2 Problem

Rules expressed with SWRL incr ease the visual com-

plexity o f an ontology. With complex mathematical

formu las invoking SWRL built-ins, rules can easily

stretch over several lines which makes reading and

comprehending difﬁcult. However, in pra ctical indus-

trial applicatio ns highly complicated rules cannot be

avoided as expressing engineering problems requires

mathematical formulas that lead to extensive use of

built-ins inducing high complexity. Th is makes it dif-

ﬁcult if not impossible to follow the logical structure

of the rules, even for domain experts. So far, Prot´eg´e

only o ffers limited op tions to search and ide ntify spe-

ciﬁc rules. A n integrated graphical visualisation w ill

lead to higher transparency and a b etter overview, ma-

king the rules more comprehensible. A new graphical

notation format for SWRL rules with higher transpa-

rency need s to be deﬁned.

See http://protege-project.136.n4.nabble.com/

Visualisation-tool-for-OWL-and-SWRL-rules-

td4667578.html - (accessed on 06/01/2018)

Nguyen, J., Geyer, J., Farrenkopf, T. and Guckert, M.

Aided OWL Notation (AOWLN): Conceptual Modelling and Visualisation of Advanced SWRL Rules.

DOI: 10.5220/0006917701750182

In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 2: KEOD, pages 175-182

ISBN: 978-989-758-330-8

175

1.3 Idea

The contribution of this work is a proposal for a

set of notation elements that a re able to portray the

main logical constructs used in SWRL. We will spe-

cify an algor ithm that composes the newly deﬁned

notation elements into a diagram. In our initial a p-

proach e s we attempted to model SWRL rules using

UML and BPMN notation elements. However, the

elements available there are semantically inapprop ri-

ate an d can lead to BPMN and UML diagrams con-

tradicting the SWRL logic. Furtherm ore, we pr esent

prototy pical visualisation tool that can be implemen-

ted as a Pr ot´eg´e plugin.

1.4 Outline of the Paper

The following section provides a technology review,

giving an overview of the most important existing so-

lutions for visualising SWRL rules, inter alia, Prot

Axiom

e which is a known visualisation plugin for

Prot´eg´e. Section 3 introduces a new set of notation

elements for the graphical visualisation and in section

4 an example is p resented as proof of concept. This

example demonstrates the transformation of r ule gi-

ven in textual description into our graphical notation.

Finally, the implementation of the visualisation plugin

is described.

2 RELATED WORK

In this section, other approaches to visualise ru le s in

ontologies are discussed.

2.1 Prot

e Axiom

Prot´eg´e Axiom´e was developed by the creators of

Prot´eg´e. It is a plugin that consists of ﬁve main func ti-

onal areas (Hassanpour et al., 2009). Th e ﬁrst functi-

onal area is a rule gr a ph for visualising th e interde-

pendencies between individual rules to repr esent an

entire rule base. The rules are portrayed as nodes

that are connected through directed edges. Besides

this, the tool also offers an option for rule para phra-

sing. This option enables the creation of English like

text representations for individual rules and catego-

rises them based on their syntactic structure. Addi-

tionally, a rule elicitation function was implemente d

that creates templates for adding new rules to th e ru le

base. Prot´eg´e Axiom´e visualisation uses a tree struc-

ture cre a te d by applying Depth First Search to chain

the variables (Hassanpour et al., 2009). By cha ining

variables a simple ﬂowchart diagram which visualises

the basic logical sequence for data and ob je ct proper-

ties is derived. However, the tool neither differentiates

between existing SWRL e lements nor does it clarify

the application of built-ins (see Fig. 1). A more ap-

propriate modellin g concept for visualisation should

include more information about the rule and its con-

stituents. Furthermore, the tool at this stage is not up-

to-date as it has not been ported to the current version

of Prot´eg´e 5.0.

³F´KDV2ZQHU´S´

³S´KDV'ULYHU/LFHQVH³G´ ³S´FDQ'ULYH³F´

)LJXUH

Figure 1: Axiom´e – individual rule visualisation.

2.2 Poznan University of Technology

Graph-based Editor

In 2013, Jaroslaw Bak and his team fro m Poznan Uni-

versity of Technology published a prototypical imple-

mentation of a graphed-based editor for SWRL rules.

The edito r focuses on the visu alisation of individual

SWRL rules. It is based on a set of new modelling

elements for the illustration of rules in diagrams (see

Fig. 2).

&ODVV &ODVV,QVWDQFH 2EMHFW'DWD3URSHUW\ 9DOXH

)LJXUH

Figure 2: Set of notation elements.

This approach distinguishe s separate taxonomies for

Classes, Data Properties, and Object Properties (Bak

et al., 2013). The ed itor creates a diagram for each of

the three taxonomies, allowing the user to choose be-

tween different pe rspectives. The diagrams are split

into two sections (see Fig. 3) (Bak et al., 2013). The

left-hand section portra ys th e condition elements (a n-

tecedent) of an SWRL rule whereas the right-hand

section shows the conclusion (consequent).

FDQ'ULYH

"S "F

KDV'ULYHU/LFHQVH KDV2ZQHU

3HUVRQ"S

'ULYHU/LFHQVH"G &DU"F

&RQGLWLRQV &RQFOXVLRQ

)LJXUH

Figure 3: Poznan Graph Editor - SWRL visualisation.

In general, this mo delling approach offers a lot of po-

tential as it is visually self-explaining, but it is limi-

ted when tryin g to show the impact of built-ins or

KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development

176

restrictions. However, built-ins are essential compo-

nents of SWRL necessary to implem ent mathematical

operations. The sepa ration of the representation into

different views can be considered a deﬁciency. A uni-

ﬁed diagram for all three perspectives may improve

general understanding of the rule. Despite this, we

agree that the visual separation of rule antecedent and

consequent is as a good approach.

2.3 Graph Inscribed Logic (Grailog)

Grailog is a combination of g eneralised graph con-

structs fo r visualising data, inter alia, Horn logic

(Boley, 2013). The visualisation is adapted to the

industry standard RuleML. With Grailog a new

concept of hypergraphs is introduce d which is a

proposed enhancement in compar iso n to directed

labelled graphs (Boley, 2013). According to Boley,

directed labelled graphs (DLG) are a good starting

point for visual knowledge representation but come

with major disadvantages when trying to illustrate

non-binary relationships (Boley, 201 3). This is why

he created hyperarcs as specialised arrows for h is

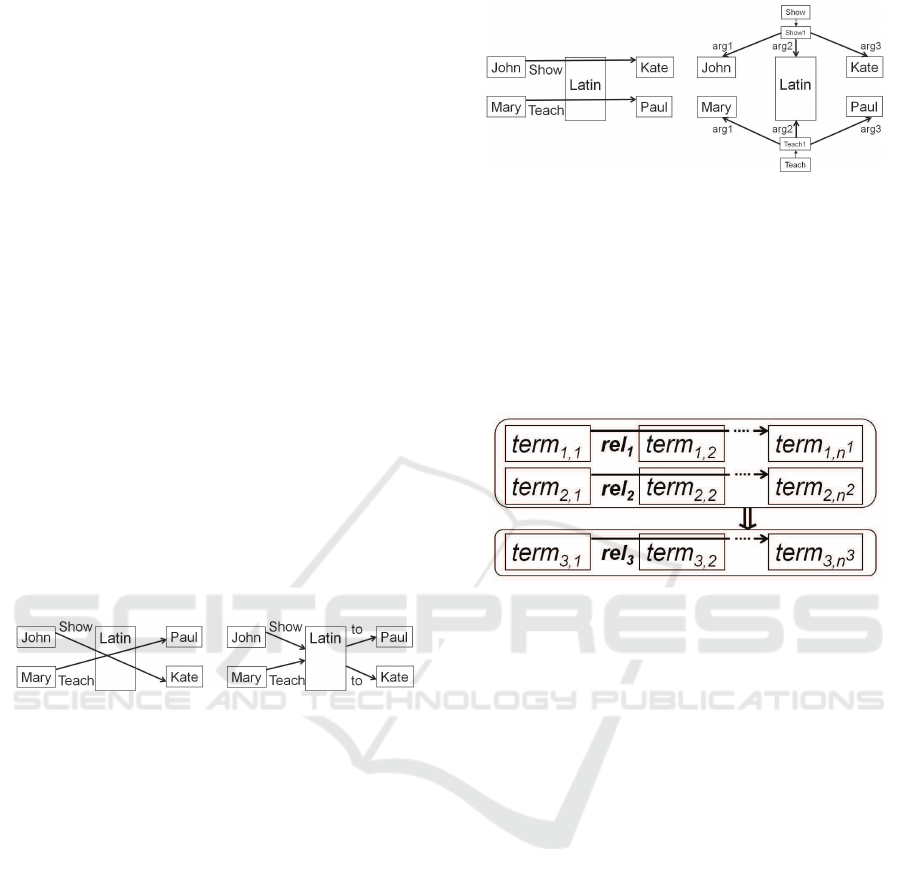
notation. The following graphs show a c omparison

of a hypergraph on the left-hand side and a directed

labelled graph on the right-hand side (see Fig. 4).

Figure 4: Hypergraphs in comparison to DLG 1 (Boley,

2013).

Both diagrams in Fig . 4 show the two statements:

”John shows Latin to Kate”

”Mary teaches Latin to Paul”

Using a directed labelled gr a ph has the disadvantage

of losing th e context of input and output arrows

(Boley, 2013). This means that the graph may also

be misin te rpreted as “John shows Latin to Paul”

and “Mary teaches Latin to Kate”. However, the

hypera rcs provide a means to unmistakably deﬁne

the non -binary relationship. When trying to correctly

and unambiguously illustrate the two given sentences

as a DLG, the graph becom es signiﬁcantly more

complex, demonstrating a major advantage of Grailog

Hypergraphs (see Fig. 5).

Grailog also offers the possibility to formulate advan-

ced logic using the idea of so called c omplex nodes.

According to Grailog, a graph can co nsist of elemen-

tary nodes such as John and Kate. Moreover, a com-

plex node is able to contain othe r grap hs, making it an

Figure 5: Hypergraphs in comparison to DLG 2 (Boley,

2013).

enclosing entity. Based on this, it is also possible to

express Horn Logic using a combination of complex

nodes in Grailog ( see Fig. 6) (Bo ley, 2013). Although

Grailog can describe Horn Logic, it is not specialised

for SWRL m aking it difﬁcult to portray SWRL built-

ins. In this paper, we f ocus on a more specia lised

solution for SWRL ru le s.

Figure 6: Grailog - Horn logic (Boley, 2013).

2.4 Using UML State Diagrams for

Visualising Business Rules

In 2008, Konrad Kułakowski and Grzegorz J. Na-

lepa pu blished a modelling approach for business ru-

les using UML diagrams. The main idea is to repre-

sent a rule base as a class diagra m. Based on this,

each class repre sents a single rule. Th e class diagram

then shows dependenc ies between different rules (Ku-

lakowski and Nalepa, 200 8). Furtherm ore, each class

has its own state diagram which is describe d as a rule

deﬁnition d iagram. The paper deﬁnes rules a s plain

textual if-then statements (Kulakowski and N alepa,

2008). The rule d eﬁnition diagram expresses condi-

tions using the UML standard Object Co nstraint Lan-

guage (OCL). As the proposed modelling format is

designed for business rules in g eneral, the possibili-

ties to visualise m ore complex SWRL logic rules are

limited.

3 CONCEPTUAL MODELLING

Before we deﬁne our notation elements we give a

brief discussion of relevant aspects of ontologies and

rules.

Aided OWL Notation (AOWLN): Conceptual Modelling and Visualisation of Advanced SWRL Rules

177

3.1 OWL/SWRL Elements

OWL is a standardised general knowledge represen-

tation language for creating ontologies (McGuinness

et al., 20 04). The elements of OWL are often de no-

minated as a toms when used in rules.

An ontology O is a triple (C ,R ,I ). C is a set of c on-

cepts, R a set of relations, and I a set of individual

objects. Concepts (i.e. Classes) formally d e note sets

of objects. From a perspective of formal logic, these

sets are the extension of concepts while con c epts de-

ﬁne the intentional r e presentation of the correspon-

ding set of objects. An obje ct that belongs to a con-

cept is called an instance of that concept. The ele-

ments of R are relations (also called roles or object

properties, as they manife st links on the level o f the

instances) having subsets of C as domain and range.

The extension of a role then is a set of pairs (c, d)

with c, d elements of I . Additionally, instances can

have data properties through which they get linked to

primitive data e.g. strings or numbers. Typically, on-

tologies are formulated by means of description lo-

gics with differing levels of expressiveness (Baader,

2003). Usually description logics are proper subsets

of ﬁrst order logic where expressiveness has been tra-

ded for decidability. Inf erence knowledge is impli-

citly given by the underlying mechan ism s of the avai-

lable reasoning instruments. Apar t from this, SWRL

as an extension also includes elements for restricti-

ons and built-ins (McGuin ness et al., 2004). Built-ins

can be de scribed as operators similar to methods or

functions respectively in conventional pro gramming

languag es. For instance, mathematical operatio ns and

data type restrictions can be expressed through built-

ins. The following table summarises the mo st signiﬁ-

cant elements and the corresponding syntactic struc-

ture when used in SWRL rule s.

Table 1: OWL/SWRL E lements.

OWL/SWRL Element Syntax

Class Person

Individual /

Class instance

Person(bob) /

Person(alice)

Data Property canDrive(bob, true)

Object Property isSon(bob, alice)

Built-ins swrlb:lessThan(?age,18)

Restrictions integer[> 0]

Variable ?age

3.2 SWRL Syntax Diagram

Horrocks (2004) d e ﬁnes a SWRL rule as a pair (A,

C) in which both, antece dent A and conseq uent C are

sets of atoms S

and S

(see Fig. 7).

Implies( )



antecedent consequent

Antecedent(

atom

)

Consequent(

atom

)

SWRL Rule

Antecedent

Consequent



Figure 7: SWRL syntax diagram 1.

An atom element r

must be de c la red w ith an atom

name ∈ B

∪C

∪ O

∪ D

for which B

is th e

set of built-in names, C

the set of c lass names, O

the set of object property names, D

the set of data

pro perty names and ﬁnally D

the set o f data ranges.

A built-in name b

is followed by zero or one built-

inID and at least one or more d-objects. The built-in

ID is a variable in which the built-in output is written.

A d- object can be a data literal o r a d-va riable which

in the second case is an URI reference to an entity de-

ﬁned in the ontology. A class name C

is followed

by an i-object which can either be an individual-ID or

an i-variable. An i-variable is an URI reference to an

entity deﬁned in the ontology. Apart fr om this, an ob-

ject property name o

is followed by a pair (i-object,

i-object) and a data property name d

compleme nted

by a pair (i-obje c t, d-object). A data range d

is fol-

lowed by a single d-object (see Fig. 8).

Atom

builtInName ( builtInID

d-object

)

className

(

i-object

objectPropertyName

(

i-object

dataRange

(

d-object

dataPropertyName

(

i-object

URIreference

BuiltInID

i-variable

Individual-ID

i-object

d-variable

dataLiteral

d-object

URIreferenceI-variable(

)

URIreferenceD-variable(

)

d-variable

i-variable

Figure 8: SWRL syntax diagram 2.

3.3 AOWLN Graph Structure

As discussed before, directed labelled graphs are we ll

suited to visualise logical sequences (see Section 2).

In order to visualise SWRL rules, a corresponding

KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development

178

graphica l symbol for each of the existing semantic

OWL/SWRL elements has been mapped a nd c an be

composed into a graph.

For a given SWRL rule R

we deﬁne a Graph G and

map the components of R

to nodes of G. Th e graph

consists of a heterogeneous set o f vertices V = R ∪

O ∪ T ∪ D (R be ing a set of rectangles (class nodes),

O a set of ovals (property nodes), T a set of trapeziums

(variable nodes) and D a set of d iamond shapes (built-

in collection nodes) an d edges E = D

∪ O

∪ B

)

being a set of unlabelled solid arrows ( data pro-

perty edges), O

a set of dashed unlabelled arrows

(object property edg es) and B

a set of solid and la-

belled arrows (built-in edges). T he mapp ing is des-

cribed in ﬁgure 9.

&ODVVHV

'DWD3URSHUW\

2EMHFW3URSHUW\

9DULDEOH

%XLOWLQ&ROOHFWLRQ

%XLOW,Q

(

$

%XLOWLQ1DPH

2EMHFW3URSHUW\

(

Figure 9: AOWLN elements.

According to this mapping, classes are represented

by rectangle shapes and properties by oval shapes.

Properties associated with classes are connected to

the corresponding class e le ment with an edge. E dges

are unlabelled and directed. Wh ile class nodes a nd

data properties as well as variables are connected

with solid lines, ed ges associated with object p ro-

perties are dashe d. Variables are re presented by

trapezium shapes. In SWRL data type restrictions

and operations can be expressed with built-ins.

Data type re strictions are written into the lower half

of a property symbol, sepa rated by a dashed line.

Moreover, built-ins are visualised by labelling the

edge that progresses towards the resulting variable.

If multiple built-ins result in the same variable, these

built-ins are summarised into a new diamond shaped

Built-in Collection element.

For both rule antecedent and consequent separate

graphs a re created which are displayed in juxtaposi-

tion. The following pseudocode sketches th e creation

of the graph.

List aowlnElements

List aowlnEdges

function createAOWLNGraph(RuleFragment rf)

for each classAtom in rf

if classAtom not in aowlnElements

aowlnElements add classAtom

completeLogicalSequence(classAtom, rf)

for each ObjectPropAtom in rf

if classAtom is firstArg:

appendAtom (classAtom, ObjectPropAtom)

classAtom = ObjectPropAtom.SecondArg

completeLogicalSequence(classAtom, rf)

endIf

endFor

aowlnGraph = new Graph(aowlnElements, aowlnEdges)

function appendAtom (startAtom, nextAtom)

aowlnElements add nextAtom

aowlnEdges add new Edge(startAtom, nextAtom)

function completeLogicalSequence(classAtom, ruleFragment)

for each DataPropAtom in ruleFragment

if classAtom is firstArg:

appendAtom (classAtom, DataPropAtom)

currentAtom = DataPropAtom

while (successorAtom not null) do

successorAtom =

findLogicalSuccessor(successorAtom, ruleFragment)

appendAtom(currentAtom, successorAtom)

currentAtom = successorAtom

endWhile

varElement = currentAtom.getResultingVar()

appendAtom(currentAtom, varElement)

endIf

endFor

By convention, for e a ch variable instance of a

class, a class node is crea te d explicitly. Furthermore,

the last variable of a logical sequence must be

indicated. A logical sequence is the concatenation of

SWRL atoms through joint references to variables.

However, variables th a t are passed on to consequen-

tial properties or built-ins ma y be skipped in the

visualisation to avoid redundant graph elem e nts. For

logical sequences that end with a class a tom no de

(i.e. objec t properties) the variable node at the end

of the sequence can be omitted as class atoms are

explicitly created for each variable instance of a class.

The algorithm de scribed above requir es a sequ ential

ordering of the atoms in the SWRL rule:

1. Class 1

a. class1DataProperty1

b. class1TransitiveNextProperty1

i. c1TNP1BuiltIn1

ii. c1TNP1BuiltIn 2

iii. c1TNP1Restriction

c. class1TNP2

Aided OWL Notation (AOWLN): Conceptual Modelling and Visualisation of Advanced SWRL Rules

179

d. class1TNPN

2. Class2

3. ...

4. ClassN

(1) objectProperty 1

(2) objectProperty 2

(3) ...

(4) objectProperty N

⇒ Conclusion

The rule conclusion is processed just like that. The

ordering en sures the afﬁliation of transitive e le ments

simplifying the implementation. Built-ins which only

use a single variable in position one will not be visu-

alised. See the following example:

1. add(?ageNew, ?age, 10)

2. add(?ageNew, 6, 10)

The SWRL math built-in, swrlb:add() is used. This

built-in is satisﬁed if the ﬁrst argument is equal to the

arithmetic sum of the f ollowing arguments (Horrocks

et al., 2004). Henc e, the built-in writes the result into

the ﬁrst variable ?newAge. In the ﬁrst case, the varia-

ble ?newAge is derived from the variable ?age. In th e

second case the ope rands of the summation are con-

stants a nd will no t be visualised because they are not

part of a logical sequence. This en hances the reada-

bility of the graph by eliminating nodes of low mea-

ningfulness.

4 EXAMPLE OF APPLICATION

The following example demonstrates the use of the

notation elements.

Textual Description:

Individuals under the age of 18 as a potential driver of

a vehicle with a weight of less than 26,000 lbs are able

to drive in California if they possess an out-of-state

driver’s license except for New York and are visiting

the state for less than 10 days. For this, the person

must be the owner of the car.

Table 2: AOWLN Elements Mapping.

Concept / Class Data Property

→ Built-In

Object Property

Person(?p) hasAge(?p,?g)

→ lessThan(18)

ownsCar(?p,?c)

Car(?c) numberOfVisiting-

InDaysInCA(?p,?x)

→ lessThan(10)

hasDriverLicence(?p,?d)

DriverLicense(?d) issuedStateOf(?d,?s)

→ notEqual(s,”CA”)

→ notEqual(s,”NY”)

hasWeightInLBS(?x,?w)

3HUVRQS

KDV'ULYHU

/LFHQVH

LVVXHG6

WDWH2I

KDV$JH

QXPEHU2I9LVLWLQJ

'D\V,Q&$

&DUF

RZQV

&DU

KDV:HLJKW,Q/%6

&RQFOXVLRQ

3HUVRQS

FDQ

'ULYH

'ULYHU/LFHQVHG

[

&DUF

)LJXUH

SWRL:

Person(?p) ∧ hasAge(?p, ?g) ∧ swrlb : lessT han

(?g, 18) ∧ numberO fVisitngDaysInCA(?p, ?x) ∧

swrlb : lessT han(?x, 10) ∧ D riverLicense(?d) ∧

hasDriverLice nse(?p, ?d) ∧ issuedInStateO f (?d, ?s)

∧ swrlb : notEqual(?s,

′′

) ∧ swrlb : notEqual

(?s,

′′

) ∧ Car(?c) ∧ hasWeightInLB S(?c, ?w) ∧

swrlb : lessT han(?w, 26000) ∧ ownsCar(?p, ?c)

⇒ Person(?p) ∧Car(?c) ∧ canDrive(?p, ?c)

AOWLN:

As the Fig. 10 displays, there is a separatio n of rule

conditions and the rule conclusion similar to the Po-

znan graph editor (see Sectio n 2.2). This separation

helps making the graph more m anageable when rules

are getting more c omplex. However, the visualisation

does not use sep arate taxonom ie s. Built-in s a re inclu-

ded in the visualisation. The names of the built-ins are

used to label the edges. In case that multiple built-ins

result in the same variable, the built-ins are summ a-

rised in a built-in collection symbol. Fig. 10 shows,

that it is po ssible to reduce the rule illustration to the

most essential and necessary elements to portray the

logical sequ ence. This makes working with rule ba-

sed systems signiﬁcantly easier.

3HUVRQS

KDV'ULYHU

/LFHQVH

LVVXHG6

WDWH2I

KDV$JH

QXPEHU2I9LVLWLQJ

'D\V,Q&$

&DUF

RZQV

&DU

KDV:HLJKW,Q/%6

&RQFOXVLRQ

3HUVRQS

FDQ

'ULYH

'ULYHU/LFHQVHG

[

&DUF

)LJXUH

Figure 10: Example rule – AOWLN graph.

KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development

180

5 IMPLEMENTATION

In this section we addre ss th e prototypical implemen-

tation of the visu alisation p lugin for Prot´eg´e.

5.1 Design

The plugin will be seamlessly integrated into the

Prot´eg´e environment. The application includes a

full-text search to simplify the work with th e rule set.

Based on this, the user is given the option to select

rules for which an AOWLN diagram will be created.

The implementation of the visualisation engine is

separated from the display unit and the ontology. This

makes the engine independ ent for future applications

as shown in the following co mponent diagram. A

completely assembled system can use Prot´eg´e as an

ontology editor to d ocument and generate the o nto-

logy. The AOWLN modelling engine extracts SWRL

rules th rough the OWL/SWRL API and produces a

diagram as an image ﬁle or as an interactive graph

(see Fig. 11).

<<component>>

Ontology Editor

<<component>>

Ontology

<<component>>

Display Unit

<<component>>

AOWLN Modelling

Engine

OWL/SWRL API

Graph Visualisation Framework

Display Ontology

gets diagram

extracts rules

models ontology

Figure 11: Component diagram.

5.2 Modelling Engine for Graphical

Abstraction (MEGA)

The impleme ntation is based on a three-layer-

approa c h has been developed to process rule data

from the ontology into the required graph format that

can be v isu alised (see Fig. 12). In Laye r 0, the SWRL

API

is the fundamental componen t. The SWRL

API (an extension of th e OWL API) reads the on-

tology and provides a set of SWRLAtoms. As the

SWRLAtom class from the SWRL API includes un-

necessary information for the visualisation, a custom

SWRL atom structure has been deﬁne d wh ic h is il-

lustrated as Layer 1. The createCustomSWRLAtoms()

method transforms the given SWRL atoms from the

SWRL API in to the custom SWRL atom structur e .

This makes it easier to focus on the most essential

See https://github.com/protegeproject/swrlapi - (acces-

sed on 06/01/2018)

informa tion for the visualisation. In a second step,

the createAOWLNElements() method creates a sepa-

rate list for both, AOWLN nodes and edges for La yer

2 based on the custom SWRL atoms in Layer 1. Ed-

ges contain references for a start and a target node.

6:5/$3,6:5/$WRPV

&XVWRP6:5/$WRPV

$2:/1(OHPHQWV

FUHDWH&XVWRP6:5/$WRPV

FUHDWH$2:/1(OHPHQWV

/D\HU

/D\HU

/D\HU

Figure 12: MEGA – t hree-layer-approach.

5.3 Prototype

The prototype has the following features: search and

select rules f rom the rule base, visualise the rules as

an AOWLN graph an d it includes an option to edit

and update a selected rule in the rule base. The pro-

totypical Prot´eg´e plugin is written in Java as both, the

Prot´eg´e environment and the SWRL API are also im-

plemented in Java. For the graph visualisation, we

make use of the open source library Graphviz.

6 CONCLUSION AND FUTURE

WORK

This p aper deﬁnes a graphical notation format for the

visualisation of SWRL rules and describes a prototy-

pical Prot´eg´e plugin for rule visualisation. AOWLN

offers mean s for visu alising all types of componen ts

of SWRL elements especially built-ins. For this, the

form of representation is a pair o f directed labelled

graphs to po rtray rule antecedent and consequent.

The implemented plugin offers options to search and

select rules from the rule base, visualise the ru le s

as an AOWLN grap h and includes an op tion to edit

and update a selected rule. As proof of concept

the plugin is currently used in an indu stria l digi-

tisation project which enabled several feedback loops.

Further fu nctions to im prove usability and error hand-

ling will make working with the visualisation tool

See https://www.graphviz.org/ - (accessed on

20/01/2018)

Aided OWL Notation (AOWLN): Conceptual Modelling and Visualisation of Advanced SWRL Rules

181

Figure 13: AOWLN Prot´eg´e Plugin – Protoype.

more efﬁcient. Since the prototype was written as a

component inde pendent from both the ontology and

the display unit, it can ea sily be integrated into lar-

ger systems e.g. the plug in can easily be extended

to a graphical editor that allows for interactive cre-

ation and modiﬁcation of SWRL rules. Further fo r-

malisation and generalisation to make the algorithm

work with arbitrary SWRL rules will be carried out.

We will provid e the source code for the AOWLN

project on g ithub. The repository can be acc essed

under the following URL: https://githu b.com/KITE-

Cloud/AOWLN

REFERENCES

Baader, F. (2003). The description logic handbook: Theory,

implementation and applications. Cambridge univer-

sity press.

Bak, J., Nowak, M., and Jedrzejek, C. (2013). Graph-based

editor for swrl rule bases. In RuleML (2). Citeseer.

Boley, H. (2013). Grailog 1.0: Graph-Logic Visualization

of Ontologies and Rules. In Proc. 7th International

Web Rule Symposium: Research Based and Industry

Focused (RuleML 2013), Seattle, Washington, USA,

volume 8035 of Lecture Notes in Computer Science,

pages 52–67. Springer.

Guarino, N., Oberle, D., and Staab, S. (2009). What is an

ontology? In Handbook on ontologies, pages 1–17.

Springer.

Hassanpour, S., O’Connor, M. J., and Das, A. K. ( 2009).

Axiom´e: A tool for the elicitation and management

of SWRL rules. In Proceedings of the 5th Internati-

onal Workshop on OWL: Experiences and Directions

(OWLED 2009), Chantilly, VA, United States, October

23-24, 2009.

Horrocks, I., Patel-Schneider, P. F., Boley, H., Tabet, S.,

Grosof, B., Dean, M., et al. (2004). Swrl: A semantic

web rule language combining owl and ruleml. W3C

Member submission, 21:79.

Kulakowski, K. and Nalepa, G. J. (2008). Using uml state

diagrams for visual modeling of business rules. In

Computer Science and Information Technology, 2008.

IMCSIT 2008. International Multiconference on, pa-

ges 189–194. IEEE.

McGuinness, D. L., Van Harmelen, F., et al. (2004). Owl

web ontology language overview. W3C recommenda-

tion, 10(10):2004.

KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development

182