Applying Cartesian Genetic Programming to Evolve Rules for Intrusion

Detection System

Hasanen Alyasiri

, John Clark

and Daniel Kudenko

Department of Computer Science, University of York, U.K.

Department of Computer Science, University of Shefﬁeld, U.K.

Keywords:

Cartesian Genetic Programming, Intrusion Detection System, Stacking Ensemble.

Abstract:

With cyber-attacks becoming a regular feature of daily business and attackers continuously evolving their

techniques, we are witnessing ever more sophisticated and targeted threats. Various artiﬁcial intelligence

(AI) algorithms have been deployed to analyse such incidents. Extracting knowledge allows the discovery

of new attack methods, intrusion scenarios, and attackers’ objectives and strategies, all of which can help

distinguish subsequent attacks from legitimate behaviour. Amongst AI approaches, Evolutionary Computation

(EC) techniques have seen signiﬁcant application, particularly in the area of intrusion detection. In this paper,

we show how one EC approach, namely Cartesian Genetic Programming (CGP), can construct rules (checks)

for detecting malicious behaviour in a system. Experiments are conducted on up-to-date datasets and compared

with state of the art approaches. We also introduce an ensemble learning paradigm, indicating how CGP can

be used as stacking technique to improve learning performance.

1 INTRODUCTION

“Intrusion detection is the process of monitoring the

events occurring in a computer system or network

and analysing them for signs of possible incidents,

which are violations or imminent threats of violation

of computer security policies, acceptable use policies,

or standard security practices” (Scarfone and Mell,

2007). In recent years, security threats have had a

major effect on the conﬁdentiality, privacy and inte-

grity of on-line services. Intrusion detection can help

prevent or mitigate some of these threats. Intrusion

detection relies extensively on the analysis of attack

vectors and intentions. However, IDS systems face

various problems such as large trafﬁc volumes, unba-

lanced data distributions, the need to recognize nor-

mal and abnormal behaviour, and continuously chan-

ging environments (Wu and Banzhaf, 2010).

Researchers have applied a variety of machine le-

arning and data mining approaches to address IDS

problems. Evolutionary Computation (EC) techni-

ques have been used by researchers to tackle nume-

rous tasks in IDSs, for example searching for an op-

timal probe placement, automatic model design, and

learning of classiﬁers (Wu and Banzhaf, 2010). EC

approaches have a number of attractive features, such

as producing readable outputs, producing lightweight

rules, and an ability to make trade-offs between con-

ﬂicting objectives (Sen, 2015). These features are

very signiﬁcant for security teams (Orﬁla et al., 2009).

In addition, EC makes possible the automated synthe-

sis of computer programs. It is often used when the

desired solution is an ‘expression’ or program. EC-

based techniques can be data distribution free, i.e., no

prior knowledge is needed about the statistical distri-

bution of the data and the approaches can operate di-

rectly on the data in their original form.

Various researchers have reported the use of some

sort of EC for evolving IDS rules. In this paper we use

a form of Genetic Programming (GP) called Cartesian

Genetic Programming (CGP). CGP was introduced in

(Miller and Thomson, 2000). CGP individuals take

the form of directed acyclic graphs instead of the tree

structures used by standard forms of GP. It represents

these graphs as a two-dimensional grid of computati-

onal nodes (Miller, 2011). An individual’s genotype

is a linear string of integers that decodes to a directed

graph. A set of predeﬁned inputs and functions, en-

coded as graph nodes, are then sequentially evaluated

(‘executed’) to give the desired output. CGP has been

applied in a signiﬁcant number of domains and pro-

blems (Miller and Smith, 2006). This paper demon-

strates the use of CGP to discover intrusion detection

rules.

176

Alyasiri, H., Clark, J. and Kudenko, D.

Applying Cartesian Genetic Programming to Evolve Rules for Intrusion Detection System.

DOI: 10.5220/0006925901760183

In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 176-183

ISBN: 978-989-758-327-8

Section 2 summarises past use of EC algorithms

for IDS rule synthesis. Section 3 introduces our pro-

posed method. Section 4 introduces the experimen-

tal datasets and the standard CGP implementation re-

sults. Section 5 introduces the stacking ensemble con-

cept, implementation and results. The last section gi-

ves conclusions and identiﬁes future work.

2 RELATED WORK

(Crosbie et al., 1995) gave the ﬁrst GP application to

intrusion detection, training autonomous agents to de-

tect intrusive behaviours. Obvious intrusions that are

misclassiﬁed during the evolution process are penali-

sed heavily. (Folino et al., 2005) presented a GP en-

semble for a distributed IDS. GP runs on a distributed

hybrid multi-island model-based environment to mo-

nitor security-related activity within a network. Each

island contains a cellular genetic program whose aim

is to generate a decision-tree predictor, trained on the

local data stored in the node and enhanced with the

boosting algorithm AdaBoost.M2. Every genetic pro-

gram operates cooperatively, yet independently of the

others. After the classiﬁers compute their results, ma-

jority voting is used to form an ensemble. (Abraham

et al., 2007) use three GP variants: linear genetic pro-

gramming, multi-expression programming and gene

expression programming to build an intrusion de-

tection program. The evolved detectors are effective

against a variety of attacks such as denial of service,

probe, user-to-root and remote-to-local attacks. The

work demonstrated the ability of GP techniques to de-

velop lightweight and accurate detection rules com-

pared to some of the conventional intrusion detection

systems based on machine learning paradigms. (Sen

and Clark, 2011) applied GP and Grammatical Evo-

lution (GE), another evolutionary computation para-

digm, to build IDS rules for deployment in mobile

ad hoc networks (MANETs). Their research shows

that GP and GE can be used to evolve efﬁcient detec-

tors automatically for known attacks, namely ad hoc

ﬂooding and route disruption against the routing pro-

tocol on MANETs. The experimental outcomes show

that GP and GE are good at discovering complex re-

lations on MANET data and that GP gives a better

performance than GE under their (approximation to)

optimal parameter settings.

3 CARTESIAN GENETIC

PROGRAMMING

“CGP is a form of automatic evolution of compu-

ter programs and other computational structures using

ideas inspired by Darwin’s theory of evolution by na-

tural selection” (Miller, 2011). In CGP, a program is

encoded as a linear string of integers representing a

directed graph. Each program is divided into subsets

of genes (i.e. genotype) of the same length, represen-

ting the nodes of the graph.

The genotype describes from where a node re-

ceives its data, what operations the node carries out

on the data, and how user output data is extracted.

When the genotype is decoded, some nodes are ig-

nored. This happens when a node’s outputs are not

subsequently used in the calculation of output data.

When this happens, we refer to the nodes and their ge-

nes as ‘inactive’. Previous investigations (Miller and

Thomson, 2000)(Miller and Smith, 2006) have shown

how a signiﬁcant percentage of inactive nodes can

help the efﬁciency of the evolution process. Unlike a

tree structure, where there is always a unique path be-

tween any pair of nodes, graphs permit more than one

path between any pair of nodes. If we assume all no-

des perform some computational function, graph re-

presentations of functions are more compact than tree

representations since they permit the reuse of previ-

ously calculated subgraphs. EC algorithms are also

susceptible to bloat, a phenomenon where a large por-

tion of the evolved program code has no inﬂuence on

the ﬁtness but whose execution still consumes resour-

ces (and so typically extends execution times). CGP

avoids such bloat (Miller and Smith, 2006).

CGP’s genotype decoding process is recursive in

nature. Decoding starts with the output genes. CGP

programs may have as many output nodes as ne-

cessary. These ﬁnal output nodes are deemed to

be ‘active’. The decoding process identiﬁes the no-

des whose outputs are used as inputs to these nodes.

These input nodes themselves become ‘active’ and

the same procedure is repeatedly applied until the full

function is identiﬁed, ending with the identiﬁcation

of appropriate terminal input nodes. The decoding

process extracts the active nodes; inactive nodes are

not processed and so having inactive genes presents

little computational overhead. Consider the example

shown in Figure 1.

There are three input nodes, which are indexed by

0,1, and 2. (These do not form part of the genotype,

but may be indexed by it.) The remaining (computati-

onal) nodes of the system are now numbered contigu-

ously, from 3 to 8. System inputs and computational

Applying Cartesian Genetic Programming to Evolve Rules for Intrusion Detection System

177

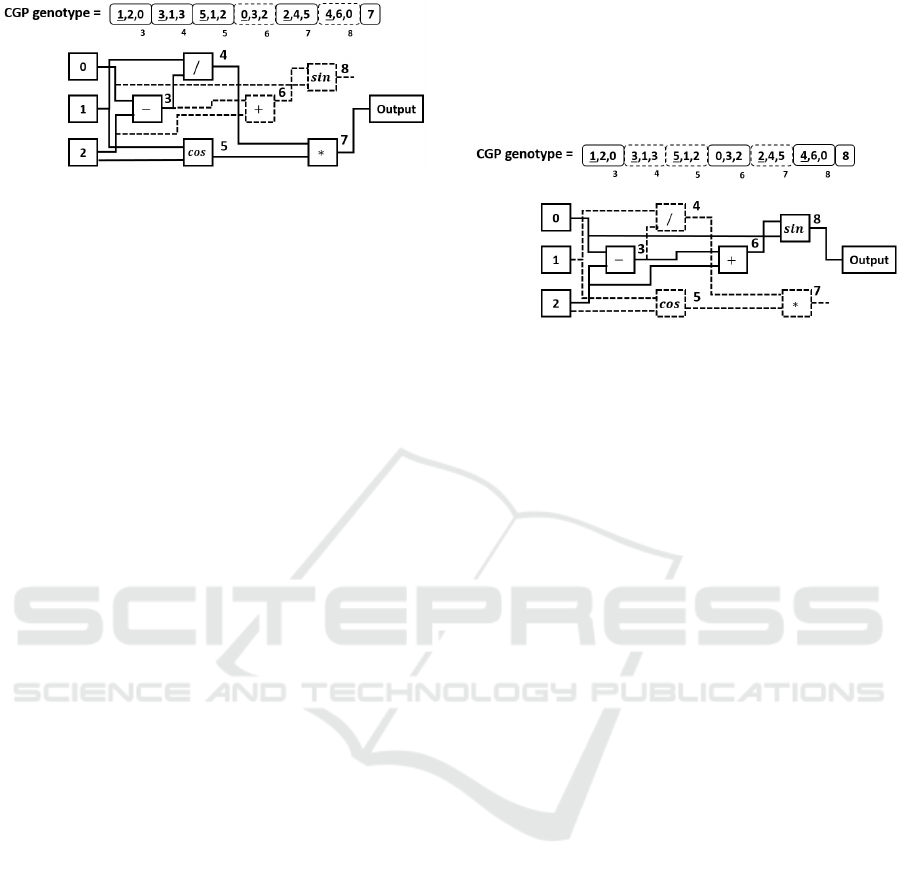
Figure 1: CGP genotype and corresponding phenotype.

nodes are therefore numbered contiguously over the

range 0 to 8.

The genotype contains structures of three integers

for each of its computational nodes. The underlined

genes in the genotype encode the speciﬁc function for

each node. There are six possible functions, denoted

by the integers 0 to 5: add (0), subtract (1), multi-

ply (2), divide (3), sin (4) and cos (5). The remaining

integers in each node structure are associated with ter-

minal inputs or with other function nodes that are lo-

cated to the left. The number of actual inputs depends

on the arity of the function. The number of formal

inputs to a computational node is the maximum arity

of any function in the function set. Any extra inputs

will be neglected by function nodes that require fewer

inputs than this maximum.

The last nodes in the genotype identify the output

nodes. Here there is only one such node, which takes

the value 7. The choice of node 7 as the output node

coupled with the value of earlier node triples induces

the active and inactive status of all earlier nodes.

Crossover operators have not been widely adop-

ted in CGP. Originally, a one-point crossover operator

was used (similar to the n-point crossover in genetic

algorithms) but was found to disrupt the subgraphs

within the chromosome (Miller, 2011). In another in-

vestigation (Clegg et al., 2007), a new ﬂoating-point

crossover operator was found to improve performance

for symbolic regression problems. However, further

work is needed on a range of problems in order to

evaluate its advantages. In a point mutation, a value at

a randomly chosen gene location is changed to anot-

her valid random value. If a function gene is selected

for mutation, then a valid value is the label of any

function in the function set, whereas if an input gene

is selected for mutation, then a valid value is the la-

bel of the output of any previous node in the genotype

or of any program input. In addition, a valid value

for a program output gene is the label of the output

of any node in the genotype or the label of a program

input. The user deﬁnes the number of genes in the ge-

notype that can be mutated in a single application of

the mutation operator. An example of the point mu-

tation operator is shown in ﬁgure 2. A single point

mutation takes place in the program gene, altering the

output node input connection from 7 to 8. This makes

nodes 6 and 8 to become active, whilst making nodes

4, 5 and 7 inactive. The inactive areas are shown in

dashes. This highlights how a small change in the ge-

notype can sometimes produce a large change in the

phenotype.

Figure 2: CGP genotype and corresponding phenotype after

mutation.

For individual selection the (1+ λ) Evolutionary

Strategy (ES) is normally used in CGP. Usually λ is

chosen to be 4. ES conﬁgures a single parent to breed

four children using mutation at each generation. The

best individual among the parent and children is kept

in the next generation and the process is repeated. In

an ES approach, child genotypes are favoured over the

parent. The parent is replaced by one of its offspring

when offspring genotypes have the same ﬁtness as the

parent and there is no offspring that is better than the

parent. This is an important characteristic of the algo-

rithm, which makes good use of redundancy in CGP

genotypes (Miller, 2011).

The method we propose uses a supervised lear-

ning CGP algorithm for detecting the Internet and

computer network threats. We will use existing data-

sets for which reasonable features have already been

extracted. The training phase will ﬁnish when one of

two criteria met: either all instances are categorised

correctly; or an identiﬁed maximum number of gene-

rations have been produced. Then, the best evolved

rules are evaluated in a test phase.

3.1 Parameter Settings for CGP

The ECJ (Luke, 1998) toolkit is used for the CGP

implementation. The population size chosen was 5.

CGP generally uses very small population sizes and

large numbers of generations (Miller, 2011). The

number of generation was 10,000, except for the mo-

dern DDoS dataset where a value of 2,000 was adop-

ted. This is because we did not witness any change in

the ﬁtness value after reaching 2,000 generation for

all runs. The mutation rate used was 0.01. The max-

imum number of nodes was 500. (This does not in-

clude inputs and outputs nodes.) These settings were

determined empirically via preliminary experimenta-

tion. We do not claim that these values are optimal.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

178

Function nodes consist of a set of mathematical, re-

lational and logical operators. The single input arity

functions used were sin, cos, log, log1p, sqrt, abs,

exp, ceil, f loor, tan and tanh. The binary functi-

ons were +, −, ∗, protected (/), power, max, min,

percent, >, ≥, ≤, <, =, 6=, AND and OR. The rest of

the parameters were determined automatically by the

packages. In our implementation, we evolve two out-

put nodes and compare them using the ” > ” function

to obtain a binary classiﬁcation decision (normal vs.

anomaly).

3.2 CGP Performance Measure

The effectiveness of proposed algorithms can be me-

asured according to how malicious and normal be-

haviours are classiﬁed. Our datasets are labelled as

normal or anomalous. We calculate the numbers of:

true positives (TP), where malicious events are accu-

rately classiﬁed as such; true negatives (TN), where

normal events are classiﬁed as such; false positives

(FP), where normal events are classiﬁed as malici-

ous; and false negatives FN), where malicious events

are classiﬁed as normal. Both false classiﬁcations are

problematic. FPs waste a great deal of time and can

lead to loss of conﬁdence and FN are examples of the

detector system not performing its primary task, i.e.

they are attacks that go undetected.

Three derived performance metrics are used to as-

sess our IDS optimize rule. The Detection Rate (DR)

(

T P

(T P+F N)

) indicates the fraction of real attacks that

are detected; this is sometimes is referred to as Re-

call. Accuracy (

(T P+T N)

(T N+T P+FN+FP)

) deﬁnes the fraction

of all instances (attacks or non-attacks) that are cor-

rectly classiﬁed. IDS experts consider both False

Positive Rate (FPR) (

(FP+T N)

) and False Negative

Rate (FNR) (

(FN+T P)

) to be as important as the de-

tection accuracy. Finally, the False Alarm Rate (FAR)

(

(FPR+FNR)

) gives the rate of misclassiﬁed instances.

3.3 Cost Function

The cost function measures how much an indivi-

dual’s performance deviates from the ideal. The

cost function used in our experiments is deﬁned

as ((

T P−Anomaly Count

Anomaly Count

)

+ (

T N−Normal Count

Normal Count

)

). When

classiﬁcation is perfect the cost is 0.

4 EXPERIMENT

The performance of the proposed techniques have

been evaluated using four different datasets: Kyoto

2006+ (Song et al., 2011), Phishing websites (Mo-

hammad et al., 2015), UNSW-NB15 (Moustafa and

Slay, 2015), and modern DDoS (Alkasassbeh et al.,

2016). These datasets are fully labelled and contain

realistic normal and malicious scenarios. Extracted

features are numeric, symbolic or binary. However,

we did not employ all sets of features available for dif-

ferent aspects. We did not want to increase learning

algorithm complexity by processing symbolic featu-

res such as protocol type, packet type and ﬂag. Some

attributes, such as IP addresses and port numbers,

may be changing constantly for a variety of reasons.

Any detectors relying on these attributes may not ge-

neralise well in real world applications. To obtain a

statistically signiﬁcant measure that does not depend

on the initial random seed, CGP algorithm results cor-

respond to an average of 20 independent runs. The

results from the testing phase are presented here.

4.1 Description of the Benchmark

Datasets

The datasets used in this study are publicly accessible

labelled and suitable datasets for training and testing

intrusion detection system. Four widely different ty-

pes of environment are used to generate them. The

scientiﬁc community is currently using these datasets.

More details on the feature names, types, possible va-

lues and descriptions of environments and threats are

given in the corresponding references.

To allow a fair comparison with the published re-

sults of other detection systems, the same dataset sam-

ples and splitting percentages (training/testing) are

chosen for evaluation . The relation between accuracy

of the best evolved program out of all runs from each

dataset and number of generations is examined and

demonstrated in ﬁgure 3. The best program shows

a performance on the testing dataset almost as good

as that on the training dataset, except on UNSW-

NB15 dataset due to its complexity (Moustafa and

Slay, 2016).

4.2 Results

Table 1 shows the performance of the evolved rules.

Table 1: Proposed method performance (%).

Dataset

CGP

DR FAR Accuracy

Kyoto 2006+ 99.65 0.70 99.35

Phishing Websites 89.99 8.31 91.88

UNSW-NB15 94.20 13.46 87.31

Modern DDoS 87.38 7.13 97.19

Applying Cartesian Genetic Programming to Evolve Rules for Intrusion Detection System

179

(a) Kyoto 2006+ (b) Phishing Websites

Figure 3: CGP: Relation between classiﬁcation accuracy and number of generations from each of the datasets.

To demonstrate the performance of the propo-

sed method, results obtained by CGP are compared

with those of other paradigms. (Ambusaidi et al.,

2016) build an IDS using Least Square Support Vec-

tor Machine algorithm integrated with feature se-

lection algorithm Flexible Mutual Information Based

Feature Selection (LSSVM-IDS+FMIFS). The main

idea is to remove redundant and irrelevant features in

data, as these features not only slow the classiﬁcation

process but also affect IDS classiﬁcation accuracy.

The evaluation showed that feature selection algo-

rithm contributes more critical features for LSSVM-

IDS to achieve better accuracy and lower computatio-

nal cost. The performance of LSSVM-IDS+FMIFS

tested on Kyoto 2006+ dataset were 99.64% DR,

0.13% FPR ,and 99.77% accuracy, while CGP accom-

plished 99.65% DR, 1.06% FPR, and 99.35% accu-

racy. To combat phishing website threats, (Thabtah

et al., 2016) proposed anti-phishing model deploying

improved Self-Structuring Neural Network (iSSNN)

combined with a feature selection method. Informa-

tion Gain, Chi-Square and Gain Ratio have been utili-

zed for the purpose of feature selection. iSSNN when

epoch size is set to 500 combined with Information

Gain for preprocessing achieved the higher perfor-

mance in most cases. iSSNN-500 experiment results

were 93.06%, 92.30%, 91.12%, 93.71% of accuracy,

F1-score, recall and precision respectively. This com-

pare to 91.88%, 90.69%, 89.99%, and 91.44% achie-

ved by CGP. (Moustafa and Slay, 2016) have imple-

mented Network Anomaly Detection System (NIDS)

using ﬁve techniques, namely, Na

ıve Bayes, Deci-

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

180

sion Tree (DT), Artiﬁcial Neural Network, Logis-

tic Regression, and Expectation-Maximisation Clus-

tering. NIDS was tested on nine types of modern

attacks fashions and new patterns of normal trafﬁc.

The DT technique accomplishes the highest accuracy

(i.e. 85.56%) and the lowest FAR (i.e. 15.78%) tes-

ted on UNSW-NB15 dataset. Finally, (Alkasassbeh

et al., 2016) proposed an IDS to detect and classify

Distributed Denial of Service Attacks (DDoS) using

three well-known data mining techniques: Multilayer

Perceptron (MLP), Na

ıve Bayes and Random Forest.

The IDS were evaluated on the modern DDoS dataset.

The experimental results show that MLP achieved the

highest accuracy of 98.63%.

So far, we have focused on developing an IDS

using standard algorithm implementations. However,

modern IDS model building can be integrated with a

wide variety of machine learning methods. For in-

stance, feature selection, various ensemble and hy-

brid techniques, and these methods generally produce

favourable results (Aburomman and Reaz, 2017).

These approaches are commonly used combined with

a single stage learner. An ensemble approach gene-

rally produces better performance than the individual

classiﬁers. Another advantage of ensemble approa-

ches is their design. Ensembles allow substitution one

or more algorithms with more accurate ones. Conse-

quently, we adopt an ensemble technique in our lear-

ning phase.

5 ENSEMBLE

The concept of combining a collection of weak lear-

ners and forming a single, strong learner is referred to

as an ensemble. An ensemble may combine multiple

(heterogeneous or homogeneous) models to obtain re-

liable and more accurate prediction. Different sche-

mas can be considered to generate the detectors and

to combine them, i.e. the same learning algorithm can

be trained on different datasets or/and different algo-

rithms can be trained on the same dataset (Folino and

Pisani, 2015). Popular conventional ensemble met-

hods include bagging, boosting and stacking (Abu-

romman and Reaz, 2017). Stacking is the abbreviated

term used to refer to Stacked Generalization (Wolpert,

1992). The main idea behind stacking is ﬁnding the

optimal combination of a collection of base learners.

Stacking is a class of algorithms that involves training

a second level “meta-learner” to ﬁnd the combination.

Unlike bagging and boosting, the goal in stacking is

to combine strong, diverse sets of learners. Moreo-

ver, ensemble techniques like bagging and boosting

are often used to generate homogeneous ensembles,

whereas stacking can be used to produce heterogene-

ous ensembles.

The algorithms used to generate the pool of clas-

siﬁers for this experiment are implemented in the

H2O.ai platform (H2O.ai, 2018). H2O.ai includes

many common machine learning algorithms and im-

plements best in class algorithms at scale. It also in-

cludes a stacked ensemble method that ﬁnds the op-

timal combination of a collection of prediction algo-

rithms using stacking. The Automatic Machine Le-

arning (AutoML) function in the platform is used to

build base learning models. This function automates

the supervised machine learning model-training pro-

cess. AutoML performs basic data preprocessing if

required such as imputation, one-shot encoding and

standardization. During the model generation stage,

it implements random grid search and model parame-

ter tuning using the validation set to produce best per-

forming models. AutoML trains and cross-validates

a Distributed Random Forest (DRF), an Extremely-

Randomized Forest (XRT), a random grid of Gra-

dient Boosting Machines (GBMs), a ﬁxed grid of

Generalized Linear Model (GLM), a random grid of

Deep Neural Nets (DNNs). In AutoML, the maxi-

mum number of models to generate is set to 10 and

the rest of the parameters determined automatically

by the platform. Note it is possible to produce more

than one model from the same family. However these

models may have different parameters.

5.1 Evolving Stacking through CGP

In this work, various algorithms are applied to the

same dataset to create different learner models. Af-

ter a number of models are created usually utilizing

part of the dataset i.e. training, the decisions of these

models are combined and a common decision is ta-

ken. In phase two, CGP is applied to create the ac-

tual ensemble model. Ensembles are coded as genetic

programs, each individual act as a possible aggrega-

tion of the available base learners. More speciﬁcally,

each ensemble is represented as a graph, while input

vector elements (i.e. base learners ) are input nodes.

We considered the continuous outputs of the base le-

arners, rather than the discrete outputs. This ensemble

model is then used to predict class labels for a new da-

taset (i.e.the testing dataset). To avoid a further phase

of training, we split the training dataset into 80% trai-

ning used to train base learners and 20% validation set

used to build stacked ensemble model through CGP

(see ﬁgure 4).

CGP offers an intelligent self-conﬁguration

environment to perform dynamic model selection

and integration for constructing the ensemble. The

Applying Cartesian Genetic Programming to Evolve Rules for Intrusion Detection System

181

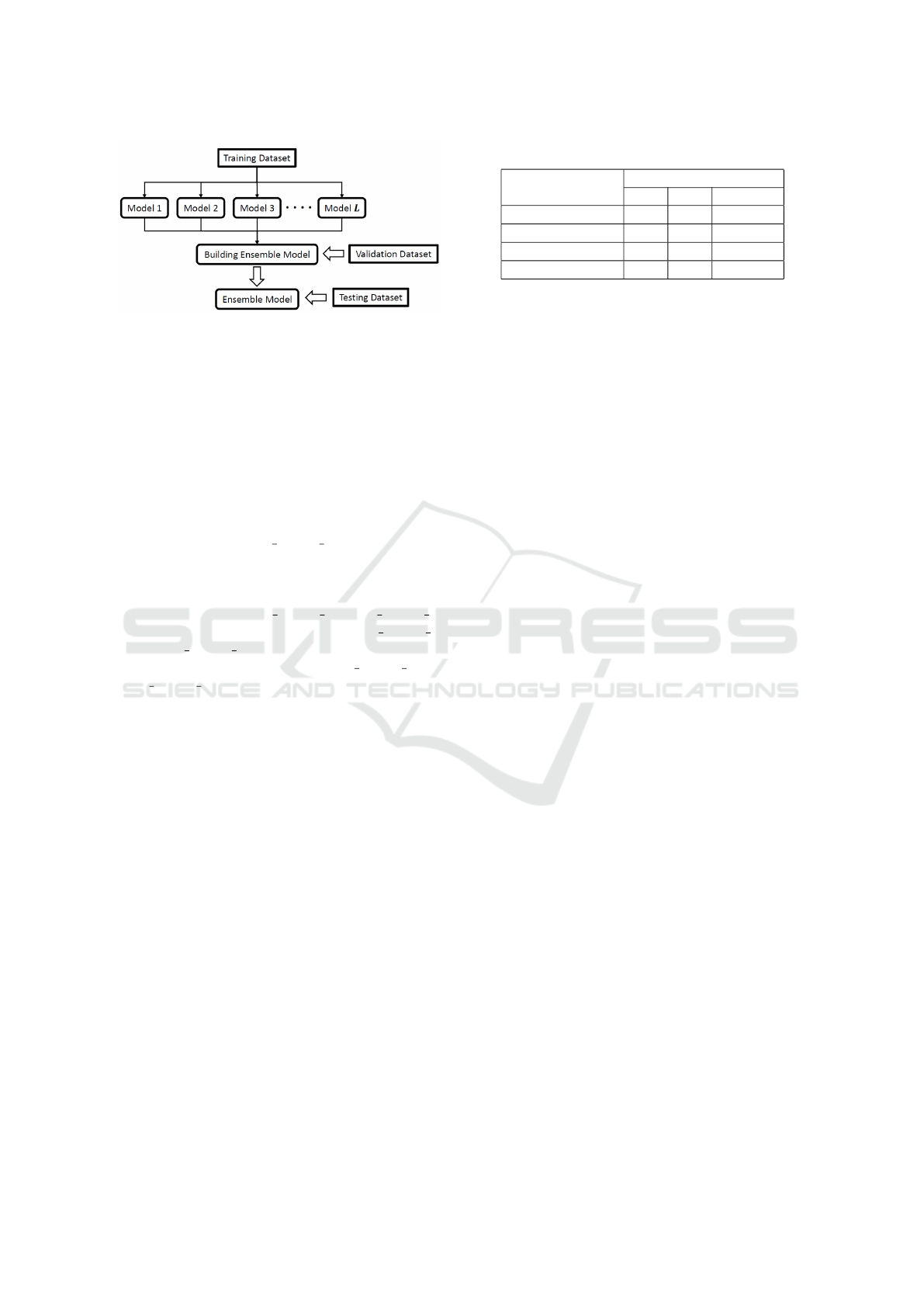
Figure 4: Proposed ensemble.

CGP parameter settings introduced in section 3 are

extended to evolve a detection rule of the ensemble

model. However, all CGP stacking runs used 2,000

generations. An example of CGP generated output

of the stacking model (taken from UNSW-NB15

dataset) are shown in ﬁgure 5. Besides being readable

output and ready for deployment, the solution showed

the 6 learner models that were selected out of 10.

This helps experts to understand how the ensemble

model works. Furthermore, it can be seen from this

ﬁgure that the cos GBM Model 4 node is reused 3

times in this rule which shows one of CGP graph

representation’s advantages.

o0 = sqrt (− (cos GBM Model 4) GBM Model 3)

o1 = log (/ (power (+ (sqrt DNN) GBM Model 1)

(cos GBM Model 4)) (sqrt (exp (min(exp XRT )

(min (sqrt (cos GBM Model 4))(=

GBM Model 3 DRF))))))

Figure 5: CGP stacking output.

5.2 Stacking Experiment Results

In practice, the default cross-validation folds in Au-

toML is 5 while training the base learners. The results

of applying the proposed technique to the testing data-

sets are shown in table 2. Comparing the standard and

ensemble implementations, it can be seen that adop-

ting the ensemble learning phase helped to enhance

the DR, reduce FAR and improve overall accuracy.

The most striking result to emerge was the CGP per-

formance on the phishing dataset. In this dataset, our

CGP stacking can provide a score of 96.29% F1-score

and 95.28% precision. CGP demonstrated a supe-

rior performance for all datasets except for modern

DDoS. Although CGP stacking managed to improve

DR compared to standard CGP, FAR and accuracy

performances slightly declined. It is worth noting that

this is the only unbalanced dataset distribution and

we treated both classes as equally important in this

implementation. Finally, ensemble synthesis by me-

ans of stacking heterogeneous base learners produced

Table 2: Stacking method performance (%).

Dataset

CGP Stacking

DR FAR Accuracy

Kyoto 2006+ 99.94 0.14 99.87

Phishing Websites 97.33 3.22 96.70

UNSW-NB15 96.29 11.29 89.47

Modern DDoS 87.40 7.18 97.10

the best classiﬁer performance compared with other

detection systems tested on the same dataset in most

cases.

6 CONCLUSIONS

This paper investigates an application of CGP to

the automated discovery of intrusion detection ru-

les. CGP has not been previously considered for this

problem. We used four publicly available datasets.

These datasets contain contemporary threats gathered

from various environments. Our proposed approaches

are capable of mapping the input vector space into a

decision space to allow effective discrimination bet-

ween classes (i.e. normal vs. anomaly). In addition,

we have considered the use of stacking to ensemble

synthesis to improve intrusion detection performance.

CGP stacking was generally able to generate, given a

domain, a good stacking conﬁguration. Our approach

determines not only which base learners must be pre-

sent but also the combining method of these learners.

The obtained results highlight clearly the beneﬁts of

adopting stacking heterogeneous ensembles over ot-

her paradigms.

One interesting feature of the approach is the abi-

lity to evolve a detector that can detect a wide range

of threats. However, we now intend to investigate

CGP ability to cope with new attacks (i.e. zero-day

attacks). Though we have not done so here, it should

also be possible to examine how the use of comple-

mentary classiﬁers can be applied to the problem at

hand (i.e. we would aim to synthesise classiﬁers for

complementary weaknesses).

ACKNOWLEDGEMENTS

Hasanan Alyasiri would like to thank the Iraqi Mini-

stry of Higher Education and Scientiﬁc Research and

the University of Kufa for supporting his PhD study.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

182

REFERENCES

Abraham, A., Grosan, C., and Martin-Vide, C. (2007). Evo-

lutionary design of intrusion detection programs. IJ

Network Security, 4(3):328–339.

Aburomman, A. A. and Reaz, M. B. I. (2017). A survey

of intrusion detection systems based on ensemble and

hybrid classiﬁers. Computers & Security, 65:135–

152.

Alkasassbeh, M., Al-Naymat, G., Hassanat, A. B., and

Almseidin, M. (2016). Detecting distributed denial of

service attacks using data mining techniques. Inter-

national Journal of Advanced Computer Science and

Applications, 7(1).

Ambusaidi, M. A., He, X., Nanda, P., and Tan, Z. (2016).

Building an intrusion detection system using a ﬁlter-

based feature selection algorithm. IEEE transactions

on computers, 65(10):2986–2998.

Clegg, J., Walker, J. A., and Miller, J. F. (2007). A new cros-

sover technique for cartesian genetic programming. In

Proceedings of the 9th annual conference on Gene-

tic and evolutionary computation, pages 1580–1587.

ACM.

Crosbie, M., Spafford, G., et al. (1995). Applying genetic

programming to intrusion detection. In Working No-

tes for the AAAI Symposium on Genetic Programming,

pages 1–8. Cambridge, MA: MIT Press.

Folino, G. and Pisani, F. S. (2015). Combining ensemble

of classiﬁers by using genetic programming for cyber

security applications. In European Conference on the

Applications of Evolutionary Computation, pages 54–

66. Springer.

Folino, G., Pizzuti, C., and Spezzano, G. (2005). Gp ensem-

ble for distributed intrusion detection systems. Pattern

Recognition and Data Mining, pages 54–62.

H2O.ai (2018). h2o: R Interface for H2O. Package version

3.18.0.2.

Luke, S. (1998). ECJ evolutionary computation li-

brary. Available for free at http://cs.gmu.edu/

∼eclab/projects/ecj/.

Miller, J. F. (2011). Cartesian genetic programming. In

Cartesian Genetic Programming, pages 17–34. Sprin-

ger.

Miller, J. F. and Smith, S. L. (2006). Redundancy and com-

putational efﬁciency in cartesian genetic program-

ming. IEEE Transactions on Evolutionary Computa-

tion, 10(2):167–174.

Miller, J. F. and Thomson, P. (2000). Cartesian genetic pro-

gramming. In European Conference on Genetic Pro-

gramming, pages 121–132. Springer.

Mohammad, R. M., McCluskey, L., and Thabtah, F.

(2015). UCI machine learning repository: Phis-

hing websites data set. https://archive.ics.uci.edu/

ml/datasets/Phishing+Websites.

Moustafa, N. and Slay, J. (2015). Unsw-nb15: a com-

prehensive data set for network intrusion detection

systems (unsw-nb15 network data set). In Mili-

tary Communications and Information Systems Con-

ference (MilCIS), 2015, pages 1–6. IEEE.

Moustafa, N. and Slay, J. (2016). The evaluation of net-

work anomaly detection systems: Statistical analysis

of the unsw-nb15 data set and the comparison with

the kdd99 data set. Information Security Journal: A

Global Perspective, 25(1-3):18–31.

Orﬁla, A., Estevez-Tapiador, J. M., and Ribagorda, A.

(2009). Evolving high-speed, easy-to-understand net-

work intrusion detection rules with genetic program-

ming. In Workshops on Applications of Evolutionary

Computation, pages 93–98. Springer.

Scarfone, K. and Mell, P. (2007). Guide to intrusion de-

tection and prevention systems (idps). NIST special

publication, 800(2007):94.

Sen, S. (2015). A survey of intrusion detection systems

using evolutionary computation. Bio-Inspired Com-

putation in Telecommunications, pages 73–94.

Sen, S. and Clark, J. A. (2011). Evolutionary computation

techniques for intrusion detection in mobile ad hoc

networks. Computer Networks, 55(15):3441–3457.

Song, J., Takakura, H., Okabe, Y., Eto, M., Inoue, D., and

Nakao, K. (2011). Statistical analysis of honeypot

data and building of kyoto 2006+ dataset for nids eva-

luation. In Proceedings of the First Workshop on Buil-

ding Analysis Datasets and Gathering Experience Re-

turns for Security, pages 29–36. ACM.

Thabtah, F., Mohammad, R. M., and McCluskey, L. (2016).

A dynamic self-structuring neural network model to

combat phishing. In Neural Networks (IJCNN), 2016

International Joint Conference on, pages 4221–4226.

IEEE.

Wolpert, D. H. (1992). Stacked generalization. Neural net-

works, 5(2):241–259.

Wu, S. X. and Banzhaf, W. (2010). The use of computa-

tional intelligence in intrusion detection systems: A

review. Applied Soft Computing, 10(1):1–35.

Applying Cartesian Genetic Programming to Evolve Rules for Intrusion Detection System

183