
Expansion: A Novel Mutation Operator for Genetic Programming
Mohiul Islam
1
, Nawwaf Kharma
1
and Peter Grogono
2
1
Department of Electrical & Computer Engineering, Concordia University, Montreal, Canada
2
Department of Computer Science & Software Engineering, Concordia University, Montreal, Canada
Keywords:
Evolutionary Computation, Computational Intelligence, Program Synthesis, Genetic Programming, Monte
Carlo Simulation, Monte Carlo Tree Search, Symbolic Regression.
Abstract:
Expansion is a novel mutation operator for Genetic Programming (GP). It uses Monte Carlo simulation to
repeatedly expand and evaluate programs using unit instructions, taking advantage of the granular search space
of evolutionary program synthesis. Monte Carlo simulation and its heuristic search method, Monte Carlo Tree
Search has been applied to Koza-style tree-based representation to compare results with different variation
operations such as sub-tree crossover and point mutation. Using a set of benchmark symbolic regression
problems, we prove that expansion have better fitness performance than point mutation, when included with
crossover. It also provides significant boost in fitness when compared with GP using only crossover on a
diverse problem set. We conclude that the best fitness can be achieved by including all three operators in GP,
crossover, point mutation and expansion.
1 INTRODUCTION
Genetic Programming (GP) is a stochastic generate-
and-test approach to inductive program synthesis
(Krawiec, 2016). Monte Carlo Tree Search (MCTS),
also being a stochastic search method is yet to be ef-
fectively applied to evolutionary program synthesis
(White et al., 2015) (Lim and Yoo, 2016). GP search
space is extremely granular while the fitness lands-
cape is exceptionally multi-modal. MCTS could take
advantage of this granularity if every level of this se-
arch tree expands a unit instruction set. Traversing a
tree made of programs using Monte Carlo Simulation
can provide interesting advantages to program expan-
sion with increased fitness.
2 PROGRAM SYNTHESIS
The earliest and the most commonly used method of
program synthesis is the evolution of a tree struc-
ture of programs. Here representation is made using
variable-length expressions from a functional pro-
gramming language, like symbolic expressions (S-
expr.) in LISP (Koza, 1992). Tree-based genetic pro-
gramming (TGP) is the classic approach to GP where
inner nodes of program trees hold functions (instructi-
ons) while leaves hold terminals which are input vari-
able or constants.
When evolving programs are represented using
computational nodes in a Cartesian coordinate sy-
stem, the method can aptly be named Cartesian Ge-
netic Programming (CGP) (Miller, 2011). It was first
used by Miller for evolving digital circuits (Miller
et al., 1997), but later became a general form of pro-
gram evolution (Miller and Thomson, 2000). This
representation can also be considered as a directed
acyclic graph. Its genotypes are integers containing a
node’s input data source, operation and output desti-
nation. The genotype passes through a decoding pro-
cess to result in an evolved program, which is its phe-
notype.
In Linear Genetic Programming (LGP) (Brameier
and Banzhaf, 2010) the term linear refers to the struc-
ture of the program representation. Here programs
in a population are represented as a sequence of in-
structions from an imperative programming language
or machine language (Nordin et al., 1999). The main
motivation of using a linear structure in LGP is the li-
near representation of the DNA molecule. Just as the
DNA is divided into gene codes, a linear represen-
tation of a program can be divided into instructions,
where each line of a single instruction is analogous to
a gene.
The most obvious challenges to robust and sca-
lable program synthesis, identified by Krawiec, is
Islam, M., Kharma, N. and Grogono, P.
Expansion: A Novel Mutation Operator for Genetic Programming.
DOI: 10.5220/0006927800550066
In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 55-66
ISBN: 978-989-758-327-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
55

the size of the search space, its multimodal fitness
landscape, externalized semantics of instructions and
their complex interactions (Krawiec, 2016). In his re-
cent study he identifies scalar evaluation of programs,
which is the normalized count of successfully passing
test cases, as a bottle neck. To solve this problem,
he defines program semantics as a vector of program
outputs for particular tests, providing more informa-
tion about program behaviour than conventional sca-
lar evaluation. The origin of Semantic Genetic Pro-
gramming (SGP) comes from the belief that to scale
evolutionary program synthesis, the algorithm needs
to take program semantics into account (Krawiec and
Lichocki, 2010). Also if we can exploit the geometry
of its semantic space, it is possible to come up with
more efficient search methods. The key intuition for
Geometric Semantic Programming (GSGP) (Morag-
lio et al., 2012) focuses specifically on the geome-
tric (metric-related) properties of program semantics.
With this in mind different crossover operators such
as Approximate Geometric Crossover (KLX) (Kra-
wiec and Lichocki, 2009) and exact geometric cros-
sover (GSGX) are defined (Krawiec, 2016).
Despite all the different methods using varied re-
presentations and variation operators, evolutionary
program synthesis is still not efficient enough for
practical software development. GP can only solve
elementary small problems using enormous computa-
tional effort. Most of this effort is spent on the multi-
tude of evaluations required on all different combina-
tions of programs. It is imperative for GP to be more
efficient in finding the optimum program with fewer
evaluations.
3 MONTE CARLO TREE
SEARCH
Monte-Carlo simulation is a highly effective method
which depends on repeated random sampling. Monte
Carlo Tree Search (MCTS) is a heuristic search algo-
rithm which uses Monte-Carlo simulation to evaluate
the nodes of a search tree. As a new paradigm for se-
arch, MCTS (Coulom, 2007b), has revolutionised not
only computer Go (Gelly and Silver, 2011) (Coulom,
2007a), but also General Game Playing (Finnsson and
Björnsson, 2008), Amazons (Lorentz, 2008), Line of
Action (Winands and Björnsson, 2010), multi-player
card games (Sturtevant, 2008) and real time strategy
games (Balla and Fern, 2009). Replacing other tra-
ditional search methods, MCTS uses self-play, by si-
mulating thousands of random games from its current
position in the tree. Ideally an MCTS algorithm for
game playing will contain the following four steps
(Chaslot et al., 2008).
Selection. Selection is the process of selecting
children of any node of the tree. Selection of the
children provides for balance between exploration
and exploitation of the search tree. Any method which
can be applied for sampling can also be used for node
child selection, depending on the problem being sol-
ved.
Expansion. This is the decision process of whether
a node’s children will be expanded for evaluation or
not. For game playing the simplest strategy is to ex-
pand one node per simulated game (Coulom, 2007b).
This step can be performed before or after simulation.
Simulation. For Go players this is the step where
players play pseudo random moves of self play until
the end of the game. Interesting moves and patterns
are applied, to come up with game strategies. It is dif-
ficult to come up with an efficient strategy, to balance
between exploration and exploitation. Having a stra-
tegy too stochastic results in weak moves where the
level of Monte-Carlo program decreases. In contrast,
having a deterministic strategy increases exploitation,
which also decreases the level of Monte-Carlo pro-
gram (Chaslot et al., 2008).
Figure 1: Monte Carlo Tree of Programs.
Backpropagation. This is the step in which results
are propagated backwards from the leaf node. For the
game of Go it could be the penalty of losing the game,
or reward of winning it. A ratio of this win/loss va-
lue will be propagated backwards, to update its parent
nodes about the outcome of this path.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
56
3.1 Monte Carlo Tree of Programs
The Monte Carlo Tree (MCT) of programs can be de-
fined using the definition of a unit instruction.
Unit Instruction. A unit instruction consists of a
single operator (+, -, /, cos, log, etc.) and its operands
(x, y, z, etc.). Here the number of operands depends
on whether the instruction is unary or binary. The list
of possible unit instructions consist of all combina-
tion of operators with all possible operands that can
be attached to that operator.
We define an MCT of programs consisting of no-
des similar to that of MCTS, where each node is a
program (Figure 1). For MCT the root node is the ini-
tial program. Expansion is a mutation operator where
the parent program that is selected for mutation is the
root node of the MCT. The first level of this tree, right
after the root node consists of the possible ways the
root node can be expanded using a unit instruction.
So each node of this level is a program expanded from
the initial program by one unit instruction. The next
level of MCT of programs consist of all possible ways
the programs of the first level can be expanded using
one unit instruction. Defined in the following section,
the Expansion mutation operator simply traverses this
MCT to find the best possible extension for the parent
program.
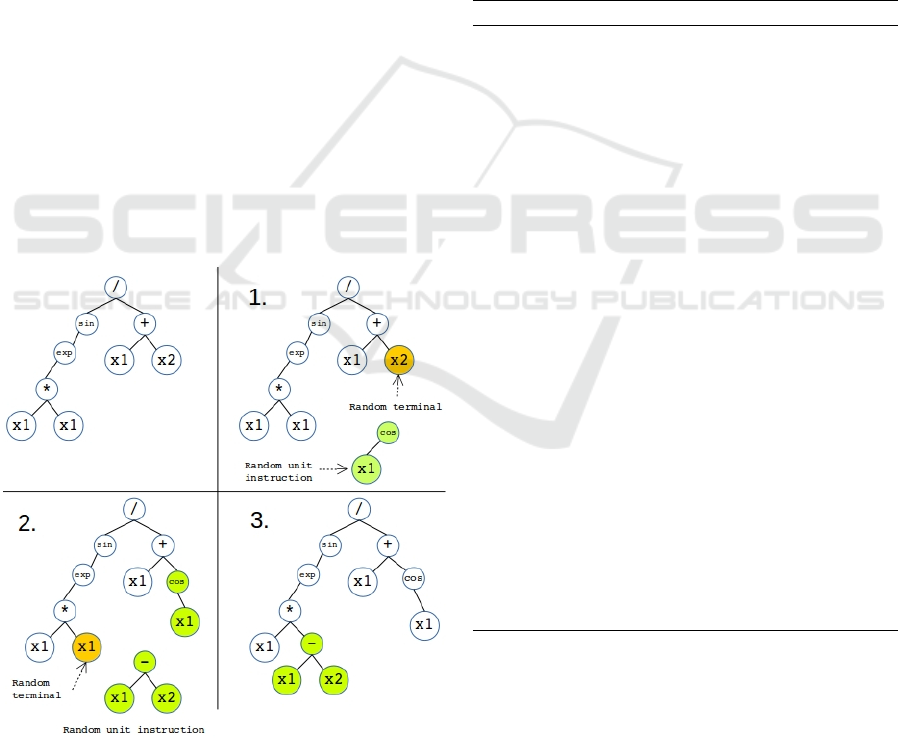
Figure 2: Program expanded with Monte Carlo Tree using
a single simulation with a depth of 2.
3.2 Expansion: The Mutation Operator
Expansion, the mutation operator can be defined
using the following terms.
Single Step Expansion. A single step expansion
starts by selecting a random terminal from the s-
expression of the initial program. Then a unit in-
struction is randomly selected from the list of possi-
ble unit instructions (Figure 2 step 1). Both of these
processes perform uniform random selection. The se-
lected terminal is then replaced by the unit instruction
expanding the s-expression (Figure 2 step 2). For the
next single step expansion this new expanded pro-
gram is passed as the initial program (Figure 2 step
3).
Algorithm 1: Expansion using Monte Carlo simulation.
1: procedure SIMULATE(currentIndividual, bestIndividual)
2: for 1 to noO f Simulation do
3: randomDistance ← random no. between 1 and maxDistance
4: Create rootNode using currentIndividual
5: simulateRecursive(rootNode, randomDistance)
6: end for
return list of betterNewIndividuals
7: end procedure
8: procedure SIMULATERECURSIVE(node,depth)
9: if depth = 0 then
10: evaluate(node.program)
11: else
12: Create childNode
13: childNode.program ← clone of node.program
14: terminalList ← f indTerminals(childNode.program)
15: randomTerminal ← select random terminal from terminalList
16: Grow/Create random unit newGPnode
17: newGPnode.parent ← randomTerminal.parent
18: childrenList ← children of randomTerminal.parent
19: Replace randomTerminal with newGPnode in childrenList
20: evaluate(childNode.program)
21: simulateRecursive(childNode,depth − 1)
22: end if
23: end procedure
24: procedure EVALUATE(node)
25: node. f itness ← Evaluate fitness by executing test cases
26: if node. f itness > bestIndividual. f itness then
27: Add node to list of betterNewIndividuals
28: end if
29: end procedure
Single Simulation. A single simulation consists of
one or more single step expansions to the parent pro-
gram. Maximum depth of expansion is a constant
defined as a parameter for the algorithm. Initially a
random depth is generated between one and the max-
imum depth. For one simulation, starting from the pa-
rent program, the algorithm recursively keeps execu-
ting single step expansions up to that depth constraint.
Expansion: A Novel Mutation Operator for Genetic Programming
57

In this way the algorithm performs a constraint num-
ber of simulation, also defined as a constant parameter
at the beginning of the execution (Algorithm 1, Table
1).
The parent selection process for the expansion
mutation operator is made using tournament se-
lection. Once a parent is selected using a tournament,
the algorithm also sorts the current population of pro-
grams by fitness, selecting the current best program
in the population. Two constraints are passed to the
algorithm as constant parameters. One is the maxi-
mum depth of expansion, while the other is the num-
ber of simulations. Using the parent program the al-
gorithm starts performing simulations (Algorithm 1).
At each single step expansion of each simulation the
newly expanded program is evaluated for fitness. If
the fitness for the new program is better than the best
program in the population then it is added to a list of
better programs. Once the algorithm completes all the
simulation, the list of better new programs are sorted
by fitness from which the best new program replaces
the parent (Algorithm 2).
It is worth mentioning that the new programs ge-
nerated by expansion, are compared with the current
best in the population, instead of their own parent as
this method maintains diversity in the entire GP po-
pulation. If we compare with the current parent, there
will be more individuals added by expansion to the
population in each generation, reducing diversity.
Thus we can observe that MCTS can effectively
be applied to program expansion. Expansion, the new
mutation operator, is inspired by MCTS. Each step of
MCTS is reflected in this algorithm. It uses uniform
random for selection of (MCT) nodes to expand. Af-
ter selection simulations are performed using a series
of expansions. Once all the simulation is complete,
the algorithm backpropagates to the initial program
only to attach the extension from all the simulation
which provided the best fitness.
4 ECJ: EVOLUTIONARY
COMPUTATION LIBRARY
The Evolutionary Computation Library in Java (ECJ)
(Luke, 1998) is one of the oldest open source, uni-
fied metaheuristic toolkits, with strength in the im-
plementation of Genetic Programming (GP) (Luke,
2017). The evolving architecture and support of ECJ
has played a pivotal role in making it a widely used li-
brary for experimenting almost any algorithm in evo-
lutionary computation. Its flexible object oriented de-
sign is very easy to extend and customize. Also it is
written in the most widely used object oriented lan-
guage, Java. ECJ’s GP implementation is influenced
by John Koza’s Genetic Programming (Koza, 1992)
and succeeding texts. Also Koza’s "Simple Lisp" has
been used as the programming language for GP evo-
lution in ECJ. That is why ECJ’s Koza-style imple-
mentation of Genetic Programming has been used for
evaluating the performance of the Expansion muta-
tion operator.
Algorithm 2: Expansion pipeline.
1: procedure PRODUCE
2: individual ← Grab random individual from Reproduction Pipeline
3: bestIndividual ← Find current best individual from the population
4: betterNewIndividuals ← simulate(individual, bestIndividual)
5: bestNewIndividual ← best from list of betterNewIndividuals
6: replace individual with bestNewIndividual
7: end procedure
ECJ’s top level evolutionary loops are designed
for execution of any evolving algorithm. It is a sim-
ple loop over individuals in a population with steps of
initialization, evaluation, breeding, exchanging and
finally terminating, when the algorithm reaches the
maximum number of generations or best fitness eva-
luation.
In ECJ, the structure and operation of an experi-
ment is defined using a set of parameter files, where
the Problem is written by the researcher. Using sim-
ple scripting with the parameter files, it is possible to
make major architecture change in the execution of
the evolving algorithm. In this library the population
contains a set of sub-populations, which can be evol-
ved independently and also asynchronously. This can
be helpful for algorithms involving co-evolution or is-
land models.
Each individual in ECJ contains a representation
and fitness both of which can have many variations.
For generational breeding, the experimenter is suppo-
sed to specify one or more Breeding Pipelines, which
is a combination of selection, mutation and recom-
bination procedures. These processes define an indi-
vidual’s method of selection, copy, modification and
addition into a new population.
Genetic Programming in ECJ. Originally desig-
ned for GP, ECJ implements the Koza-style GP using
trees of nodes. Each GPIndividual object contains fo-
rests of GPTree, which in turn holds a tree of GPNo-
des. Using a set-based Strongly-Typed Genetic Pro-
gramming, each node’s parent and child slots are aug-
mented with a set of types. Similar is the case for the
tree’s root slot. Parent slots may attach to other node’s
child slots, or to the tree’s root slot, given their two
set’s intersection is nonempty.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
58

4.1 Crossover Pipeline
Being a subclass of GPBreedingPipeline, Crossover-
Pipeline performs strongly-typed version of Koza-
style "Subtree Crossover". After selecting two
random individuals (Figure 3), a single tree is cho-
sen from each individual having similar GPTreeCon-
straints, meaning their tree type, builder and function
set are the same. The selection of random nodes in
each tree is done making sure that each node’s return
type is compatible with the argument type of the pa-
rent’s slot which contains the other node. Also if this
swap exceeds the maximum depth constraint, the en-
tire operation is discarded and repeatedly tried again
to a constrained number of times. If a successful cros-
sover fails to occur, within that limited number then
the two individuals are ’reproduced’ to the new sub-
population without any change. For the work presen-
ted in the paper, no change was made to the default
ECJ implementation and parameters of crossover.
Figure 3: GP Pipelines including expansion. Diagram ex-
tended from (Luke, 2017)
4.2 Mutation Pipeline
Koza’s definition of Point Mutation (Koza, 1992) be-
gins by selecting a point at random within the tree
which could be a terminal or a non-terminal. A rand-
omly generated subtree is inserted at that point af-
ter removing whatever is currently there at that point.
In ECJ, MutationPipeline is another type of GPBree-
dingPipeline which implements a strongly-typed ver-
sion of the point mutation. In addition it provides a
depth restriction where if the tree becomes larger than
a maximum depth, it is discarded, while the process
is repeated until satisfying this constraint. Similar to
crossover (Section 4.1), if the number of repeat con-
straints is violated, then the individual is reproduced
to the new population as it is. The default ECJ im-
plementation and parameters of this process were not
changed for any experiments for the research presen-
ted in the paper.
4.3 Expansion Pipeline
The ExpansionPipeline is also an extension of the
GPBreedingPipeline, and is the primary contribution
of this paper. The process is described in Algorithm
2. An individual is selected using ECJ’s default Tou-
rnament Selection, which is also used for both the
crossover (Section 4.1) and mutation (Section 4.2) pi-
pelines. After sorting the current sub-population, the
current best individual is also picked. Using the se-
lected individual a simulation is performed with MCT
(Section 3.1), which executes randomized single step
expansion and evaluation on randomly selected ter-
minals of the tree. Each simulation is performed up
to a maximum depth for a certain number of times
(max depth and no. of simulation in table 1). This si-
mulation and expansion process is explained in detail
using algorithms 1 and 2 (Section 3.2). As each unit
expansion is evaluated, the new individual’s fitness is
compared with the fitness of the best individual in the
sub-population. If better, it is added to a list of better
individuals. Once simulations are complete the list of
better individuals are again sorted to come up with the
best from that list, which replaces the original indivi-
dual picked from the population.
5 EXPERIMENTS AND RESULTS
Before our discussion on the experimental procedure
we describe the problem set that was used to find best
possible comparison for expansion (Section 5.1).
5.1 Benchmark
To avoid the simplicity of historically used GP pro-
blems and to tackle real world complexities, (McDer-
mott et al., 2012) and (White et al., 2013) suggested a
set of benchmark problems which is currently consi-
dered a standard for evaluating any version of GP al-
gorithms. The benchmark problem set has the charac-
teristics of being difficult to choose, varied, relevant
to the field, fast to execute, easy to interpret and com-
pare while being precisely defined. From the diffe-
rent type of problems (regression, classification, pre-
dictive modeling, etc) that received consensus of the
research community, a variety of symbolic regression
problems have been used in this research to evalu-
ate performance of expansion, as a mutation operator.
Out of the 53 symbolic regression problems (McDer-
mott et al., 2012), Pagie-1 (
1
1+x
−4
+
1
1+y
−4
) has the re-
Expansion: A Novel Mutation Operator for Genetic Programming
59

(a) Variation of max depth - avg. of 50 executions (b) Variation of max depth - best of 50 executions
(c) Variation of no. of simulation - avg. of 100 executions (d) Variation of no. of simulation - best of 100 executions
(e) Varying ratio of expansion - avg. of 50 executions (f) Varying ratio of expansion- best of 50 executions
Figure 4: Comparison of different parameters and ratio of Expansion. In the above graphs the horizontal axis contain number
of generation, while the vertical axis is the Koza fitness of the best individual in the population in that generation. (a, c, e)
contain average of 50 executions, while (b, d, f) contain the best run of 50 executions. (a, b) compare the Maximum Depth
parameter varying from 3 to 20. Without any apparent pattern we can observe Maximum depth 10 has the best overall fitness.
In (c, d) we compare the Number of Simulation parameter varying from 1 to 10, where the value of 1 seem to provide the
best result. (e, f) tell us the best ratio of Expansion with Crossover, where we find only 5% expansion provides the optimum
output. These graphs also did not following any obvious pattern. Problem source: (Pagie and Hogeweg, 1997).
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
60
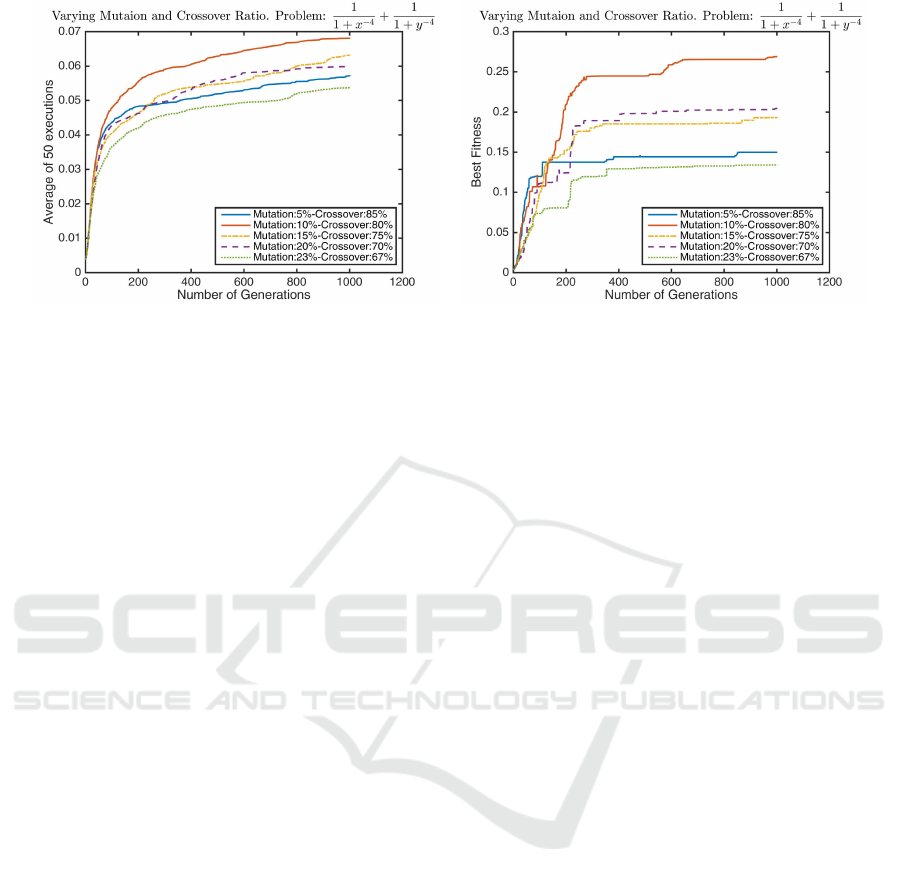
(a) Variation of Mutation ratio - avg. of 50 executions (b) Variation of Mutation ratio - best of 50 executions
Figure 5: Comparison of different Point Mutation (Section 4.2) and Crossover (Section 4.1) Ratio. In the above graphs the
horizontal axis contain number of generation, while the vertical axis is the Koza fitness of the best individual in the population
in that generation. (a) contains average of 50 executions, while (b) contains the best run of 50 executions. We can observe
without any apparent pattern 10% of Point Mutation performs best with 80% of Crossover.
putation of being particularly challenging (Pagie and
Hogeweg, 1997), as it has a rugged fitness landscape
and limited number of possible solutions. That is why
Pagie-1 has been used for the comparison study of
different parameter variation for expansion (Section
5.3, 5.4). After selecting reasonably best parameters,
a comparison study has been done on other diverse
problems from the benchmark (Section 5.6). ECJ has
a complete implementation of all the Benchmark pro-
blems, optimized using the Reproduction, Crossover
(Section 4.1) and Mutation (Section 4.2) pipelines.
For this study ExpansionPipeline was added to ECJ
and its best ratio was compared with crossover and
mutation.
Koza Fitness. Described in (Koza, 1992), Koza fit-
ness is a fitness measure used in ECJ to normalize
the error rate of the benchmark symbolic regression
problems. Here fitness f = 1/(1 + e), where e is the
summation of the errors from all the tests. All results
presented in this paper use this measure of fitness.
5.2 Experimental Procedure
Program expansion using MCT is most effective
when it is used along with the crossover (Section 4.1)
and mutation (Section 4.2) pipeline in ECJ. Executing
GP using only expansion did not provide a competi-
tive result. All experiments in the following sections
were done up to 1000 generations. The average fit-
ness curves were generated from 50 consecutive exe-
cutions. For comparison (Section 5.6) problems from
(Keijzer, 2003) and (Vladislavleva et al., 2009) were
selected as they were difficult enough not to reach
their best fitness within 1000 generations. ECJ Repro-
ductionPipeline which is a type of breeding pipeline
that simply makes a copy of the individuals it recei-
ves from its source (Figure 3) maintains a constant
ratio of 10% in all the experiments (Table 1). Com-
plete source code of the ExpansionPipeline, parame-
ters and results associated to experiments presented in
this paper can be found at (Islam, 2018).
5.3 Expansion Parameters
To evaluate performance of the ExpansionPipeline,
the initial experiments were designed to find the rela-
tively optimum point of its two significantly important
parameters maximum depth and number of simulation
(Figure 4 a,b,c,d).
Using one of the most difficult problems from
benchmark, Pagie-1 (Pagie and Hogeweg, 1997) dif-
ferent depth variations were applied for the simula-
tions performed (Figure 4 a,b). The other parame-
ters for this experiment remained constant (ratio of
expansion: 5%, crossover: 85%, no. of simulation:
1). Maximum depth was varied from 3 to 20 with
different intervals where the best fitness performance
was found at 10, for both the average and the best fit-
ness of all 50 executions. These results are explained
as follows: if the maximum depth of each simulation
is too high, the search space of the programs in the
population is larger, resulting in bad fitness. Also if
the depth is too small then expansion has very little
impact.
Similarly, number of simulation was varied bet-
ween 1 to 10 in figure 4(c,d), were a single simula-
tion seemed to have the optimum impact for incre-
asing overall fitness in both average and best of 50
experiments.
Expansion: A Novel Mutation Operator for Genetic Programming
61

5.4 Expansion Ratio
Once a reasonable parameter choice was found, the
next step is to find the best ratio between expansion
and crossover (Section 5.4). As compared in figure
4(e,f), the best fitness impact comes from very little
expansion, only 5%. This can be explained as increa-
sing the program size too quickly has negative impact
on fitness performance. Because it also increases the
size of the search space, it is harder for GP to find the
optimum program.
5.5 Mutation Ratio
Expansion being a mutation operator, it is important
that we compare it with other mutation operators, na-
mely the most widely used Point Mutation by Koza
(Koza, 1992) (Section 4.2). Before this comparison
study, an experiment was done to find the best ra-
tio between point mutation and crossover pipelines in
ECJ. Figure 5 contains the average and best results of
50 executions where 10% point mutation rate along
with 80% crossover seems to have the best impact in
fitness.
5.6 Comparison
ECJ’s default Koza-style GP implementation uses
only crossover. So when we have the best ratio be-
tween expansion-crossover and mutation-crossover,
the final comparison is done between only-crossover,
expansion-mutation-crossover and the two above.
Four GP variations (Table: 1) are executed 50 times
on a variety of symbolic regression problems from the
benchmark list (Section 5.1). These results are pre-
sented in figures 6, 7, 8. The problems were selected
avoiding the ones which are too simple to reach their
optimum fitness within 1000 generations. Algorithms
with version 3 and 4 from Table 1 contain the best ra-
tio of expansion with its reasonably optimum parame-
ters (depth, no of simulation). They both start with a
population of 1024, but due to the additional evaluati-
Table 1: Parameters for compared versions.
Version
Population
Reproduction
Crossover
Mutation
Expansion
Max Depth
Number of Simulation
Average number of
Evaluations/Generation
1 1120 10% 90% 0 0 - - 1120
2 1120 10% 80% 10% 0 - - 1120
3 1024 10% 85% 0 5% 10 1 1120
4 1024 10% 75% 10% 5% 10 1 1120
ons of every step of expansion, the average number of
evaluations per generation increases to 1120. Version
1 and 2 is for only-crossover and mutation-crossover,
where the population has been purposefully increased
to 1120 so that the average number of evaluations per
generation remains the same for all three versions of
the algorithms. ECJ’s implementation of a single exe-
cution of the CrossoverPipeline start with two rand-
omly selected individuals, and ends in evaluating two
new ones. MutationPipeline evaluates only one newly
mutated individual. So without making any changes
to the existing ECJ implementation, the only way to
increase the number of evaluations for version 1 and
2 was to increase the population. Increasing the po-
pulation also provides an added advantage to version
1 and 2 of the algorithms as it provides a larger search
space for GP combinatorial search. This advantage
is slightly less (population 1024) for version 3 and 4,
were expansion is applied.
6 ANALYSIS
Analysing the comparison results of figures 6, 7, 8, we
can observe that version 4 with expansion-mutation-
crossover almost always provided the best fitness
over 1000 generations of 50 executions. Version 3
with expansion-crossover is competitive with Version
2 which is mutation-crossover, where both of them
have performed better than version 1, only-crossover.
Overall Version 2 performs worse than version 3 and
4 (in most cases). This result was obtained after pro-
viding added advantage of an increased population to
version 1 and 2, and having the same number of eva-
luations per generation for all four. A small ratio of
expanding with unit instructions and fitness evalua-
tion of each step of this process has a large impact in
overall GP performance. In GP, crossover has always
provided the highest impact as a variation operator
(Koza, 1992). But we can observe from the compa-
rison study that a little expansion can boost this per-
formance significantly.
Expansion also performs better than point muta-
tion. With number of simulation as 1 for expansion,
their algorithmic difference is the step by step evalu-
ation of each unit expansion, which does not happen
to programs when point mutation is applied. Expan-
sion as a mutation operator takes into consideration
the granularity of programs at the level of unit in-
structions, which is lacking in point mutation, where
sub-trees are added, replaced or removed.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
62

(a) keijzer2 (b) keijzer4
(c) keijzer5 (d) keijzer6
(e) keijzer10 (f) keijzer11
Figure 6: Comparison between Crossover, Mutation and Expansion Ratio. In the above graphs the horizontal axis contain
number of generation, while the vertical axis is the Koza fitness of the best individual in the population in that generation.
All these problems were picked from the benchmark list (McDermott et al., 2012), from which their names originate (keijzer
2,4,5, etc.). For all figures 5% expansion has provided a boost in performance. For (a, b, c, e and f) version 4 (5% expansion,
10% mutation and 75% crossover) was able to reach the best fitness. For (d) version 3 (5% expansion and 85% crossover)
seems to be doing slightly better than version 4 (Keijzer, 2003).
Expansion: A Novel Mutation Operator for Genetic Programming
63

(a) keijzer12 (b) keijzer13
(c) keijzer14 (d) keijzer15
Figure 7: Comparison between Crossover, Mutation and Expansion Ratio. In the above graphs the horizontal axis contain
number of generation, while the vertical axis is the Koza fitness of the best individual in the population in that generation. The
problem set is from the same source as figure 6 (Keijzer, 2003). Version 4 (5% expansion, 10% mutation and 75% crossover)
has provided the best fitness is all cases.
7 CONCLUSION
Monte Carlo simulation has been an effective met-
hod in diverse fields (Eckhardt, 1987) (Benov, 2016).
MCTS has created impact for problems involving
large search space (Section 3). Combinatorial opti-
mization techniques such as genetic programming is
a search over an infinitely large space of combinations
of programs. That is why we can apply MCTS in vari-
ous new and effective ways to program synthesis. The
mutation operator expansion, presented in this paper
is only one of these ways. Using a comparison study
with crossover and point mutation the effectiveness of
the Monte Carlo method can be observed in program
synthesis. The benchmark symbolic regression pro-
blems used in this study are considered as the com-
munity standard, with which we prove that expansion
have a better fitness performance than point mutation
when included with crossover. Also fitness is signifi-
cantly boosted on a variety of problems when a small
ratio of expansion is added to crossover and mutation,
compared to GP using only-crossover and crossover-
mutation. It is worth emphasising that for all cases
the expansion algorithm achieves such improvement
using the same number of fitness evaluations. Also
we reach the conclusion that the best fitness can be
achieved by including all three operators in GP, cros-
sover, point mutation and expansion.
A study of the impact of program bloating is re-
quired on expansion, which is currently being done
by the authors.
REFERENCES
Balla, R.-K. and Fern, A. (2009). Uct for tactical assault
planning in real-time strategy games. In Proceedings
of the 21st International Jont Conference on Artifical
Intelligence, IJCAI’09, pages 40–45, San Francisco,
CA, USA. Morgan Kaufmann Publishers Inc.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
64

(a) vladislavleva1 (b) vladislavleva2
(c) vladislavleva3 (d) vladislavleva4
(e) vladislavleva5 (f) vladislavleva7
Figure 8: Comparison between Crossover, Mutation and Expansion Ratio. In the above graphs the horizontal axis contain
number of generation, while the vertical axis is the Koza fitness of the best individual in the population in that generation. All
these problems were picked from the benchmark list (McDermott et al., 2012), from which their names originate (vladislavleva
1,2,3, etc.). For all figures 5% expansion has provided a boost in performance. For (a, c, d, e and f) version 4 (5% expansion,
10% mutation and 75% crossover) was able to reach the best fitness. For (b) version 3 (5% expansion and 85% crossover)
seems to be doing better than version 4 (Vladislavleva et al., 2009).
Expansion: A Novel Mutation Operator for Genetic Programming
65

Benov, D. M. (2016). The manhattan project, the first elec-
tronic computer and the monte carlo method. Monte
Carlo Methods and Applications, 22(1):73–79.
Brameier, M. F. and Banzhaf, W. (2010). Linear Genetic
Programming. Springer Publishing Company, Incor-
porated, 1st edition.
Chaslot, G. M. J.-B., Winands, M. H. M., van Den Herik,
H. J., Uiterwijk, J. W. H. M., and Bouzy, B. (2008).
Progressive strategies for monte-carlo tree search.
New Mathematics and Natural Computation (NMNC),
04(03):343–357.
Coulom, R. (2007a). Computing Elo Ratings of Move Pat-
terns in the Game of Go. In van den Herik, H. J.,
Winands, M., Uiterwijk, J., and Schadd, M., edi-
tors, Computer Games Workshop, Amsterdam, Net-
herlands.
Coulom, R. (2007b). Efficient selectivity and backup ope-
rators in monte-carlo tree search. In Proceedings
of the 5th International Conference on Computers
and Games, CG’06, pages 72–83, Berlin, Heidelberg.
Springer-Verlag.
Eckhardt, R. (1987). Stan Ulam, John von Neumann, and
the Monte Carlo Method. Los Alamos Science, pages
131–143.
Finnsson, H. and Björnsson, Y. (2008). Simulation-based
approach to general game playing. In Proceedings
of the 23rd National Conference on Artificial Intelli-
gence - Volume 1, AAAI’08, pages 259–264. AAAI
Press.
Gelly, S. and Silver, D. (2011). Monte-carlo tree search and
rapid action value estimation in computer go. Artif.
Intell., 175(11):1856–1875.
Islam, M. (2018). ECJ evolutionary computation library v25
with expansion pipeline. https://github.com/mohiul/
ecj-v25-expansion/ releases. Accessed: 2018-05-23.
Keijzer, M. (2003). Improving symbolic regression with in-
terval arithmetic and linear scaling. In Proceedings
of the 6th European Conference on Genetic Program-
ming, EuroGP’03, pages 70–82, Berlin, Heidelberg.
Springer-Verlag.
Koza, J. R. (1992). Genetic Programming: On the Pro-
gramming of Computers by Means of Natural Se-
lection. MIT Press, Cambridge, MA, USA.
Krawiec, K. (2016). Behavioral Program Synthesis with
Genetic Programming, volume 618 of Studies in Com-
putational Intelligence. Springer International Publis-
hing. http://www.cs.put.poznan.pl/kkrawiec/bps.
Krawiec, K. and Lichocki, P. (2009). Approximating geo-
metric crossover in semantic space. In Proceedings of
the 11th Annual Conference on Genetic and Evolutio-
nary Computation, GECCO ’09, pages 987–994, New
York, NY, USA. ACM.
Krawiec, K. and Lichocki, P. (2010). Using Co-solvability
to Model and Exploit Synergetic Effects in Evolution,
pages 492–501. Springer Berlin Heidelberg, Berlin,
Heidelberg.
Lim, J. and Yoo, S. (2016). Field report: Applying monte
carlo tree search for program synthesis. In Sarro, F.
and Deb, K., editors, Search Based Software Engi-
neering, pages 304–310, Cham. Springer Internatio-
nal Publishing.
Lorentz, R. J. (2008). Amazons discover monte-carlo. In
Proceedings of the 6th International Conference on
Computers and Games, CG ’08, pages 13–24, Berlin,
Heidelberg. Springer-Verlag.
Luke, S. (1998). ECJ evolutionary computation li-
brary. Available for free at http://cs.gmu.edu/∼eclab/
projects/ecj/.
Luke, S. (2017). Ecj then and now. In Proceedings
of the Genetic and Evolutionary Computation Con-
ference Companion, GECCO ’17, pages 1223–1230,
New York, NY, USA. ACM.
McDermott, J., White, D. R., Luke, S., Manzoni, L., Cas-
telli, M., Vanneschi, L., Jaskowski, W., Krawiec, K.,
Harper, R., De Jong, K., and O’Reilly, U.-M. (2012).
Genetic programming needs better benchmarks. In
Proceedings of the 14th Annual Conference on Gene-
tic and Evolutionary Computation, GECCO ’12, pa-
ges 791–798, New York, NY, USA. ACM.
Miller, J., editor (2011). Cartesian Genetic Programming.
Springer Berlin Heidelberg, Berlin, Heidelberg.
Miller, J. F. and Thomson, P. (2000). Cartesian Genetic
Programming, pages 121–132. Springer Berlin Hei-
delberg, Berlin, Heidelberg.
Miller, J. F., Thomson, P., Fogarty, T., and Ntroduction, I.
(1997). Designing electronic circuits using evolutio-
nary algorithms. arithmetic circuits: A case study.
Moraglio, A., Krawiec, K., and Johnson, C. G. (2012). Geo-
metric Semantic Genetic Programming, pages 21–31.
Springer Berlin Heidelberg, Berlin, Heidelberg.
Nordin, P., Banzhaf, W., and Francone, F. (1999). Efficient
evolution of machine code for cisc architectures using
instruction blocks and homologous crossover. In Ad-
vances in Genetic Programming 3, chapter 12, pages
275–299. MIT Press.
Pagie, L. and Hogeweg, P. (1997). Evolutionary consequen-
ces of coevolving targets. Evol. Comput., 5(4):401–
418.
Sturtevant, N. R. (2008). An analysis of uct in multi-player
games. In Proceedings of the 6th International Con-
ference on Computers and Games, CG ’08, pages 37–
49, Berlin, Heidelberg. Springer-Verlag.
Vladislavleva, E. J., Smits, G. F., and Den Hertog, D.
(2009). Order of nonlinearity as a complexity me-
asure for models generated by symbolic regression
via pareto genetic programming. Trans. Evol. Comp,
13(2):333–349.
White, D. R., McDermott, J., Castelli, M., Manzoni, L.,
Goldman, B. W., Kronberger, G., Ja
´
skowski, W.,
O’Reilly, U.-M., and Luke, S. (2013). Better gp
benchmarks: community survey results and propo-
sals. Genetic Programming and Evolvable Machines,
14(1):3–29.
White, D. R., Yoo, S., and Singer, J. (2015). The program-
ming game: Evaluating mcts as an alternative to gp
for symbolic regression. In Proceedings of the Com-
panion Publication of the 2015 Annual Conference
on Genetic and Evolutionary Computation, GECCO
Companion ’15, pages 1521–1522, New York, NY,
USA. ACM.
Winands, M. H. M. and Björnsson, Y. (2010). Evaluation
function based monte-carlo loa. In Proceedings of the
12th International Conference on Advances in Com-
puter Games, ACG’09, pages 33–44, Berlin, Heidel-
berg. Springer-Verlag.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
66
