
Selecting Relevance Thresholds to Improve a Recommender System in a
Parliamentary Setting
Luis M. de Campos, Juan M. Fern
´
andez-Luna, Juan F. Huete and Luis Redondo-Exp
´
osito
Departamento de Ciencias de la Computaci
´
on e Inteligencia Artificial,
ETSI Inform
´
atica y de Telecomunicaci
´
on, CITIC-UGR,
Universidad de Granada, 18071 Granada, Spain
Keywords:
Recommendation Systems, Automatic Classification, Parliamentary Documents, Relevance Thresholds.
Abstract:
In the context of building a recommendation/filtering system to deliver relevant documents to the Members
of Parliament (MPs), we have tackled this problem by learning about their political interests by mining their
parliamentary activity using supervised classification methods. The performance of the learned text classifiers,
one for each MP, depends on a critical parameter, the relevance threshold. This is used by comparing it with
the numerical score returned by each classifier and then deciding whether the document being considered
should be sent to the corresponding MP. In this paper we study several methods which try to estimate the
best relevance threshold for each MP, in the sense of maximizing the system performance. Our proposals are
experimentally tested with data from the regional Andalusian Parliament at Spain, more precisely using the
textual transcriptions of the speeches of the MPs in this parliament.
1 INTRODUCTION
In a recent paper (de Campos et al., 2018) we
considered the problem of building a recommenda-
tion/filtering system (Hanani et al., 2001; Pazzani and
Billsus, 2007) in a parliamentary setting. The pro-
posed system was able to learn about the political in-
terests of the Members of Parliament (MPs) by min-
ing their parliamentary activity. The goal was, given
new documents entering the Parliament, to automat-
ically decide which MPs should be informed about
the existence of each one of these documents, on the
basis of the matching degree between the individual
interests of each MP and the document content. With
this objective in mind we built a set of text classifiers,
one for each MP, starting from their interventions in
the parliamentary debates. We could therefore use all
these (binary) classifiers for each new incoming doc-
ument to recommend it to the appropriate subset of
MPs.
However, it may happen that if the classifier asso-
ciated to an MP is not selective enough, she can be
overloaded with more information than she needs; on
the contrary, if the classifier is too restrictive then the
MP could miss some information that probably would
be interesting to her. This fact may depend essentially
on the type of classifier being built. If the classifier is
able to provide a numerical output, representing a de-
gree or probability of relevance of the document be-
ing classified for the corresponding MP, then it is cru-
cial to determine appropriately the relevance thresh-
old. If the score generated by the classifier, given an
input document, is greater than or equal to this thresh-
old then we assume that this document is relevant for
the MP associated to the classifier. If this threshold
is too large then the classifier can be very restrictive
and if it is very small, the classifier can be too per-
missive. This is the question that we consider in this
paper, namely to study methods to try to determine
the relevance threshold that we should use with the
classifier associated to each MP in our recommenda-
tion/filtering system, in order to maximize the system
performance.
The remaining of this paper is organized as fol-
lows: Section 2 sets the reader in the context of the
study, by giving some details about the recommenda-
tion/filtering system implemented in our parliamen-
tary domain. In Section 3 we explain the different ap-
proaches considered to determine the best relevance
thresholds for each of the classifiers associated to the
MPs. Section 4 describes the experimentation pro-
cess and the results obtained using a collection of MP
interventions from the Spanish regional Andalusian
Parliament. Finally, Section 5 contains the conclud-
ing remarks and introduces possible future works.
186
Campos, L., Fernández-Luna, J., Huete, J. and Redondo-Expósito, L.
Selecting Relevance Thresholds to Improve a Recommender System in a Parliamentary Setting.
DOI: 10.5220/0006928701860193
In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 1: KDIR, pages 186-193
ISBN: 978-989-758-330-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 OVERVIEW OF THE
RECOMMENDATION/
FILTERING SYSTEM
The subjects of our case study are the MPs belonging
to a (regional, national or transnational) parliament,
M P = {MP
1
, . . . , MP
n
}. In order to distribute the dif-
ferent documents that arrive to the parliament among
MPs, we have built a system to carry out this filter-
ing process. More precisely, we use a set of n binary
classifiers, one for each MP. The data used to train
these classifiers is extracted from the interventions of
MPs in the parliamentary debates
1
. So, associated to
MP
i
we have a set of documents D
i
= {d
i1
, . . . , d
im
i
},
each d
i j
being the transcription of the speech of MP
i
when she intervened in the discussion of a parliamen-
tary initiative. The set D = ∪
n
j=1
D
j
containing the
interventions of all the MPs constitutes our document
collection.
We use support vector machines (SVM) (Cristian-
ini and Shawe-Taylor, 2000) to build the classifier for
each MP, because they are considered a state-of-the-
art approach for text classification. These classifiers
use the terms appearing in the MP interventions as
features. However, SVM, as other classifiers need
to be trained with positive (relevant documents) and
negative (irrelevant documents) examples. The set of
positive instances for MP
i
clearly corresponds to her
own parliamentary interventions, i.e. D
i
, but we do
not have a real set of negative instances. Instead, we
have an amount of unlabeled instances that represent
the interventions of the other MPs, D \ D
i
. In our par-
liamentary context, assuming that all the interventions
of the other MPs represent negative training data for
MP
i
is not reasonable, because some of these inter-
ventions may be about the same topics which are of
interest for MP
i
, hence probably they can be relevant
to MP
i
. Therefore, the set D \ D
i
will contain both
positive and negative instances for MP
i
, so that it is
safe to initially consider these instances as unlabeled.
For that reason we use positive unlabeled learn-
ing (PUL) methods (Zhang and Zuo, 2008), with the
purpose of finding trustworthy negative training data
N
i
from the unlabeled data D \ D
i
, in order to im-
prove the quality of the binary classifier. The goal
is to remove the unlabeled instances which are near
to the positive instances, avoiding in this way the ap-
pearance of noise in the training data. The specific
PUL method we use is based on a modification of the
K-means clustering algorithm: We use two clusters
(K=2), the positive and the negative clusters, initial-
1
The transcriptions of their speeches, collected in the
records of parliamentary proceedings.
ized with the positive documents in D
i
and the unla-
beled documents in D \ D
i
, respectively. Then, in the
iterative process we allow the unlabeled examples to
move between the two clusters, but forbid the positive
examples to escape from the positive cluster. When
the algorithm finishes, the unlabeled examples that
still remain in the negative cluster form the set N
i
,
see (de Campos et al., 2018) for more details.
As the set D \ D
i
is much larger than D
i
, and
therefore probably N
i
is also much larger than D
i
, we
have considered the use of a method to manage the
class imbalance problem. More precisely, the syn-
thetic minority over-sampling technique (SMOTE)
(Chawla et al., 2002) has been considered. This
method tries to increase the number of examples in
the minority class (in our case the positive class) by
creating new artificial examples from existing cases
of this class.
Therefore, for each MP
i
we build two classifiers:
one which is not balanced, using D
i
and N
i
as positive
and negative training instances, respectively, and an-
other one which applies SMOTE to get an additional
set of artificial positive instances A
i
, and then uses
D
i
∪ A
i
and N
i
as positive and negative training in-
stances, respectively.
3 APPROACHES TO DETERMINE
THE RELEVANCE
THRESHOLDS
Let d be a new document that must be filtered to the
appropriate MPs, according to its content and their
political interests. Then we use the selected n clas-
sifiers (one for each MP) and we obtain n numerical
values p
i
(d), i = 1 . . . , n, representing the probability
of relevance of document d for MP
i
.
Now, in order to make a decision concerning
whether d should be sent to MP
i
, we need to cali-
brate to what extent p
i
(d) is large enough. Perhaps
the most natural and simplest strategy would be to
compare the probability of d being relevant for MP
i
with the probability of being irrelevant, 1 − p
i
(d). If
p
i
(d) ≥ 1− p
i
(d), and this happens when p
i
(d) ≥ 0.5,
then we should send d to MP
i
. Therefore, the obvious
option is to choose the relevance threshold equal to
0.5 for all the MPs.
Generalizing this strategy, we could select a
threshold t, with 0 ≤ t ≤ 1, and assume that d is rel-
evant for MP
i
if p
i
(d) ≥ t. This may have sense in
case that, for some reason, the classifiers have the ten-
dency to generate very low or very large probability
values. Going a step further, it can be the case that the
Selecting Relevance Thresholds to Improve a Recommender System in a Parliamentary Setting
187

behavior of the classifiers for different MPs is differ-
ent. This may be due, for example, to a very different
number of interventions of the MPs in the debates,
which gives rise to very different training set sizes.
Or perhaps the difference can be due to the fact that
the range of political interests is wider for some MPs
than for others, which translates into the participation
of some MPs in many committees devoted to differ-
ent topics (and this fact generates speeches which are
more diverse or heterogeneous). In this case it would
be better to use a threshold t
i
which depends on the
specific MP
i
being considered. Then, we would send
document d to MP
i
only if p
i
(d) ≥ t
i
. Obviously, the
question now is how to select the most appropriate rel-
evance threshold t
i
for each MP
i
. Moreover, this se-
lection will almost surely depend on the type of clas-
sifier (balanced or not) selected for each MP. In turn,
the decision of using either a balanced or an imbal-
anced classifier may also depend on some features of
the MPs.
Therefore, the hypotheses that drive our work are:
(1) the baseline threshold (0.5) is not the best thresh-
old; (2) each MP has an individual best threshold; (3)
the best thresholds are correlated to some features of
the MPs.
In this section we are going to propose several ap-
proaches to try to determine appropriate thresholds
for all the MPs. These methods will be experimen-
tally compared in the next section.
3.1 Using a Validation Set to Estimate
the Thresholds
Perhaps the most standard approach to estimate the
threshold to be used by a classifier (and in general
to determine any other configuration parameter of
the classifier) is to use a validation set (Sebastiani,
2002). In this approach, the available training set
T S for building the classifier is randomly divided into
two disjoint subsets: a new and smaller training set
ST S and a validation set V S (T S = ST S ∪V S). The
new training subset ST S is used to learn the classifier.
Then we use it with all the instances in the validation
set V S, thus obtaining a value p(d) for each instance
in VS. Assuming that we have some way to measure
the performance of the classifier (the concrete perfor-
mance measures considered will be specified in the
next section), we can try to use different relevance
thresholds and to determine the one, t, which obtains
the best overall results. Finally we retrain the classi-
fier with the complete training set and use it in com-
bination with the threshold t.
This approach relies on the assumption that the
classifier will behave similarly when processing in-
stances in the validation set and in the test set. A pos-
sible difficulty is that, as we do not induce the classi-
fier from all the available training data T S but from a
subset ST S, its behavior may be different from that of
the classifier which finally we are going to use, espe-
cially if the available number of instances is not suf-
ficiently large. Related to this, another possible prob-
lem is that the number of instances in the validation
set V S may be not large enough to allow to extract
reliable conclusions about the best threshold.
3.2 Using the Own Training Set to
Estimate the Thresholds
Instead of using a validation subset extracted from the
original training set, our proposal is to use the com-
plete training set to both induce the classifier and es-
timate the best threshold. In this way we use all the
instances in T S to learn the classifier. Now, we use it
to obtain a value p(d) for all the instances in T S and
try different relevance thresholds, evaluating the over-
all performance and selecting the threshold that offers
the best results.
This approach tries to solve the problems of using
a separate validation set: on the one hand the number
of instances used to select the best threshold is much
larger; on the other hand, we are using to estimate the
threshold exactly the same classifier that finally will
be employed. However, clearly a new problem ap-
pears: we take the risk of overfitting, as we are clas-
sifying the same instances used for training. What it
is not clear is whether this possible overfitting can be
directly translated into a poor estimation of the thresh-
old.
3.3 Relating the Thresholds with some
Features of the MPs
Looking at previous experiments (de Campos et al.,
2018), where we obtained the best reachable thresh-
olds looking at the best value of the performance mea-
sure in the test set
2
, we could notice that the thresh-
olds obtained when we do not balance any MP were
generally low. On the other hand, when we proceeded
balancing all the MPs, the best reachable thresholds
obtained in this case were commonly situated near the
middle of the interval [0,1]. This behaviour led us to
think about the possibility that the key of making the
decision between balancing or not an MP could be
given by some features of her own profile, since when
we altered the training set of an MP balancing it, the
2
Thus using the “privileged” information that offers this
set.
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
188
threshold changed and in many cases this effect was
rather positive.
In view of this hypothesis, we have extracted some
features from the MPs profiles in order to try to find
which ones are better correlated with their respective
best balanced and not balanced thresholds. We have
tried many features from the profiles but finally we
only use those which have best Gini index (with the
best threshold) in order to perform our experiments.
The features considered are: the number of interven-
tions (interventions) of the MP, the total number of
different terms in all those interventions after (terms)
and before (NP-Term) processing the text, the aver-
age of terms per intervention after (meanTermInterv)
and before (NP-meanTermInterv) processing the text
and finally the lexical density (lexicalDensity) (Ure,
1971), which represents the ratio between the number
of lexical units (nouns, verbs, adjectives, adverbs) and
the total number of terms.
We want to study the correlations that we can ob-
tain between each one of these features and the best
threshold. A high correlation, either positive or neg-
ative, between a feature and the threshold would be
a signal that this feature could be important to deter-
mine the most appropriate threshold for an MP. More-
over, we also want to build some prediction model us-
ing all these features together.
4 EXPERIMENTAL EVALUATION
The experimental evaluation will be carried out us-
ing all the 5,258 parliamentary initiatives (containing
12.633 different interventions of MPs) discussed in
the 8th term of office of the Andalusian Parliament
3
at
Spain, marked up in XML (de Campos et al. 2009)
4
.
80% of the initiatives were used for training the
classifiers and the remaining 20% for testing purposes
(playing the role of input documents that need to be
filtered to the MPs). This 80-20 random partition was
repeated five times. The obtained results are then av-
eraged.
From the initiatives in the training set we extracted
the interventions of the MPs, thus obtaining the sets
D
i
. We only considered the 132 MPs who intervene
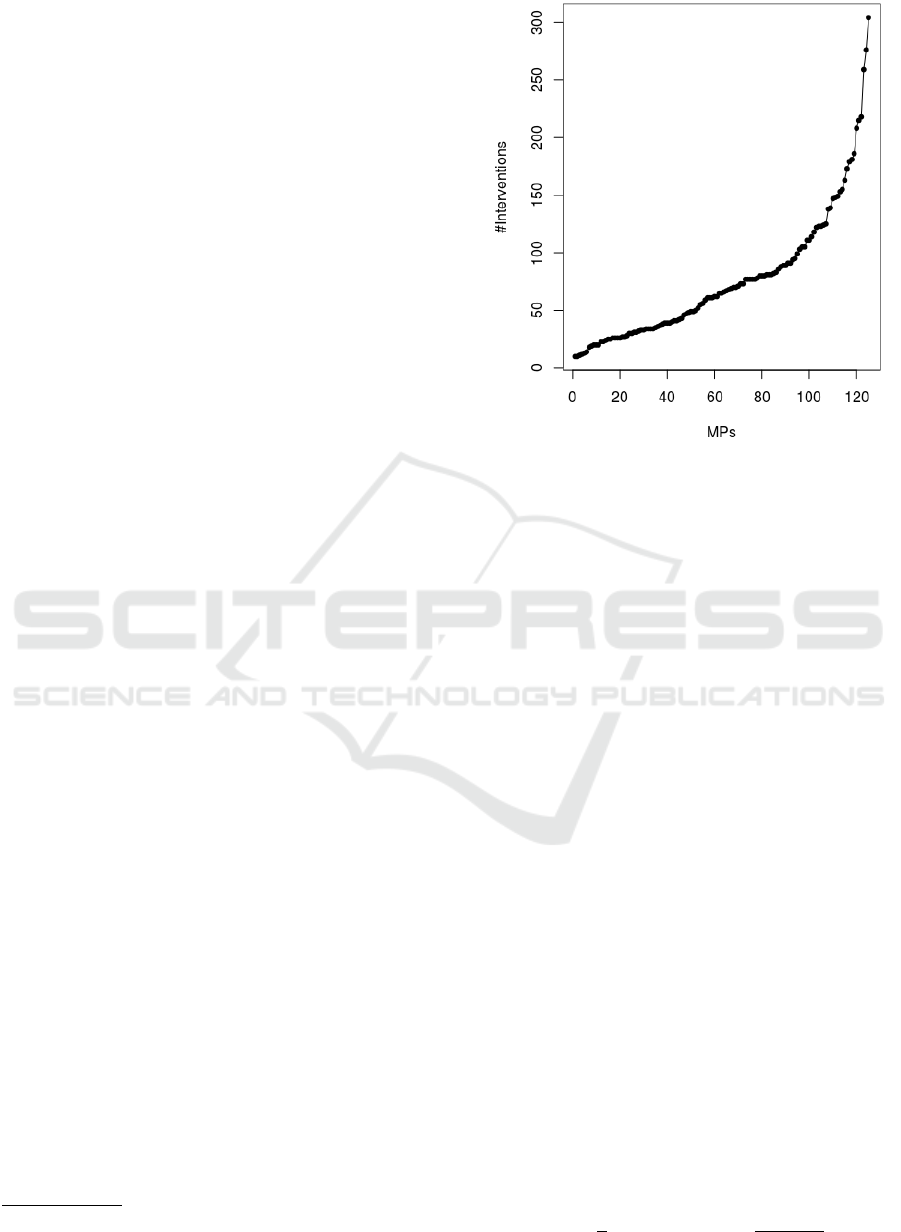
at least in 10 different initiatives. Figure 1 displays
the number of interventions associated to each MP.
We can observe that there is a great variability, which
also translates into training data of different quality.
Before building the classifiers, the text contained in
the documents was pre-processed by removing gen-
eral stopwords (articles, prepositions, etc.), removing
3
http://www.parlamentodeandalucia.es
4
http://irutai2.ugr.es/ColeccionPA/legislatura8.tgz.
Figure 1: Number of interventions of each MP.
terms with high occurrence and no relevance, and per-
forming a stemming process.
Then we built the 132 classifiers (both balanced
and non balanced versions) as specified in Section 2.
Next, we used these classifiers with the initiatives in
the test set. The ground truth that we are assuming,
with respect to who the relevant MPs are for each test
initiative, is: those MPs that intervened in the debate
of the initiative.
Once we have computed the values p
i
(d) for every
initiative d in the test set and for each MP
i
(really we
compute two values for each i, p
n
i
(d) and p
b
i
(d), from
the non balanced and the balanced classifiers associ-
ated to MP
i
, respectively), we compare these values
with the selected thresholds t
i
(really we also have
two selected thresholds for each i, t
n
i
and t
b
i
), in or-
der to decide whether document d is recommended to
MP
i
.
In this way we can compute, for each MP
i
, the
number of True Positives (TP
i
), False Positives (FP
i
)
and False Negatives (FN
i
), in order to get the standard
performance measures for text classification (Sebas-
tiani, 2002): precision (ρ
i
) and recall (r
i
). We com-
pute also the F-measure (F
i
), i.e. the harmonic mean
of precision and recall, which displays a global vision
of the classifier quality. To summarize the measures
associated to each MP
i
and obtain a general evalua-
tion of the system, we shall use the macro-averaged
and micro-averaged F measures (Tsoumakas et al.,
2010), MF and mF, respectively:
MF =
1
n
n
∑
i=1
F
i
, mF =
2mρmr
mρ + mr
, (1)
Selecting Relevance Thresholds to Improve a Recommender System in a Parliamentary Setting
189

where
mρ =
∑
n
i=1
T P
i
∑
n
i=1
(T P
i
+ FP
i
)
, mr =
∑
n
i=1
T P
i
∑
n
i=1
(T P
i
+ FN
i
)
(2)
The previous process will be carried out once we
have selected the threshold t
i
for each classifier, and
gives us an indirect idea of the quality of the threshold
selection method being considered by evaluating the
system performance obtained after using this method.
But previously we have to select the more convenient
threshold for each classifier. The possible relevance
thresholds t
i
considered to look for the best one will
range from 0.1 to 0.9 with a step size of 0.1, indepen-
dently on the approach used to estimate them.
For the experiments where we use the own train-
ing set to estimate the best thresholds, we simply
carry out the same previous process but using the
documents in the training set instead of those in the
test set to compute the measures F
i
, for each possible
threshold, selecting the one offering the best F value.
For the experiments where we use a validation set,
we first randomly divide each training set to extract a
new training subset (80% of the training instances)
and a validation set (20% of the training instances).
Then we build another set of classifiers from these
training subsets and use them to evaluate the instances
in the validation sets, once again computing, for each
possible threshold, the measures F
i
, and selecting the
threshold which gets the best F value.
In addition to using both the imbalanced and the
balanced versions of the classifiers separately, we
have also tried a combined method: for each MP
i
we
evaluate (using either the validation set or the training
set) both classifiers, obtain the best threshold for each
one, t
n
i
and t
b
i
, and select the classifier that gets the
best results.
4.1 Results
The results of our experiments are summarized in Ta-
ble 1. In addition to the experiments using the vali-
dation sets and the own training sets, we also display
results of the baseline approach which fixes the rele-
vance thresholds at 0.5 for all the classifiers. We re-
port results from both the balanced, the non balanced
and the combined versions of the classifiers.
Regarding the baseline approach, we can observe
that the results in terms of micro-F are quite simi-
lar for both the balanced and imbalaced approaches
(with a slight advantage for the second one), but the
balanced approach is clearly better in the case of us-
ing the macro-F measure. This seems to indicate that
balancing the training data particularly improves the
results of those MPs having less interventions (which
are precisely those having more imbalanced training
data). These MPs have the same importance than
other MPs having more interventions from the point
of view of computing MF, although they are less im-
portant when computing mF.
The results obtained when using a validation set
are discouraging, as we systematically get worse re-
sults than the baseline (between 3% and 8% of wors-
ening). Therefore, although the use of a separate val-
idation set is the standard practice to estimate the pa-
rameters of classifiers, in our case study this approach
does not work properly. We believe that the reason
may be the (low) number of documents in the valida-
tion sets associated to many MPs (only around 16%
of the interventions of an MP will appear in her vali-
dation set
5
), which is not enough to capture the char-
acteristics of these MPs.
In order to overcome the problem of the low num-
ber of documents in the validation sets, we tried the
same procedure with the whole training data. What
we are expecting is that the bigger is the number of
documents the better the thresholds will fit. Look-
ing at the results in Table 1 we can corroborate that
this assumption is mostly true in the non balanced ap-
proach, where both the macro and micro F-measures
improve with respect to the baseline results (9% and
5% respectively). Regarding the micro F-measure,
the improvement is most remarkable because we get
the best result for this measure in all the classifiers.
We think that this happens because the thresholds of
the MPs with a strong training set are well estimated.
Nevertheless, the macro F-measure is not so good in
absolute terms. Perhaps this is due to the fact that,
in this measure, we are giving the same importance
to all the MPs, independently on the quality of their
training set and the thresholds of the MPs with a weak
training set are not well estimated. The combined bal-
anced/non balanced approach in this case does not
improve in any case the results of the non balanced
approach alone. Finally, the balanced approach once
again obtains worse results than the baseline.
To put into perspective the results obtained us-
ing the validation and the training sets, we have also
displayed in Table 1 the ideal results we could get
with the balanced, non balanced and combined ap-
proaches. These values are computed by selecting the
best thresholds (and in the last case also choosing for
each MP whether balancing him or not) on the ba-
sis of the results on the test set. These results show
that the combined approach could be useful, at least
in theory, if we were able to decide when the training
data associated to an MP should be balanced or not:
5
For example an MP having 20 interventions will have
only 3 in the validation set.
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
190

Table 1: Values of the macro and micro F-measures obtained in all the experiments.
Baseline Static Threshold (0.5)
Macro F-measure micro F-measure
Not Balanced 0.2343 0.2967
Balanced 0.2722 0.2944
Variable Threshold (Validation)
Macro F-measure micro F-measure
Not Balanced 0.2275 0.2767
Balanced 0.2612 0.2709
Combined Balanced/Not Balanced 0.2436 0.2844
Variable Threshold (Train)
Macro F-measure micro F-measure
Not Balanced 0.2556 0.3129
Balanced 0.2385 0.2912
Combined Balanced/Not Balanced 0.2541 0.3079
Ideal Reachable Solution (Test)
Macro F-measure micro F-measure
Not Balanced 0.2807 0.3322
Balanced 0.3193 0.3273
Combined Balanced/Not Balanced 0.3220 0.3435
We obtain improvements of 15% and 1% for macro-F
and of 3% and 5% for micro-F, with respect to the non
balanced and the balanced approaches respectively.
We can also observe that, from the point of view of
the micro-F measure, is preferable not to balance the
data sets, whereas the opposite is true for the macro-
F measure. For the micro-F measure, the best result
found is to use the complete training set to estimate
the thresholds and not to balance (obtaining 91% of
the ideal performance). For the macro-F measure, the
best we can do is to use the default threshold and to
balance (reaching 85% of the ideal performance).
For the sake of completeness, we display in Table
2 the values of (micro and macro) precision and recall
corresponding to the F-measures displayed in Table
1. We can observe that when we use the validation
set, the non balanced classifiers obtain relatively high
precision but very low recall. However, when using
the training set we get a slightly lower precision but
much better recall. It should be noticed that in our fil-
tering application, recall is probably more important
than precision. The behavior of the balanced classi-
fiers is more erratic when using either the validation
or the training set: in the first case recall is consider-
ably higher than precision whereas in the second case
the opposite happens. This seems to indicate that the
thresholds being selected in these cases are consider-
ably different, very low in the case of using the vali-
dation set and very high when using the training set.
Regarding the approach of trying to relate the se-
lected thresholds with some features of the MPs, the
obtained correlation coefficients between each fea-
ture and the best thresholds (either balanced or not)
are displayed in Table 3. Even when the Gini index
showed that the selected features were the most im-
portant among all those being considered, the corre-
lation between them and the threshold is negligible.
The conclusion is therefore clear: none of these fea-
tures is important in order to determine the value of
the threshold.
We also tried to combine these features, to test
whether their combination was able to predict at some
extent the best values of the threshold. To do that we
trained a linear regression model with these features,
using 80% of the MPs for training and 20% for test.
Next, we computed for the MPs in the test set the dif-
ferences between the truly best threshold and the pre-
dicted threshold. The result also were discouraging.
5 CONCLUDING REMARKS
In this work we have considered different ways to deal
with the problem of finding the best relevance thresh-
olds to be used in combination with a set of binary
text classifiers. The objective is to calibrate the nu-
merical output generated by each classifier, given an
input document, in order to decide whether the docu-
ment can be considered as relevant or not. In our case
study, the classifiers are built from the interventions
of the MPs in the parliamentary debates, and their ob-
jective is to filter new documents to the appropriate
MPs according to their political interests. The basic
assumption of our system is that the interests and pref-
Selecting Relevance Thresholds to Improve a Recommender System in a Parliamentary Setting
191

Table 2: Values of the macro and micro precision and recall obtained in all the experiments.
Baseline Static Threshold (0.5)
Macro Precision micro Precision Macro Recall micro Recall
Not Balanced 0.3117 0.3593 0.2434 0.2527
Balanced 0.2689 0.2500 0.3810 0.3580
Variable Threshold (Validation)
Macro Precision micro Precision Macro Recall micro Recall
Not Balanced 0.3258 0.3914 0.1886 0.2046
Balanced 0.2679 0.2203 0.3792 0.3514
Combined Balanced/Not Balanced 0.3575 0.3754 0.2312 0.2289
Variable Threshold (Train)
Macro Precision micro Precision Macro Recall micro Recall
Not Balanced 0.3216 0.3411 0.2762 0.2891
Balanced 0.3307 0.3523 0.2446 0.2481
Combined Balanced/Not Balanced 0.3278 0.3391 0.2740 0.2811
Ideal Reachable Solution (Test)
Macro Precision micro Precision Macro Recall micro Recall
Not Balanced 0.3512 0.3692 0.2929 0.3020
Balanced 0.3743 0.3728 0.3071 0.2917
Combined Balanced/Not Balanced 0.3814 0.3772 0.2984 0.3153
Table 3: Correlations between different features of the MPs and the best thresholds, for the non balanced and the balanced
cases.
Non Balanced Threshold Balanced Threshold
interventions -0.1331 -0.2214
terms -0.0553 -0.1941
meanTermInterv -0.0283 -0.1475
NP-Terms -0.0709 -0.2057
NP-MeanTermInterv 0.0556 -0.0469
lexicalDensity 0.1348 0.0064
erences of the MPs can be extracted from their inter-
ventions (you are what you speak).
Taking into account that the training sets for the
classifiers associated to the MPs can be quite imbal-
anced (they contain the interventions of an MP as pos-
itive instances and a possibly large subset of the inter-
ventions of all the other MPs as negative instances),
we also considered the possibility of using a tech-
nique to balance these training sets.
The first, baseline approach to tackle the problem
is by fixing a static threshold (the most “natural” one,
equal to 0.5), whereas the other proposals guess an
individual threshold for each MP, either using a vali-
dation subset or the whole training set. We have also
tried to relate the appropriate threshold for each MP
with some features of her discourse.
After carrying out an experimental evaluation of
the different approaches using data from the Parlia-
ment of Andalusia at Spain, we can extract some con-
clusions. First, although the use of a validation set is a
quite standard practice, in our case its results are quite
bad, worse than those of the baseline. Second, the use
of the same instances with which we train the mod-
els to estimate the best threshold, although it takes the
risk of overfitting, performs reasonably good in our
case study, improving the baseline results appreciably.
Third, balancing the training data prior to building the
classifiers is not useful in general, although it tends
to improve the macro-F measure, probably because
balancing is able to improve the classifiers associ-
ated to MPs having few interventions, although at the
cost of worsening the classifiers associated to other
MPs. However, balancing systematically gets worse
results with respect to the micro-F measure. Fourth,
all our attempts to relate some features of the MPs
with the type of threshold which is more appropriate
have failed. We tried many features, as the number of
interventions of each MP, or the total number of dif-
ferent terms in all those interventions and attempted
to correlate them with the ideal thresholds (obtained
from the test set). The found correlations were always
very low. We even tried a regression model using all
these features to predict the threshold also with very
poor results.
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
192

Therefore, we conclude that the best approach
among those considered in this paper is to estimate
the thresholds using the whole training sets without
using balancing.
For future work, we plan to continue studying in
more detail which features or combination of fea-
tures could be useful to both detect the most appro-
priate thresholds for each MP and to decide when
the balancing process should be carried out. An-
other interesting line of research could be to use more
sophisticated multi-label classification techniques in-
stead of a simple set of independent binary classifiers
(Tsoumakas and Katakis, 2007).
ACKNOWLEDGEMENTS
This work has been funded by the Spanish “Minis-
terio de Econom
´
ıa y Competitividad” under project
TIN2016-77902-C3-2-P and the European Regional
Development Fund (ERDF-FEDER).
REFERENCES
Chawla, N.V., Bowyer, K.W., Hall, L.O., Kegelmeyer,
W.P. (2002). Smote: synthetic minority over-sampling
technique. Journal of Artificial Intelligence Research,
16:321–357.
Cristianini, N., Shawe-Taylor, J. (2000). An introduction
to Support Vector Machines and other kernel-based
learning methods. Cambridge University Press.
de Campos, L.M., Fern
´
andez-Luna, J.M., Huete, J.F.,
Martin-Dancausa, C.J., Tur-Vigil, C., Tagua, A.
(2009). An integrated system for managing the An-
dalusian parliament’s digital library. Program: Elec-
tronic Library and Information Systems 43:121–139.
de Campos, L.M., Fern
´
andez-Luna, J.M., Huete, J.F.,
Redondo-Exp
´
osito, L. (2018). Positive unlabeled
learning for building recommender systems in a
parliamentary setting. Information Sciences, 433-
434:221–232.
U. Hanani, U., B. Shapira, B., P. Shoval, P. (2001). Informa-
tion filtering: Overview of issues, research and sys-
tems. User Modelling and User-Adapted Interaction,
11:203–259.
Pazzani, M., Billsus, D. (2007). Content-based Recommen-
dation Systems. In: The Adaptive Web, LCNS vol.
4321, 2007, pages 325–341.
Sebastiani F. (2002). Machine learning in automated text
categorization. ACM Computing Surveys, 34:1–47.
Tsoumakas, G., Katakis, I. (2007). Multi-label classifi-
cation: An overview. International Journal of Data
Warehousing and Mining, 3:1–13.
Tsoumakas, G., Katakis, I., Vlahavas, I.P. (2010). Mining
multi-label data. In: O. Maimon, L. Rokach (Eds.),
Data Mining and Knowledge Discovery Handbook,
Springer-Verlag, 2010, pages 667–685.
Ure, J. (1971). Lexical density and register differentia-
tion. In: G. Perren, J.L.M. Trim (Eds.), Applications
of Linguistics, London: Cambridge University Press,
pages 443–452.
Zhang, B., Zuo, W. (2008). Learning from positive and un-
labeled examples: a survey. In: International Sympo-
siums on Information Processing, pages 650–654.
Selecting Relevance Thresholds to Improve a Recommender System in a Parliamentary Setting
193
