PrCP: Pre-recommendation Counter-Polarization

Mahsa Badami

, Olfa Nasraoui

and Patrick Shafto

Knowledge Discovery and Web Mining Lab, Computer Science and Computer Engineering Department,

University of Louisville, Louisville, KY, U.S.A.

Department of Mathematics and Computer Science, Rutgers University - Newark, Newark, NJ, U.S.A.

Keywords:

Recommender System, Polarization, Controversy, Big data, Algorithmic Bias.

Abstract:

Personalized recommender systems are commonly used to ﬁlter information in social media, and recommen-

dations are derived by training machine learning algorithms on these data. It is thus important to understand

how machine learning algorithms, especially recommender systems, behave in polarized environments. We

investigate how ﬁltering and discovering information are affected by using recommender systems. We study

the phenomenon of polarization within the context of the users interactions with a space of items and how

this affects recommender systems. We then investigate the behavior of machine learning algorithms in such

environments. Finally we propose a new recommendation model based on Matrix Factorization for existing

collaborative ﬁltering recommender systems in order to combating over-specialization in polarized environ-

ments toward counteracting polarization in human-generated data and machine learning algorithms.

1 INTRODUCTION

The growing popularity of Recommender Systems

(RS) to help ﬁlter data to the users, has led to a dyna-

mic interplay between the information that users can

discover and the algorithms that ﬁlter such informa-

tion (Badami et al., 2018; Sun et al., 2018). This

has given rise to several side effects, such as algo-

rithmic biases (Dandekar et al., 2013; Baeza-Yates,

2016), ﬁlter bubbles (Liao and Fu, 2014), and human-

algorithm iterated bias (Shafto and Nasraoui, 2016)

and polarization (Badami et al., 2017). Recent re-

search has studied different types of biases genera-

ted due to algorithms, including bias and fairness

in machine learning (Hardt et al., 2016; Fish et al.,

2016); as well as algorithmic bias(Hajian et al., 2016;

Lambrecht and Tucker, 2018), and assimilation bias

(Zhang et al., 2017). Polarization around controver-

sial issues have arguably affected recommender sys-

tems (and vice-versa) (Garimella et al., 2016b). An

effective and efﬁcient recommender system should

be able to provide the most suitable recommenda-

tion method even in the presence of a set of polarized

items. When such issues emerge on social media, we

often observe the creation of echo chambers or “Filter

Bubbles”, where there is greater interaction between

like-minded people who reinforce each others opinion

(Garimella et al., 2016b). These individuals do not get

exposed to the views of the opposing side, and this in

turn exacerbates polarization (Dandekar et al., 2013).

Allowing users to discover different viewpoints could

allow them to develop unique tastes and diverse per-

spectives (Knijnenburg et al., 2016).

In order to give the users a choice to see more

items, we believe that a recommender system should

enables users to discover novel items whose discovery

may become hindered as a result of the users continu-

ous engagement with a system This is not necessa-

rily the same as recommending a random item by trial

and error or by diversifying the recommendation list,

to increase diversity and serendipity. It is important to

note that recommender systems that improve diversity

and serendipity are not the same as polarization aware

recommender systems. This is because the former ge-

nerally require diversity in the actual description or

nature of items, which in turn requires content data.

Our work primarily focuses on items that can cross

polarization boundaries, where polarization is based

on how users interact with the items (via ratings) and

not their content.

Research on polarization in recommender systems

has emerged rapidly, in recent years, as an important

interdisciplinary topic (Dandekar et al., 2013; Gari-

mella et al., 2016b; Mejova et al., 2014; Nasraoui

and Shafto, 2016; Abisheva et al., 2016; Matakos and

Tsaparas, 2016; Garimella et al., 2016a), with some

efforts trying to decrease online polarization (Gari-

mella et al., 2016b; Liao and Fu, 2014; Garimella et

282

Badami, M., Nasraoui, O. and Shafto, P.

PrCP: Pre-recommendation Counter-Polarization.

DOI: 10.5220/0006938702820289

In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 1: KDIR, pages 282-289

ISBN: 978-989-758-330-8

(a) Φ

= 1 (b) Φ

= 0 (c) Φ

= 0 (d) Φ

= 0

(e) Φ

= 0

Figure 1: Polarization scores for different rating histograms.

al., 2016a; Badami et al., 2017) However, most cur-

rent work on polarization has either been limited to

simple problems (Dandekar et al., 2013), has relied

on textual content to detect sentiment and then po-

larization, or has been conﬁned to speciﬁc domains

within the context of political (or other controversial

domain) news and blogs. In this paper, we are more

interested in studying the emergence and aggravation

of polarization as a result of using collaborative ﬁlte-

ring recommender systems.

Aiming toward alleviating the important problems

of over-specialization and concentration bias, especi-

ally in a polarized environment, we propose a new

approach to generating recommendation lists based

on a modiﬁed Non-Negative Matrix Factorization ap-

proach. We formulate theoretically-grounded scena-

rios for polarization which will allow a simulation-

based analysis of the emergence of polarization, as

well as designing new counter-polarization strategies

for recommender systems. Our proposed approach al-

ters only the input ratings based on the automatically

detected polarization of the items and the users pre-

speciﬁed tolerance for discovery. The proposed mo-

del aims to achieve a trade-off between accurate per-

sonalized recommendations and expanding the space

of items that can be discovered, hence escaping a ﬁl-

ter bubble. Whether humans prefer to discover more

or less is beyond the scope of this paper. The propo-

sed pre-recommendation approach is useful for other

applications where a dataset should be either publis-

hed by an online recommender system provider or by

researchers. In addition, we propose an Interactive

Recommender System (IRS) inspired by (Dandekar

et al., 2013) to assess the effect of the proposed stra-

tegy on the diversity of recommendations in a polari-

zed environment. We see the proposed simulation ap-

proach as a complementary method to investigate the

performance of a recommendation process in a pola-

rized environment in an experimental setting.

The remainder of this paper is organized as fol-

lows. Section 2 presents our proposed methods, fol-

lowed by experiments in Section 3. Finally, we make

our conclusions in Section 4.

2 PROPOSED METHOD

In this section, we propose a strategy that can coun-

teract population polarization, independent of a RS

algorithm. This means that it can later be employed

in a pre-ﬁltering stage along with any recommender

system algorithm. Our proposed approach can be

used to handle polarization without compromising too

much on relevance-based (i.e. pure rating) predictive

accuracy. This is a useful strategy since most online

system providers are using a RS as a black box; hence,

it is difﬁcult to look into the inner workings of the al-

gorithm to modify it.

One might also think of alternatives such as a

straightforward counter-polarization approach, con-

sisting of just including some randomly selected items

from the opposite view. Temporarily, this would seem

to solve the ﬁlter bubble problem and increase the di-

versity of the recommended list. However it would

cause much information loss which leads to recom-

mending irrelevant items and eventually risks redu-

cing user satisfaction with the system. In addition,

such a remedy is not able to solve the ﬁlter bubble

problem for a long period.

Finally, our proposed approach works in the con-

text of the classical collaborative ﬁltering (CF) Re-

commender system algorithm, however, unlike these

recommender systems, our proposed algorithm al-

lows each user to control how much information to

see from opposite views. Similar to CF recommen-

der systems, we also use latent factor models, spe-

ciﬁcally Non-negative Matrix (NMF), to characterize

both items and users based on a set of factors inferred

from user-item rating patterns. However, the propo-

sed approach is not speciﬁc to NMF and can be easily

extended to any RS method. The goal of our propo-

sed recommender system is to avoid guiding the user

toward the most popular items and rather to include

items that help users become aware of other items that

they are not able to discover on their own.

PrCP: Pre-recommendation Counter-Polarization

283

2.1 Problem Deﬁnition

We start with our deﬁnition of polarization and then

deﬁne the problem of polarization-aware collabora-

tive ﬁltering (CF).

In the absence of polarization, the distribution of

opinions is either J-shaped as in ﬁgure 1d and

ﬁgure 1e, or bell shaped, as in ﬁgure 1c. However,

as polarization emerges, the resulting distribution

shifts to a U-shaped distribution, see ﬁgure 1a, with

two peaks emerging around the two dominant and

confronted opinions at the extreme sides of the rating

scale (Badami et al., 2017; Matakos and Tsaparas,

2016). There are some cases with a ﬂat distribution,

1-b, which represent diverse opinions toward an item.

Different examples of such distributions are shown in

ﬁgure 1

Deﬁnition 1 - Polarization:

Given an environment G = (U, I, R), user u ∈ R

1×n

had rated item i ∈ R

m×1

with rating r

∈ R

m×n

a scale of x to y. Item i’s polarization score φ

is a

measure that captures the presence of a gap between

opposite concentration poles or opposite polarity

peaks of the histogram of all users’ ratings r

, when

such poles exist. We say the item is polarized if

≥ δ. This deﬁnition is subjective and tries to deﬁne

an intuitive but data-driven notion of polarization.

Instead of using an explicit formula to calculate this

score, we compute it using a data driven machine

learning model that learns to automatically assign

a polarization score to any rating histogram after

training the model on real item rating histograms

that have been manually labeled according to their

polarization level (Badami et al., 2017)

Deﬁnition 2 - Polarization-aware Collaborative

Filtering Recommendation:

Given a set of ratings R ∈ R

m×n

collected from a set

of users U ∈ R

1×n

for a set of items I ∈ R

m×1

, the

problem of polarization-aware collaborative ﬁltering

recommendation (CF) can be modeled by the triplet

(U, I, R), in a way that a recommender system should

recommend a ranked item set i

, ..., i

∈ I according to

1) the relevance of the item to the user’s interest, and

2) the item’s polarization score. As a realization from

deﬁnition 2, (U, I, R) can be denoted by (u, i, r) which

means that user u rated item i with value r.

Each distribution belongs to a movie crawled from

IMDb by (Badami et al., 2017) with polarization score, φ,

calculated by the method presented in the paper.

2.2 Pre-recommendation: Countering

Polarization (PrCP)

In this step, we aim to transform the source data in

such a way that it mitigates extreme ratings that make

an item polarized. By doing this, we still keep the

user’s relative preferences, yet make it more moderate

so that no extreme recommendation can be generated

from a standard recommender system algorithm. We

perform a controlled distortion of the training data ba-

sed on which a recommender system is trained to help

the users receive more useful recommendations, in the

presence of polarization. This transformation is based

both on the user’s willingness to discover more items

and on the item’s polarization score.

The proposed solution to counteract polarization

by making the training dataset less polarized, employs

a stochastic mapping function as deﬁned below:

f : (U,I, R) → (U, I,R

) with probability p

(1)

The function transforms a user-item rating, r

(for

user u on item i) into rating r

, based on the rating

itself, population average rating, item’s polarization

score and user’s chosen discovery factor, as follows.

= r

− λ

× (¯r +

max

) × Φ

if r

≥ δ

= r

+ λ

× (¯r −

max

) × Φ

if r

< δ

(2)

where λ

∈ [0, 1] is the user’s selected discovery

factor. At one extreme, it is 1 when the user indi-

cates that s/he is interested in discovering more items,

especially from the opposite view. At the opposite ex-

treme, if the user sets λ = 0, the result reduces to using

only the classical recommendation algorithm which

aims to minimize the squared error on the set of raw

ratings. Note that if a user expresses an interest in

considering items from the opposite view, it does not

necessary mean that s/he would deﬁnitely like or pur-

chase those items. The goal here, is to simply give an

option to the users to be able to burst out of their ﬁl-

ter bubbles. Φ

∈ [0, 1] is the polarization score which

is computed using the Polarization Detection Classi-

ﬁer (Badami et al., 2017). g

∈ [0, 1] indicates the gap

between the two rating extreme ranges for a polari-

zed item, in other words it measures how polarized

the user population’s ratings are for item i. We deﬁne

the gap g

as the difference between an item’s typical

minimum rating when it is liked and its typical max-

imum rating when it is disliked. In other words, the

gap g

captures the difference between extreme opini-

ons regarding an item. We deﬁne g

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

284

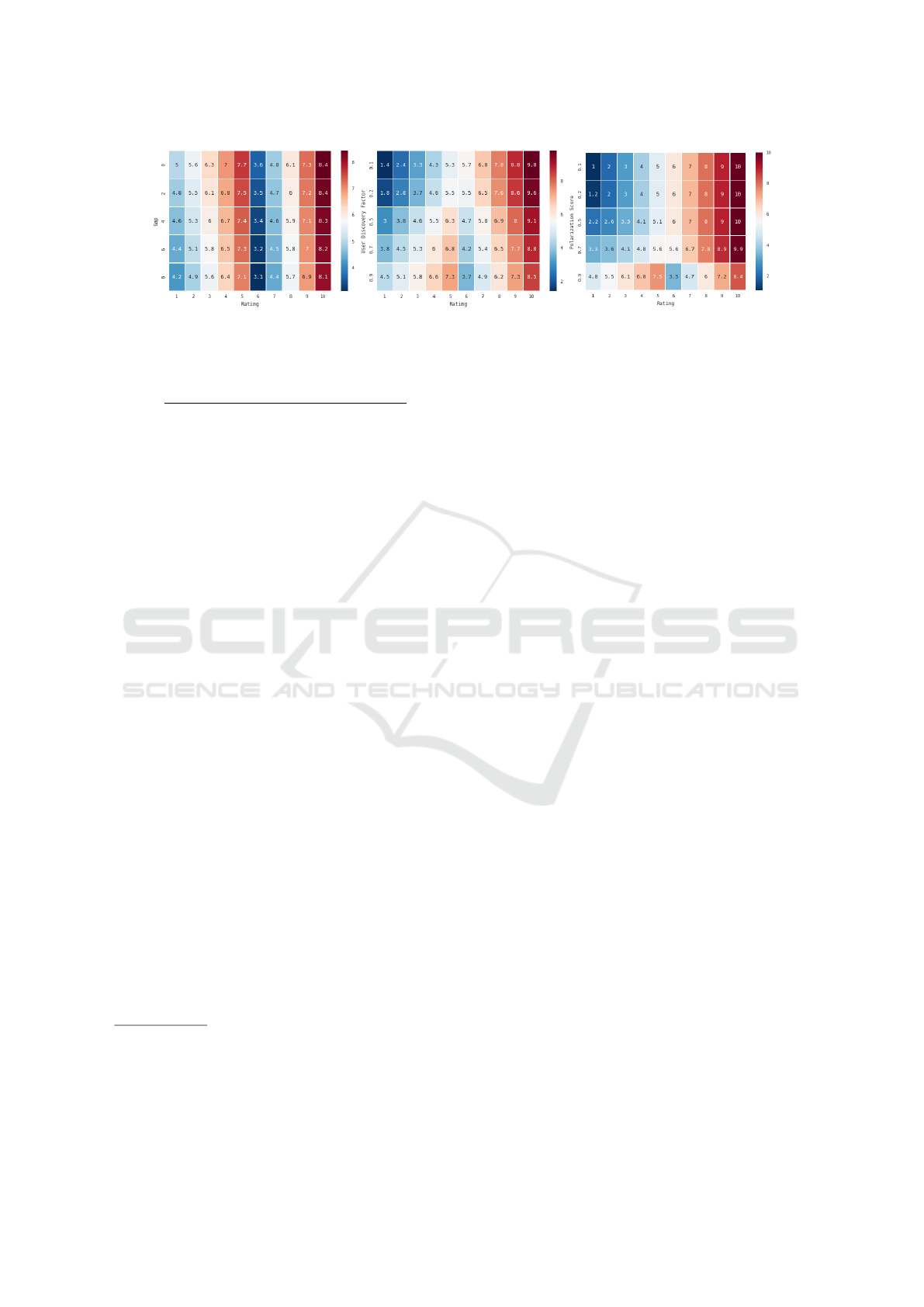
(a) g and r

(b) λ and r

Figure 2: Correlation between user discovery factor (λ), polarization score (Φ), rating (r

) and gap (g) in the pre-

recommendation style counter-polarization approach.

max

u∈Liked(i)

) − min

u∈U nliked(i)

)

max

) − min

)

(3)

where Liked(i) is the set of users who liked item(i)

(i.e. r

≥ δ) and Unliked(i) is the set of users who

didn’t like item(i) (i.e. r

< δ).

Note that the denominator normalizes the gap by

the extremes of the population ratings. g

max

is simply

the difference between the maximum and minimum

rating that a typical user can provide for any item,

using the system’s rating scale. The more polarized a

population gets, the higher g

gets. δ indicates which

ratings are considered as liked versus disliked.

3 EXPERIMENTS

In order to evaluate the impact of our proposed

counter-polarization approach, we will take a deeper

look at the view space coverage and effects of polari-

zation on the algorithms.

To empirically validate our proposed pre-

recommendation scheme, we ﬁrst studied how factors

, Φ

, g

would affect the mapping function from

section 1. Figures 2a-2c show how the difference

among extreme values affects the initial rating r

i j

in a polarized environment if a user u has a high

discovery factor λ. In ﬁgure 2a, we assume that

ratings are on a scale of 1 to 10 and that all items

have the same polarization score, ∀i ∈ I,φ

= 0.9.

As mentioned before, g

represents the difference

between extreme opinions of an item

. Similarly,

ﬁgure 2b indicates how the transformation affects

the initial ratings for an arbitrary item i, where

= 2 and the user discovery factor λ is 1. Finally,

For example if g

= 2, item i has received two diverging

sets of ratings from users. Users who liked this item rated

it 10,9,8,7, while those who did not enjoy the item as much

had given ratings in the range of 1 to 4. So there is a 2-gap

between the given ratings; hence, the item ratings histogram

looks like ﬁgure 3

we study the effect of the user’s chosen discovery

factor on transforming the source data. Here, we

assumed that g

= 2 and that the item is polarized,

with φ

= 0.9. As shown in ﬁgure 2c, we performed a

controlled distortion of the training data from which

a recommender system is learned to help the users

receive more recommendations in the presence of

polarization. By doing this, we still keep the users’

preferences, yet make it more moderate so that, less

extreme recommendations are generated when using

a conventional recommender system algorithm.

3.1 Experimental Settings

Most data publishers provide information regarding

the data collection process, yet there are often hidden

biases which affect the recommendation process (Ba-

dami et al., 2017; Nasraoui and Shafto, 2016; Baeza-

Yates, 2016). Hence, we study the effect of pola-

rization on recommender systems on multiple users

in a ﬁxed environment, inspired by (Dandekar et al.,

2013).

We evaluate the performance of our approach in

terms of rating prediction accuracy, using the Mean

Squared Error (MSE) (Koren et al., 2009). As part

of studying polarization. We also deﬁne the Oppo-

site View Hit Rate (OVHR) ratio based on the ratio of

the number of items from the opposite view to the to-

tal number of recommended items. Considering each

user, if any of the items from the opposite view is in-

cluded in the recommendation list, then a hit occur-

red.

3.2 Simulating the Interactive

Recommendation Process

We consider the following simple environment: Let

G = (U, I, R) be an environment where user u ∈ U

can rate item i ∈ I with rating r

∈ R on a scale of

x to y. The item could be a book, web page, news

article, movie, etc. We deﬁne a recommender system

PrCP: Pre-recommendation Counter-Polarization

285

Figure 3: Rating histograms of the items in environment G with polarization ratio 0.25.

algorithm as follows:

Deﬁnition 3: Let the number of users, |U| = n and

number of items, |I| = m. A recommender system al-

gorithm takes environment G as input along with a

user u ∈ U, and outputs a set of items i

, ..., i

∈ I.

Thus, given an environment G, representing which

users have rated which items and a speciﬁc user u,

a recommender system algorithm’s output is a list of

items to be recommended to u. We assume that u has

to pick only one item from the recommendation list

and that s/he then provides a rating r

for the selected

item.

We generate a rating environment with 50 users

and 200 items where items are evenly divided in two

opposite viewpoint sets that we refer to as red items

and blue items. Users are also divided into two groups

based on whether they like Red or Blue items

. Each

user u ∈ U rates half of the items of I, in such a way

that the rating r

is greater than δ

if s/he likes item

i, and less than δ if s/he does not like it. This pro-

cess forms environment G. We also assume that users

are rational and are truly expressing their preferen-

ces with ratings on a scale of 1 to 10. In order to

make the environment polarized, we assume that user

∈ GroupA likes red items more than blue ones, and

hence all of his/her ratings for the red items are hig-

her than all of his/her ratings for the blue ones. Si-

milarly, we assume that user u

∈ GroupB likes blue

items more than red ones and hence all of his/her ra-

tings for the blue items are higher than all of his/her

ratings for the red ones. Finally, we generated envi-

ronment G with different values of Gap, g and user’s

discovery factor, λ

In order to understand the Interactive Recommen-

der System (IRS), we start by showing some experi-

ments that illustrate examples of how such a system

works in environment G. In all of the examples, we

These labels are purely for the purpose of analysis and

they obviously do not affect the recommender system algo-

rithms.

For concreteness, we assumed δ = 5.

set the number of factors in the latent space, k

, to 5

and we compute the list of top k

= 5 items to be re-

commended to each user. The user will give a rating

for only one of the selected items and we take this

rating value from the true source of ratings, i.e. the

ground-truth data. We repeat this procedure 100 times

(there are 100 unrated items for each user) to simulate

an interactive recommender system scenario. In each

iteration, we measure MSE from the training and tes-

ting phases. We also keep track of the items to which

a user decided to react by providing a rating.

Figure 4 shows traces from the interactive recom-

mendation system for user u ∈ GroupA, which me-

ans s/he likes red items more. We generate environ-

ment G considering for example that gap g

of 2 me-

ans that 7 ≤ r

≤ 10 if u ∈ GroupA likes item i while

1 ≤ r

≤ 4 if u ∈ GroupA does not like item i. Fi-

gure 3 shows the rating histogram of items and we

can clearly see that the difference between the range

of the two sub-populations of ratings given to an item

is 2. Figure 4, upper row, shows that a classic state

of the art recommender system, in our case NMF, is

always going to recommend red items, to which the

user had previously shown more interest. Although

the red items are relevant, the user Red is trapped in

a ﬁlter bubble that does not allow him/her to explore

any items from the opposite color/view, at least not

before the user has seen all of the Red items, the num-

ber of which may be enormous in a real life setting.

This ﬁnding is in line with ﬁnding in most of the lite-

rature (Lord et al., 1979; Flaxman et al., 2016; Dan-

dekar et al., 2013). The second row shows the testing

MSE error for user u

. MSE decreases as the user pro-

vides ratings in each iteration; hence, there are fewer

unrated items for the user. We repeated the same ex-

periment for user u

∈ GroupB who likes blue items

more than red items and we observed the same pattern

as user u

but with Blue items.

Figure 5 shows the results of applying our propo-

sed pre-recommendation counter polarization (PrCP)

strategy on the traditional NMF-based algorithm in

environment G for user u

. As we can see, the user

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

286

Figure 4: Traces of the Interactive Recommendation process with the classical NMF-based CF recommendation algorithm in

environment G with different polarization ratio and gap values, for user u

who had liked red items more. Although the red

items are relevant, the user Red is trapped in a ﬁlter bubble that does not allow him/her to explore any items from the opposite

color/view, at least not before the user has seen all of the Red items.

Figure 5: Traces of the Interactive Recommendation process when applying the pre-recommendation counter polarization

(PrCP) strategy for user u

. As we can see, the user gets to see items from different a color/view even in a very polarized

environment.

gets to see items from a different color/view even in

a very polarized environment. The second row shows

the testing MSE error for user u

which follows the

same trend as before since PrCP doesn’t change the

updating function.

To make a more comprehensive evaluation of per-

formance of the proposed counter-polarization appro-

aches, we repeat the experiment with varying the pa-

rameter λ for the proposed counter-polarization met-

hodology. We consider two scenarios: (a) All users

have the same λ, i.e. λ

= c ∀u ∈ U, where c is a

constant ∈ [0, 1]. (b) User u has his/her own unique

λ, λ

= c

for user u and λ

= 0 ∀u ∈ U − u, where

∈ [0, 1], is a user deﬁned constant.

PrCP: Pre-recommendation Counter-Polarization

287

Table 1: Comparison of the counter-polarization methodologies with the classical NMF-based Recommender system in terms

of accuracy (on training and testing set, respectively) and opposite view ratio (OV HR

,OV HR

). There are two scenarios:

Scenario (a): same λ for all users and Scenario (b): only user u has λ

6= 0.

Opposite View Ratio MSE

Train

MSE

Test

OV HR

mean, std mean, std mean, std mean, std

Classic NMF 0.0 ± 0.00 22.02 ± 5.27 138.96 ± 12.55

PrCP

Scenario (a)

= 0.2 4.8% ± 0.06 25.0% ± 0.035 126.57 ± 38.13 807.30 ± 70.51

= 0.5 4.8% ± 0.07 28.0% ± 0.41 122.38 ± 37.16 805.33 ± 71.77

= 1.0 5.0% ± 0.06 2.9% ± 0.21 120.14 ± 34.40 800.23 ± 64.91

Scenario (b)

= 0.2 5.4% ± 0.073 4.9% ± 0.021 123.92 ± 36.76 813.01 ± 36.76

= 0.5 6.2% ± 0.075 5.2% ± 0.042 122.56 ± 39.081 804.01 ± 75.88

= 0.7 7.0% ± 0.075 5.8% ± 0.033 120.97 ± 35.19 803.65 ± 64.65

The intuition behind this experiment is to study

the effect of a user population on recommending

items to a single user and to all users. We run the

experiments for different λ ∈ [0.2, 0.7, 1] in environ-

ment G with gap = 2. Then, we compute MSE

test

MSE

train

and OV HR for each user and then take an

average over all 50 users. In order to have a compre-

hensive comparison, we compute OV HR in two ways:

(a) OV HR

: Compute the ratio of number of items

from the opposite view to what the user has picked

from the recommendation list. (b) OV HR

: the ratio

of number of items recommended to the user from an

opposite view.

Table 1 shows that the effects of the two metrics

strongly vary depending on the chosen recommenda-

tion algorithm and strategy. Trends in varying para-

meters, show that the higher the user-deﬁned para-

meter λ, the more she will be recommended items

from the opposite view, as desired by the user. When

comparing the traditional NMF-based RS with our

polarization-aware RS, we see that the traditional

NMF-based algorithm achieves good accuracy in ra-

ting prediction, yet it is not able to recommend any

item from the opposite view. In contrast, Our pro-

posed pre-recommendation scheme can be added to

a traditional NMF-based RS and the Polarization-

Aware RS would recommend signiﬁcantly more items

(p ≤ 0.05) from the opposite view compared to the

baseline approach, for all the degrees of user-deﬁned

discovery factors. These differences between diffe-

rent recommendation processes would go unnoticed

if only accuracy measures were considered.

In addition, table 1 shows that having the same

user discovery factor for all users has less effect com-

pared to increasing the user discovery factor for a spe-

ciﬁc user. As we can see in Scenario (b), having

an enthusiastic population does not always result in

counter-polarization. This effect is even more severe

in the polarization-aware strategy where the users do

not see any item from the opposite view even when

the user population has λ

= 0.5 ∀u ∈ U.

Finally, by looking at the number of recommended

items over time in ﬁgure 5, we can see our proposed

methodology succeeds to cover items from the oppo-

site view after a few iterations and broadens the vie-

wpoint spectrum even faster if the user is more inte-

rested in discovering items from different viewpoints.

4 CONCLUSIONS

In this paper, we investigated the mechanism of ﬁlte-

ring and discovering information while using recom-

mender systems. We found that environments with

different polarization degrees engender different pat-

terns. We proposed a counter-polarization methodo-

logy that succeeds to cover items from the opposite

view after a few iterations and can broaden the vie-

wpoint spectrum even faster if the user is more inte-

rested in discovering items from different viewpoints.

The ability of the user to tune the degree of discovery

into the opposite viewpoint is an important feature in

a polarization-aware recommender system because it

allows the users to make decisions about their explo-

ration space. This also contributes to the transparency

of a RS algorithm.

ACKNOWLEDGEMENTS

This research was supported by NSF Grant NSF IIS-

1549981.

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

288

REFERENCES

Abisheva, A., Garcia, D., and Schweitzer, F. (2016). When

the ﬁlter bubble bursts: collective evaluation dynamics

in online communities. In Proceedings of the 8th ACM

Conference on Web Science, pages 307–308. ACM.

Badami, M., Nasraoui, O., Sun, W., and Shafto, P. (2017).

Detecting polarization in ratings: An automated pi-

peline and a preliminary quantiﬁcation on several ben-

chmark data sets. In Big Data (Big Data), 2017 IEEE

International Conference on. IEEE.

Badami, M., Tafazzoli, F., and Nasraoui, O. (2018). A case

study for intelligent event recommendation. Interna-

tional Journal of Data Science and Analytics, pages

1–20.

Baeza-Yates, R. (2016). Data and algorithmic bias in the

web. In Proceedings of the 8th ACM Conference on

Web Science, pages 1–1. ACM.

Bobadilla, J., Ortega, F., Hernando, A., and Guti

errez, A.

(2013). Recommender systems survey. Knowledge-

based systems, 46:109–132.

Bozdag, E. (2013). Bias in algorithmic ﬁltering and per-

sonalization. Ethics and information technology,

15(3):209–227.

Caliskan, A., Bryson, J. J., and Narayanan, A. (2017). Se-

mantics derived automatically from language corpora

contain human-like biases. Science, 356(6334):183–

186.

Dandekar, P., Goel, A., and Lee, D. T. (2013). Biased as-

similation, homophily, and the dynamics of polariza-

tion. Proceedings of the National Academy of Scien-

ces, 110(15):5791–5796.

Fish, B., Kun, J., and Lelkes,

A. D. (2016). A conﬁdence-

based approach for balancing fairness and accuracy.

In Proceedings of the 2016 SIAM International Con-

ference on Data Mining, pages 144–152. SIAM.

Flaxman, S., Goel, S., and Rao, J. (2016). Filter bubbles,

echo chambers, and online news consumption. Public

Opinion Quarterly, page nfw006.

Garimella, K., De Francisci Morales, G., Gionis, A., and

Mathioudakis, M. (2016a). Quantifying controversy

in social media. In Proceedings of the Ninth ACM In-

ternational Conference on Web Search and Data Mi-

ning, pages 33–42. ACM.

Garimella, K., Morales, G. D. F., Gionis, A., and Mathiou-

dakis, M. (2016b). Balancing opposing views to re-

duce controversy. arXiv preprint arXiv:1611.00172.

Hajian, S., Bonchi, F., and Castillo, C. (2016). Algorithmic

bias: From discrimination discovery to fairness-aware

data mining. In Proceedings of the 22nd ACM

SIGKDD international conference on knowledge dis-

covery and data mining, pages 2125–2126. ACM.

Hardt, M., Price, E., Srebro, N., et al. (2016). Equality of

opportunity in supervised learning. In Advances in

neural information processing systems, pages 3315–

3323.

Isenberg, D. J. (1986). Group polarization: A critical review

and meta-analysis. Journal of personality and social

psychology, 50(6):1141.

Kamishima, T., Akaho, S., and Sakuma, J. (2011). Fairness-

aware learning through regularization approach. In

Data Mining Workshops (ICDMW), 2011 IEEE 11th

International Conference on, pages 643–650. IEEE.

Kirkpatrick, K. (2016). Battling algorithmic bias: How do

we ensure algorithms treat us fairly? Communications

of the ACM, 59(10):16–17.

Knijnenburg, B. P., Sivakumar, S., and Wilkinson, D.

(2016). Recommender systems for self-actualization.

In Proceedings of the 10th ACM Conference on Re-

commender Systems, pages 11–14. ACM.

Koren, Y., Bell, R., and Volinsky, C. (2009). Matrix factori-

zation techniques for recommender systems. Compu-

ter, 42(8).

Lambrecht, A. and Tucker, C. E. (2018). Algorithmic bias?

an empirical study into apparent gender-based discri-

mination in the display of stem career ads.

Liao, Q. V. and Fu, W.-T. (2014). Can you hear me now?:

mitigating the echo chamber effect by source position

indicators. In Proceedings of the 17th ACM confe-

rence on Computer supported cooperative work & so-

cial computing, pages 184–196. ACM.

Lord, C. G., Ross, L., and Lepper, M. R. (1979). Bi-

ased assimilation and attitude polarization: The ef-

fects of prior theories on subsequently considered evi-

dence. Journal of personality and social psychology,

37(11):2098.

Matakos, A. and Tsaparas, P. (2016). Temporal mechanisms

of polarization in online reviews. In Advances in So-

cial Networks Analysis and Mining (ASONAM), 2016

IEEE/ACM International Conference on, pages 529–

532. IEEE.

Mejova, Y., Zhang, A. X., Diakopoulos, N., and Castillo,

C. (2014). Controversy and sentiment in online news.

arXiv preprint arXiv:1409.8152.

Melville, P. and Sindhwani, V. (2011). Recommender sy-

stems. In Encyclopedia of machine learning, pages

829–838. Springer.

Morales, A., Borondo, J., Losada, J. C., and Benito,

R. M. (2015). Measuring political polarization:

Twitter shows the two sides of venezuela. Chaos:

An Interdisciplinary Journal of Nonlinear Science,

25(3):033114.

Munson, S. A. and Resnick, P. (2010). Presenting diverse

political opinions: how and how much. In Procee-

dings of the SIGCHI conference on human factors in

computing systems, pages 1457–1466. ACM.

Nasraoui, O. and Shafto, P. (2016). Human-algorithm inte-

raction biases in the big data cycle: A markov chain

iterated learning framework. CoRR, abs/1608.07895.

Shafto, P. and Nasraoui, O. (2016). Human-recommender

systems: From benchmark data to benchmark cogni-

tive models. In Proceedings of the 10th ACM Con-

ference on Recommender Systems, pages 127–130.

ACM.

Sun, W., Nasraoui, O., and shafto, P. (2018). Iterated algo-

rithmic bias in the interactive machine learning pro-

cess of information ﬁltering. In Proceedings of the

10th Of the Knowledge Discovery and Information

Retrieval conference.

Zhang, X., Zhao, J., and Lui, J. C. (2017). Modeling the

assimilation-contrast effects in online product rating

systems: Debiasing and recommendations. In Procee-

dings of the Eleventh ACM Conference on Recommen-

der Systems, RecSys ’17, pages 98–106, New York,

NY, USA. ACM.

PrCP: Pre-recommendation Counter-Polarization

289