
Scheduling of Streaming Data Processing with Overload of Resources
using Genetic Algorithm
Mikhail Melnik, Denis Nasonov and Nikolay Butakov
ITMO University, Saint-Petersburg, Russia
Keywords: Stream Data Processing, Adaptive Scheduling, Performance Modeling, Simulation, Cloud Computing.
Abstract: The growing demand for processing of streaming data contributes to the development of distributed
streaming platforms, such as Apache Storm or Flink. However, the volume of data and complexity of their
processing is growing extremely fast, which poses new challenges and tasks for developing new tools and
methods for improving the efficiency of streaming data processing. One of the main ways to improve a
system performance is an effective scheduling and a proper configuration of the computing platform.
Running large-scale streaming applications, especially in the clouds, requires a high cost of computing
resources and additional efforts to deploy and support an application itself. Thus, there is a need for an
opportunity to estimate the performance of the system and its behaviour before real calculations are made.
Therefore, in this work we propose a model for distributed data stream processing, stream scheduling
problem statement and a developed simulator of the streaming platform, immediately allowing to explore
the behaviour of the system under various conditions. In addition, we propose a genetic algorithm for
efficient stream scheduling and conducting experimental studies.
1 INTRODUCTION
The processing of data flows is increasingly being
introduced into our daily life through the
development of Internet of Things, social networks,
online streams, monitoring centers. The industry and
the scientific community are also confronted with
the constantly increasing volume and processing
complexity of streaming data. This poses new
challenges and tasks for researchers of developing
tools and methods for processing of data streams.
Currently, there are distributed platforms for
streaming data processing. One of the most common
is Apache Storm, Spark Streaming, Flink, S4.
Operators of streaming applications, which process
data, are assigned to nodes of a computing cluster on
which the platform was deployed. The functionality
of such platforms involves mechanisms for scaling
by adding new nodes and replication of application’s
operators. Such functionality is especially important
when a platform is deployed in clouds (Amazon
EC2, Microsoft Azure), where new nodes can be
added or terminated depending on the density of
application’s workload.
The optimal configuration of both the platform
and the application may improve the performance of
data processing in terms of throughput, latency,
energy consumption. Choosing the optimal number
of nodes, correct platform parameters and the
optimal distribution of applications' operators across
the computing nodes can achieve maximum
performance of the system. Moreover, there are
options for modifying the structure of streaming
application (Hirzel et al., 2014). For example, the
union of operators to get rid of serialization, or
permutation of operators to reduce the amount of
data transferred between them.
To solve optimization problems, new methods
and algorithms for scheduling of composite
applications in distributed computing environments
are developed. In comparison to data processing in
batch mode, the scheduling of streaming data is
characterized by the continuous arrival of new tuples
of data that require their immediate processing. It
created the need for simultaneous work of all
application’s operators. Due to the continuity, the
final amount of data for processing can’t be
determined. However, the density of incoming
workload can be predicted, and the received system
load estimates can be taken into account during the
scheduling of streaming application. Since the
workload density is dynamic and may have a peak
232
Melnik, M., Nasonov, D. and Butakov, N.
Scheduling of Streaming Data Processing with Overload of Resources using Genetic Algorithm.
DOI: 10.5220/0006951902320241
In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 232-241
ISBN: 978-989-758-327-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

and off-peak time intervals, it is possible to
distribute operators of streaming application in such
a way as to combine peak intervals with off-peak
ones to increase resources utilization and improve
system’s performance without losing the
performance of overloaded resources.
Therefore, the main idea of this work is to
investigate the scheduling problem of streaming data
processing with an ability to overload the
computational resources in order to combine peak
and off-peak workload densities of application’s
operators on the basis of predictive and performance
modeling. The contribution of the work is:
Modeling and problem statement of scheduling of
applications for streaming data processing taking
into account the forecasting of incoming
workload and overloading of computing nodes;
Development of the distributed streaming
platform simulator that allows exploring the
behavior of the system under various conditions
and scenarios;
Development of a genetic algorithm for
scheduling of streaming data processing.
The article is further structured as follows.
Section 2 is devoted to a review of the related works
to the scheduling of streaming data processing.
Sections 3 presents the background of streaming
data processing. The model and problem statement
of scheduling problem are described in section 4.
Section 5 is devoted to the development of simulator
and genetic algorithm to solve the scheduling
problem. Experimental studies and analysis of their
results are carried out in section 6. Section 7
includes a conclusion and future works.
2 RELATED WORKS
In general, the field of task scheduling in distributed
computing environments has long been at sight of
the scientific community. There is a huge amount of
works devoted to the scheduling of batch data
processing in a form of composite applications or,
for example, MapReduce applications in various
computing environments (Singh and Singh, 2013;
Wu et al., 2015). In such works, a lot of algorithms
of different classes, such as heuristic (Arabnejad,
2013; Topcuoglu et al., 2002), metaheuristic (Liu et
al., 2013; Nasonov et al., 2015) and possible
multiple modifications or hybrid schemes are
developed and investigated (Rahman et al., 2013;
Tsai et al., 2014; Yin et al., 2011). However,
compared to batch processing, the area of scheduling
of streaming data processing is currently poorly
explored and is at the development stage.
Most of the existing algorithms are sharpened for
a particular streaming platform (Storm, Spark
Streaming).
A resource-aware scheduling algorithm for Storm
is proposed in (Peng et al., 2015). The algorithm is
aimed at increasing the throughput of the system due
to the tight placement of application’s operators. The
allocation is based on the calculation of the minimal
difference between the available resource on node
and operator’s requirements to these resources.
Another algorithm (Xu et al., 2014), which is also
a modification of the Storm platform is aimed at
minimizing the inter-node interaction. The algorithm
works with an allocation matrix of operators on
computing nodes. Calculation and update of this
matrix are based on a monitoring of system’s
workload.
Authors of (Eskandari et al., 2016) present a
hierarchical algorithm for Storm. The main idea of the
algorithm lies in the two-phase partitioning of
application’s topology graph into roughly equal parts
for uniform placement of operators across computing
nodes. The partition is made by minimizing the sum
of edges’ weights between subgraphs. Moreover,
before the partitioning, the optimal number of
required nodes is estimated.
Two algorithms for the Storm platform are
suggested in (Aniello et al., 2013). The first is an
offline algorithm that tries to determine the most
related parts of the topology and place them on one or
nearby nodes. The second algorithm uses monitoring
data of resources utilization and traffic between nodes
for further periodic adaptation of previous schedules.
The next work is devoted to Spark Streaming (Liao
et al., 2016). There, one of the most influential
system’s parameters, which should be correctly
selected, is the time window for microbatching. Thus,
the work is focused on dynamical adaptation of the
time window for the microbatching, depending on a
number of entering events in the system.
Besides platform oriented algorithms, there are
works devoted to generalized modeling and
investigation of the streaming data processing. In
such works, the scheduling problem is presented in a
more generalized form, with determination of
indicators and performance characteristics of the
system and ways to evaluate and improve them.
The method for grouping incoming tuples across
operators is proposed in (Rivetti et al., 2016),
allowing the computational workload to be balanced.
Due to the evaluation of the execution time of tuples
and their distribution to less loaded operators, the
Scheduling of Streaming Data Processing with Overload of Resources using Genetic Algorithm
233
proposed algorithm achieves the balance between
execution time of tuples.
In (De Matteis 2017), authors study questions
related to the elasticity of streaming platforms and
how to achieve elasticity by prediction. In the paper,
performance models of streaming data processing
are described in detail, such as bandwidth model,
tuple execution time, resource consumption, and a
reconfiguration model of the system.
3 BACKGROUND
In this section, we’ll look at typical application
organization for streaming data processing. An
application for streaming data processing is a graph
where vertexes are computational operators, and
edges represent data transfer between operators.
Such a graph is abstract structure, just as a definition
of operator also will be considered as a logical unit.
For the direct processing of data and to enable the
application to scale, a certain number of operator
instances are created, which also can be called tasks.
The data stream is defined as an unlimited flow of
tuples through operator instances of application’s
graph. A tuple is a logically complete unit of data,
i.e., can be processed by the operator. Tuples can be
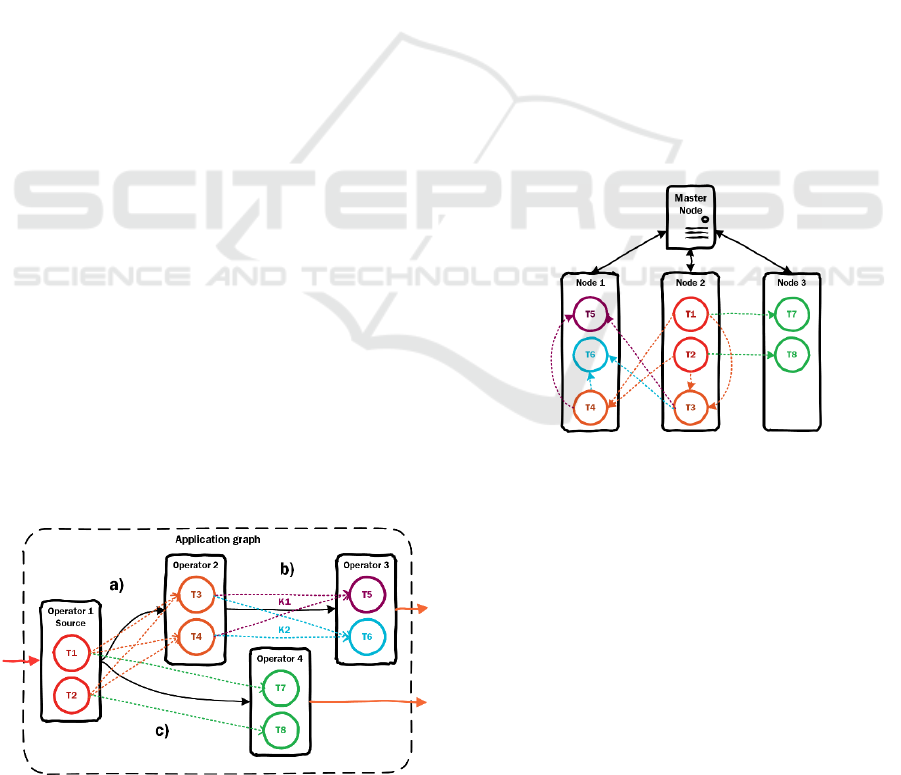
different both in volume and in type. Fig. 1 shows an
example of a graph where black color corresponds to
logical structures (operators and dependencies
between them), while other colors indicate physical
operator instances and physical data flows.
There are various strategies for organizing the
transfer of data flows between instances of
operators:
random distribution of tuples through operator
instances (a);
each instance processes tuples with only a certain
key (b);
custom routing of tuples (c).
Figure 1: Example of application graph with logical (black
color) and physical (other colors) levels of objects.
A similar representation can be found in the most
streaming platforms. For example, in Storm, a graph
is called topology with bolts or spouts as operators.
Spark Streaming works with stages (operators) and
tasks (operator instances). In the Apache Flink, the
logical abstraction of an application is named
JobGraph, which is composed of JobVertexes
(operators), while on the physical level, application
graph called ExecutionGraph with corresponding
ExecutionVertexes as operator instances.
The computing environment is presented in the
form of a set of computing nodes (physical or
virtual). Some of the resources are allocated for the
management system of the platform itself and other
system needs, for example, cluster managers, etc.
(Zookeeper, Yarn, Mesos). The remaining resources
are used to place and launch instances of operators
(tasks) and directly process incoming data (streams
of tuples). The distribution of computing resources
(CPU, memory) between placed tasks can be carried
out in different ways. Resources can be allocated for
each process, and can also be shared by all running
processes on the machine. In this paper, we focus on
the principle with shared computing resources. Thus,
we assume the possibility of overloading the node in
order to achieve maximum utilization of resources.
Figure 2: Example of a computing environment with
allocated tasks across computing nodes.
To start an application for streaming data
processing, it is required to provide a schedule
(Fig. 2). The schedule includes the configuration of
the application itself, a configuration of the
computing environment and the assignment of
application’s tasks to the nodes of the environment.
Effective scheduling allows improving the
performance of the system by optimizing for
selected criteria. The criteria can be the
maximization of throughput, resource utilization,
minimization of latency and cost of resources. In
addition, during scheduling, it is worth considering
possible constraints, for example, budget, reliability.
Therefore, there is a need to develop effective
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
234

scheduling algorithms capable of producing
schedules that would satisfy the identified
constraints and optimize the selected criteria.
4 MODELLING AND PROBLEM
STATEMENT
In this section, models of application, computing
environment, performance models will be presented
together with a problem statement for scheduling of
streaming data processing.
4.1 Computing Environment
The computing environment consists of a set of
computing nodes (hosts) =
{
ℎ
}
. Each node is a
set of characteristics or resources that are allocated
to tasks for their execution.
ℎ
=
{
}
=(
,
,
,…)
(1)
The set of resources may include the number and
frequency of CPU cores, volumes of RAM or GPU,
and others. In this paper, we assume that tasks
hosted on the same host share its resources in the
proportion of their workload densities. Assuming
work in the cloud environment and taking into
account virtualization technologies, the computing
environment can be changed during the
scheduling process. So, if a task needs a certain
amount of resources for its allocation, then a new
virtual machine can be allocated from any of the
suitable hosts, which satisfies the task's requirement.
4.2 Workload
The workload consists of composite applications for
streaming data processing, each of which has a set of
operators. Thus, workload =(,) is a graph,
consisting of the set of all operators ={
} of
these applications and the set of dependencies
between them ={
,
}. Edge
,
stands for a
logical data dependency from the parent operator
to the child operator
. Parent operators will be
denoted by function:
(
)
={
∈|
,
∈}
(2)
Similarly, the set of child operators is defined by the
function:
(
)
= {
∈|
,
∈}
(3)
Operators that don’t have ancestors are called
sources, and operators that don’t have children are
sinks. Just like the computing environment can be
changed during scheduling, the workload’s operators
can also be reconfigured.
Since operators are logical structures, each
operator is characterized by its performance models,
the structure of input and output data. These
performance models can be obtained empirically by
analysing the statistical data of monitoring system or
theoretically derived by the application developer.
The following functions can be included in
performance models for each operator
:
(
)
– function, which estimates the amount
of resources for the complete processing of
input tuples;
,
(,) – is a number of input tuples, obtained
by operator
from the parent operator
∈
(
), which will be processed, depending on
the total number of input tuples (or set of
tuples) and the set of resources, assigned for the
task;
,
() – is a number of output tuples, which
will be transmitted to the child operator
∈
(
) depending on the number of processed
input tuples .
Each operator
has a set of its operator instances
{
|
∈
}. All next definitions are directed to a
task
of operator
. Operator instance or task is
the immediate object that processes the incoming
data.
=(
,
,
)
(4)
Therefore, task
is characterized by the input
and output
flows of tuples, as well as the queue of
tuples
, which accumulates when the capacity of
this instance doesn’t allow to process all incoming
tuples
()=
() +
() .
Input dataflow of tuples
is a set of stochastic
processes:
() = {
()} ∈ {1, …}
(5)
where =|(
)| is equal to the number of
parent operators of
. Similarly, the output stream
of processed tuples
is a set of stochastic
processes:
() =
(), ∈{1,…},
(6)
Scheduling of Streaming Data Processing with Overload of Resources using Genetic Algorithm
235
where =|(
)| is a number of child
operators.
The queue of not processed tuples:
() =
()
,∈{1,…}
(7)
is a set of stochastic processes that coincides with
the dimension of
. Therefore, the total number of
tuples of stream
, that are waiting for their
processing by the task at a time is:
(
)
=
()+
(−Δ),
(8)
where Δ – is a time step. Each next value of the
queue can be estimated as:
(
)
=
()−
,
(
(),
()),
(9)
where
() – are the node’s resources, allocated for
operator instance
at the moment of time ,
,
is
a performance model of operator
and
={
} is
the set of total amount of input tuples for processing.
It is assumed, that resources
of node ℎ
,
which allocate task
∈
, run a set of tasks
=
{
|
∈∩
∩ℎ
} with the corresponding total
amount of input tuples
̅
={
} can be calculated as:
(
)
=ℎ
(
())
∑
(
())
∈
̅
(10)
The resulting number of output tuples as a result of
data processing can be estimated as:
(
)
=
,
(
,
(
(),
()))
(11)
Suppose that the application was started at time
.
During the time
we collected data on the densities
of input, output streams, as well as the queues of all
operator instances from . For further use by
schedulers, these stochastic processes can be
modeled and forecasted for a further period of
time Δ. Suppose that there is a model that allows to
predict the flow of incoming tuples
. Using the
model, we can obtain the forecast
for the next
time period Δ, from the current time
to the
moment of time
=
+Δ. Further, by analogy
with the calculation of
and
on the basis of
input stream
, we can predict the queue
and
density of output stream
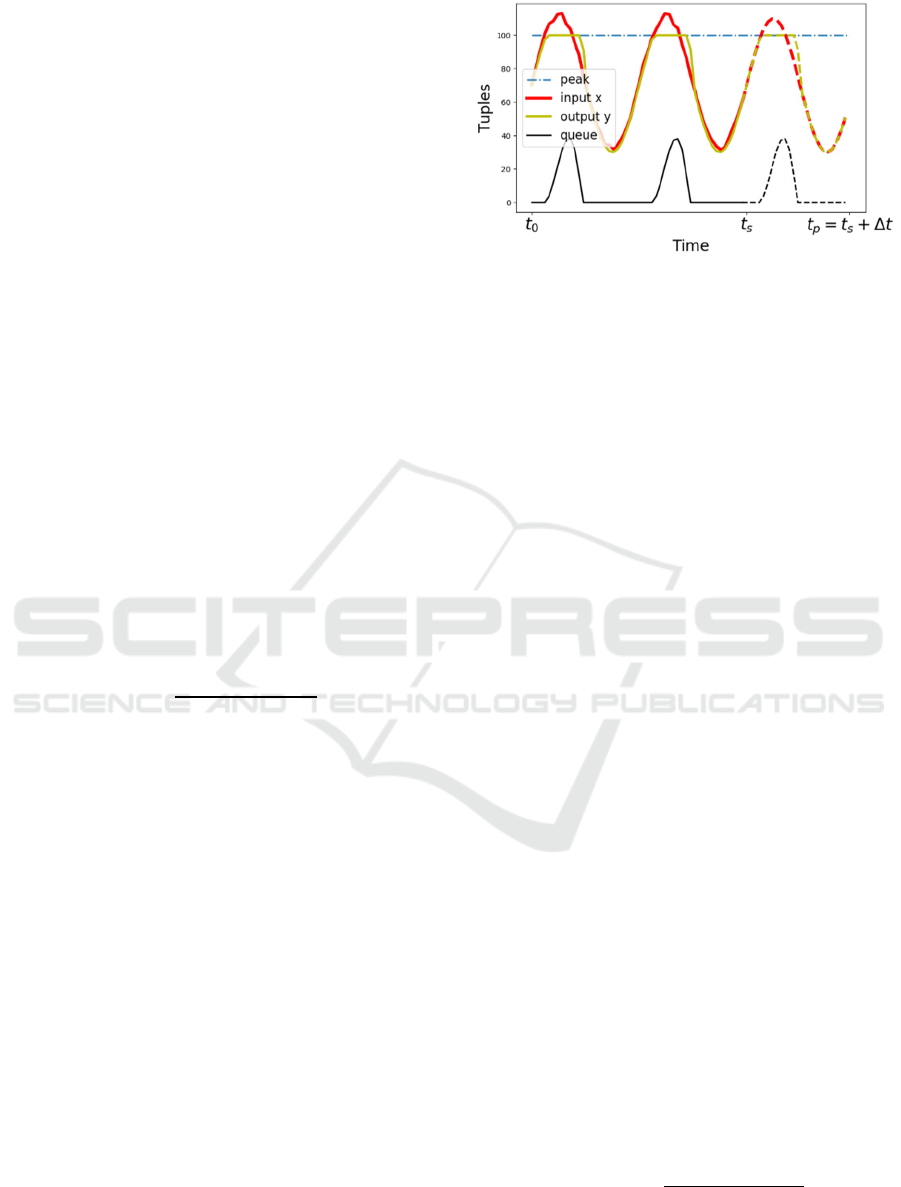
. An example of a data
flow through an operator and its forecast is shown in
Figure 3.
Figure 3: Example of data flow over one operator instance.
In Figure 3, it is assumed, that node cannot
process more than 100 tuples for the single
timestamp. The peak workload of input stream
exceeds the possible number of tuples. During these
periods of time, the queue is growing. When the
workload density decreases, the tuples from the
queue are processed, and the queue itself is
reducing.
4.3 Performance Models
After we described the compute nodes, operators
and data streams passing through the running
instances of the operators, we can proceed to
determine the characteristics of the performance of
the task, resource or the entire application.
Throughput of the entire application will be
considered as the sum of the output tuples from all
instances of operators whose operators are sinks, i.e.,
don’t have child operators ={|
∈
,
(
)
=∅}.
ℎ
(
)
=
()
∈
(12)
A latency is usually understood as the time to
process a tuple fully. In other words, the time from
the arrival of the tuple in the application, until the
result of its processing. In this paper, we are dealing
with flows of tuples instead of particular tuples.
Therefore, the delay will be considered a relative
value, defined as the average ratio of the total input
tuples of the problem to the processed tuples for all
tasks of the application. Therefore, the latency for
task
of operator
can be evaluated as average
ratio through all input streams:
(
)
=
(
)
,
(),
()
(13)
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
236

Utilization of resources determines how tightly the
resources of the computing nodes are occupied. For
each node ℎ
, which runs the tasks ̅ ={
|
∈
}, the recycling of this resource is considered as:
(
)
=min
∈{,,,…}
∑
()
∈
(14)
The function () expresses the total utilization of
the resource . However, in cases when the node is
overloaded, the lack of node’s characteristics for
correct processing the entire amount of input data
will be determined by the function:
(
)
=max
∈{,,,…}
∑
(
())
(15)
The cost of used resources is calculated on the basis
of the tariffs of the cloud environment, which
provides computing resources and the time of use
of each of the nodes ℎ
. A node is considered to be
used during the time
, if at least one task has been
started during this time
, and the rent for the
resource is a function (ℎ
). Thus, the total cost
is calculated as:
=
(
ℎ
)
∙
(16)
4.4 Scheduling Problem Statement
The schedule =(
,
,) consists of a
configuration of the computational workload
′
=
{
}, a configuration of the computing environment
′
={ℎ
} and a distribution of instances of
operators from
′
across nodes
′
.
=
,ℎ
||
(17)
is the set of pairs composed of the tasks
and the
computing node, on which this task should be
started.
Let’s consider a set of different optimization
criteria or objectives =
{
(
)}
, where each
() is a function of a schedule.
We assume that we would like to maximize all
the criteria
(). In a case of minimization, we
easily can use negative criteria −
().
Beside optimization criteria, an optimization
problem may include different constraints =
{
()}.
=
(
)
,
(
)
,…
|
|
(
)
(18)
A produced solution should satisfy all these
restrictions. There are two types of constraints. Hard
constraints, when a schedule must satisfy the
constraint, otherwise a solution is not valid. The
second type is soft constraints, which can be
exceeded, but with penalties.
Considering all criteria and constraints, we can
show the problem definition. The main goal is to find
such optimal schedule
, that:
∃
:∀
≠
:
≥
(
)
,∀
∈
≤
(
)
,∀
∈
(19)
In other words, the optimal solution must maximize
all criteria and don't exceed constraints, and the
equation above is mostly applicable for a multi-
objective problem.
Problem can be rewritten as single-objective
problem by defining two sets of weights α and β.
These weights are used to determine the significance
of a particular criterion or restriction.
∑
|
|
−
∑
|
|
≥
∑
(
)
|
|
−
∑
(
)
|
|
,
(20)
Thus, we can determine the result estimation of each
schedule and develop an algorithm, which will find
the optimal one.
5 SIMULATION AND
SCHEDULING
In this section, the developed simulator for
streaming data processing will be described.
Moreover, we present a genetic algorithm for
scheduling, which is integrated into this simulator.
The simulator is the agent-based model, and is
developed on the basis of MASON (Cioffi-revilla
and Sullivan, 2005) Java library for discrete-event
multiagent simulation. We have two main types of
agents: OperatorAgent and NodeAgent.
Evidently, OperatorAgent is described by the
operator instance model from section 4 with such
fields as input and output data flows with their
forecasts and queue. NodeOperator represents
computing node with a set of computing resources
(CPU, RAM) on which operators are placed to
process a flow of data tuples.
Scheduling of Streaming Data Processing with Overload of Resources using Genetic Algorithm
237

Beside the operators and nodes, there is another
ScenarioAgent. It determines all events that will
occur during the simulation. The scenario may
include the following events:
NewNodeEvent – add a new node to cluster;
NewOperatorEvent – add a new operator to
current workload;
KillNodeEvent – remove a node from
cluster;
KillOperatorEvent – remove an operator
from workload;
ScheduleEvent – launch of scheduling
algorithm and apply its result schedule.
During step() function, OperatorAgent
receives new value of input tuples, updates queue
and evaluate a number of output tuples at current
moment of time. Further, new points are predicted
for forecasts of input and output flows.
The simulator may work in both online and
offline mode. Offline mode allows quickly obtaining
the result of the simulation, while the online mode
allows monitoring the behavior of the simulated
system during all the simulation process.
The simulator includes interface for scheduling
algorithm to allocate tasks across nodes when the
ScheduleEvent occurs. The algorithm is able to use
all the monitoring data about operators' input and
output data flows.
For the scheduling, we developed a Genetic
algorithm (GA). GA is one of the most known
evolutionary algorithms. GA evolves a population of
individuals (or chromosomes), which represent
solutions to an optimization problem. The fitness
function is used to estimate the quality of each
solution according to specified optimization criteria
and restrictions. GA imitates the evolutionary
process by using further operators:
Selection – the more adapted individuals have
more chances to survive during evolution;
Mutation – random change in the individual’s
genotype;
Crossover – generation of children individuals by
combining features of parents.
For the development of GA, it is required to define
the representation of candidate solutions, mutation
operator, crossover operator, and the most important
– fitness function. In our development algorithm, the
chromosome is represented as a mapping of
operators (tasks) to nodes. The example of the
chromosome is presented in Fig. 4.
Figure 4: Example of chromosome (candidate solution).
The next step is to develop appropriate mutation
and crossover operators. For the mutation, we
developed two options. The first option is to change
node for one of the operators. The second option is
to swap two nodes of two randomly chosen
operators.
Crossover is an evolutionary operator that
recombine the properties of two parents and produce
a new solution. In our algorithm, the crossover is
performed by random selection of assigned node for
each operator between two parents.
Figure 5: Example of two mutation operators and
crossover operator with two parents.
The examples of two mutations and crossover
are shown in Fig. 5.
GA can take any set of criteria and constraints to
evaluate the quality of candidate solutions by
building an appropriate fitness function. Moreover,
advantages of GA also include the possibility of its
modification. In particular, the algorithm can be
extended to work with multi-criteria optimization
problems. In addition, any problem oriented
heuristic algorithms may be integrated into an initial
population of GA to speed up the evolution process
of finding the optimal solution.
In offline experiments (Table 1) we used
following GA’s parameters: crossover probability
for each pair of individuals = 0.3; mutation
probability = 0.2; elitism = 3; population size = 100;
iterations = 1000. The algorithm has generational
evolution strategy, and the initial population is
initiated randomly. Fitness function considers
optimization by resources utilization and a number
of used nodes with penalties for overloading of
nodes.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
238

6 EXPERIMENTAL STUDIES
For the experimental study in this paper, we used
sinusoidal signal as input dataflow for all operators
in workload. A scenario for an experiment can be
constructed as follows:
// params: event time, node id, CPU
cores;
NewNodeEvent(0.0, "n0", 20);
NewNodeEvent(0.0, "n1", 20);
// params: event time, operator id,
baseline=a, amplitude=b, period=c,
phase=d;
// x(t)=a+b*sin(2*π*t/c+d);
NewSinusOperatorEvent(0.0, "t0", 249,
40, 40, 0);
NewSinusOperatorEvent(0.0, "t1", 249,
40, 40, PI);
NewSinusOperatorEvent(200.0,"t2",249,40
,40, PI/2);
NewSinusOperatorEvent(200.0,"t3",249,40
,40, PI/2*3);
// params: event time;
ScheduleEvent(0.0);
ScheduleEvent(100.0);
ScheduleEvent(300.0);
Parameters of objects are indicated above them.
Here, we define the launch of two nodes with 20
CPU cores on each. This number of cores was taken
in accordance with the number of available cores on
physical nodes of our cluster (32 cores, but 12 are
used for system needs). Further, we define that the
workload will consist of two operators with a
sinusoidal input signals at the moment time 0.0, and
two additional operators that will arrive to the
system at the moment 200.0.
We add three scheduling events to the scenario at
moments 0, 100 and 300. At the initial time 0,
Figure 6: Result RStorm schedule of 12 signals with 5
used resources.
statistical data about operators' workload will not be
collected yet. Therefore, the scheduling algorithm
(GA) would produce a poor-quality random
schedule. Then, at the moment time 100, when
statistical data are collected, the algorithm should
find the optimal solution where signals are placed in
pair at one node. At the time point 200, new
operators will arrive and start to collect input tuples.
Since they are not yet located on nodes, these input
tuples will be accumulated in their queues. Then, at
the time point 300.0, the last scheduling event will
be performed at time point 300, where all four
operators should be scheduled.
Further experiments were conducted in offline
mode. The aim of these experiments is to investigate
the ability of GA to find the optimal allocation of
many sinusoidal signals with various parameters
across the computing nodes. Despite the fact, that
built GA represents simple structure, this work
provides opportunities for further experiments with
more sophisticated algorithms, designed for the
given problem. In these experiments, we varied the
number of available nodes, operators and parameters
of their sinusoidal input streams of tuples. In all
cases we assume, that peak throughput of each node
is 500 tuples per time unit (the specific of target
application, that was simulated here). All operators’
input signals are generated with random parameters
within defined bounds for sinusoids’ baseline and
amplitude.
For comparison, we implemented RStorm
algorithm with only CPU as resource for allocation
of tasks. We compared the result of our GA with
RStorm algorithm. Result of all experiments are
presented in Table 1. Each experiment was
conducted 20 times with new random samples of
operators’ input signals. Values in table represent
average values among performed experiments.
Figure 7: Result schedule of 12 signals, obtained by GA
with 4 used resources.
Scheduling of Streaming Data Processing with Overload of Resources using Genetic Algorithm
239

Table 1: Results of experiments on scheduling of sinusoidal input dataflows.
Exp # Operators Nodes
Used nodes Avg utility, %
GA avg
overload, %
RStorm GA RStorm GA
Input params: Min baseline = 100; Max baseline = 200; Min ampl = 40; Max ampl = 60
1 12 9 5.3 4.3 69.3 86.2 0.01
2 50 25 19.7 18.2 75.5 82.9 0.02
3 100 50 38.8 35.8 77.1 83.7 0.02
4 200 100 73.7 72.8 78.1 81.6 0.02
Input params: Min baseline = 90; Max baseline = 150; Min ampl = 30; Max ampl = 80
5 50 25 16.8 15.5 71.0 78.4 0.01
6 100 50 33.0 31.6 72.4 78.9 0.01
7 200 100 61.6 60.2 72.5 78.4 0.01
The result of one of these experiments (#1) is
shown in Fig. 6 and Fig. 7 for RStorm and GA
schedules accordingly. In the GA schedule, only 4
nodes were used instead of 5 used nodes in the
RStorm schedule.
Due to the optimal combination of peak and off-
peak input dataflows, the algorithm allows to save
nodes and increase utilization of used resources. In
order to estimate obtained solutions, we used the
number of used nodes, the average load on them and
the average overload of resources (only among
overloaded ones). Despite the assumed limit on the
peak workload (500 tuples / s), GA results have
minor overloads of resources, but not exceeding
0.03%. However, it can be controlled by using
penalties for overload of resources. To meet strict
constraints, stronger penalties should be imposed in
fitness function, or such solutions should be
considered as invalid. In comparison with GA,
RStorm algorithm does not impose the overloading.
Both algorithms found optimal-like solutions in
presented experiments, and it was difficult for GA to
find a solution with fewer used nodes. Nevertheless,
proposed GA is able to grow better schedules with
1.6 less number of used nodes and with 6.2% greater
resources utilization in average among experiments
even with a large dimension of the optimization
problem (200x100). For large-scale problems, it
makes sense to divide a full-dimension problem into
sub-problems to preserve the effectiveness and the
execution time of both algorithms.
7 CONCLUSION AND FUTURE
WORKS
In this paper, we investigated the problem of
scheduling the streaming data processing in
distributed computing environments. We put
emphasis on the sharing of resources between
operators, which allows nodes to be overloaded and
allocate operators in such a way to combine peak
and off-peak input dataflows to improve resources
utilization and system performance. For that
purposes, we presented the model of streaming data
processing, based on input and output workload
densities and their forecasting. Further, we
developed the simulator of streaming platform,
based on the proposed model. The simulator allows
investigating the behavior of a system under various
conditions. This is important, since running real
streaming applications requires additional efforts
and time, and more importantly, can have the cost of
renting computing resources. The use of simulator
will allow configuring the system and improving the
performance of streaming data processing before the
application is directly launched. Along with the
simulator, we developed genetic algorithm for
scheduling of workload on the resources of the
computing environment. Results of the experiments
show the ability of algorithm to find optimal
solutions in terms of increasing of resources
utilization and reducing the number of used nodes
even with large dimensions of problem.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
240

Currently, the simulator is under development
and available on GitHub (StreamSim) with
additional results and experiments. There are many
features, which can be added, including the ability to
create complex composite streaming applications
with the ability to reconfigure their internal
structures during the execution. We also plan to
implement more of reviewed algorithms (T-Storm,
etc.) and evaluate their effectiveness in various
conditions.
ACKNOWLEDGEMENTS
This research is financially supported by The
Russian Foundation for Basic Research, Agreement
#18-37-00416 and The Russian Science Foundation,
Agreement #17-71-10253.
REFERENCES
Aniello, L. et al., 2013. Adaptive Online Scheduling in
Storm. Proc. 7th ACM Int. Conf. Distrib. event-based
Syst. 207–218.
Arabnejad, H., 2013. List Based Task Scheduling
Algorithms on Heterogeneous Systems-An overview.
Dr. Symp. Informatics Eng.
Cioffi-revilla, C., Sullivan, K., 2005. MASON : A
Multiagent Simulation Environment. Simulation 81,
517–527.
De Matteis, T., Mencagli, G., 2017. Proactive elasticity
and energy awareness in data stream processing. J.
Syst. Softw. 127, 302–319.
Eskandari, L. et al., 2016. P-Scheduler: Adaptive
Hierarchical Scheduling in Apache Storm Leila. Proc.
Australas. Comput. Sci. Week Multiconference -
ACSW ’16 1–10.
Hirzel, M. et al., 2014. A catalog of stream processing
optimizations. ACM Comput. Surv. 46.
Liao, X. et al., 2016. An enforcement of real time
scheduling in Spark Streaming. 2015 6th Int. Green
Sustain. Comput. Conf.
Liu, R. et al., 2013. A Multipopulation PSO Based
Memetic Algorithm for Permutation Flow Shop
Scheduling. Sci. World J.
Nasonov, D., Melnik, M., Shindyapina, N., Butakov, N.,
2015. Metaheuristic Coevolution Workflow
Scheduling in Cloud Environment. 7th Int. Jt. Conf.
Comput. Intell. 1, 252–260.
Peng, B., Hosseini, M., Hong, Z., Farivar, R., Campbell,
R., 2015. R-Storm: Resource-Aware Scheduling in
Storm. Proc. 16th Annu. Middlew. Conf. 149–161.
Rahman, M.., Hassan, R.., Ranjan, R.., Buyya, R.., 2013.
Adaptive workflow scheduling for dynamic grid and
cloud computing environment. Concurr. Comput.
Pract. Exp. 25, 1816–1842.
Rivetti, N. et al., 2016. Online Scheduling for Shuffle
Grouping in Distributed Stream Processing Systems.
Proc. 17th Int. Conf. Middlew. 1–12.
Singh, L., Singh, S., 2013. A Survey of Workflow
Scheduling Algorithms and Research Issues. Int. J.
Comput. Appl. 74.
StreamSim [WWW Document], URL
https://github.com/HighExecutor/StreamSim
Topcuoglu, H., Hariri, S., Wu, M.-Y., 2002. Performance-
effective and low-complexity task scheduling for
heterogeneous computing. IEEE Trans. Parallel
Distrib. Syst. 13, 260–275.
Tsai, C. et al., 2014. A Hyper-Heuristic Scheduling
Algorithm for Cloud. IEEE Trans. Cloud Comput. 2,
236–250.
Wu, F. et al., 2015. Workflow scheduling in cloud: a
survey. J. Supercomput. 71, 3373–3418.
Xu, J., Chen, Z., Tang, J., Su, S., 2014. T-storm: Traffic-
aware online scheduling in storm. Proc. - Int. Conf.
Distrib. Comput. Syst. 535–544.
Yin, M. et al., 2011. A novel hybrid K-harmonic means
and gravitational search algorithm approach for
clustering. Expert Syst. Appl. 38, 9319–9324.
Scheduling of Streaming Data Processing with Overload of Resources using Genetic Algorithm
241
