
Usability of Concordance Indices in FAST-GDM Problems
Marcelo Loor
1,2
, Ana Tapia-Rosero
2
and Guy De Tr
´
e
1
1
Dept. of Telecommunications and Information Processing, Ghent University,
Sint-Pietersnieuwstraat 41, B-9000, Ghent, Belgium
2
Dept. of Electrical and Computer Engineering, ESPOL Polytechnic University,
Campus Gustavo Galindo V., Km. 30.5 Via Perimetral, Guayaquil, Ecuador
Keywords:
Flexible Consensus Reaching, Group Decision-Making, Intuitionistic Fuzzy Sets, IFS Contrasting Charts.
Abstract:
A flexible attribute-set group decision-making (FAST-GDM) problem boils down to finding the most suitable
option(s) with a general agreement among the participants in a decision-making process in which each option
can be described by a flexible collection of attributes. The solution to such a problem can involve a consensus
reaching process (CRP) in which the participants iteratively try to reach a general agreement on the best
option(s) based on the attributes that are relevant for each participant. A challenging task in a CRP is the
selection of an adequate method to determine the level of concordance between the evaluations given by each
participant and the collective evaluations computed for the group. To gain insights in this regard, we performed
a pilot test in which a group of persons were asked to estimate the level of concordance between individual and
collective evaluations obtained while other participants tried to solve a FAST-GDM problem. The perceived
concordance levels were compared with several theoretical concordance indices based on similarity measures
designed to compare intuitionistic fuzzy sets. This paper presents our findings on how each of the chosen
theoretical concordance indices reflected the perceived concordance levels.
1 INTRODUCTION
Consider a situation in which a group of viniculturists
are trying to reach a consensus about the best grape-
vine(s) for winemaking from a collection of grapevi-
nes that have been developed for the industry. In this
situation, a consensus can be reached using a process
where the viniculturists, under the supervision of a
moderator, can iteratively reconsider their evaluations
to be in agreement with the group and, thus, to decide
on the best grapevine(s) for winemaking (Bouyssou
et al., 2013). Assuming that the viniculturists have a
similar expertise, the moderator can ask them to eva-
luate each grapevine (i.e., each option) using a prede-
fined collection of attributes, which denote the featu-
res or characteristics inherent to any of the grapevi-
nes under evaluation. As such, this situation can be
deemed to be an example of a multi-attribute group
decision-making (MA-GDM) problem (Dong et al.,
2016; Liu et al., 2016).
A different situation is one in which a heteroge-
neous group of participants have different opinions
on how the attributes (or features) of the given op-
tions should be evaluated. In this case, the problem
of finding a consensus with a flexible collection of
attributes comes to light. As an example, one can
consider another situation where three untrained vi-
niculturists, say Alice, Bob and Chloe, are trying to
reach a consensus on the best grapevine(s) for wine-
making from the aforementioned collection of grape-
vines: while Alice considers that one of the grape-
vines, say ‘GV1’, is almost the best for winemaking
due to its reddish color, Bob considers this grapevine
to be unacceptable for winemaking because it is ex-
pensive; meanwhile, Chloe considers that ‘GV1’ is a
good grapevine for winemaking because of its appe-
tizing aroma, but it is not the best due to its strong
flavor. Notice in this example that, since they are un-
trained viniculturists, Alice, Bob and Chloe evaluate
‘GV1’ according to the attributes that each of them
might consider to be relevant on this grapevine for
deciding whether or not it is the best for winemaking.
In this case, a consensus can be reached using a pro-
cess where these persons iteratively reconsider their
evaluations based on the attributes of the grapevines
that were initially unobserved by some of them but
observed by others. This last situation can be seen as
an example of a flexible attribute-set group decision-
making (FAST-GDM) problem (Loor et al., 2018).
The solution to such group decision-making pro-
Loor, M., Tapia-Rosero, A. and De Tré, G.
Usability of Concordance Indices in FAST-GDM Problems.
DOI: 10.5220/0006956500670078
In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 67-78
ISBN: 978-989-758-327-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
67

blems can involve a consensus reaching process
(CRP) in which the participants (experts or non-
experts) iteratively try to reach a collective agreement
on the best option(s) (Kacprzyk and Fedrizzi, 1988;
Herrera et al., 1996; Kacprzyk and Zadro
˙
zny, 2010).
A challenge in this process is to find a consistently
good method by which one can determine the level of
concordance between the individual evaluations given
by a participant and the collective evaluations compu-
ted for the group.
To gain insights about what can be accepted as a
good indicator of the level of concordance in FAST-
GDM problems, we conducted a pilot test in which an
easy-to-reach group of persons were asked to make an
estimation of the level of concordance that they per-
ceive between the individual and the collective eva-
luations obtained during the iterations of a CRP in
a FAST-GDM problem. To make such estimations,
those persons were provided with IFS contrasting
charts, a novelty of this work, which depict the evalu-
ations characterized as intuitionistic fuzzy sets (IFSs)
(Atanassov, 1986; Atanassov, 2012). Then, those esti-
mations were compared with several theoretical con-
cordance indices to determine the usability of each
index. By means of such comparisons, we aim to de-
termine how well those theoretical concordance indi-
ces could reflect a perceived level of concordance in a
FAST-GDM problem.
It is worth mentioning that, although the CRP pro-
posed for FAST-GDM problems is based on an aug-
mented variant of IFSs called augmented Atanassov
intuitionistic fuzzy sets (Loor and De Tr
´
e, 2017a), in
this test we use similarity measures designed to com-
pare traditional IFSs because the computation of con-
cordance indices can be done by using only the mem-
bership and nonmembership levels (Loor et al., 2018).
A practical motivation in this regard is to study the ap-
plicability of the tools included in the IFS framework
to the solution of decision-making problems where
participants having different expertise are given the
freedom to perform positive or negative evaluations
according to what they consider to be relevant.
To present the results of the pilot test, this paper
has been structured as follows. In Section 2, we pre-
sent some preliminary concepts, as well as the formu-
lation of a FAST-GDM problem. Then, in Section 3,
we describe the pilot test and introduce the novel IFS
contrasting charts. Before concluding this paper, we
present the results and our findings in Section 4 and
some related work in Section 5.
2 PRELIMINARIES
When there are different opinions on how the attribu-
tes (or features) of a predefined collection of potential
options should be evaluated, an evaluation might be
accompanied by some suggestions about what have
been focused on during the evaluation process. For
instance, in the second introductory example Alice
has considered that ‘GV1’ is almost the best grapevine
for winemaking due to its reddish color. To characte-
rize this kind of evaluations, the idea of an augmen-
ted appraisal degree (AAD) has been introduced in
(Loor and De Tr
´
e, 2017a). In the context of decision-
making, such an augmented appraisal degree idea can
be described as follows:
Consider a discrete collection X = {x
1
, ⋯, x
n
} of
potential solutions, called options, for a particular
problem, where each x
i
∈ X has a collection of fea-
tures F
i
. Consider also that a collection of suitable
options for this problem in X is denoted by A, i.e.,
A ⊆ X . Finally, consider a person P who has been as-
ked to evaluate the level to which an option x
i
∈ X sa-
tisfies the proposition “p : x
i
is a member of A.” With
these considerations, an augmented appraisal degree
of x
i
, say ˆµ
A@P
(x
i
), is a pair µ
A@P
(x
i
), F
µ
A
@P
(x
i
)
that denotes the level µ
A@P
(x
i
) to which x
i
satisfies
the proposition p, as well as the collection of features
F
µ
A
@P
(x
i
) ∈ F
i
considered by P while appraising the
proposition p.
For instance, consider the collection of grapevines
X = {‘GV1’, ‘GV2’, ‘GV3’}. Consider also a unit in-
terval scale where 0 and 1 represent the lowest and
the highest level of satisfiability respectively. In this
context, after denoting (the collection of) the best gra-
pevine(s) for winemaking by the letter A, one can
characterize Alice’s evaluation by ˆµ
A@Alice
(‘GV1’) =
0.9, {‘reddish color’}.
In the second introductory example, Chloe has
considered that ‘GV1’ is a good grapevine for wine-
making because of its appetizing aroma, but it is not
the best due to its strong flavor. Notice is this case that
one can provide an evaluation denoting not only how
acceptable but also how unacceptable an option could
be. To characterize this kind of evaluations, the inclu-
sion of AADs into the definition of an IFS has been
proposed in (Loor and De Tr
´
e, 2017a). Such augmen-
ted version of an IFS, called augmented (Atanassov)
intuitionistic fuzzy set (AAIFS), can be described as
follows:
Keep X , A, p and P as given above. Recall
that x
i
∈ X has a collection of features F
i
and as-
sume that F = F
1
∪⋯ ∪F
n
. Assume also I = [0, 1].
Let ˆµ
A@P
(x
i
)= µ
A@P
(x
i
), F
µ
A
@P
(x
i
) and
ˆ
ν
A@P
(x
i
)=
ν
A@P
(x
i
), F
ν
A
@P
(x
i
) in I, F be two AADs deno-
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
68

ting the evaluations given by P on how acceptable and
how unacceptable x
i
is for fulfilling the proposition p
respectively. In this context, an AAIFS is a collection
ˆ
A
@P
that describes the correspondence between each
x
i
∈ X and both ˆµ
A@P
(x
i
) and
ˆ
ν
A@P
(x
i
) through the
expression
ˆ
A
@P
={x
i
, ˆµ
A@P
(x
i
),
ˆ
ν
A@P
(x
i
) (x
i
∈ X)
∧(0 ≤ µ
A@P
(x
i
)+ν
A@P
(x
i
) ≤ 1)}. (1)
Notice in this expression that the consistency condi-
tion, i.e., 0 ≤ µ
A@P
(x
i
)+ν
A@P
(x
i
) ≤ 1, has been inher-
ited from the original definition of an IFS (Atanassov,
1986; Atanassov, 2012). Hence, an AAIFS can be
used for the characterization of evaluations like the
given by Chloe even if the evaluations are marked by
hesitation. Because of this and given that an AAIFS
can be used in situations when no constraint on the
attributes of the collection of potential options has
been established, the AAIFS concept has been used
in the formulation of a FAST-GDM problem as fol-
lows (Loor et al., 2018):
Consider a discrete collection X = {x
1
, ⋯, x
n
} of
potential options for a particular problem, and con-
sider that A ⊆ X represents a collection of suitable
options for this problem. Consider also a collection
E = {E
1
, ⋯, E
m
} that represent a group of participants,
experts or non-experts, who were asked to evaluate to
which level each option in X is member of A. Let
ˆ
A
@E
j
=
x
i
, ˆµ
A@E
j
(x
i
),
ˆ
ν
A@E
j
(x
i
) (x
i
∈ X)
∧
0 ≤ µ
A@E
j
(x
i
)+ν
A@E
j
(x
i
) ≤ 1
(2)
be an AAIFS characterizing the individual evaluati-
ons given by E
j
∈ E. Let
ˆ
A ={x
i
, ˆµ
A
(x
i
),
ˆ
ν
A
(x
i
) (x
i
∈ X)
∧(0 ≤ µ
A
(x
i
)+ν
A
(x
i
) ≤ 1)} (3)
be an AAIFS characterizing the collective evaluati-
ons computed for the group of participants E. Finally,
let cix(
ˆ
A
@E
j
,
ˆ
A) be a function, called concordance in-
dex, that computes the level of concordance between
ˆ
A
@E
j
and
ˆ
A, where a higher value denotes a higher
concordance between
ˆ
A
@E
j
and
ˆ
A. In this context, a
FAST-GDM problem boils down to finding the most
suitable option(s) in such a way that the average of all
the concordance indices, i.e.,
1
m
∑
E
j
∈E
cix(
ˆ
A
@E
j
,
ˆ
A),
is maximized.
As can be noticed, the computation of a concor-
dance index is a very influential step in a FAST-GDM
problem. For this reason, the selection of an adequate
method for its computation is deemed to be an impor-
tant and challenging task.
An option to perform such computation is through
a function, say S, that computes the similarity bet-
ween
ˆ
A
@E
j
and
ˆ
A, i.e., a concordance index can be
computed by
cix(
ˆ
A
@E
j
,
ˆ
A) = S(
ˆ
A
@E
j
,
ˆ
A). (4)
As will be shown in the next section, in this work
we use similarity measures that have been designed
to compare traditional IFSs.
3 PILOT STUDY
As was mentioned in Section 1, the aim of this pa-
per is to study how well a theoretical concordance in-
dex could reflect a perceived level of concordance be-
tween individual and collective evaluations in FAST-
GDM problems. Hence in this section, we describe a
procedure to get evaluations from people with diffe-
rent opinions on how the attributes of the given opti-
ons should be evaluated. Then, we explain how this
procedure has been used to get evaluations from a he-
terogeneous group of participants who tried to reach
consensus about the best smooth dip(s) to pair with
banana chips. After that, we describe how the indivi-
dual and the collective evaluations given by the afore-
mentioned group of participants have been compared
by theoretical concordance indices and perceived le-
vels of concordance.
3.1 Getting Evaluations
To get evaluations from persons who express not only
the level to which but also the reasons why a potential
option is suitable (or unsuitable) for a problem, we
use a form like the one shown in Figure 1. Notice
that, through this kind of form, a person can indicate
how suitable and how unsuitable an option could be
along with (some of) the reasons that justify his/her
appraisal.
hardly
hardly
highly
highly
suitable...
... due to
... due to
unsuitable...
To which degree option 1 is suitable for problem XYZ?
feature 01
feature 04
feature 03
Figure 1: Form for evaluating an option.
The evaluations of the potential options filled out
by a person, say P, in such a form can easily be cha-
racterized as an AAIFS by means of the following
procedure:
Usability of Concordance Indices in FAST-GDM Problems
69

Consider a discrete collection X = {x
1
, ⋯, x
n
} of
potential options for the problem under study, and
consider that A ⊆ X represents a collection of suit-
able options for this problem. Then, consider that
the levels of suitability and unsuitability filled out
by P for any x
i
∈ X can be linked to two values in
a unit interval scale, say ˇµ
A@P
(x
i
) and
ˇ
ν
A@P
(x
i
) re-
spectively, where 1 denotes the highest value and 0
the lowest. Finally, consider that the features fil-
led out for any x
i
∈ X can be included in two col-
lections, say F
µ
A@P
(x
i
) and F
ν
A@P
(x
i
). With these
considerations, compute η = max(1, (ˇµ
A@P
(x
i
) +
ˇ
ν
A@P
(x
i
))), ∀x
i
∈ X . After that, obtain an AAIFS
element x
i
, ˆµ
A@P
(x
i
),
ˆ
ν
A@P
(x
i
) for each option x
i
∈
X such that ˆµ
A@P
(x
i
) = ˇµ
A@P
(x
i
)η, F
µ
A@P
(x
i
) and
ˆ
ν
A@P
(x
i
) =
ˇ
ν
A@P
(x
i
)η, F
ν
A@P
(x
i
).
Round
r
...
...
E
1
E
2
E
j
E
ˆ
A
@E
1
ˆ
A
@E
1
ˆ
A
@E
j
ˆ
A
@E
1
ˆ
A
@E
2
ˆ
A
@E
1
ˆ
A
X
x
n
x
3
x
2
x
1
evaluation
aggregation
Figure 2: Getting evaluations.
We followed the above procedure to obtain the
evaluations from 11 persons, 6 women and 5 men,
who tried to reach consensus about the best smooth
dip(s), among 3 potential dips, to pair with banana
chips. This CRP was modeled using the notation in-
troduced in Section 2 as follows: the collection of po-
tential dips was denoted by X = {x
1
, x
2
, x
3
}; the col-
lection of the best smooth dip to pair with banana
chips was denoted by A; the group of participants was
denoted by E = {E
1
, ⋯, E
11
}; the individual evaluati-
ons given any participant E
j
∈ E were represented by
an AAIFS
ˆ
A
@E
j
; and the collective evaluations com-
puted for the group were represented by an AAIFS
ˆ
A (see Figure 2). This means that 12 AAIFSs (1
AAIFS representing the collective evaluations and 11
AAIFSs representing the individual evaluations) were
obtained in each of the 2 rounds completed by these
11 persons. In the next part, we show how these eva-
luations have been compared to each other.
3.2 Contrasting Evaluations
To compare a collection of individual evaluations, say
ˆ
A
@E
j
, with the collection of collective evaluations,
say
ˆ
A, obtained during each round of the CRP, we use
theoretical concordance indices and perceived level of
concordance as explained below.
3.2.1 Theoretical Concordance Indices
Round
r
ˆ
A
@E
1
ˆ
A
@E
1
ˆ
A
@E
j
ˆ
A
@E
1
ˆ
A
@E
2
ˆ
A
@E
1
ˆ
A
quantication
of concordance (cix)
XVBr-0.5
SK1
SK2
SK3
SK4
cix ( , )
ˆ
A
@E
j
ˆ
A
XVBr-0.5
cix ( , )
ˆ
A
@E
j
ˆ
A
SK1
cix ( , )
ˆ
A
@E
j
ˆ
A
SK2
cix ( , )
ˆ
A
@E
j
ˆ
A
SK3
cix ( , )
ˆ
A
@E
j
ˆ
A
SK4
Figure 3: Quantification of theoretical concordance indices.
The concordance index between each
ˆ
A
@E
j
and
ˆ
A was computed by means of (4), where S was cho-
sen among five (configurations of) similarity mea-
sures designed to compare traditional IFSs, namely
XVBr-0.5 (Loor and De Tr
´
e, 2017b), SK1, SK2, SK3
and SK4 (Szmidt and Kacprzyk, 2004) (see Figure 3).
A flat operator, ê ⋅ ⊩, which turns an AAIFS into an
IFS by excluding the collections of features recorded
in each AAIFS element, was used for converting
ˆ
A
@E
j
and
ˆ
A into two IFSs, say J and A respectively, that are
used as input for any of the chosen similarity measu-
res. Regarding XVBr-0.5, it refers to a configuration
of
S
α
@A
(J, A) = ∆
@A
⋅S
α
(J, A), (5)
in which α has been set to 0.5. In this equation,
∆
@A
∈ [0, 1] is a factor that was computed through
the method spotRatios proposed in (Loor and De Tr
´
e,
2017b) and S
α
(J, A) is given by
S
α
(J, A) = 1 −
1
n
n
i=1
(µ
A
(x
i
)−µ
J
(x
i
)) (6)
+ α(h
A
(x
i
)−h
J
(x
i
))
.
With respect to SK1, SK2, SK3 and SK4, they refer to
following similarity measures:
S
SK1
(J, A) = 1 − f (l(J, A), l(J, A
c
)), (7)
S
SK2
(J, A) =
1 − f (l(J, A), l(J, A
c
))
1 + f (l(J, A), l(J, A
c
))
, (8)
S
SK3
(J, A) =
(1 − f (l(J, A), l(J, A
c
)))
2
(1 + f (l(J, A), l(J, A
c
)))
2
(9)
and
S
SK4
(J, A) =
e
− f (l(J,A),l(J,A
c
))
−e
−1
1 −e
−1
. (10)
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
70

Herein, A
c
is the complement of A, i.e.,
A
c
= {x
i
, ν
A
(x
i
), µ
A
(x
i
)(x
i
∈ X) (11)
∧(0 ≤ µ
A
(x
i
)+ν
A
(x
i
) ≤ 1)},
l(J, A) has been set as the Hamming distance between
J and A (Szmidt and Kacprzyk, 2004), i.e.,
l(J, A)=
1
2n
n
i=1
µ
A
(x
i
)−µ
J
(x
i
)+ (12)
+ν
A
(x
i
)−ν
J
(x
i
)+h
A
(x
i
)−h
J
(x
i
)
,
and
f (l(J, A), l(J, A
c
)) =
l(J, A)
l(J, A)+l(J, A
c
)
. (13)
The interest reader is referred to (Loor and De Tr
´
e,
2017c) for an open-source implementation of the
above-mentioned similarity measures.
To obtain the perceived levels of concordance bet-
ween each
ˆ
A
@E
j
and
ˆ
A, the AAIFSs were graphically
represented by means of IFS contrasting charts as ex-
plained in the next part.
3.2.2 Perceived Levels of Concordance
Aiming to facilitate the interpretation of the evaluati-
ons given by a person or computed for a group during
a CRP, we propose a novel visual representation of an
IFS, which is called IFS contrasting chart or IFSCC
for short.
The idea behind an IFSCC can be described
through the following analogy. Consider that the eva-
luation of an option, say x
i
, is a buoy floating on the
surface of the sea. The air column inside this buoy
corresponds to the level to which x
i
is a suitable op-
tion, i.e., the air column corresponds to µ
A
(x
i
). Like-
wise, the ballast in the buoy corresponds to the level
to which x
i
is an unsuitable option, i.e., the ballast
corresponds to ν
A
(x
i
). This means that the buoyancy
of the buoy, say ρ
A
(x
i
), results from the difference
between µ
A
(x
i
) and ν
A
(x
i
), i.e., the buoyancy corre-
sponds to ρ
A
(x
i
) = µ
A
(x
i
)−ν
A
(x
i
). While a positive
value of ρ
A
(x
i
) suggests that x
i
is a suitable option,
a negative value suggests that x
i
is an unsuitable op-
tion. The height of buoy is limited to the unit inter-
val [0, 1] because of the consistency condition, i.e.,
0 ≤ µ
A
(x
i
)+ν
A
(x
i
) ≤ 1, which is expressed in the de-
finition of an IFS. Figure 4 illustrates the evaluations
of two options, x
1
and x
2
, using this analogy.
We can use the above analogy to represent the ap-
praisal levels in an AAIFS, say
ˆ
A
@E
11
, which charac-
terizes the evaluations of the collection of potential
dips performed by person E
11
during the first round.
This representation is shown in Figure 5. Notice in
1
1
0
0
μ
A
ρ
A
x
1
(x )
1
ρ
A
(x )
2
x
2
ν
A
above sea level => suitable
below sea level => unsuitable
Figure 4: Idea behind an IFS contrasting chart.
this figure that the collection of potential dips is de-
noted by X = {x
1
, x
2
, x
3
}. Notice also that the ‘buoy’
related to dip x
1
has equal parts of ‘air’ and ‘bal-
lasts’, i.e., µ
A
(x
1
) = ν
A
(x
1
), and, thus, the buoyancy
of x
1
is 0. This suggests that x
1
has some ‘positive’
features but also some ‘negative’ features that make
E
11
to think that x
1
neither satisfies nor dissatisfies
the membership in the collection of the best smooth
dips to pair with banana chips. In a similar way,
notice that the ‘buoy’ related to dip x
2
has less ‘air’
than ‘ballasts’ and, thus, x
2
has a negative buoyancy
(ρ
A
(x
2
) = −0.48). This indicates that x
2
might not be
included by E
11
in the collection of the best smooth
dips. Finally, notice that the ‘buoy’ related to dip x
3
has more ‘air’ than ‘ballasts’ and, thus, x
3
has a posi-
tive buoyancy (ρ
A
(x
3
) = 0.39). This suggests that E
11
might include x
3
in the collection of the best smooth
dips.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.00
−0.48
0.39
Figure 5: Evaluations of the dips x
1
, x
2
and x
3
given by E
11
.
It is worth mentioning that, although the hesita-
tion margin, i.e., h
A
(x
i
) = 1 −(µ
A
(x
i
)+ν
A
(x
i
)) (Ata-
nassov, 1986; Atanassov, 2012), is not explicitly de-
picted in an IFSCC, it can be inferred. For instance,
Figure 6 depicts the evaluations given by E
10
. Notice
that µ
A
(x
1
) and ν
A
(x
1
) are equal to 0. This suggests
that the evaluation of dip x
1
has been missed or that
E
10
did not try dip x
1
during the first round. Hence,
considering x
1
as a member (or not) of the collection
of the best dips is marked by a high hesitation in this
case.
Notice in Figure 5 and Figure 6 that an IFSCC
shows a holistic view of the evaluations given by a
participant in a CRP. Thus, to obtain the perceived
level of concordance between the individual and col-
lective evaluations in the CRP about the best smooth
Usability of Concordance Indices in FAST-GDM Problems
71

1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.00
0.10
0.83
Figure 6: Evaluations of the dips x
1
, x
2
and x
3
given by E
10
.
dips, we built the IFSCCs of the 24 AAIFSs (22 re-
presenting individual evaluations and 2 representing
collective evaluations) obtained after the 2 rounds of
this CRP.
We made use of those IFSCCs, which are depicted
in Figures 12 and 13 (see Appendix), to make 22 pairs
of IFSCCs in such a way that the individual evaluati-
ons given by each participant could be compared with
the computed collective evaluations in each round –
i.e., 11 pairs of IFSCCs corresponding to pairs of
AAIFSs
ˆ
A
@E
j
,
ˆ
A, j = 1, ⋯, 11, were built for each
round.
Round
r
... ...
P
1
P
2
P
k
P
.
ˆ
A
ˆ
A
@ E
j
ˆ
A
@E
1
ˆ
A
@E
1
ˆ
A
@E
1
ˆ
A
@E
j
ˆ
A
@E
1
ˆ
A
quantication
of perceived concordance (PLoC)
PLoC( , )
ˆ
A
@E
j
ˆ
A
P
1
PLoC( , )
ˆ
A
@E
j
ˆ
A
P
1
PLoC( , )
ˆ
A
@E
j
ˆ
A
P
1
PLoC( , )
ˆ
A
@E
j
ˆ
A
P
1
PLoC( , )
ˆ
A
@E
j
ˆ
A
P
k
Figure 7: Quantification of perceived levels of concordance.
Using those 22 pairs of IFSCCs, we asked a group
of 13 persons having managerial roles to quantify the
level of concordance that each of them perceives bet-
ween each pair of IFSCCs (see Figure 7). To indicate
so, the use of a unit interval scale where 1 and 0 repre-
sent the highest and the lowest level of concordance
respectively was recommended.
3.2.3 Theoretical vs. Perceived Concordance
To compare the perceived levels of concordance gi-
ven by the group of 13 people with the theoretical
concordance indices computed by the similarity me-
asures mentioned in Section 3.1, we followed two
approaches: a macro approach in which the average
of the perceived levels of concordance is contrasted
with each concordance index; and a micro approach
in which each perceived level of concordance is con-
trasted with each concordance index. These compa-
risons are as follows. Consider that P = {P
1
, ⋯, P
13
}
represents the group of the 13 persons. Consider also
that PLoC
P
k
(
ˆ
A
@E
j
,
ˆ
A) represents the level of concor-
dance between
ˆ
A
@E
j
and
ˆ
A perceived by any P
k
∈ P.
With these considerations, in the macro comparison
we first compute the average of the perceived levels
for each pair
ˆ
A
@E
j
,
ˆ
A by means of
PLoC(
ˆ
A
@E
j
,
ˆ
A) =
1
P
P
k
∈P
(PLoC
P
k
(
ˆ
A
@E
j
,
ˆ
A)), (14)
where P denotes the number of persons having ma-
nagerial roles. Then, we compute the absolute error
between the average of the perceived level of con-
cordance and a given concordance index, say cix, for
each pair
ˆ
A
@E
j
,
ˆ
A by means of
∆
cix
(
ˆ
A
@E
j
,
ˆ
A) = PLoC(
ˆ
A
@E
j
,
ˆ
A)−cix(
ˆ
A
@E
j
,
ˆ
A),
(15)
where ⋅ denotes the absolute value. After that, we
compute a macro mean absolute error by means of
∆
cix
=
1
E
E
j
∈E
∆
cix
(
ˆ
A
@E
j
,
ˆ
A), (16)
where E represents the number of participants in E.
In this case, a value of ∆
cix
close to 0 means that cix
reflects well the perceived level of concordance.
Regarding the micro comparison, we compute for
a given person in P, say P
k
, the absolute error bet-
ween the perceived level of concordance and a given
concordance index, say cix, for each pair
ˆ
A
@E
j
,
ˆ
A
by means of
δ
cix,P
k
(
ˆ
A
@E
j
,
ˆ
A)= PLoC
P
k
(
ˆ
A
@E
j
,
ˆ
A)−cix(
ˆ
A
@E
j
,
ˆ
A).
(17)
Then, we aggregate all these absolute errors through
a micro mean absolute error computed by
δ
cix
=
1
E×P
E
j
∈E,P
k
∈P
δ
cix,P
k
(
ˆ
A
@E
j
,
ˆ
A). (18)
A value of δ
cix
close to 0, as analogous to ∆
cix
, means
that cix reflects well the perceived level of concor-
dance.
The results obtained after performing the afore-
mentioned comparisons are shown in the next section.
4 RESULTS AND DISCUSSION
In this section, we present the results and our findings
on how well each of the chosen theoretical concor-
dance indices reflected the perceived levels of con-
cordance.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
72

Table 1: Theoretical Concordance Indices and Average of
Perceived Levels of Concordance (Round 1).
Pair XVBr-0.5 SK1 SK2 SK3 SK4 PLoC
ˆ
A
@E
1
,
ˆ
A 0.75 0.58 0.41 0.17 0.46 0.54
ˆ
A
@E
2
,
ˆ
A 0.19 0.48 0.32 0.10 0.36 0.20
ˆ
A
@E
3
,
ˆ
A 0.59 0.41 0.26 0.07 0.29 0.50
ˆ
A
@E
4
,
ˆ
A 0.00 0.42 0.27 0.07 0.30 0.29
ˆ
A
@E
5
,
ˆ
A 0.76 0.59 0.42 0.18 0.47 0.53
ˆ
A
@E
6
,
ˆ
A 0.45 0.55 0.38 0.14 0.43 0.62
ˆ
A
@E
7
,
ˆ
A 0.88 0.55 0.38 0.14 0.42 0.59
ˆ
A
@E
8
,
ˆ
A 0.50 0.53 0.36 0.13 0.41 0.32
ˆ
A
@E
9
,
ˆ
A 0.25 0.47 0.31 0.10 0.35 0.35
ˆ
A
@E
10
,
ˆ
A 0.74 0.54 0.37 0.14 0.42 0.63
ˆ
A
@E
11
,
ˆ
A 0.43 0.52 0.35 0.12 0.40 0.60
Table 2: Theoretical Concordance Indices and Average of
Perceived Levels of Concordance (Round 2).
Pair XVBr-0.5 SK1 SK2 SK3 SK4 PLoC
ˆ
A
@E
1
,
ˆ
A 0.43 0.49 0.33 0.11 0.37 0.43
ˆ
A
@E
2
,
ˆ
A 0.40 0.52 0.35 0.13 0.40 0.18
ˆ
A
@E
3
,
ˆ
A 0.00 0.34 0.21 0.04 0.24 0.15
ˆ
A
@E
4
,
ˆ
A 0.20 0.50 0.34 0.11 0.38 0.14
ˆ
A
@E
5
,
ˆ
A 0.68 0.61 0.43 0.19 0.48 0.43
ˆ
A
@E
6
,
ˆ
A 0.55 0.65 0.48 0.23 0.53 0.68
ˆ
A
@E
7
,
ˆ
A 0.54 0.66 0.49 0.24 0.54 0.76
ˆ
A
@E
8
,
ˆ
A 0.53 0.45 0.29 0.08 0.33 0.36
ˆ
A
@E
9
,
ˆ
A 0.50 0.61 0.44 0.19 0.49 0.46
ˆ
A
@E
10
,
ˆ
A 0.53 0.49 0.33 0.11 0.37 0.52
ˆ
A
@E
11
,
ˆ
A 0.56 0.65 0.48 0.23 0.53 0.50
4.1 Results
The computed theoretical concordance indices, iden-
tified by XVBr-0.5, SK1, SK2, SK3 and SK4, along
with the macro average of the perceived levels of con-
cordance, which is denoted by PLoC and computed
by (14), are shown in Table 1 and Table 2: while the
data in the former table correspond to the 11 pairs of
IFSCCs obtained during the first round (see Figure 12
in Appendix), the data in the latter table correspond
to the 11 pairs of IFSCCs obtained during the second
round (see Figure 13 in Appendix).
We make use of the data in the aforementioned ta-
bles as inputs of (15) to compute ∆
cix
(
ˆ
A
@E
j
,
ˆ
A) for
each of the theoretical concordance indices. The re-
sults are depicted as bars in Figure 8 (Round 1) and
Figure 9 (Round 2). For instance, in Figure 8(a)
the lowest and the highest absolute errors between
XVBr-0.5 and PLoC are related to the pairs
ˆ
A
E
2
,
ˆ
A
and
ˆ
A
E
4
,
ˆ
A, which result from ∆
XVBr-0.5
(
ˆ
A
@E
2
,
ˆ
A) =
0.19 − 0.20 = 0.01 and ∆
XVBr-0.5
(
ˆ
A
@E
4
,
ˆ
A) = 0 −
0.29 = 0.29 respectively.
For the sake of a better macro comparison, a fre-
quency distribution of the absolute errors correspon-
ding to the two rounds are depicted in Figure 10.
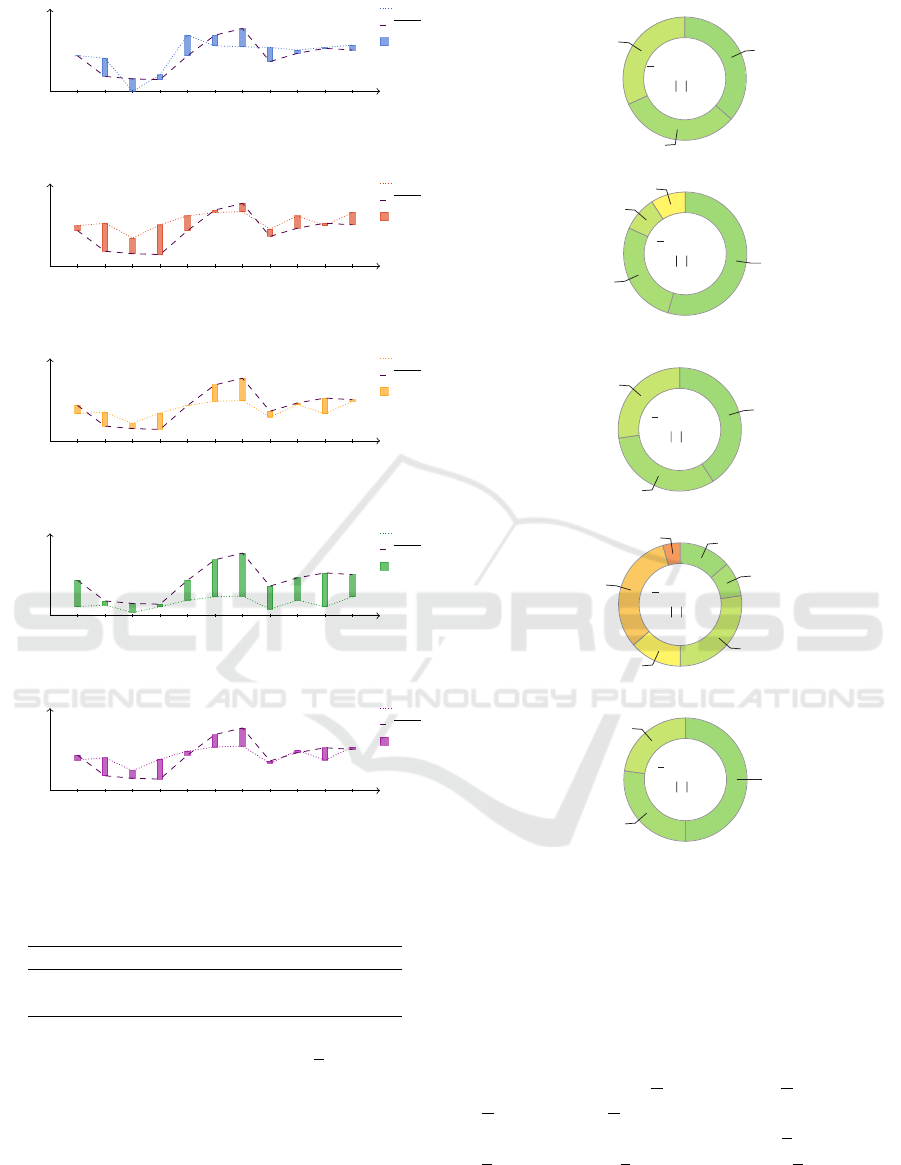
As an example of the frequency distribution, in Fi-
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
XVBr-0.5
PLoC
Abs.Err.
(a) XVBr-0.5.
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
SK1
PLoC
Abs.Err.
(b) SK1.
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
SK2
PLoC
Abs.Err.
(c) SK2.
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
SK3
PLoC
Abs.Err.
(d) SK3.
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
SK4
PLoC
Abs.Err.
(e) SK4.
Figure 8: Absolute Errors (Round 1).
gure 10(b) it is shown that, while 12 out of 22 (i.e.,
54.54%) of the computed absolute errors between
SK1 and PLoC are placed in the interval [0, 0.1],
6 out of 22 (i.e., 27.27%) are located in the inter-
val (0.1, 0.2]. The values computed by (16) are also
shown in Figure 10. For instance, the macro mean ab-
solute error between SK1 and PLoC, i.e., ∆
SK1
= 0.13,
is indicated in the center of Figure 10(b).
Regarding the comparisons using a micro appro-
ach, a frequency distribution of the results compu-
ted by (17) and (18) are depicted in Figure 11. In
Figure 11(c), e.g., it is shown that, while 68 out of
286 (i.e., 23.77%) of the computed absolute errors
between SK1 and PLoC are located in the interval
[0, 0.1], 74 out of 286 (i.e., 25.87%) are placed in the
Usability of Concordance Indices in FAST-GDM Problems
73
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
XVBr-0.5
PLoC
Abs.Err.
(a) XVBr-0.5.
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
SK1
PLoC
Abs.Err.
(b) SK1.
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
SK2
PLoC
Abs.Err.
(c) SK2.
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
SK3
PLoC
Abs.Err.
(d) SK3.
Concordance Level
0
1
⟨
ˆ
A
E
1
,
ˆ
A⟩
⟨
ˆ
A
E
2
,
ˆ
A⟩
⟨
ˆ
A
E
3
,
ˆ
A⟩
⟨
ˆ
A
E
4
,
ˆ
A⟩
⟨
ˆ
A
E
5
,
ˆ
A⟩
⟨
ˆ
A
E
6
,
ˆ
A⟩
⟨
ˆ
A
E
7
,
ˆ
A⟩
⟨
ˆ
A
E
8
,
ˆ
A⟩
⟨
ˆ
A
E
9
,
ˆ
A⟩
⟨
ˆ
A
E
10
,
ˆ
A⟩
⟨
ˆ
A
E
11
,
ˆ
A⟩
SK4
PLoC
Abs.Err.
(e) SK4.
Figure 9: Absolute Errors (Round 2).
Table 3: Macro and micro mean absolute errors.
XVBr-0.5 SK1 SK2 SK3 SK4
¯
∆
cix
0.14 0.13 0.13 0.31 0.12
¯
δ
cix
0.21 0.21 0.22 0.33 0.21
interval (0.1, 0.2]. In this case, the micro mean abso-
lute error between SK2 and PLoC, i.e., δ
SK2
= 0.22, is
indicated in the center of Figure 11(c). The results are
summarized in Table 3.
4.2 Discussion
The results listed in Table 3 suggest that the con-
cordance indices (based on the similarity measures)
∆
XVBr-0.5
= 0.14
2 ×
E = 22
“[0, 0.1]”: 8 (36.36%)
“(0.1, 0.2]”: 7 (31.82%)
“(0.2, 0.3] ”: 7 (31.82%)
(a) XVBr-0.5.
∆
SK1
= 0.13
2 ×
E = 22
“[0, 0.1]”: 12 (54.54%)
“(0.1, 0.2]”: 6 (27.27%)
“(0.2, 0.3]”: 2 (9.09%)
“(0.3, 0.4]”: 2 (9.09%)
(b) SK1.
∆
SK2
= 0.13
2 ×
E = 22
“[0, 0.1]”: 9 (40.91%)
“(0.1, 0.2]”: 7 (31.82%)
“(0.2, 0.3] ”: 6 (27.27%)
(c) SK2.
∆
SK3
= 0.31
2 ×
E = 22
“[0, 0.1]”: 3 (13.64%)
“(0.1, 0.2]”: 2 (9.09%)
“(0.2, 0.3]”: 6 (27.27%)
“(0.3, 0.4]”: 3 (13.64%)
“(0.4, 0.5]”: 7 (31.82%)
“(0.5, 0.6] ”: 1 (4.54%)
(d) SK3.
∆
SK4
= 0.12
2 ×
E = 22
“[0, 0.1]”: 11 (50%)
“(0.1, 0.2]”: 6 (27.27%)
“(0.2, 0.3]”: 5 (22.73%)
(e) SK4.
Figure 10: Distribution of Abs. Errors (Macro compari-
sons).
XVBr-0.5, SK1, SK2 and SK4 reflect to an acceptable
extent the perceived level of concordance between the
individual and the collective evaluations.
As far as one can see, SK4 slightly outperforms
XVBr-0.5, SK1 and SK2 according to both the ma-
cro and the micro mean absolute errors. Notice that,
while the expression (∆
SK4
= 0.12) < (∆
SK1
= 0.13) ≤
(∆
SK2
=0.13) <(∆
XVBr-0.5
=0.14) holds for the macro
mean absolute errors, the expression (δ
SK4
= 0.21) ≤
(δ
SK1
= 0.21) ≤ (δ
XVBr-0.5
= 0.21) < (δ
SK2
= 0.22)
holds for the micro mean absolute errors. However,
such a slightly advantage of SK4 can disappear if so-
meone focuses only on the frequency of the abso-
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
74

δ
XVBr-0.5
= 0.21
2 ×
E P = 286
“[0, 0.1]”: 97 (33.92%)
“(0.1, 0.2]”: 62 (21.68%)
“(0.2, 0.3]”: 54 (18.88%)
“(0.3, 0.4]”: 42 (14.69%)
“(0.4, 0.5]”: 15 (5
.
24%)
“(0.5, 0.6]”: 10 (3
.5%)
“(0.6, 0.7]”: 5 (1
.
75%)
“(0.7, 0.8]”: 1 (0
.
35%)
(a) XVBr-0.5.
δ
SK1
= 0.21
2 ×
E P = 286
“[0, 0.1]”: 76 (26.57%)
“(0.1, 0.2]”: 65 (22.73%)
“(0.2, 0.3]”: 57 (19.93%)
“(0.3, 0.4]”: 56 (19.58%)
“(0.4, 0.5]”: 25 (8
.
74%)
“(0.5, 0.6]”: 7 (2.45%)
(b) SK1.
δ
SK2
= 0.22
2 ×
E P = 286
“[0, 0.1]”: 68 (23.77%)
“(0.1, 0.2]”: 74 (25.87%)
“(0.2, 0.3]”: 70 (24.48%)
“(0.3, 0.4]”: 40 (13.98%)
“(0.4, 0.5]”: 19 (6
.
64%)
“(0.5, 0.6]”: 12 (4.19%)
“(0.6, 0.7]”: 3 (1
.
05%)
(c) SK2.
δ
SK3
= 0.33
2 ×
E P = 286
“[0, 0.1]”: 64 (22.38%)
“(0.1, 0.2]”: 41 (14.34%)
“(0.2, 0.3]”: 31 (10.84%)
“(0.3, 0.4]”: 31 (10.84%)
“(0.4, 0.5]”: 42 (14.69%)
“(0.5, 0.6]”: 34 (11.89%)
“(0.6, 0.7]”: 24 (8.39%)
“(0.7, 0.8]”: 11 (3.85%)
“(0.8, 0.9]”: 8 (2
.
.8%)
(d) SK3.
δ
SK4
= 0.21
2 ×
E P = 286
“[0, 0.1]”: 66 (23.08%)
“(0.1, 0.2]”: 71 (24.82%)
“(0.2, 0.3]”: 80 (27.97%)
“(0.3, 0.4]”: 41 (14.34%)
“(0.4, 0.5]”: 19 (6.64%)
“(0.5, 0.6]”: 8 (2 .8%)
“(0.6, 0.7]”: 1 (0
.
35%)
(e) SK4.
Figure 11: Distribution of Abs. Errors (Micro Compari-
sons).
lute errors between the concordance indices and the
average of perceived levels of concordance located in
the interval [0, 0.1] (i.e., ∆
cix
∈ [0, 0.1]) – notice in Fi-
gure 10 that the frequency of ∆
SK1
∈[0, 0.1], i.e., 12, is
slightly greater than the frequency of ∆
SK4
∈ [0, 0.1],
i.e., 11. That advantage can also disappear when so-
meone only takes into account the frequency of the
absolute errors between the concordance indices and
the perceived levels of concordance located in the in-
terval [0, 0.1] (i.e., δ
cix
∈[0, 0.1]) – notice in Figure 11
that the frequency of δ
XVBr-0.5
∈ [0, 0.1], i.e., 97, is
greater than the frequency of δ
SK4
∈ [0, 0.1], i.e., 66.
Hence, we can say that, although SK4 has a slightly
advantage, in this pilot study the concordance indi-
ces based on the similarity measures XVBr-0.5, SK1,
SK2 and SK4 are comparatively alike when reflecting
the perceived levels of concordance between the in-
dividual and the collective evaluations. A practical
implication of these results is that these concordance
indices can be accepted as good indicators of the level
of concordance in FAST-GDM problems.
Regarding the concordance index based on the si-
milarity measure SK3, the computed macro and mi-
cro mean absolute errors suggest that this index might
not reflect well the perceived level of concordance.
Notice in Figure 10(d) and Figure 11(d) that roughly
50% of the computed absolute errors are located in
the interval (0.30, 1].
It is worth mentioning that, although in the first
round the individual evaluations characterized by
ˆ
A
@E
4
(see Figure 12(e)) and the collective evaluations
characterized by
ˆ
A (see Figure 12(a)) can lead to po-
tential opposite decisions about the options x
1
, x
2
and
x
3
, the average of the perceived level of concordance
related to the pair
ˆ
A
@E
4
,
ˆ
A, i.e., PLoC(
ˆ
A
@E
4
,
ˆ
A) =
0.29, is appreciably greater than the expected theo-
retical value for this case, i.e., 0 (Loor and De Tr
´
e,
2017b). A potential explanation for this result might
be that a more clear indication of the potential deci-
sion that can be taken after studying the evaluations
represented in an IFSCC is needed. In this regard,
conducting a follow-up study in which the perceived
levels of concordance would be obtained by compa-
ring IFSCCs that have been augmented with additio-
nal information (e.g., an explicit ranking of the opti-
ons, or a linguistic summary about a potential deci-
sion (Kacprzyk and Zadro
˙
zny, 2005)) is suggested.
Another suggested study concerns the use of sca-
les of measurement formed from linguistic labels such
as ‘highly concordant’ or ‘hardly concordant’ to map
or express the results of the concordance indices, as
well as the perceived levels of concordance (Her-
rera et al., 1996; Herrera et al., 1997). Since the
macro averages computed for the concordance indi-
ces XVBr-0.5, SK1, SK2 and SK4 are roughly 0.12,
we foresee that a scale consisting of 5 linguistic la-
bels, for instance ‘hardly concordant’, ‘not specially
concordant’,‘slightly concordant’,‘fairly concordant’
and ‘highly concordant’, can further improve the level
to which those concordance indices reflect the percei-
Usability of Concordance Indices in FAST-GDM Problems
75

ved levels of concordance.
5 RELATED WORK
Methods that obtain the level of concordance (or
agreement) between the evaluations given by two in-
dividuals by means of a similarity (or distance) me-
asure defined in the IFS framework can be found in
the literature. For instance, in (Szmidt and Kacprzyk,
2002; Szmidt and Kacprzyk, 2003; Szmidt and Ka-
cprzyk, 2004) Szmidt and Kacprzyk proposed the use
of either similarity or distance measures between two
IFSs to compute the level of agreement between two
participants whose evaluations have been characteri-
zed as IFSs. However, to the best of our knowledge,
no empirical study oriented to determine how well the
results computed by such similarity measures reflect
the perceived levels of concordance in a consensus re-
aching process has been published so far.
Regarding the visual representations of IFSs, se-
veral geometrical interpretations of IFSs are availa-
ble in the literature. The standard interpretation, in
which the membership and the nonmembership com-
ponents, i.e., µ
A
(x) and ν
A
(x), are depicted in a com-
mon region (or band) of height 1, is the most accep-
ted visual representation of IFSs according to Atanas-
sov (Atanassov, 2012). A variant of the standard in-
terpretation is one in which is depicted (1 − ν
A
(x))
instead of ν
A
(x). This variant leads to a represen-
tation where each element in an IFS is depicted a
unit segment. Another representation, called IFS-
interpretational triangle, is based on a right triangle
having two sides of length 1: one for µ
A
(x) and the
other for ν
A
(x) (Atanassov, 1986; Atanassov, 2012).
While an advantage of the IFS-interpretational tri-
angle is that an operation over an IFS element can, in
general, be easily visualized, a disadvantage of this
representation is that a holistic view of all the IFS
elements can be unclear. As a variant of the IFS-
interpretational triangle, the idea of a ‘unit cube’ to
additionally represent the hesitation margin has been
introduced in (Szmidt and Kacprzyk, 2004). Using
a different approach, the representation of an IFS by
means of radar charts has been proposed in (Atanas-
sova, 2010). Since radar charts are typically used in
a business-oriented environment, an IFS radar chart
can be considered as a business-oriented representa-
tion of an IFS. However, the representation of the two
components in the same circle (or band) can be con-
fusing when the representation of the buoyancy of the
elements of an IFS is needed. Because of this, we
propose a novel business-oriented representation of
an IFS by means of an IFSCC. As could be noticed
throughout this paper, two bands, one for µ
A
(x) and
the other for ν
A
(x), are used within an IFSCC to de-
pict in a holistic way the buoyancy of each element in
an IFS.
6 CONCLUSIONS
In this paper, we have described a pilot study in which
several theoretical concordance indices based on si-
milarity measures designed to compare intuitionis-
tic fuzzy sets (IFSs) have been tested to determine
their usability in flexible attribute-set group decision-
making (FAST-GDM) problems.
During the study, the evaluations obtained from
a group of participants who tried to find a solution
for a FAST-GDM problem were characterized as aug-
mented Atanassov intuitionistic fuzzy sets (AAIFSs).
Then, each of those AAIFSs was graphically repre-
sented by means of a novel business-oriented repre-
sentation called IFS contrasting chart (IFSCC). After
that, a group of persons having managerial roles were
asked to estimate the level of concordance between
the individual and the collective evaluations depicted
respectively in two IFSCCs. The perceived levels of
concordance given by this group were then compared
to the values computed by the theoretical concordance
indices.
The results of this pilot study suggest that, among
the five theoretical concordance indices chosen for the
test, four reflected to an acceptable extent the percei-
ved level of concordance between the individual and
the collective evaluations. However, a more exten-
ded study should corroborate the usability of these
concordance indices in practical situations involving
FAST-GDM problems.
It was found a case in which the perceived level
of concordance between the individual and collective
evaluations is not the lowest even though such evalua-
tions lead to complete opposite decisions. A possible
explanation for this case might be that a more clear
indication of the potential decisions is needed in the
two IFSCCs representing such evaluations. Hence,
a follow-up study in which additional information
about a potential decision is incorporated into an IF-
SCC is suggested. Another suggested study concerns
the usability of scales of measurement formed from
linguistic labels to quantify both theoretical and per-
ceived concordance levels.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
76

REFERENCES
Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy sets
and Systems, 20(1):87–96.
Atanassov, K. T. (2012). On Intuitionistic Fuzzy Sets The-
ory, volume 283 of Studies in Fuzziness and Soft Com-
puting. Springer Berlin Heidelberg, Berlin, Heidel-
berg.
Atanassova, V. (2010). Representation of fuzzy and intuiti-
onistic fuzzy data by radar charts. Notes on Intuitio-
nistic Fuzzy Sets, 16(1):21–26.
Bouyssou, D., Dubois, D., Prade, H., and Pirlot, M. (2013).
Decision Making Process: Concepts and Methods.
John Wiley & Sons.
Dong, Y., Xiao, J., Zhang, H., and Wang, T. (2016). Ma-
naging consensus and weights in iterative multiple-
attribute group decision making. Applied Soft Com-
puting, 48:80 – 90.
Herrera, F., Herrera-Viedma, E., and Verdegay, J. L. (1996).
A model of consensus in group decision making un-
der linguistic assessments. Fuzzy Sets and Systems,
78(1):73 – 87.
Herrera, F., Herrera-Viedma, E., and Verdegay, J. L. (1997).
A rational consensus model in group decision making
using linguistic assessments. Fuzzy Sets and Systems,
88(1):31 – 49.
Kacprzyk, J. and Fedrizzi, M. (1988). A ‘soft’ measure of
consensus in the setting of partial (fuzzy) preferences.
European Journal of Operational Research, 34(3):316
– 325.
Kacprzyk, J. and Zadro
˙
zny, S. (2005). Linguistic database
summaries and their protoforms: towards natural lan-
guage based knowledge discovery tools. Information
Sciences, 173(4):281 – 304. Dealing with Uncertainty
in Data Mining and Information Extraction.
Kacprzyk, J. and Zadro
˙
zny, S. (2010). Soft computing and
web intelligence for supporting consensus reaching.
Soft Computing, 14(8):833–846.
Liu, Y., Fan, Z.-P., and Zhang, X. (2016). A method
for large group decision-making based on evaluation
information provided by participators from multiple
groups. Information Fusion, 29:132–141.
Loor, M. and De Tr
´
e, G. (2017a). On the Need for Augmen-
ted Appraisal Degrees to Handle Experience-Based
Evaluations. Applied Soft Computing, 54C:284 – 295.
Loor, M. and De Tr
´
e, G. (2017b). In a Quest for Suitable
Similarity Measures to Compare Experience-Based
Evaluations. In Merelo, J. J., Rosa, A., Cadenas, J. M.,
Correia, A. D., Madani, K., Ruano, A., and Filipe,
J., editors, Computational Intelligence: International
Joint Conference, IJCCI 2015 Lisbon, Portugal, No-
vember 12-14, 2015, Revised Selected Papers, volume
669 of Studies in Computational Intelligence, pages
291–314. Springer International Publishing.
Loor, M. and De Tr
´
e, G. (2017c). An open-source software
package to assess similarity measures that compare
intuitionistic fuzzy sets. In 2017 IEEE International
Conference on Fuzzy Systems (FUZZ-IEEE), pages 1–
6.
Loor, M., Tapia-Rosero, A., and De Tr
´
e, G. (2018). Refo-
cusing attention on unobserved attributes to reach con-
sensus in decision making problems involving a hete-
rogeneous group of experts. In Kacprzyk, J., Szmidt,
E., Zadro
˙
zny, S., Atanassov, K. T., and Krawczak,
M., editors, Advances in Fuzzy Logic and Technology
2017, pages 405–416, Springer International Publis-
hing.
Szmidt, E. and Kacprzyk, J. (2002). Evaluation of
agreement in a group of experts via distances bet-
ween intuitionistic fuzzy preferences. In Proceedings
First International IEEE Symposium Intelligent Sys-
tems, volume 1, pages 166–170 vol.1.
Szmidt, E. and Kacprzyk, J. (2003). A consensus rea-
ching process under intuitionistic fuzzy preference re-
lations. International Journal of Intelligent Systems,
18(7):837–852.
Szmidt, E. and Kacprzyk, J. (2004). A concept of simila-
rity for intuitionistic fuzzy sets and its use in group
decision making. In IEEE International Conference
on Fuzzy Systems, pages 1129–1134.
APPENDIX
Evaluations about the ‘best smooth dip’
This appendix presents the evaluations given by 11
persons who tried to reach a consensus about the best
smooth dip(s), among 3 potential dips, to pair with
banana chips. These evaluations have been graphi-
cally represented by means of IFS contrasting charts
(IFSCCs) (see Section 3.2).
Figure 12 shows the IFSCCs corresponding to the
evaluations given or computed during the first round
of the consensus reaching process: while Figure 12(a)
represents the collective evaluations computed for the
group, Figures 12(b)-12(l) represent the individual
evaluations given by these 11 persons respectively.
In a similar way, Figure 13 shows the IFSCCs corre-
sponding to the evaluations given or computed during
the second round.
Usability of Concordance Indices in FAST-GDM Problems
77
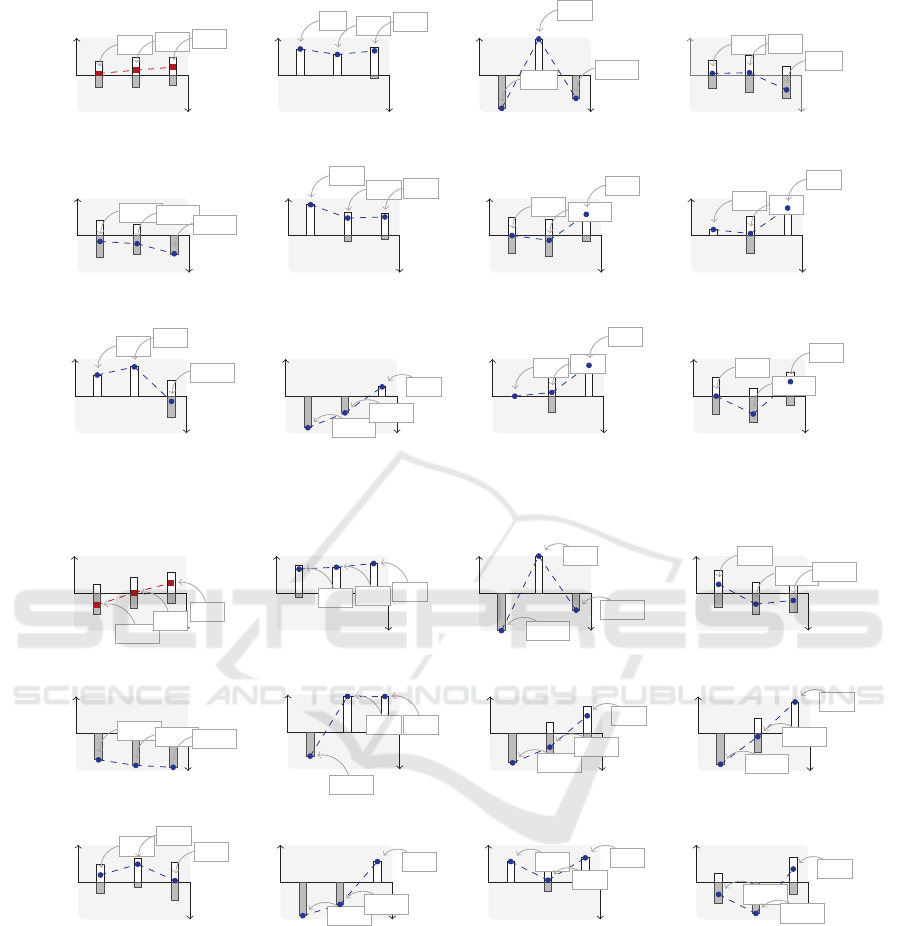
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.04
0.13
0.21
(a)
ˆ
A.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.7
0.55
0.65
(b)
ˆ
A
@E
1
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.9
0.97
−0.63
(c)
ˆ
A
@E
2
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.04
0.06
−0.4
(d)
ˆ
A
@E
3
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.16
−0.22
−0.49
(e)
ˆ
A
@E
4
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.83
0.47
0.50
(f)
ˆ
A
@E
5
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.00
−0.13
0.57
(g)
ˆ
A
@E
6
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.16
0.05
0.74
(h)
ˆ
A
@E
7
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.57
0.79
−0.14
(i)
ˆ
A
@E
8
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.85
−0.45
0.25
(j)
ˆ
A
@E
9
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.00
0.10
0.83
(k)
ˆ
A
@E
10
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.00
−0.48
0.39
(l)
ˆ
A
@E
11
.
Figure 12: Evaluations obtained during Round 1.
Figure 12: Evaluations obtained during Round 1.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.32
0.02
0.28
(a)
ˆ
A.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.65
0.70
0.80
(b)
ˆ
A
@E
1
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−1.00
1.00
−0.45
(c)
ˆ
A
@E
2
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.24
−0.29
−0.19
(d)
ˆ
A
@E
3
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.70
−0.85
−0.90
(e)
ˆ
A
@E
4
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.65
0.95 0.95
(f)
ˆ
A
@E
5
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.78
−0.36
0.48
(g)
ˆ
A
@E
6
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.82
−0.08
0.85
(h)
ˆ
A
@E
7
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.19
0.48
0.04
(i)
ˆ
A
@E
8
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.90
−0.60
0.55
(j)
ˆ
A
@E
9
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
0.55
0.05
0.65
(k)
ˆ
A
@E
10
.
1
1
0 0
µ
A
ν
A
x
1
x
2
x
3
−0.33
−0.84
0.35
(l)
ˆ
A
@E
11
.
Figure 13: Evaluations obtained during Round 2.
Figure 13: Evaluations obtained during Round 2.
IJCCI 2018 - 10th International Joint Conference on Computational Intelligence
78
