
New Value Metrics using Unsupervised Machine Learning, Lexical Link
Analysis and Game Theory for Discovering Innovation from Big Data
and Crowd-sourcing
Ying Zhao
1
, Charles Zhou
2
and Jennie K. Bellonio
1
1
Naval Postgraduate School, Monterey, CA, U.S.A.
2
Quantum Intelligence, Inc., Cupertino, CA, U.S.A.
Keywords:
Lexical Link Analysis, Crowd-Sourcing, Game Theory, Big Data, Unsupervised Learning, Nash Equilibrium,
Social Welfare, Pareto Superior, Pareto Efficient
Abstract:
We demonstrated a machine learning and artificial intelligence method, i.e., lexical link analysis (LLA) to
discover innovative ideas from big data. LLA is an unsupervised machine learning paradigm that does not
require manually labeled training data. New value metrics are defined based on LLA and game theory. In this
paper, we show the value metrics generated from LLA in a use case of an internet game and crowd-sourcing.
We show the results from LLA are validated and correlated with the ground truth. The LLA value metrics can
be used to select high-value information for a wide range of applications.
1 INTRODUCTION
Traditionally in social networks, the importance of
a network node as one form of high-value informa-
tion, for example, the leadership role in a social net-
work (CASOS, 2009)(Girvan and Newman, 2002) is
measured according to centrality measures (Freeman,
1979). Among various centrality measures, sorting
and ranking information based on authority is com-
pared with page ranking of a typical search engine.
Current automated methods such as graph-based ran-
king used in PageRank (Brin and Page, 1998), re-
quire established hyperlinks, citation networks, social
networks (e.g., Facebook), or other forms of crowd-
sourced collective intelligence. Similar to the Page-
Rank algorithm, HITS (Kleinberg, 1999), TextRank
(Mihakcea and Tarau, 2004) and LexRank (Erkan and
Radev, 2004) have been used for keyword extraction
and document summarization. The authority of each
node is determined by computing an authority score
that equals the number of times cited by the other no-
des.
However, these methods are not applicable to si-
tuations where there exist no pre-established relati-
onships among network nodes. For example, there
are few hyperlinks available in DoD data or public
data that cross-reference data are not reliable or can
be manipulated. This makes the traditional centrality
measures or PageRank-like methods difficult to apply.
Furthermore, current methods mainly score popular
information and do not rank emerging and anomalous
information that are important for some applications.
An example is that crowd-sourcing and distribu-
ted collaboration are becoming increasingly impor-
tant in driving production and innovation in a net-
worked world. It is important to identify innovative
ideas using content from crowd-sourcing. Since the
content is freshly generated, cross-referencing is rare,
therefore, traditional methods to rank important infor-
mation are not applicable in the situation.
In this paper, the goal is to show a set of novel me-
trics from the lexical link analysis (LLA)(Zhao et al.,
2015a)(Zhao et al., 2015b) to discover and rank high-
value information directly from content data. The
contribution of present work is that the LLA is a uni-
fied methodology of discovering high-value informa-
tion from structured and unstructured heterogeneous
data sources illustrated in a crowd-sourcing context
and big data use case. The definition of high-value
information can vary depending on the applications;
however, we can apply the LLA to categorize any in-
formation into popular or authoritative, emerging and
anomalous ones. Such categorization can greatly fa-
cilitate the discovery of high-value information based
on an application’s requirement.
Zhao, Y., Zhou, C. and Bellonio, J.
New Value Metrics using Unsupervised Machine Learning, Lexical Link Analysis and Game Theory for Discovering Innovation from Big Data and Crowd-sourcing.
DOI: 10.5220/0006959403270334
In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 2: KEOD, pages 327-334
ISBN: 978-989-758-330-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
327

2 LEXICAL LINK ANALYSIS
(LLA)
In a LLA, a complex system can be expressed in a list
of attributes or features with specific vocabularies or
lexicon terms to describe its characteristics. LLA is
a data-driven text analysis. For example, word pairs
or bi-grams as lexical terms can be extracted and le-
arned from a document repository. Figure 1 shows
an example of such a word network discovered from
data. For a text document, words are represented as
nodes and word pairs (or bi-grams) as the links bet-
ween nodes. A word center (e.g., ”energy” in Figure
1) is formed around a word node connected with a
list of other words to form more word pairs with the
center word ”energy”. ”Clean energy”, ”renewable
energy” are two bi-gram word pairs. LLA automati-
cally discovers word pairs, clusters of word pairs and
displays them as word pair networks. LLA is rela-
ted to but significantly different from so called bag-
of-words (BOW) methods such as Latent Semantic
Analysis (LSA (Dumais et al., 1988), Probabilistic
Latent Semantic Analysis (PLSA) (Hofmann, 1999),
WordNet (Miller, 2003), Automap (Newman, ), and
Latent Dirichlet Allocation (LDA) (Blei et al., 2003).
LDA uses a bag of single words (e.g., associations
are computed at the word level) to extract concepts
and topics. LLA uses bi-gram word pairs as the basis
to form word networks and therefore network theory
and methods can be readily applied here. No quan-
titative comparison with LDA can be provided since
LDA does not compute the value metrics discussed in
this paper.
Figure 1: LLA Example.
2.1 Extending LLA to Structured Data
Bi-gram also allows LLA to be extended to data ot-
her than text (e.g., numerical or categorical data). For
example, for structured data such as attributes from
databases, they can be discretized or categorized to
word-like features. The word pair model can further
be extended to a context-concept-cluster model(Zhao
and Zhou, 2014). In this model, a context is a word or
word feature that is shared by multiple data sources.
A concept is a specific word feature. A context can be
also a location, a time point or an object that is shared
across data sources. Using LLA to analyze structured
data is not the focus of this paper.
2.2 Three Categories of High-value
Information and Value Metrics
The word pairs in LLA are divided into groups or the-
mes. Each theme is assigned to one of the three cate-
gories based on the number of connected word pairs
(edges) within a cluster (intra-cluster) and the number
of edges between the themes (inter-cluster):
• Authoritative or popular (P) themes: These the-
mes resemble the current search engines ranking
measures where the dominant eigenvectors are
ranked high. These represent the main topics in
a data. They can be insightful information in two
folds: 1) These word pairs are more likely to be
shared or cross-validated across multiple diversi-
fied domains, so they are considered authoritative.
2) These themes could be less interesting because
they are already in the public consensus and awa-
reness and they are considered popular.
• Emerging (E) themes: These themes tend to be-
come popular or authoritative over time. An emer-
ging theme has the intermediate number of inter-
connected word pairs.
• Anomalous (A) themes: These themes may not
seem to belong to the data domain as compared to
others. They are interesting and could be high-
value for further investigation. An example of
an anomalous theme has the smallest number of
inter-connected word pairs.
Community detection algorithms have been illus-
trated in Newman (Newman, 2006)(Newman, ), a
quality function (or Q-value), as specifically defined
as the modularity measure, i.e., the fraction of edges
that fall within communities, minus the expected va-
lue of the same quantity if edges fall at random wit-
hout regard for the community structure, is optimized
using a dendrogram like greedy algorithm. The Q-
value for modularity is normalized between 0 and 1
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
328

with 1 to be the best and can be compared across data
sets. It was further pointed (Newman, ) that formation
of the modularity matrix is closely analogous to the
covariance matrix whose eigenvectors are the basis
for Principal Component Analysis (PCA). Modularity
optimization can be regarded as a PCA for networks.
Related methods also include Laplacian matrix of the
graph or the admittance matrix, and spectral cluste-
ring (Ng et al., 2002). Newmans modularity assumes
a subgraph deviates substantially from its expected to-
tal number of edges to be considered anomalous and
interesting, therefore, all the clusters or communities
(i.e.,popular, emerging and anomalous themes) found
by the community detection algorithm are considered
to be interesting. However, this anomalousness metric
does not consider the difference among the communi-
ties.
In LLA, we improve the modularity metric by
considering a game theoretic framework detailed in
Section 3.
In a social network, the most connected nodes are
typically considered the most important nodes. Ho-
wever, in a text document, we consider emerging and
anomalous information are more interesting and cor-
related to innovations. Also, for a piece of informa-
tion, the combination of popular, emerging and ano-
malous contributes to the total value of the informa-
tion. Therefore, we define a value metric as follows:
Let the popular, emerging and anomalous value
of the information i be P(i), E(i) and A(i) computed
from LLA respectively, the total value V (i) for i, and
V (i) = P(i) + E(i) + A(i) (1)
In the use case in Section 4, we show that the
value metrics are correlated with 1) the innovations
selected and analyzed by human analysts which can
be viewed as ”ground truth”; 2) how many posts fol-
lowing the information as a measure of actual interest.
3 GAME-THEORETIC
FRAMEWORK OF LLA
Previously, game-theoretic frameworks of search en-
gine and information retrieval have studied but rarely
content based(Zhai, 2015). Also, it is important to
point out that the game of information ranking and
retrieval is not a zero-sum game, thus it is different
from a game such as chess or poker in this sense.
As we discussed, value can be defined differently
in different context. When it is defined, the value of
an information can be learned and trained using super-
vised machine learning methods with two conditions:
1) if data can be collected and value are measured and
labeled; 2) if the definition of the value in the context
does not consistently change therefore the historical
train data can be used for prediction.
In real-life, such data is difficult to collect and va-
lue is dynamically changing in many context, there-
fore, supervised machine learning method is difficult
to apply. We introduce a game-theoretic perspective
to justify the value metric in (1).
Game theory is a field of applied mathematics.
It formalizes the conflict between collaborating and
competing players has found applications ranging
from economics to biology(Nowak and Sigmund,
1999)(Rasmusen, 1995). The players can both coope-
rate and compete to exploit their environment to max-
imize their own rewards. This is often can be modeled
as a process to search for a Nash equilibrium. The
whole system including all the players reaches a sta-
ble state, where a player can not unilaterally change
her actions to improve her reward.
When designing a good value metric for an infor-
mation player, there are a couple of other factors that
need attention:
The whole system has to be Pareto efficient or su-
perior. That is to say, the system can not make at least
one player better off without making any other player
worse off is called at a Pareto efficient state. Here,
better off is often interpreted as having higher value
or being in a preferred position, for example, more
central or with a higher degree. If no Pareto impro-
vement can be made in a system, the system is Pa-
reto efficient. Searching for a Nash equilibrium may
not achieve a full Pareto efficiency at the collective le-
vel or to achieve the so-called social welfare measure,
i.e., a total value of a set of players.
LLA can be set up as a game-theoretic framework:
one player is an information provider and the rest of
the world is the other player who responds with the
interest for the information generated by the informa-
tion provider player (or player).
In Figure 2, a LLA player has two rewards: the
authority and expertise reward. The authority from
the popular information and the expertise rewards
from the emerging and anomalous information. An
authority reward measures the correlation (r
i j)
of
Player i to Player j. The expertise reward b
j
(X
t
) for
Player j measures her own unique information to the
whole system.
Traditional search engine algorithms only con-
sider the cumulative authority part of the recursion
(e.g., using the Power method to compute the eigen-
vector for the largest of eigenvalue of the adjacency
or correlation matrix). LLA introduces the expertise
part of the recursion as the total value of collabora-
tive learning agents. By weighing expertise more than
New Value Metrics using Unsupervised Machine Learning, Lexical Link Analysis and Game Theory for Discovering Innovation from Big
Data and Crowd-sourcing
329

Figure 2: The recursion to compute the overall value (total reward) of a system R(t, j).
Table 1: LLA Game Reward Matrix.
Authority Expertise
Authority (R
2
j
,1 − R
2
j
) (0,b
02
)
Expertise (b
2
,0) (0,0)
authority, the resulting information ranking mecha-
nism values new and unique information more than
authoritative and popular information. The trade-off
between authority and expertise is controlled by the
coefficients w
1
and w
2
, as shown in Figure 2. In LLA,
a correlation coefficient is computed for the correla-
tion of two players using the following formula:
r
i j
=
(Overlapped Words Player i and j)
p
(Words Player i)(Words Player j)
(2)
As a game-theoretic framework, the reward matrix
for LLA is described in Table 1.
In Table 1, the row player is j and all ot-
her players are the column player, as in a net-
work game. There are two pure strategies, aut-
hority including popular themes or expertise inclu-
ding emerging and anomalous themes , for each
player j. The game is similar to a strategic com-
plement game such as the chicken game(Fudenberg
and Tirole, 1991) in which the authority strategy
is similar to the chicken out (C) strategy and the
expertise strategy is similar to the dare (D) stra-
tegy. Therefore, the CG has two Nash equilibria:
(Authority,Expertise) and (Expertise, Authority) if
b
2
> R
2
j
and (Expertise,Authority) if b
02
> 1 − R
2
j
.
As a baseline model, as shown in Figure 4, if a
network of players only play authoritative informa-
tion, the solution is a total value 1 distributed among
the network players associated with the eigenvector
corresponding to the maximum absolute eigenvalue
of the correlation matrix r
i j
in (2). When the player
uses an expertise strategy, she is rewarded with b
2
.
Let the reward vector be
~
R and
~
R =
R
1
R
2
.
.
.
R
N
(3)
R
2
1
+R
2
2
+...+R
2
N
= 1. If a node is isolated, i.e., Node
k, then R
k
= 0. The eigenvector can be computed from
the following iteration:
~
R(t + 1) = λr
~
R(t) (4)
where λ > 1, r denotes the correlation matrix r
i j
in
(2) and N is the number of players.
~
R converges to
the eigenvector of the maximum absolute eigenvalue
of r when for any small ε and |
~
R(t + 1) −
~
R(t)| < ε
(Jackson and Zenou, 2014). Note that this solution
is not a Nash equilibrium because when b
2
> R
2
j
, the
player j tries to play b
2
since it provides higher reward
as shown in Table 1.
In game theory, mixed strategies are often used
where authority and expertise in (6) are used mixed
with probabilities. The player plays mixed strategies
w
1
> 0 & w
2
> 0; w
1
+w
2
= 1 when w
1
and w
2
repre-
sent the probabilities of providing authority and ex-
pertise information, respectively. The reward is for
the player as an information provider is the interest
generated by the other players. The convergence of
R(t) shows that a Nash equilibrium can be achieved
through the recursive scheme shown in Figure 2 when
w
2
= 0, which is the distribution of the total authority
score 1 among the players. The Player j possesses
a value with a component R
2
j
from the total autho-
rity plus the additional expertise component b
2
to a
new self-value
ˆ
R
2
j
in (6). Using the same reasoning as
in the chicken game, the mixed strategies Nash equi-
librium result in w
1
=
b
2
b
2
+R
2
j
, because to be able to
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
330

mix and reach an equilibrium, the information provi-
der player must be indifferent over the actions of the
other players, i.e., how the rest of the world might re-
spond (A or E in the first row of Table 1). Therefore,
from Table 1, we have the following equation and so-
lution of w
1
:
w
1
R
2
j
= (1 − w
1
)b
2
w
1
=
b
2
b
2
+ R
2
j
(5)
The total reward for Player j for the mixed strategies
is
ˆ
R
2
j
= w
1
R
2
j
+ w
2
b
2
(6)
Total value of the whole system is the following
relation in (7):
Pareto superior :1 > w
1
+ w
2
b
2
> b
2
when b
2
< 1
(7)
If the information provider player uses mixed stra-
tegies including both authority and expertise informa-
tion, she can reach a Nash equilibrium because her
own total self-value is maximized, meanwhile, she
can help generate a higher social welfare, therefore
the whole system reaches a higher Pareto superior
state (not a full Pareto efficient state) than play exper-
tise alone when the total system’s reward is b
2
than
using authority or expertise alone. The total value of
the whole system w
1
+ w
2
b
2
in Figure 7 is more than
the total value b
2
using expertise alone (i.e., w
1
= 0)
but less than authority alone (i.e., w
2
= 0, which is
not a Nash equilibrium). In essence, the information
provider (player) plays mixed strategies by providing
both authoritative (i.e., popular information) and ex-
pertise (i.e.,emerging and anomalous information) to
reach the optimal value for herself and also incre-
ase the reward or value of the total system, because
the authoritative or popular information can propa-
gate through the system and create a higher total so-
cial welfare value as in (7).
4 USE CASE: MASSIVE
MULTIPLAYER ONLINE
WAR-GAME LEVERAGING
THE INTERNET (MMOWGLI)
Crowd-sourcing and distributed collaboration are be-
coming increasingly important in driving production
and innovation in a networked world. New innova-
tive, idea generation platforms are being implemented
in many organizations. Using crowd-sourcing techni-
ques, for example, the Department of Defense (DoD)
is capable of searching for new innovations that can
be implemented so that there is an increase in effi-
ciency, effectiveness, overall mission readiness. One
of these platform is the so-called Massive Multiplayer
Online War-game Leveraging the Internet (MMO-
WGLI) which allows innovators to virtually submit
and collaborate on ideas on how to improve a specific
topic.
Each individual game produces massive amounts
of data. At present, there is not an efficient way to
analyze, sort and rank the big data to uncover innova-
tive ideas for decision makers.
We go through one of the MMOWGLI games in
this paper as a use case and illustration for the ana-
lysis process. The process of a MMOWGLI game is
described as follows:
1. Start the call to action video: Each MMOWGLI
game begins with a Call to Action video. The call
to action gives few top-level questions to get play-
ers to wrap their minds around a big idea question.
2. Register Players: Players must create a player
profile that consists of a user name, an affiliation,
a location and an expertise.
3. Create Idea Cards: The input idea each player gi-
ves during a game. There are also different types
of idea cards. Players have the option to counter,
expand, explore, or adapt to the idea card that they
are responding to. The idea card creation and idea
card response can continue for anywhere from 48
hours to weeks to months.
4. Create Action Plans: After some amount of time,
determined by the game masters, the game gets
away from the idea cards and turns into creating
action plans. The action plans are created to go
deeper into a specific idea and are meant to des-
cribe how to solve game challenges and achieve
motivating goals (MMOWGLI Portal). There is
another 24-48-hour window in which action plans
can be created and posted.
In a nutshell, if an idea card is selected and turned into
an action plan, it is a success and can be considered a
”ground truth” of innovative idea.
4.1 LLA Analysis of the MMOWGLI
Game
There were about 8000 idea cards in this game, the
meta data needs to be fused from the action plans and
players’ profiles. Idea card ids were used to link the
three data sources together into a fused data.
New Value Metrics using Unsupervised Machine Learning, Lexical Link Analysis and Game Theory for Discovering Innovation from Big
Data and Crowd-sourcing
331
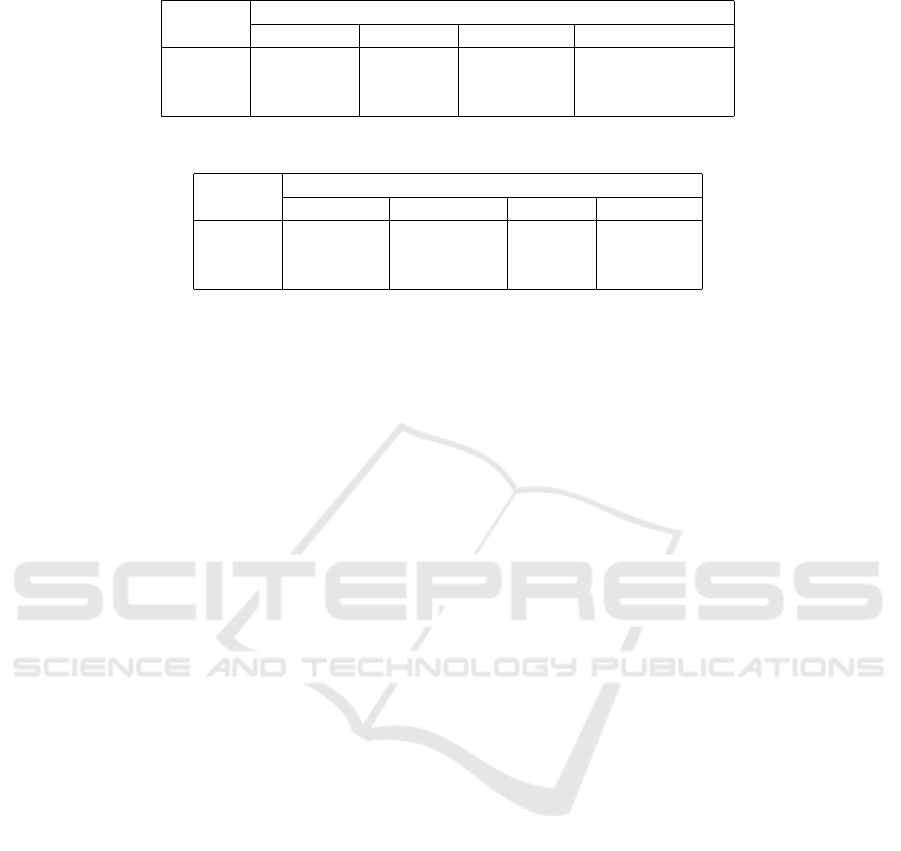
Table 2: Statistics Significance Tests for the Meta Data Variables.
Metrics Categories in Data
Highest Total # Authored # of Ideas Below
A 6.9 5.9 9.5 12.26
Non-A 6.5 4.8 7.7 0.86
p-value 0.0734933 0.001333 0.149908 < .0001
Table 3: Statistics Significance Tests.
Metrics Categories Generated by LLA
Value Anomalous Popular Emerging
A 6.38 3.23 0.85 2.29
Non-A 4.44 2.13 0.60 1.69
p-value 0.000368
a
0.002173 0.1 0.036
LLA organizes the data into content and meta
data. The text of idea cards are content in this case.
The other tags of the idea cards are meta data, compri-
sing the information of the content (idea cards) such
as time stamp, whether the idea card is turned into an
action plan, author, date, card id, level, move num-
ber, type, super interesting, text, affiliation, location,
expertise and total number of cards played below the
idea, and how many thumbs up in the action plan for
the idea.
To validate the patterns we observed from the
LLA visualization. We divided the idea cards popula-
tion into the two sets below and performed the statis-
tical t-tests to show the average of the value metrics
are indeed different.
• Population A: The idea cards were selected as
seed cards by human analysts for action plans and
can be viewed as ”ground truth” of innovative
ideas that were selected by human analysts.
• Population Not-A: The rest of idea cards that were
not selected.
Table 2 shows the means of some the original
MMOWGLI variables for Population A and Not-A
and the p-values for the t-tests when comparing the
two sets. These variables were not derived variables,
they were in the original MMOWGLI data collection
and included in the meta data. As we described intui-
tively, the number of ideas below was the best meta
data that explained the human analysts’ selections of
innovative ideas.
Table 2 shows the means of the LLA metrics of
popular, emerging and anomalous metrics and value
for Population A and Not-A and the p-values for the t-
tests when comparing the two sets. As shown in Table
2, the value metric as the mixed strategies from the
game-theoretic framework is better than the popular,
emerging and anomalous metrics alone.
In Figure 3, the x-axis shows the percentage of the
idea cards population and the y-axis shows the per-
centage of the summation of the thumbs measure, the
different curves are the plots sorted by the original
meta data variables and the LLA metrics that are lis-
ted in Table 2 and Table 3. As shown in Figure 3,
the number of idea below shows the best gain (hig-
hest curve up) with respect to a random selection (the
straight line). All the LLA metrics have gains, howe-
ver, the value metric has the second best gain.
5 CONCLUSIONS
In this paper, LLA was applied to the MMOWGLI
data set to filter, identify, and visualize the most rele-
vant innovations and new ideas. The findings from the
LLA and MMOWGLI data set were then used to cor-
relate with the analyses from the surrogates of ground
truth of innovative ideas.
We focused on analyzing the idea cards of a large
internet crowd-sourcing game. If an idea card was se-
lected and turned into an action plan, we viewed this
fact as one of the surrogates of the ground truth of in-
novative ideas. The number of ideas below an idea in
examination collected in the data is the other and best
surrogate of ground truth. Although this attribute is
a direct measure of the interest generated by an idea,
it is not based on content. We showed that the LLA
value metrics based only on content. We also showed
the game-theoretic foundation of the LLA metrics and
how they are correlated with the surrogates of ground
truth.
ACKNOWLEDGEMENTS
Thanks to the Naval Research Program at the Naval
Postgraduate School and the Office of Naval Research
(ONR) for the SBIR contract N00014-07-M-0071 for
the research of lexical link analysis and collaborative
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
332

Figure 3: The gains chart show that all the LLA metrics have gains and the value metric has the best gain.
learning agents. The views and conclusions contained
in this document are those of the authors and should
not be interpreted as representing the official policies,
either expressed or implied of the U.S. Government.
REFERENCES
Blei, D., Ng, A., and Jordan, M. (2003). Latent dirichlet
allocation. In Journal of Machine Learning Research,
3:993-1022.
Brin, S. and Page, L. (1998). The anatomy of a large-scale
hypertextual web search engine. In Computer Net-
works and ISDN Systems, 30:107-117.
CASOS (2009). Center for computational analysis of social
and organizational systems automap: extract, analyze
and represent relational data from texts.
Dumais, S. T., Furnas, G. W., Landauer, T. K., and Deer-
wester, S. (1988). Using latent semantic analysis to
improve information retrieval. In CHI88: Conference
on Human Factors in Computing, pages 281–285.
Erkan, G. and Radev, D. R. (2004). Lexrank: graph-based
lexical centrality as salience in text summarization.
22:457–479.
Freeman, L. (1979). Centrality in social networks i: con-
ceptual clarification. In Social Networks, 1: 215-239.
Fudenberg, D. and Tirole, J. (1991). Game theory. The MIT
Press, Cambridge, Massachusetts; London,England.
Girvan, M. and Newman, M. E. J. (2002). Community
structure in social and biological networks. In the Na-
tional Academy of Sciences, 99(12),7821–7826.
Hofmann, T. (1999). Probabilistic latent semantic analysis.
Stockholm, Sweden.
Jackson, M. and Zenou, Y. (2014). Games on networks.
Kleinberg, J. M. (1999). Authoritative sources in a hyper-
linked environment. In Journal of the ACM, 46 (5):
604.
Mihakcea, R. and Tarau, P. (2004). Textrank: bringing order
into texts. In the 2004 Conference on Empirical Met-
hods in Natural Language Processing (EMNLP 2004),
July 2004, Barcelona, Spain.
Miller, G. A. (2003). Wordnet: a lexical database for eng-
lish. In Communications of the ACM, 38(11).
Newman, M. E. J. Finding community structure in networks
using the eigenvectors of matrices. In Phys. Rev. E,
vol. 74, no. 3.
Newman, M. E. J. (2006). Fast algorithm for detecting com-
munity structure in networks.
Ng, A., Jordan, M., and Weiss, Y. (2002). On spectral clus-
tering: analysis and an algorithm. In T. Dietterich, S.
Becker, and Z. Ghahramani (Eds.), Advances in Neu-
ral Information Processing Systems 14, pp. 849–856,
MIT Press.
New Value Metrics using Unsupervised Machine Learning, Lexical Link Analysis and Game Theory for Discovering Innovation from Big
Data and Crowd-sourcing
333

Nowak, M. A. and Sigmund, K. (1999). Phage-lift for game
theory. In Nature, 398, 367368. doi:10.1038/18761.
Rasmusen, E. (1995). Games and information: An intro-
duction to game theory (4th ed.). ISBN:1405136669.
Publisher: Blackwell Publishers.
Zhai, C. (2015). Towards a game-theoretic framework for
information retrieval.
Zhao, Y., Gallup, S., and MacKinnon, D. (2015a). System
self-awareness and related methods for improving the
use and understanding of data within dod. In Software
Quality Professional, 13(4): 19-31.
Zhao, Y., Mackinnon, D. J., and Gallup, S. P. (2015b). Big
data and deep learning for understanding dod data. In
Journal of Defense Software Engineering, Special Is-
sue: Data Mining and Metrics.
Zhao, Y. and Zhou, C. (2014). System and method for kno-
wledge pattern search from networked agents. US pa-
tent 8903756.
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
334
