
Assessing Similarity Value between Two Ontologies
Aly Ngon
´
e Ngom
1
, Guidedi Kaladzavi
1,2
, Fatou Kamara-Sangar
´
e
1
and Moussa Lo
1
1
LANI, Gaston Berger University, BP 234, Saint - Louis, Senegal
2
University of Maroua, Cameroon
Keywords:
Ontologies Similarity, Concepts Similarity, Semantic Similarity.
Abstract:
The aim of this paper is to present an appraoch for assessing similarity between ontolgies. This approach
is based on set theory, edges-based semantic similarity and features based similarity. We first determine the
set of concepts that is shared by two ontologies and the sets of concepts that are different from them. Then
we extend ontologies by using the set of concepts shared by the two ontologies. Then we redetermine set of
concepts shared by the two extended ontologies. finally, we end with the assessment of the similarity between
ontologies by using the average values of similarity of the sets of specific concepts to each not extended
ontologies, and the set of concepts shared by extended ontologies.
1 INTRODUCTION
Ontologies allow to formalize knowledge related to
the description of the world by making them accessi-
ble and shareable across the Web. They introduce the
semantic layer into the architecture of the on based-
systems (Dram
´
e, 2014). When several ontologies are
used for an application, it is necessary that these on-
tologies present some similarity. The assessing of si-
milarity between ontologies may be very interesting.
Indeed, it can make easy the choice of ontologies in
the case of elaboration of a system, which uses them.
In addition, it can help to evaluate the ontology evo-
lution by comparing its different versions. In (Ngom
et al., 2017), we have proposed an approach for as-
sessing similarity between two ontolgies O
1
and O
2
.
This approach has given good results. However, it
would be interesting to take into account some proper-
ties (relations, axioms) for extending the formed sets
(set of resemblance and set of differences) in the goal
to improve this approach. The aim of this paper is to
present another approach which improves our propo-
sition in (Ngom et al., 2017).
This paper continues by presenting our research con-
text. Section 2 presents the related work. Then, we
present our approach in section 3 before making its
experimentation in section 4. In section 5, we ana-
lyse the results obtained by the experimentation and
compare them to the results obtained in (Ngom et al.,
2017). We end with conclusion and perspectives of
this work.
2 RELATED WORKS
There are several works, which are dedicated to the
evaluation of similarity between two concepts in an
ontology. However, there are not many works which
deal with evaluation of similarity between ontologies.
The following are some works about similarity bet-
ween two ontologies.
Maedche and Staab (Maedche and Staab, 2002) pro-
pose a method for comparing two ontologies. This
method is based on two levels:
• the Lexical level which consists of investigation
on how terms are used to convey meanings ;
• the Conceptual level which is the investigation of
what conceptual relations exist between terms.
The Lexical comparison allows to find concepts by
assessing syntaxic similarity between concepts. It is
based on Levenshtein (Levenshtein., 1966) edit dis-
tance (ed) formula which allows to measure the mi-
nimum number of change required to transform one
string into another, by using a dynamic programming
algorithm. The Conceptual Comparison Level allows
to compare the semantic of structures of two ontolo-
gies. Authors use Upwards Cotopy (UC) to compare
the Concept Match (CM). Then, they use the CM to
determine the Relation Overlap (RO). Finally they as-
sess the average of RO.
This approach allows to assess similarity between
two ontologies by using the Lexical and Conceptual
Comparison Level. However, if we reverse the posi-
Ngom, A., Kaladzavi, G., Kamara-Sangaré, F. and Lo, M.
Assessing Similarity Value between Two Ontologies.
DOI: 10.5220/0006959903430350
In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 2: KEOD, pages 343-350
ISBN: 978-989-758-330-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
343

tion of some concepts in the hierarchy, we can get the
same results because the method only considers the
presence of the concept in the hierarchy.
In (Ngom et al., 2017), we have proposed an ap-
proch which assesses similaty between two ontolo-
gies. The approach is based on set theory, edges ba-
sed (Ngom., 2015) and feature-based similarity ba-
sed (Tversky, 1977). It is composed of three steps.
The first step consists to determine the different sets :
set of concepts shared by the two ontologies and sets
of concepts specific to each ontology. In the second
step, we have assessed the average similarity values
between concepts for each sets thanks to semantic si-
milarity measures. Finally, in the last step, we have
assessed similarity between ontologies by redefining
Tversky’s measure relying to the two first steps.
To assess similarity between two ontologies, we
have defined a measure which readjust the Tversky
measure. This measure takes into acount shared fe-
atures and differences of ontologies. Applying the
Tversky measure, the similarity between O
1
and O
2
is given by the formula 1.
T vr
(O
1
,O
2
)
=
f (O
1
∩O
2
)
f (O
1
∩O
2
)+α. f (O
1
\O
2
)+β. f (O
2
\O
1
)
(1)
Instead of the function f, we use Wu and Palmer (Wu
and Palmer, 1994) semantic similarity measure. for
every determined set, we have computed the average
of the similarity values between concepts. Using Wu
and Palmer similarity measure, the similarity between
two concepts c
1
and c
2
is given by the formula 2.
Sim(c
1
,c
2
) =
2 × depth(c
3
)
depth(c
1
) + depth(c
2
)
(2)
The concept c
3
represents the Least Common Subsu-
mer (LCS) of concepts c
1
and c
2
. By replacing the
terms of the Tversky measure with the average of the
similarity values between concepts of the determined
sets, formula 1 becomes formula 3.
T
Ngom
(O
1
,O
2
) =
θ.x
O
1
+ω.x
O
2
θ.x
O
1
+ω.x
O
2
+α.y
(O
1
\O
2
)
+β.z
(O
2
\O
1
)
(3)
with :
• θ =
cardinality(O
1
∩ O
2
)
cardinality(O
1
)
;
• ω =
cardinality(O
1
∩ O
2
)
cardinality(O
2
)
;
• α =
cardinality(O
1
\O
2
)
cardinality(O
1
)
;
• and β =
cardinality(O
2
\O
1
)
cardinality(O
2
)
;
• cardinality(O) is the number of elements (con-
cepts) of the set (ontology) O ;
and where :
• x
O
1
(respectively x
O
2
) is the average value of si-
milarity between concepts (x
i
,x
j
) in ontology O
1
(respectively (x
i
,x
j
) in ontology O
2
). i, j ∈ N and
i 6= j.
• y
(O
1
\O
2
)
(respectively z
(O
2
\O
1
)
) is the average va-
lue of similarity between concepts (y
i
,y
j
) (re-
spectively (z
i
,z
j
)) present in ontology O
1
but not
in O
2
(respectively present in ontology O
2
but not
in O
1
). i, j ∈ N and i 6= j.
• the coefficients θ, ω, α and β allow to take into ac-
count the similarity values in relation to the num-
ber of concepts of the sets and number of concepts
of ontologies.
The measure presented by formula 3 respects this pro-
perties :
• the measure is symetric : T
Ngom
(O
1
,O
2
) =
T
Ngom
(O
2
,O
1
) ;
• the measure is bounded between 0 and 1 ;
• if T
Ngom
(O
1
,O
2
) = 1 then O
1
= O
2
.
The method we have proposed in (Ngom et al., 2017)
gives satisfactory results. Indeed, it allows to assess
similarity between two ontologies while taking into
account the semantic links that exist between the con-
cepts in ontologies. However, it doesn’t take into ac-
count properties of concepts for extending the formed
sets (set of resemblance and set of difference). In this
paper, we propose another approach which takes into
account relation ”is-a” between concepts for the ex-
tension of the set of concepts shared by O
1
and O
2
.
3 OUR APPROACH
3.1 Principe
The approach we propose is an improvement of our
previous paper (Ngom et al., 2017). As in our previ-
ous works, this approach is based on set theory, ed-
ges based (Ngom., 2015) and feature-based similarity
based (Tversky, 1977). It can be summarized in five
steps :
• Step 1 consists to determine the sets (O
1
\O
2
),
(O
2
\O
1
) and (O
1
∧ O
2
).
• Once the sets are determined, we assess the
average of the semantic similarity values between
concepts of each set in step 2.
• In step 3, we extend ontologies O
1
and O
2
by
using the set (O
1
∧ O
2
). In this step, for each
concept c of (O
1
∧ O
2
), we search there sons x
i
(i ∈ N) in O
1
(respetively O
2
) and we add them
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
344

as sons of c in O
2
(respetively O
1
) if they don’t
exist in this ontology. At the end of this step,
we obtain two ontologies : O
0
1
(respectively O
0
2
)
which extends O
1
(respectively O
2
) with concepts
of O
2
(respectively O
1
). Thus, extension of onto-
logies allows us to determine the set of concepts
(O
0
1
∧ O
0
2
) shared by the two ontologies.
• In Step 4, we determine (O
0
1
∧O
0
2
) which is the set
of shared concepts by ontologies O
0
1
and O
0
2
.
• Finally, in the step 5, we assess similarity between
ontologies by using the results of the step 2 and 4
in our measure which is a redefinition of the T
Ngom
measure (Ngom et al., 2017).
In summary, for assessing similarity between ontolo-
gies, we use sets (O
1
\O
2
), (O
2
\O
1
) and (O
0
1
∧ O
0
2
);
i.e we consider the difference between O
1
and O
2
by
using sets (O
1
\O
2
) and (O
2
\O
1
), and the resemblance
between the two ontologies by using set (O
0
1
∧ O
0
2
).
Figure 1 represents the differents that we use for as-
sessing similarity beetween ontologies O
1
and O
2
. In
Figure 1: Representation of extensions of ontologies O
0
1
and
O
0
2
with Tversky’s feature model.
figure 1, we distinguish three parts :
• (O
1
\O
2
) = {A,C, E} : set of concepts present in
O
1
and not in O
2
;
• (O
2
\O
1
) = {R,S, T,W,X,Y } : set of concepts
present in O
2
and not in O
1
;
• (O
0
1
∧ O
0
2
) = {B,C,D,E,F,G} : set of concepts
present in O
0
1
and O
0
2
.
3.2 Measure
The measure we present in this paper is an impro-
vement of our measure T
Ngom
(Ngom et al., 2017)
which redifines Tversky’s (Tversky, 1977) similarity
measure. For assessing similarity between two on-
tologies O
1
and O
2
, our measure takes into account
the difference between the two ontologies by asses-
sing the average similarity values of sets (O
1
\O
2
) and
(O
2
\O
1
), and their common concepts by extending
the ontologies (O
1
to O
0
1
and O
2
to O
0
2
) and assessing
the average similarity values of the set of common
concepts of extended ontologies ((O
0
1
∧ O
0
2
)). We use
Wu and Palmer measure (Wu and Palmer, 1994) for
computing semantic similarity between concepts of
sets in ontologies. The measure is given by the for-
mula 4:
N
Plus
(O
1
,O
2
) =
(θ.x
O
0
1
+I
2
)+(ω.x
O
0
2
+I
1
)
(θ.x
O
0
1
+I
2
)+(ω.x
O
0
2
+I
1
)+α.y
(O
1
\O
2
)
+β.z
(O
2
\O
1
)
(4)
with :
• θ =
cardinality(O
0
1
∩ O
0
2
)
cardinality(O
1
) + n
1
+ n
2
;
• ω =
cardinality(O
0
1
∩ O
0
2
)
cardinality(O
2
) + n
1
+ n
2
;
• α =
cardinality(O
1
\O
2
)
cardinality(O
1
)
;
• β =
cardinality(O
2
\O
1
)
cardinality(O
2
)
;
• I
1
=
1
1 + n
2
;
• I
2
=
1
1 + n
1
;
• x
O
0
1
(respectively x
O
0
2
) is the average value of
similarity between concepts (x
i
,x
j
) in ontology
O
0
1
(respectively (x
i
,x
j
) in ontology O
0
2
). i, j ∈ N
and i 6= j.
• y
(O
1
\O
2
)
(respectively z
(O
2
\O
1
)
) is the average
value of similarity between concepts (y
i
,y
j
)
(respectively (z
i
,z
j
)) present in ontology O
1
but
not in O
2
(respectively present in ontology O
2
but
not in O
1
). i, j ∈ N and i 6= j.
• cardinality(O) is the number of elements (con-
cepts) of the set (ontology) O ;
• I
i
: Integrity coefficient of Ontology O
i
(i ∈ N);
• n
i
: number of concepts of O
i
added for extending
O
j
(i, j ∈ N);
• As in (Ngom et al., 2017), θ, ω, α and β are para-
meters which allow to take into account the simi-
larity values in relation to the number of concepts
of the sets and number of concepts of ontologies.
The integrity coefficient of Ontology (I
i
) is a value
which is related to the number of concepts of ontology
Assessing Similarity Value between Two Ontologies
345

O
j
(n
j
) that we have to add to O
i
in goal to extend it
(i, j ∈ N). The larger is n
j
, the smaller is I
i
. We have
the expression 5:
(
lim
n→∞
I = lim
n→∞
1
1 + n
= 0;
lim
n→0
I = lim
n→0
1
1 + n
= 1;
(5)
with (n ∈ N).
We note that measure presented by formula 4 like
formula 3 respects this properties :
• the measure is symetric : N
Plus
(O
1
,O
2
) =
N
Plus
(O
2
,O
1
) ;
• the measure is bounded between 0 and 1 ;
• if N
Plus
(O
1
,O
2
) = 1 then O
1
= O
2
.
In the next section, we will introduce some important
algorithms.
3.3 Algorithms
In this section, we will present the important algo-
rithms that we can implement to assess similarity be-
tween ontologies. The algorithms we define here
are based on different steps that we have mentio-
ned in section 3.1 to evaluate the similarity between
the ontologies. The algorithms 1 and 2 allow re-
spectively to form the sets of concepts that repre-
sent differences and resemblances between two onto-
logies O
1
and O
2
. Algorithm 1 implements a met-
Algorithm 1: diffOnto. /* Differences between two ontolo-
gies */
hod named di f f Onto(stackO
1
,stackO
2
) which al-
lows to extract the difference between two ontolo-
gies. In input, we have two set of concepts stored on
stacks. stackO
1
(respectively stackO
2
) store all O
1
’s
concepts (respectively O
2
’s concepts). The function
checkConcept(c, stackO
2
) checks if concepts c is pre-
sent in ontology O
2
. If c is not in O
2
, then c will be
added in the stack of difference stackDi f f . In out-
put, the method di f f Onto(stackO
1
,stackO
2
) returns
a stack of concepts which represents all concepts pre-
sent in O
1
and not in O
2
.
Algorithm 2: cCOnto. /* (Common Concept of Ontologies)
Resemblance between two ontologies */
Algorithm 2 called cCOnto(stackO
1
,stackO
2
) al-
lows to get the set of concepts that belong to on-
tologies O
1
and O
2
. In input, as for algorithm
1, we have the stacks of concepts stackO
1
and
stackO
2
which store, respectively, the concepts of O
1
and O
2
. The method sizeO f (stackO
1
) (respectively
sizeO f (stackO
2
)) gives the size of the stack stackO
1
(respectively stackO
2
) and the method checkConcept
checks, if a concept, belongs to the stack of concept.
If the result is true, then, the concept is added in the
stack stackCommon. In output, we have a stack of
concepts stackCommon which store all concepts that
belong to O
1
and O
2
.
Algorithm 3 is defined to assess the average of si-
milarity values between concepts of a set of concepts
(set of differences and set of resemblance). In input,
we have a stack of concept (stackConcept) and an on-
tology (O). The stack stackConcept represents a set
of concepts (set of difference or set of resemblance).
The algorithm compute similarity between all con-
cepts of the set and assess the average of values of
similarity. For that, we extract the first concept out of
the stack and fix a pointer to the new first concept of
the stack in the goal to assess similarity between con-
cepts. The function Sim(c
i
,c
j
,O) (i, j ∈ N and i 6= j)
implements an edge-based semantic similarity mea-
sure among measures studied in (Ngom et al., 2017).
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
346

Algorithm 3: aSV. /* (Average Similarity Value) Assess the
average of similarity values between concepts of a set of
concepts */
The variable meter allows to count the number of si-
milarity values evaluated and valueSim is the sum of
similarity values. These operations are repeated until
there is no concept in the stack stackConcept. In out-
put, the algorithm computes the average and returns it
as the final result of the algorithm.
The algorithm 3 gives the average of semantic simila-
rity values of a set of concepts in an ontology. Since
edge-based similarity measures are symmetric, then
instead to select Sim(c
i
,c
j
,O) and Sim(c
j
,c
i
,O) in
the calcul, we choose one of those values, because
Sim(c
i
,c
j
,O) = Sim(c
j
,c
i
,O). The algorithm also
does not assess the similarity between a concept and
itself.
Algorithm 4 defines a method which extends an
ontology O
2
by adding concepts of another ontology
O
1
.
Algorithm 4 : extensionOntology. /* extension of O
2
by
adding concepts of O
1
*/
In algorithm 4 takes in input the stacks of
common concepts (stackCommon) of ontologies
O
1
and O
2
, and the two ontologies. Function
copyStack(stackCommon,stackCommonCopy) co-
pies all concepts of stackCommon in another stack
(stackCommonCopy) for not loosing the elements
of stack when we depile them. Once stackCommon
has been copied, we use its copy for searching
concepts of O
1
to insert to O
2
for its extention. For
each concept c
1
of O
1
stored in stackCommonCopy
(c
1
∈ O
1
and c
1
∈ stackCommonCopy), we stack all
its direct sons in stackO f Sons thanks to function
stackSons(c
1
,O
1
). Then, for each c
2
son of c
1
(c
2
∈ O
1
), we use function f indInOntology(c
2
,O
2
)
for checking if c
2
is not in O
2
. If c
2
doesn’t belong to
O
2
(c
2
/∈ O
2
), we insert c
2
as a son of c
1
in O
2
thanks
to function insertAsSonO f (c
2
,c
1
,O
2
). In result, we
obtain the ontology O
2
extended by concepts of O
1
.
Finally, the last algorithm (algorithm 5) imple-
ments the expression 4 defined in the section 3.2.
Algorithm 5 allows to assess similarity value bet-
ween two ontologies O
1
and O
2
. In input, we have the
two ontologies. The ontologies are stored on stacks
stackO
1
and stackO
2
thanks to a function stack(O)
which stores all concepts of an ontology O in a stack.
After storing the concepts in the stacks, the sets of
Assessing Similarity Value between Two Ontologies
347

Algorithm 5 : simOnto. /* Assess similarity between two
ontologies */
resemblance (stackCommon) and difference
(stackDi f f
(O
1
\O
1
)
,O
2
) and stackDi f f
(O
1
\O
2
)
,O
1
))
are determined by calling the algorithms 1
and 2. Once the sets have been determined,
we extend ontologies thanks to the function
extensionOntology(stackCommon, O
2
,O
1
) which
extends O
1
(respectively O
2
) by adding sons of
concepts of O
2
(respectively O
1
) included in the
stack stackCommon but not in O
1
(respectively O
2
).
After extending the ontologies, we redefine the stacks
of concepts of ontologies for re-evaluating the stack
of concepts that they share (stackCommonFinal).
We also compute n
1
and n
2
respectively the number
of concepts of O
1
added to O
2
, and the number of
concepts of O
2
added to O
1
. Then, we assess the
integrity indexes I
1
and I
2
before initializing parame-
ters α, β, θ and ω. Finally, we compute similarity of
two ontologies and return the final result. The result
is equal to -1 if there are errors in the calculation
process.
4 EXPERIMENTATIONS
Example 1:
The example 1 is about a fragment of Wordnet
1
that
we have used in our previous works (Ngom et al.,
2016b) and (Ngom et al., 2016a). The ontologies are
represented by figures 2 and 3.
We obtain the following results:
• aSV (stackCommonFinal, O
0
3
) = 0.5 ;
• aSV (stackCommonFinal, O
0
4
) = 0.5 ;
• aSV (stackDi f f
(O
3
\O
4
)
,O
3
) = 0 ;
1
http ://wordnet.princeton.edu
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
348
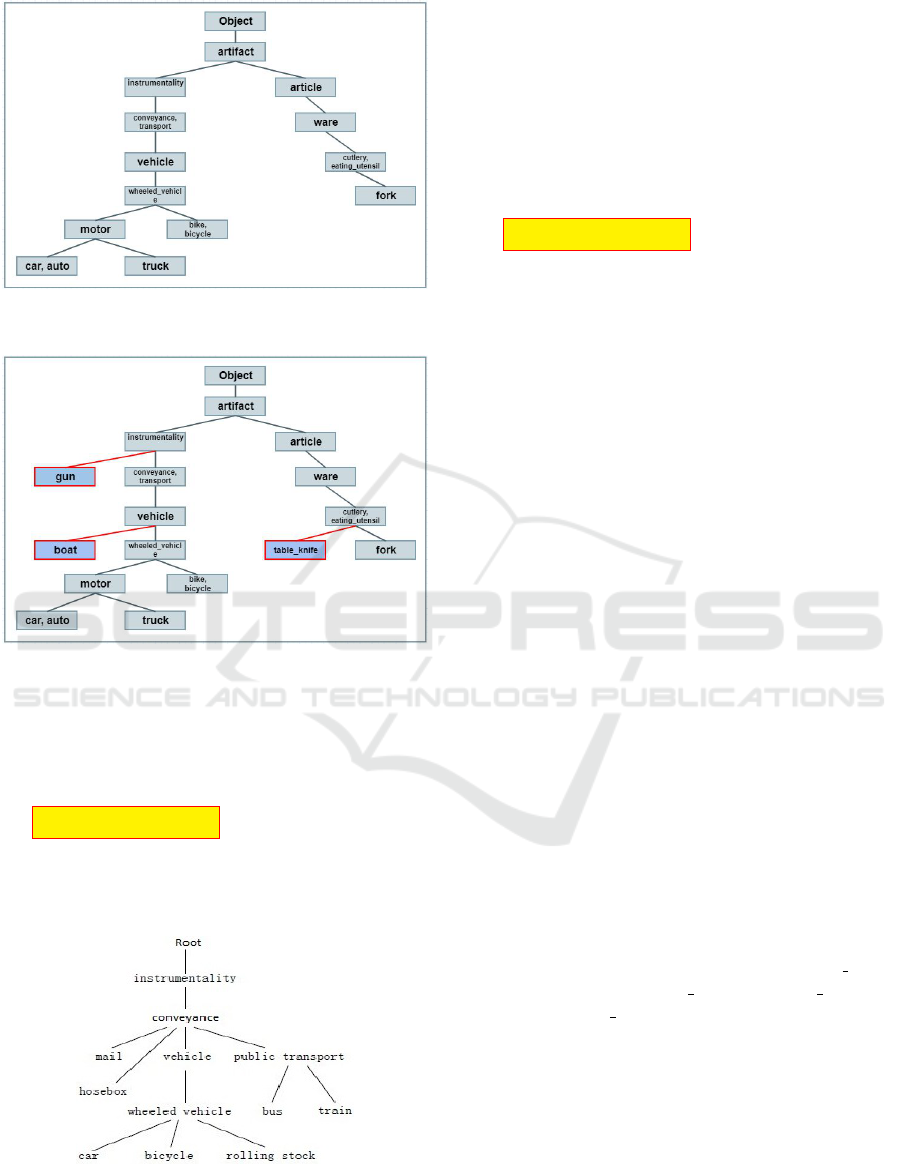
Figure 2: Representation of an ontology extracted from
WordNet (O
3
).
Figure 3: Representation of an ontology extracted from
WordNet and extended with some concepts (O
4
).
• aSV (stackDi f f
(O
4
\O
3
)
,O
4
) = 0.2875 ;
• θ = 1 ; ω = 0.85 ; α = 0 ; β = 0.18 ;
• I
3
= 1/4 ; I
4
= 1 ; n
3
= 0 ; n
4
= 3 ;
• N
Plus
(O
3
,O
4
) = 0.98
In this example, we illustrate our proposition by
assessing the similarity between the ontology of the
figure 2 and that of the figure 4.
Figure 4: Representation of an ontology extracted from
WordNet (O
5
).
We obtain the following results:
• aSV (stackCommonFinal, O
0
3
) = 0.69 ;
• aSV (stackCommonFinal, O
0
5
) = 0.62 ;
• aSV (stackDi f f
(O
3
\O
5
)
,O
3
) = 0.51 ;
• aSV (stackDi f f
(O
5
\O
3
)
,O
5
) = 0.68 ;
• θ = 11/19 ; ω = 11/18 ; α = 3/7 ; β = 6/13 ;
• I
3
= 1/5 ; I
5
= 1/2 ; n
3
= 1 ; n
5
= 4 ;
• N
Plus
(O
3
,O
5
) = 0.74
5 ANALYSIS AND
COMPARISONS
In the Experimentation section (section 4), we have
given two examples for illustrating our proposition.
This section is about analysis of obtained results. We
also compare this results to the results obtained in
(Ngom et al., 2017) with same examples.
Example 1:
Ontologies O
3
and O
4
present a good similarity va-
lue (N
Plus
(O
3
,O
4
) = 0.98). Then, we can say that
the similarity value between two ontologies is good.
We note that ontologies have respectively 14 con-
cepts for O
3
and 17 concepts for O
4
. The ontology
O
4
contains all O
3
’s concepts and 3 more concepts.
Initially, in the different sets, we have 14 concepts
in the stack stackCommon which represents the set
(O
3
∩ O
4
), 0 concept in the set (O
3
\O
4
) stored in
the stack stackDi f f
(O
3
\O
4
)
and 3 concepts in the set
(O
4
\O
3
) stored in the stack stackDi f f
(O
4
\O
3
)
. After
extension of ontologies, we have 17 concepts in O
0
3
and 17 concepts in 17 concepts in O
0
4
. O
0
4
does not
change but O
0
3
has 3 more concepts than O
3
. In O
0
3
,
the insertions of concepts have been done following
this rules : ”gun” is inserted as a son of ”instrumen-
tality” (”gun” is-a ”instrumentality”), ”boat” as a son
of ”vehicle” (”boat” is-a ”vehicle”) and ”table knife”
as a son of ”cutlery, eating utensil” (”table knife” is-
a ”cutlery, eating utensil”). Finally, the set (O
3
∩ O
4
)
becomes (O
0
3
∩ O
0
5
) and contains 17 concepts stored
in the stack stackCommonFinal.
Example 2:
The similarity value between ontologies O
3
and O
5
is equal to 0.74 (N
Plus
(O
3
,O
5
) = 0.57). This simi-
larity value is good. The ontologies have respecti-
vely 14 concepts for O
3
and 13 for O
5
. Before ex-
tending ontologies, in the different sets, we have 7
Assessing Similarity Value between Two Ontologies
349

concepts in the stack stackCommon which represents
the set (O
3
∩ O
5
), 6 concept in the set (O
3
\O
5
) sto-
red in the stack stackDi f f
(O
3
\O
5
)
and 6 concepts in
the set (O
5
\O
3
) stored in the stack stackDi f f
(O
5
\O
3
)
.
After the extension of ontologies, we have respecti-
vely 18 concepts in O
0
3
and 14 concepts in O
0
5
. The
set (O
3
∩ O
5
) is extended and becomes (O
0
3
∩ O
0
5
).
(O
3
∩ O
5
) contains 11 concepts stored in the stack
stackCommonFinal. In O
0
3
, the insertions of con-
cepts have been done following this rules : in first,
”mail”, ”hosebox” and ”public transport” are inserted
as a sons of ”conveyance” (”mail” is-a ”conveyance”,
”hosebox” is-a ”conveyance” and ”public transport”
is-a ”conveyance”), and then, ”rolling stock” is in-
serted as a son of ”Wheeled vehicle” (”rolling stock”
is-a ”wheeled vehicle”). The ontology O
0
5
is exten-
ded following that ”motor” is inserted as a son of
”wheeled vehicle” (”motor” is-a ”wheeled vehicle”).
The Table 1 allows to compare the results obtai-
ned in this paper to the results of our previous works
(Ngom et al., 2017).
Table 1: Comparison of results of N
Plus
and T
Ngom
.
N
Plus
T
Ngom
(O
3
,O
4
) 0.98 0.95
(O
3
,O
5
) 0.74 0.57
In Table 1, we find that the measure N
Plus
gives
better results compared to the measure T
Ngom
. In-
deed, we have : N
Plus
(O
3
,O
4
) > T
Ngom
(O
3
,O
4
) (0.98
> 0.95) and N
Plus
(O
3
,O
5
) > T
Ngom
(O
3
,O
5
) (0.74 >
0.57). The N
Plus
measure increases the T
Ngom
mea-
sure thanks to the extension of the set of their com-
mon concepts.
6 CONCLUSION
In this paper, we proposed an approach for assessing
similarity between two ontologies. The approach that
we adopt is based on set theory, edges based semantic
similarity (Ngom., 2015) and feature-based similarity
(Tversky, 1977). It can be summarized in 5 steps. In
step 1, we have determined the sets of concepts which
characterize the concepts shared by the two ontolo-
gies and the sets of concepts that are different from
them. Once the sets have been determined, we have
assessed the average of the semantic similarity values
between concepts of each set in step 2. Step 3 is de-
dicated to the extension of ontologies. After the step
3, we have extended set of concepts that ontologies
share in Step 4. Finally, we assessed similarity be-
tween ontologies in step 5. The approach proposed
in this paper improve our proposition in (Ngom et al.,
2017) by extending the set of concepts shared by the
two ontologies. The extension on this set is realized
by taking into account the concepts of ontologies lin-
ked with concepts of the set by the ”is-a” relation. In
perspectives, we will propose an approach to assess
similarity between an ontology and a speech in text
format to check if the text and the ontology refer to
the same theme.
ACKNOWLEDGMENT
The authors would like to thank the CEA-MITIC (The
African Center of Excellence in Mathematics, Com-
puter Science and ICT) which partially funded this
work.
REFERENCES
Dram
´
e, K. (2014). Contribution
`
a la construction
d’ontologies et
`
a la recherche d’information : appli-
cation au domaine m
´
edical. PhD thesis, Universit
´
e De
Bordeaux.
Levenshtein., I. V. (1966). Binary codes capable of cor-
recting deletions, insertions, and reversals. In Cyber-
netics and Control Theory, 10(8), pages 707 – 710.
Maedche, A. and Staab, S. (2002). Measuring similarity
between ontologies. In In: G
´
omez-P
´
erez A., Ben-
jamins V.R. (eds) Knowledge Engineering and Kno-
wledge Management: Ontologies and the Semantic
Web. EKAW 2002. Lecture Notes in Computer Science,
vol 2473. Springer, Berlin, Heidelberg, pages 251 –
263.
Ngom., A. N. (2015). Etude des mesures de similarit
´
e
s
´
emantique bas
´
ee sur les arcs. In CORIA, Paris,
France, pages 535 – 544.
Ngom, A. N., Diallo, P. F., Kamara-Sangar
´
e, F., and LO,
M. (2016a). A method to validate the insertion of a
new concept in an ontology. In SITIS 2016 : The 12th
International Conference on Signal Image Technology
and Internet Systems, Naples, pages 275 – 281.
Ngom, A. N., Kamara-Sangar
´
e, F., and Lo, M. (2017). Pro-
position of a method for assessing similarity between
two ontologies. In 4th Annual Conf. on Computatio-
nal Science & Computational Intelligence (CSCI’17)
— Dec 14-16, 2017 — Las Vegas, Nevada, USA, pages
174 – 179.
Ngom, A. N., Traore, Y., Diallo, P., Sangare, F., and Lo,
M. (2016b). A method to update an ontology : si-
mulation. In Int’l Conf, Information and Knowledge
Engineering, IKE’16, Las Vega, Nevada, USA, pages
92 – 96.
Tversky, A. (1977). Features of similarity. In Psychological
Review, 84(4), pages 327– 352.
Wu, Z. and Palmer, M. (1994). Verbs semantics and lexical
selection. In U.A.f.C.L. Stroudsburg, PA (ed.), In Pro-
ceedings of the 32nd annual meeting on ACL, volume
2 de ACL ’94, pages 133 – 138.
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
350
