Comparing of Term Clustering Frameworks for Modular Ontology

Learning

Ziwei Xu, Mounira Harzallah and Fabrice Guillet

LS2N, Polytech’Nantes, Rue Christian Pauc, 44300, Nantes, France

Keywords: Text Mining, Feature Extraction, Ontology Learning, Term Clustering.

Abstract: This paper aims to use term clustering to build a modular ontology according to core ontology from domain-

specific text. The acquisition of semantic knowledge focuses on noun phrase appearing with the same

syntactic roles in relation to a verb or its preposition combination in a sentence. The construction of this co-

occurrence matrix from context helps to build feature space of noun phrases, which is then transformed to

several encoding representations including feature selection and dimensionality reduction. In addition, the

content has also been presented with the construction of word vectors. These representations are clustered

respectively with K-Means and Affinity Propagation (AP) methods, which differentiate into the term

clustering frameworks. Due to the randomness of K-Means, iteration efforts are adopted to find the optimal

parameter. The frameworks are evaluated extensively where AP shows dominant effectiveness for co-

occurred terms and NMF encoding technique is salient by its promising facilities in feature compression.

1 INTRODUCTION

Ontology building is a complex process composed of

several tasks: term or concept acquisition, concept

formation, taxonomy definition, ad-hoc relation

definition, axiom definition, etc. (Fernández-López et

al., 1997). The ever-increasing access to textual

sources has motivated the development of ontology

learning approaches based on techniques of different

fields, like natural language processing, data mining

and machine learning. Many works are focused on

the taxonomy definition and more especially on the

hypernym relation extraction. A term t1 is a

hypernym of a term t2 if the former categorizes the

later. This relation is also known as a terminological

« is-a » relation. For its extraction from texts, several

approaches based on Harris’ distributional hypothesis

are proposed. This hypothesis states that words/terms

in the same context can have similar meanings

(Harris, 1954). Then, each term can be represented as

a vector of contexts, forming a matrix of co-

occurrence or colocation (i.e. co-occurrence of the

second order). Based on the semantic similarity in a

vector space, non-supervised methods are applied for

term clustering. Each cluster is expected to include

semantically similar terms (i.e. synonyms or related

by the hypernym relation) or semantically connected

terms.

However, obtained clusters are not necessarily

relevant for the ontology to build. Moreover, these

approaches may have a poor performance due to the

sparsity of the co-occurrence matrix (Buitelaar et al.,

2004). Dimensionality reduction becomes a crucial

issue. It can be performed by feature selection. In

statistical stage, feature selection could be achieved

by the frequency of terms or the weighting of Tf-Idf

(term frequency- inverse document frequency).

In our work, we are interested in term clustering

according to core ontology in order to build a modular

ontology (Kutz and Hois, 2012). A core ontology of

a domain is a basic and minimal ontology composed

only of the minimal concepts (i.e core concepts) and

the principal relations between them that allow

defining the other concepts of the domain (Oberle et

al., 2006; Burita et al., 2012). This step (i.e. term

clustering according to a core ontology) is the first

stage towards a taxonomy definition. Indeed, a term

of each cluster is expected to be synonym or hyponym

of the core concept that corresponds to its cluster.

Later, inside of each cluster, other hypernym relations

between terms have to be extracted.

In this paper, we analyze and evaluate two

frameworks of terms clustering following the

processing workflow of Figure 1. We discuss some

works dealing with term clustering in section 2. We

then describe the resources used for our experiments

128

Xu, Z., Harzallah, M. and Guillet, F.

Comparing of Term Clustering Frameworks for Modular Ontology Learning.

DOI: 10.5220/0006960401280135

In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 2: KEOD, pages 128-135

ISBN: 978-989-758-330-8

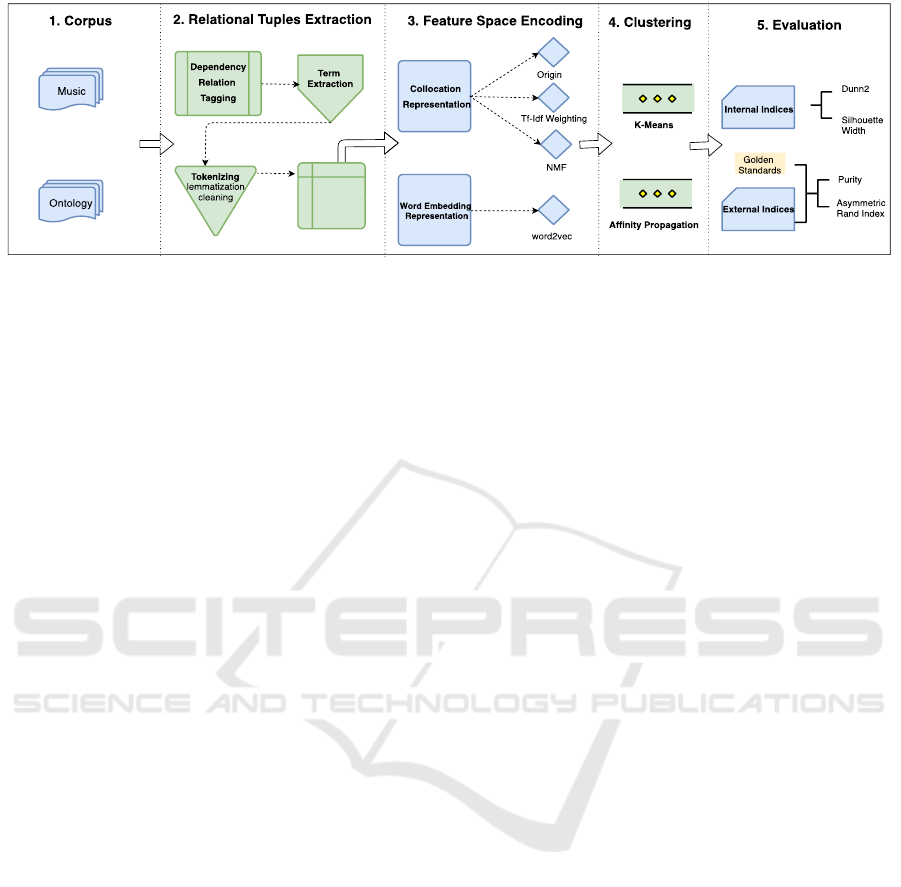
Figure 1: The Processing Workflow.

and preprocessing steps performed in section 3 and

expose feature space representation in section 4.

Sequently, we discuss the parameters of two

clustering techniques, analysis their results and give

instructions on future work.

2 RELATED WORK

In the field of knowledge acquisition on feature

selection, clauses and their functional equivalent

entities are apparent linguistic elements to collect

syntagmatic information. Cimiano et al. (2004)

describe the local context by extracting triples of

nouns, their syntactic roles, and co-occurred verbs.

They consider only verbs/object relations, so as to

emphasize partial features of terms working as object

by conditional probability measure. Similarly,

ASIUM (Faure and Nedellec,1998) acquires semantic

knowledge from case frames which include the

headword of noun phrases, verbs, and their

preposition or syntactic roles. For examples, for this

sentence “Bart travels by boat”, we get

Besides syntactic dependency, one recent work

by Gábor et al. (2016) extract co-occurring couples of

entities and present their semantic relations with

pattern-based representation. To interpret these

appearances, terms(entities) are presented by vectors

with frequent sequential pattern as components. Then

pattern-based feature space is constructed for

relation discovery. Moreover, according to Word2vec

(Mikolov et al., 2013), a term is statistically encoded

with analogies from its appearance in different

context, where the similarity of encoding vectors

reflect the semantic relations between terms.

Feature transformation is consistently discussed

in order to emphasize characteristics of extracted

phrases or sentences. Gábor et al. (2016) proposed to

apply PPMI weighting (positive pointwise mutual

information) to reduce bias in rare contexts, in which

values below 0 are replaced by 0. Tf-Idf (term

frequency-inverse document frequency) also

contribute to weight terms by their specificity to

documents. The computational complexity grows

exponentially with the size of the lattice, where NMF

(non-Negative Matrix Factorization) (Lee and Seung,

1999) is dedicated to solving the dimensionality

reduction problem by performing feature

compression.

Hierarchical clustering is preferred in terms

aggregation, which provides subsumption relation of

concepts for ontology learning. Based on that,

ASIUM creates conceptual clustering to aggregate

clusters for new concepts discovery. Besides, non-

hierarchical clustering organizes terms with different

relations. Affinity Propagation (Frey and Dueck,

2007) gives the link of terms represented by context

concepts of message passing between data points.

3 RESOURCES AND

PREPROCESSING

3.1 Resources

For the purpose of term clustering experiments, we

choose two corpora about two different domains:

music domain and ontology learning domain. For

each corpus, we possess a golden standard, which

includes a set of extracted terms that are classified

manually over the core concepts in the domain.

Music Corpus, is composed of 100M-word

documents, includes Amazon reviews, music

biographies and Wikipedia pages about theory and

music genres (Competitions.codalab.org, 2018). We

deliberately selected 2000 documents from 105,000

whose content includes the great proportion of terms

in predefined golden standards. Also, we have

Comparing of Term Clustering Frameworks for Modular Ontology Learning

129

Ontology Learning Corpus with 16 scientific articles

from the journal in the domain of ontology learning.

As shown in Table 1, these two corpora are

different in terms of domain and the amounts of docs,

however, a great contrast could help researchers to

figure out whether different strategies have a stable

performance of taxonomy discovery.

The aforementioned core concepts are predefined

for each domain in the golden standard. As Table 2

shown, 190 relevant terms were labeled into 5 classes

for Music golden standard, while larger terms were

labeled into 8 classes for Ontology learning golden

standard.

Table 1: Corpus Size and Statistics.

Corpus

Document

Size

Sampling

Sentences

Words

/documents

Music

105,000

2,000

33,051

762,180

381

Ontology

16(none)

4901

112,628

7,040

Table 2: Golden Standard.

Corpus

#core

concepts

nb. of terms

classified under

core concepts

Labels of Core Concepts

Music

190

Album, Musician, Music

Genre, Instruments,

Performance

Ontology

742

Component, Technique,

Ontology, Domain, Tool,

User, Step, Resource

3.2 Pre-processing

According to the syntactic roles, the skeleton of a

sentence is composed by subject and object along

with its corresponding verb. In other words, terms

with important syntactic roles cover the most

descriptive information in a sentence. Thus noun

phrases (NP), acting as subject or object, turn to be

highlighted in concept extraction, while verbs

reflecting the contextual components are used to

present the concrete connection between NPs.

From POS parsing stage, syntactic information is

extracted in order to identify NPs acting as subject or

object and their co-occurred verbs. In our lab, we

propose to use spaCyr (Kenneth and Akitaka, 2018)

as a parser tool. It decomposes an entire typical

syntactic tree, which shows the overwhelming

convenience in postprocessing, comparing to other

parser tools, such as cleanNLP and coreNLP.

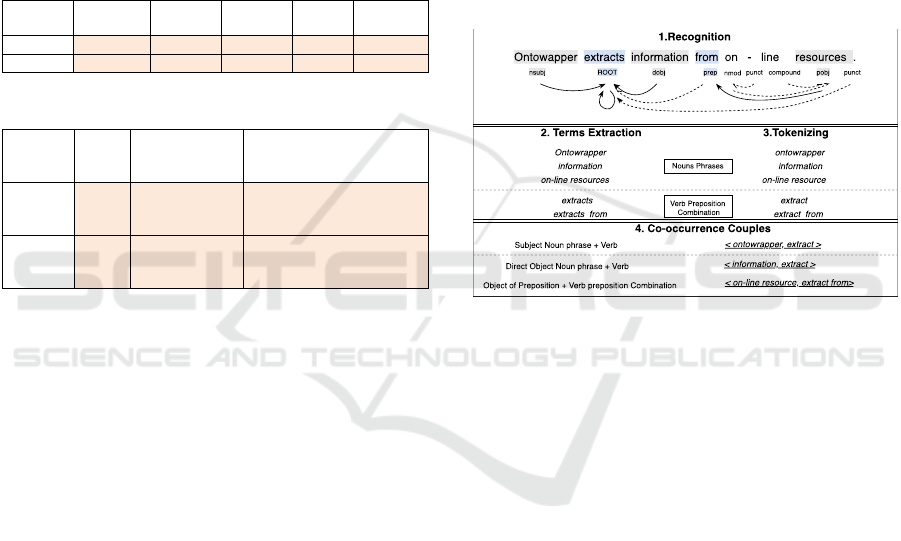
We start with skeleton terms recognition in each

sentence. As shown in the top of Figure 2, terms in a

sentence are presented with dependency relation,

where the shaded terms have been tagged as subject

(nsubj), ROOT and object. Subject (‘ontowrapper’)

and Direct Object (‘information’) point to ROOT

(‘extract’) with the solid line, while Proposition

Object (‘on-line resource’) indirectly points to ROOT

(‘extract from’) with the solid line. For non-skeleton

dependency, they are shown in dashed lines. Further,

we need to pay attention to the distinction between

passive and active sentence. To simplify the

composition of couples, it is feasible to record Passive

Subject (nsubjpass) as Direct Object (dobj).

Terms extraction is followed in the subpart of

Figure 1. With the help of head pointers, presenting

with the dashed line, noun phrases (NPs) and verb-

preposition combinations (VPCs) are gathered and

extracted in compound format. Then, they are cleaned

and lemmalised after tokenization. Finally, the

couples of ROOT and skeleton terms are tagged with

roles of subject or object within sentences and

recorded as intermediate data in replacement of raw

context.

Figure 2: Instantiated Co-occurrence Couples Extraction.

4 FEATURE

REPRESENTATIONS

We discuss hereinafter two disparate approaches to

build basic feature representations. One of the

fundamental vector spaces takes advantage of the

frequency of NPs and VPCs couples, while another

feature representation uses entire context for word

embedding. They differ in the range of terms

colocation, for which the fundamental method

facilitates syntactic roles for co-occurrence couples

within a sentence, while the word embedding method

takes into account the surrounding context of all

appearance places of a term. Additionally, to tackle

the sparseness of phrases, dimensionality reduction

techniques are employed to condense feature

representation.

4.1 Co-occurrence Representation

The aforementioned couples are extracted and

transformed into a co-occurrence frequency matrix,

KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development

130

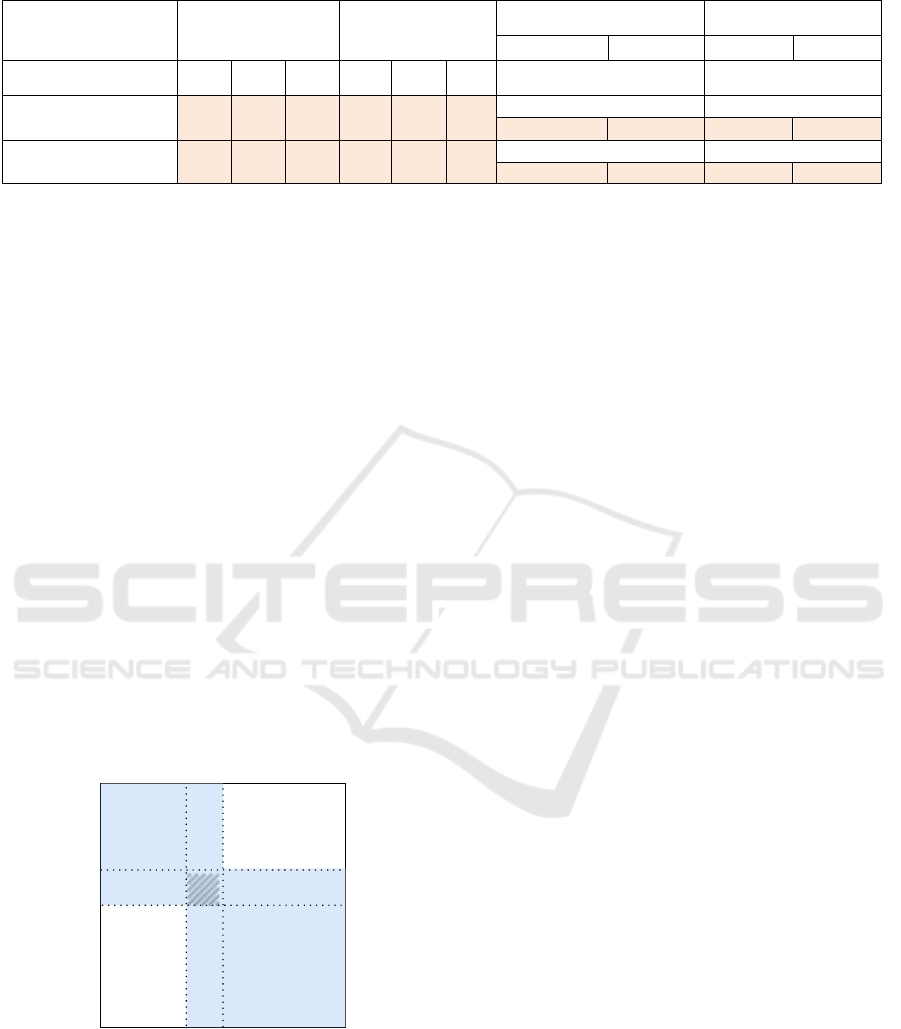
Table 3: Dimensionality Reduction after Threshold.

#NPs

#VPCs

Reduction with

Frequency

Reduction with

Tf-Idf

#NPs

#VPCs

#NPs

#VPCs

Corpus

subj.

obj.

both

subj.

obj.

both

Threshold 𝜎

Summation of frequency

Threshold 𝜎

Summation of value

Music

3138

7272

1560

254

3054

532

𝜎

573

660

582

456

Ontology

401

1643

281

889

219

𝜎

602

505

563

502

where VPCs are features of NPs. Since we notice the

big gap of functionality between subject and object,

they are organized into separate co-occurrence

couples, named subject co-occurrence and object co-

occurrence.

Actually, one type of the co-occurrence couples,

either subject or object, could only cover segmental

linguistic context. It is required to deliberatively

combine subject and object co-occurrence couples. In

Figure 3, we differentiate NPs and VPCs into ‘pure

subject’, ‘pure object’ and common part. The

common part means NPs and VPCs appear in both

subject and object. Entirely, the merged matrix

comprises 9 subparts, where the non-existing couples

present to be all zero (blank rectangles) and the ‘pure

couples’ (subject or object) present respective

frequency in two blue rectangles. Common couples

(shaded rectangles) , overlapping between subject

rectangle and object rectangle, are filled with the

cumulate frequency of subject couples and object

couples. Positively, as long as subject and object co-

occurrence couples join together, the merged matrix

Figure 3: Merged Co-occurrence Matrix.

theoretically emcompasses complete linguistic

information. Hence, it would work as primary

representation if encoding techniques are required in

the following part.

4.2 Dimensionality Reduction

The sparseness of the merged co-occurrence matrix

becomes a significant issue. Row and column

reduction are simultaneously required to decrease the

noise effect. In Table 3, a frequency-based threshold

𝜎

could be used to eliminate most common and rare

elements. Similarly, Tf-Idf encoding representation

provides bi-directional selection respecting to the

relevance of NPs to specific VPCs. While NMF

encoding is dedicated to reducing feature space.

4.2.1 Weighted Co-occurrence

Based on the merged representation, we would like to

weight values to decrease the impact of common and

rare NPs and differentiate the importance of co-

occurrence couples. Tf-Idf, is designed with this

discriminative purpose. Basically, it extracts the most

descriptive terms of documents, which could also

extend to weight the most significant NPs to their

VPCs, instead of documents. With certain thresholds

in rows and columns, only distinguishing NPs and

their co-occurred VPCs are kept at last. Thanks to the

derivation of Tf-Idf, the strong associated NPs and

VPCs are selected according to threshold 𝜎

in Table

3 so that the weighted co-occurrence matrix gets

refined with reduced dimensionality.

4.2.2 NMF Co-occurrence

Term co-occurrences could be separated into 3 levels

according to the identity of words in context

(Gamallo and Bordag, 2011). In first-order co-

occurrence, terms appear together in identical

context. As for two terms are associated by means of

second-order co-occurrence, they share at least one-

word context and have strong syntactic relations.

Besides, terms do not co-occur in context with the

same words but between words that can be related

through indirect co-occurrences, namely third

(higher) order co-occurrence. To manipulate this,

NMF (Lee and Seung, 1999) is applied to condense

isolated VPCs into encoded features. From previous

NPs as subj.

NPs as obj.

NPs as both

VPCs with subj.

VPCs with both

VPCs with obj.

Comparing of Term Clustering Frameworks for Modular Ontology Learning

131

Figure 4: Clustering and Evaluation.

related works, it is reasonable to set the number of

features to be 100 during experiments. Then NPs with

indirect co-occurrence are signified in the new dense

feature space.

4.3 Word Embedding Representation

From the distribution of contextual information, it

allows building feature vectors that adapt for

semantic similarity tasks. Word embedding

representation was trained using word2vec (Mikolov

et al., 2013) algorithm under the skip-gram model. In

the local aspect, terms can be represented by vectors

of its colocated words within certain window size,

called colocating vectors. The sum of colocating

vectors around appearance place of a term constitute

the context vectors. As for the global aspect, the sum

of context vectors at all appearance places of a term

gives the construction of word vectors. It integrates

all the contextual features of a word and statistically

present with encoded similarity. One of the

advantages of word2vec is that it embeds techniques

to achieve dimension reduction purposes by

indicating the required amount of features. To be

comparable with NMF encoding technique, the

number of features with word2vec is also given by

100.

5 CLUSTERING

The most typical clustering technique is k-means

(Hartigan and Wong, 1979). One of the drawbacks is

that k-means is quite sensitive to the initial set of

seeds. On the other hand, affinity propagation uses

graph distance that performs in a ‘message passing’

way between data points (Frey and Dueck, 2007). It

does not need to determine the number of clusters in

advance and the centroid of each cluster is specified

after calculation, which turns out to be helpful for

interpretation. As for distance measurement in

clustering, cosine dissimilarity is preferred in both

techniques because of the high dimension of feature

space. As shown in Figure 4, clustering iterates with

adjusted parameters k ranging from 2 to 50, indicating

the variation of the number of clusters. Each iteration

allows for analysis of clustering performance

respecting to internal indices and external indices.

6 EVALUATION

6.1 Evaluation Indices

A large number of indices provide possibilities to

assess the clustering quality (Aggarwal and Zhai,

2012). In order to simplify the discrimination process,

we select two distinct indices respectively for internal

evaluation and external evaluation.

6.1.1 Indices for Internal Evaluation

Silhouette width (Rdrr.io., 2018) and adjusted Dunn

Index are chosen as indices of internal evaluation.

Silhouette method specifies how well each object lies

within its cluster.

𝑠

(

𝑖

)

𝑏

(

𝑖

)

− 𝑎(𝑖)

max⁡(𝑎

(

𝑖

)

, 𝑏

(

𝑖

)

(1)

In equation 1, 𝑎(𝑖) represents average dissimilarity

between i and all other points of the cluster to which

i belongs. For all other clusters⁡𝑑(𝑖, 𝐶), denotes

average dissimilarity of i to all observations of C.

𝑏(𝑖)is set by the smallest 𝑑(𝑖, 𝐶)and can be seen as

the dissimilarity between i and its “neighbor” cluster.

A high average silhouette width indicates a good

clustering according to features.

Adjusted Dunn Index proposed by Pal and Biswas

(1997) overcomes the presence of noise comparing to

original Dunn Index (Dunn, 1974). In general, they

are both dedicated for the identification of “compact

and well-separated clusters”. Higher values are

preferred, which shows a good performance of

compactness. Notably, the Dunn Index family does

not exhibit any trend with respect to the number of

clusters, of which this property is exceedingly

welcomed since the number of clusters varies in

different iterations.

NPs

feature

space

iterate with parameter k of clustering

cluster with

adjusted k

Golden

Standard

Internal Indices

External Indices

Evaluation

KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development

132

6.1.2 Indices for External Evaluation

In the case of external evaluation, the indices are

slightly different from formers because of the use of

a golden standard. According to expected core

concept classes, Purity and Asymmetric Rand Index

are representative of clustering quality measurement.

To compute purity, each cluster firstly is assigned

with a label that is most frequent in it, according to

the gold standard, then this assignment is calculated

by counting the number of correctly assigned

elements dividing by all elements. High purity is easy

to achieve when the number of clusters is large. A

larger amount of clusters may refine the branches of

structure in ontology building, however, it incurs

complexity to label clusters with core concepts,

performing as the first step of ontology learning. Thus

we could not use only purity to trade off the quality

of clustering against the number of clusters.

The Asymmetric Rand Index proposed by Hubert

L. and Arabie P. (1985) is also considered, for which

it provides the comparison between 2 different sets of

labels of same extracted data. It differs from typical

Rand Index because it allows for inclusion from a

greater number of partitions to relevant partitions. For

example, the partitions varied with clustering are

always larger than classes of core concepts. The

characteristic of inclusion provides a more accurate

calculation.

6.2 Repetitions with Number of

Clusters

To weaken the impact of randomness of clustering,

each experiment is repeated 10 times to go through all

parameters of k ranging from 2 to 50, so as to get the

convincing results with mean values. Thus each index

is statistically averaged to be presented for

evaluation. For example, as Figure 5 shows, curves of

all indices for NP_VPC representations are plotted

separately in Ontology Corpus and in Music Learning

Corpus. To select the optimal amount of clusters, we

attempt to solve the multicriteria optimization

problem by finding the first peak of a fluctuating line

and assuring a rather higher summation over the

entire indices. The dashed lines indicate the final

parameter choice for this specific representation.

Besides, optimal parameters of the rest

representations are selected with the same rules and

are directly given by our extensive experiments. This

process could be achieved automatically by inserting

algorithms of corresponding rules. However, the

choice in Figure 5 is manually selected for the time-

saving purpose.

It seems better to choose a locally optimal k

around the number of core concepts, so as to restrict

the number of clusters within a suitable range for

ontology learning purpose. This assumption takes the

characteristics of primitive concepts into

considerations. However, it rejects the possibilities of

high-quality clustering along with smaller clusters.

Therefore, in replace of the local optimization

approach, global optimization of all indices is

preferred to choose parameters of k-means clustering

for every representation.

(1)

(2)

Figure 5: Example of Parameter Selection with K-Means.

6.3 Interpretation of Clustering

Term clustering of feature representations is expected

to capture core concepts labels in relevant with its

syntactic context. Apart from the two distinct

methods of feature extraction, such as NPs-VPCs

number of clusters

Comparing of Term Clustering Frameworks for Modular Ontology Learning

133

couples and word embedding techniques, the

influence of encoding techniques also changes the

clustering quality.

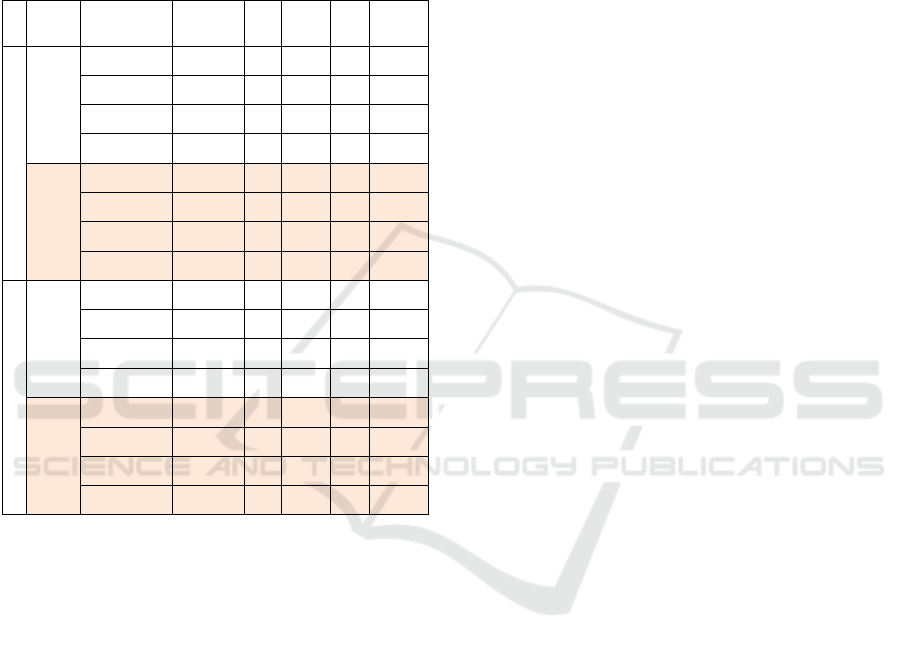
Table 4 indicates the evaluation of clustering with

golden standards. Encoding representations of NPs

are denoted with corresponding techniques, such as

‘NP_VPC_tfidf’ and ‘NP_VPC_NMF’. While the

word embedding representation is said as ‘NP_w2v’.

Table 4: K-Means and Affinity Propagation Evaluation.

Corpus

Feature

Representation

# optimal

cluster/#core

concepts

Purity

Asymm

Rand

Index

Dun2

Index

Silhouette

Width

Ontology

NP_VPC

2.5(20/8)

0.430

0.009

0.553

0.196

NP_VPC_tfidf

1.875(15/8)

0.391

0.007

0.927

0.394

NP_VPC_NMF

3.375(27/8)

0.545

0.067

0.381

0.390

NP_w2v

2.25(18/8)

0.535

0.149

0.648

0.147

Music

NP_VPC

6(30/5)

0.906

0.6696

0.075

0.126

NP_VPC_tfidf

2(10/5)

0.060

0.085

NP_VPC_NMF

3.4(17/5)

0.761

0.348

0.559

0.292

NP_w2v

4(20/5)

0.871

0.736

0.688

0.135

Ontology

NP_VPC

1.87(15/8)

0.450

0.044

0.730

-0.131

NP_VPC_tfidf

1.75(14/8)

0.410

0.738

-0.078

NP_VPC_NMF

2.625(21/8)

0.492

0.096

0.743

-0.108

NP_w2v

1.5(12/8)

0.445

0.048

0.789

-0.099

Music

NP_VPC

0.6(3/5)

0.666

-0.11

0.921

- 0.02

NP_VPC_tfidf

0.4(2/5)

0.75

NP_VPC_NMF

0.8(4/5)

0.666

-0.66

0.860

- 0.03

NP_w2v

2.4(12/5)

0.445

0.048

0.789

- 0.09

In the upper half part of Table 4, diverse feature

representations are clustered with k-means. In the

aspect of the corpus, it is evident that Music corpus

gives higher purity and higher Asymmetric Rand

Index than that of Ontology Learning corpus. It can

be due to that bigger corpus (Music Corpus) provides

significant contextual features to cluster terms with

taxonomic relations. On contrary, poor Dunn2 Index

and Silhouette width in Music Corpus indicate terms

do not compact closely with others, implying that

features in bigger corpus have less similarity to

others.

In the bottom part of Table 4, terms are clustered

with affinity propagation algorithm. It is noticeable

that NP_VPC representation family outperforms

word2vec representation in Music Corpus. For

NP_VPC representation family, the number of

clusters in Music corpus is rather lower than that in

Ontology Learning Corpus and the purity stays in a

higher level. It is reasonable to infer that NP_VPC

family are well suitable for AP clustering algorithm.

Comparing these two clustering methods, AP has

a higher Dunn2 Index than that of K-Means, which

means clusters of AP compact well. However, the

negative silhouette width with AP indicates the

intersection of clusters, which means feature similar

terms probably share different labels. That is

inevitable in linguistic because the similar context of

terms could not straightly infer to the same meaning

of them.

In terms of the encoding representations, Tf-Idf

representations provide unevenly lower accuracy and

higher compactness in clusters. While NMF

representations have a good clustering quality overall.

In general, NP_VPC family representations

appear to have a better clustering quality with AP

clustering method than word2vec representation. On

the other hand, encoding representations show an

enhanced quality of clustering with K-Means.

Precisely, NMF representations are prominent in

most clustering situations.

7 CONCLUSIONS

Many works suggest making use of core ontology to

build the modular ontology. However, most of these

efforts are manually constructed and seldom in

automatic approach. Term clustering according to a

core ontology supports modular ontology

construction without artificial demands. Taxonomic

relations are constructed by gathering of NPs

appearing with prominent syntactic roles after VPCs

respecting to core concepts. Successfully we

constructed feature space with these characteristics

from two specialized corpora. To tackle the problem

of sparsity, we benefit from feature selection and

feature extraction techniques, such as adjusted Tf-Idf

algorithm and NMF technique. Apart from that,

word2vec is also compared as a benchmark. Along

with all the extended representations, terms are

clustered by K-Means and affinity propagation

algorithm. We found that co-occurrence feature space

appearing with syntactic roles, is proved to have a

better clustering quality with the affinity propagation

algorithm than that of K-Means. Furthermore, the

usage of NMF on co-occurrence matrix could

prominently improve clustering performance.

From the comparison of term clustering

frameworks, we recommend beginning with a bigger

domain-specific corpora. Since the syntactic relations

between noun phrases and verbs are insufficient as

features representation, with the assistance of

encoding techniques, it gives rather convincing

results in term clustering, which provides us a

guideline for modular ontology building.

KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development

134

In the future work, we would like to benefit from

prior knowledge of core concepts to assist in term

selection process, so as to consider the characteristics

of terms that related to core ontology. Furthermore,

the morphological analysis could also help to merge

specific terms into a general concept, which gives

more distinguishing features of term clustering.

REFERENCES

Aggarwal, C.C. and Zhai, C., 2012. A survey of text

clustering algorithms. In Mining text data (pp. 77-128).

Springer, Boston, MA.

Borgo, S. and Leitão, P., 2004, October. The role of

foundational ontologies in manufacturing domain

applications. In OTM Confederated International

Conferences" On the Move to Meaningful Internet

Systems" (pp. 670-688). Springer, Berlin, Heidelberg.

Buitelaar, P., Olejnik, D. and Sintek, M., 2004, May. A

protégé plug-in for ontology extraction from text based

on linguistic analysis. In European Semantic Web

Symposium (pp. 31-44). Springer, Berlin, Heidelberg.

Burita, L., Gardavsky, P. and Vejlupek, T., 2012. K-GATE

Ontology Driven Knowledge Based System for

Decision Support. Journal of Systems Integration, 3(1),

p.19.

Cimiano, P., de Mantaras, R.L. and Saitia, L., 2004.

Comparing conceptual, divisive and agglomerative

clustering for learning taxonomies from text. In 16th

European Conference on Artificial Intelligence

Conference Proceedings (Vol. 110, p. 435).

Competitions.codalab.org. (2018). CodaLab - Competition.

[online] Available at: https://competitions.codalab.org/

competitions/17119#learn_the_details-terms_and_

conditions [Accessed 12 Jun. 2018].

Dunn, J.C., 1974. Well-separated clusters and optimal

fuzzy partitions. Journal of cybernetics, 4(1), pp.95-

104.

Faure, D. and Nédellec, C., 1998. Asium: Learning

subcategorization frames and restrictions of selection.

Fernández-López, M., Gómez-Pérez, A. and Juristo, N.,

1997. Methontology: from ontological art towards

ontological engineering.

Frey, B.J. and Dueck, D., 2007. Clustering by passing

messages between data points. science, 315(5814),

pp.972-976.

Gábor, K., Zargayouna, H., Tellier, I., Buscaldi, D. and

Charnois, T., 2016, October. Unsupervised Relation

Extraction in Specialized Corpora Using Sequence

Mining. In International Symposium on Intelligent

Data Analysis (pp. 237-248). Springer, Cham.

Gamallo, P. and Bordag, S., 2011. Is singular value

decomposition useful for word similarity extraction?.

Language resources and evaluation, 45(2), pp.95-119.

Gillis, N., 2014. The why and how of nonnegative matrix

factorization. Regularization, Optimization, Kernels,

and Support Vector Machines, 12(257).

Gruber, T.R., 1993. A translation approach to portable

ontology specifications. Knowledge acquisition, 5(2),

pp.199-220.

Harris, Z., 1954. Distributional structure.(J. Katz, Ed.)

Word Journal Of The International Linguistic

Association, 10 (23), 146-162.

Hartigan, J.A. and Wong, M.A., 1979. Algorithm AS 136:

A k-means clustering algorithm. Journal of the Royal

Statistical Society. Series C (Applied Statistics), 28(1),

pp.100-108.

Hubert, L. and Arabie, P., 1985. Comparing partitions.

Journal of classification, 2(1), pp.193-218.

Kenneth, B. and Akitaka, M. (2018). [online] Cran.r-

project.org. Available at: https://cran.r-project.org/

web/packages/spacyr/spacyr.pdf [Accessed 12 Jun.

2018].

Kutz, O. and Hois, J., 2012. Modularity in ontologies.

Applied Ontology, 7(2), pp.109-112.

Lee, D.D. and Seung, H.S., 1999. Learning the parts of

objects by non-negative matrix factorization. Nature,

401(6755), p.788.

Mikolov, T., Chen, K., Corrado, G. and Dean, J., 2013.

Efficient estimation of word representations in vector

space. arXiv preprint arXiv:1301.3781.

Nlp.stanford.edu. (2018). Evaluation of clustering. [online]

Available at: https://nlp.stanford.edu/IR-book/html/

htmledition/evaluation-of-clustering-1.html

Oberle, D., Lamparter, S., Grimm, S., Vrandečić, D., Staab,

S. and Gangemi, A., 2006. Towards ontologies for

formalizing modularization and communication in

large software systems. Applied Ontology, 1(2),

pp.163-202.

Pal, N.R. and Biswas, J., 1997. Cluster validation using

graph theoretic concepts. Pattern Recognition, 30(6),

pp.847-857.

Rdrr.io. (2018). silhouette: Compute or Extract Silhouette

Information from Clustering [online] Available at:

https://rdrr.io/cran/cluster/man/silhouette.html

[Accessed 6 Jun. 2018].

Smith, J., 1998. The book, The publishing company.

London, 2

edition.

Comparing of Term Clustering Frameworks for Modular Ontology Learning

135