
A Roadmap towards Tuneable Random Ontology Generation Via
Probabilistic Generative Models
Pietro Galliani, Oliver Kutz and Roberto Confalonieri
Free University of Bozen-Bolzano, Faculty of Computer Science, 39100, Bozen-Bolzano, Italy
Keywords:
Ontology Generation, Benchmarking, Testing.
Abstract:
As the sophistication of the tools available for manipulating ontologies increases, so does the need for novel
and rich ontologies to use for purposes such as benchmarking, testing and validation. Ontology repositories
are not ideally suited for this need, as the ontologies they contain are limited in number, may not generally
have required properties (e.g., inconsistency), and may present unwelcome correlations between features. In
order to better match this need, we hold that a highly tuneable, language-agnostic, theoretically principled tool
for the automated generation of random ontologies is needed. In this position paper we describe how a proba-
bilistic generative model (based on features obtained via the analysis of real ontologies) should be developed
for use as the theoretical back-end for such an enterprise, and discuss the role of the DOL metalanguage in it.
1 INTRODUCTION
Due to the ever-increasing practical importance of Se-
mantic Web technologies, in recent years there has
been a remarkable increase in the pacing of the study
and development of algorithms and tools for ma-
nipulating, analyzing or exploring ontologies (Cris-
tani and Cuel, 2005; Katifori et al., 2007). Every
month, sophisticated novel techniques are developed
for identifying and resolving inconsistencies in on-
tologies (Plessers and De Troyer, 2006; Troquard
et al., 2018), representing and answering queries over
them (Wache et al., 2001; Zhang et al., 2018), alig-
ning ontologies (Choi et al., 2006; Granitzer et al.,
2010; Dragisic et al., 2014), and assisting human
users in their creation and manipulation (Choi et al.,
2006; Zablith et al., 2015).
The problem of testing and validating such techni-
ques, as well as the problem of comparing their per-
formance with that of related approaches, cannot be
solved without a steady supply of new, independently
generated ontologies satisfying specific criteria (e.g.,
language choice, size, height and tree-width of indu-
ced class hierarchy, distribution of the operator depth
in logical expressions and so forth).
The existence of Ontology Repositories (e.g., Bi-
oPortal (Matentzoglu and Parsia, 2018) and Onto-
hub (Codescu et al., 2017)) making publicly available
a number of human-generated ontologies of practical
importance is not, in itself, a satisfactory solution to
this need. In more detail:
1. Although the number of ontologies contained in
such repositories is not small, it is not sufficient
for performing each instance of testing or ben-
chmarking on a truly novel corpus of ontologies.
This is especially problematic in the case of tools
designed to be used for specific subclasses of on-
tologies, for which few examples may be availa-
ble in such repositories, or for tools that make use
of machine learning methodologies (and which,
therefore, need to be trained, cross-validated and
tested on different corpora of ontologies).
2. Tools for solving certain highly important types of
problems, like ontology repair, operate on ontolo-
gies with properties (e.g inconsistency) which are
not generally shared by the ontologies uploaded
to public repositories. It is, of course, possible to
induce artificially such properties via ad-hoc met-
hods (e.g., adding random axioms to an ontology
until it is made inconsistent), but it then becomes
rather opaque whether the resulting corpus of on-
tologies bears any resemblance to the typical real
use cases.
3. In many cases, it would be important to be able
to examine how the performance of a tool is af-
fected by various changes in the properties of the
input ontologies. However, it is not generally pos-
sible to sample from repositories adequately rich
corpora of ontologies which differ with respect
Galliani, P., Kutz, O. and Confalonieri, R.
A Roadmap towards Tuneable Random Ontology Generation Via Probabilistic Generative Models.
DOI: 10.5220/0006961103510357
In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 2: KEOD, pages 351-357
ISBN: 978-989-758-330-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
351

to certain features and are not statistically distin-
guishable with respect to others: instead, diffe-
rent features are generally highly correlated. For
instance: if the larger ontologies of a repository
tend to be little more than taxonomies, having
relatively few complex axioms in comparison to
the smaller ontologies of the repository, then sam-
pling ontologies of different sizes from it in order
to study the effect of ontology dimension on the
performance of an algorithm might lead unwary
researchers to outright incorrect conclusions.
One additional difficulty worth mentioning, mo-
reover, is that there does not, at the moment, exist
a truly comprehensive, experimentally validated set
of ontology features with respect to which to validate
and compare tools and algorithms. Certainly, the clas-
sification of ontologies is not unexplored territory al-
together; but the features thus far studied in the lite-
rature, though certainly interesting and worth of furt-
her analysis, have not for the most part been obtained
through systematic exploration of the available cor-
pora but rather as a result of the researchers’ own in-
terests in certain properties of ontologies.
To bridge this gap, the development of a new
generation of tools, based on principled theoretical
foundations, for the automatic generation of random
ontologies, is required. These tools should be tune-
able with respect to a variety of (logic-agnostic) fe-
atures, and these features should in turn be extracted
and justified through the study of corpora via network
analysis-inspired techniques and probabilistic model-
ling.
We here outline a possible roadmap towards such
an achievement, discussing furthermore the current
approaches to ontology generation and their limita-
tions.
2 TOWARDS TUNEABLE
RANDOM ONTOLOGY
GENERATION
Against the above mentioned background, it is clear
that extracting a selection of human-readable, com-
prehensive ontology features and using them for the
generation of random ontologies suitable for testing
purposes is a major and challenging task.
Our overall aim is then to:
Develop a tuneable, language-agnostic gene-
rator of random ontologies suitable for the
testing and benchmarking of algorithms and
tools. Relevant features will be extracted semi-
automatically from corpora of ontologies. These
features will be used for the development of
Markov Chain Monte Carlo (MCMC)-like sam-
pling algorithms over ontologies.
The usefulness of the resulting generator for
benchmarking and testing purposes will be ex-
perimentally verified.
To achieve the general aims outlined above, we be-
lieve that the following three specific objectives need
to be solved.
Objective 1 – Ontology Features: A fundamental
prerequisite for tuneable ontology generation is
to first generate and justify, on empirical grounds,
a set of language-agnostic ontology features and
study their distribution and correlations in corpora
of human-created ontologies. We will then need
to find (possibly multiple) choices of default va-
lues for these features that may be used to direct
the generation of realistic random ontologies,
barring users choosing different values for them
(cf. Figure 1, Node 1: Feature Analyzer). It is
worth remarking here that obtaining such features
and classifying real ontologies with respect to
them will result in a product of inherent value
for the scientific community, even aside from
their intended application to random ontology
generation: indeed, it will provide the basis for a
reliable, empirically grounded, language-agnostic
taxonomy of ontologies.
Objective 2 – Generative Probabilistic Model:
The thus obtained ontology features and statistics
will then serve as the basis for a Generative Pro-
babilistic Model (see Figure 1, Node 3: Ontology
Generator) for ontologies which, for any given
choice of parameters, will provide a mechanism
for producing novel, random ontologies. The
precise structure of such a model will, of course,
depend heavily on the nature of the features
found as well as on their probabilistic distribution
over the corpora; but as a preliminary hypothesis,
we think that an agent-based approach in which
multiple artificial agents add or remove certain
patterns of expressions to the ontology with
a probability which depends on the values of
certain features is likely to be a profitable one in
this context, in such a way that the overall proba-
bility distribution of features is as required. This
can be seen, after a fashion, as a generalisation
of Markov Chain Monte Carlo approaches to
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
352
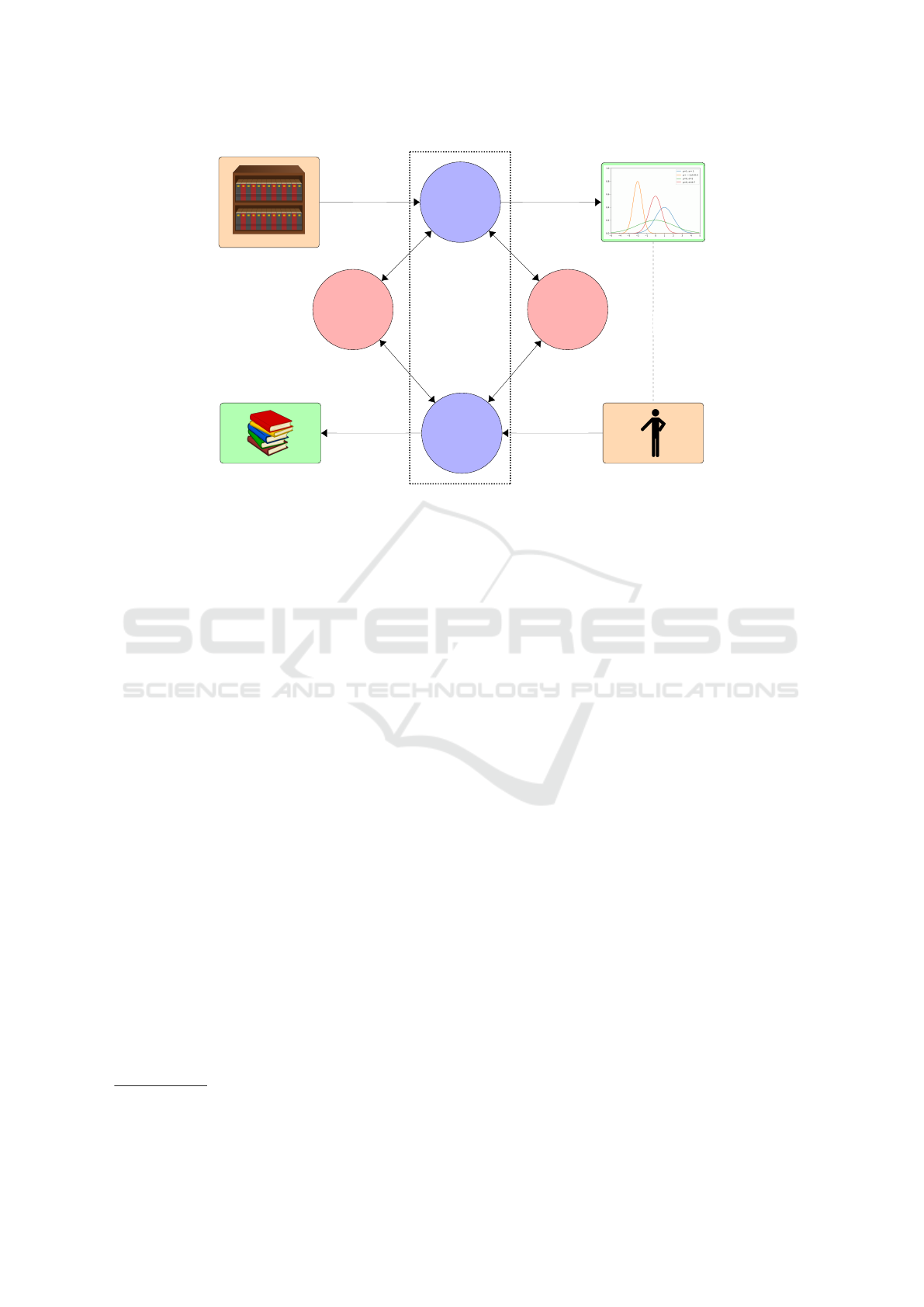
Real Repositories
– 1 –
Feature
Analyser
Parameter Distribution
– 4 –
DOL
Specification
(swappable)
– 2 –
Reasoner
(swappable)
user
– 3 –
Ontology
Generator
Random Ontologies
Samples
Feature Values
Chosen Parameters
Random Ontology
Typical
Parameters
Ontorator
Figure 1: Tuneable Ontology Generation: workflow, structure and modules.
random sampling.
Objective 3 – Implementation and Validation: We
will then implement the thus obtained theoretical
model. The implementation will also be language
agnostic, in the sense that it will be applicable to
ontologies described in any language as long as a
DOL specification and a suitable reasoner will be
provided (see Nodes 2 and 4 of Figure 1, as well
as the discussion below). This implementation
will then be validated by means of comparing
the performance of algorithms over real-world
ontologies and over synthetic ones.
3 THE ROLE OF DOL
The Distributed Ontology, Modeling, and Specifica-
tion Language (DOL) (Mossakowski et al., 2015) was
submitted in November 2015 to the Object Manage-
ment Group (OMG), and formally adopted in 2016 as
an international standard. The finalisation of this lan-
guage for heterogeneous logical specification invol-
ved more than 50 international experts overall.
1
DOL
has support for logical heterogeneity, structuring, lin-
king, and modularisation, i.e., crucial features to orga-
nise a large number of ontologies into structured re-
positories. Also, several key technologies have been
developed in the DOL ecosystem, most importantly
the OntoHub repository and reasoning platform (Co-
descu et al., 2017).
2
1
See http://ontoiop.org
2
See http://ontohub.org
The availability of DOL is thus essential to the
overall feasibility of the research proposed here, for
at least three different reasons:
• In its role as a unifying meta-language, it allows
our approach to be truly language-agnostic, in that
it will be able to generate random ontologies (or
estimate feature parameter distributions given cor-
pora) for any formalisms for which DOL speci-
fications and reasoners can be provided (see Fi-
gure 1);
• The OntoHub repository, which, as already men-
tioned, is part of the DOL ecosystem and provides
a rich collection of ontologies in various specifi-
cation languages, will be essential for our work in
feature selection over ontologies as well as for the
testing of the resulting framework.
• The rich linking and modularisation constructs of
DOL support specifically two crucial operations:
1) the systematic build-up of larger ontologies
from smaller parts, and 2) the recording of rela-
tionships between ontologies in different logical
formalisms, e.g. recording the approximation of
an ontology in a less expressive language, via a
theory interpretation. Note that operationalising
this structural information is non-destructive, i.e.,
the parts of a larger ontology can be recovered
from the structural links.
A Roadmap towards Tuneable Random Ontology Generation Via Probabilistic Generative Models
353

4 EXTRACTING FEATURES
FROM ONTOLOGY CORPORA
As the size and the practical importance of ontologies
increased, it is not surprising that the interest in the
development of ontology metrics – that is, numerical
quantities that summarize the overall features of on-
tologies – has also grown (Lozano-Tello and G
´
omez-
P
´
erez, 2004; Garc
´
ıa et al., 2010; Kang et al., 2012;
Sicilia et al., 2012; McDaniel et al., 2018).
Such metrics have been introduced for different
purposes, such as assessing the quality of an ontology
(McDaniel et al., 2018), predicting the performance
of reasoners (see e.g., (Tempich and Volz, 2003;
Kang et al., 2012)) or measuring the cognitive com-
plexity of OWL justifications (Horridge et al., 2011).
Approaches along these lines seem to have been
fairly effective in predicting the results of benchmarks
in real ontologies. Their effectiveness for evaluating
ontology quality seems more limited, owing to some
degree to the greater intangibility and complexity of
the concept, but nonetheless such metrics can have a
useful role in this context (Tartir and Arpinar, 2007;
Duque-Ramos et al., 2011; Sicilia et al., 2012; Neu-
haus et al., 2013; McDaniel et al., 2018).
These metrics, in general, are hand-crafted by re-
searchers on the basis of their intuitions and expe-
rience with ontologies. We think that, in this con-
text, it would be instead useful to take inspiration
from approaches to representation learning on graphs
(see (Hamilton et al., 2017b) for a survey) such as
node2vec (Grover and Leskovec, 2016) and Grap-
hSAGE (Hamilton et al., 2017a) to automatically ex-
tract the salient features from a corpus of ontologies.
Automatically extracted features, however, will
not suffice for our needs: indeed, for our purposes we
need to find not only features over ontologies which
are suitable for clustering and prediction tasks or for
ontology generation, but also those features which
can be understood and used as parameters by humans.
Therefore, we envision a two-stage approach to
the extraction of features from ontologies:
1. Automated feature learning techniques can be
used to extract statistically significant (but not ne-
cessarily human-readable) features from ontology
corpora;
2. These features can then be further analysed, at-
tempting to either (a) find intuitively comprehen-
sible, human-readable analogues or (b) decom-
pose them in terms of multiple human-readable
features.
5 A GENERATIVE
PROBABILISTIC MODEL FOR
ONTOLOGIES
A natural source of inspiration for the study of ge-
nerative models for ontologies is the study of such
models for graphs. This is a very rich topic, and
many such models, like Exponential Random Graphs
(Erd
¨
os and R
´
enyi, 1959; Robins et al., 2007), the Ba-
rab
´
asi-Albert model (Albert and Barab
´
asi, 2002), sto-
chastic block models (Airoldi et al., 2008) and Kro-
necker graphs (Leskovec et al., 2010) have been ex-
tensively studied in the literature.
It is difficult to predict in advance the exact struc-
ture of the model which we will develop, as much will
of course depend on the results of our previous inves-
tigation about ontology features.
We think, in analogy with some recent works on
graph generation (see e.g., (You et al., 2018)), that
a potentially fruitful approach might be to create a
MCMC-like model in which various transformations
(e.g., axiom additions, deletions and modifications)
might be applied to an ontology with a probability
that depends on the current values of its features.
By assigning correct weights to the probability of
each transformation, it would be then possible to en-
sure that the probability distribution over the features
would indeed match the specified one; and, by sam-
pling from this distribution, we could indeed obtain
random ontologies for any choice of parameter value.
As an added advantage, this type of model - repre-
sented as a set of possible transformation over ontolo-
gies, with pre-requisites and weights - would be fairly
human-interpretable and could be modified manually
if desired.
6 IMPLEMENTATION, TESTING
AND COMPARISON
The best known and most used frameworks for the
benchmarking of tools over ontologies are the Lehigh
University Benchmark (LUBM) (Guo et al., 2005)
and the University Ontology Benchmark (UOBM)
(Ma et al., 2006). Albeit certainly useful, the general
applicability of these two frameworks for generating
ontologies is hindered by at least three factors:
1. The languages of the ontologies generated
through these two frameworks are fixed (to a sub-
set of OWL Lite and to the complete OWL Lite or
OWL DL respectively) and not easy to change;
2. The structure of the TBoxes obtained via these ap-
proaches are fairly static, and not necessarily re-
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
354

flective of that of all real ontologies;
3. Although there are options for changing somew-
hat the properties of the ontologies generated via
these approaches, the amount of fine-tuning that
is possible to perform with respect to the features
of the ontology is very limited.
The programme sketched in this work is thus con-
siderably more ambitious than LUBM and UOBM:
indeed, as we argued before, it would be highly desi-
rable to develop a tool for the generation of random
ontologies that was highly tuneable, language agnos-
tic, theoretically well founded, and capable of gene-
rating ontologies whose statistical features are ana-
logous to those of arbitrary real world ontologies.
Despite their undeniable practical success, LUBM
and UOBM are quite far indeed from this mark.
A more general approach, much closer in con-
cept to our research perspectives, is the one employed
by the OTAGen ontology generator (Ongenae et al.,
2008). In short, given a number of parameter choi-
ces (e.g., number of classes, number of logically de-
fined classes, number of individuals, minimum and
maximum number that non-functional object proper-
ties are instantiated and so forth), OTAGen genera-
tes a random ontology ex novo. Still, the selection of
adjustable parameters is arguably somewhat idiosyn-
cratic in that it reflects the structure of the ontology
generation algorithm employed (rather than conside-
rations regarding the importance of these specific pa-
rameters for the testing and benchmarking of ontolo-
gies); and, furthermore, the ontologies thus generated
are not necessarily “typical” or structurally similar to
real-world ontologies with the same parameter values.
Another work worth mentioning in this context is
Mips Benchmark (Zhang et al., 2015), an automatic
generator of incoherent ontologies for the purpose of
measuring the effectiveness of tools for solving the
minimal incoherence preserving sub-terminologies
(Mips) problem (Schlobach et al., 2007). This is
more special-purpose than our intended approach, and
while experimental evaluation suggests that the tune-
able parameters of this generator are relevant to the
analysis of the complexity of the Mips problem once
more there is no particular concern about whether the
ontologies thus generated are structurally analogous
to real-world use cases.
After devoting some effort to the principled search
for relevant ontological features and to the develop-
ment of a generative probabilistic mathematical mo-
del of ontology generation, we believe that it would be
possible to build and validate a general-purpose, the-
oretically sound, highly tuneable generator of struc-
turally plausible (in the sense of “having statistical
structural properties close to those of real ontologies”)
random ontologies; and, as mentioned before, such a
generator - aside from its direct possible application
to the testing and benchmarking of algorithms over
ontologies - would constitute a useful step towards
the integration of statistical and symbolic reasoning
via probabilistic inference.
Our generator will also need to be validated. In or-
der for this validation to be successful, we will require
the following three requirements to be all satisfied:
Correctness: The probability distribution of the fea-
tures of the generated ontologies will match the
predictions of the probabilistic model (in other
words, our generator will be a correct implemen-
tation of our probabilistic model);
Suitability: The ontologies generated by our tool
will be suitable for use in testing, benchmarking
and algorithm validation purposes (as verified, for
instance, by comparison with other benchmarking
approaches and with real ontologies);
Verisimilitude: For adequate choices of parameters,
the ontologies generated will be structurally close
to real ones, as verified both by direct inspection
and by automated exploration of relevant proper-
ties.
7 CONCLUSION
In this work we presented a roadmap towards the
automated generation of random ontologies for tes-
ting/benchmarking purposes.
This preliminary discussion left several open is-
sues in need of further exploration, and it is a foregone
conclusion that many ulterior difficulties and insights
(quite possibly, ones which would prove themselves
valuable in a much wider scope than that of the spe-
cific problem of random ontology generation) will be
encountered in the process of developing the theoreti-
cally principled, tuneable, practically useable tool that
we envision.
Nonetheless, we hope to have convinced the rea-
der that the problem of random ontology generation is
a surprisingly complex, subtle, and potentially fruitful
one, and to have provided some insights regarding the
difficulties inherent to it and the possible ways to sur-
pass them.
As a final comment, we further speculate that re-
solving the problem of random ontology generation
– and, in particular, doing so via the generative pro-
babilistic approach discussed here – has the potential
to provide a useful avenue towards the integration of
symbolic and statistical reasoning. Indeed, genera-
tive probabilistic models such as the ones envisioned
A Roadmap towards Tuneable Random Ontology Generation Via Probabilistic Generative Models
355

in this roadmap can in principle be also used for in-
ferential reasoning over ontologies: very briefly, the
probability distributions over ontologies provided by
such a model can be used to calculate quantities such
as e.g. the probability that an axiom will be contained
in an ontology given that certain other axioms are in
it and so forth. It is not possible to say much more at
this juncture regarding the feasibility of this type of
approach to statistical inference over ontologies; but
it is an intriguing idea that would certainly be deser-
ving of further examination after the development of
an adequate model for the generation of random on-
tologies.
REFERENCES
Airoldi, E. M., Blei, D. M., Fienberg, S. E., and Xing, E. P.
(2008). Mixed membership stochastic blockmodels.
Journal of Machine Learning Research, 9(Sep):1981–
2014.
Albert, R. and Barab
´
asi, A.-L. (2002). Statistical mecha-
nics of complex networks. Reviews of modern physics,
74(1):47.
Choi, N., Song, I.-Y., and Han, H. (2006). A survey on
ontology mapping. ACM Sigmod Record, 35(3):34–
41.
Codescu, M., Kuksa, E., Kutz, O., Mossakowski, T., and
Neuhaus, F. (2017). Ontohub: A semantic repository
engine for heterogeneous ontologies. Applied Onto-
logy, 12(3–4):275–298.
Cristani, M. and Cuel, R. (2005). A survey on onto-
logy creation methodologies. International Journal
on Semantic Web and Information Systems (IJSWIS),
1(2):49–69.
Dragisic, Z., Eckert, K., Euzenat, J., Faria, D., Ferrara, A.,
Granada, R., Ivanova, V., Jim
´
enez-Ruiz, E., Kempf,
A. O., Lambrix, P., et al. (2014). Results of the onto-
logy alignment evaluation initiative 2014. In Proc. of
the 9th Int. Conf. on Ontology Matching-Volume 1317,
pages 61–104. CEUR-WS. org.
Duque-Ramos, A., Fern
´
andez-Breis, J. T., Stevens, R.,
Aussenac-Gilles, N., et al. (2011). Oquare: A square-
based approach for evaluating the quality of ontolo-
gies. Journal of Research and Practice in Information
Technology, 43(2):159.
Erd
¨
os, P. and R
´
enyi, A. (1959). On random graphs, I. Pu-
blicationes Mathematicae (Debrecen), 6:290–297.
Garc
´
ıa, J., JoseGarc
´
ıa-Pe
˜
nalvo, F., and Ther
´
on, R. (2010).
A survey on ontology metrics. In World Summit on
Knowledge Society, pages 22–27. Springer.
Granitzer, M., Sabol, V., Onn, K. W., Lukose, D., and Toch-
termann, K. (2010). Ontology alignmenta survey with
focus on visually supported semi-automatic techni-
ques. Future Internet, 2(3):238–258.
Grover, A. and Leskovec, J. (2016). node2vec: Scalable
feature learning for networks. In Proc. of the 22nd
ACM SIGKDD Int. Conf. on Knowledge discovery and
data mining, pages 855–864. ACM.
Guo, Y., Pan, Z., and Heflin, J. (2005). LUBM: a bench-
mark for OWL knowledge base systems. Web Seman-
tics: Science, Services and Agents on the World Wide
Web, 3(2-3):158–182.
Hamilton, W., Ying, Z., and Leskovec, J. (2017a). Inductive
representation learning on large graphs. In Advan-
ces in Neural Information Processing Systems, pages
1025–1035.
Hamilton, W. L., Ying, R., and Leskovec, J. (2017b). Re-
presentation learning on graphs: Methods and appli-
cations. arXiv preprint arXiv:1709.05584.
Horridge, M., Bail, S., Parsia, B., and Sattler, U. (2011).
The cognitive complexity of owl justifications. In
International Semantic Web Conference, pages 241–
256. Springer.
Kang, Y.-B., Li, Y.-F., and Krishnaswamy, S. (2012). Pre-
dicting reasoning performance using ontology me-
trics. In International Semantic Web Conference, pa-
ges 198–214. Springer.
Katifori, A., Halatsis, C., Lepouras, G., Vassilakis, C.,
and Giannopoulou, E. (2007). Ontology visualization
methodsa survey. ACM Computing Surveys (CSUR),
39(4):10.
Leskovec, J., Chakrabarti, D., Kleinberg, J., Faloutsos, C.,
and Ghahramani, Z. (2010). Kronecker graphs: An
approach to modeling networks. Journal of Machine
Learning Research, 11(Feb):985–1042.
Lozano-Tello, A. and G
´
omez-P
´
erez, A. (2004). Ontometric:
A method to choose the appropriate ontology. Journal
of database management, 2(15):1–18.
Ma, L., Yang, Y., Qiu, Z., Xie, G., Pan, Y., and Liu, S.
(2006). Towards a complete OWL ontology bench-
mark. In European Semantic Web Conference, pages
125–139. Springer.
Matentzoglu, N. and Parsia, B. (2018). BioPortal. last
accessed, 2018/26/05.
McDaniel, M., Storey, V. C., and Sugumaran, V. (2018).
Assessing the quality of domain ontologies: Metrics
and an automated ranking system. Data & Knowledge
Engineering.
Mossakowski, T., Codescu, M., Neuhaus, F., and Kutz, O.
(2015). The Road to Universal Logic: Festschrift for
the 50th Birthday of Jean-Yves B
´
eziau, Volume II.
chapter The Distributed Ontology, Modeling and Spe-
cification Language – DOL, pages 489–520. Springer
International Publishing, Cham.
Neuhaus, F., Vizedom, A., Baclawski, K., Bennett, M.,
Dean, M., Denny, M., Gr
¨
uninger, M., Hashemi, A.,
Longstreth, T., Obrst, L., et al. (2013). Towards on-
tology evaluation across the life cycle. Applied Onto-
logy, 8(3):179–194.
Ongenae, F., Verstichel, S., De Turck, F., Dhaene, T.,
Dhoedt, B., and Demeester, P. (2008). OTAGen: A tu-
nable ontology generator for benchmarking ontology-
based agent collaboration. In 32nd Annual IEEE
Int. Computer Software and Applications Conf., pages
529–530.
KEOD 2018 - 10th International Conference on Knowledge Engineering and Ontology Development
356

Plessers, P. and De Troyer, O. (2006). Resolving inconsis-
tencies in evolving ontologies. In European Semantic
Web Conference, pages 200–214. Springer.
Robins, G., Pattison, P., Kalish, Y., and Lusher, D. (2007).
An introduction to exponential random graph (p*) mo-
dels for social networks. Social networks, 29(2):173–
191.
Schlobach, S., Huang, Z., Cornet, R., and Van Harmelen, F.
(2007). Debugging incoherent terminologies. Journal
of Automated Reasoning, 39(3):317–349.
Sicilia, M., Rodr
´
ıguez, D., Garc
´
ıa-Barriocanal, E., and
S
´
anchez-Alonso, S. (2012). Empirical findings on
ontology metrics. Expert Systems with Applications,
39(8):6706–6711.
Tartir, S. and Arpinar, I. B. (2007). Ontology evaluation
and ranking using OntoQA. In Semantic Computing,
2007. ICSC 2007. International Conference on, pages
185–192. IEEE.
Tempich, C. and Volz, R. (2003). Towards a benchmark
for semantic web reasoners-an analysis of the daml
ontology library. In EON, volume 87.
Troquard, N., Confalonieri, R., Galliani, P., Pe
˜
naloza, R.,
Porello, D., and Kutz, O. (2018). Repairing onto-
logies via axiom weakening. In Proceedings of the
Thirty-Second AAAI Conference on Artificial Intelli-
gence, pages 1981–1988.
Wache, H., Voegele, T., Visser, U., Stuckenschmidt, H.,
Schuster, G., Neumann, H., and H
¨
ubner, S. (2001).
Ontology-based integration of information-a survey of
existing approaches. In IJCAI-01 workshop: onto-
logies and information sharing, volume 2001, pages
108–117. Citeseer.
You, J., Ying, R., Ren, X., Hamilton, W. L., and Leskovec,
J. (2018). GraphRNN: A deep generative model for
graphs. arXiv preprint arXiv:1802.08773.
Zablith, F., Antoniou, G., d’Aquin, M., Flouris, G., Kondy-
lakis, H., Motta, E., Plexousakis, D., and Sabou, M.
(2015). Ontology evolution: a process-centric survey.
The knowledge engineering review, 30(1):45–75.
Zhang, F., Ma, Z., and Cheng, H. (2018). A review of
answering queries over ontologies based on databases.
In Information Retrieval and Management: Concepts,
Methodologies, Tools, and Applications, pages 2267–
2286. IGI Global.
Zhang, Y., Ouyang, D., and Ye, Y. (2015). An automatic
way of generating incoherent terminologies with pa-
rameters. In IWOST-1, pages 117–127.
A Roadmap towards Tuneable Random Ontology Generation Via Probabilistic Generative Models
357
