Forest Fire Area Estimation using Support Vector Machine as an

Approximator

Nittaya Kerdprasop

, Pumrapee Poomka

, Paradee Chuaybamroong

and Kittisak Kerdprasop

Data and Knowledge Engineering Research Unit, School of Computer Engineering,

Suranaree University of Technology, Nakhon Ratchasima, Thailand

Department of Environmental Science, Thammasat University, Thailand

Keywords: Forest Fire Area Estimation, Machine Learning, Data Modelling, Approximator, Support Vector Machine,

Kernel Function.

Abstract: Forest fire is critical environmental issue that can cause severe damage. Fast detection and accurate

estimation of forest fire burned area can help firefighters to effectively control damage. Thus, the purpose of

this paper is to apply state of the art data modeling method to estimate the area of forest fire burning using

support vector machine (SVM) algorithm as a tool for area approximation. The dataset is

real forest fires

data from the Montesinho natural park in the northeast region of Portugal. The original dataset comprises of

517 records with 13 attributes. We randomly sample the data 10 times to obtain 10 data-subsets for building

estimation models using two kinds of SVM kernel:

radial basis function and polynomial function. The

obtained models are compared against other proposed techniques to assess performances based on the two

measurement metrics: mean absolute error (MAE) and root mean square error (RMSE). The experimental

results show that our SVM predictor using polynomial kernel function can precisely estimate forest fire

damage area with the MAE and RMSE as low as 6.48 and 7.65, respectively. These errors are less than

other techniques reported in the literature.

1 INTRODUCTION

Forest fire is a severe disaster for humans and other

wild lives. The fires, either intentionally manmade

or a natural phenomenon, are unwanted situation and

they should be getting into control as fast as possible

in order to reduce loss. Predicting accurately the

spread of the fires is one effective way to control

and limit the burned area. In practice, controlling the

fire area is based on the experience of firefighters.

At present, with the advance of computational

modeling methods, estimating the burned area can

be made more accurate with the new technology.

Computational modeling efficiency is mainly

due to the advancement in machine learning

technology. The recent invention of support vector

machine (Cortes and Vapnik, 1995; Vapnik, 2013)

has made machine being able to learn both linear

and non-linear classification models based on the

application of specific kind of kernel functions.

Support vector machine, or SVM, has been proven

an efficient learner and extensively applied in

environmental science and other numerous research

areas. Some examples of SVM applications to

support natural phenomenon study includes the

estimation of horizontal global solar radiation (Baser

and Demirhan, 2017), landslide assessment due to

rainfall effect (Lin et al., 2017), and the prediction

of wind power (Yuan et al., 2017).

However, it is not a straightforward task to apply

SVM successfully in every domain because SVM is

a parametric learning approach that needs a proper

setting of parameters best suitable for each specific

data domain. Data analysts, therefore, need some

experiences and prior knowledge regarding the

nature of SVM before applying it efficiently.

In this work, we propose an empirical study of

applying SVM to estimate the burned area of forest

fires in the largest natural park of Portugal, named

Montesinho. We show in our experimental setting

that using different kinds of kernel function results

in different yields. We explain major characteristics

of SVM as a background knowledge for general

readers in the next section. We then explain our

modeling method and SVM setting in section 3. The

Kerdprasop, N., Poomka, P., Chuaybamroong, P. and Kerdprasop, K.

Forest Fire Area Estimation using Support Vector Machine as an Approximator.

DOI: 10.5220/0007224802690273

In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 269-273

ISBN: 978-989-758-327-8

269

experimental results are shown in section 4 and the

conclusion is provided in section 5.

2 SVM CHARACTERISTICS

SVM is a very fast and effective algorithm for

learning a classification model. The term model

means a concise form that can be used to classify

future data into their correct class. SVM learns to

build a model and represents it as a plane or a linear

line. This line is called a classifier. Figure 1

illustrates the idea of learning SVM classification

model from the available data of mixed classes: the

one that is represented by dark dot, and the other

class shown by light dot. The learning objective of

SVM is to find a linear line being able to separate

correctly data of one class from another.

In this simple example, a classification model is

represented as a linear blue line in the middle of the

figure. There are many possible linear lines being

qualified to be a classifier, but there is only one

optimal classifier. Optimality is judged from the

farthest distance between the classification line and

the data at the border lines. In Figure 1, the dashed

lines on both sides of the classification line are

boundaries for selecting the optimal model in such a

way that the distance between the classification line

to both borders are the wideset one. Data on the

dashed lines are called support vectors.

Figure 1: SVM learning on linearly separable data.

Figure 2: The application of kernel function to learn

classifier for non-linear separable data.

For data that cannot be separated easily with the

linear line, some transformation function is needed

to change the orientation of data to be conveniently

separable through the straight line. Figure 2

illustrates the idea of data transformation. The

function that transforms data from normal plane to a

hyperplane is called a kernel function. With the

power of data transformation through the application

of proper kernel function, SVM can efficiently learn

classifier that can classify non-linear data.

There are many possible kernel functions to

transform data to be in a higher feature space that

can help SVM linearly separating data. Among

many existing functions, the most applicable one is

the radial basis function. Its computation (Cristianini

and Shawe-Taylor, 2000) is shown in (1) and (2). In

our work, we also consider a simpler kernel

function, called polynomial, as shown in (3).







,



=−



−









(1)

=−

2





(2)







,



=



,



+





(3)

where γ is gamma parameter, X

is a vector of input

variables, X

is the target variable, σ is a free

variable, q is the degree of polynomial function, and

is the bias.

3 RESEARCH METHODOLOGY

3.1 Study Area and Data Preparation

The forest fire data used in our study are historical

events occurred at the Montesinho natural park

(Figure 3).

Figure 3: Location of Montesinho natural park in the

northeast of Portugal.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

270

This park covers 748 km

, or 74,229 ha, in the

mountainous region of the northeast Portugal with

altitude ranges from 438 m in the lower valley to

1481 m over the mountain top (Castro et al., 2010).

The forest fire data are publicly available at the

UCI machine learning repository (https://archive.ics.

uci.edu/ml/datasets/forest+fires). Fire data had been

collected from January 2000 to December 2003

comprising of 517 records with 13 attributes in each

record. In our study, we select only 9 attributes to be

used in the modeling process. The attribute details

are summarized in Table 1.

Table 1: Forest fire data attributes and meaning.

Attribute name Description Unit

FFMC Fine Fuel Moisture Code --

DMC Duff Moisture Code --

DC Drought Code --

ISI Initial Spread Index --

Temp Temperature

RH Relative Humidity %

Wind Wind speed km/h

Rain Rain volume mm/m

Area Total burned area ha

The attributes FFMC, DMC, DC, ISI are parts of

major components to compute the danger rating

scales of forest fires (Taylor and Alexander, 2006).

The FFMC determines influence of litters for the

ignition and spread of fire. The DMC and DC

identify fire intensity, while ISI correlates to the fire

velocity spread. The other four attributes (temp, RH,

wind, rain) are meteorological data that can also

affect fire spread. The target of our modeling is the

last attribute, area.

3.2 Modeling Techinque

Prior to the modeling process of fire area estimation,

we have to explore the distributions of our data.

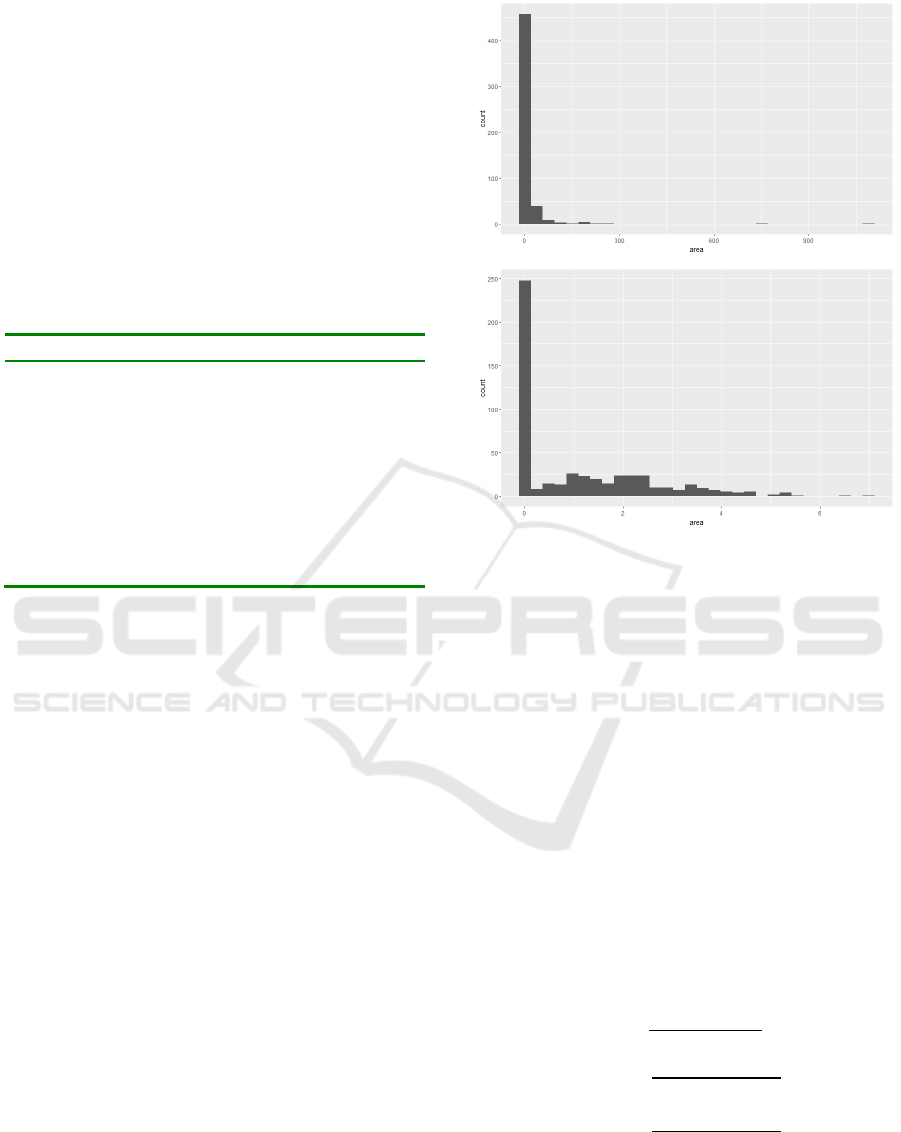
From data exploration, we have found that from the

517 records, there are 247 records (almost 48%) that

burned area is zero. This is due to the data collection

threshold that burned area less than 100 m

shall not

be recorded. We, therefore, have to rescale the

burned area with the formula shown in (4).

burned_area = ln(area + 1) (4)

The comparison of original burned area and the

new one after transformation is graphically shown in

Figure 4. The transformation makes data less skew

and hence can increase correctness on burned area

prediction.

Figure 4: Distributions of the burned area in the original

data (above) compared to the area after logarithmic scaling

(below), where vertical axis is frequency of fires and

horizontal axis is the burned area.

We then randomly select ten datasets of equal

size for the purpose of ten iterations of train SVM to

build model and test the built model (10-fold cross

validation). For the SVM learning with radial basis

kernel function, we set the gamma (γ) parameter to

be 80. For the SVM training with polynomial kernel

function, the learning parameters q = 7, γ = 1, and

θ = 1.

The model testing has been performed ten times

and the model’s performances are evaluated with the

mean absolute error (MAE) and root mean square

error (RMSE) metrics. The computations (Al Janabi,

Al Shourbaji, and Salman, 2017) of MAE and

RMSE are shown in (5) and (6), respectively.

=

∑





−















(5)

=



∑





−

















(6)

where 



is the actual value of burned area, 





the estimated burned area, and n is the number of

data records.

Forest Fire Area Estimation using Support Vector Machine as an Approximator

271

4 RESULTS AND DISCUSSION

The results of forest fire burned area prediction from

the ten iterations of SVM learning algorithm using

polynomial and radial basis kernel functions are

illustrated in Table 2. For the specific application of

natural phenomenon prediction such as forest fires,

polynomial kernel produces more accurate

estimation than the radial basis function. The

prediction results are graphically shown in Figure 5.

Table 2: Error evaluation results from the ten iterations of

SVM-polynomial and SVM-radial basis kernel functions.

MAE RMSE

No.

SVM-

polynomial

SVM-

radial basis

SVM-

polynomial

SVM-

radial basis

1 6.4814 11.0621 7.6575 56.0906

2 6.4813 11.0619 7.6577 56.0906

3 6.4814 11.0618 7.6578 56.0906

4 6.4814 11.0620 7.6576 56.0906

5 6.4813 11.0624 7.6575 56.0907

6 6.4813 11.0621 7.6574 56.0906

7 6.4812 11.0619 7.6574 56.0906

8 6.4814 11.0623 7.6577 56.0907

9 6.4816 11.0620 7.6577 56.0906

10 6.4815 11.0620 7.6577 56.0907

Avg.

6.4814

11.0620

7.6576

56.0906

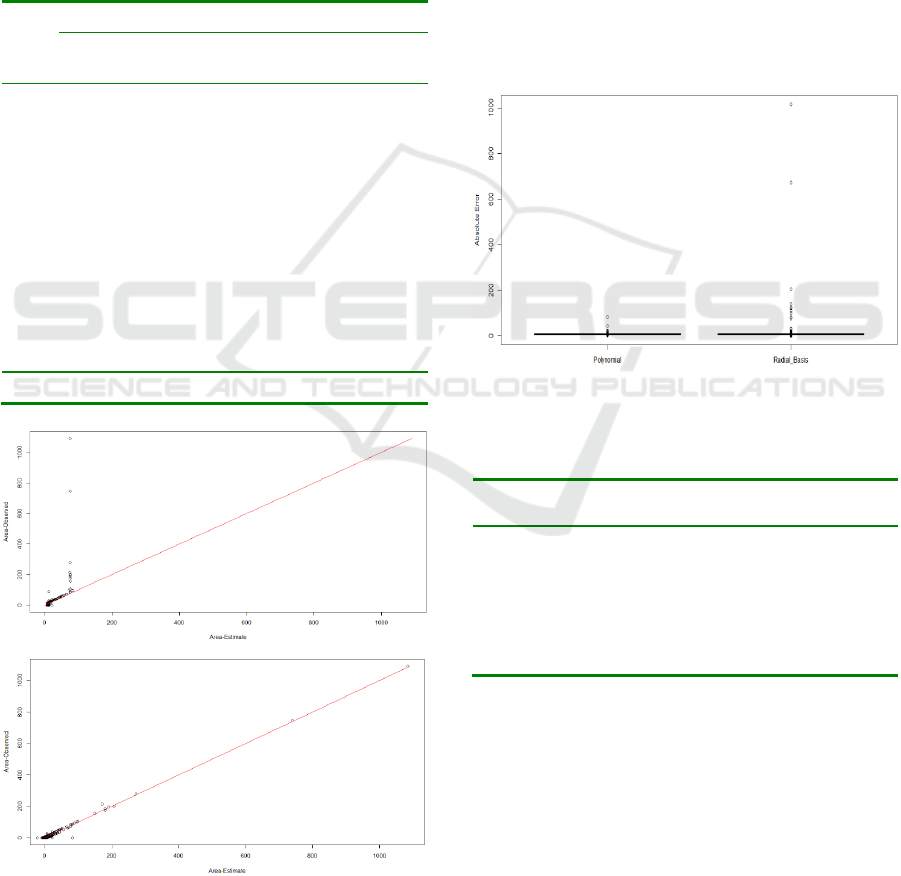
Figure 5: Comparative plots showing estimation errors of

radial basis kernel (above) and polynomial kernel (below).

From the prediction plots in Figure 5, it is

noticeable that the radial basis kernel cannot predict

correctly burned area wider than 100 ha. To analyze

absolute errors, we show the boxplot in Figure 6 and

the errors made by radial basis kernel are from the

too high approximation.

The SVM learning using exactly the same set of

forest fire data also appears in the literature (Al

Janabi, Al Shourbaji, and Salman, 2017; Cortez and

Morais, 2007). But the kernel application, the data

attribute selection, and SVM parameter setting are

different from our work. The prediction results of

our work as compared to others are also summarized

and shown in Table 3.

From the comparative results, it is our SVM with

polynomial kernel model that performs the most

accurate prediction of forest fire burned area.

Figure 6: Boxplot showing absoluter errors of polynomial

kernel (left) against the radial basis kernel (right).

Table 3: Comparative performance of SVM predictors.

Modeling method RMSE MAE

Our SVM with polynomial kernel

7.65 6.48

Our SVM with radial basis kernel 56.09 11.06

SVM by Cortez and Morais (2007) 64.70 12.71

SVM by Al Janabi et al. (2017) 54.00 282.40

5 CONCLUSIONS

In this work, we study the performance of support

vector machine (SVM) algorithm when it has been

applied to the environmental domain to predict

burned area of the forest fires. SVM and other

computational models such as logistic regression,

artificial neural network, and particle swarm

intelligence have recently been applied to the

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

272

modeling of forest fire spread and intensity. The

advantage of accurate prediction with computational

models is to efficiently control the damage caused

by forest fires.

It has been reported by many research teams that

SVM yield the most promising results. But most

applications of SVM employ a sophisticate radial

basis function as the kernel of SVM. We

demonstrate in our experiment that for some specific

application, a simpler kernel such as polynomial

function performs better than the complex one. The

polynomial SVM predicts correctly burned area with

the root mean square error as low as 7.65, whereas

the radial basis kernel yields higher error at 56.09.

ACKNOWLEDGEMENTS

This work was financially supported by grants from

the Thailand Toray Science Foundation, the National

Research Council of Thailand, and Suranaree

University of Technology through the funding of the

Data and Knowledge Engineering Research Units.

REFERENCES

Al Janabi, S., Al Shourbaji, I., Salman, M. A., 2017.

Assessing the suitability of soft computing approaches

for forest fires prediction.

Applied Computing and

Informatics, Available at https://doi.org/10.1016/j.aci.

2017.09.006

Baser, F., Demirhan, H., 2017. A fuzzy regression with

support vector machine approach to the estimation of

horizontal global solar radiation.

Energy, vol. 123, pp.

229-240.

Castro, J., de Figueiredo, T., Fonseca, F., Castro, J. P.,

Nobre, S., Pires, L. C., 2010. Motesinho natural park:

general description and natural values. In N.

Evelpidou, T. Figueiredo, F. Mauro, V. Tecim, and A.

Vassilopoulos (eds), Natural Heritage from East to

West, Springer

Cortes, C., Vapnik, V., 1995. Support-vector network.

Machine Learning, vol. 20, no. 3, pp. 273-297.

Cortez, P., Morais, A., 2007. A data mining approach to

predict forest fires using meteorological data. In 13

EPIA – Portuguese Conference on Artificial

Intelligence, pp. 512-523.

Cristianini, N., Shawe-Taylor, J., 2000. An Introduction to

Support Vector Machines and Other Kernel-based

Learning Methods, Cambridge University Press.

Lin, G. F., Chang, M. J., Huang, Y. C., Ho, J. Y., 2017.

Assessment of susceptibility to rainfall-induced

landslides using improved self-organizing linear

output map, support vector machine, and logistic

regression. Engineering Geology, vol. 224, pp. 62-74.

Taylor, S. W., Alexander, M. E., 2006. Science,

technology, and human factors in fire danger rating:

the Canadian experience. International Journal of

Wildland Fire, vol. 15, no. 1, pp. 121-135.

Yuan, X., Tan, Q., Lei, X., Yuan, Y., Wu, X., 2017. Wind

power prediction using hybrid autoregressive

fractionally integrated moving average and least

square support vector machine. Energy, vol. 129, pp.

122-137.

Vapnik, V. 2013. The Nature of Statistical Learning

Theory, Springer Science & Business Media.

Forest Fire Area Estimation using Support Vector Machine as an Approximator

273