Low Level Big Data Processing
Jaime Salvador-Meneses
1
, Zoila Ruiz-Chavez
1
and Jose Garcia-Rodriguez
2
1
Universidad Central del Ecuador, Ciudadela Universitaria, Quito, Ecuador
2
Universidad de Alicante, Ap. 99. 03080, Alicante, Spain
Keywords:
Big Data, Compression, Processing, Categorical Data, BLAS.
Abstract:
The machine learning algorithms, prior to their application, require that the information be stored in memory.
Reducing the amount of memory used for data representation clearly reduces the number of operations requi-
red to process it. Many of the current libraries represent the information in the traditional way, which forces
you to iterate the whole set of data to obtain the desired result. In this paper we propose a technique to process
categorical information previously encoded using the bit-level schema, the method proposes a block proces-
sing which reduces the number of iterations on the original data and, at the same time, maintains a processing
performance similar to the processing of the original data. The method requires the information to be stored in
memory, which allows you to optimize the volume of memory consumed for representation as well as the ope-
rations required to process it. The results of the experiments carried out show a slightly lower time processing
than the obtained with traditional implementations, which allows us to obtain a good performance.
1 INTRODUCTION
The number of attributes (also called dimension) in
many datasets is large, and many algorithms do not
work well with datasets that have a high dimension.
Currently, it is a challenge to process data sets with
a high dimensionality such as censuses conducted in
different countries (Rai and Singh, 2010).
Latin America, in the last 20 years, has tended to
take greater advantage of census information (Feres,
2010), this information is mostly categorical informa-
tion (variables that take a reduced set of values). The
representation of this information in digital media can
be optimized given the categorical nature.
A census consists of a set of m observations (also
called records) each of which contains n attributes.
An observation contains the answers to a question-
naire given by all members of a household (Bruni,
2004).
This paper proposes a mechanism for proces-
sing categorical information using bit-level operati-
ons. Prior to processing, it is necessary to encode
(compress) the information into a specific format.
The mechanism proposes compressing the informa-
tion into packets of a certain number of bits (16, 32,
64 bits), in each packet a certain number of values are
stored.
Bitwise operations (AND, OR, etc.) are an impor-
tant part of modern programming languages because
they allow you to replace arithmetic operations with
more efficient operations (Seshadri et al., 2015).
This document is organized as follows: Section 2
summarizes the standard that defines the algebraic
operations that can be performed on data sets as
well as some of the main libraries that implement
it, Section 3 presents an alternative for information
processing based on the BLAS Level 1 standard,
Section 4 presents several results obtained using the
proposed processing method and, finally, Section 5
presents some conclusions.
2 BLAS SPECIFICATION
In this section we present a summary of some libraries
that implements the BLAS specification and a brief
review about encoding categorical data.
Basic Linear Algebra Subprograms (BLAS) is a
specification that defines low-level routines for per-
forming operations related to linear algebra. Opera-
tions are related to scalar, vector and matrix process.
BLAS define 3 levels:
• BLAS Level 1 defines operations between vector
scales
• BLAS Level 2 defines operations between scales
Salvador-Meneses, J., Ruiz-Chavez, Z. and Garcia-Rodriguez, J.
Low Level Big Data Processing.
DOI: 10.5220/0007227103470352
In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 1: KDIR, pages 347-352
ISBN: 978-989-758-330-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
347

and matrices
• BLAS Level 3 defines operations between scales,
vectors and matrices
This document focuses on the BLAS Level 1 spe-
cification.
2.1 BLAS Level 1
This level specifies operations between scales and
vectors and operations between vectors. Table 1 lists
all the functions described in BLAS Level 1.
2.2 Libraries that Implement BLAS
This section describes some of the libraries that im-
plement the BLAS Level 1 specification. The ap-
proach is based on implementations without GPU
graphics acceleration.
All the libraries described below make extensive
use of vector and matrix operations and therefore re-
quire an optimal representation of this type of alge-
braic structure (vectors and matrices).
Most of the libraries described in this section re-
present the information as arrangements of float or
double elements, so the size in bytes needed to re-
present a vector is:
total = number o f elements ∗4
2.2.1 ViennaCL
ViennaCL’s approach is to provide a high-level ab-
straction using C++ for the data represented on a GPU
(Rupp et al., 2010). To work with GPUs, ViennaCL
maintains two approaches, the first based on CUDA
1
, while the second is based on OpenCL
2
.
In the event that the underlying system running
ViennaCL does not support GPU acceleration, Vien-
naCL makes use of the multi-processing associated
with the processor (CPU).
ViennaCL is extensible, the data types provided
can be invoked from other libraries such as Armadillo
and uBLAS (Rupp et al., 2016). The information is
represented in a scheme similar to STL
3
, for the case
of vectors the data type is:
vector < T,aligment >
where T can be a primitive type like char, short,
int, long, float, double.
1
https://developer.nvidia.com/cuda-zone
2
http://www.khronos.org/opencl/
3
https://isocpp.org/std/the-standard
2.2.2 uBLAS
uBLAS is a C++ library which provides support for
dense, packed and sparse matrices
4
. uBLAS is part
of the BOOST project and corresponds to a CPU im-
plementation of the BLAS standard (all levels) (Tillet
et al., 2012).
The information is represented in a scheme similar
to STL, for the case of vectors the data type is:
vector < T >
where T can be a primitive type like char, short,
int, long, float, double.
2.2.3 Armadillo
Armadillo is an open source linear algebra library
written in C++. The library is useful in the develop-
ment of algorithms written in C++. Armadillo pro-
vides efficient, object-like implementations for vec-
tors, arrays, and cubes (tensors) (Sanderson and Cur-
tin, 2016).
There are libraries that use Armadillo for its im-
plementation, such as MLPACK
5
which is written using
the matrix support of Armadillo (Curtin et al., 2012).
Armadillo represents arrays of elements using a
column or row oriented format using the classes Col
and Row respectively. The two types of data need as a
parameter the type of data to be represented within the
vector, these types of data can be: uchar, unsigned int
(u32), int (s32), unsigned long long (u64), long long
(s64), float, double
6
.
The size in bytes needed to represent a vector cor-
responds to:
total = number o f elements ∗sizeo f (element type)
2.2.4 LAPACK
Linear Algebra Package (LAPACK) is a library of
routines written in Fortran which implements the
functionality described in the BLAS specification.
There are additional modules which allow the library
to be used from C++ or other programming langua-
ges.
LAPACK is the industry standard for interacting
with linear algebra software (Cao et al., 2014), it sup-
ports the BLAS Level 1 functions using native vec-
tors of the programming language used, C++ in this
4
http://www.boost.org/doc/libs/1 65 1/libs/numeric/
ublas/doc/index.html
5
http://mlpack.org/index.html
6
u64 and s64 supported only in 64 bit systems
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
348

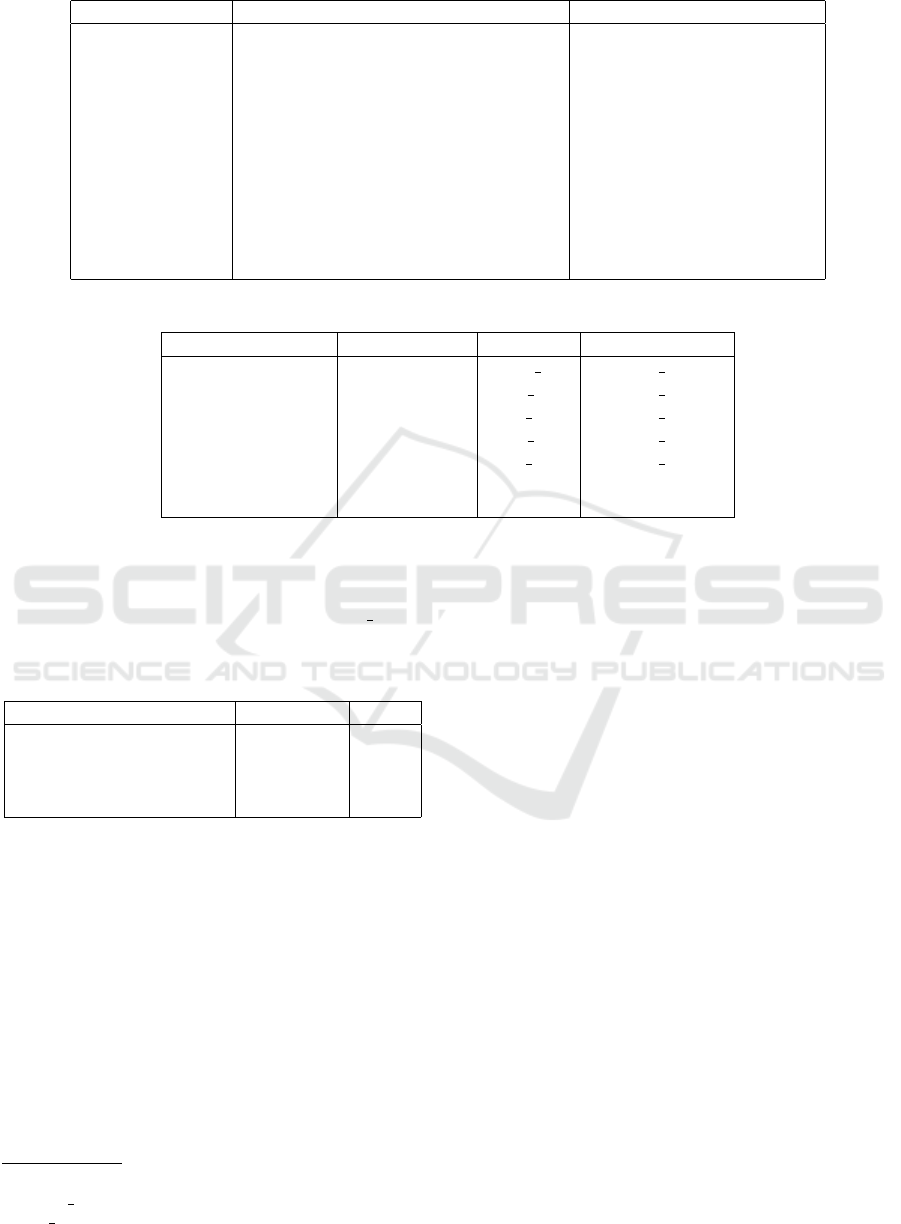
Table 1: BLAS Level 1 functions.
Function Description Mathematical Formula
Swap Exchange of two vectors y ↔ y
Stretch Vector scaling x ←αx
Assiggment Copy a vector y ← x
Multiply add Sum of two vectors y ← αx + y
Multiply subtract Subtraction of two vectors y ← αx −y
Inner dot product Dot product between two vectors α ← x
T
y
L
1
norm L
1
norm α ← ||x||
1
L
2
norm Vector 2-norm (Euclidean norm in R
2
) α ← ||x||
2
L
∞
norm Infinite norm α ← ||x||
∞
L
∞
norm index Infinite-index norm i ← max
i
|x
i
|
Plane rotation Rotation (x,y) ← (αx + βy, −βx + αy)
Table 2: Armadillo suported vector format.
Input vector type Armadilo type Col Row
unsigned char - uchar vec uchar rowvec
unsigned int u32 u32 vec u32 rowvec
int s32 s32 vec s32 rowvec
unsigned long long u64 u64 vec u64 rowvec
long long s64 s64 vec s64 rowvec
float - fvec frowvec
double - vec,dvec rowvec,drowvec
case. Additionally, it supports operations with com-
plex numbers.
Table 3 shows the detail of the norm2 function and
the prefix used to name the functions (cblas Xnrm2
where X represents the prefix)
7
.
Table 3: LAPACK supported vector format.
Input vector Result type Prefix
Vector of float float S
Vector of double double D
Vector of complex float float SC
Vector of domplex double double DZ
As shown in the above table, vectors are represen-
ted as arrays of float or double elements, so the size
in bytes needed to represent a vector is:
total = number o f elements ∗4
2.3 Current Compression Algorithms
As shown in the previous sections, the libraries descri-
bed above work with uncompressed data. In most ca-
ses the information is represented as one-dimensional
vectors containing 32-bit elements (float, int). When
working with categorical data, there are some options
for working with this type of information.
7
https://www.ibm.com/support/knowledgecenter/en/
SSFHY8 5.5.0/com.ibm.cluster.essl.v5r5.essl100.doc/
am5gr hsnrm2.htm
Some options for compressing/representing one-
dimensional (vector) data sets are described below.
Run-length Encoding. Consecutive data streams
are encoded using a (key, value) pair (Elgohary et al.,
2017).
Offset-list encoding. Unlike the previous method,
correlated pairs of data are encoded (Elgohary et al.,
2017).
GZIP. This type of method overloads the CPU
when decompressing the data (Chen et al., 2001).
Bit-level Compression. A data set is packaged in
32-bit blocks (De Grande, 2016).
3 PROCESSING APPROACH
In this section we propose a new mechanism for pro-
cessing categorical data, the processing method pro-
posed corresponds to a variation of the processing of
data compressed using bit level compression method
described in Section 2.3. The processing method de-
veloped corresponds to a process of bit-level elements
with bit-shifting operations.
Low Level Big Data Processing
349

3.1 Algorithms
The algorithm consists of representing within 4-bytes
n-categorical values of a variable. This means that to
access the value of a particular observation, a double
indexing is necessary:
1. Access the index of the value (4-bytes) containing
the searched element.
2. Index within 32 bits to access the value.
For the implementation of the proposed method
we use a mixture of arithmetic and bit-wise operati-
ons, specifically:
• Logical AND (&)
• Logical OR (|)
• Logical Shift Left ()
• Logical Shift Right ()
As an example, in this section we implement the
L
2
norm algorithm. As you can see, all the functions
described in the BLAS Level 1 can be implemented
in the same way.
3.1.1 L
2
Norm Algorithm
Algorithm 1 represents the algorithm for calculating
the L
2
norm of a compressed vector. It should be no-
ted that for each iteration on the compressed vector
(vector), n-elements represented in 32 bits of data are
accessed.
The input values correspond to:
• vector: Input vector stored as compressed vector
of dataSize bits.
• size: Vector size.
• dataSize: Bit size used for representation.
The algorithm iterates over each element of the
compressed vector and then iterates inside each block.
The number of elements contained in each block cor-
responds to:
elementsPerBlock ← 32/dataSize
It is possible to optimize the iteration within the
block by performing bit-wise operations. The Algo-
rithm 2 shows the implementation of the same algo-
rithm using bit-wise operations. For a given dataSize,
a code block is generated that operates on the bits in
such a way that iteration on the block is avoided.
The Algorithm 2 ahows the Algorithm 1 modified.
Algorithm 1: Calculate L
2
norm - version 1.
Data: vector, size, dataSize
1 elementsPerBlock ← 32/dataSize;
2 mask ← sequence of dataSize-bits with value
= 1
3 sum ←0;
4 for index ←0 to size −1 do
5 value ← vector1[index];
6 for i ←0 to elementsPerBlock −1 do
7 v ←value1  (i ∗dataSize) & mask;
8 sum ←sum + v ∗v;
9 end
10 end
11 norm2 ←
√
sum
4 EXPERIMENTS
This section presents the result of the processing of
random generated vectors. The memory consumption
of the representation of the data in the main memory
of a computer was not analyzed, instead the proces-
sing speed was measured.
All libraries were tested on Ubuntu 16.04 LTE
using GCC 5.0.4 as compiler with the default settings.
None were compiled with optimizations for the test
platform.
4.1 Test Platform
Several vector sizes were considered for testing: 10
3
,
10
4
,..., 10
9
elements. The test data set contains rand-
omly generated items in the range [0.119]. All the
libraries mentioned in the Section 2.2 use vector re-
presentation with float-type elements.
The platform on which the tests were performed
corresponds to:
• Procesador: Intel(R) Core(TM) i5-5200 CPU
• Processor speed: 2.20GHz
• RAM Memory: 16.0GB
• Operating System: Ubuntu 16.04LTE 64 bits
• Compiler: GCC 5.04 64bits
Some libraries provide particular implementations
of the vector data type:
• LAPACK uses native float * implementation
• uBLAS uses the ublas::vector<float> imple-
mentation
• Armadillo uses the arma::vec implementation
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
350

Algorithm 2: Calculate L
2
norm - version 2.
Data: vector, size, dataSize
1 function SUM 06 SQUARE(int b, int mask )
→ int
2 {
3 b1 ← ((b >> 0) & mask);
4 b2 ← ((b >> 6) & mask);
5 b3 ← ((b >> 12) & mask);
6 b4 ← ((b >> 18) & mask);
7 b5 ← ((b >> 24) & mask);
8 return b1*b1 + b2*b2 + b3*b3 + b4*b4
+ b5*b5;
9 }
10 function SUM 07 SQUARE(int b, int mask )
→ int
11 {
12 b1 ← ((b >> 0) & mask);
13 b2 ← ((b >> 7) & mask);
14 b3 ← ((b >> 14) & mask);
15 b4 ← ((b >> 21) & mask);
16 return b1*b1 + b2*b2 + b3*b3 + b4*b4;
17 }
18 elementsPerBlock ← 32/dataSize;
19 mask ← sequence of dataSize-bits with value
= 1
20 sum ←0;
21 nn ←dataSize;
22 for index ←0 to size −1 do
23 value ← vector1[index];
24 sum ←
sum + SUM nn SQUARE(value,mask);
25 end
26 norm2 ←
√
sum
• ViennaCL uses the STL std::vector<float>
implementation
The function that were verified correspond to L
2
norm of the BLAS Level 1 (operations between vec-
tors and scalars). Below are some results obtained,
from the second graph the values of ViennaCL for
vectors of size 10
9
were omitted due to the considera-
ble time needed for the process.
4.2 Results: L
2
Norm
This section presents results obtained when perfor-
ming operations with vectors represented in traditi-
onal formats (Section 2.2) and in compressed format.
For testing purposes, a vector similar to the one des-
cribed in the previous section is used.
Figure 1 and Table 4 show the time taken to cal-
culate the L
2
norm for vectors of different sizes.
10
5
10
6
10
7
10
8
10
9
10
−4
10
−3
10
−2
10
−1
10
0
10
1
10
2
Vector size (# elements)
Time (seconds)
LPACKT
uBLAS
Armadillo
ViennaCL
Block compressed
Figure 1: L
2
- Processing time.
As we can see, the block compressed approach has
a better performance than the others methods and is
similar to Armadillo in performance but it uses low
memory. We can expect the other algebraic functions
to behave similarly.
5 CONCLUSIONS
In this document we reviewed some of the most com-
mon libraries which implement the algebraic opera-
tions that constitute the core for the implementation
of machine learning algorithms. In general, it can be
concluded that the categorical information processing
proposed slightly reduces the processing time of the
information compared to similar implementations un-
der the BLAS Level 1 standard. The encoded data
representation allows to reduce the amount of me-
mory needed to represent the information as well as
the number of iterations over the data.
In the case of the test dataset, the calculation of the
L
2
norm showed a slight reduction in the processing
time (for more details, see Table 4). In the case of
operations involving two vectors, it is recommended
to encode both vectors using the same scheme.
Future work is proposed to (1) implement all the
functions described in the BLAS Level 1 standard and
test more sophisticated functions like matrix operati-
ons, (2) extend representation and processing to ma-
trix data structures and (3) implement the representa-
tion and processing using parallel programming with
Graphics Processing Unit (GPU).
Low Level Big Data Processing
351

Table 4: L
2
norm - Processing time.
Time (seconds)
Vector size (# elements) LAPACK uBLAS Armadillo ViennaCL Bit by bit
10
3
0 0 0 0 0
10
4
0 0 0 0 0
10
5
0.0002 0.0001 0.0001 0.0002 0.0001
10
6
0.0018 0.0013 0.0017 0.0024 0.0007
10
7
0.0190 0.0135 0.0073 0.0241 0.0065
10
8
0.1918 0.1242 0.0748 0.2576 0.0666
10
9
2.0787 1.7273 0.9916 53.4602 0.6696
ACKNOWLEDGEMENTS
The authors would like to thank to Universidad Cen-
tral del Ecuador and its initiative called Programa de
Doctorado en Inform
´
atica for the support during the
writing of this paper. This work has been supported
with Universidad Central del Ecuador funds.
REFERENCES
Bruni, R. (2004). Discrete models for data imputation. Dis-
crete Applied Mathematics, 144(1-2):59–69.
Cao, C., Dongarra, J., Du, P., Gates, M., Luszczek, P., and
Tomov, S. (2014). clMAGMA: High Performance
Dense Linear Algebra with OpenCL. Proceedings
of the International Workshop on OpenCL 2013 {&}
2014, pages 1:1—-1:9.
Chen, Z., Gehrke, J., and Korn, F. (2001). Query optimiza-
tion in compressed database systems. ACM SIGMOD
Record, 30(2):271–282.
Curtin, R. R., Cline, J. R., Slagle, N. P., March, W. B., Ram,
P., Mehta, N. A., and Gray, A. G. (2012). MLPACK:
A Scalable C++ Machine Learning Library. pages 1–
5.
De Grande, P. (2016). El formato Redatam. ESTUDIOS
DEMOGR
´
AFICOS Y URBANOS, 31:811–832.
Elgohary, A., Boehm, M., Haas, P. J., Reiss, F. R., and
Reinwald, B. (2017). Scaling Machine Learning via
Compressed Linear Algebra. ACM SIGMOD Record,
46(1):42–49.
Feres, J. C. (2010). XII . Medici
´
on de la pobreza a trav
´
es de
los censos de poblaci
´
on y vivienda. pages 327–335.
Rai, P. and Singh, S. (2010). A Survey of Clustering Techni-
ques. International Journal of Computer Applicati-
ons, 7(12):1–5.
Rupp, K., Rudolf, F., and Weinbub, J. (2010). ViennaCL-a
high level linear algebra library for GPUs and multi-
core CPUs. Intl.˜Workshop on GPUs and Scientific
Applications, pages 51–56.
Rupp, K., Tillet, P., Rudolf, F., and Weinbub, J. (2016).
ViennaCL—Linear Algebra Library for Multi-and
Many-Core Architectures. SIAM Journal on.
Sanderson, C. and Curtin, R. (2016). Armadillo: a template-
based C++ library for linear algebra. The Journal of
Open Source Software, 1:26.
Seshadri, V., Hsieh, K., Boroumand, A., Lee, D., Kozuch,
M. A., Mutlu, O., Gibbons, P. B., and Mowry, T. C.
(2015). Fast Bulk Bitwise and and or in DRAM. IEEE
Computer Architecture Letters, 14(2):127–131.
Tillet, P., Rupp, K., and Selberherr, S. (2012). An Auto-
matic OpenCL Compute Kernel Generator for Basic
Linear Algebra Operations. Simulation Series, 44(6).
KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval
352