Multi-objective Evolutionary Approach in the Linear Dynamical

System Inverse Modeling

Ivan Ryzhikov

1,2

, Christina Brester

1,2

, Eugene Semenkin

and Mikko Kolehmainen

Department of Environmental and Biological Sciences, University of Eastern Finland, Kuopio, Finland

Institute of Computer Science and Telecommunications, Reshetnev Siberian State University of Science and Technology,

Krasnoyarsk, Russia

Keywords: Time-invariant System, Dynamical System, Linear Differential Equation, Inverse Problem, Multi-objective

Optimization, System Identification, Initial Value.

Abstract: In this study, we consider an inverse mathematical modeling problem for dynamical systems with a single

output. Generally, the final solution of this problem is an approximation of a system transient process and a

system state at some time point. Only those classes of models, which describe the transient process properly,

can portray the system behavior and can be applicable for prediction and optimal control problems. One of

possible mathematical representations of dynamical systems is differential equations, in particular, linear

differential equations for linear systems. While solving the inverse problem, we aim to identify a differential

equation order and parameters, an initial system state. Since all the parameters are interrelated, we propose

to identify them by solving a two-criterion optimization problem, which includes the model adequacy (i.e. a

distance between model outputs and observations) and the closeness of the initial value estimation to the

observation data. To solve this complex optimization problem, we apply a Real-valued Cooperative Multi-

Objective Evolutionary Algorithm which effectiveness has been proved on the set of high-dimensional test

problems. We investigate the dependency between the considered criteria by depicting the Pareto front

approximation. Then, having the same amount of computational resources, we vary the system order, the

number of control inputs and the initial state to analyze changes in the algorithm effectiveness based on

each criterion and estimate basic limitations. Finally, we conclude that the optimization problem considered

is quite challenging and it might be used for testing and comparing various heuristics.

1 INTRODUCTION

Inverse mathematical modeling problems of

dynamical systems occur in different scientific and

practical fields. In most cases, identification

approaches are applicable only for processes and

systems for which the transient processes and the

initial state are known or there are some acceptable

assumptions about them. Basically, one needs to

approximate the system parameters so that the model

output would fit the observation data in the best

way. However, when we solve the identification

problem in a general case, there is no information

about the following things: the mathematical

operator class of the transient process, mathematical

model parameters and the initial system state.

Moreover, all these variables have a complex

influence on the model adequacy.

In this study, we consider the inverse modeling

problem reduction to a two-criterion optimization

problem. The reduced problem includes the

following criteria: the first one reflects the distance

between the observation data and the model output

and the other one means the distance between the

initial value estimation and the data at the beginning

of the process observation. This multi-objective

problem formulation exposes the relation between

the transient process and the initial system state. The

main idea behind this two-objective problem is that

different initial system states can produce different

optimization problems for parameters and vice-

versa. Therefore, the system initial state and the

transient process must be approximated

simultaneously (Ryzhikov et al., 2016).

The approximation of the transient process

differs from the standard regression problem

because the identification is applied to the field of

differential operators and the system input is not the

element of the vector field, but the piecewise

continuous function. In this study, we assume that

Ryzhikov, I., Brester, C., Semenkin, E. and Kolehmainen, M.

Multi-objective Evolutionary Approach in the Linear Dynamical System Inverse Modeling.

DOI: 10.5220/0007228402810288

In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 281-288

ISBN: 978-989-758-327-8

281

the dynamical system can be described with the

linear differential equation. Thus, the inverse

modeling problem can be reduced to the

identification of the differential equation order, its

parameters and the initial state vector. In previous

studies, such as (Ryzhikov et al., 2016) and

(Ryzhikov and Semenkin, 2017), we have

considered one-criterion approaches. We discovered

that solving this problem requires some specific and

problem-oriented algorithm modifications.

Nevertheless, these studies lack thorough

experiments for systems with different orders, the

number of control inputs and different initial states.

To solve the two-criterion optimization problem,

we use a Real-valued Multi-Objective Evolutionary

Algorithm based on the island model cooperation,

which includes the following heuristics as the

parallel working islands: the Strength Pareto

Evolutionary Algorithm (SPEA2) (Zitzler et al.,

2002), the Preference-Inspired Co-Evolutionary

Algorithm with goal vectors (PICEA-g) (Wang,

2013), and the Non-dominating Sorting Genetic

Algorithm II (NSGA-II) (Deb et al., 2002).

Previously, the proposed algorithm with the binary

solution representation was successfully applied for

solving different optimization problems (Brester and

Semenkin, 2015) and particular inverse modeling

problems (Brester et al., 2016a), (Semenkina et al.,

2014) and (Brester et al., 2016b).

In the study (Ryzhikov et al., 2017), the inverse

modeling problem for chemical disintegration

reaction was reduced to the multi-criteria

optimization problem, which was solved with the

cooperation of the multi-objective evolutionary

algorithms. That considered approach achieved the

promising results and allowed us to solve the general

inverse problem for the linear dynamical system.

Our goal is to explore the algorithm performance for

this problem and estimate how its efficiency changes

when varying the initial problem parameters: the

system order, the number of control inputs and the

initial state vector. This is needed to reveal when

and how the complexity changes.

2 INVERSE MATHEMATICAL

MODELING PROBLEM FOR

LINEAR DYNAMICAL

SYSTEMS

Let us consider a linear time-invariant system

inverse modeling problem. It is assumed that the

initial system can be determined with a linear

differential equation (LDE)

   

()

i j j

a x t b u t



  



(1)

where

 

()

: , 0,

x t i n

is the system state i-

th derivative,

 

: , 1,

u t j m

is the j-th

input function, n and m are the differential equation

order and the number of input functions,

respectively. Here, with the notation

 

(0)

mean the function

 

itself.

Using the equation (1), we can evaluate the

model output on some particular set of inputs if we

know the system state at the initial time

. Let us

denote the system state as

v

, so

 

x t v

and

that would lead us to the following Cauchy problem

   

()

i j j

a x t b u t



  



 

x t v

(2)

Now let the sets

   

, , 1,

Y y T t i s  

be an

observation data, where

y 

are the system

output measurements at times

t 

, and

is the

number of observations. It is assumed, that the

system output and the observations can be

determined with the following equation

( ) , 1,

i i i

y x t i s   

(3)

where

: ( ) 0, ( )ED     

is a random value and

()

is the solution of the Cauchy problem (2) at

the time point

tt

In this study, we assume that the order of the

differential equation (1) is given. Thus, we need to

identify the parameters of the differential equation

(1) and the initial value of the related Cauchy

problem (2). In other words, the problem can be

reduced to determine the parameters and initial

values, which would maximize fitting the

observation data by the solution of the Cauchy

problem

     

( ) ( )

i j j

x t a x t b u t





   



 

x t v

 

mintT

(4)

where

a

b 

and

v

. The Cauchy

problem (4) is modified, because if we know the

LDE order, then its first coefficient cannot be equal

to 0 and, thus, the equation (2) can be transformed to

the equation (4), by dividing all its coefficients by

this coefficient.

According to the model representation (4) and

using the observation data

and

, the inverse

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

282

modeling problem can be reduced to the two-

criterion optimization problem with the following

criteria:

 

ˆˆ

min

a b v

y x t









(5)

 

argmin

min min

C y x T  

(6)

The first criterion (5) is a standard one that

estimates the model adequacy. The second criterion

(6) is the measure of the closeness of the initial

value estimation to the observation data set. In this

study, the norm of each criterion is chosen as the

Manhattan norm. The reason for this decision is its

better robustness against the abnormal values.

As one can see, the LDE coefficients have no

influence on the second criterion, but the initial

value estimation influences the main criterion (5).

The solution of the problem considered is the

Pareto set of non-dominated alternatives. The Pareto

set can be determined as

 

 

n m n m

P p z z p

   

    

, where

with the notation

we mean that both

   

1 1 1 2

С z С z

and

   

2 1 2 2

С z С z

conditions

are met and at least one of the following conditions

is met:

   

1 1 1 2

С z С z

   

2 1 2 2

С z С z

. It is

impossible to calculate the Pareto set analytically, as

well as, the Pareto front for the problem (5)-(6), and,

thus, we need to approximate it.

The solution of the Cauchy problem (4) is

evaluated with the Runge-Kutta 4-th order numerical

integration scheme. For each particular considered

Cauchy problem, the initial and final integration

time points are known and the integration step is

equal to 0.05.

All the identification problems considered in this

study have been generated without the additive

noise. We can consider the performance of the

modeling approach, regardless the distortion of the

observation data.

3 MULTI-OBJECTIVE

COOPERATIVE GENETIC

ALGORITHM WITH THE

ISLAND META-HEURISTIC

In multi-objective optimization, we aim at achieving

a compromise between competing criteria. The

Pareto-dominance idea (Goldberg, 1989) is widely

used to compare alternative solutions. While solving

multi-criteria problems, we expect to obtain a set of

non-dominated points, which cannot be preferred to

one another based on all the objectives considered.

Evolutionary-based algorithms (in particular,

Genetic Algorithms (GAs)) operate with a set of

solutions at each generation, and therefore, they

were considered as an effective tool to find Pareto

set and front approximations. Nevertheless, there are

some open questions researchers usually face when

they apply Multi-Objective Evolutionary Algorithms

(MOEAs) in practical problems.

Firstly, different fitness assignment strategies

might be proposed (Zitzler, 2004): the dominance

depth, the dominance rank or the dominance count

might be used to assign a fitness function.

Next, various diversity preservation techniques

might be applied. In (Silverman, 1986) these

techniques are introduced: nearest neighbour

techniques, kernel methods, histograms.

Furthermore, the idea of elitism has been

proposed to avoid the loss of good individuals

during the stochastic algorithm execution. There are

two ways to implement it: to merge the parent

population with the offspring and then to employ

environmental selection or to use an additional set

for keeping promising solutions.

Remembering these issues, we decided to apply a

cooperative MOEA (Brester and Semenkin, 2015)

which includes three algorithms based on different

heuristics. The cooperative MOEA enables us to

eliminate the choice of the appropriate algorithm and

avoid many experiments with different MOEAs. The

cooperative MOEA uses an island model (Whitley et

al., 1997) and includes NSGA-II, PICEA-g, and

SPEA2 as its islands work in a parallel way. The

initial number of individuals is spread across

subpopulations equally. The fitness function

evaluation for different subpopulations is

implemented in parallel threads. At each T-th

generation algorithms exchange the best solutions

(migration). There are two parameters: migration

size, the number of candidates for migration, and

migration interval, the number of generations

between migrations.

Moreover, the island model topology should be

determined, in other words, the scheme of migration.

The fully connected topology is applied, meaning

that each algorithm shares its best solutions with all

other algorithms included in the island model.

Originally, GAs operate with binary strings,

however, for real-valued optimization problems a

number of genetic operators have been developed.

Multi-objective Evolutionary Approach in the Linear Dynamical System Inverse Modeling

283

To select effective solutions for the offspring

generation, we apply binary tournament selection.

As a crossover operator, we use intermediate

recombination. In a mutation operator, we

implement the next scheme (Liu et al., 2009):

( ), ,

j j j j

x b a















   



(7)

With

(2 ) 1, if 0.5

1 (2 2 ) , otherwise

rand U

rand















  



  

(8)

where U is a uniformly random number [0, 1]. There

are two control parameters: the mutation rate



, where n is the chromosome length, and the

distribution index



is equal to 1.0.

and

are

the lower and the upper bounds of the j-th variable

in the chromosome.

The cooperative MOEA was investigated on the

set of complex benchmark problems CEC 2009

(Zhang, 2008) and proved its effectiveness (Brester

and Semenkin, 2015).

4 INVERSE MODELING

PROBLEM SOLVING

In the experiments conducted, we considered

different LDEs and Cauchy problems: we varied the

order of the LDE, the initial values and the number

of the inputs. To solve all the considered problems,

the proposed MOEA was applied. The maximum

number of objective function evaluations was 30000

for each algorithm in the island model. Each

algorithm had 300 generations and 100 individuals

for its population. The migration interval was 25

generations and the migration set size was 10. The

limitation of the total amount of the fitness function

evaluations was 90000. For each problem, the

MOEA was launched for 20 times.

The initial population was generated randomly

within the hypercube

 

1,1

nm



, and the borders for

the heuristic search were

 

5, 20

nm



. The

influence of the initial population generation on the

algorithm efficiency is beyond the scope of this

article.

First, we analyzed the influence of the LDE

order. The coefficients of the LDE are given in

Table 1. The input function for these experiments

was chosen as the unit-step function,

   

,1u t t m  

. The initial values of the system

and the coefficients of the control inputs were equal

R

and 1, respectively, and

was the LDE

order. The fixed control coefficients and initial

values allowed us to estimate the complexity

growth, which was caused only by the order

increase. The initial time was equal to 0 for all the

Cauchy problems. The final time was equal to 10 for

problems of orders 2 or 3 and 20 for problems of

other orders.

Table 1: Cauchy problems: orders and equation

coefficients.

Order

Parameters

 

1, 2a 

 

1, 2,1a 

 

1, 2, 4,1a 

 

0.25,1.75, 4.75, 6.25, 4a 

 

0.25, 2,6.5,11,10.25,5a 

 

0.125,1.25, 5.25,12,16.125,12.75, 5.5a 

The results obtained are given in Figures 1 and 2

for the first criterion (5) and the second one (6),

respectively, and boxplots reflect the algorithm

efficiency. The best solution, according to each

criterion, was chosen from the Pareto front

estimation in each particular algorithm run. We can

see that the first criterion (5) values become worse

with the increase of the LDE order and this

deterioration is nonlinear. The second criterion (6)

values are close to 0, which is not informative, in

contrast to the first one, therefore, we exclude it

from the further analysis and focus on the Pareto

front estimations and the first criterion (5)

distribution.

Figure 1: Pareto front estimation statistics for different

LDE orders. The first criterion (5).

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

284

Figure 2: Pareto front estimation statistics for different

LDE orders. The second criterion (6).

In Figures 3 and 4, the Pareto front estimation

distributions are presented for the system of the 2nd

order and for the system of the 7th order,

respectively.

The heat maps show that the distribution of the

solutions for the system of the 7

order is more

complex. For the 2

order systems the distribution

of the front approximation is closer to 0 by the first

criterion (5). At the same time, for the 7

order the

distribution is much closer to 0 by the second

criterion (6).

Figure 3: The Pareto front distribution for the 2

order

inverse problem (Table 1). X-axis corresponds to the first

criterion, Y-axis corresponds to the second criterion.

Figure 4: The Pareto front distribution for the 7

order

inverse problem (Table 1). X-axis corresponds to the first

criterion, Y-axis corresponds to the second criterion.

The next factor is the number of control inputs

and their influence on the problem complexity. To

investigate it, we performed the same experiment for

the system of the 2

order from Table 1, for which

the control inputs are listed in Table 2. The initial

values were equal to 0 and the final integration time

was 10.

Table 2: Cauchy problems: control inputs.

Number of

inputs,

Input:

 





   

u t t

   

sinu t t

   

cosu t t

 

u t t

   

sin 2u t t

   

cos 2u t t

   

ln 1u t t

The results of the Pareto front estimation for

problems with different number of inputs are given

in Figure 5. The distributions of the Pareto front for

one and seven control inputs are given in Figures 6

and 7, respectively.

Figure 5: Pareto front estimation statistics for the different

number of inputs. The first criterion (5).

Figure 6: The Pareto front distribution for the 2

order

inverse problem (Table 1) and one control input (Table 2).

Multi-objective Evolutionary Approach in the Linear Dynamical System Inverse Modeling

285

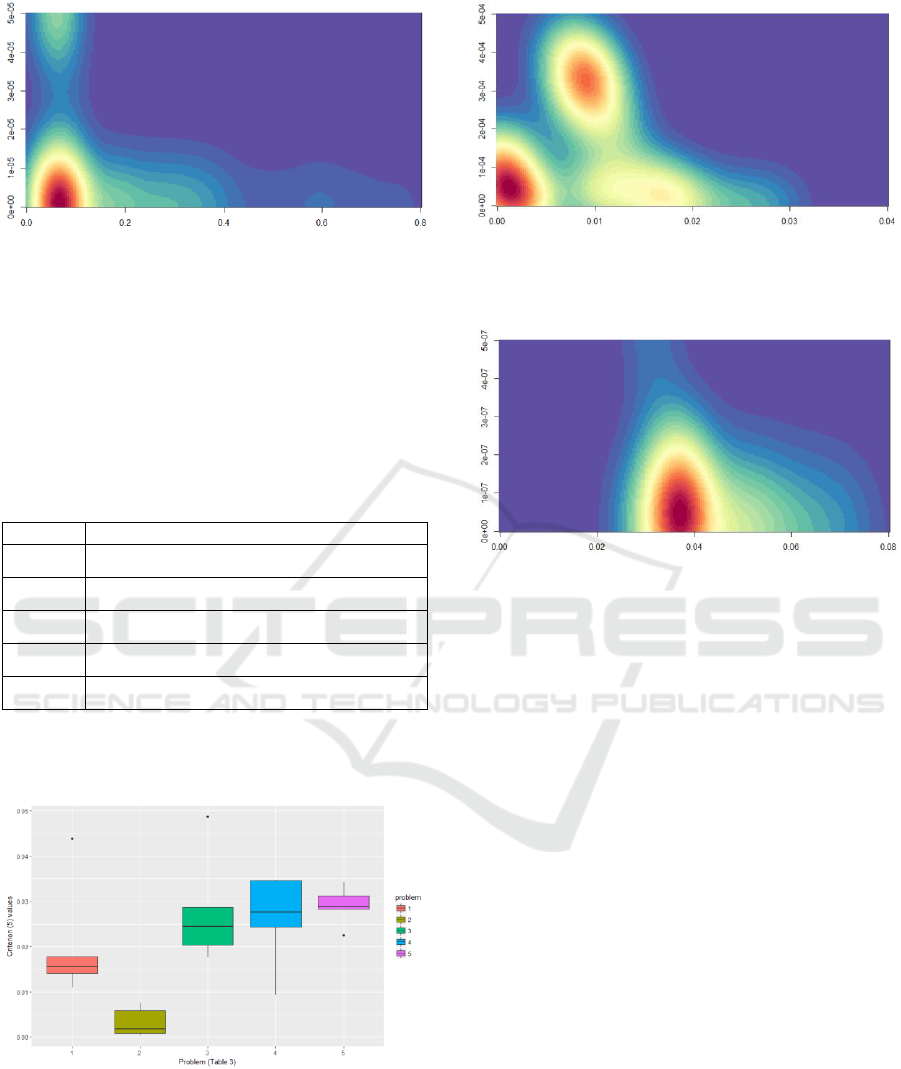
Figure 7: The Pareto front distribution for the 2

order

inverse problem (Table 1) and seven control inputs (Table

2).

Then, we considered the initial value of the

system and its influence on the problem complexity.

For this experiment, we took the system of the 4

order from Table 1. The different initial values are

given in Table 3. The final integration time was

equal to 15 and the input was the unit-step function.

Table 3: Cauchy problems: initial values.

Problem

Initial value

 

0000v 

 

1 0 0 0v 

 

0 1 0 0v 

 

0 0 1 0v 

 

0 0 0 1v 

The results of the Pareto front estimations for the

different combinations of the initial values are given

in Figures 8, 9 and 10.

Figure 8: Pareto front estimation statistics for different

initial values (Table 3). The first criterion (5).

All the Cauchy problems were considered for the

stable LDEs. Here the stable system was generated

via the characteristic equation so that each root had

the negative real part.

Figure 9: The Pareto front distribution for the 4

order

inverse problem (Table 1) and the 2

initial value (Table

3).

Figure 10: The Pareto front distribution for the 2

order

inverse problem (Table 1) and the 5

initial value (Table

3).

As the Pareto front distribution approximations

show, the front is localized but still has a complex

structure. Anyway, the inverse mapping of the close

Pareto front elements could give us completely

different alternatives, which makes the inverse

modeling problem complex.

5 CONCLUSION

In this study, the inverse mathematical modeling

problem was reduced to the two-criterion

optimization problem on the real vector space,

which was solved by the real-valued cooperative

MOEA.

The complexity of the problem considered

depends on the LDE order, the number of inputs and

the initial values. The complexity growth can be

estimated by changing the objective criterion values,

which are found by the MOEA. In our experiments,

the computational resources were the same for all

the problems, so it was possible to estimate the

influence of the certain parameter, such as the

differential equation order, the number of inputs and

the initial state.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

286

The order of the differential equation has the

strongest effect on the algorithm efficiency and thus,

the problem complexity. The possible reason for that

is not only the increased dimension of the search

space, but also the increased variance and the

maximum absolute value of the LDE coefficients,

which makes the search space wider. The increase of

the order by 1 increases the dimension by 2, since

each order is related to the coefficient and the initial

value.

The number of control inputs also determines the

search space dimension and makes the reduced

problem more complex, when the number of inputs

increases. There is another significant detail, which

is hard to be formalized: when the number of inputs

increases, their impacts overlap and this can mislead

the algorithm.

The search space dimension does not change

when we vary the initial values. However, the

problem becomes more challenging, as there are the

initial values of the high orders, which are not equal

to 0. Therefore, changing the analyzed parameters,

we may create various challenging test problems for

MOEAs.

Future research will be related to the estimation

of the computational resources, which would be

required to keep the algorithm performance at the

same level while changing the parameters. This

study is a prior to the development of the automatic

identification of the causative control inputs and the

differential equation order. The gathered information

also would be used to develop the problem-oriented

algorithms with higher performance.

ACKNOWLEDGEMENTS

The reported research was funded by Russian

Foundation for Basic Research and the government

of the region of the Russian Federation, grant № 18-

41-243007.

REFERENCES

Brester, C., Kauhanen, J., Tuomainen, T.P., Semenkin, E.,

Kolehmainen, M., 2016. A. Comparison of two-

criterion evolutionary filtering techniques in

cardiovascular predictive modelling. Proceedings of

the 13th International Conference on Informatics in

Control, Automation and Robotics (ICINCO’2016),

Lisbon, Portugal, vol. 1: pp. 140–145.

Brester, C., Semenkin, E., 2015. Cooperative

Multiobjective Genetic Algorithm with Parallel

Implementation. Advances in Swarm and

Computational Intelligence, LNCS 9140: pp. 471–

478.

Brester, C., Semenkin, E., Sidorov, M., 2016. B. Multi-

objective heuristic feature selection for speech-based

multilingual emotion recognition. Journal of Artificial

Intelligence and Soft Computing Research, vol. 6, no.

4: pp. 243-253.

Deb, K., Pratap, A., Agarwal, S., Meyarivan, T., 2002. A

fast and elitist multiobjective genetic algorithm:

NSGA-II. IEEE Transactions on Evolutionary

Computation 6 (2): pp. 182-197.

Goldberg, D., 1989. Genetic algorithms in search,

optimization, and machine learning. Addison-wesley.

Liu, M., Zou, X., Chen, Y., Wu, Z., 2009. Performance

assessment of DMOEA-DD with CEC 2009 MOEA

competition test instances. 2009 IEEE Congress on

Evolutionary Computation.

Ryzhikov, I., Semenkin, E., 2017. Restart Operator Meta-

heuristics for a Problem-Oriented Evolutionary

Strategies Algorithm in Inverse Mathematical MISO

Modelling Problem Solving. IOP Conference Series:

Materials Science and Engineering, vol. 173.

Ryzhikov, I., Semenkin, E., Panfilov, I., 2016.

Evolutionary Optimization Algorithms for Differential

Equation Parameters, Initial Value and Order

Identification. ICINCO (1) 2016: pp. 168-176.

Ryzhikov I., Brester Ch., Semenkin E. Multi-objective

dynamical system parameters and initial value

identification approach in chemical disintegration

reaction modelling. Proceedings of the 14th

International Conference on Informatics in Control,

Automation and Robotics (ICINCO’2017), Madrid,

Spain, vol. 1: pp. 497-504.

Semenkina, M., Akhmedova, Sh., Brester, C., Semenkin,

E., 2016. Choice of spacecraft control contour variant

with self-configuring stochastic algorithms of multi-

criteria optimization. Proceedings of the 13th

International Conference on Informatics in Control,

Automation and Robotics (ICINCO’2016), Lisbon,

Portugal, vol. 1: pp. 281–286.

Silverman, B., 1986. Density estimation for statistics and

data analysis. Chapman and Hall, London.

Wang, R., 2013. Preference-Inspired Co-evolutionary

Algorithms. A thesis submitted in partial fulfillment

for the degree of the Doctor of Philosophy, University

of Sheffield: p. 231.

Whitley, D., Rana, S., and Heckendorn, R., 1997. Island

model genetic algorithms and linearly separable

problems. Proceedings of AISB Workshop on

Evolutionary Computation, vol.1305 of LNCS: pp.

109-125.

Zhang, Q., Zhou, A., Zhao, S., Suganthan, P. N., Liu, W.,

Tiwari, S., 2008. Multi-objective optimization test

instances for the CEC 2009 special session and

competition. University of Essex and Nanyang

Technological University, Tech. Rep. CES–487, 2008.

Zitzler, E., Laumanns, M., Bleuler, S., 2004. A Tutorial on

Evolutionary Multiobjective Optimization. In:

Gandibleux X., (eds.): Metaheuristics for

Multi-objective Evolutionary Approach in the Linear Dynamical System Inverse Modeling

287

Multiobjective Optimisation. Lecture Notes in

Economics and Mathematical Systems, Vol. 535,

Springer.

Zitzler, E., Laumanns, M., Thiele, L., 2002. SPEA2:

Improving the Strength Pareto Evolutionary Algorithm

for Multiobjective Optimization. Evolutionary

Methods for Design Optimisation and Control with

Application to Industrial Problems EUROGEN 2001

3242 (103): pp. 95-100.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

288