A Tandem Drone-ground Vehicle for Accessing Isolated Locations for

First Aid Emergency Response in Case of Disaster

Marcos Calle

, Jose Luis Andrade-Pineda

, Pedro Luis González-R

, Jose Miguel Leon-Blanco

and David Canca Ortiz

Department of Industrial Organization and Enterprise Management I, University of Seville,

Cº Descubrimientos, Seville, Spain

Robotic, Vision and Control Group, University of Seville, Cº Descubrimientos, Seville, Spain

Keywords: Genetic Algorithm, UAV, Humanitarian Mission, Disaster Area.

Abstract: The collapse of infrastructures is very often a complicating factor for the early emergency actuations after a

disaster. A proper plan to better cover the needs of the affected people within the disaster area while

maintaining life-saving relief operations is mandatory hence. In this paper, we use a drone for flying over a

set of difficult-to-access locations for imaging issues to get information to build a risk assessment as the

earliest stage of the emergency operations. While the drone provides the flexibility required to visit

subsequently a sort of isolated locations, it needs a commando vehicle in ground for (i) monitoring the

deployment of operations and (ii) being a recharging station where the drone gets fresh batteries. This work

proposes a decision-making process to plan the mission, which is composed by the ground vehicle stopping

points and the sequence of locations visited for each drone route. We propose a Genetic Algorithm (GA)

which has proven to be helpful in finding good solutions in short computing times. We provide experimental

analysis on the factors effecting the performance of the output solutions, around an illustrative test instance.

Results show the applicability of these techniques for providing proper solutions to the studied problem.

1 INTRODUCTION

The collapse of infrastructures is very often a

complicating factor for the emergency actuations

after a disaster. In the case of developing countries,

this leads to the appearance of isolated areas to be

provided with first healthcare aid. For instance, it is

sometimes necessary to send blood supplies to the

injured in their spots instead of bringing them to the

hospitals for blood infusions (Wen et al., 2016). In

view of the lack of trained pilots as well as helicopters

and land-based local personnel in the disaster areas

(Rabta et al., 2018), humanitarian organizations are

more and more incorporating Unmanned Aerial

Vehicles (UAVs) or drones in their supply of life-

saving commodities such as blood (Wen et al., 2016)

or pharmaceuticals.

By using UAVs, they can also get a quick and

flexible access to certain locations of interest, aiming

at collecting crucial information for the ulterior

efficient development of the emergency mission

itself. Aside from overcoming the accessibility issues,

UAVs can be useful for reducing the worker exposure

to danger (e.g. in structural integrity assessment after

an earthquake or in gauging radiation levels in a

nuclear accident (Greenwood, 2015)).

The maximal operation time or endurance for an

UAV depends on a variety of factors, such as the type

of drone (fixed wing vs. rotorcraft), the flying altitude

(e.g., propellers of rotor-crafts must rotate faster at

higher altitudes because of lower air density), the

weather conditions and obviously, the weight of the

UAV.

In this work, we propose using a UAV consisting

of a multirotor system that will be operated with

battery swaps to overcome the endurance limitation.

The UAV will fly over a set of challenging locations

for imaging them with the purpose of collecting

information to make a risk assessment as the earliest

stage of the emergency operations. We will suppose

the UAV is equipped to acquire the needed images of

the difficult-to-access locations, although this

research focuses not in the imagery itself, but in the

optimization of the completion time for the quick

recognisee of the target locations. This differs from

other reported studies in the emergency literature

Calle, M., Andrade-Pineda, J., González-R, P., Leon-Blanco, J. and Ortiz, D.

A Tandem Drone-ground Vehicle for Accessing Isolated Locations for First Aid Emergency Response in Case of Disaster.

DOI: 10.5220/0007230702890296

In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 289-296

ISBN: 978-989-758-327-8

289

where the challenge is in getting the consecutive

overlapping of aerial images to build an up-to-date

map of a wide area (Qi et al., 2016). We are more

interested in analysing the combination of UAVs and

alternative means of transport in difficult-to-access

areas, which with certain exceptions (Mosterman et

al., 2014), (Chowdhury et al., 2017), remains

relatively unexplored.

2 PROBLEM DESCRIPTION

The UAV provides us with the flexibility required to

visit subsequently a subset of locations (namely, a

route), although for practical convenience, an

individual would be on charge of monitoring and

controlling the flight operations. Thus, we assume

that a ground vehicle (GV) will act as a commando

vehicle.

The number of target locations to visit on each

flight is clearly limited to the capacity (power) of the

batteries in the UAV. Our assumption is that the GV

will further play the role of recharging station, so that

at the end of each of its sorties the UAV will land on

it for battery swaps. Aside from being conditioned by

the total weight on board (see Figure 1 for an example

of an energy consumption pattern), it is noticeable

that the number of locations that the UAV is able to

visit on each sortie is also limited because of the

capacity of the data storage device used for recording

the imagery task.

Our problem can shortly be described as how best

defining the routing planning for the tandem UAV-

GV used to deploy the recognisee task.

Figure 1: Power pattern in an hexacopter UAV,

approximately linear with the total load on board (Source:

(Dorling et al.,2017)).

In Figure 2, we sketch one of the flight routes of

our UAV in the studied scenario. As a first approxi-

mation to the constrained freedom of movements of

the GV in the disaster area, our assumption is that the

GV just moves along a straight line between two

points.

Observe that the route consists of the UAV’s take-

off from the GV, its visit to a subset of the planned

locations (circles) and its flight to intercept the GV

trip with the purpose of landing on it and swapping its

batteries. In the while, the GV has been moving along

the practical road (between rectangles).

Figure 2: Target Scenario: UAV and GV moves separately.

The dashed lines represent fly paths for UAV.

In spite of the sketched example, it is possible that

a launch and a rendezvous of the UAV occurs at the

same point. Namely, the GV is allowed to stay at a

position for a time while the UAV complete a route

visiting a variety of sites, if the optimization analysis

found it convenient for the general objective of

minimizing the time to accomplish the whole task.

This differs from many of the tandem UAV-GV

approaches in the literature, which mainly turn

around the commercial supply chain context with a

last-mile delivery based on UAVs. There are very few

works considering UAV load capacity greater than

one (Luo, et al., 2017), (Rahman, 2017), thereby more

than one parcel allowed for serving a certain

customer. The fact that the GV can move the UAV

between two deployment locations such that it does

not spend any energy is a feature that is sometimes

considered in such a literature. For instance, (Mathew

et al., 2015) assume the UAV travelling through a

street network joint to a truck as GV till the tandem

gets nearby a customer’s doorstep, when the UAV fly

to deliver parcels one customer at a time. Differently,

(Ha et al., 2018) allows UAV’s route comprised of

several customers, excluding the possibility to have a

launch and rendezvous in the same point though. The

latter is allowed in (Mathew et al., 2015) and in the

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

290

closely related work by (Bin Othman et al., 2017),

although none of them considers that the UAV can

visit a set of customers in a single flight mission, as is

required in our scenario. Nevertheless, the last three

referenced works apply a Travelling Salesman

Problem with Drone (TSP-D) approach that is

relevant to our research. The name TSP with drone is

first used in (Agatz et al., 2016) referring to the

problem in which a drone helps a traditional transport

system like a truck or a van in the delivery of goods.

3 PLANNING DECISIONS

The proposed decision-making process to plan our

imagery mission covering all the difficult-to-access

locations would provide the following:

 The GV stopping points, with the arriving time

and for how long the GV stays at it.

 The sequence of locations visited for each UAV’s

route, the start point for every route –i.e. the point

in take-off- and its landing point.

 The details of the hitch and ride of the UAV over

the GV (namely, when the UAV travels carried on

the GV while it moves from a position to another).

We approach it using a multiple travelling salesman

problem (mTSP) baseline: the target locations

(henceforth referred to as “customers”) which have to

be visited by a number of routes. According to the

mTSP terminology (Bektas, 2006), our case study

concerns to the ‘nonfixed destination case within the

multiple depot variation of mTSP’, since the UAV

can either return to the starting GV position (at which

the UAV taken off) or to a different ending position.

3.1 Assumptions

We first introduce the notation for the input

parameters used within our planning problem:

 : Customers to visit;

 



: Euclidean distance between two positions;

 : Maximum number of customers that can be

‘mapped’ before running out of the storage

memory;

 : UAV flight speed;

 : GV moving speed;

 : Endurance or maximum flight time;

Then, we list certain assumptions we make to

simplify our analysis.

Firstly, that the road travels of GV and the UAV

flight between locations occur both at constant speed.

The latter comes from our assumption that the energy

consumed during the emergency mission is

approximately the same as that consumed during

hover (Dorling et al., 2017).

Secondly, that the extreme points for each route

are taken from stopping positions for the GV (which

moves only along the straight road depicted in Figure

2).

Thirdly, that we have to manage the

synchronisation of GV and UAV. Specifically, we

assume that the GV opening time at a certain position

occurs always before than the arrival of the UAV

planned for landing on this position. Namely, that the

UAV’s end of route is planned so that it does not have

to wait for the arrival of the GV.

Finally, notice that the minimum number of routes

that may arise is



/



. However, depending on the

distance of flight paths, the limited endurance  could

force a route to be serving to less than H customers.

From it, the worst case is that every route was only

serving one customer, and hence the valid set of route

indices are:

∈









,…,

(1)

Although the assumptions considered in this work

have been considered individually in the literature, it

is noteworthy the novelty of considering them in a

joint way in the same problem.

3.2 Variables

Let 



be a binary variable indicating that the

route visits node  immediately after node .

Besides, assume that the visiting sequence order of

the customers served by a certain route is μ



. As we

explain below, these ordering variables are used for

subtour eliminations.

Let 



be the time at the take-off of the UAV on

its route , and 



the land time for the UAV flight

from the customer  as the last flight of route . In

order to be ready to check endurance, let us consider

the cumulative flight time of the UAV when arrive at

the node , denoted 



, and the total flight time for

the whole route  accounting for the final flight from

the last customer  to the GV, denoted 



. Let







be the arrival time for the GV at the

interception point at which the route  is terminating.

Finally let





 be the time the GV stay at this

stopping point.

3.3 Constraints

 A route cannot terminate at a customer.

 Each customer  must be visited just once, belong-

A Tandem Drone-ground Vehicle for Accessing Isolated Locations for First Aid Emergency Response in Case of Disaster

291

ing to only one route.

 There is exactly one input flight and exactly one

output flight from every customer visited by a

route.

 The endurance  is an upper bound for the

cumulative flight time variables 



and 



 The early arrival time for the UAV is treated as a

hard constraint. Thus, if 







, then node

 cannot be part of the route , since the GV is not

ready at time.

 The early leave time for the GV from the take-off

point under study is treated as a hard constraint. If















, then the GV is not

ready to be the take-off point for the UAV on its

route, since the GV has left.

 The subtour elimination constraint, which can be

written using  as follows:



μ







   1,

, ∈ ,  , ∈ 

(2)

3.4 Methodological Proposal

Deriving from the previous discussed issues, the

planning for covering the set of challenging locations

will emerge from solving a MILP formulation with

similarities to the non-fixed destination multiple

depot m-TSP minimizing the Total Mission Time

(TMT).

We recall here that the mTSP is a relaxation of the

Vehicle Routing Problem (VRP), being well-known

that this problem is NP-Hard (Bektas, 2006). In the

VRP literature there are many solution approaches

initially valid for the mTSP, but they may not be

efficient to the mTSP.

Precisely, we have focused our research in getting

quick good solutions to the practical decision problem

studied. To this aim, we have developed a Genetic

Algorithm (GA) tailored for our case study.

4 GA

A Genetic Algorithm (GA), as proposed by Holland

(1975), is a population-based metaheuristic inspired

by the evolution of species. The algorithm starts with

a population of randomly generated solutions (each

solution represented by a chromosome), and then

continues with a procedure to improve the candidate

solutions obtained generation after generation, by

using selection, crossing and mutation operators. The

improvement of the solutions occurs when a lower

value for a fitness function arises. The variable TMT

is the fitness to evaluate a solution in our problem,

evaluated by finding the time when the UAV-GV

tandem arrives to the end of the road, after all

customers have been visited.

In general, a GA is an unconstrained method,

which usually handles constraints by penalizing the

objective function. In our case, the constraints not

included in the calculation of TMT are those relating

to:

 The maximum number of customers per route

 The maximum flight time or endurance, 

 The time that the UAV is waiting for the GV

arrival at the rendezvous location.

 The total moving time of the UAV-GV tandem.

Next, we detail our GA implementation, where the

objective function is to minimize the TMT, defined as

the summation of the cumulative flight time of the

UAV and cumulative moving time of the UAV-GV

tandem.

4.1 Coding Scheme

The chromosomes in our study are comprised of 3

genes.

The first  components are devoted to code the

position of the take-off point for each route (which

would be contained in the straight road in Figure 2),

measured from the origin, 



. Next  components

are the distance specification of the selected landing

points,



. The last  components define the route

assigned to serve each customer, 



. Thus, we code

each solution according to the following structure:

.







,… 



,



,…



,



,…





(3)

Thus, each chromosome is explicitly representing the

take-off and rendezvous points for routes and the

assignment of routes to each customer. Nevertheless,

other performance details such as the number of

routes, the time at which the GV arrive at a point and

the lapse time spent there, implicitly are also

contained into it.

4.2 Pseudo-code

The pseudo-code for the GA can be resumed in

pseudocode (algorithm 1):

1: generate population of candidate solutions

2: compute fitness of candidate solutions

3: while termination criterion is false

4: generate children solutions by crossover

5: mutate children solutions

6: compute fitness of new candidate solutions

7: replace parent solutions

8: return best solution

Algorithm 1: Pseudo-code of the Genetic Algorithm.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

292

At line 1, the candidate solutions are randomly

initialized over the entire search space. Prior to the

first iteration of the GA, the algorithm evaluates the

candidate solutions of the generated population, at

line 2. After a fixed number of iterations (that were

experimentally determined to get good solutions

within reasonable computing time), a termination

criterion is applied at line 3.

The crossover operation is the first step at every

iteration of the GA, involving two parent solutions

and generating two child solutions (at line 4). In fact,

three variants of this two-point crossover have been

implemented in our algorithm: a crossover variant for

the take-off points of the flights, a crossover variant

for the rendezvous locations of the flights, and a

crossover variant for the assignments of the

customers to the UAV flights. Then, the algorithm

proceeds with the application of a mutation operator

on the children solutions (at line 5), by inverting a

subsection of the mutating solution. Again, three

different mutation operations have been implemented

depending on whether we were mutating the take-off

points of the flights, the rendezvous locations of the

flights, or the assignments of the customers to the

UAV flight missions. Once done the evaluation of the

new candidate solutions generated at the concerned

iterations (at line 6), the algorithm proceeds to replace

the parent solutions by the children solutions (at line

7). We apply elitism, where the n best solutions of the

parents’ generation replace the worst solutions of the

children’s generation.

4.3 Implementation

We have implemented this algorithm with Python 3

programming language with the help of the

evolutionary algorithm toolkit DEAP (Fortin et al.,

2012), an abbreviation for ‘Distributed Evolutionary

Algorithms in Python’. DEAP is an evolutionary

computation framework that allows rapid prototyping

of diverse genetic algorithms, including genetic

algorithms, genetic programming, evolution

strategies, covariance matrix adaptation evolution

strategy, particle swarm optimisation, and many

more.

In our GA, the data set obtained after assessing a

particular solution consists of (a) the best visiting

sequence of the customers assigned to each flight, (b)

the flight time of the UAV for each flight, (c) the

waiting time of the GV for each flight, and (d) the

total moving time of the UAV-GV tandem.

In order to test our solution approach, we have

used clouds of spread locations taken from the

clients’ position within Capacitated VRP benchmark

instances. For example, the CVRPLIB - Capacitated

Vehicle Routing Problem Library.

In what follows, we present the performance

obtained when tackling with the A-n32-k5 instance

proposed by Uchoa et al., (2014).

We have studied the possible influence of three

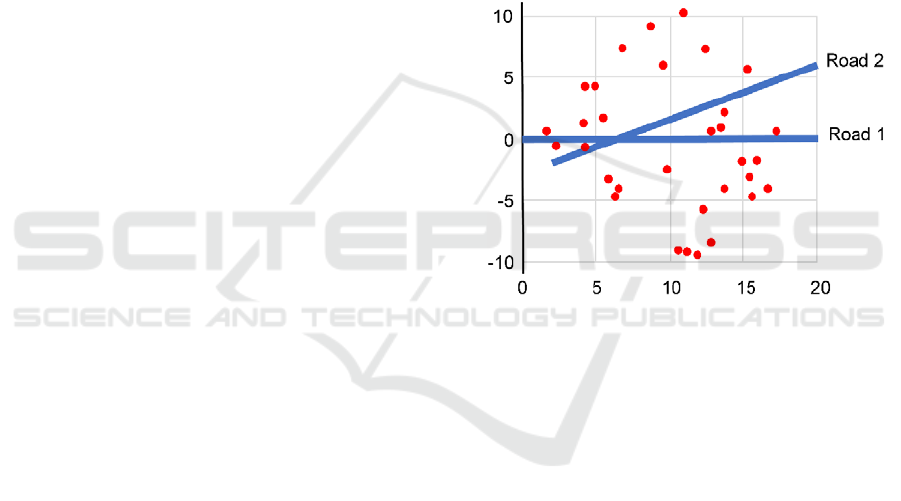
factors. To study the influence of the customers

layout, two different roads have been included in the

first factor, (see Figure 3). As the second factor, two

different UAV speeds have been studied, (a) =20

km/h and (b) =30 km/h. In both cases, the GV and

UAV-GV tandem moves at same speed, which is

=60 km/h. As the third factor, we have studied three

different values for the maximum number of visits in

each route: H=3,4,5. The endurance of the UAV is in

all the cases limited to E=1.2 hours.

Figure 3: Problem layout.

The GA implemented in this study starts with an

initial population of 100 solutions randomly

generated, and it stops after 100 generations. We have

repeated this for 30 runs, and written down the

average times of best solution over the 30 runs. Each

of the formerly described mutation operator is applied

to each of the three components with a probability of

a 2%. Similarly, each of the mentioned crossover

operators is applied with a 50% probability.

5 COMPUTATIONAL RESULTS

This section presents the results obtained by the

proposed GA.

Table 1 contains the averages of 30 runs of the

algorithm for each combination of problem

parameters, namely, road configuration, UAV flying

speed and maximum number of visits in each route.

This makes 360 runs. The ‘Mission time’ caption

refers to the TMT, expressed as the hours passed

between the depart from the origin of the road and the

A Tandem Drone-ground Vehicle for Accessing Isolated Locations for First Aid Emergency Response in Case of Disaster

293

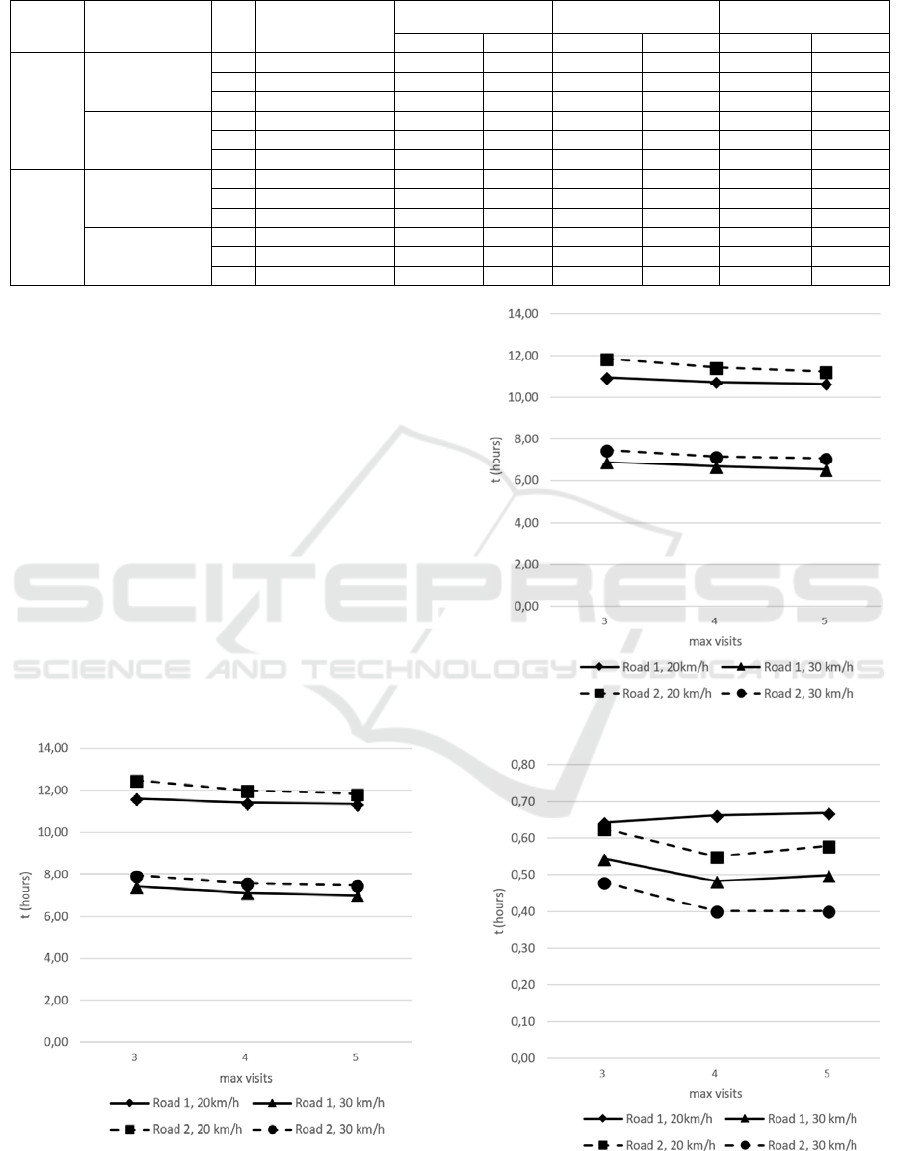
Table 1: Summary of experimental average results.

Road

UAV speed

(km/h)

Mission time

(hours)

Tandem time UAV flight time GV waiting time

(hours) % (hours) % (hours) %

3 11.60 0.64 5.54 10.96 94.46 10.78 92.89

4 11.41 0.66 5.81 10.74 94.19 10.56 92.60

5 11.34 0.67 5.89 10.68 94.11 10.47 92.30

3 7.43 0.54 7.33 6.88 92.67 6.69 90.00

4 7.14 0.48 6.77 6.65 93.23 6.46 90.49

5 7.02 0.50 7.11 6.52 92.89 6.32 90.06

3 12.49 0.63 5.01 11.86 94.99 11.68 93.57

4 12.00 0.55 4.58 11.45 95.42 11.27 93.91

5 11.82 0.58 4.90 11.24 95.10 11.07 93.65

3 7.95 0.48 6.04 7.47 93.96 7.29 91.77

4 7.57 0.40 5.30 7.17 94.70 7.01 92.63

5 7.49 0.40 5.35 7.09 94.65 6.94 92.66

arrival of the GV carrying the UAV to the end of the

road. The ‘Tandem time’ caption refers to the total

average traveling time of the GV carrying the UAV

and the percentage it weights in total mission time.

The ‘UAV flight time’ caption presents the average

total flying time of the UAV. The ‘GV waiting time’

caption shows the average total time that the GV

spends waiting for the UAV. Observe we have

included the percentage referred to the TMT value,

thereby allowing for quickly reading the weights of

Tandem time, UAV flight time and GV waiting time.

We further include illustrations for the four time

columns in Table 1.

Figure 4 shows total mission time for each

scenario. Figure 5 shows the average UAV flight time

vs . Figure 6 shows variability in the time spent by

the GV-UAV tandem, in their short travels between

flights.

Figure 4: Average total mission time vs .

Figure 5: UAV average total flying time vs .

Figure 6: GV-UAV tandem average total traveling time.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

294

Finally, Figure 7 shows the total time that the GV

spends waiting for the UAV return (once deployed

the recognisee route). Noticeably, the GV is most of

time in the status ‘stopped’.

Figure 7: GV average total waiting time.

As shown in the results, the factors (a) the UAV

speed and (b) the maximum number of visits in each

route influence the planning, and therefore the

resulting TMT. Thus, as the UAV speed increases

and/or the number of visits is less restricted, the value

TMT is reduced.

In these scenarios, the moving time of the UAV-

GV tandem is significantly low, between 5% and 7%

of the total mission time, so the moving speed of the

GV is not the most influential issue on the total

mission time. This implies that the UAV flight speed

is the most relevant factor on the total mission time,

which ranges from 93% to 95% of the mission time.

The relevance of the UAV speed justifies the need to

continue the research line of planning optimization of

these missions.

As a final remark, we notice that the studied

scenarios exhibit long waiting times for the GV at

rendezvous locations, which ranges from 90% to 94%

of the total mission time.

6 CONCLUSIONS

In this work, we propose using an UAV to visit a set

of challenging locations in a humanitarian mission, in

tandem with a GV for monitoring and controlling the

flight operations, which is used as well as a

recharging station for restoring the endurance of the

UAV. To solve the problem of planning the tandem’s

operations, we have implemented a GA algorithm

able to find good quality solutions in reasonable

computing times. The algorithm has been

programmed using Python 3 and DEAP library.

This work has considered a set of practical

considerations: (1) the limitations of the GV to access

the locations to visit, and (2) the different limitations

imposed by the drone in this type of missions. This

set of limitations does not allow us for comparing the

results obtained in this work with other nearby

approaches proposed in the literature.

Although the results are promising, we need to

improve different aspects to incorporate more

constraints that bring the problem closer to reality,

such as considering the aerodynamics. The obtained

results highlight the high relevance of the UAV flight

speed in this mission type, which justifies the need to

continue the research line of planning optimization of

these missions. Next step in this research consists in

employing other methods, such as PSO, which results

could be compare with the current results.

ACKNOWLEDGEMENTS

This research has been supported by the VI Plan

Propio de Investigación y Transferencia de la

Universidad de Sevilla, under the project DADS:

Sistemas Avanzados de Distribución Basados en

Drones.

REFERENCES

Agatz, N., Bouman, P., Schidt, M. 2018. Optimization

Approaches for the Traveling Salesman Problem with

Drone. Transportation Science, vol. April, 2018.

Bektas, T. 2006. The multiple traveling salesman problem:

An overview of formulations and solution procedures.

Omega, vol. 34, no. 3, 209–219.

Bin Othman, M. S. bin, Shurbevski, A., Karuno, Y., &

Nagamochi, H. 2017. Routing of Carrier-vehicle

Systems with Dedicated Last-stretch Delivery Vehicle

and Fixed Carrier Route. Journal of Information

Processing, vol. 25, pp. 655–666.

Chowdhury, S., Emelogu, A., Marufuzzaman, M., & Nurre,

S. G. 2017. Drones for disaster response and relief

operations: A continuous approximation model. Intern.

Journal of Production Economics, vol. 188, no.

February, pp. 167–184.

Dorling, K., Heinrichs, J., Messier, G. G., & Magierowski,

S. 2017. Vehicle Routing Problems for Drone Delivery.

IEEE Transactions on Systems, Man, and Cybernetics:

Systems, vol. 47, no. 1, pp. 70–85.

A Tandem Drone-ground Vehicle for Accessing Isolated Locations for First Aid Emergency Response in Case of Disaster

295

Drones for Disaster Response and Relief Operations. 2015,

(April). Measure & American Red Cross.

Fortin, F.A., De Rainville, F.M., Gardner, M.A., Parizeau,

M., & Gagné, C. 2012. DEAP: Evolutionary

Algorithms Made Easy. Journal of Machine Learning

Research, vol. 13, pp. 2171-2175.

Greenwood, F., 2015. Above and Beyond: Humanitarian

Uses of Drones. World Politics Review. Available from:

http://www.worldpoliticsreview.com/articles/16750/ab

ove-and-beyond-humanitarian-uses-of-drones

[Accessed 30/07/18].

Ha, Q. M., Deville, Y., Pham, Q. D., & Hà, M. H. 2018. On

the min-cost Traveling Salesman Problem with Drone.

Transportation Research Part C: Emerging

Technologies, vol. 86, pp. 597–621.

Holland, J., 1975. Adaptation in Natural and Artificial

Systems. University of Michigan Press.

Luo, L., Liu, Z. & Shi, J., 2017. A Two-Echelon Cooperated

Routing Problem for a Ground Vehicle and Its Carried

Unmanned Aerial Vehicle. Sensors, vol. 17, no. 5, pp.

1-17.

Mathew, N., Smith, S. L., & Waslander, S. L. 2015.

Planning Paths for Package Delivery in Heterogeneous

Multirobot Teams. IEEE Transactions on Automation

Science and Engineering, vol. 12, no. 4, 1298–1308.

Mosterman, P. J., Sanabria, D. E., Bilgin, E., Zhang, K., &

Zander, J., 2014. A heterogeneous fleet of vehicles for

automated humanitarian missions. Computing in

Science & Engineering, vol. 16, no. 3, pp. 90-95.

Qi, J., Song, D., Shang, H., Wang, N., Hua, C., Wu, C., …

Han, J. 2016. Search and Rescue Rotary-Wing UAV

and Its Application to the Lushan Ms 7. 0 Earthquake.

Journal of Field Robotics, vol. 33, no. 3, pp. 290–321.

Rabta, B., Wankmüller, C., & Reiner, G. 2018. A drone

fleet model for last-mile distribution in disaster relief

operations. International Journal of Disaster Risk

Reduction, vol. 28, pp.107–112.

Rahman, M. M., 2017. Two-Echelon Vehicle Routing

Problems Using Unmanned Autonomous Vehicles.

Ph.D. thesis. North Dakota State University.

Ryan, J.L., Bayley, G., Moore, J.T., & Carlton, W.B. 2013.

Reactive Tabu Search in Unmanned Aerial

Reconnaissance Simulations. Journal of Chemical

Information and Modeling, vol. 53, no. 9, pp. 1689–

1699.

Uchoa, E., Pecin, D., Pessoa, A., Poggi, M., Subramanian,

A., & Vidal, T., 2014. New Benchmark Instances for

the Capacitated Vehicle Routing Problem.

Optimization Online, vol. 257, no 3, pp. 845-858.

Wen, T., Zhang, Z., & Wong, K. K. L. 2016. Multi-

Objective Algorithm for Blood Supply via Unmanned

Aerial Vehicles to the Wounded in an Emergency

Situation. PloS one, vol. 11, no. 5, pp. 1–22.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

296