
On inclusive 1-Distance Vertex Irregularity Strength of Firecracker,
Broom, and Banana Tree
Ikhsanul Halikin, Ade Rizky Savitri, and Kristiana Wijaya
Graphs, Combinatorics, and Algebra Research Group
Department of Mathematics, Faculty of Mathematics and Natural Sciences
University of Jember (UNEJ), Jl. Kalimantan 37 Jember, Indonesia 68121
Keywords: Inclusive 1-Distance Vertex Irregular Labelling, Inclusive 1-Distance Vertex Irregularity Strength,
Firecracker, Broom, Banana Tree.
Abstract: Let k be a natural number and G be a simple graph. An inclusive d-distance vertex irregular labelling of a
graph G is a function
so that the weights at each vertex are different. Let v be a
vertex of G. The weight of v V(G), denoted by wt(v), is the sum of the label of v and all vertex labels up to
distance 1 from v. An inclusive 1-distance vertex irregularity strength of G, denoted by
is the
minimum k for the existence of an inclusive 1-distance vertex irregular labelling of a G. Here, we find the
exact value of an inclusive 1-distance vertex irregularity strength of a firecracker, a broom, anda banana
tree.
1 INTRODUCTION
Suppose that is an undirected and finite graph
without loop and parallel edges. For a vertex v in a
graph G, the degree of v with notation d(v) is the
number of edges in G that are incident to v. For two
vertices u and v in a graph G (not necessarily
distinct), a u – v walk in G is defined as a sequence
of vertices and edges in G, starting with u and
ending at v such that consecutive vertices are
connected by an edge. A path defined as a u – v walk
with different vertices. The length of the shortest
path from vertex u to vertex v is said to be a distance
from u to v and denoted by d(u,v) (see Chartrand,
Lesniak & Zhang, (2011) for another terminology).
The labelling in graph is one of research topics
introduced in the 1960s. The labelling of a graph is a
function from a set of graph elements (vertices or
edges or both) onto a set of numbers (usually natural
numbers) with certain condition. There are many
kinds of graph labelling that have been introduced
(see Gallian (2016) for a complete survey).
Chartrand et al. suggested the concept of an irregular
labelling in 1988. The problem of this labelling is
how to assign natural numbers label to the edges of a
graph so that the sum of edge labels at each vertex is
different. In this labelling also introduced a notion,
called irregularity strength, i.e. the minimum largest
label among all of the possible irregular assignments
of a graph (Chartrand et al., 1988).
In 2007, Bačá et al. introduced the similar
assignment but apply to both edges and vertices of a
graph. This labelling is called the irregular total k-
labelling. A total k-labelling is a mapping from the
vertex set and edge set to the set of natural numbers
. The minimum k for such labelling is said
to be the total irregularity strength. Furthermore,
Mirka, Rodger & Simanjuntak (2003) introduced
another kind labelling, which is called distance
magic labelling.
Motivated by Mirka and Bačá, Slamin (2017)
introduced a distance vertex irregular labelling of
graphs. A distance vertex irregular labelling of a
graph G is a function
such that
the weight of every vertex v in G is different. The
weight of a vertex, denoted by wt(v),is the
sum of the labels of all the vertices of distance1
from v. Moreover, Bong, Lin & Slamin (2017),
generalized concept of a distance irregular vertex
labelling to inclusive vertex irregular d-distance
vertex labelling. Inclusive in this labelling means
that the weight of the vertex v included the label of a
vertex v. The minimum k for the existence of this
labelling is said to bea distance irregularity strength
of G and denoted by
. Furthermore, Bong,
Lin & Slamin (2017) obtained
, for G are a
path P
n
for n= 3k, , a star
and a double
228
Halikin, I., Savitri, A. and Wijaya, K.
On inclusive 1-Distance Vertex Irregularity Strength of Firecracker, Broom, and Banana Tree.
DOI: 10.5220/0008519802280232
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 228-232
ISBN: 978-989-758-407-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

star with . In the same paper, they
gave the lower bound for caterpillar, cycle and
wheel. In 2018, Bačá et al. determined the exact
value of the inclusive distance vertex irregularity
strength of a complete graph, complete bipartite
graph, path, fan, and cycle.
In this paper, we discuss an inclusive 1-distance
vertex irregular labelling and find the exact value of
an inclusive 1-distance vertex irregularity strength of
a firecracker, broom, and banana tree.
2 DEFINITION AND USEFUL
PROPERTIES
Before we start the further discussion, we will
present the definition and some useful properties of
an inclusive 1-distance vertex irregular labelling.
Definition 1.Let k be a natural number. An inclusive
d-distance vertex irregular labelling of a graph G is
a function
so that the weights
of two vertices u and v are different for each
. The weight of a vertex vV(G), denoted by
wt(v), is defined as the sum of the label of v and all
vertex labels up to distance d from v, namely
where is distance from vertex u to v.
The smallest k for the largest labelling this
labelling is called an inclusive d-distance
irregularity strength of G and denoted by
.
Since in this paper we take , we denote it with
. Not all graphs G have an inclusive 1-
distance irregularity strength of G, and we say that
= ∞.
Bong, Lin & Slamin (2017), gave the lower
bound of the inclusive 1-distance irregularity
strength of G, by the following lemma.
Lemma 1. For a connected graph G with n vertices,
δ,∆ as minimum and maximum degree, respectively
then
.
Next, Bačá et al. (2018) proved the sufficient and
necessary condition for
= ∞.
Lemma 2. For a connected graph G,
= ∞ if
and only if there exist two different vertices
such that
, where
N(u) is the set of all neighborhood of u(distance 1
from u).
As the firecracker, broom, and banana graphs are
the kind of the tree graph, that clearly not satisfy the
Lemma 2, so we can find the inclusive 1-distance
vertex irregular labelling of them. The definition of
firecracker, broom, and banana tree graphs are as
follow:
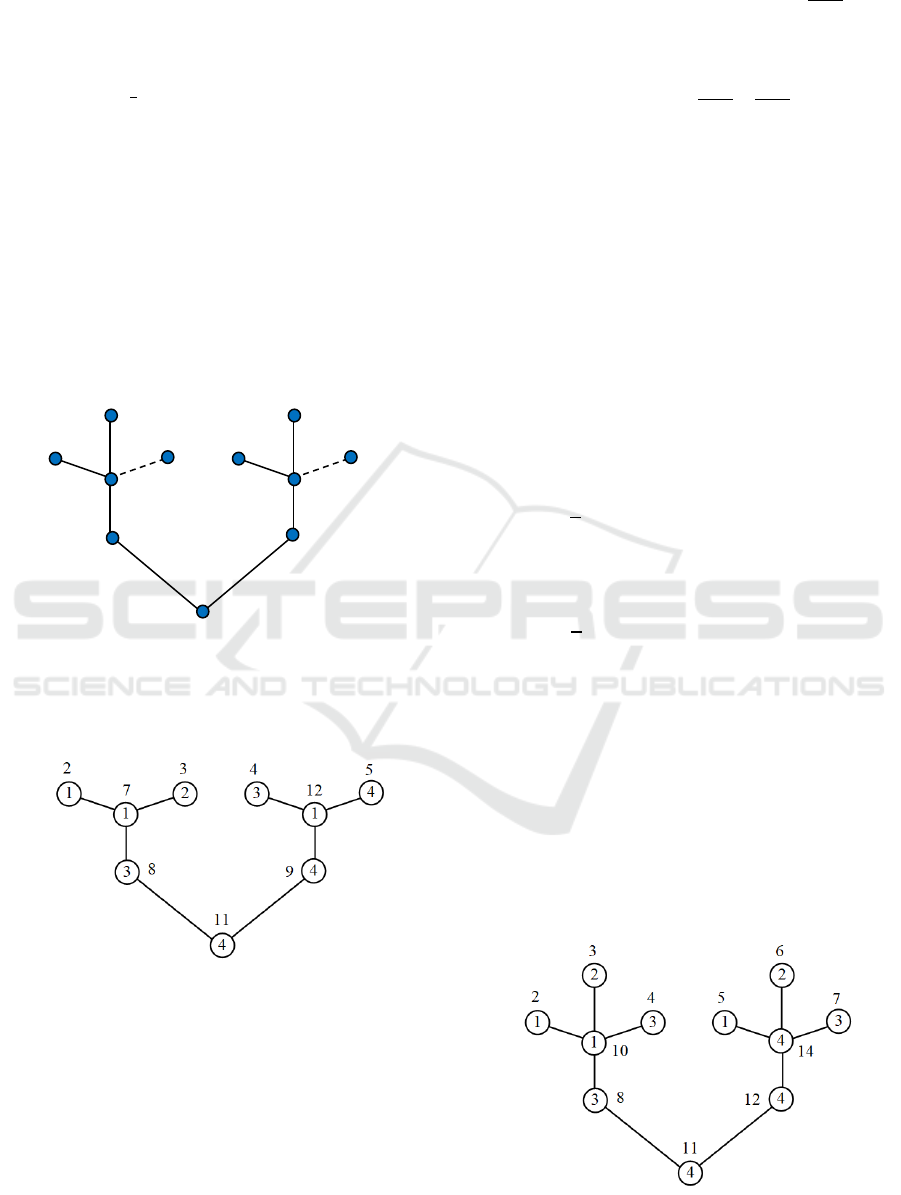
Definition2. A firecracker graph
is a graph
formed by connecting one vertex of degree one from
each of n copies of a star
.
Definition3. A broom
is a graph formed from
identifying one end leaf of a path P
n
with the center
of a star
.
Definition4. A banana tree
is a graph obtained
from connecting one vertex of degree one from each
of n copies of a star
with a new vertex.
In this paper, we determine an inclusive 1-
distance vertex irregularity strength of a firecracker
, a broom
, and a banana tree
.
3 MAIN RESULTS
In this section, we discuss an inclusive 1-distance
irregularity strength of firecracker
, broom
,
and banana tree
.
Theorem 1. Let
be a firecracker graph with
. Then
.
Proof. Suppose
where
,
, and
, and for ,
.
As illustration, the vertex notation of
can be
seen in Figure 1.
Figure 1: The notation of vertices of a firecracker
.
On inclusive 1-Distance Vertex Irregularity Strength of Firecracker, Broom, and Banana Tree
229

u
1
u
2
u
3
v
1
v
2
v
3
v
4
v
m
We know that a firecracker
has 4n vertices,
and
. Based on Lemma 1,
we get
.
To show that
we define an
inclusive irregular 1-distance vertex labelling λ of
with label as follow:
So, the vertices weight of
are
We obtain that all vertices of a graph
have
distinct weight. Hence,
Therefore, we can conclude that
Theorem 2. Let
be a broom with then
.
Proof. Suppose that
is the vertex set of a broom
,
where the vertices
and
are leaves of a broom
for each and
is the vertex of
degree (see Figure 2). Then, the broom
has leaves. So, all leaves of a broom
must have distinct weight, where
and
. Obviously that
the smallest weight of a leaf of a broom
is at
least 2 and minimum of the largest weight of a leaf
of a broom
is at least . To obtain
distinct weight of leaves
, the leaves
must have
different label for each . Hence, minimum
of the largest label of leaves from a broom
is
at least . It means that
.
Figure 2: The notation of vertices of a broom
.
Now, we show that
. We define
the inclusive irregular 1-distance vertex labelling λ
as follow,
So, the corresponding weights of each vertex of a
broom
are
The differences of every vertex weight in a
broom graph
can be verified easily. Since the
largest label of a vertex of a broom
is at most
,
Therefore, we can conclude
that
Theorem 3. Let
be a banana tree with
then
Proof. Let
be the
vertex set of a banana tree
, where the only two
vertices adjacent to z are
and
,
, and the others are leaves. The notation
of vertices of a banana tree
as depicted in
Figure 3. First, we will find the lower bound of the
inclusive 1-distance irregularity strength for a
banana tree
. To find this, we consider 2 cases.
Case1. For
Suppose the vertex set of a banana tree
is
. A banana tree
ICMIs 2018 - International Conference on Mathematics and Islam
230
x
0
x
1
x
2
x
3
x
m
y
0
y
1
y
2
y
3
y
m
z
has 4 leaves, namely
. The smallest
weight of a leaf of a banana tree
is at least 2,
and minimum of the largest weight of a leaf of a
banana tree
is at least 5. So, the label of each
leaf is at least
. Without loss of generality, it
causes
and
. However,
minimum of the largest weight of all vertices of a
banana tree
is at least 10. If the largest vertex
label of a banana tree
is 3, then the vertex with
weight 10 should be
. It cause
and the
possibility of weight of
is either 6, 7, or 8. On the
other hand, the possibility of weight of
is either 6
or 7. Two possibilities of weight of
will cause
two of vertices
and
have the same
weight. Hence, the largest label of each vertex of a
banana tree
is at least 4. So,
.
Figure 3: The notation of vertices of a banana tree
.
To show that
, we can label of a
banana tree
as depicted in Figure 4.
Figure 4: The labelling of banana tree
.
Figure 4 shows the inclusive irregular 1-distance
vertex labelling, where the number outside the cycle
shows the weight of the given vertex.
Case2. For
A banana tree
has
leaves. The
smallest weight of a leaf of a
is at least 2 and
minimum of the largest weight of a leaf of a
is
at least . So, minimum of the largest leaf
label of a banana tree
is at least
.
Meanwhile, minimum of the largest weight for every
vertex of a graph
is at least . Therefore,
minimum of the largest vertex label of a banana tree
is at least min
. So,
.
To show that
, let the inclusive
irregular1-distance vertex labelling λ is defined in
the following way:
So, the corresponding weights of each vertex of a
banana tree
are as follows.
The differences of every vertex weight can be
verified easily, and the largest label is m. So,
. Therefore, we can conclude that
For example, the inclusive irregular 1-distance
vertex labelling of a banana tree
can be seen in
Figure 5.
Figure 5: The labelling of banana tree
.
On inclusive 1-Distance Vertex Irregularity Strength of Firecracker, Broom, and Banana Tree
231

ACKNOWLEDGMENT
This research was supported by Hibah Kelompok-
Riset (Graphs, Combinatorics, and Algebra),
Mathematics Department, Faculty of MIPA,
Universitas Jember, No. 2400/STe/UN25.3.1/LT.
REFERENCES
Arumugam, S.,& Kamatchi, N., 2012. On (a, d)-distance
antimagic graphs. Australasian Journal of
Combinatorics 54, pp. 279-287.
Bačá, M., Jendrol, S., Miller, M. & Ryan, J., 2007. On
irregular total labelling. Discrete Math. 307, pp. 1378-
1388.
Bačá, M., Fenovcıková, A. S., Slamin, & Sugeng, K. A.,
2018. On inclusive distance vertex irregular labelling.
EJGTAVol 6 No. 1, pp 61-83.
Bong, N.H., Lin, Y., & Slamin, 2017.On inclusive and
non-inclusive vertex irregular d-distance vertex
labelling, submitted to JCMCC.
Chartrand, G., Jacobson, M. S., Lehel, J., Oellermann, O.
R.,Ruiz, S. & Saba, F., 1988. Irregular networks.
Congr. Numer. 64, pp. 187-192.
Chartrand, G., Lesniak, L. & Zhang, P., 2011. Graphs and
Digraphs, Taylor & Francis Group.
Gallian, J. A., 2016. A dynamic survey of graph labelling.
Electron. J. Combin, #DS6.
Miller, M., Rodger, C. & Simanjuntak, R., 2003. Distance
magic labellings of graphs. Australasian Journal of
Combinatorics 28, pp. 305-315.
Slamin, 2017. On distance irregular labellings of graphs.
Far East Journal of Mathematical Sciences (FJMS)
102 (5), pp. 919-932.
ICMIs 2018 - International Conference on Mathematics and Islam
232
